Exploration of Sp-Sp2 Carbon Networks: Advances in Graphyne Research and Its Role in Next-Generation Technologies
Abstract
1. Introduction
1.1. Overview of the Article
1.2. Scope
1.3. Introduction to Graphyne
2. Computational Approach
2.1. Density Functional Theory
2.2. GW Approximation
2.3. Semi-Empirical Tight-Binding Method
2.4. Non-Equilibrium Green’s Function Method
3. Experimental Approach
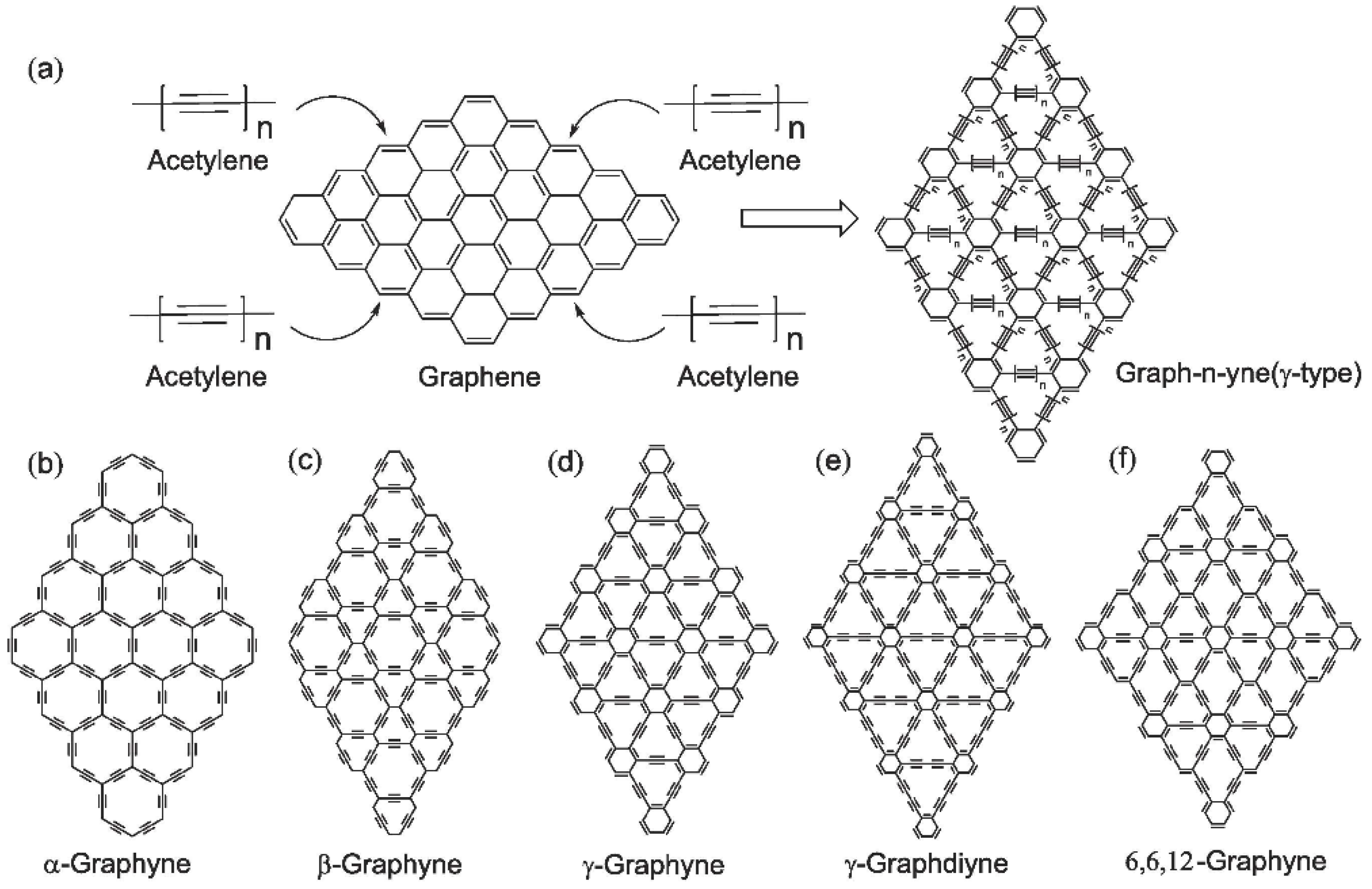
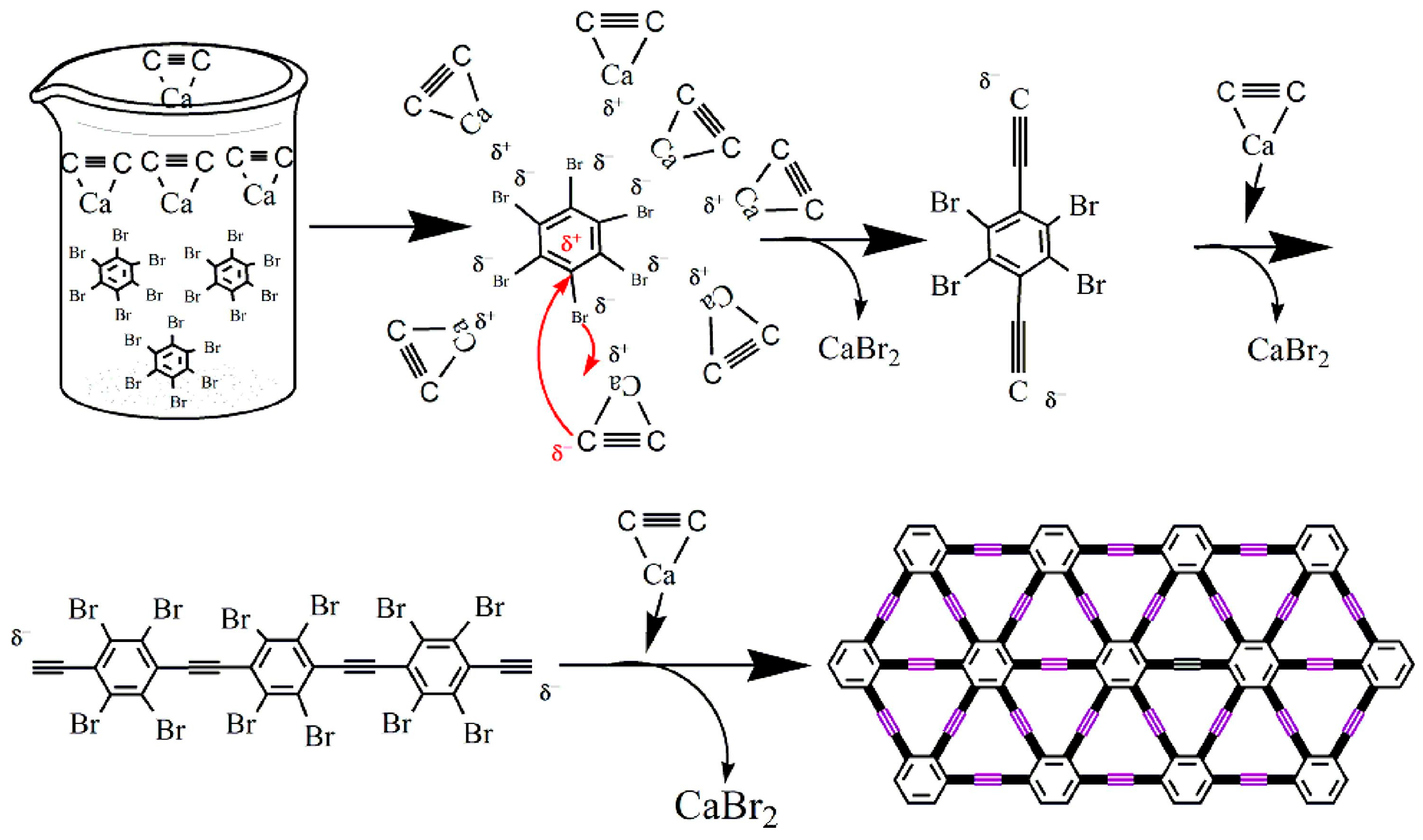
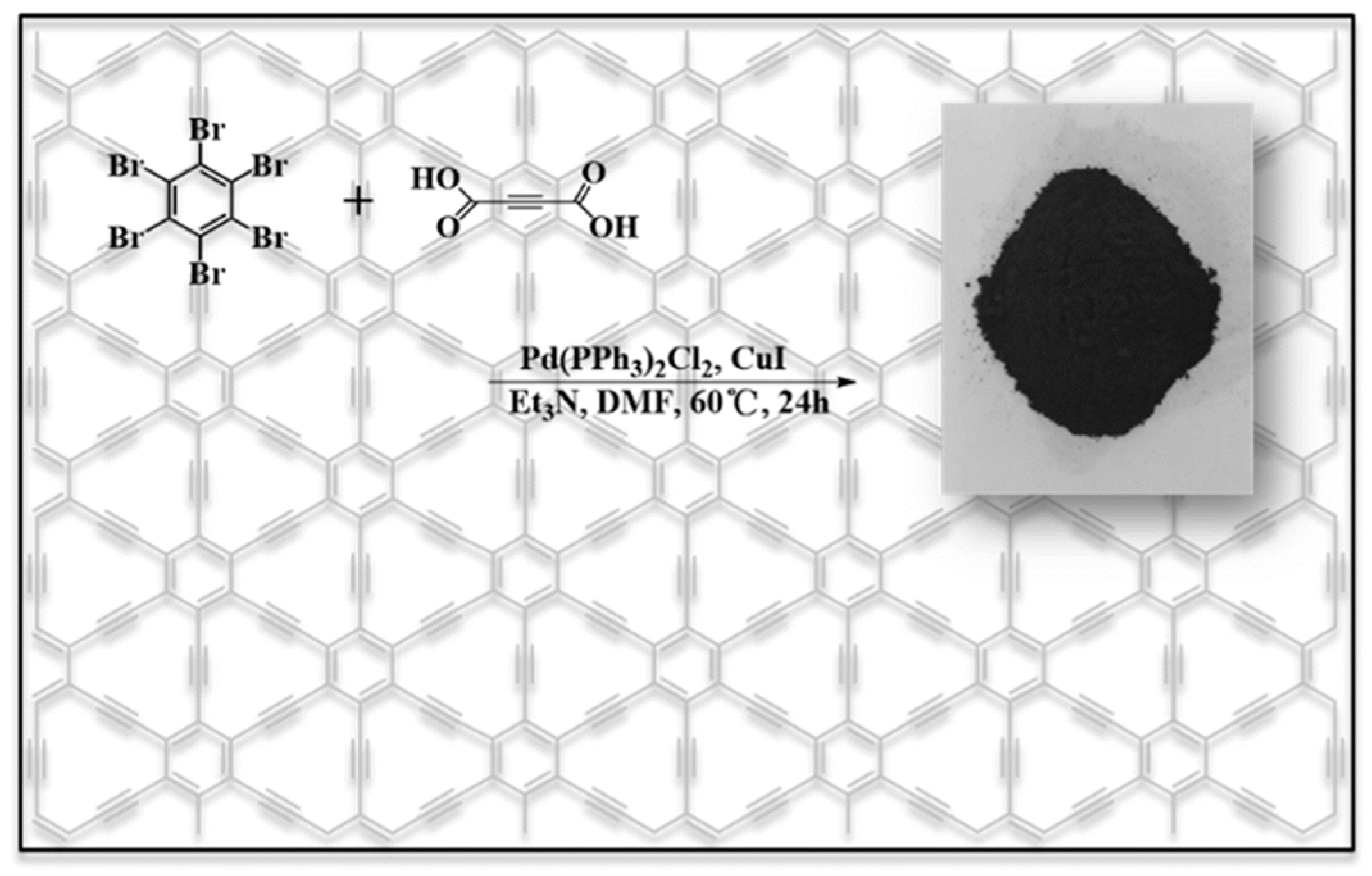
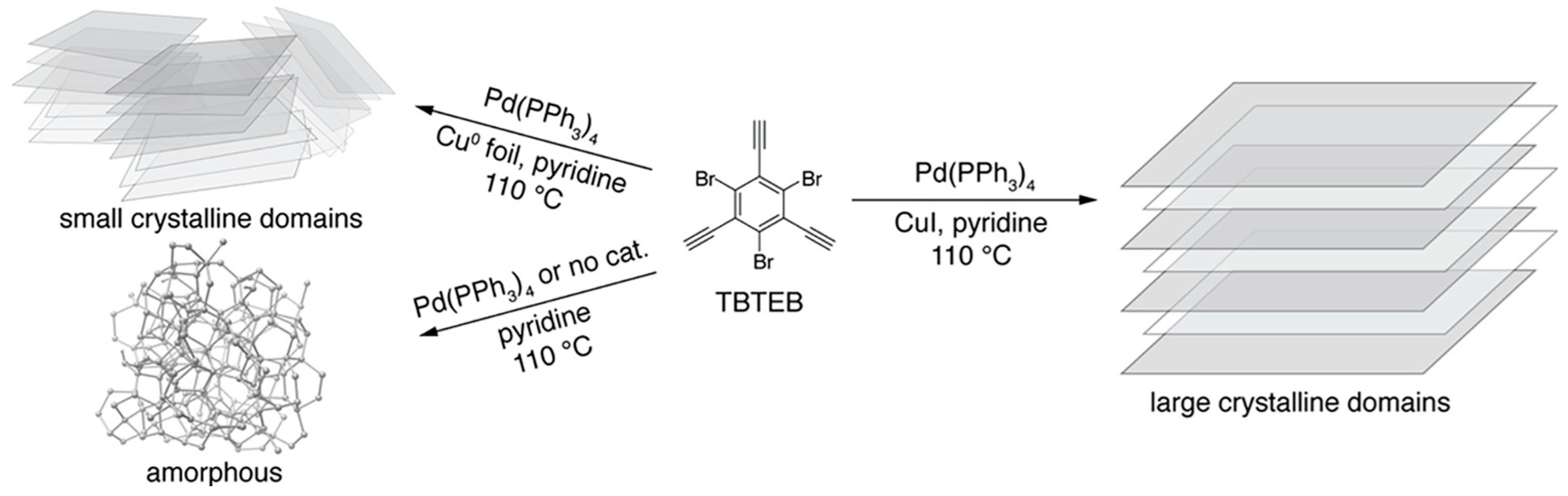
3.1. Synthesis of GR
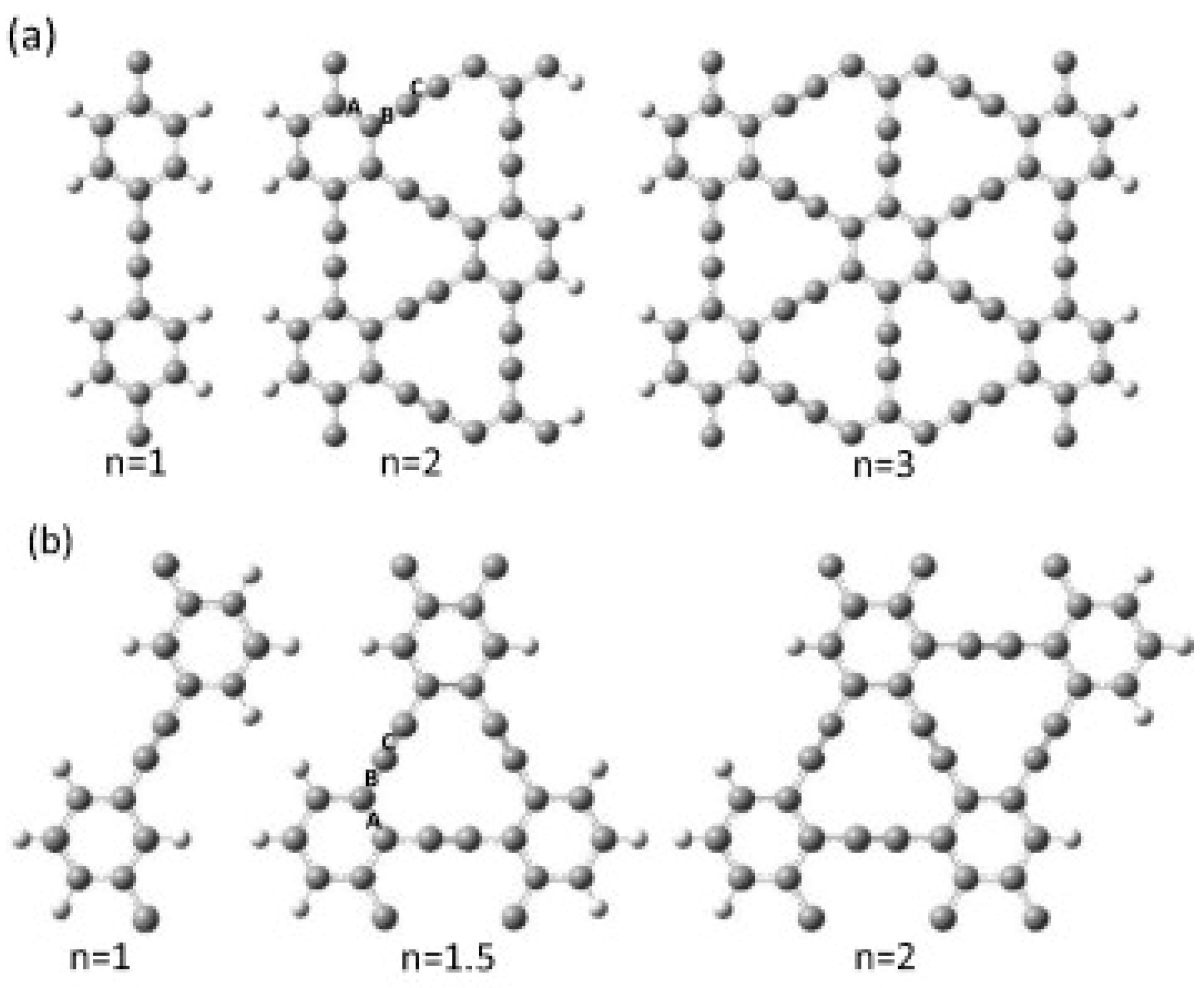
3.2. α-Graphyne
3.3. β-Graphyne
3.4. γ-Graphyne
3.5. 6,6,12-Graphyne
4. Properties of GR
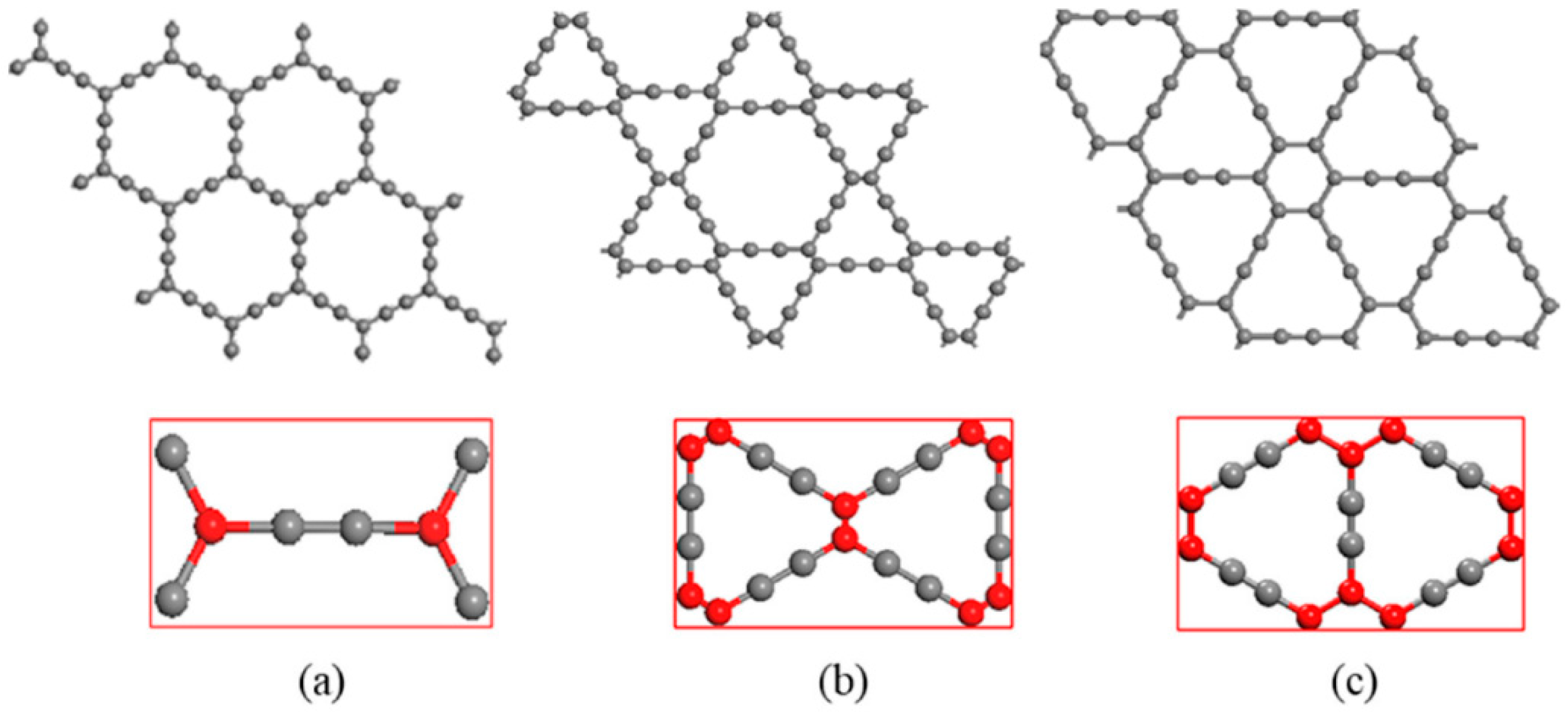
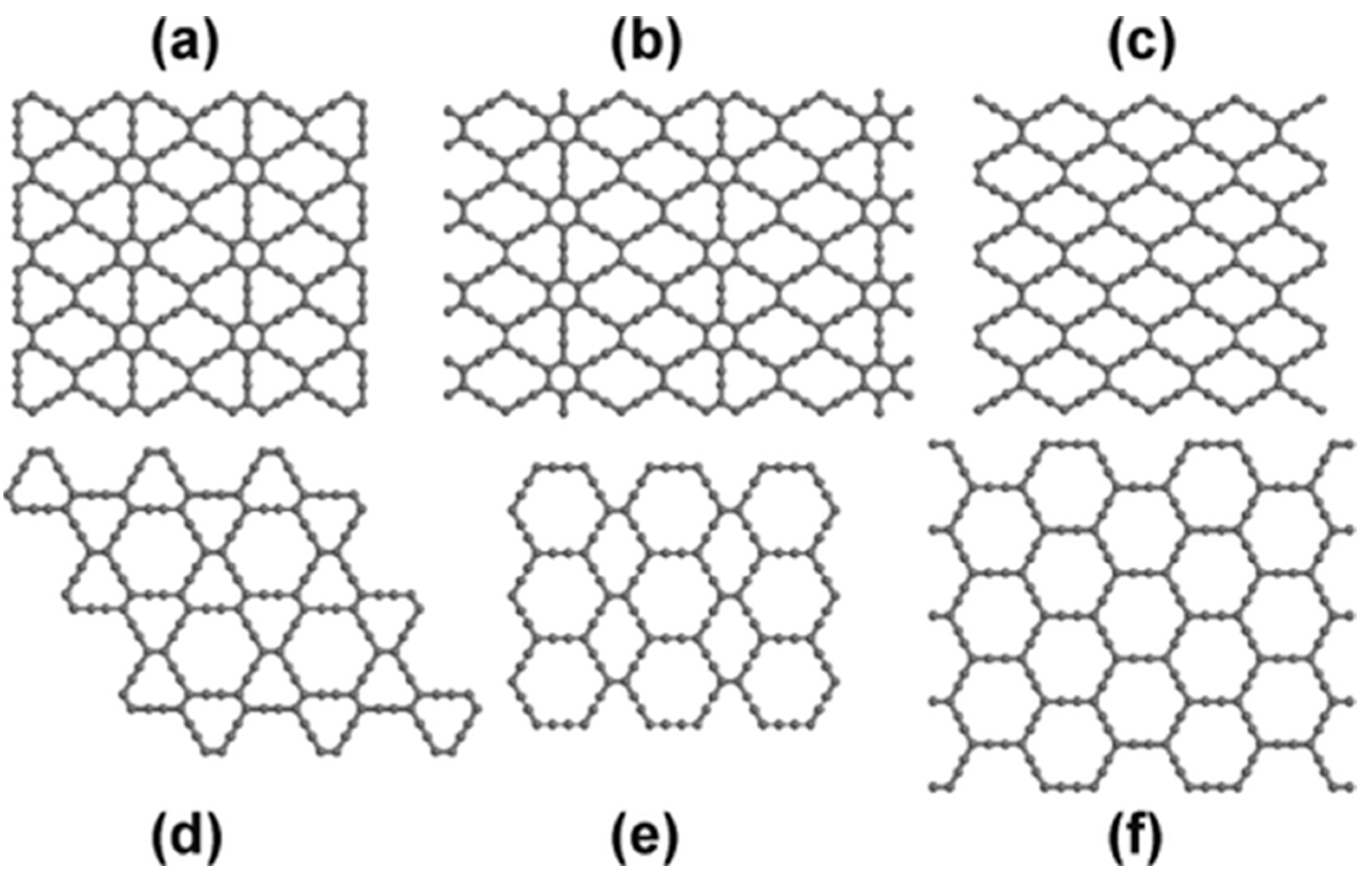
4.1. Structure
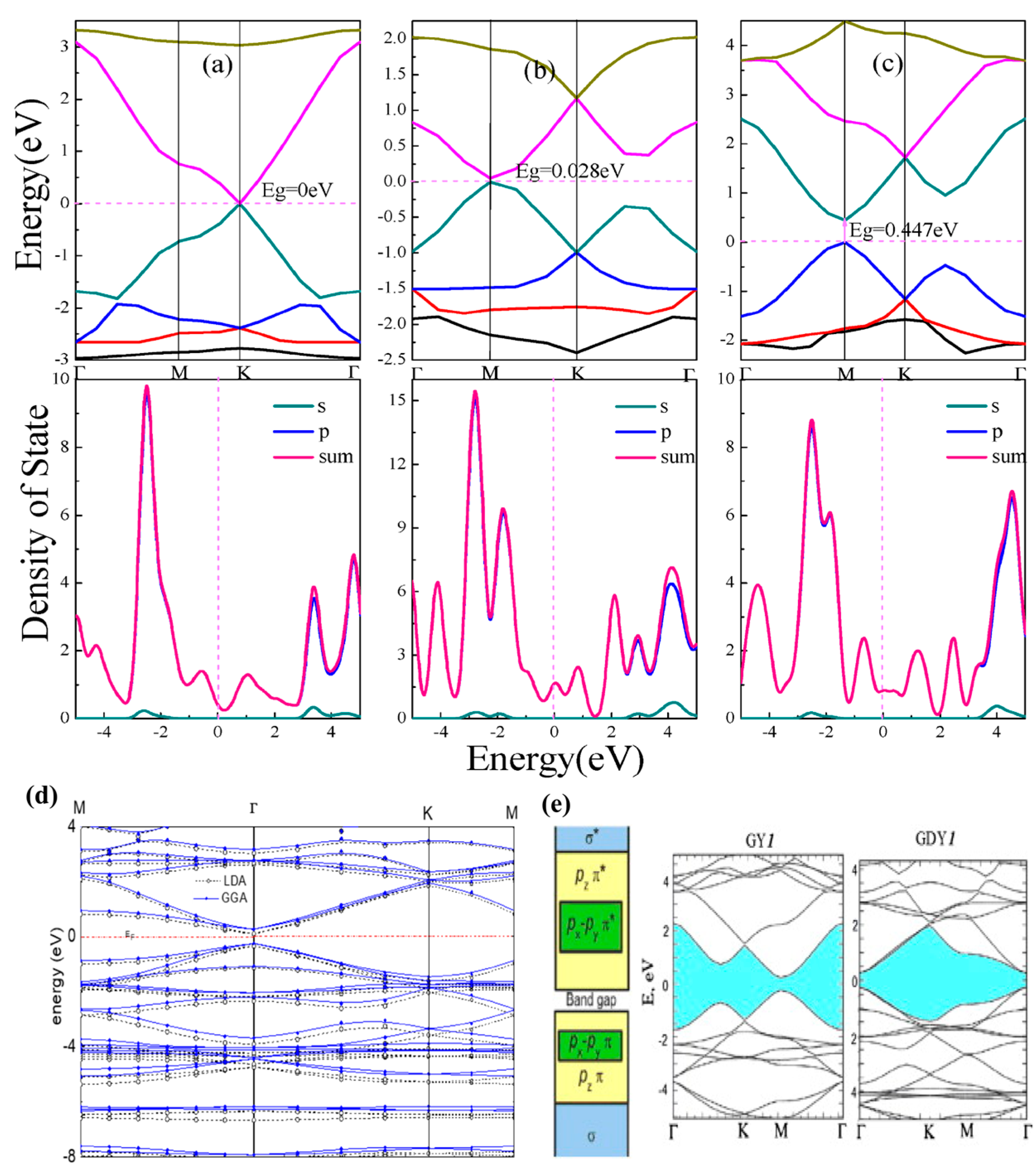
4.2. Electronic Properties
4.3. Mechanical Properties
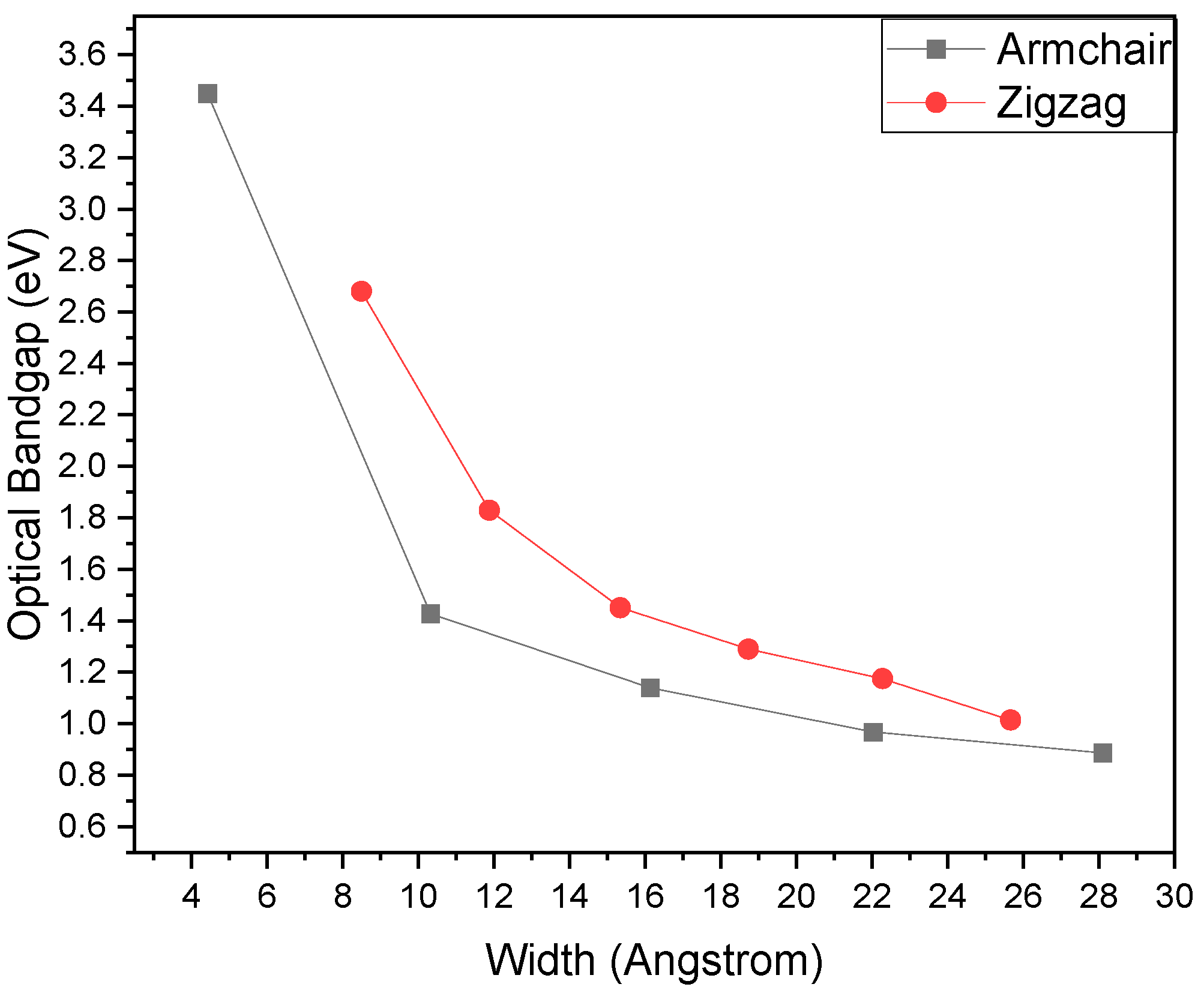
4.4. Band Properties
| Property | Graphene | α-Graphyne | β-Graphyne | γ-Graphyne | Graphdiyne |
|---|---|---|---|---|---|
| Carbon Hybridization | sp2 | sp + sp2 [113] | sp + sp2 [113] | sp + sp2 [113] | sp + sp2 [70] |
| Lattice Structure | Hexagonal | Hexagonal [105] | Hexagonal [105] | Hexagonal [105] | Hexagonal [54] |
| Acetylenic Linkage % | 0% | 100% [70] | 66.67% [70] | 33.33% [70] | Varied (more than γ) [54] |
| Band Gap | 0 eV | ~0.44 eV [106] | ~0.52 eV [106] | ~0.47 eV [106] | 0.5–1.1 eV [54,121] |
| Carrier Mobility (cm2/V·s) | ~105 [128] | High, anisotropic [128] | High [128] | High (5 × 105) [128] | Moderate–High [129] |
| Thermal Conductivity | ~5000 W/m·K [132] | Lower than graphene [140] | Lower [140] | Lower (~50 W/m·K) [140] | Much lower (~10–20 W/m·K) [140] |
| Mechanical Strength | ~1 TPa [47] | Moderate [78] | Moderate [78] | Moderate [78] | Lower than graphene [106] |
| Synthesis Status | Scalable [9] | Theoretical [70] | Theoretical [141] | Synthesised [94,95,96,97,98,99] | Synthesised [54,56] |
| Stability | High | Low (due to 100% triple bonds) [105] | Medium [105] | Medium–High [105] | Medium [54] |
| Applications | Transistors, sensors, composites [33,34,35] | Theoretical electronics [70] | Theoretical semiconductors [70] | Catalysis, desalination, batteries [94,95,96,97,98,139,142,143] | Sensors, photovoltaics, membranes [54,61,67] |
4.5. Electronic Transport Properties
4.6. Thermal Properties
4.7. Thermoelectric Effect
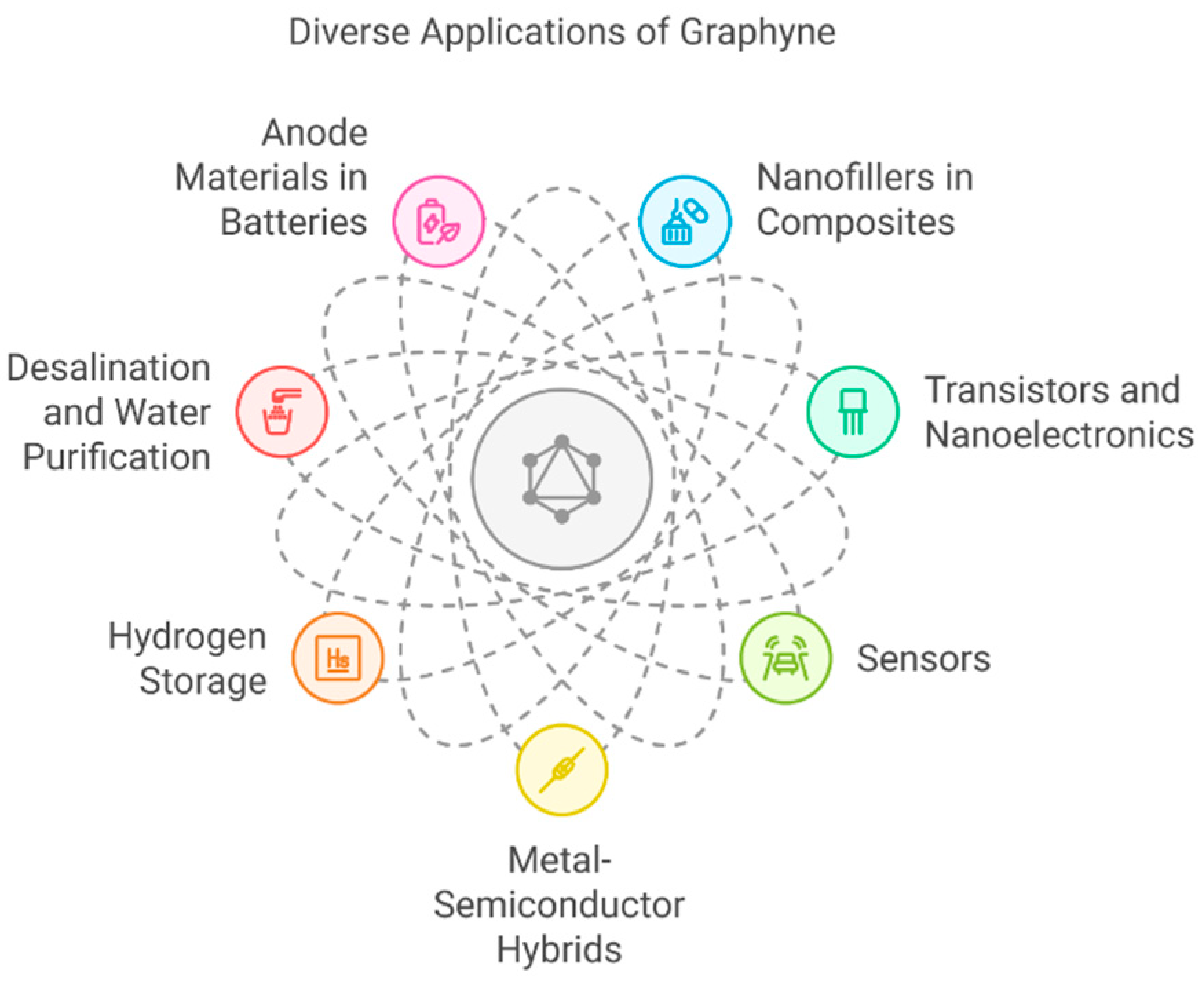
5. Applications
5.1. Nanofillers
5.2. Transistors
5.3. Sensors
5.4. Metal Hybrids SC
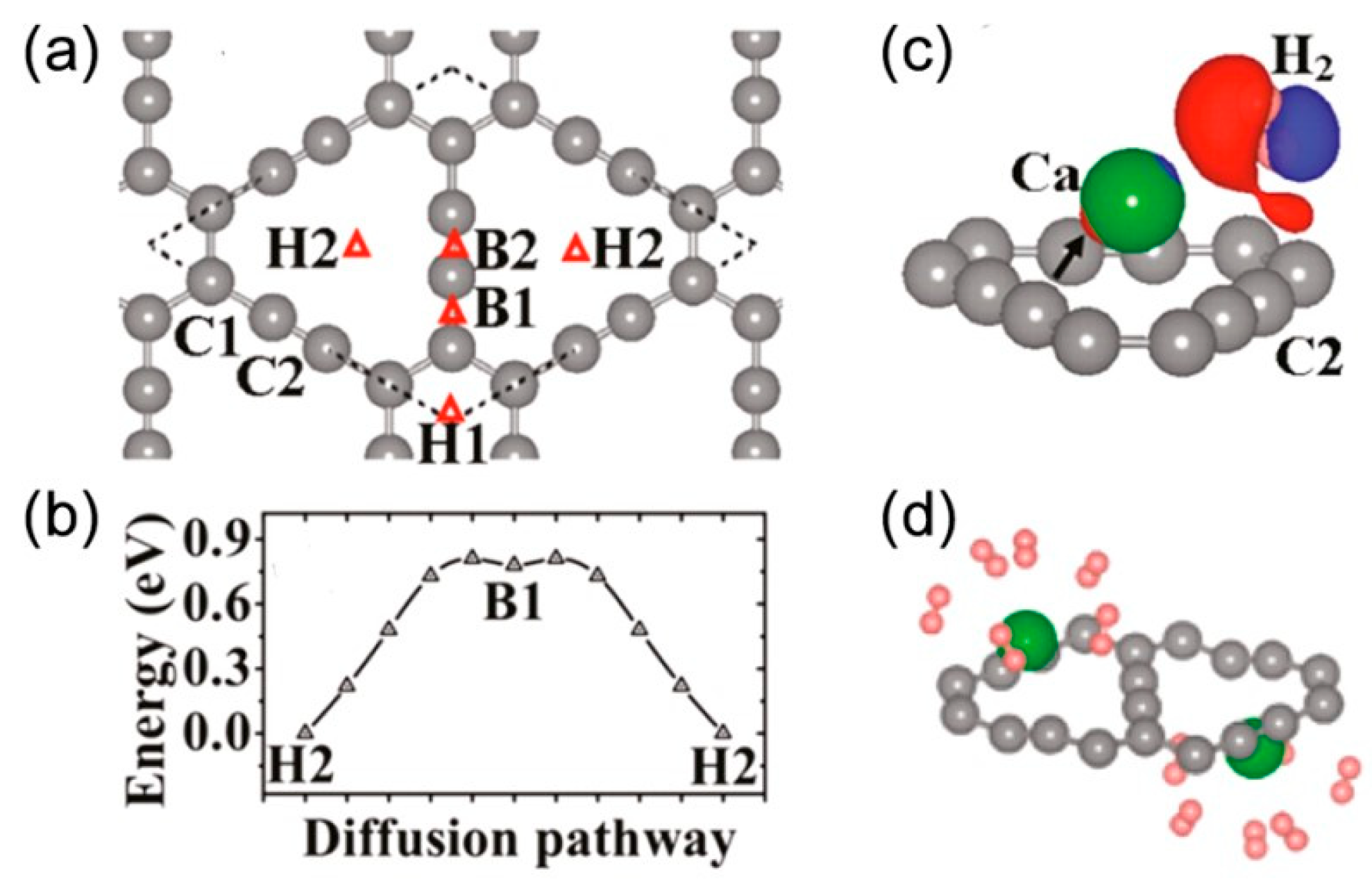
5.5. H2 Storage
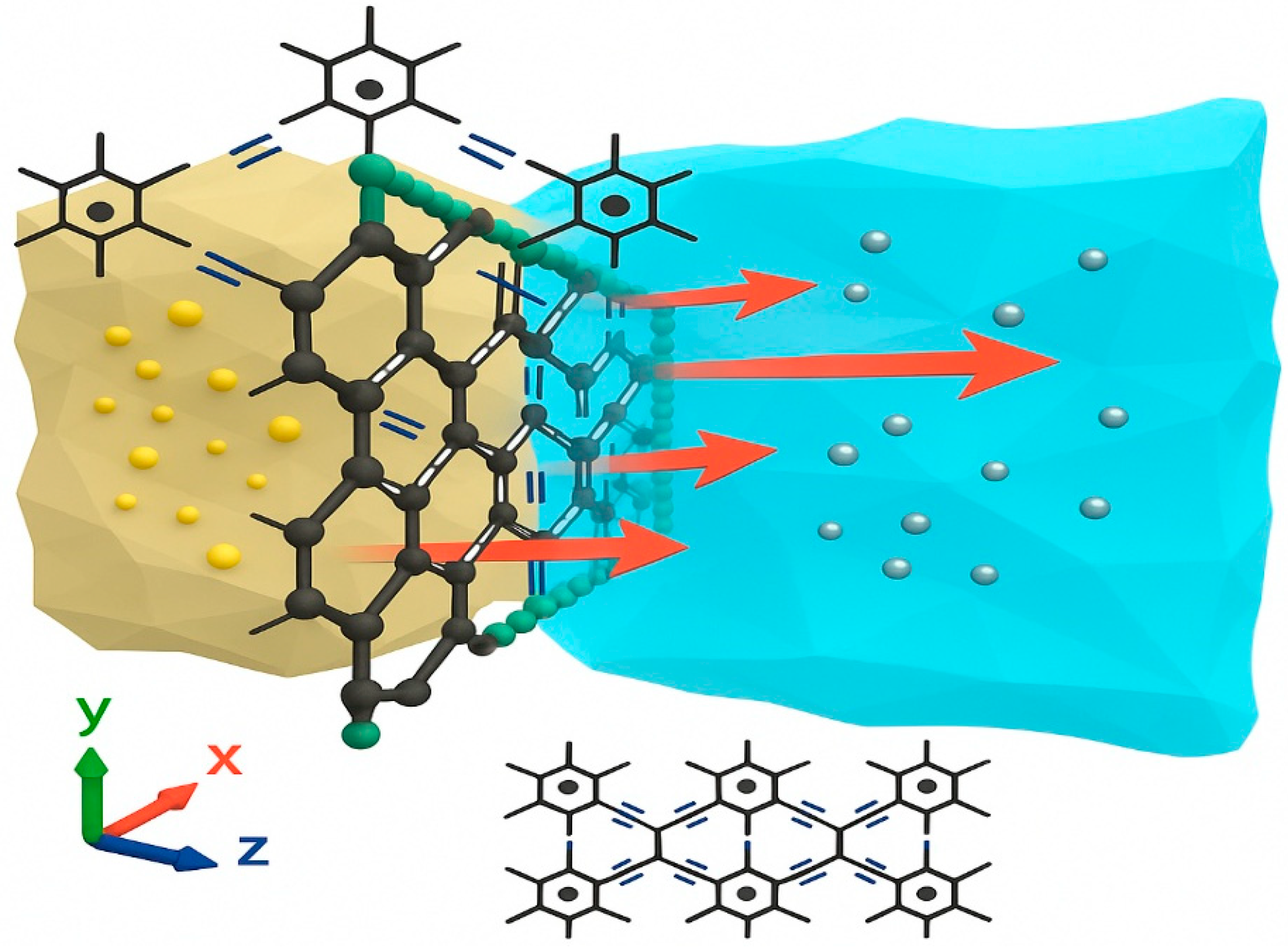
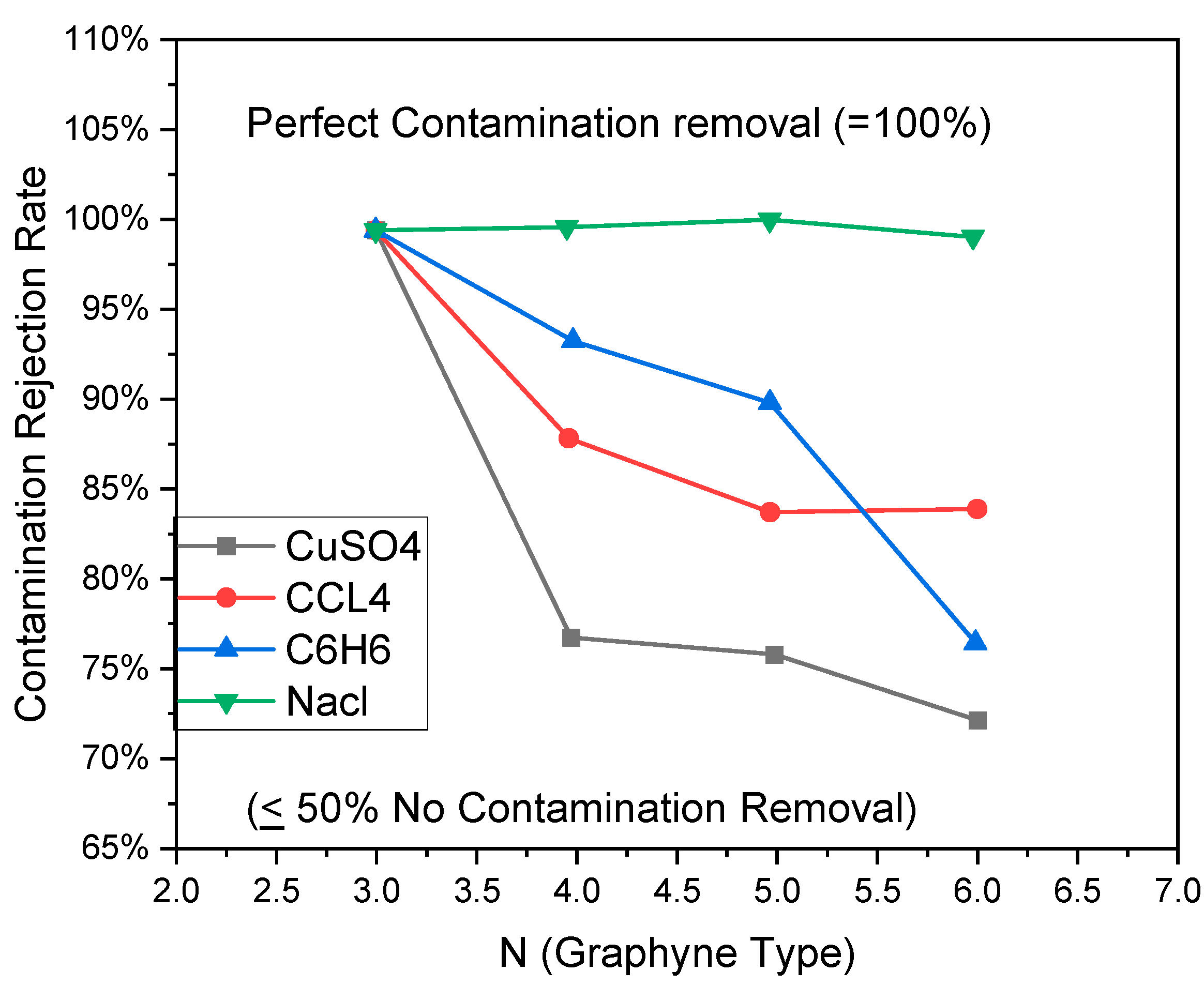
5.6. Desalination
5.7. Anode Applications
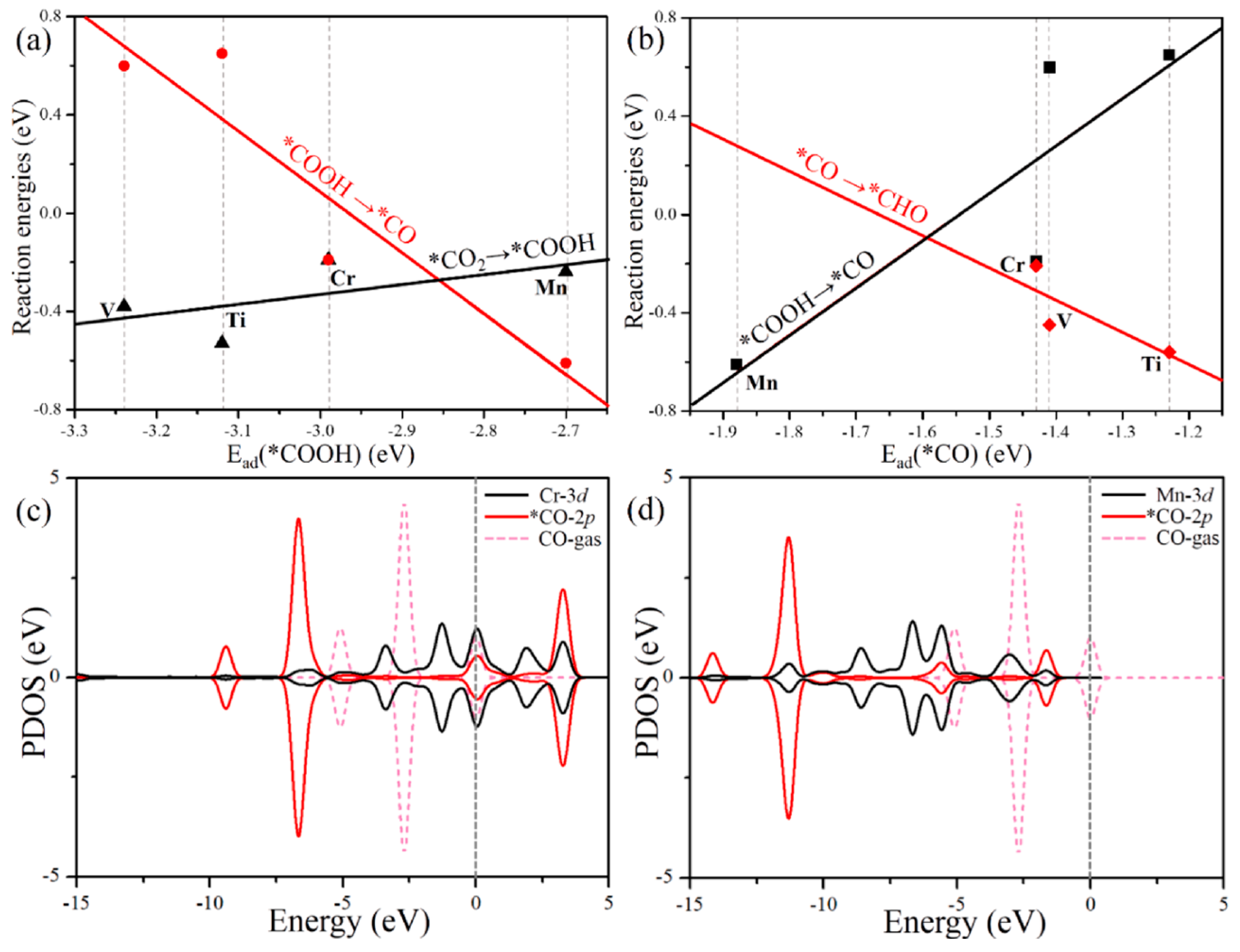
5.8. Electrocatalyst
6. Summary
7. Future Prospects
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weidmann, E.; Anderson, J. Structure and growth of oriented tellurium thin films. Thin Solid Film. 1971, 7, 265–276. [Google Scholar] [CrossRef]
- Fu, B.; Abid, M.; Liu, C.-C. Systematic study on stanene bulk states and the edge states of its zigzag nanoribbon. New J. Phys. 2017, 19, 103040. [Google Scholar] [CrossRef]
- Majid, F.; Wahid, I.; Ata, S.; Bibi, I.; Ali, M.D.; Malik, A.; Alwadai, N.; Iqbal, M.; Nazir, A. Cationic distribution of nickel doped NixCoX-1Fe2O4 nanparticles prepared by hydrothermal approach: Effect of doping on dielectric properties. Mater. Chem. Phys. 2021, 264, 124451. [Google Scholar] [CrossRef]
- Wang, Q.K.; Kalantar-Zadeh, A.; Kis, J.N.; Coleman, M.S. Electronics and Optoelectronics of Two-Dimensional Transition Metal Dichalcogenides. Nat. Nanotechnol 2012, 7, 699. [Google Scholar] [CrossRef]
- Liu, H.; Neal, A.T.; Zhu, Z.; Luo, Z.; Xu, X.; Tománek, D.; Ye, P.D. Phosphorene: An unexplored 2D semiconductor with a high hole mobility. ACS Nano 2014, 8, 4033–4041. [Google Scholar] [CrossRef]
- Zhuang, J.; Xu, X.; Peleckis, G.; Hao, W.; Dou, S.X.; Du, Y. Silicene: A promising anode for lithium-ion batteries. Adv. Mater. 2017, 29, 1606716. [Google Scholar] [CrossRef]
- Mirza, F.S.; Aftab, Z.-e.-H.; Ali, M.D.; Aftab, A.; Anjum, T.; Rafiq, H.; Li, G. Green synthesis and application of GO nanoparticles to augment growth parameters and yield in mungbean (Vigna radiata L.). Front. Plant Sci. 2022, 13, 1040037. [Google Scholar] [CrossRef]
- Hirsch, A. The era of carbon allotropes. Nat. Mater. 2010, 9, 868–871. [Google Scholar] [CrossRef]
- Baughman, R.; Eckhardt, H.; Kertesz, M. Structure-property predictions for new planar forms of carbon: Layered phases containing sp 2 and sp atoms. J. Chem. Phys. 1987, 87, 6687–6699. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.-E.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Ali, M.D.; Aslam, A.; Zeeshan, T.; Mubaraka, R.; Bukhari, S.A.; Shoaib, M.; Amami, M.; ben Farhat, I.; ben Ahmed, S.; Abdelhak, J. Robust effectiveness behavior of synthesized cobalt doped Prussian blue graphene oxide ferrite against EMI shielding. Inorg. Chem. Commun. 2022, 137, 109204. [Google Scholar] [CrossRef]
- Li, G.; Li, Y.; Liu, H.; Guo, Y.; Li, Y.; Zhu, D. Architecture of graphdiyne nanoscale films. Chem. Commun. 2010, 46, 3256–3258. [Google Scholar] [CrossRef]
- Jia, Z.; Li, Y.; Zuo, Z.; Liu, H.; Huang, C.; Li, Y. Synthesis and Properties of 2D Carbon Graphdiyne. Acc. Chem. Res. 2017, 50, 2470–2478. [Google Scholar] [CrossRef]
- Qian, X.; Liu, H.; Huang, C.; Chen, S.; Zhang, L.; Li, Y.; Wang, J.; Li, Y. Self-catalyzed growth of large-area nanofilms of two-dimensional carbon. Sci. Rep. 2015, 5, 7756. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Li, Y.; Qian, X.; Liu, H.; Lin, H.; Chen, N.; Li, Y. Construction of Tubular Molecule Aggregations of Graphdiyne for Highly Efficient Field Emission. J. Phys. Chem. C 2011, 115, 2611–2615. [Google Scholar] [CrossRef]
- Qian, X.; Ning, Z.; Li, Y.; Liu, H.; Ouyang, C.; Chen, Q.; Li, Y. Construction of graphdiyne nanowires with high-conductivity and mobility. Dalton Trans. 2012, 41, 730–733. [Google Scholar] [CrossRef]
- Zhou, J.; Gao, X.; Liu, R.; Xie, Z.; Yang, J.; Zhang, S.; Zhang, G.; Liu, H.; Li, Y.; Zhang, J.; et al. Synthesis of Graphdiyne Nanowalls Using Acetylenic Coupling Reaction. J. Am. Chem. Soc. 2015, 137, 7596–7599. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Li, J.; Du, R.; Zhou, J.; Huang, M.; Liu, R.; Li, J.; Xie, Z.; Wu, L.; Liu, Z.; et al. Direct Synthesis of Graphdiyne Nanowalls on Arbitrary Substrates and Its Application for Photoelectrochemical Water Splitting Cell. Adv. Mater. 2017, 29, 1605308. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, H.; Huang, C.; Cui, G.; Li, Y. Bulk graphdiyne powder applied for highly efficient lithium storage. Chem. Commun. 2015, 51, 1834–1837. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, S.; Liu, H.; Li, Y.; Cui, G.; Li, Y. Graphdiyne for high capacity and long-life lithium storage. Nano Energy 2015, 11, 481–489. [Google Scholar] [CrossRef]
- Wang, S.; Yi, L.; Halpert, J.E.; Lai, X.; Liu, Y.; Cao, H.; Yu, R.; Wang, D.; Li, Y. A novel and highly efficient photocatalyst based on P25–graphdiyne nanocomposite. Small 2012, 8, 265–271. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Gao, X.; Liu, B.; Feng, Q.; Li, X.-B.; Huang, M.-Y.; Liu, Z.; Zhang, J.; Tung, C.-H.; Wu, L.-Z. Graphdiyne: A metal-free material as hole transfer layer to fabricate quantum dot-sensitized photocathodes for hydrogen production. J. Am. Chem. Soc. 2016, 138, 3954–3957. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Zhou, J.; Du, R.; Xie, Z.; Deng, S.; Liu, R.; Liu, Z.; Zhang, J. Robust superhydrophobic foam: A graphdiyne-based hierarchical architecture for oil/water separation. Adv. Mater. 2016, 28, 168–173. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Zhou, J.; Gao, X.; Li, J.; Xie, Z.; Li, Z.; Zhang, S.; Tong, L.; Zhang, J.; Liu, Z. Graphdiyne filter for decontaminating lead-ion-polluted water. Adv. Electron. Mater. 2017, 3, 1700122. [Google Scholar] [CrossRef]
- Kuang, C.; Tang, G.; Jiu, T.; Yang, H.; Liu, H.; Li, B.; Luo, W.; Li, X.; Zhang, W.; Lu, F. Highly efficient electron transport obtained by doping PCBM with graphdiyne in planar-heterojunction perovskite solar cells. Nano Lett. 2015, 15, 2756–2762. [Google Scholar] [CrossRef]
- Xiao, J.; Shi, J.; Liu, H.; Xu, Y.; Lv, S.; Luo, Y.; Li, D.; Meng, Q.; Li, Y. Efficient CH3NH3PbI3 perovskite solar cells based on graphdiyne (GD)-modified P3HT hole-transporting material. Adv. Energy Mater. 2015, 5, 1401943. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.; Firsov, A.A. Two-dimensional gas of massless Dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Peng, Q.; Crean, J.; Dearden, A.K.; Huang, C.; Wen, X.; Bordas, S.P.; De, S. Defect engineering of 2D monatomic-layer materials. Mod. Phys. Lett. B 2013, 27, 1330017. [Google Scholar] [CrossRef]
- Xu, M.; Liang, T.; Shi, M.; Chen, H. Graphene-like two-dimensional materials. Chem. Rev. 2013, 113, 3766–3798. [Google Scholar] [CrossRef]
- Ali, M.D.; Majid, F.; Aslam, A.; Malik, A.; Wahid, I.; Dildar, S.; Waseem, S.; Dahshan, A. Dielectric and electrical properties of synthesized PBGO/Fe3O4 nanocomposite. Ceram. Int. 2021, 47, 26224–26232. [Google Scholar] [CrossRef]
- Peng, Q.; Ji, W.; De, S. Mechanical properties of the hexagonal boron nitride monolayer: Ab initio study. Comput. Mater. Sci. 2012, 56, 11–17. [Google Scholar] [CrossRef]
- Peng, Q.; De, S. Tunable band gaps of mono-layer hexagonal BNC heterostructures. Phys. E Low-Dimens. Syst. Nanostructures 2012, 44, 1662–1666. [Google Scholar] [CrossRef]
- Peng, Q.; Zamiri, A.R.; Ji, W.; De, S. Elastic properties of hybrid graphene/boron nitride monolayer. Acta Mech. 2012, 223, 2591–2596. [Google Scholar] [CrossRef]
- Peng, Q.; Ji, W.; De, S. First-principles study of the effects of mechanical strains on the radiation hardness of hexagonal boron nitride monolayers. Nanoscale 2013, 5, 695–703. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, X.J.; Ji, W.; De, S. Chemically tuning mechanics of graphene by BN. Adv. Eng. Mater. 2013, 15, 718–727. [Google Scholar] [CrossRef]
- Peng, Q.; Liang, C.; Ji, W.; De, S. A first principles investigation of the mechanical properties of g-TlN. Model. Numer. Simul. Mater. Sci. 2012, 2, 76–84. [Google Scholar] [CrossRef][Green Version]
- Peng, Q.; Liang, C.; Ji, W.; De, S. A first principles investigation of the mechanical properties of g-ZnO: The graphene-like hexagonal zinc oxide monolayer. Comput. Mater. Sci. 2013, 68, 320–324. [Google Scholar] [CrossRef]
- Peng, Q.; Chen, X.-J.; Liu, S.; De, S. Mechanical stabilities and properties of graphene-like aluminum nitride predicted from first-principles calculations. RSC Adv. 2013, 3, 7083–7092. [Google Scholar] [CrossRef]
- Peng, Q.; Liang, C.; Ji, W.; De, S. A first-principles study of the mechanical properties of g-GeC. Mech. Mater. 2013, 64, 135–141. [Google Scholar] [CrossRef]
- Peng, Q.; Liang, C.; Ji, W.; De, S. Mechanical properties of g-GaN: A first principles study. Appl. Phys. A 2013, 113, 483–490. [Google Scholar] [CrossRef]
- Peng, Q.; Wen, X.; De, S. Mechanical stabilities of silicene. Rsc Adv. 2013, 3, 13772–13781. [Google Scholar] [CrossRef]
- Kara, A.; Enriquez, H.; Seitsonen, A.P.; Voon, L.L.Y.; Vizzini, S.; Aufray, B.; Oughaddou, H. A review on silicene—New candidate for electronics. Surf. Sci. Rep. 2012, 67, 1–18. [Google Scholar] [CrossRef]
- Jose, D.; Datta, A. Structures and chemical properties of silicene: Unlike graphene. Acc. Chem. Res. 2014, 47, 593–602. [Google Scholar] [CrossRef]
- Peng, Q.; De, S. Outstanding mechanical properties of monolayer MoS2 and its application in elastic energy storage. Phys. Chem. Chem. Phys. 2013, 15, 19427–19437. [Google Scholar] [CrossRef]
- Peng, Q.; De, S. Mechanical properties and instabilities of ordered graphene oxide C 6 O monolayers. RSC Adv. 2013, 3, 24337–24344. [Google Scholar] [CrossRef]
- Aslam, A.; Ali, M.D.; Fakhar, U.; Ahmad, A.; Khalid, U.; Amami, M.; Dahshan, A. Electrical, dielectric, IV and antimicrobial behavior of cobalt incapacitated Prussian blue graphene ferrites composite. Inorg. Chem. Commun. 2022, 141, 109548. [Google Scholar] [CrossRef]
- Iqbal, K.; Ishaq, M.A.; Ahmad, A.; Ali, M.D.; Zeeshan, T.; Tahir, W.; Aslam, A.; Amami, M.; ben Farhat, I.; ben Ahmed, S. Fabrication and characterizations of hybrid materials based on polyaniline, metal oxide, and graphene nano-platelets for supercapacitor electrodes. Inorg. Chem. Commun. 2022, 137, 109201. [Google Scholar] [CrossRef]
- Ivanovskii, A. Graphynes and graphdyines. Prog. Solid State Chem. 2013, 41, 1–19. [Google Scholar] [CrossRef]
- Li, Y.; Xu, L.; Liu, H.; Li, Y. Graphdiyne and graphyne: From theoretical predictions to practical construction. Chem. Soc. Rev. 2014, 43, 2572–2586. [Google Scholar] [CrossRef]
- Peng, Q.; Dearden, A.K.; Crean, J.; Han, L.; Liu, S.; Wen, X.; De, S. New materials graphyne, graphdiyne, graphone, and graphane: Review of properties, synthesis, and application in nanotechnology. Nanotechnol. Sci. Appl. 2014, 7, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-M.; Jenkins, K.A.; Valdes-Garcia, A.; Small, J.P.; Farmer, D.B.; Avouris, P. Operation of graphene transistors at gigahertz frequencies. Nano Lett. 2009, 9, 422–426. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-M.; Dimitrakopoulos, C.; Jenkins, K.A.; Farmer, D.B.; Chiu, H.-Y.; Grill, A.; Avouris, P. 100-GHz transistors from wafer-scale epitaxial graphene. Science 2010, 327, 662. [Google Scholar] [CrossRef] [PubMed]
- Liao, L.; Lin, Y.-C.; Bao, M.; Cheng, R.; Bai, J.; Liu, Y.; Qu, Y.; Wang, K.L.; Huang, Y.; Duan, X. High-speed graphene transistors with a self-aligned nanowire gate. Nature 2010, 467, 305–308. [Google Scholar] [CrossRef]
- Narita, N.; Nagai, S.; Suzuki, S.; Nakao, K. Optimized geometries and electronic structures of graphyne and its family. Phys. Rev. B 1998, 58, 11009. [Google Scholar] [CrossRef]
- Kang, J.; Li, J.; Wu, F.; Li, S.-S.; Xia, J.-B. Elastic, electronic, and optical properties of two-dimensional graphyne sheet. J. Phys. Chem. C 2011, 115, 20466–20470. [Google Scholar] [CrossRef]
- Srinivasu, K.; Ghosh, S.K. Graphyne and graphdiyne: Promising materials for nanoelectronics and energy storage applications. J. Phys. Chem. C 2012, 116, 5951–5956. [Google Scholar] [CrossRef]
- Diederich, F.; Kivala, M. All-carbon scaffolds by rational design. Adv. Mater. 2010, 22, 803–812. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A. The rise of graphene. Nat. Mater 2007, 6, 183–191. [Google Scholar]
- Novoselov, K.S.; Fal′ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Kong, X.Y.; Ding, Y.; Yang, R.; Wang, Z.L. Single-crystal nanorings formed by epitaxial self-coiling of polar nanobelts. Science 2004, 303, 1348–1351. [Google Scholar] [CrossRef] [PubMed]
- Nasibulin, A.G.; Pikhitsa, P.V.; Jiang, H.; Brown, D.P.; Krasheninnikov, A.V.; Anisimov, A.S.; Queipo, P.; Moisala, A.; Gonzalez, D.; Lientschnig, G. A novel hybrid carbon material. Nat. Nanotechnol. 2007, 2, 156–161. [Google Scholar] [CrossRef]
- Malko, D.; Neiss, C.; Vines, F.; Görling, A. Competition for graphene: Graphynes with direction-dependent dirac cones. Phys. Rev. Lett. 2012, 108, 086804. [Google Scholar] [CrossRef]
- Narita, N.; Nagai, S.; Suzuki, S.; Nakao, K. Electronic structure of three-dimensional graphyne. Phys. Rev. B 2000, 62, 11146. [Google Scholar] [CrossRef]
- Haley, M.M.; Brand, S.C.; Pak, J.J. Carbon networks based on dehydrobenzoannulenes: Synthesis of graphdiyne substructures. Angew. Chem. Int. Ed. Engl. 1997, 36, 836–838. [Google Scholar] [CrossRef]
- Kehoe, J.M.; Kiley, J.H.; English, J.J.; Johnson, C.A.; Petersen, R.C.; Haley, M.M. Carbon networks based on dehydrobenzoannulenes. 3. synthesis of graphyne substructures1. Org. Lett. 2000, 2, 969–972. [Google Scholar] [CrossRef]
- Haley, M.M. Synthesis and properties of annulenic subunits of graphyne and graphdiyne nanoarchitectures. Pure Appl. Chem. 2008, 80, 519–532. [Google Scholar] [CrossRef]
- Xie, L.; Wang, X.; Lu, J.; Ni, Z.; Luo, Z.; Mao, H.; Wang, R.; Wang, Y.; Huang, H.; Qi, D. Room temperature ferromagnetism in partially hydrogenated epitaxial graphene. Appl. Phys. Lett. 2011, 98, 193113. [Google Scholar] [CrossRef]
- Gao, X.; Liu, H.; Wang, D.; Zhang, J. Graphdiyne: Synthesis, properties, and applications. Chem. Soc. Rev. 2019, 48, 908–936. [Google Scholar] [CrossRef] [PubMed]
- Diederich, F. Carbon scaffolding: Building acetylenic all-carbon and carbon-rich compounds. Nature 1994, 369, 199–207. [Google Scholar] [CrossRef]
- Bunz, U.H.; Rubin, Y.; Tobe, Y. Polyethynylated cyclic π-systems: Scaffoldings for novel two and three-dimensional carbon networks. Chem. Soc. Rev. 1999, 28, 107–119. [Google Scholar] [CrossRef]
- Coluci, V.; Braga, S.; Legoas, S.; Galvao, D.; Baughman, R. Families of carbon nanotubes: Graphyne-based nanotubes. Phys. Rev. B 2003, 68, 035430. [Google Scholar] [CrossRef]
- Baughman, R.H.; Galvão, D.S.; Cui, C.; Wang, Y.; Tománek, D. Fullereneynes: A new family of porous fullerenes. Chem. Phys. Lett. 1993, 204, 8–14. [Google Scholar] [CrossRef]
- Balaban, A.; Rentia, C.C.; Ciupitu, E. Chemical graphs. 6. Estimation of relative stability of several planar and tridimensional lattices for elementary carbon. Rev. Roum. Chim. 1968, 13, 231–247. [Google Scholar]
- Wang, L.; Hao, Z.; Chen, S.; Chen, H.; Lou, Y.; He, C.; Chen, Y.; Cui, X. Critical review on mechanochemical fabrication of full-carbon graphyne material. Prog. Mater. Sci. 2024, 146, 101327. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Jiang, D.; Schedin, F.; Booth, T.; Khotkevich, V.; Morozov, S.; Geim, A.K. Two-dimensional atomic crystals. Proc. Natl. Acad. Sci. USA 2005, 102, 10451–10453. [Google Scholar] [CrossRef]
- Ma, Y.; Dai, Y.; Guo, M.; Huang, B. Graphene-diamond interface: Gap opening and electronic spin injection. Phys. Rev. B 2012, 85, 235448. [Google Scholar] [CrossRef]
- Brumfiel, G. Graphene gets ready for the big time: Physicists are talking about how to make practical use of a former laboratory curiosity. Nature 2009, 458, 390–392. [Google Scholar] [CrossRef]
- Kaloni, T.P.; Cheng, Y.; Schwingenschlögl, U. Electronic structure of superlattices of graphene and hexagonal boron nitride. J. Mater. Chem. 2012, 22, 919–922. [Google Scholar] [CrossRef]
- Elias, D.C.; Nair, R.R.; Mohiuddin, T.; Morozov, S.; Blake, P.; Halsall, M.; Ferrari, A.C.; Boukhvalov, D.; Katsnelson, M.; Geim, A. Control of graphene’s properties by reversible hydrogenation: Evidence for graphane. Science 2009, 323, 610–613. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.K.; Yakobson, B.I. Electronics and magnetism of patterned graphene nanoroads. Nano Lett. 2009, 9, 1540–1543. [Google Scholar] [CrossRef]
- Balog, R.; Jørgensen, B.; Nilsson, L.; Andersen, M.; Rienks, E.; Bianchi, M.; Fanetti, M.; Lægsgaard, E.; Baraldi, A.; Lizzit, S. Bandgap opening in graphene induced by patterned hydrogen adsorption. Nat. Mater. 2010, 9, 315–319. [Google Scholar] [CrossRef]
- Burgess, J.S.; Matis, B.R.; Robinson, J.T.; Bulat, F.A.; Perkins, F.K.; Houston, B.H.; Baldwin, J.W. Tuning the electronic properties of graphene by hydrogenation in a plasma enhanced chemical vapor deposition reactor. Carbon 2011, 49, 4420–4426. [Google Scholar] [CrossRef]
- Castellanos-Gomez, A.; Wojtaszek, M.; Arramel; Tombros, N.; van Wees, B.J. Reversible hydrogenation and bandgap opening of graphene and graphite surfaces probed by scanning tunneling spectroscopy. Small 2012, 8, 1607–1613. [Google Scholar] [CrossRef]
- Topsakal, M.; Cahangirov, S.; Ciraci, S. The response of mechanical and electronic properties of graphane to the elastic strain. Appl. Phys. Lett. 2010, 96, 091912. [Google Scholar] [CrossRef]
- Pei, Q.-X.; Sha, Z.-D.; Zhang, Y.-W. A theoretical analysis of the thermal conductivity of hydrogenated graphene. Carbon 2011, 49, 4752–4759. [Google Scholar] [CrossRef]
- Dillon, A.; Heben, M. Hydrogen storage using carbon adsorbents: Past, present and future. Appl. Phys. A 2001, 72, 133–142. [Google Scholar] [CrossRef]
- Şahin, H.; Ataca, C.; Ciraci, S. Magnetization of graphane by dehydrogenation. Appl. Phys. Lett. 2009, 95, 222510. [Google Scholar] [CrossRef]
- Kang, B.; Liu, H.; Lee, J.Y. Oxygen adsorption on single layer graphyne: A DFT study. Phys. Chem. Chem. Phys. 2014, 16, 974–980. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Ceperley, D.M.; Alder, B.J. Ground state of the electron gas by a stochastic method. Phys. Rev. Lett. 1980, 45, 566. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Hedin, L. New method for calculating the one-particle Green’s function with application to the electron-gas problem. Phys. Rev. 1965, 139, A796. [Google Scholar] [CrossRef]
- Hybertsen, M.S.; Louie, S.G. Electron correlation in semiconductors and insulators: Band gaps and quasiparticle energies. Phys. Rev. B 1986, 34, 5390. [Google Scholar] [CrossRef] [PubMed]
- Slater, J.C.; Koster, G.F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 1954, 94, 1498. [Google Scholar] [CrossRef]
- Brandbyge, M.; Mozos, J.-L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 2002, 65, 165401. [Google Scholar] [CrossRef]
- Wang, J.-S.; Wang, J.; Lü, J. Quantum thermal transport in nanostructures. Eur. Phys. J. B 2008, 62, 381–404. [Google Scholar] [CrossRef]
- Yoshimura, T.; Inaba, A.; Sonoda, M.; Tahara, K.; Tobe, Y.; Williams, R.V. Synthesis and Properties of Trefoil-Shaped Tris(hexadehydrotribenzo[12]annulene) and Tris (tetradehydrotribenzo [12] annulene). Org. Lett. 2006, 8, 2933–2936. [Google Scholar] [CrossRef]
- Majidi, R. Density functional theory study on structural and mechanical properties of graphene, T-graphene, and R-graphyne. Theor. Chem. Acc. 2017, 136, 109. [Google Scholar] [CrossRef]
- Yang, J.; Bi, Z.; Zhang, S.; Zeng, L.; Zhang, Y.; Wang, Y.; Yan, J.; Zhao, W.; Dai, Y.; Yun, J. Synthesis of γ-graphyne by modified mechanochemistry with enhanced adsorption of organic dyes. Diam. Relat. Mater. 2022, 129, 109336. [Google Scholar] [CrossRef]
- Li, Q.; Yang, C.; Wu, L.; Wang, H.; Cui, X. Converting benzene into γ-graphyne and its enhanced electrochemical oxygen evolution performance. J. Mater. Chem. A 2019, 7, 5981–5990. [Google Scholar] [CrossRef]
- Ding, W.; Sun, M.; Zhang, Z.; Lin, X.; Gao, B. Ultrasound-promoted synthesis of γ-graphyne for supercapacitor and photoelectrochemical applications. Ultrason. Sonochem. 2020, 61, 104850. [Google Scholar] [CrossRef]
- Yang, C.; Li, Y.; Chen, Y.; Li, Q.; Wu, L.; Cui, X. Mechanochemical Synthesis of γ-Graphyne with Enhanced Lithium Storage Performance. Small 2019, 15, 1804710. [Google Scholar] [CrossRef]
- He, S.; Wu, B.; Xia, Z.; Guo, P.; Li, Y.; Song, S. One-pot synthesis of gamma-graphyne supported Pd nanoparticles with high catalytic activity. Nanoscale Adv. 2023, 5, 2487–2492. [Google Scholar] [CrossRef]
- Desyatkin, V.G.; Martin, W.B.; Aliev, A.E.; Chapman, N.E.; Fonseca, A.F.; Galvão, D.S.; Miller, E.R.; Stone, K.H.; Wang, Z.; Zakhidov, D. Scalable synthesis and characterization of multilayer γ-graphyne, new carbon crystals with a small direct band gap. J. Am. Chem. Soc. 2022, 144, 17999–18008. [Google Scholar] [CrossRef]
- Liu, X.; Cho, S.M.; Lin, S.; Chen, Z.; Choi, W.; Kim, Y.-M.; Yun, E.; Baek, E.H.; Lee, H. Constructing two-dimensional holey graphyne with unusual annulative π-extension. Matter 2022, 5, 2306–2318. [Google Scholar] [CrossRef]
- Li, J.; Li, S.; Liu, Q.; Yin, C.; Tong, L.; Chen, C.; Zhang, J. Synthesis of Hydrogen-Substituted Graphyne Film for Lithium–Sulfur Battery Applications. Small 2019, 15, 1805344. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, C.; Pan, Q.; Jin, Y.; Lyu, R.; Martinez, V.; Huang, S.; Wu, J.; Wayment, L.J.; Clark, N.A. Synthesis of γ-graphyne using dynamic covalent chemistry. Nat. Synth. 2022, 1, 449–454. [Google Scholar] [CrossRef]
- Li, J.; Han, Y. Artificial Carbon Allotrope γ-Graphyne: Synthesis, Properties, and Applications. Giant 2023, 13, 100140. [Google Scholar] [CrossRef]
- Narang, G.; Bansal, D.; Joarder, S.; Singh, P.; Kumar, L.; Mishra, V.; Singh, S.; Tumba, K.; Kumari, K. A Review on the Synthesis, Properties, and Applications of Graphynes. FlatChem 2023, 40, 100517. [Google Scholar] [CrossRef]
- Hou, X.; Xie, Z.; Li, C.; Li, G.; Chen, Z. Study of electronic structure, thermal conductivity, elastic and optical properties of α, β, γ-graphyne. Materials 2018, 11, 188. [Google Scholar] [CrossRef] [PubMed]
- Puigdollers, A.R.; Alonso, G.; Gamallo, P. First-principles study of structural, elastic and electronic properties of α-, β-and γ-graphyne. Carbon 2016, 96, 879–887. [Google Scholar] [CrossRef]
- Cranford, S.W.; Buehler, M.J. Mechanical properties of graphyne. Carbon 2011, 49, 4111–4121. [Google Scholar] [CrossRef]
- Cranford, S.W.; Brommer, D.B.; Buehler, M.J. Extended graphynes: Simple scaling laws for stiffness, strength and fracture. Nanoscale 2012, 4, 7797–7809. [Google Scholar] [CrossRef]
- Zhang, Y.; Pei, Q.; Wang, C. Mechanical properties of graphynes under tension: A molecular dynamics study. Appl. Phys. Lett. 2012, 101, 081909. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, L.; Song, B.; Du, S.; Gao, H.-J. Graphyne-and graphdiyne-based nanoribbons: Density functional theory calculations of electronic structures. Appl. Phys. Lett. 2011, 98, 173102. [Google Scholar] [CrossRef]
- Georgakilas, V.; Perman, J.A.; Tucek, J.; Zboril, R. Broad family of carbon nanoallotropes: Classification, chemistry, and applications of fullerenes, carbon dots, nanotubes, graphene, nanodiamonds, and combined superstructures. Chem. Rev. 2015, 115, 4744–4822. [Google Scholar] [CrossRef]
- He, J.; Ma, S.Y.; Zhou, P.; Zhang, C.; He, C.; Sun, L. Magnetic properties of single transition-metal atom absorbed graphdiyne and graphyne sheet from DFT+ U calculations. J. Phys. Chem. C 2012, 116, 26313–26321. [Google Scholar] [CrossRef]
- Peng, Q.; Ji, W.; De, S. Mechanical properties of graphyne monolayers: A first-principles study. Phys. Chem. Chem. Phys. 2012, 14, 13385–13391. [Google Scholar] [CrossRef] [PubMed]
- Yue, Q.; Chang, S.; Kang, J.; Qin, S.; Li, J. Mechanical and electronic properties of graphyne and its family under elastic strain: Theoretical predictions. J. Phys. Chem. C 2013, 117, 14804–14811. [Google Scholar] [CrossRef]
- Rodrigues, F.C.; Silvestre, N.; Deus, A.M. Nonlinear mechanical behaviour of γ-graphyne through an atomistic finite element model. Comput. Mater. Sci. 2017, 134, 171–183. [Google Scholar] [CrossRef]
- Hernandez, S.A.; Fonseca, A.F. Anisotropic elastic modulus, high Poisson’s ratio and negative thermal expansion of graphynes and graphdiynes. Diam. Relat. Mater. 2017, 77, 57–64. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, X. Mechanical properties of graphyne and its family–A molecular dynamics investigation. Comput. Mater. Sci. 2012, 61, 83–88. [Google Scholar] [CrossRef]
- Pei, Y. Mechanical properties of graphdiyne sheet. Phys. B Condens. Matter 2012, 407, 4436–4439. [Google Scholar] [CrossRef]
- Ducere, J.-M.; Lepetit, C.; Chauvin, R. Carbo-graphite: Structural, mechanical, and electronic properties. J. Phys. Chem. C 2013, 117, 21671–21681. [Google Scholar] [CrossRef]
- Qu, J.; Zhang, H.; Li, J.; Zhao, S.; Chang, T. Structure-dependent mechanical properties of extended beta-graphyne. Carbon 2017, 120, 350–357. [Google Scholar] [CrossRef]
- Wei, X.; Fragneaud, B.; Marianetti, C.A.; Kysar, J.W. Nonlinear elastic behavior of graphene: Ab initio calculations to continuum description. Phys. Rev. B 2009, 80, 205407. [Google Scholar] [CrossRef]
- Zhao, H.; Min, K.; Aluru, N.R. Size and chirality dependent elastic properties of graphene nanoribbons under uniaxial tension. Nano Lett. 2009, 9, 3012–3015. [Google Scholar] [CrossRef]
- Meille, S.; Garboczi, E.J. Linear elastic properties of 2D and 3D models of porous materials made from elongated objects. Model. Simul. Mater. Sci. Eng. 2001, 9, 371. [Google Scholar] [CrossRef]
- Luo, G.; Qian, X.; Liu, H.; Qin, R.; Zhou, J.; Li, L.; Gao, Z.; Wang, E.; Mei, W.-N.; Lu, J. Quasiparticle energies and excitonic effects of the two-dimensional carbon allotrope graphdiyne: Theory and experiment. Phys. Rev. B 2011, 84, 075439. [Google Scholar] [CrossRef]
- Huang, H.; Duan, W.; Liu, Z. The existence/absence of Dirac cones in graphynes. New J. Phys. 2013, 15, 023004. [Google Scholar] [CrossRef]
- Sha, X.; Krowne, C.M. Many-Body Quantum Calculations for Graphyne for Electronic Devices. arXiv 2020, arXiv:2012.07958. [Google Scholar]
- Kim, B.G.; Choi, H.J. Graphyne: Hexagonal network of carbon with versatile Dirac cones. Phys. Rev. B 2012, 86, 115435. [Google Scholar] [CrossRef]
- Asadpour, M.; Jafari, M.; Asadpour, M.; Jafari, M. Optical properties of two-dimensional zigzag and armchair graphyne nanoribbon semiconductor. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2015, 139, 380–384. [Google Scholar] [CrossRef]
- Zheng, J.-J.; Zhao, X.; Zhang, S.B.; Gao, X. Tight-binding description of graphyne and its two-dimensional derivatives. J. Chem. Phys. 2013, 138, 244708. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, G.; Yao, H.; Liu, L.; Jiang, L.; Zheng, Y. A simple tight-binding model for typical graphyne structures. New J. Phys. 2012, 14, 113007. [Google Scholar] [CrossRef]
- Van Miert, G.; Juričić, V.; Smith, C.M. Tight-binding theory of spin-orbit coupling in graphynes. Phys. Rev. B 2014, 90, 195414. [Google Scholar] [CrossRef]
- Huang, S.; Liang, Y.; Yang, L. Exciton spectra in two-dimensional graphene derivatives. Phys. Rev. B 2013, 88, 075441. [Google Scholar] [CrossRef]
- Jiang, P.; Liu, H.; Cheng, L.; Fan, D.; Zhang, J.; Wei, J.; Liang, J.; Shi, J. Thermoelectric properties of γ-graphyne from first-principles calculations. Carbon 2017, 113, 108–113. [Google Scholar] [CrossRef]
- Chen, J.; Xi, J.; Wang, D.; Shuai, Z. Carrier mobility in graphyne should be even larger than that in graphene: A theoretical prediction. J. Phys. Chem. Lett. 2013, 4, 1443–1448. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.; Wang, D.; Shuai, Z. Electronic properties and charge carrier mobilities of graphynes and graphdiynes from first principles. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2015, 5, 215–227. [Google Scholar] [CrossRef]
- Zhang, Y.; Pei, Q.; Wang, C. A molecular dynamics investigation on thermal conductivity of graphynes. Comput. Mater. Sci. 2012, 65, 406–410. [Google Scholar] [CrossRef]
- Chen, X.-K.; Liu, J.; Du, D.; Chen, K.-Q. Anomalous thermal conductance of graphyne under lower temperature. J. Phys. Condens. Matter 2017, 29, 455702. [Google Scholar] [CrossRef]
- Tan, X.; Shao, H.; Hu, T.; Liu, G.; Jiang, J.; Jiang, H. High thermoelectric performance in two-dimensional graphyne sheets predicted by first-principles calculations. Phys. Chem. Chem. Phys. 2015, 17, 22872–22881. [Google Scholar] [CrossRef]
- Jing, Y.; Hu, M.; Gao, Y.; Guo, L.; Sun, Y. On the origin of abnormal phonon transport of graphyne. Int. J. Heat Mass Transf. 2015, 85, 880–889. [Google Scholar] [CrossRef]
- Hu, M.; Jing, Y.; Zhang, X. Low thermal conductivity of graphyne nanotubes from molecular dynamics study. Phys. Rev. B 2015, 91, 155408. [Google Scholar] [CrossRef]
- Wang, X.-M.; Mo, D.-C.; Lu, S.-S. On the thermoelectric transport properties of graphyne by the first-principles method. J. Chem. Phys. 2013, 138, 204704. [Google Scholar] [CrossRef]
- Ouyang, T.; Chen, Y.; Liu, L.-M.; Xie, Y.; Wei, X.; Zhong, J. Thermal transport in graphyne nanoribbons. Phys. Rev. B 2012, 85, 235436. [Google Scholar] [CrossRef]
- Zhou, Y.-H.; Zeng, J.; Chen, K.-Q. Spin filtering effect and magnetoresistance in zigzag 6, 6, 12-graphyne nanoribbon system. Carbon 2014, 76, 175–182. [Google Scholar] [CrossRef]
- Hashmi, K.; Ahmad, M.I.; Raza, S.; Mishra, N.; Joshi, S.; Khan, T. Graphyne-Based Carbon Nanomaterials for Green Energy Applications. Carbon-Based Nanomater. Green Appl. 2024, 7, 163–197. [Google Scholar]
- Zhang, L.; He, B.; Li, Y.; Yun, J.; Yao, L.; Zhao, H.; Yan, J.; Zhao, W.; Zhang, Z. Nitrogen-Doped Graphyne as a Promising Material for Sensing Volatile Organic Compounds in Human Breath. ACS Sens. 2025, 10, 2499–2509. [Google Scholar] [CrossRef] [PubMed]
- Jalilvand, S.; Mousavi, H.; Irani, M. Metal-semiconductor transition in Ψ-graphene. Mater. Today Commun. 2022, 33, 104833. [Google Scholar] [CrossRef]
- Ataca, C.; Aktürk, E.; Ciraci, S. Hydrogen storage of calcium atoms adsorbed on graphene: First-principles plane wave calculations. Phys. Rev. B—Condens. Matter Mater. Phys. 2009, 79, 041406. [Google Scholar] [CrossRef]
- Guo, Y.; Jiang, K.; Xu, B.; Xia, Y.; Yin, J.; Liu, Z. Remarkable hydrogen storage capacity in Li-decorated graphyne: Theoretical predication. J. Phys. Chem. C 2012, 116, 13837–13841. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Wu, F.; Li, S.-S.; Xia, J.-B.; Wang, L.-W. High capacity hydrogen storage in Ca decorated graphyne: A first-principles study. J. Phys. Chem. C 2011, 115, 23221–23225. [Google Scholar] [CrossRef]
- Postel, S.L.; Daily, G.C.; Ehrlich, P.R. Human appropriation of renewable fresh water. Science 1996, 271, 785–788. [Google Scholar] [CrossRef]
- Xue, M.; Qiu, H.; Guo, W. Exceptionally fast water desalination at complete salt rejection by pristine graphyne monolayers. Nanotechnology 2013, 24, 505720. [Google Scholar] [CrossRef]
- Lin, S.; Buehler, M.J. Mechanics and molecular filtration performance of graphyne nanoweb membranes for selective water purification. Nanoscale 2013, 5, 11801–11807. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, M.; He, X.; Wang, Z.; Zhang, X.; Liu, X. High mobility and high storage capacity of lithium in sp–sp2 hybridized carbon network: The case of graphyne. J. Phys. Chem. C 2011, 115, 8845–8850. [Google Scholar] [CrossRef]
- Kundu, J.; Kwon, T.; Lee, K.; Choi, S.I. Exploration of metal-free 2D electrocatalysts toward the oxygen electroreduction. Exploration 2024, 4, 20220174. [Google Scholar] [CrossRef]
- He, S.; Wang, Y.; Wang, T.; Wu, D.; La, J.; Hu, J.; Xiao, J.; Wang, W. Direction- and polarization-tunable spontaneous emission beneficial from diffraction orders of a square R6G-nanopore array. Nanoscale Adv. 2023, 5, 3521–3526. [Google Scholar] [CrossRef] [PubMed]
- Yao, F.; Wang, W.; Shi, H.; Xu, Z.; Zeng, M.; Hu, Y.; Liu, L.; Ji, X. Graphynes: Electronic properties, synthesis, and applications in catalysis. ACS Catal. 2021, 11, 14122–14147. [Google Scholar] [CrossRef]
- Gao, S.; Yi, X.; Shang, J.; Liu, G.; Li, R.-W. Organic and hybrid resistive switching materials and devices. Chem. Soc. Rev. 2019, 48, 1531–1565. [Google Scholar] [CrossRef]
- Fu, L.; Wang, R.; Zhao, C.; Huo, J.; He, C.; Kim, K.-H.; Zhang, W. Construction of Cr-embedded graphyne electrocatalyst for highly selective reduction of CO2 to CH4: A DFT study. Chem. Eng. J. 2021, 414, 128857. [Google Scholar] [CrossRef]
- Kang, J.; Wei, Z.; Li, J. Graphyne and its family: Recent theoretical advances. ACS Appl. Mater. Interfaces 2018, 11, 2692–2706. [Google Scholar] [CrossRef]
- Lasisi, K.H.; Abass, O.K.; Zhang, K.; Ajibade, T.F.; Ajibade, F.O.; Ojediran, J.O.; Okonofua, E.S.; Adewumi, J.R.; Ibikunle, P.D. Recent advances on graphyne and its family members as membrane materials for water purification and desalination. Front. Chem. 2023, 11, 1125625. [Google Scholar] [CrossRef]
- Barua, M.; Saraswat, A.; Rao, C. A novel method for synthesis of γ-graphyne and their charge transfer properties. Carbon 2022, 200, 247–252. [Google Scholar] [CrossRef]
- Nath, S.; Bandyopadhyay, A.; Sen, S.; Jana, D. First principles investigation of structural, electronic and optical properties of synthesized radiaannulene oligomers for 6, 6, 12-graphyne. J. Phys. Chem. Solids 2021, 153, 109990. [Google Scholar] [CrossRef]








| Name | Ultimate Strength σx (N/m) | Ultimate Strength σy (N/m) | Poisson’s Ratio vx | Poisson’s Ratio vy | In-Plane Stiffness Cx (N/m) | In-Plane Stiffness Cy (N/m) | Ultimate Stain εx (%) | Ultimate Stain εy (%) |
| Graphyne | 17.84 [121] | 18.83 [121] | 0.417 [56], 0.416 [122] | 0.42 [123] | 166 [56], 170.4 [115] | 224.0 [115], 169.2 | 20 [121] | 20 [121] |
| 16.68 [117] | 21.16 [117] | 0.429 [121], 0.42 [123] | 0.38 [124] | 166.3 [122]. 162.1 [121] | 162.5 [123], 159.6 [124] | 11.2 [117] | 14.8 [117] | |
| 14.34 [115] | 31.97 [115] | 0.39 [124] | 150 [125], 170.2 [117] | 8.19 [115] | 13.24 [115] | |||
| 14.44 [125] | 20.47 [125] | 164 [123], 163.0 [124] | 11.2 [125] | 17.7 [125] | ||||
| Graphadiyne | 10.71 [116] | 13.54 [116] | 0.446 [122], 0.4 [124] | 0.40 [124] | 123.1 [122], 150.2 [116] | 185.2 [116], 117.5 [124] | 6.3 [116] | 8.0 [116] |
| 9.54 [125] | 20.84 [125] | 0.453 | 100 [125], 118.6 [124] | 10.9 [125] | 20.8 [125] | |||
| 121.8 [126] | ||||||||
| α-Graphyne | 10.88 [117] | 12.18 [117] | 0.863 [113], 0.87 [114] | 0.72 [124] | 39.9 [117], 24 [113] | 40.2 [117], 42.4 [124] | 15.6 [117] | 17.8 [117] |
| 0.874 [127], 0.72 [124] | 21.98 [114], 22.48 [127] | |||||||
| 42.8 [124] | ||||||||
| β-Graphyne | 12.75 [117] | 15.50 [117] | 0.49 [128], 0.647 [113] | 0.51 [124] | 87.1 [117], 83 [128] | 87.4 [117], 92.1 [124] | 13.0 [117] | 16.2 [117] |
| 0.67 [114], 0.52 [124] | 77 [113], 73.07 [114] | |||||||
| 93.6 [124] | ||||||||
| 6,6,12-Graphyne | 13.09 [117] | 20.64 [117] | 0.39 [124] | 0.49 [124] | 117.3 [117], 121.1 [124] | 149.1 [117], 152.1 [124] | 11.6 [117] | 14.7 [117] |
| Graphene | 34.71 [117] | 41.94 [117] | 0.164 [122], 0.169 [129] | 347.0 [122], 348 [129], 333 [117] | 0.134 [117] | 0.191 [117] | ||
| 30.15 [130] | 35.85 [130] | 0.18 [114] | 341.09 [114] | 0.13 [130] | 0.2 [130] |
| Name | Direction | μh (×104 cm2/Vs) | μe (×104 cm2/Vs) |
|---|---|---|---|
| Graphene | X | 35.12 | 32.02 |
| Y | 32.17 | 33.89 | |
| Graphdiyne | X | 1.91 | 17.22 |
| Y | 1.97 | 20.81 | |
| 6,6,12-Graphyne | X | 12.29 | 24.48 |
| Y | 42.92 | 54.10 | |
| β-Graphyne | X | 0.856 | 0.798 |
| Y | 1.076 | 0.892 | |
| α-Graphyne | X | 2.960 | 2.716 |
| Y | 3.316 | 3.3277 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.D.; Starczewska, A.; Das, T.K.; Jesionek, M. Exploration of Sp-Sp2 Carbon Networks: Advances in Graphyne Research and Its Role in Next-Generation Technologies. Int. J. Mol. Sci. 2025, 26, 5140. https://doi.org/10.3390/ijms26115140
Ali MD, Starczewska A, Das TK, Jesionek M. Exploration of Sp-Sp2 Carbon Networks: Advances in Graphyne Research and Its Role in Next-Generation Technologies. International Journal of Molecular Sciences. 2025; 26(11):5140. https://doi.org/10.3390/ijms26115140
Chicago/Turabian StyleAli, Muhammad Danish, Anna Starczewska, Tushar Kanti Das, and Marcin Jesionek. 2025. "Exploration of Sp-Sp2 Carbon Networks: Advances in Graphyne Research and Its Role in Next-Generation Technologies" International Journal of Molecular Sciences 26, no. 11: 5140. https://doi.org/10.3390/ijms26115140
APA StyleAli, M. D., Starczewska, A., Das, T. K., & Jesionek, M. (2025). Exploration of Sp-Sp2 Carbon Networks: Advances in Graphyne Research and Its Role in Next-Generation Technologies. International Journal of Molecular Sciences, 26(11), 5140. https://doi.org/10.3390/ijms26115140








