Effects of Electrode Materials on Electron Transport for Single-Molecule Junctions
Abstract
1. Introduction
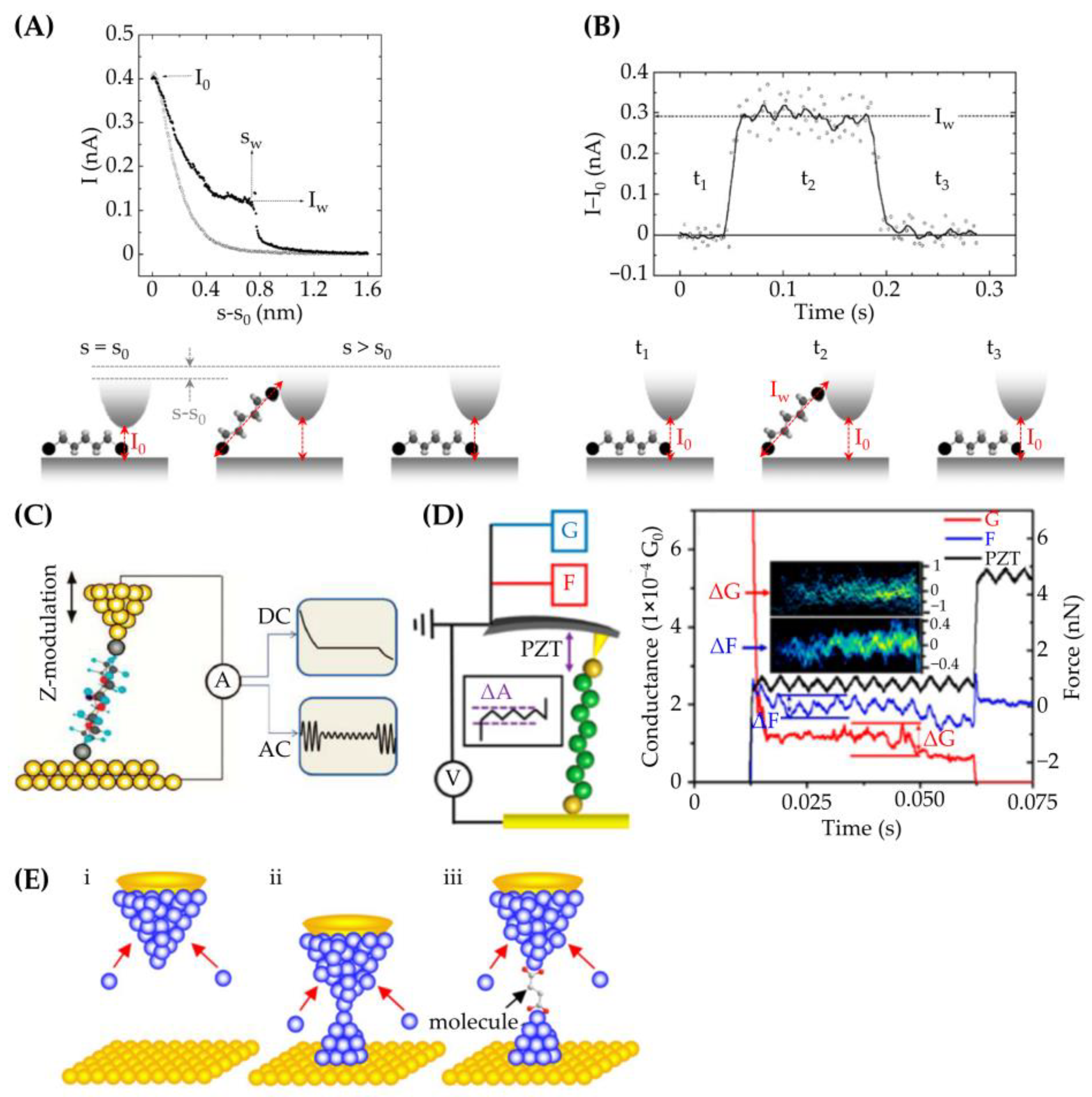
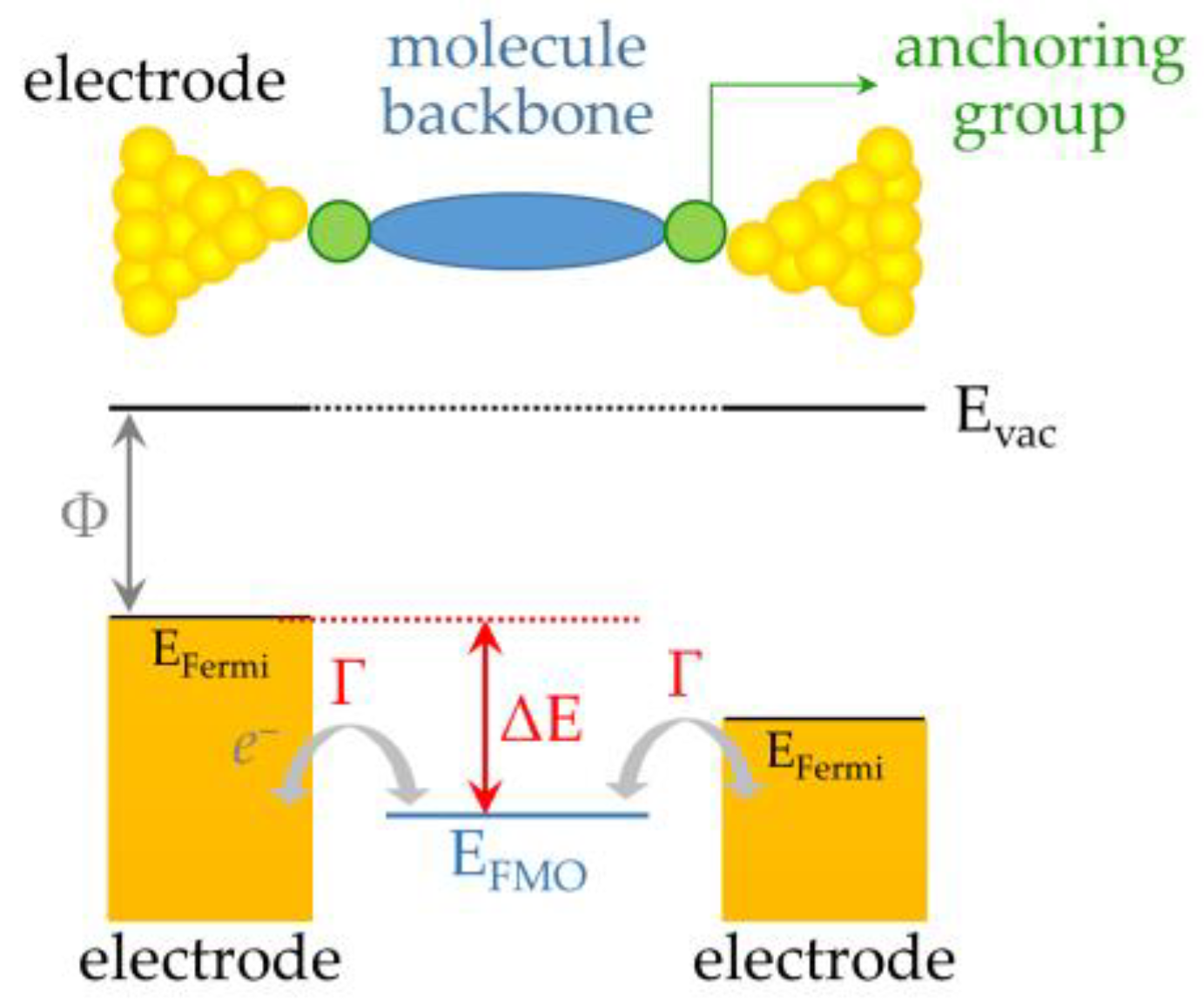
2. Effects of Electrodes on Molecular Conductance
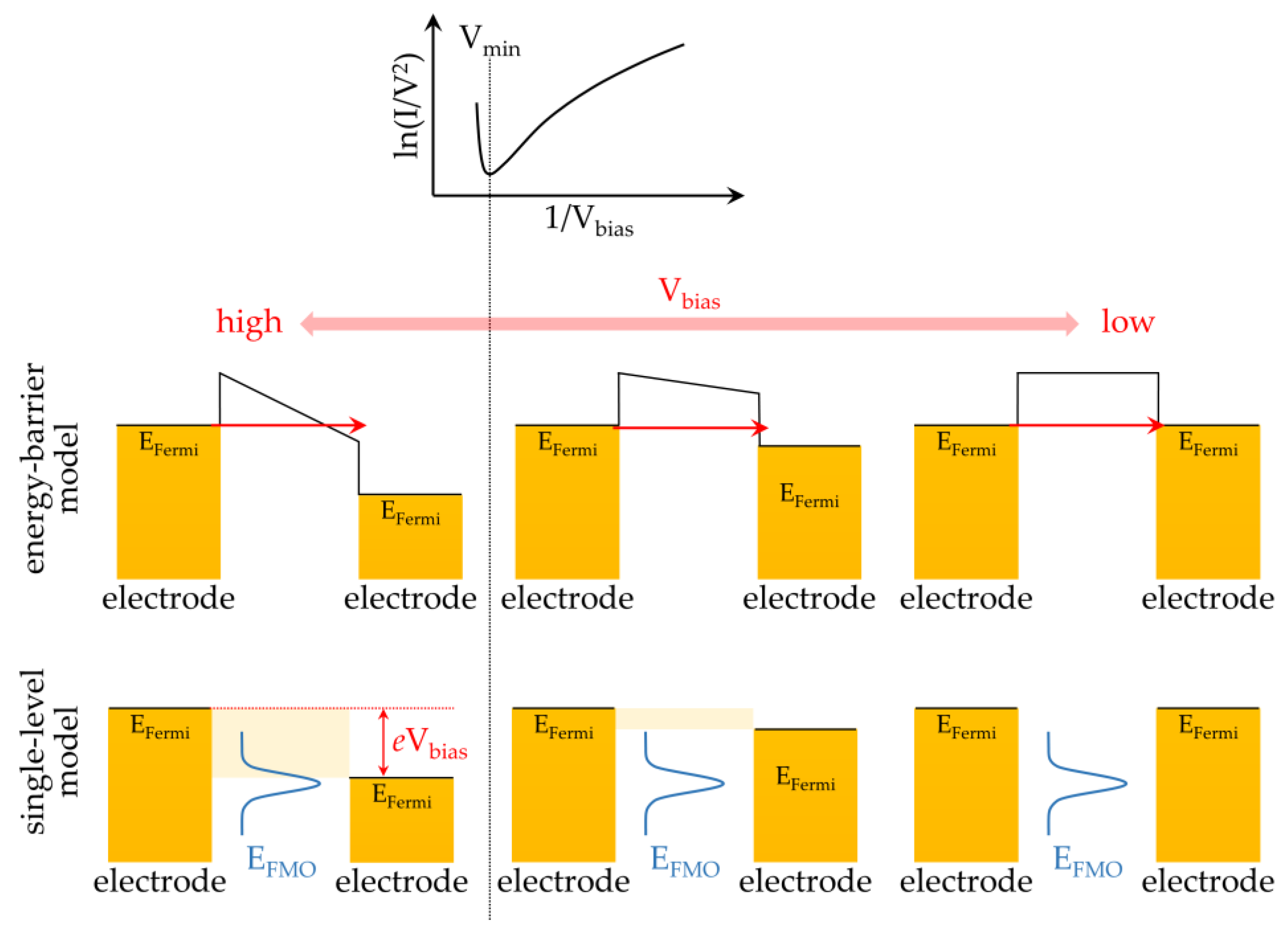
2.1. Basic Principles
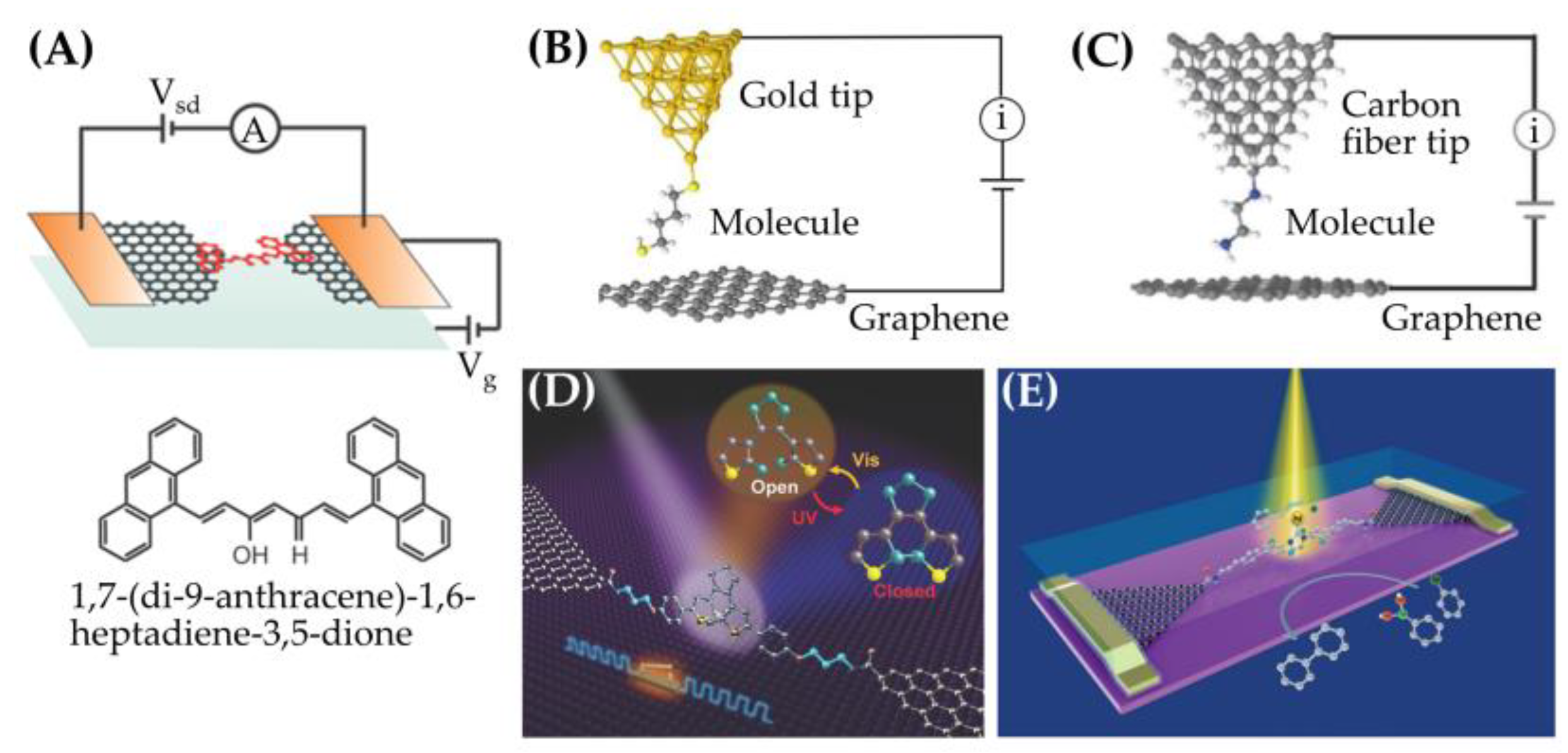
2.2. Characterization Methods
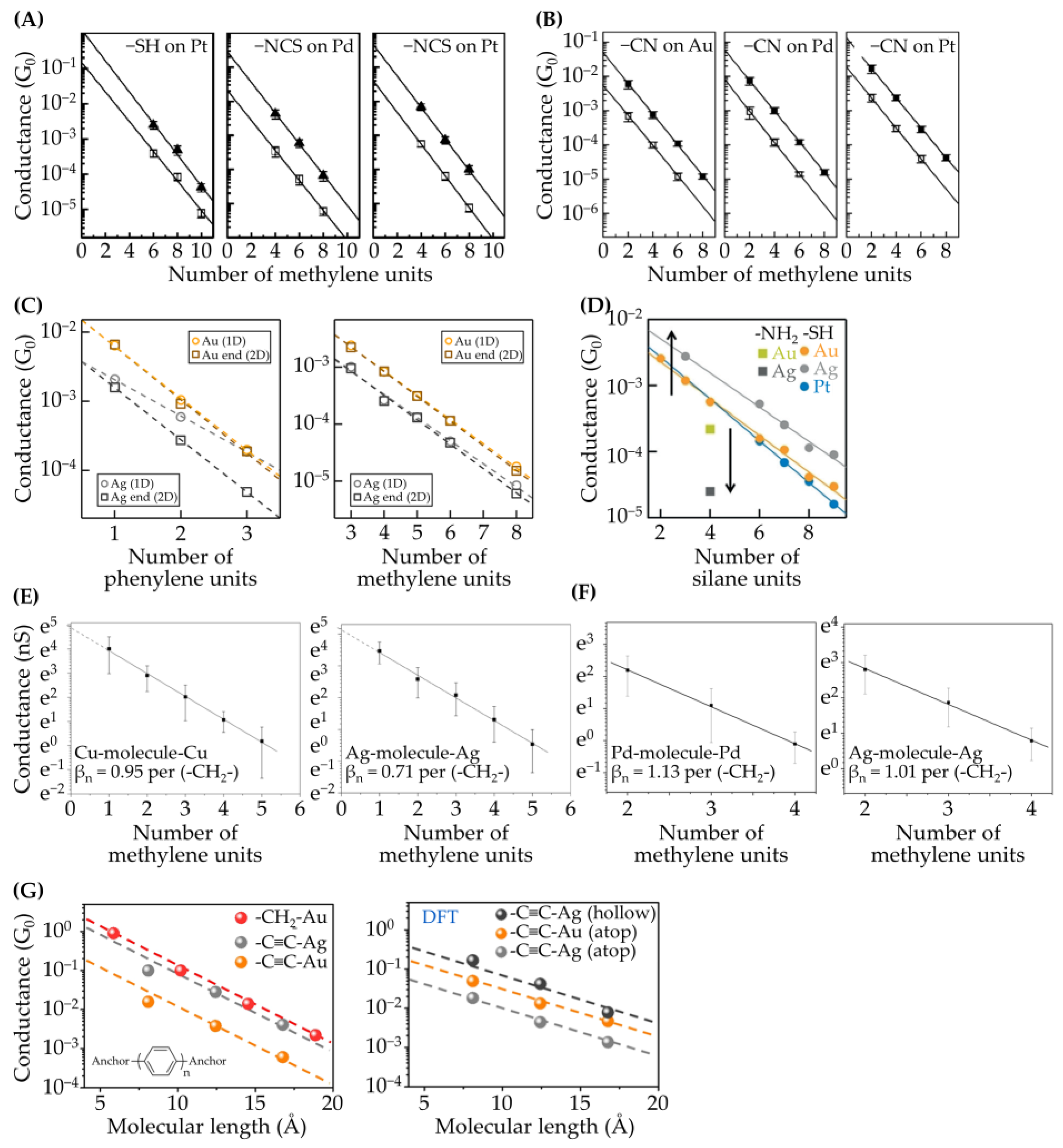
3. Metallic Material Electrodes
3.1. Pt, Pd, Ag, and Cu Electrodes
3.2. Fe, Co, and Ni Electrodes
3.3. Junctions of Ni-Au Pairs
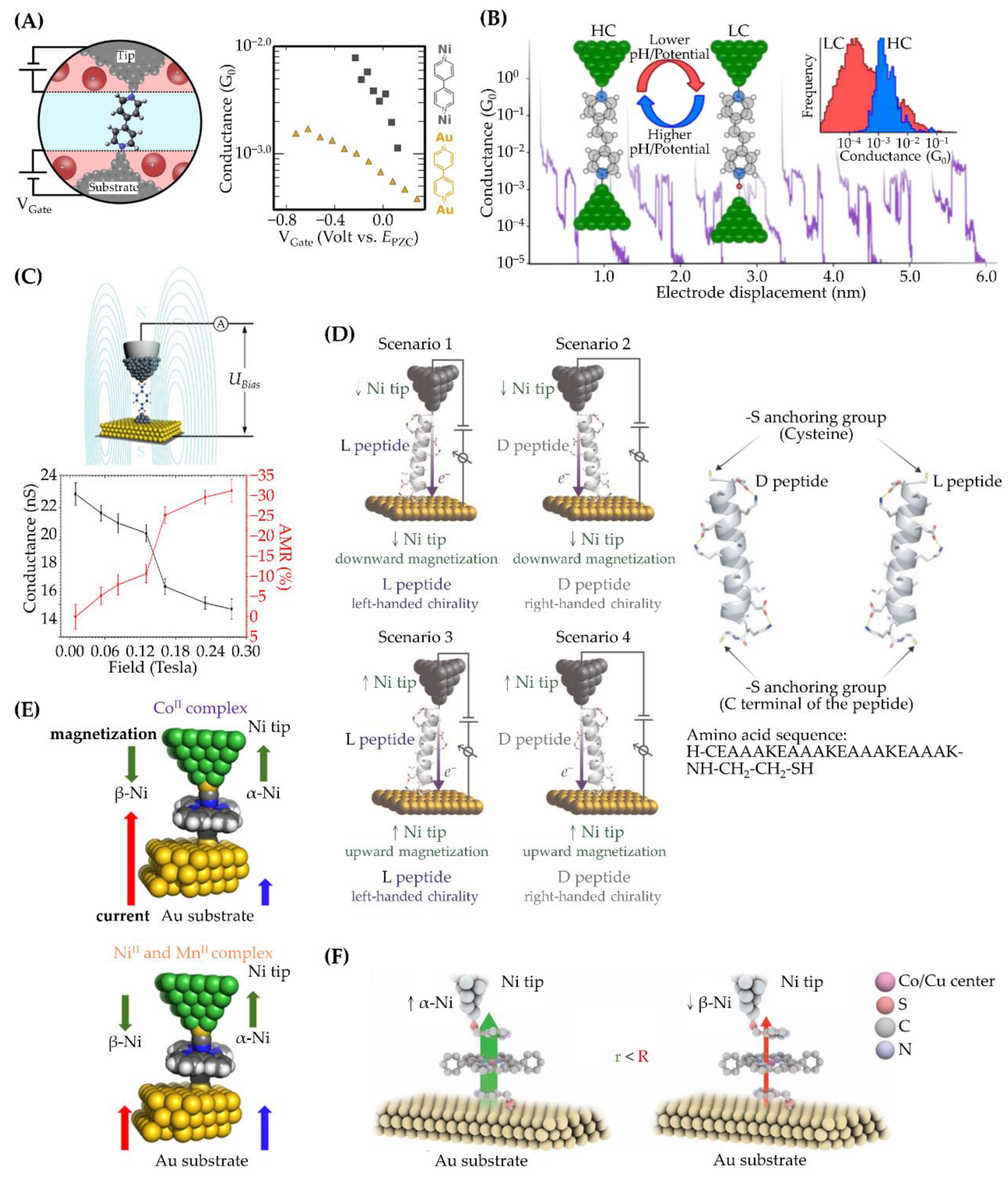
3.4. Bimetallic Electrodes
4. Carbon-Based Material Electrodes
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aviram, A.; Ratner, M.A. Molecular rectifiers. Chem. Phys. Lett. 1974, 29, 277–283. [Google Scholar] [CrossRef]
- Garner, M.H.; Li, H.; Chen, Y.; Su, T.A.; Shangguan, Z.; Paley, D.W.; Liu, T.; Ng, F.; Li, H.; Xiao, S.; et al. Comprehensive suppression of single-molecule conductance using destructive σ-interference. Nature 2018, 558, 415–419. [Google Scholar] [CrossRef]
- Li, Y.; Buerkle, M.; Li, G.; Rostamian, A.; Wang, H.; Wang, Z.; Bowler, D.R.; Miyazaki, T.; Xiang, L.; Asai, Y.; et al. Gate controlling of quantum interference and direct observation of anti-resonances in single molecule charge transport. Nat. Mater. 2019, 18, 357–363. [Google Scholar] [CrossRef] [PubMed]
- Lauhon, L.J.; Ho, W. Single-molecule chemistry and vibrational spectroscopy: Pyridine and benzene on Cu(001). J. Phys. Chem. A 1999, 104, 2463–2467. [Google Scholar] [CrossRef]
- Czap, G.; Wagner, P.J.; Xue, F.; Gu, L.; Li, J.; Yao, J.; Wu, R.; Ho, W. Probing and imaging spin interactions with a magnetic single-molecule sensor. Science 2019, 364, 670–673. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Low, J.Z.; Wilhelm, J.; Liao, G.; Gunasekaran, S.; Prindle, C.R.; Starr, R.L.; Golze, D.; Nuckolls, C.; Steigerwald, M.L.; et al. Highly conducting single-molecule topological insulators based on mono- and di-radical cations. Nat. Chem. 2022, 14, 1061–1067. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, L.; Lu, C.; Zhou, S.; Li, X.; Li, Y.; Yang, Y.; Li, Y.; Liu, Z.; Yang, J.; et al. Unveiling the full reaction path of the Suzuki–Miyaura cross-coupling in a single-molecule junction. Nat. Nanotechnol. 2021, 16, 1214–1223. [Google Scholar] [CrossRef]
- Reed, M.A.; Zhou, C.; Muller, C.J.; Burgin, T.P.; Tour, J.M. Conductance of a molecular junction. Science 1997, 278, 252–254. [Google Scholar] [CrossRef]
- Xu, B.; Tao, N.J. Measurement of single-molecule resistance by repeated formation of molecular junctions. Science 2003, 301, 1221–1223. [Google Scholar] [CrossRef]
- van Zalinge, H.; Schiffrin, D.J.; Bates, A.D.; Haiss, W.; Ulstrup, J.; Nichols, R.J. Single-molecule conductance measurements of single- and double-stranded DNA oligonucleotides. ChemPhysChem 2006, 7, 94–98. [Google Scholar] [CrossRef]
- Haiss, W.; van Zalinge, H.; Higgins, S.J.; Bethell, D.; Höbenreich, H.; Schiffrin, D.J.; Nichols, R.J. Redox state dependence of single molecule conductivity. J. Am. Chem. Soc. 2003, 125, 15294–15295. [Google Scholar] [CrossRef] [PubMed]
- Haiss, W.; Nichols, R.J.; van Zalinge, H.; Higgins, S.J.; Bethell, D.; Schiffrin, D.J. Measurement of single molecule conductivity using the spontaneous formation of molecular wires. Phys. Chem. Chem. Phys. 2004, 6, 4330–4337. [Google Scholar] [CrossRef]
- Xia, J.L.; Diez-Perez, I.; Tao, N.J. Electron transport in single molecules measured by a distance-modulation assisted break junction method. Nano Lett. 2008, 8, 1960–1964. [Google Scholar] [CrossRef]
- Wang, K.; Hamill, J.M.; Zhou, J.; Xu, B. Mapping the details of contact effect of modulated Au-octanedithiol-Au break junction by force–conductance cross-correlation. J. Am. Chem. Soc. 2014, 136, 17406–17409. [Google Scholar] [CrossRef] [PubMed]
- Ismael, A.K.; Wang, K.; Vezzoli, A.; Al-Khaykanee, M.K.; Gallagher, H.E.; Grace, I.M.; Lambert, C.J.; Xu, B.; Nichols, R.J.; Higgins, S.J. Side-group-mediated mechanical conductance switching in molecular junctions. Angew. Chem. Int. Ed. 2017, 56, 15378–15382. [Google Scholar] [CrossRef]
- Chen, I.-W.P.; Tseng, W.-H.; Gu, M.-W.; Su, L.-C.; Hsu, C.-H.; Chang, W.-H.; Chen, C.-h. Tactile-feedback stabilized molecular junctions for the measurement of molecular conductance. Angew. Chem. Int. Ed. 2013, 52, 2449–2453. [Google Scholar] [CrossRef]
- Chen, H.; Li, Y.; Chang, S. Hybrid molecular-junction mapping technique for simultaneous measurements of single-molecule electronic conductance and its corresponding binding geometry in a tunneling junction. Anal. Chem. 2020, 92, 6423–6429. [Google Scholar] [CrossRef]
- Xiao, X.; Nagahara, L.A.; Rawlett, A.M.; Tao, N. Electrochemical gate-controlled conductance of single oligo(phenylene ethynylene)s. J. Am. Chem. Soc. 2005, 127, 9235–9240. [Google Scholar] [CrossRef]
- Bai, J.; Daaoub, A.; Sangtarash, S.; Li, X.; Tang, Y.; Zou, Q.; Sadeghi, H.; Liu, S.; Huang, X.; Tan, Z.; et al. Anti-resonance features of destructive quantum interference in single-molecule thiophene junctions achieved by electrochemical gating. Nat. Mater. 2019, 18, 364–369. [Google Scholar] [CrossRef]
- Brooke, R.J.; Jin, C.; Szumski, D.S.; Nichols, R.J.; Mao, B.-W.; Thygesen, K.S.; Schwarzacher, W. Single-molecule electrochemical transistor utilizing a nickel-pyridyl spinterface. Nano Lett. 2015, 15, 275–280. [Google Scholar] [CrossRef]
- Naghibi, S.; Sangtarash, S.; Kumar, V.J.; Wu, J.-Z.; Judd, M.M.; Qiao, X.; Gorenskaia, E.; Higgins, S.J.; Cox, N.; Nichols, R.J.; et al. Redox-addressable single-molecule junctions incorporating a persistent organic radical. Angew. Chem. Int. Ed. 2022, 61, e202116985. [Google Scholar] [CrossRef] [PubMed]
- Xiang, L.; Palma, J.L.; Li, Y.; Mujica, V.; Ratner, M.A.; Tao, N. Gate-controlled conductance switching in DNA. Nat. Commun. 2017, 8, 14471. [Google Scholar] [CrossRef] [PubMed]
- Capozzi, B.; Chen, Q.; Darancet, P.; Kotiuga, M.; Buzzeo, M.; Neaton, J.B.; Nuckolls, C.; Venkataraman, L. Tunable charge transport in single-molecule junctions via electrolytic gating. Nano Lett. 2014, 14, 1400–1404. [Google Scholar] [CrossRef] [PubMed]
- Ting, T.-C.; Hsu, L.-Y.; Huang, M.-J.; Horng, E.-C.; Lu, H.-C.; Hsu, C.-H.; Jiang, C.-H.; Jin, B.-Y.; Peng, S.-M.; Chen, C.-h. Energy-level alignment for single-molecule conductance of extended metal-atom chains. Angew. Chem. Int. Ed. 2015, 54, 15734–15738. [Google Scholar] [CrossRef] [PubMed]
- Lin, G.-M.; Lin, C.-H.; Peng, H.H.; Hsiao, H.; Wang, T.-H.; Ho, C.-H.; Hsu, H.-F.; Chen, C.-h. Effect of the chemical potentials of electrodes on charge transport across molecular junctions. J. Phys. Chem. C 2019, 123, 22009–22017. [Google Scholar] [CrossRef]
- Zhou, X.-S.; Wei, Y.-M.; Liu, L.; Chen, Z.-B.; Tang, J.; Mao, B.-W. Extending the capability of stm break junction for conductance measurement of atomic-size nanowires: An electrochemical strategy. J. Am. Chem. Soc. 2008, 130, 13228–13230. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.-S.; Liang, J.-H.; Chen, Z.-B.; Mao, B.-W. An electrochemical jump-to-contact stm-break junction approach to construct single molecular junctions with different metallic electrodes. Electrochem. Commun. 2011, 13, 407–410. [Google Scholar] [CrossRef]
- Nitzan, A. Chemical Dynamics in Condensed Phases: Relaxation, Transfer and Reactions in Condensed Molecular Systems; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Cuevas, J.C.; Scheer, E. Molecular Electronics: An Introduction to Theory and Experiment, 2nd ed.; World Scientific: Singapore, 2017. [Google Scholar]
- Karthäuser, S. Control of molecule-based transport for future molecular devices. J. Phys. Condens. Matter 2011, 23, 013001. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Why gold is the noblest of all the metals. Nature 1995, 376, 238–240. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Theoretical surface science and catalysis-calculations and concepts. Adv. Catal. 2000, 45, 71–129. [Google Scholar]
- Zhao, Z.-J.; Liu, S.; Zha, S.; Cheng, D.; Studt, F.; Henkelman, G.; Gong, J. Theory-guided design of catalytic materials using scaling relationships and reactivity descriptors. Nat. Rev. Mater. 2019, 4, 792–804. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Abild-Pedersen, F.; Studt, F.; Bligaard, T. Density functional theory in surface chemistry and catalysis. Proc. Natl. Acad. Sci. USA 2011, 108, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Gonzalez, S.; Xie, Z.; Galangau, O.; Selvanathan, P.; Norel, L.; Van Dyck, C.; Costuas, K.; Frisbie, C.D.; Rigaut, S.; Cornil, J. Homo level pinning in molecular junctions: Joint theoretical and experimental evidence. J. Phys. Chem. Lett. 2018, 9, 2394–2403. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.-J.; Hsu, L.-Y.; Fu, M.-D.; Chuang, S.-T.; Tien, F.-W.; Chen, C.-h. Conductance of tailored molecular segments: A rudimentary assessment by Landauer formulation. J. Am. Chem. Soc. 2014, 136, 1832–1841. [Google Scholar] [CrossRef]
- Beebe, J.M.; Kim, B.; Gadzuk, J.W.; Frisbie, C.D.; Kushmerick, J.G. Transition from direct tunneling to field emission in metal-molecule-metal junctions. Phys. Rev. Lett. 2006, 97, 026801. [Google Scholar] [CrossRef]
- Araidai, M.; Tsukada, M. Theoretical calculations of electron transport in molecular junctions: Inflection behavior in Fowler-Nordheim plot and its origin. Phys. Rev. B 2010, 81, 235114. [Google Scholar] [CrossRef]
- Nose, D.; Dote, K.; Sato, T.; Yamamoto, M.; Ishii, H.; Noguchi, Y. Effects of interface electronic structures on transition voltage spectroscopy of alkanethiol molecular junctions. J. Phys. Chem. C 2015, 119, 12765–12771. [Google Scholar] [CrossRef]
- Xie, Z.; Bâldea, I.; Frisbie, C.D. Determination of energy-level alignment in molecular tunnel junctions by transport and spectroscopy: Self-consistency for the case of oligophenylene thiols and dithiols on Ag, Au, and Pt electrodes. J. Am. Chem. Soc. 2019, 141, 3670–3681. [Google Scholar] [CrossRef]
- Xie, Z.; Bâldea, I.; Frisbie, C.D. Energy level alignment in molecular tunnel junctions by transport and spectroscopy: Self-consistency for the case of alkyl thiols and dithiols on Ag, Au, and Pt electrodes. J. Am. Chem. Soc. 2019, 141, 18182–18192. [Google Scholar] [CrossRef]
- Yanson, A.I.; Bollinger, G.R.; van den Brom, H.E.; Agraït, N.; van Ruitenbeek, J.M. Formation and manipulation of a metallic wire of single gold atoms. Nature 1998, 395, 783. [Google Scholar] [CrossRef]
- Trouwborst, M.L.; Huisman, E.H.; Bakker, F.L.; van der Molen, S.J.; van Wees, B.J. Single atom adhesion in optimized gold nanojunctions. Phys. Rev. Lett. 2008, 100, 175502. [Google Scholar] [CrossRef] [PubMed]
- Lawson, B.; Zahl, P.; Hybertsen, M.S.; Kamenetska, M. Formation and evolution of metallocene single-molecule circuits with direct gold-π links. J. Am. Chem. Soc. 2022, 144, 6504–6515. [Google Scholar] [CrossRef] [PubMed]
- Hong, W.; Manrique, D.Z.; Moreno-García, P.; Gulcur, M.; Mishchenko, A.; Lambert, C.J.; Bryce, M.R.; Wandlowski, T. Single molecular conductance of tolanes: Experimental and theoretical study on the junction evolution dependent on the anchoring group. J. Am. Chem. Soc. 2011, 134, 2292–2304. [Google Scholar] [CrossRef]
- Meisner, J.S.; Ahn, S.; Aradhya, S.V.; Krikorian, M.; Parameswaran, R.; Steigerwald, M.; Venkataraman, L.; Nuckolls, C. Importance of direct metal−π coupling in electronic transport through conjugated single-molecule junctions. J. Am. Chem. Soc. 2012, 134, 20440–20445. [Google Scholar] [CrossRef] [PubMed]
- Kamenetska, M.; Koentopp, M.; Whalley, A.C.; Park, Y.S.; Steigerwald, M.L.; Nuckolls, C.; Hybertsen, M.S.; Venkataraman, L. Formation and evolution of single-molecule junctions. Phys. Rev. Lett. 2009, 102, 126803. [Google Scholar] [CrossRef] [PubMed]
- Makk, P.; Tomaszewski, D.; Martinek, J.; Balogh, Z.; Csonka, S.; Wawrzyniak, M.; Frei, M.; Venkataraman, L.; Halbritter, A. Correlation analysis of atomic and single-molecule junction conductance. ACS Nano 2012, 6, 3411–3423. [Google Scholar] [CrossRef]
- Xu, B.; Xiao, X.; Tao, N.J. Measurements of single-molecule electromechanical properties. J. Am. Chem. Soc. 2003, 125, 16164–16165. [Google Scholar] [CrossRef]
- Ko, C.-H.; Huang, M.-J.; Fu, M.-D.; Chen, C.-h. Superior contact for single-molecule conductance: Electronic coupling of thiolate and isothiocyanate on Pt, Pd, and Au. J. Am. Chem. Soc. 2010, 132, 756–764. [Google Scholar] [CrossRef]
- Frei, M.; Aradhya, S.V.; Hybertsen, M.S.; Venkataraman, L. Linker dependent bond rupture force measurements in single-molecule junctions. J. Am. Chem. Soc. 2012, 134, 4003–4006. [Google Scholar] [CrossRef]
- Lovat, G.; Choi, B.; Paley, D.W.; Steigerwald, M.L.; Venkataraman, L.; Roy, X. Room-temperature current blockade in atomically defined single-cluster junctions. Nat. Nanotechnol. 2017, 12, 1050–1054. [Google Scholar] [CrossRef]
- Aragonès, A.C.; Haworth, N.L.; Darwish, N.; Ciampi, S.; Bloomfield, N.J.; Wallace, G.G.; Diez-Perez, I.; Coote, M.L. Electrostatic catalysis of a Diels–Alder reaction. Nature 2016, 531, 88–91. [Google Scholar] [CrossRef] [PubMed]
- Gu, M.-W.; Lai, C.-T.; Ni, I.-C.; Wu, C.-I.; Chen, C.-h. Increased surface density of states at the fermi level for electron transport across single-molecule junctions. Angew. Chem. Int. Ed. 2023, 62, e202214963. [Google Scholar] [CrossRef]
- Kim, T.; Vázquez, H.; Hybertsen, M.S.; Venkataraman, L. Conductance of molecular junctions formed with silver electrodes. Nano Lett. 2013, 13, 3358–3364. [Google Scholar] [CrossRef] [PubMed]
- Frei, M.; Aradhya, S.V.; Koentopp, M.; Hybertsen, M.S.; Venkataraman, L. Mechanics and chemistry: Single molecule bond rupture forces correlate with molecular backbone structure. Nano Lett. 2011, 11, 1518–1523. [Google Scholar] [CrossRef] [PubMed]
- Gu, M.-W.; Peng, H.H.; Chen, I.-W.P.; Chen, C.-h. Tuning surface d bands with bimetallic electrodes to facilitate electron transport across molecular junctions. Nat. Mater. 2021, 20, 658–664. [Google Scholar] [CrossRef]
- Ahn, S.; Aradhya, S.V.; Klausen, R.S.; Capozzi, B.; Roy, X.; Steigerwald, M.L.; Nuckolls, C.; Venkataraman, L. Electronic transport and mechanical stability of carboxyl linked single-molecule junctions. Phys. Chem. Chem. Phys. 2012, 14, 13841–13845. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Zhou, X.-Y.; Sun, Y.-Y.; Han, D.; Zheng, J.-F.; Niu, Z.-J.; Zhou, X.-S. Conductance measurement of carboxylic acids binding to palladium nanoclusters by electrochemical jump-to-contact stm break junction. Electrochim. Acta 2014, 123, 205–210. [Google Scholar] [CrossRef]
- Li, J.-J.; Chen, Z.-B.; Wang, Y.-H.; Zhou, X.-S.; Xie, L.-Q.; Shi, Z.; Liu, J.-X.; Yan, J.-W.; Mao, B.-W. Single-molecule anisotropic magnetoresistance at room temperature: Influence of molecular structure. Electrochim. Acta 2021, 389, 138760. [Google Scholar] [CrossRef]
- Smit, R.H.M.; Untiedt, C.; Yanson, A.I.; van Ruitenbeek, J.M. Common origin for surface reconstruction and the formation of chains of metal atoms. Phys. Rev. Lett. 2001, 87, 266102. [Google Scholar] [CrossRef]
- Gorelsky, S.I. AOMix: Program for Molecular Orbital Analysis. Available online: https://www.sg-chem.net/aomix/ (accessed on 1 March 2023).
- Gorelsky, S.I.; Lever, A.B.P. Electronic structure and spectra of ruthenium diimine complexes by density functional theory and INDO/S. Comparison of the two methods. J. Organomet. Chem. 2001, 635, 187–196. [Google Scholar] [CrossRef]
- Aradhya, S.V.; Frei, M.; Halbritter, A.; Venkataraman, L. Correlating structure, conductance, and mechanics of silver atomic-scale contacts. ACS Nano 2013, 7, 3706–3712. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Su, T.A.; Camarasa-Gómez, M.; Hernangómez-Pérez, D.; Henn, S.E.; Pokorný, V.; Caniglia, C.D.; Inkpen, M.S.; Korytár, R.; Steigerwald, M.L.; et al. Silver makes better electrical contacts to thiol-terminated silanes than gold. Angew. Chem. Int. Ed. 2017, 56, 14145–14148. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.-L.; Chen, Z.-B.; Zhou, X.-Y.; Sun, Y.-Y.; Liang, J.-H.; Niu, Z.-J.; Zhou, X.-S.; Mao, B.-W. Single molecule conductance of carboxylic acids contacting Ag and Cu electrodes. J. Phys. Chem. C 2012, 116, 21699–21705. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Hong, Z.-W.; Sun, Y.-Y.; Li, D.-F.; Han, D.; Zheng, J.-F.; Niu, Z.-J.; Zhou, X.-S. Tunneling decay constant of alkanedicarboxylic acids: Different dependence on the metal electrodes between air and electrochemistry. J. Phys. Chem. C 2014, 118, 18756–18761. [Google Scholar] [CrossRef]
- Cheng, Z.-L.; Skouta, R.; Vazquez, H.; Widawsky, J.R.; Schneebeli, S.; Chen, W.; Hybertsen, M.S.; Breslow, R.; Venkataraman, L. In situ formation of highly conducting covalent Au-C contacts for single-molecule junctions. Nat. Nanotechnol. 2011, 6, 353–357. [Google Scholar] [CrossRef]
- Chen, W.; Widawsky, J.R.; Vázquez, H.; Schneebeli, S.T.; Hybertsen, M.S.; Breslow, R.; Venkataraman, L. Highly conducting π-conjugated molecular junctions covalently bonded to gold electrodes. J. Am. Chem. Soc. 2011, 133, 17160–17163. [Google Scholar] [CrossRef]
- Starr, R.L.; Fu, T.; Doud, E.A.; Stone, I.; Roy, X.; Venkataraman, L. Gold–carbon contacts from oxidative addition of aryl iodides. J. Am. Chem. Soc. 2020, 142, 7128–7133. [Google Scholar] [CrossRef]
- Li, S.; Yu, H.; Chen, X.; Gewirth, A.A.; Moore, J.S.; Schroeder, C.M. Covalent Ag–C bonding contacts from unprotected terminal acetylenes for molecular junctions. Nano Lett. 2020, 20, 5490–5495. [Google Scholar] [CrossRef]
- Rocha, A.R.; García-suárez, V.M.; Bailey, S.W.; Lambert, C.J.; Ferrer, J.; Sanvito, S. Towards molecular spintronics. Nat. Mater. 2005, 4, 335. [Google Scholar] [CrossRef]
- Quek, S.Y.; Kamenetska, M.; Steigerwald, M.L.; Choi, H.J.; Louie, S.G.; Hybertsen, M.S.; Neaton, J.B.; Venkataraman, L. Mechanically controlled binary conductance switching of a single-molecule junction. Nat. Nanotechnol. 2009, 4, 230–234. [Google Scholar] [CrossRef]
- Brooke, R.J.; Szumski, D.S.; Vezzoli, A.; Higgins, S.J.; Nichols, R.J.; Schwarzacher, W. Dual control of molecular conductance through pH and potential in single-molecule devices. Nano Lett. 2018, 18, 1317–1322. [Google Scholar] [CrossRef] [PubMed]
- Li, J.-J.; Bai, M.-L.; Chen, Z.-B.; Zhou, X.-S.; Shi, Z.; Zhang, M.; Ding, S.-Y.; Hou, S.-M.; Schwarzacher, W.; Nichols, R.J.; et al. Giant single-molecule anisotropic magnetoresistance at room temperature. J. Am. Chem. Soc. 2015, 137, 5923–5929. [Google Scholar] [CrossRef] [PubMed]
- LaShell, S.; McDougall, B.A.; Jensen, E. Spin splitting of an Au(111) surface state band observed with angle resolved photoelectron spectroscopy. Phys. Rev. Lett. 1996, 77, 3419–3422. [Google Scholar] [CrossRef] [PubMed]
- Nicolay, G.; Reinert, F.; Hüfner, S.; Blaha, P. Spin-orbit splitting of the L-gap surface state on Au(111) and Ag(111). Phys. Rev. B 2001, 65, 033407. [Google Scholar] [CrossRef]
- Friedrich, R. Spin–orbit interaction in the photoemission spectra of noble metal surface states. J. Phys. Condens. Matter 2003, 15, S693. [Google Scholar]
- Aragonès, A.C.; Medina, E.; Ferrer-Huerta, M.; Gimeno, N.; Teixidó, M.; Palma, J.L.; Tao, N.; Ugalde, J.M.; Giralt, E.; Díez-Pérez, I.; et al. Measuring the spin-polarization power of a single chiral molecule. Small 2017, 13, 1602519. [Google Scholar] [CrossRef]
- Aragonès, A.C.; Aravena, D.; Valverde-Muñoz, F.J.; Real, J.A.; Sanz, F.; Díez-Pérez, I.; Ruiz, E. Metal-controlled magnetoresistance at room temperature in single-molecule devices. J. Am. Chem. Soc. 2017, 139, 5768–5778. [Google Scholar] [CrossRef]
- Aragonès, A.C.; Martín-Rodríguez, A.; Aravena, D.; di Palma, G.; Qian, W.; Puigmartí-Luis, J.; Aliaga-Alcalde, N.; González-Campo, A.; Díez-Pérez, I.; Ruiz, E. Room-temperature spin-dependent transport in metalloporphyrin-based supramolecular wires. Angew. Chem. Int. Ed. 2021, 60, 25958–25965. [Google Scholar] [CrossRef]
- Herrero, E.; Buller, L.J.; Abruña, H.D. Underpotential deposition at single crystal surfaces of Au, Pt, Ag and other materials. Chem. Rev. 2001, 101, 1897–1930. [Google Scholar] [CrossRef]
- Prins, F.; Barreiro, A.; Ruitenberg, J.W.; Seldenthuis, J.S.; Aliaga-Alcalde, N.; Vandersypen, L.M.K.; van der Zant, H.S.J. Room-temperature gating of molecular junctions using few-layer graphene nanogap electrodes. Nano Lett. 2011, 11, 4607–4611. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L.; Tao, S.; Wang, C.; Zhao, C.; González, C.; Dappe, Y.J.; Nichols, R.J.; Yang, L. Graphene as a promising electrode for low-current attenuation in nonsymmetric molecular junctions. Nano Lett. 2016, 16, 6534–6540. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Zhang, Q.; Tao, S.; Zhao, C.; Zhao, C.; Su, W.; Dappe, Y.J.; Nichols, R.J.; Yang, L. Carbon-contacted single molecule electrical junctions. Phys. Chem. Chem. Phys. 2018, 20, 24553–24560. [Google Scholar] [CrossRef] [PubMed]
- Jia, C.; Migliore, A.; Xin, N.; Huang, S.; Wang, J.; Yang, Q.; Wang, S.; Chen, H.; Wang, D.; Feng, B.; et al. Covalently bonded single-molecule junctions with stable and reversible photoswitched conductivity. Science 2016, 352, 1443–1445. [Google Scholar] [CrossRef] [PubMed]

| Headgroups (X) | Electrode Materials | n | Junction Conductance (×10−3 G0) | G-Ratio (vs. GAu) a | EFMO (eV) a | Γ (meV) a | Rupture Force (nN) b | Mechanism | Refs. No. |
|---|---|---|---|---|---|---|---|---|---|
| −SH | Pt | 8 | 0.48 | 1.85 | --- | --- | --- | coupling | [50] |
| −SH | Au | 8 | 0.26 | 1 | −0.98 | 14.88 | 1.50 | --- | [49,50] |
| −SMe | Au | 6 | 0.19 | 1 | −0.91 | 12.9 | 0.42 (±0.22) | --- | [54] |
| −SMe | Au | 4 | 1.4 | 1 | --- | --- | 0.70 | --- | [51] |
| −NH2 | Ag | 4 | 0.26 c | 0.29 | --- | --- | ELA | [55] | |
| −NH2 | Au | 4 | 0.9 c | 1 | --- | --- | 0.69 | --- | [55,56] |
| −CO2H | Ag | 6 | 0.018 | 2 | −0.99 | 3.43 | 0.83 (±0.30) | ELA | [57] |
| −CO2H | Au | 6 | 0.009 | 1 | −0.96 | 2.73 | 0.60 (±0.30) | --- | [57,58] |
| −CO2H | Pd | 2 | 0.30 | 4.17 | --- | --- | --- | coupling | [59] |
| −CO2H | Fe | 2 | 0.0065 | 0.54 | --- | --- | --- | --- | [60] |
| −CO2H | Ag | 2 | 0.17 | 2.36 | --- | --- | --- | coupling | [27] |
| −CO2H | Cu | 2 | 0.23 | 3.25 | --- | --- | --- | coupling | [27] |
| −CO2H | Au | 2 | 0.072 | 1 | --- | --- | --- | --- | [27] |
| −CN | Pd | 6 | 0.12 | 1.09 | --- | --- | --- | coupling | [36] |
| −CN | Pt | 6 | 0.29 | 2.64 | --- | --- | --- | coupling | [36] |
| −CN | Au | 6 | 0.11 | 1 | 0.69 | 6.1 | 0.43 (±0.40) | --- | [36,54] |
| −NCS | Pd | 6 | 0.59 | 2.95 | --- | --- | --- | coupling | [50] |
| −NCS | Pt | 6 | 0.73 | 3.65 | --- | --- | --- | coupling | [50] |
| −NCS | Au | 6 | 0.20 | 1 | --- | --- | 0.69 | --- | [50] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, M.-W.; Chen, C.-h. Effects of Electrode Materials on Electron Transport for Single-Molecule Junctions. Int. J. Mol. Sci. 2023, 24, 7277. https://doi.org/10.3390/ijms24087277
Gu M-W, Chen C-h. Effects of Electrode Materials on Electron Transport for Single-Molecule Junctions. International Journal of Molecular Sciences. 2023; 24(8):7277. https://doi.org/10.3390/ijms24087277
Chicago/Turabian StyleGu, Mong-Wen, and Chun-hsien Chen. 2023. "Effects of Electrode Materials on Electron Transport for Single-Molecule Junctions" International Journal of Molecular Sciences 24, no. 8: 7277. https://doi.org/10.3390/ijms24087277
APA StyleGu, M.-W., & Chen, C.-h. (2023). Effects of Electrode Materials on Electron Transport for Single-Molecule Junctions. International Journal of Molecular Sciences, 24(8), 7277. https://doi.org/10.3390/ijms24087277





