General Capacitance Upper Limit and Its Manifestation for Aqueous Graphene Interfaces
Abstract
1. Introduction
2. Results and Discussion
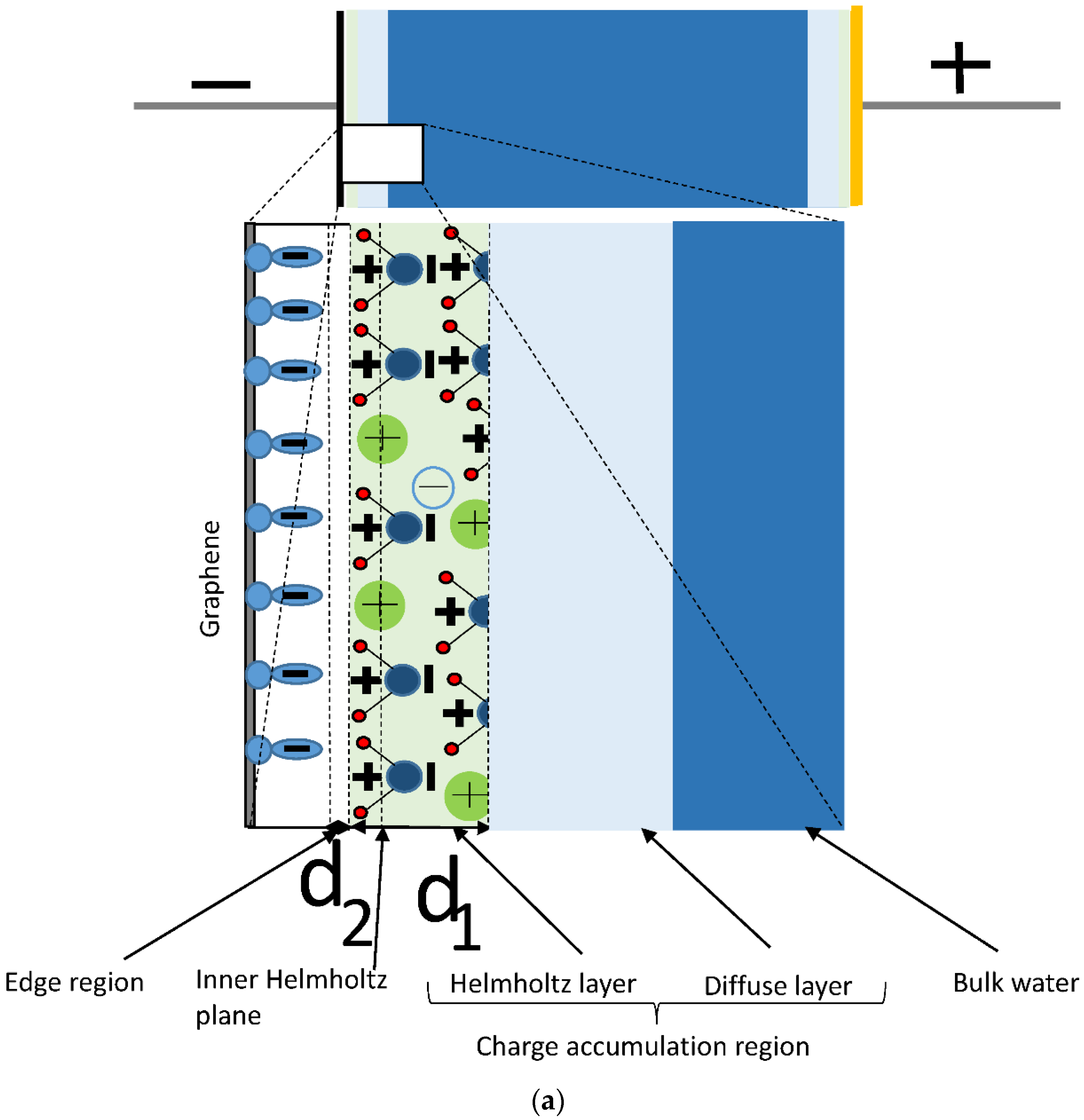
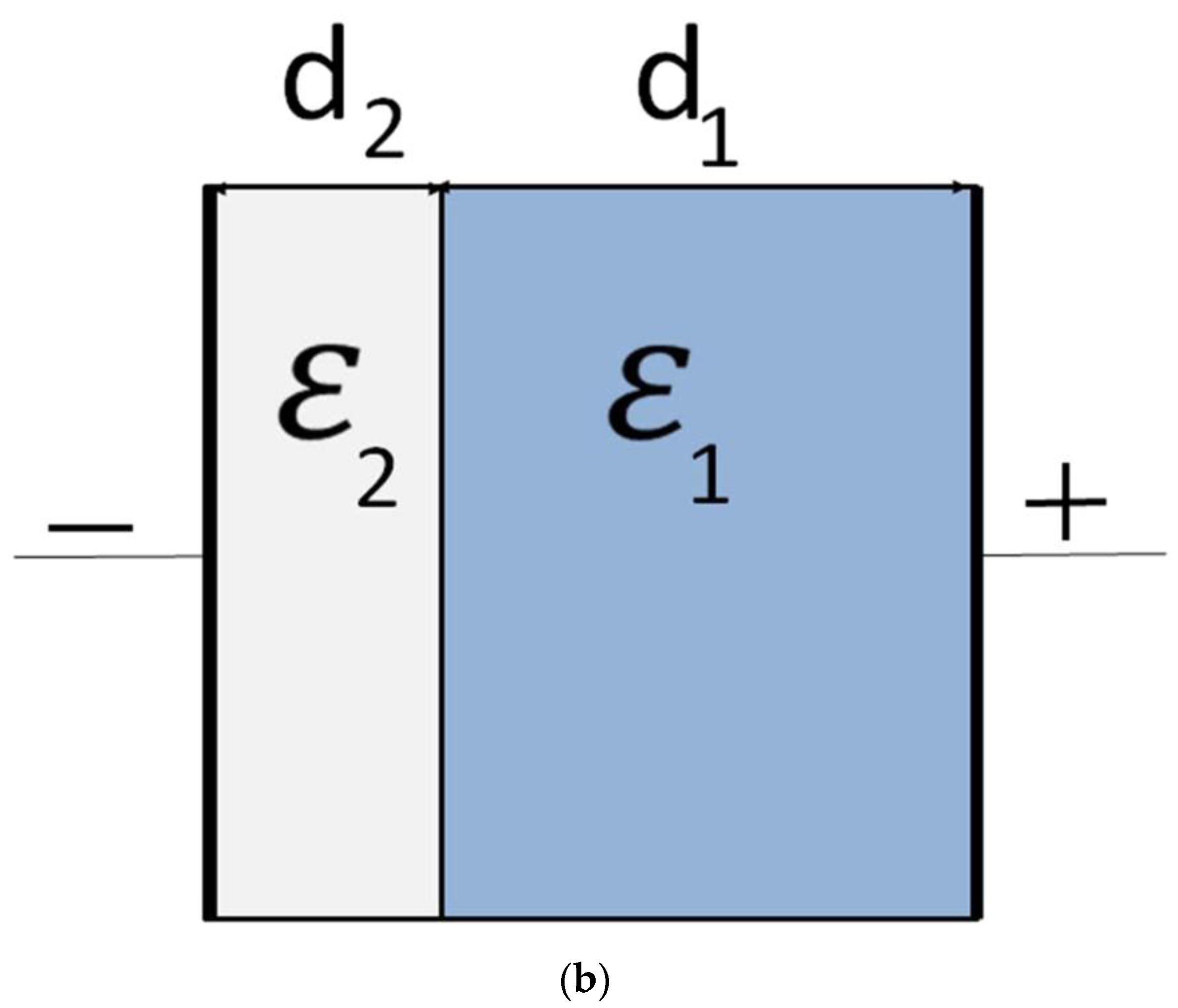
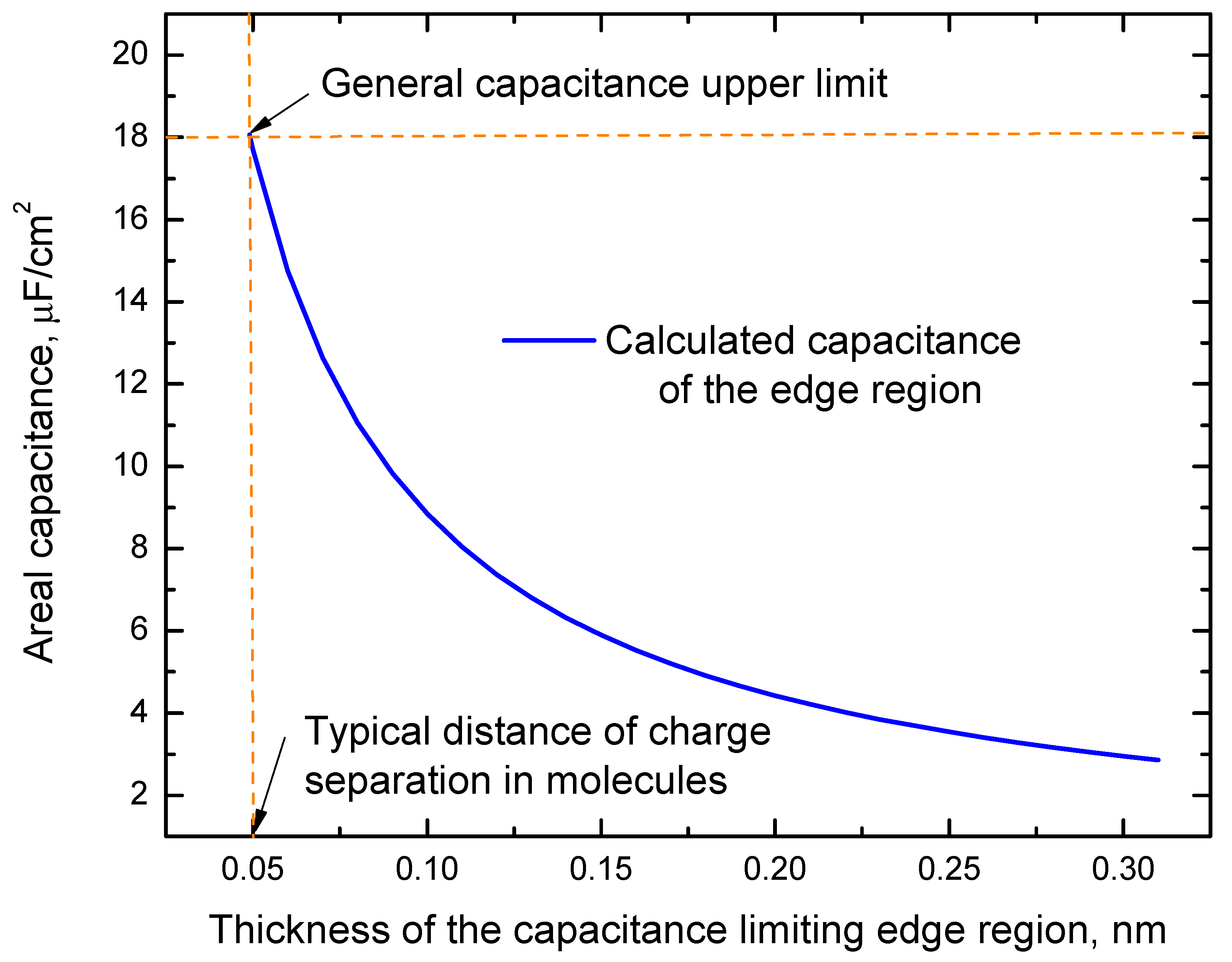
2.1. Model and Its Predictions
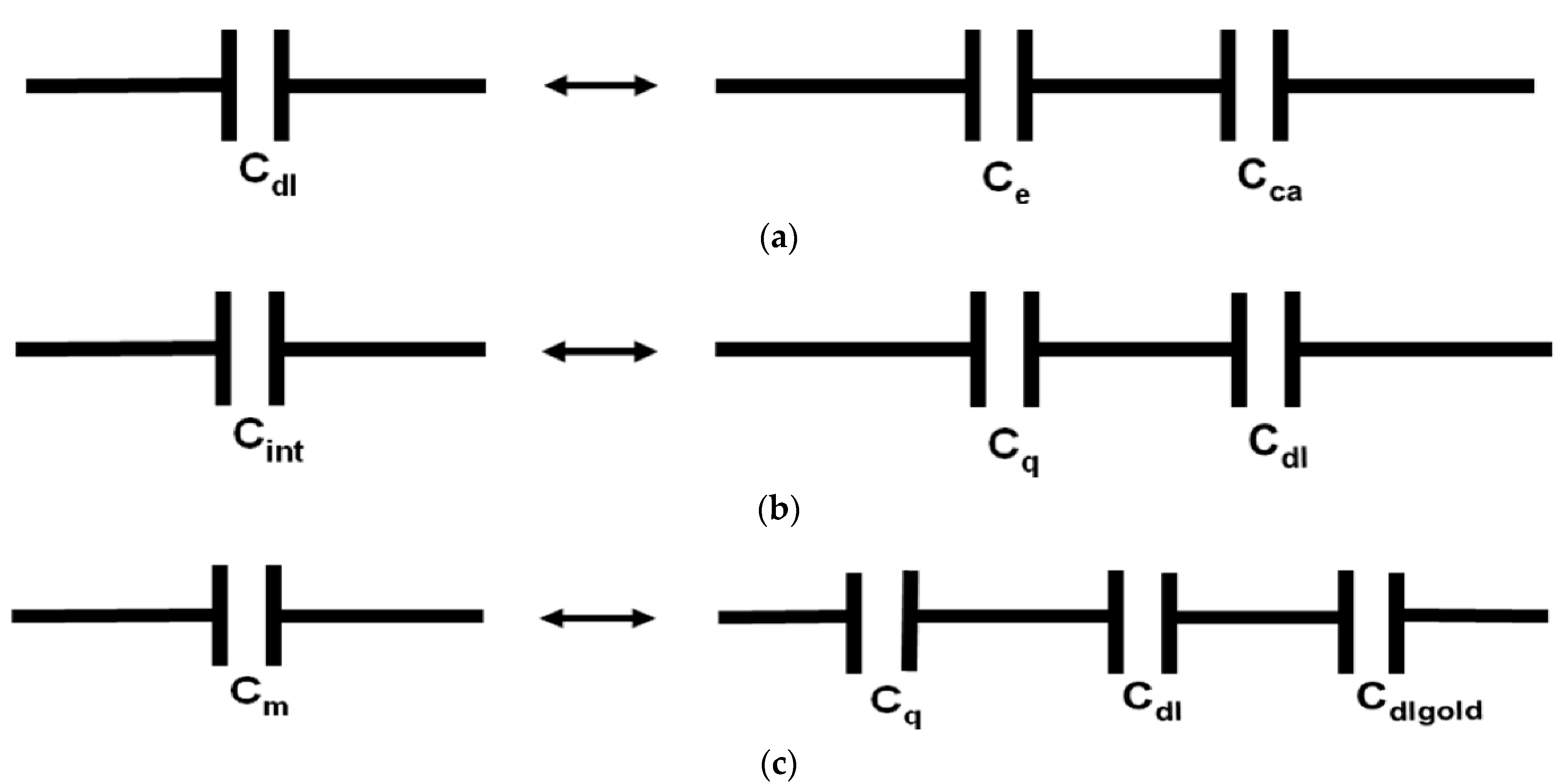
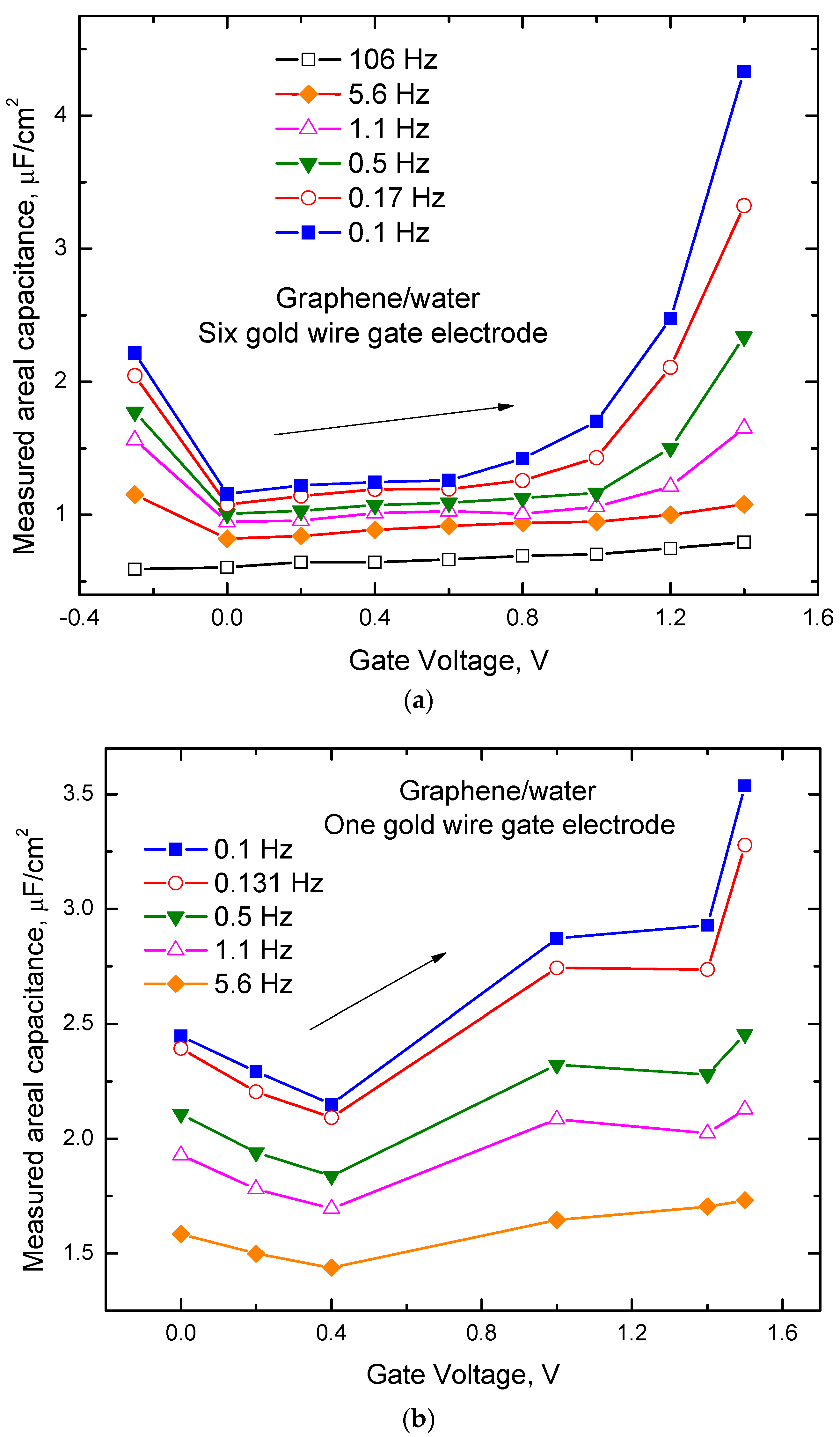
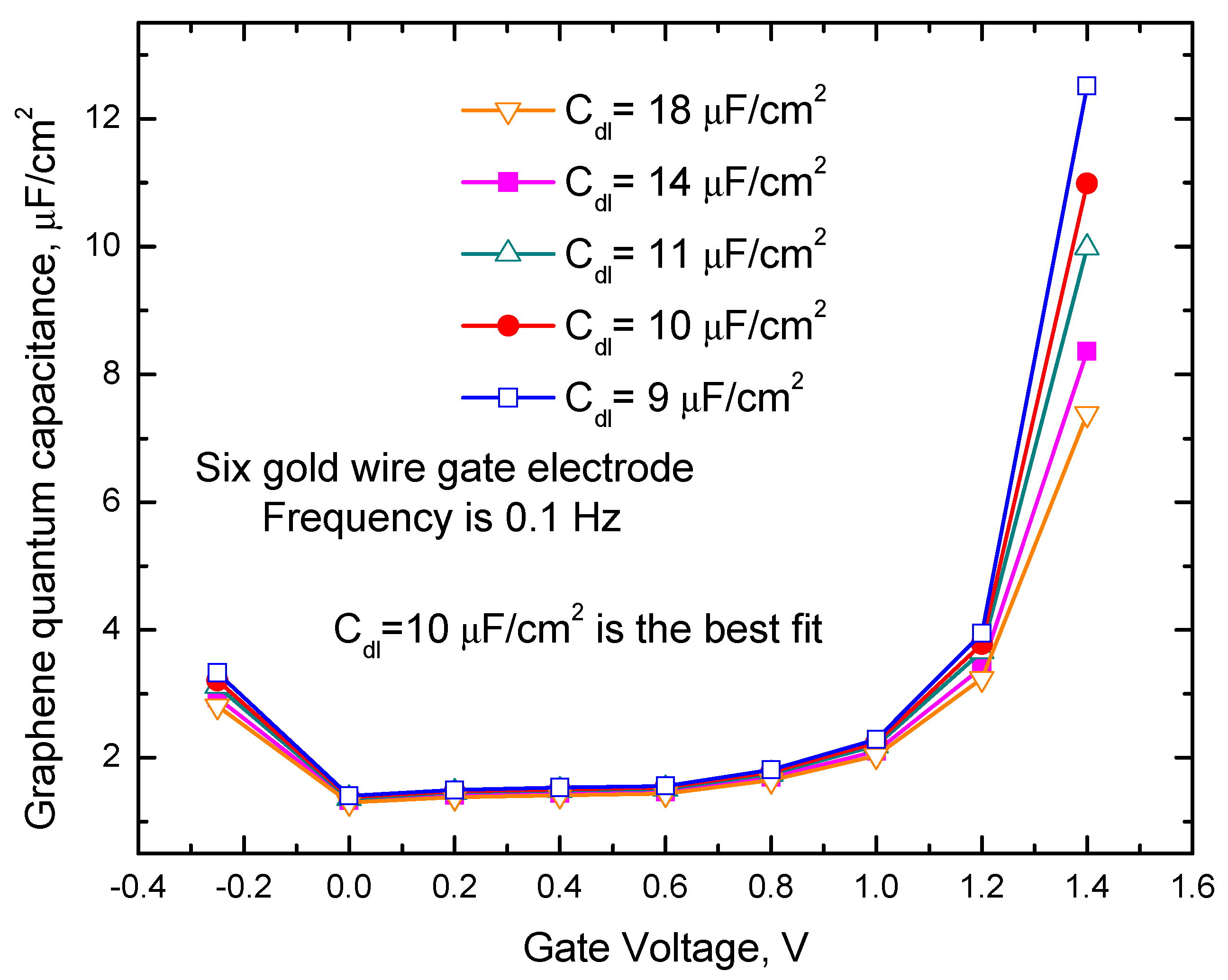
2.2. Impedance Spectroscopy Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ang, P.K.; Chen, W.; Wee, A.T.; Loh, K.P. Solution-gated epitaxial graphene as ph sensor. J. Am. Chem. Soc. 2008, 130, 14392–14393. [Google Scholar] [CrossRef] [PubMed]
- Sainz-Urruela, C.; Vera-López, S.; San Andrés, M.P.; Díez-Pascual, A.M. Graphene-based sensors for the detection of bioactive compounds: A Review. Int. J. Mol. Sci. 2021, 22, 3316. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Huang, Y.; Huang, K.; Lin, J.; Huang, P. Functional magnetic graphene composites for Biosensing. Int. J. Mol. Sci. 2020, 21, 390. [Google Scholar] [CrossRef]
- Thangamuthu, M.; Hsieh, K.Y.; Kumar, P.V.; Chen, G.-Y. Graphene- and graphene oxide-based nanocomposite platforms for electrochemical biosensing applications. Int. J. Mol. Sci. 2019, 20, 2975. [Google Scholar] [CrossRef]
- Butko, A.V.; Butko, V.Y.; Lebedev, S.P.; Lebedev, A.A.; Davydov, V.Y.; Eliseyev, I.A.; Kumzerov, Y.A. Detection of lysine molecular ions in solution gated field effect transistors based on unmodified graphene. J. Appl. Phys. 2020, 128, 215302. [Google Scholar] [CrossRef]
- Green, N.S.; Norton, M.L. Interactions of DNA with graphene and sensing applications of graphene field-effect transistor devices: A Review. Anal. Chim. Acta 2015, 853, 127–142. [Google Scholar] [CrossRef]
- Moradi, R.; Khalili, N.P.; Septiani, N.L.; Liu, C.; Doustkhah, E.; Yamauchi, Y.; Rotkin, S.V. Nanoarchitectonics for abused drug biosensors. Small 2021, 18, 2104847. [Google Scholar] [CrossRef]
- Kwak, Y.H.; Choi, D.S.; Kim, Y.N.; Kim, H.; Yoon, D.H.; Ahn, S.-S.; Yang, J.-W.; Yang, W.S.; Seo, S. Flexible glucose sensor using CVD-grown graphene-based field effect transistor. Biosens. Bioelectron. 2012, 37, 82–87. [Google Scholar] [CrossRef]
- Taniselass, S.; Arshad, M.K.M.; Gopinath, S.C.B. Graphene-based electrochemical biosensors for Monitoring Noncommunicable Disease Biomarkers. Biosens. Bioelectron. 2019, 130, 276–292. [Google Scholar] [CrossRef]
- Tehrani, Z.; Burwell, G.; Azmi, M.A.; Castaing, A.; Rickman, R.; Almarashi, J.; Dunstan, P.; Beigi, A.M.; Doak, S.H.; Guy, O.J. Generic epitaxial graphene biosensors for ultrasensitive detection of cancer risk biomarker. 2D Mater. 2014, 1, 025004. [Google Scholar] [CrossRef]
- Butko, A.V.; Butko, V.Y.; Lebedev, S.P.; Lebedev, A.A.; Davydov, V.Y.; Smirnov, A.N.; Eliseyev, I.A.; Dunaevskiy, M.S.; Kumzerov, Y.A. State memory in solution gated epitaxial graphene. Appl. Surf. Sci. 2018, 444, 36–41. [Google Scholar]
- Xia, J.; Chen, F.; Li, J.; Tao, N. Measurement of the quantum capacitance of graphene. Nat. Nanotechnol. 2009, 4, 505–509. [Google Scholar] [CrossRef] [PubMed]
- Sharma, P.; Mišković, Z.L. Capacitance of graphene in aqueous electrolytes: The effects of dielectric saturation of water and finite size of ions. Phys. Rev. B 2014, 90, 125415. [Google Scholar] [CrossRef]
- Dankerl, M.; Hauf, M.V.; Lippert, A.; Hess, L.H.; Birner, S.; Sharp, I.D.; Mahmood, A.; Mallet, P.; Veuillen, J.-Y.; Stutzmann, M.; et al. Graphene solution-gated field-effect transistor array for sensing applications. Adv. Funct. Mater. 2010, 20, 3117–3124. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Z.-B.; Ma, L.; Ahlberg, P.; Gao, X.; Qiu, Z.; Wu, D.; Ren, W.; Cheng, H.-M.; Zhang, S.-L. A graphene field-effect capacitor sensor in electrolyte. Appl. Phys. Lett. 2012, 101, 154106. [Google Scholar] [CrossRef]
- Heller, I.; Chatoor, S.; Männik, J.; Zevenbergen, M.A.; Dekker, C.; Lemay, S.G. Influence of electrolyte composition on liquid-gated carbon nanotube and Graphene Transistors. J. Am. Chem. Soc. 2010, 132, 17149–17156. [Google Scholar] [CrossRef]
- Yan, F.; Zhang, M.; Li, J. Solution-gated graphene transistors for chemical and biological sensors. Adv. Healthc. Mater. 2013, 3, 313–331. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Guo, H.; Jin, Y.; Jin, Q.; Zhao, J. Electrochemistry investigation on the graphene/electrolyte interface. Electroanalysis 2015, 27, 2760–2765. [Google Scholar] [CrossRef]
- Conway, B.E. Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications; Kluwer Academic Publisher: New York, NY, USA, 1999; pp. 105–181. [Google Scholar]
- Srinivasan, S. Fuel Cells: From Fundamentals to Applications; Springer Science & Business Media: New York, NY, USA, 2006; pp. 27–37. [Google Scholar]
- Brüesch, P.; Christen, T. The electric double layer at a metal electrode in pure water. J. Appl. Phys. 2004, 95, 2846–2856. [Google Scholar] [CrossRef]
- Hess, L.H.; Seifert, M.; Garrido, J.A. Graphene transistors for Bioelectronics. Proc. IEEE 2013, 101, 1780–1792. [Google Scholar] [CrossRef]
- Chiang, K.-Y.; Seki, T.; Yu, C.-C.; Ohto, T.; Hunger, J.; Bonn, M.; Nagata, Y. The dielectric function profile across the water interface through surface-specific vibrational spectroscopy and simulations. Proc. Natl. Acad. Sci. USA 2022, 119, e2204156119. [Google Scholar] [CrossRef]
- Olivieri, J.-F.; Hynes, J.T.; Laage, D. Confined water’s dielectric constant reduction is due to the surrounding low dielectric media and not to interfacial molecular ordering. J. Phys. Chem. Lett. 2021, 12, 4319–4326. [Google Scholar] [CrossRef]
- Bonthuis, D.J.; Gekle, S.; Netz, R.R. Dielectric profile of interfacial water and its effect on double-layer capacitance. Phys. Rev. Lett. 2011, 107, 166102. [Google Scholar] [CrossRef]
- Stoller, M.D.; Park, S.; Zhu, Y.; An, J.; Ruoff, R.S. Graphene-based ultracapacitors. Nano Lett. 2008, 8, 3498–3502. [Google Scholar] [CrossRef] [PubMed]
- Schalenbach, M.; Durmus, Y.E.; Tempel, H.; Kungl, H.; Eichel, R.-A. Double layer capacitances analysed with impedance spectroscopy and cyclic voltammetry: Validity and limits of the constant phase element parameterization. Phys. Chem. Chem. Phys. 2021, 23, 21097–21105. [Google Scholar] [CrossRef] [PubMed]
- Zeng, K.; Zhang, D. Recent progress in alkaline water electrolysis for hydrogen production and applications. Prog. Energy Combust. Sci. 2010, 36, 307–326. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butko, A.V.; Butko, V.Y.; Kumzerov, Y.A. General Capacitance Upper Limit and Its Manifestation for Aqueous Graphene Interfaces. Int. J. Mol. Sci. 2023, 24, 10861. https://doi.org/10.3390/ijms241310861
Butko AV, Butko VY, Kumzerov YA. General Capacitance Upper Limit and Its Manifestation for Aqueous Graphene Interfaces. International Journal of Molecular Sciences. 2023; 24(13):10861. https://doi.org/10.3390/ijms241310861
Chicago/Turabian StyleButko, Alexey V., Vladimir Y. Butko, and Yurii A. Kumzerov. 2023. "General Capacitance Upper Limit and Its Manifestation for Aqueous Graphene Interfaces" International Journal of Molecular Sciences 24, no. 13: 10861. https://doi.org/10.3390/ijms241310861
APA StyleButko, A. V., Butko, V. Y., & Kumzerov, Y. A. (2023). General Capacitance Upper Limit and Its Manifestation for Aqueous Graphene Interfaces. International Journal of Molecular Sciences, 24(13), 10861. https://doi.org/10.3390/ijms241310861






