Abstract
A new 1D-coordination polymer [Co(Piv)2(NH2(CH2)6NH2)]n (1, Piv is Me3CCO2− anion) was obtained, the mononuclear fragments {Co(O2CR)2} within which are linked by μ-bridged molecules of hexamethylenediamine (NH2(CH2)6NH2). For this compound, two different monoclinic C2/c (α-1) and P2/n (β-1) phases were found at room temperature by single-crystal X-ray diffraction analysis, with a similar structure of chains and their packages in unit cells. The low-temperature phase (γ-1) of crystal 1 at 150 K corresponds to the triclinic space group P-1. As the temperature decreases, the structural phase transition (SPT) in the α-1 and β-1 crystals is accompanied by an increase in the crystal packing density caused by the rearrangements of both H-bonds and the nearest ligand environment of the cobalt atom (“octahedral CoN2O4 around the metal center at room temperature” → “pseudo-tetrahedral CoN2O2 at 150 K”). The SPT was confirmed by DSC in the temperature range 210–150 K; when heated above 220 K, anomalies in the behavior of the heat flow are observed, which may be associated with the reversibility of SPT; endo effects are observed up to 300 K. The SPT starts below 200 K. At 100 K, a mixture of phases was found in sample 1: 27% α-1 phase, 61% γ-1 phase. In addition, at 100 K, 12% of the new δ-1 phase was detected, which was identified from the diffraction pattern at 260 K upon subsequent heating: the a,b,c-parameters and unit cell volume are close to the structure parameters of γ-1, and the values of the α,β,γ-angles are significantly different. Further heating leads to a phase transition from δ-1 to α-1, which both coexist at room temperature. According to the DC magnetometry data, during cooling and heating, the χMT(T) curves for 1 form a hysteresis loop with ~110 K, in which the difference in the χMT values reaches 9%. Ab initio calculations of the electronic structure of cobalt(II) in α-1 and γ-1 have been performed. Based on the EPR data at 10 K and the ab initio calculations, the behavior of the χMT(T) curve for 1 was simulated in the temperature range of 2–150 K. It was found that 1 exhibits slow magnetic relaxation in a field of 1000 Oe.
1. Introduction
Materials based on molecular complexes, for which the bistability of the physical properties is realized, attract interest from a fundamental and practical point of view, as these properties can be used in the development of smart materials for storage, the processing and transmitting of data, as well as in sensors, electronic components, etc. [1,2,3]. Particular attention has been given to systems in which magnetic effects are realized, associated with changes in the spin state (spin crossover phenomenon, charge transfer induced spin transition, super-exchange), the presence of residual magnetization, magnetization hysteresis, slow magnetic relaxation, etc. [4,5,6,7,8,9,10]. Magnetic effects in crystals of complexes are due to the electronic structure of the metal ion, the coordination environment and the nature of the ligands, packing effects, and intra- and inter-molecular interactions.
The design of molecular complexes with 3d metal ions in the 3dn (n = 4–7) configuration in combination with high-field ligands leads to compounds exhibiting spin-spin transitions between low spin (LS) and high spin (HS) states [11]. Often, valence tautomerism is observed for paramagnetic metal complexes with redox-active ligands [12]. As for molecular magnets, the key method is the control of the geometric parameters of the coordination environment of the metal centers in 4f and 3d metal complexes with orbital angular momentum. This approach should certainly be considered during the chemical assembly of single molecule (SMMs) and single ion (SIMs) magnets [13,14,15].
In addition, intermolecular interactions in crystals play a special role in determining a variety of the physicochemical characteristics of compounds, in particular, magnetism. For example, modulation of the spin state can be caused by co-crystallization involving halogen bonds [16,17], the appearance of interligand π-stacking [18,19], as well as the presence of hydrogen bonds between the ligands [20,21]. In some cases, these spin transitions are accompanied by structural phase transitions (SPTs), which are generally reversible, and are accompanied by a thermal hysteresis loop.
SPTs can occur both with minor changes in the coordination sphere of the metal ion and with the breaking of the M-L bond between the metal atom and the donor ligand atom. Using the example of cobalt(II) complexes with orbital angular momentum, it was shown that slight distortions of the coordination sphere of the metal atom are accompanied by changes in the magnetic behavior (the difference in χMT values by ~3.5% in the temperature range 240–228 K with a hysteresis loop >10 K) [22]. However, a change in the geometry of the polyhedron as a result of breaking the M–L bond can lead to an increase in the energy gap between the excited and ground states, due to which χMT forms a hysteresis loop of 14 K and the difference in χMT in the range of 135–90 K is ~10.5% [23].
This paper describes a method for the synthesis of a new 1D polymer [Co(Piv)2(NH2(CH2)6NH2)]n (1), in which the mononuclear fragments {Co(O2CR)2} are linked by μ-bridged molecules of hexamethylenediamine (NH2(CH2)6NH2). For 1, possible crystal forms were studied at different temperatures. The magnetic behavior of polymer 1 was studied and it was shown that a decrease in temperature leads to SPT due to changes in the intra- and inter-molecular H-bonds and in the coordination number of the metal atom, as a result of which the energy of the singly occupied d-orbital of cobalt(II) decreases.
2. Results and Discussion
2.1. Synthesis and Characterization
The interaction of equimolar amounts of [Co(Piv)2]n and hexamethylenediamine (NH2(CH2)6NH2)) in dry acetonitrile in an inert atmosphere led to the formation of violet crystals with a quantitative yield of the product with composition [Co(Piv)2(NH2(CH2)6NH2)]n (1).
The obtained IR-spectra of 1 (Figure S1) containing stretching vibrations at 3316, 3234, 3160 cm−1 (ν(NH)), 2975 cm−1 (νas(CH3/CH2), 2925 cm−1 (νas(CH3/CH2), 2860 cm−1 (νs(CH3/CH2), 1580 cm−1 (νas(COO)), 1540 (νas(COO)), 1470 cm−1 with shoulder at 1460 cm−1 (σas(CH3) and/or σ(CH2)), 1410 cm−1 (νs(COO)), 1360 cm−1 (σs(CH3) and σ(C(CH3)3)), 1145 cm−1 (σ(C(CH3)3)), 1083 cm−1 (C–N stretching frequency of primary amines), 807 and 792 cm−1 (NH2 bending frequencies of primary amines) and 725 cm−1 (σ(CH2)) show the vibrations of aliphatic amine and trimethylacetate ligands [24,25,26]. We also compared the IR spectra of the solid sample isolated during the synthesis with the spectra of this sample at room temperature after one-month exposure to air (Figure S1) and found no significant changes. Thus, we can conclude that compound 1 is resistant to moisture and atmospheric oxygen.
2.2. Diffraction and DSC Studies of Polycrystals and Single Crystals
It turned out that the isolated crystals 1 are not crystallographically homogeneous at different temperatures. For crystals of this compound, three identified forms were found: two monoclinic (C2/c, α-1) and (P2/n, β-1) at room temperature (selected from a set of crystals obtained in one synthesis) and triclinic (P-1, γ-1) at 150 K (Table 1). Separately, it should be noted that the cooling of the α-1 and β-1 crystals at a rate of 5 K/min leads to their destruction; therefore, cooling was carried out at a rate of ~2 K/min, which made it possible to establish the structure of the γ-1 phase, which is the same for both initial monoclinic forms at a low temperature.

Table 1.
The main crystallography data and refinement details for structures α-1, β-1, γ-1 and δ-1.
The DSC data in the temperature range 273–140 K (cooling process) for 1 showed two anomalies (exo-effects), below 250 and 205 K. The second one takes place in the temperature range 205–150 K. During heating, the anomalies with endo-effects start above 225 K and continue up to 300 K (Figure 1). It can be assumed that the observed structural changes (see below) from α-1 to γ-1 begin below 205 K (exo-effect in the region of 205–150 K), and the reverse phase transition(s) is(are) shifted to the region above 225 K. To attribute the anomalies observed in the DSC, variable-temperature powder X-ray diffraction studies (VT-PXRD) were carried out on a polycrystalline sample.
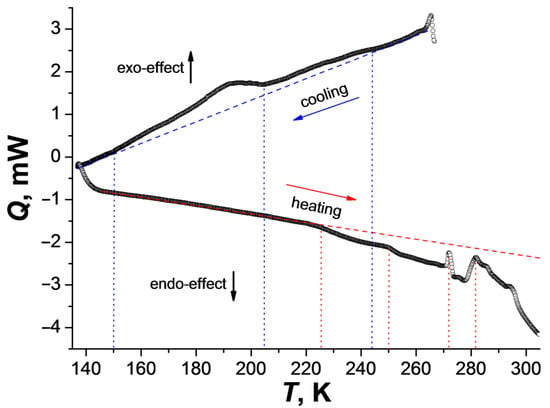
Figure 1.
Changes in the heat flux during cooling (270–135 K) and heating (135–300 K) of complex 1 (temperature rate is 10 K/min; dotted lines correspond to the deviations of the curves from the baseline (dashed lines) and the beginning of the anomaly).
The simulation of the powder diffraction pattern taken at room temperature showed that all of the observed peaks correspond to the structure with the space group C2/c (α-1 phase) (Figure S2), while the description of the experimental data, only by the second structural model with the P2/n group (β-1 phase), is markedly worse (Figure S3). Based on this, we can conclude that the crystalline sample obtained in the synthesis is predominantly a rather pure α-1 phase; therefore, in order to understand the properties of sample 1, we further focused on the prevailing presence of the α-1 phase. Compound 1 is stable at RT and maintains its crystallinity for a long time (more than 3 months).
VT-PXRD for 1 was applied in the temperature ranges 300–100 K (cooling) and 100–300 K (heating) (Figure 2 and Figure S4). When the sample is cooled with a step of 40 K, the XRD patterns change below 200 K. In this case, the peaks related to the γ-1 phase appear; however, in addition to them, a number of peaks of the new δ-1 phase are observed on the diffraction patterns. The combination of the data sets shows that the concentration of γ-1 increases with the decrease in temperature (35%, 58%, 61% at 180, 140 and 100 K, respectively; Figure 2, Figures S4 and S5; Table 2), the content of the initial phase α-1 decreases (54%, 28%, 27% at 180, 140 and 100 K, respectively; Figure 2, Figures S4 and S5; Table 2), and the intensity of the δ-1 peaks does not change significantly with further cooling (the content of δ-1 is in the range of 11–14%). When heated above 180 K, the intensity of the peaks of the δ-1 phase increases with the simultaneous disappearance of the γ-1 peaks. The unit cell parameters of the δ-1 phase were determined from the XRD data at 260 K (Figure 2 and Figure S6). Despite the close values of the a,b,c-parameters and the unit cell volumes of the γ-1 and δ-1 phases, they differ in α,β,γ-angles, which indicates the uniqueness of the δ-1 phase (Table 1). The maximum amount of δ-1 was recorded at 220–260 K (77% δ-1, 23% α-1). Subsequent heating to 300 K resulted in the formation of α-1 with δ-1 impurity (19% δ-1, 81% α-1; Figure 2 and Figure S7). Presumably, the δ-1 → α-1 transition is accompanied by endo-effects on the DSC curve above 270 K (Figure 1, heating).
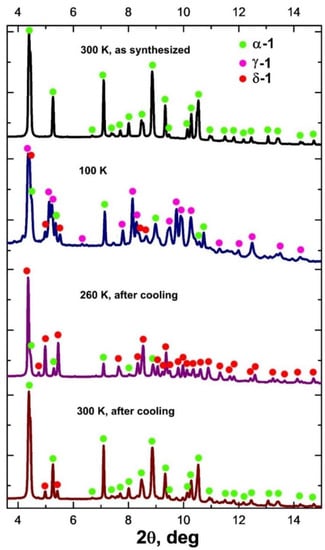
Figure 2.
Diffractograms of 1 at 300 K (as synthesized; at the top), at 100 K (second from top), at 260 K after cooling at 100 K (second from bottom), and at 300 K after cooling to 100 K (at the bottom) (λ = 0.74 Å).

Table 2.
The content of phases in sample 1 determined by the Rietveld method at different temperatures during cooling (300–100 K) and heating (100–300 K).
It was shown that the cooling and holding of sample 1 at temperatures below the onset of the phase transition (77 and ~180 K), followed by heating to RT, leads to the formation of a mixture of α-1 and δ-1 phases in the ratio δ-1:α-1 = 66:34 at 77 K and δ-1:α-1 = 43:57 at 180 K (Figures S8 and S9). The dependence of the δ-1 concentration on the cooling temperature suggests that this phase is formed as a result of the SPT of the γ-1 phase. Thus, it is likely that the δ-1 phase is an SPT intermediate (heating) of γ-1 into α-1.
It was subsequently discovered that crystals 1 (α-1 and β-1 phases) contain molecules of a coordination linear polymer in which the hexamethylenediamine bridges link the cobalt atoms, each of which is linked to two carboxylic acid ligands (Figure 3a and Figure S10). It is important to note that, in these phases, the Co(II) atom has an octahedral ligand environment (CoN2O4 chromophore; α-1 structure contains two independent Co atoms with a close environment; Table S1). The Co–O distances with the chelate carboxylate group (in α-1 (Co–O 2.085(4)‒2.260(4) Å) and β-1 (Co‒O 2.072(17)‒2.278(11) Å) differ somewhat from each other in value (~0.2 Å), which is often observed in cobalt(II) carboxylate complexes (see for example [27,28,29,30,31]). As the temperature decreases (150 K), the octahedral environment of the metal center in the γ-1 structure rearranges into a distorted trigonal-bipyramidal environment (CoN2O3 chromophore, Figure 3b, Table S1) as a result of the formal breaking of the Co‒O bond between the metal ion and the oxygen atom of one of the chelate pivalate ligands, due to the rotation of the chelate carboxyl group (Co…O 2.622 Å). However, the process does not stop there: in the low-temperature structure γ-1, a noticeable elongation of the Co-O bond from the second chelate carboxyl group (Co…O 2.369 Å) is observed, which allows us to interpret the environment (certainly with a certain degree of stipulation) of the Co(II) metal centers as distorted tetrahedral (CoN2O2 chromophore, Table S1). At the same time, the Co-N bond lengths change insignificantly (2.098(4) and 2.099(4) Å for α-1, 2.087(6) Å for β-1, 2.029(11) and 2.088(10) Å for γ-1).
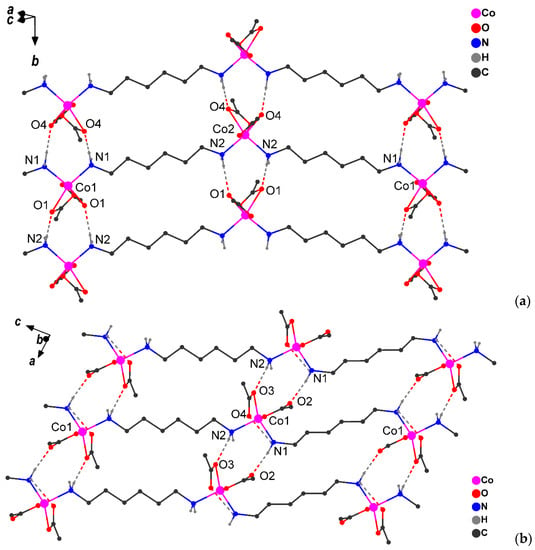
Figure 3.
Fragments of crystal packing in α-1 (a) and γ-1 (b) (H atoms bonded to carbons atoms and CH3-groups are omitted, H-bonds are shown by dotted line).
The geometry of the chains in the crystals of the high-temperature α-1 and β-1 phases corresponds to a zigzag pattern (the angle between cobalt atoms is 148.2° for both structures), while in the low-temperature γ-1 phase the chain is close to straight (the corresponding angle is 169.8°). This is due to a change in the metal polyhedron and a change in the conformation of the bridging ligand NH2(CH2)6NH2. In α-1 and β-1, the metal atom lies on the crystallographic axis 2, the substituent chains are symmetrical, the Co-N-C-C torsion angle is 178.8(3)° (for Co1) and 170.3(3)° (for Co2) for α-1 and 174.2(5)° for β-1. As a result, the structure of the polymer chains in the α-1 crystal differs slightly from that in β-1 (Figure 4a). As the temperature decreases, the symmetry of the crystal decreases, the chain conformations on the opposite sides of the metal also change and become different, and the Co1-N-C-C angles are 170.2(9) and 77.6(3)° in the high-temperature and low-temperature phases, respectively. As a consequence, the Co…Co distances within the chain change; at room temperature, they are 12.432(2) Å in α-1 and 12.431(2) Å in β-1, but 12.590(6) Å and 11.002(6) Å in γ-1. As a result, the geometry of the polymer chain at different temperatures differs significantly (Figure 4b).
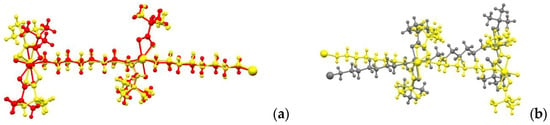
Figure 4.
Geometry overlay of polymer chains 1 at different temperatures ((a)—α-1 (yellow) vs. β-1 (red); (b)—α-1 (yellow) vs. γ-1 (grey)).
The packing of the chains in all cases represents parallel infinite layers formed by a NH…O type of hydrogen bonds (Table 3). In the crystals at RT and 150 K, each pair of coordinated amino groups form two H-bonds with the oxygen atoms of the carboxylate groups of the adjacent chain, forming supramolecular layers (Figure 3). Additionally, in γ-1, the oxygen atom of the carboxylate group forms an intramolecular H-bond with the hydrogen atom of the NH2 group of the bridging ligand (Figure 3b). The comparison of the intermolecular H-bonds upon transition from α-1 to γ-1 revealed a shortening of the N1…O interatomic distance by 0.03 Å and an elongation of N2…O by 0.07 Å (Figure 3, Table 3). Structural changes in the layer are accompanied by a decrease in the minimum Co…Co distance (by 0.1–0.2 Å) between atoms of neighboring chains: 5.710(2) Å in α-1, 5.622(2) Å in β-1, and 5.510(6) Å in γ-1.

Table 3.
Parameters of H-bonds in crystals of α-1, β-1 and γ-1.
The supramolecular layers are linked to each other by van der Waal’s interactions (Figures S11–S13). The distances between the planes drawn through the metal atoms in the layer are close and amount to 8.041(2) Å in α-1, 8.050(2) Å in β-1, and 8.102(6) Å in γ-1. Thus, the changes associated with an increase in the density of the crystals upon the decrease in the temperature are determined by the intralayer compression of the chains.
2.3. Spectral Properties
The IR spectra of the samples maintained at 77 and ~180 K are identical (Figure S1).
Changes are observed in the diffuse reflectance spectra at RT (Figure S14). Sample 1 has a broad band (400–800 nm) with a maximum at 534 nm and shoulders at 480, 500, and 680 nm. For sample 177K (sample 1 after exposure at 77 K for 5 h), a shift of the maximum of a wide band (538 nm) is observed, with shoulders at 480, 500, 575, and 690 nm. The spectral bands correspond to d-d transitions for a high-spin cobalt(II) ion surrounded by high-field ligands [32,33,34], which confirms the splitting of the characteristic band at ~500 nm. The differences in the spectra during the transition from 1 to 177K indicate changes in the electronic structure of the cobalt(II), which may be associated with the structural changes described above; namely, the formation of a mixture of δ-1 and α-1 phases, in which the ligand environment of the cobalt(II) ions changes along with the formal composition retention.
2.4. EPR Spectroscopy, DC Magnetic Data and Theoretical Calculations
According to the X-band EPR spectroscopy at a temperature of 10 K, a signal was registered for 1 (Figure S15), which was simulated using the software package EasySpin [35]. The complex is characterized by typical values of the spin Hamiltonian of the high-spin CoII ion. The spectrum simulation in the effective spin model S = 1/2 made it possible to determine the parameters for the Kramer’s doublet: gx = gy = 4.6, gz = 2.11, linewidth 30 mT. For the effective spin model S = 3/2, the following parameters of the spin Hamiltonian were obtained as a result of the best agreement between the theoretical model and the experimental data: gx = gy = 2.29, gz = 2.18 (giso = 2.25), linewidth 30 mT. The estimated value of the magnetic anisotropy parameter D of the cobalt(II) ion used in the simulation was ~23 cm−1 (the assumed value is much larger than the microwave quantum and cannot be determined from the X-band EPR spectrum). The parameter D has a positive sign, i.e., The Kramer’s doublet ±1/2 is the main one. The rhombicity parameter E of the splitting tensor in the zero magnetic field was set to zero.
The magnetic properties of 1 were studied in both static and dynamic modes. Measurements of the static magnetic susceptibility χ were carried out in a magnetic field with strength H = 5 kOe. The value of χMT at a temperature of 300 K is 2.88 cm3K/mol (Figure 5a), which significantly exceeds the theoretical pure spin value for the Co2+ ion (4F9/2, d7, C = 1.90 cm3K/mol). It can be expected that such an overestimation of the χMT values is due to the nonzero orbital contribution. As the temperature drops below 190 K, a noticeable change in the value of χMT (Figure 5a), from 2.84 cm3K/mol (at 192 K) to 2.61 cm3K/mol (at 162 K), is observed, which, as has already been shown by the single crystal and powder X-ray diffraction studies and calculations, is due to a change in the packing of the polymer chains upon the change in temperature with a corresponding change in the geometric parameters (bonds and angles) in the coordination sphere around the cobalt ions, as well as in the g-tensor and the zero-field tensor (parameters D and E). According to the DC magnetometry data, the value of χMT for 1 sharply decreases by 8% in the range of 200–150 K, which corresponds to the SPT and to the change in the magnetic behavior of the cobalt(II) ions upon the rearrangement of the coordination environment of the metal atom.
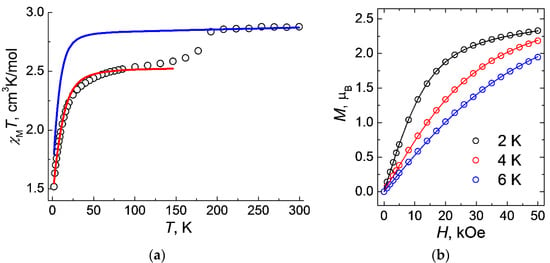
Figure 5.
Temperature dependences of χMT for 1 measured at HDC = 0.5 T (a) and magnetization vs. field measured at T = 2, 4, and 6 K (b). Theoretical curves (solid lines) are calculated at Hamiltonian (Equation (2); red line in Figure 5a) and Griffith Hamiltonian (Equation (1); blue line in Figure 5a)) and with the optimal set of parameters (see text).
χMT(T) curve calculations were performed for high- (192–300 K) and low-temperature (2–146 K) regions, taking into account the zero-field splitting of Co2+ electronic levels, in the Mjolnir [36,37] and PHI programs [38], respectively.
The high temperature region is described using the Griffith Hamiltonian (GH) [39,40,41,42], which takes into account the contribution of unquenched orbital angular momentum for octahedral Co(II) complexes (1):
where Δax and Δrh = splitting of the 4T1g ground term coming from symmetry lowering, κ = orbital reduction factor (it can vary between 0.6 and 1.0 depending on the complex), λ = spin-orbit coupling, L and S are the orbital angular momentum and spin operators, ge = free-electron g-factor (2.0023), μB is the Bohr magneton, and B is the applied magnetic field. The final plot of χMT(T) was simulated, taking into account the average parameters Δax = −1316.9 cm−1, Δrh = −153.7 cm−1 and λ = −174.54 cm−1 taken form the ab initio calculations (see details below, Table 4) and κ = 0.8 (Figure 5a). In addition, these values are quite consistent with those calculated for the distorted octahedral cobalt(II) complexes with “easy axis” anisotropy [43,44,45,46,47,48,49,50].

Table 4.
The best-fit of the experimental magnetic data for α-1 and γ-1.
For the low-temperature region, the course of the curve is described by the parameters of the effective spin Hamiltonian, which takes into account the anisotropic parameter D (2):
The calculated values were giso = 2.322(1), D = 14.3 cm−1, R2 = 3.9∙10−5 (Figure 5a). The value of axial parameter D is typical for Co2+ complexes, where metal ions are in a tetrahedral coordination environment [51,52,53,54].
To fully explain the dc-results, the parameters of the GH (1) and the effective spin Hamiltonian (3) were calculated using the CASSCF/NEVPT2 methods in the Orca 5.0.1 program [55]:
where μB—Bohr’s magneton, B—applied magnetic field, S—full spin, D and E—axial and rhombic parameters of zero field splitting (ZFS), Ŝ—full spin operator.
In the transition from α-1 to γ-1, an increase in the z-component of the g-tensor was observed (Table 4). The calculated SOC constants are of the same order as the constant of the free Co2+ ion (ζ = 533 cm−1). The calculated values of giso and D for γ-1 are close to those calculated from the EPR data (giso = 2.25, D ≈ 23 cm−1) for the model with spin S = 3/2.
The comparison of the results of the calculations and the simulation of the magnetic data confirms that SPT is accompanied by the extinction of the orbital angular momentum and a decrease in SOC for Co2+ ions, the SOC constants correspond to 523.61 and 520.43 cm−1 for α-1 and γ-1, respectively.
The structure of the high-temperature phase contains two crystallography non-equivalent cobalt atoms, each having a pseudo-octahedral environment with an axial elongation of Co-O bonds (Figure 3). In phase α-1, upon the application of a Oh crystal field (CF), the ground term 4F splits to 4T1g, 4T2g and 2Ag, where 4T1g is the lowest in energy. As a result, lowering the symmetry of each Co2+ ion from ideal Oh to D4h lifts the degeneration of the state 4T1g by 4Eg and 4A2g (Table 5), and due to the rhombic distortion, the 4Eg ground term is split in two [40,41,42,43,44,48,56].

Table 5.
CASSCF/NEVPT2-calculated relative energies of initial states and spin-orbit states (six lowest Kramer’s Doublets) for α-1 and γ-1.
In phase γ-1, upon the application of a Td crystal field, the ground term 4F splits to 4A2, 4T2 and 4T1, where 4A2 is the lowest in energy. The perfect symmetry distortion from Td to D2d splits the 4T2 term into the 4B2 and 4E terms (Table 5). State 4A2 changes to 4B1 due to the CF symmetry [54,57,58,59]. In the case of γ-1 complex, a significant increase in the 4B2 level compared to 4B1 induces easy-plane magnetic anisotropy.
In other words, lowering the temperature affects the splitting of the CF, due to a decrease in the orbital angular momentum and the SOC of the metal ions, the degeneracy of the excited states decreases.
As the electronic structure of both of the Co2+ ions in α-1 are described by the GH, their spin-orbit contribution to the total magnetic moment, in this case, is considered as a superposition of the values for the ions.
To estimate the effect of the CF on the magnetic anisotropy, the relative energies of the d-orbitals were calculated using the AILFT method [60]. For α-1, the orbital energies were calculated for each Co2+ ion from the symmetry of CF (Figure 6). The three low-lying orbitals make up the partially occupied t2g subshell separated from the singly occupied eg subshell [47,61,62].
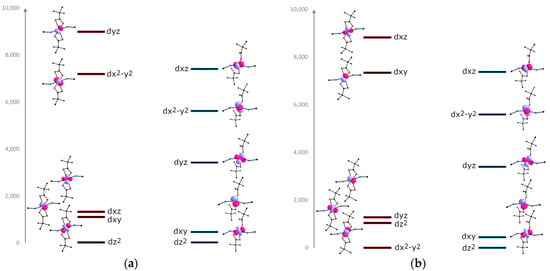
Figure 6.
CASSCF/NEVPT2-calculated relative energies of a d-orbitals for α-1 (red states) and γ-1 (blue states). Change in the splitting of orbitals for Co12+ ion (a), and for Co22+ (b).
Lowering the temperature leads to the alignment of the polymer chains in the crystal, which leads to the same symmetry of the orbitals for γ-1 (Figure 6). In the case of the Co12+ ion, the breaking of the Co–O bond is accompanied by the removal of the carboxylate group along the y axis, which leads to the strong decrease in the energy of the dyz and dx2-y2 orbitals. For the Co22+ ion, the formation of a strong σ-bond with the second oxygen atom of the carboxylate group is observed. This probably affects the increase in the energy of the dyz and dx2–y2 orbitals.
The doubly occupied dxy and dz2 orbitals forming the e subshell are almost degenerate and stabilized with respect to the singly occupied high-lying t2 (dxz, dx2-y2, dyz) orbitals [63,64,65].
As a reversible phase transition is observed for 1, which is accompanied by a change in the electronic state of cobalt(II) ions observed in the behavior of χMT(T), this effect can give rise to a thermal hysteresis loop in the magnetic susceptibility. To verify this assumption, we carried out additional measurements of the static magnetic susceptibility in a magnetic field of H = 1 kOe with a cooling of the sample from 300 to 2 K and subsequent heating up to 300 K. The behavior of the χMT(T) curve upon cooling ((χMT)cool) (Figure 7) is similar to the results described above (Figure 5a). The χMT(T) curves during cooling and heating ((χMT)heat) coincide in the temperature range of 2‒170 K. Above 170 K, the (χMT)heat values are lower than the (χMT)cool values: the difference between the (χMT)cool and (χMT)heat values in the temperature range 190–285 K is 8‒9%. The (χMT)heat curve up to 300 K does not reach the initial value (2.98 cm3K/mol vs. 3.13 cm3K/mol); as a result, an incomplete hysteresis loop of ~110 K is formed in the temperature range 170–300 K. These results are consistent with the incomplete phase transition at 300 K, as the magnetic moment for the superposition of the two phases, α-1 and δ-1, is expected to be lower than for the α-1 phase, provided that the electronic structure of the cobalt(II) ions in δ-1 differs from α-1, which is confirmed by the difference in the diffuse reflectance spectra for pure α-1 and a mixture of α-1 and δ-1 at RT (Figure S14).
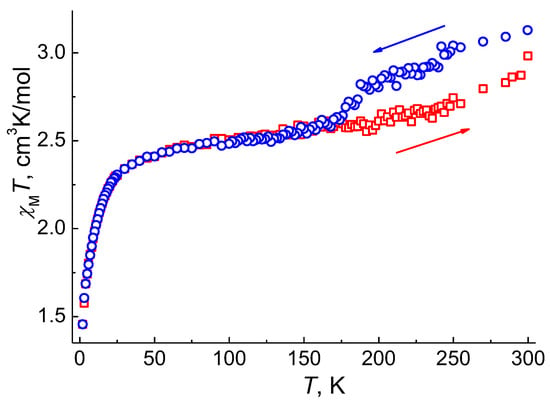
Figure 7.
Temperature dependences of χMT for 1 measured at HDC = 0.1 T (blue—cooling in the range 300–2 K; red—heating in the range 2–300 K).
2.5. AC Magnetic Data
In order to study the dynamics of the magnetic behavior of 1, measurements of the dynamic magnetic susceptibility were carried out. The measurements in a zero external magnetic field showed the absence of significant values of the imaginary component of the dynamic magnetic susceptibility at T = 2 K, which indicates a rather high relaxation rate of the system, even at such a low temperature, and/or is a consequence of the fact that the splitting parameter in the zero field D has a positive sign and the ground state is the state with mJ = ±1/2. It is well known that the application of an external magnetic field can significantly increase the magnetic relaxation time due to the suppression of the effect of quantum tunneling of magnetization (QTM).
Measurements of the dynamic magnetic susceptibility in external magnetic fields that are different from zero make it possible to detect significant values in the frequency dependences of the imaginary component of the dynamic magnetic susceptibility at a temperature of 2 K, and, consequently, slow magnetic relaxation in complex 1 under these conditions (Figure S16).
Varying the strength of the external magnetic field made it possible to determine the optimal value at which the QTM effect is most effectively suppressed, however, relaxation by the direct mechanism is the least likely to occur. For complex 1, the optimal value of H is 1000 Oe. The measurements of the ac magnetic susceptibility and approximation of the out-of-phase frequency dependences using the generalized Debye model (Figure 8) were used to plot the dependence of the relaxation time τ on T (Figure 9).
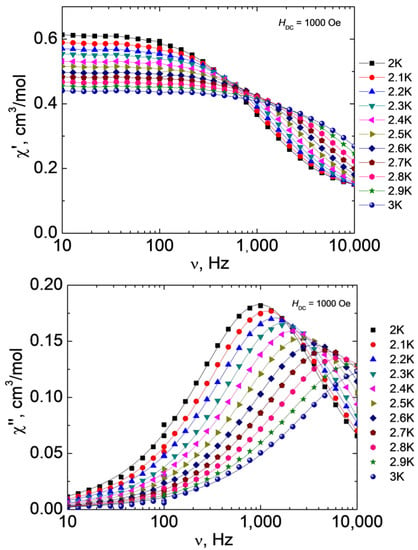
Figure 8.
Frequency dependences of the real (χ’, top) and imaginary (χ”, bottom) parts of the ac magnetic susceptibility at different temperatures for 1 at H = 1000 Oe, T = 2-3 K. Lines show approximations of the data by the generalized Debye model.
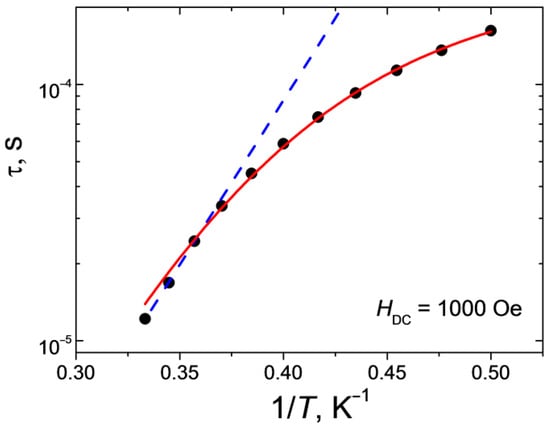
Figure 9.
Dependence of the relaxation time τ on the reciprocal temperature for 1 at H = 1000 Oe. Lines show approximations of the curves by Orbach (blue dashed line) and sum of Raman and direct (red solid line) relaxation mechanisms.
Approximation of the high-temperature linear part of the dependence τ(1/T) by the Arrhenius equation (τ = τ0·exp{ΔE/kT}) made it possible to estimate both the effective value of the remagnetization barrier and the fastest relaxation time in the system (τ0 = 6.4·10−10 s, ΔE/k = 30 K). The deviation of the dependence τ(1/T) in the semi-logarithmic coordinates from the linear one (Figure 9) points to the fact that, in addition to the above-barrier Orbach mechanism, relaxation passes through other possible paths. The best agreement between the theoretical curve and the experimental data was obtained for a linear combination of the Raman mechanism (τRaman−1 = CRaman·Tn_Raman) and direct (τdirect−1 = AdirectHn_directT) relaxation mechanism with the following parameter values: CRaman = 1.9 K-n_Ramanc−1 (±0.7), n_Raman= 9.5 (±0.4) and Adirect= 2.4·10−9 K−1Oe−n_directs−1 (±2·10−11), n_direct= 4 (fixed for Kramer’s ion). The value of the parameter nRaman obtained as a result of the best approximation is typical for the Kramer’s ions.
2.6. Discussions
For the resulting 1D polymer 1, a reversible SPT is observed with a change in the coordination environment of the metal center, which is the Co(II) ion, from octahedral to tetrahedral in the temperature range 205–150 K (according to DSC data), this rearrangement is stabilized by the transition of the coordinated carboxylate group from the chelate mode to the monodentate mode and the formation of an intramolecular H-bond. SPT was confirmed by single-crystal and powder X-ray diffraction data at different temperatures. Upon cooling and subsequent heating, the crystal loses its crystallinity. According to XRD data, cooling of polycrystalline sample 1 below 200 K is accompanied by the formation of the γ-1 phase. Cooling of 1 to 100 K leads to the formation of a mixture of phases γ-1 (61%), established by the method of single-crystal X-ray diffraction analysis, δ-1 (12%), and the initial α-1 (27%). The presence of the δ-1 phase in sample 1 at 100 K may be due to keeping the sample during the recording of the diffraction pattern at 180 K (the content of δ-1 is ~12% at 180, 140, and 100 K). This agrees with the experimental results when sample 1 is heated in the range of 100–300 K: the phase ratio α-1:γ-1:δ-1 at 100 and 140 K remains the same; above 140 K, the γ-1 phase begins to transform into δ-1. The maximum concentration of δ-1 (77%) in sample 1 was recorded at 220 and 260 K. Above 260 K, the δ-1 phase transforms into α-1 (270 K according to DSC data). The δ-1 and α-1 phases coexist at RT, what is confirmed by XRD data at RT for samples kept at 77 K (δ-1:α-1 = 66:34) and 180 K (δ-1:α-1 = 43:57). An increase in the concentration of δ-1 in sample 1 kept at 77 K confirms the transition of γ-1 to δ-1. Both phases are triclinic and have close a,b,c unit cell parameters and volume, but differ in the values of α,β,γ angles. Based on these data, the following scheme of polymorphic transformations was proposed (Scheme 1):

Scheme 1.
Polymorphic transformations for 1.
The described phase transition, which leads to a change in the geometry of the coordination environment of the cobalt(II) ion in 1 (from octahedral for α-1 to pseudo-tetrahedral for γ-1), significantly affects the magnetic behavior of sample 1 by an 8% drop in χMT in the region of 200-150 K. According to the results of the ab initio calculations, SPT is accompanied by the extinction of the orbital angular momentum and a decrease in the SOC of the cobalt(II) ions, the SOC constants correspond to 523.61 and 520.43 cm−1 for α-1 and γ-1, respectively. The difference in the electronic structure of the cobalt(II) ions in α-1 and γ-1 and the reverse phase transition being shifted higher in temperature through the δ-1 phase leads to the formation of a hysteresis loop of ~110 K on the χMT curve. The completion of the hysteresis loop is assumed to be above 300 K, as the presence of the δ-1 phase (19%) in sample 1 at 300 K underestimates the value of χMT. Furthermore, as the change in the values of (χMT)cool and (χMT)heat in the temperature range of 190–285 K is symbatic, and the cell parameters for γ-1 and δ-1 are close, we can assume that the coordination environment and the electronic structure of the cobalt(II) ions are similar in these phases.
The values of the giso (2.238) and D (17.555 cm−1) parameters for 1 at 150 K, obtained from the ab initio calculations, correspond to the EPR data at 10 K (giso = 2.25, D = ~23 cm−1) for the model with spin S = 3/2.
At helium temperatures, sample 1 exhibits slow magnetic relaxation in a field of 1000 Oe, which is often observed for cobalt(II) complexes with planar magnetic anisotropy (D > 0), for which spin-lattice relaxation occurs between lower levels Ms = ½ [66,67,68,69,70]. The observed magnetic relaxation in 1 is described by the sum of the direct mechanism and the Raman relaxation, which is consistent with the results of the ab initio calculations and the approximation of the DC data.
2.7. Conclusions
Thus, in this work, a new 1D polymer was synthesized and studied, in which the cobalt(II) atoms are linked into a chain by an aliphatic bridge, hexamethylenediamine. For this compound, a structural phase transition is observed below 205 K, which is accompanied by changes in the coordination environment of the cobalt(II) ions, the intra- and intermolecular H-bonds, and the packing density of the molecules in the crystal. We believe that the result of such structural rearrangements is a decrease in the value of χMT by 8% in the region of 200–150 K, which is due to the extinction of the orbital angular momentum of the cobalt(II) ions. According to the results of the multi-temperature X-ray diffraction analysis (RT and 150 K), the VT-PXRD (100–300 K), and the DSC (135–300 K), it was shown that, for the initial monoclinic phases α-1 and β-1, a SPT below 200 K is observed upon cooling, as a result of which the triclinic phase γ-1 is formed, from which, when heated above 140 K, the triclinic phase δ-1 is formed with close values of the unit cell parameters, and above 260 K, the initial monoclinic phase α-1 is formed. The δ-1 and α-1 phases coexist at 300 K. The shift of the reverse structural phase transition is higher in temperature and the supposed similar electronic structure of the cobalt(II) ions in γ-1 and δ-1 causes the formation of a hysteresis loop of ~110 K on the χMT(T) curve, in the range of 170–300 K, which is caused by reversible changes in the orbital angular momentum of the metal center as a result of the structural cooperative effects in the crystal and the dynamics of the Co–O bonds, similar to the previously described structural-magnetic transitions of cobalt(II) complexes [22,23]. Thus, perhaps this is the third example of the control of orbital angular momentum of cobalt(II) ions through a structural phase transition, which resulted in the formation of a hysteresis loop on the magnetic susceptibility with a record value of 110 K.
The analysis of the magnetic behavior of sample 1 in the temperature range of 150–2 K, EPR spectrum of 1 at 10 K, and ab initio calculations consistently led to a positive ZFS value for the cobalt(II) ion in the tetrahedral CoO2N2 environment. the easy-plane magnetic anisotropy for Co(II) in 1 at low temperatures is consistent with the observed slow magnetic relaxation, which is realized within the framework of a model that includes the sum of the Raman and direct relaxation mechanisms.
This study will continue with the aim of determining the completeness of the reversibility of the δ-1 to α-1 transition and the accompanying temperature changes in sample 1 over a wide temperature range. As part of the subsequent work, it is planned to refine the δ-1 structure based on the XRD data and a set of studies with multi-temperature IR experiments, DC magnetic measurements, DSC and PXRD, affecting the high-temperature region >300 K.
3. Methods and Materials
3.1. Main Methods
The IR spectra of the compound was recorded on a Perkin Elmer Spectrum 65 spectrophotometer equipped with a Quest ATR Accessory (Specac) by the attenuated total reflectance (ATR) in the range of 400–4000 cm−1. Elemental analysis of the resulting compounds was carried out with a Carlo Erba automatic C,H,N,S-analyzer.
The EPR spectra were collected using a Bruker Elexsys E580 spectrometer at X-band (9 GHz) in continuous wave mode. The spectrometer was equipped with an Oxford Instruments temperature control system, and the powder polycrystalline spectra measured at T = 10 K.
Magnetic susceptibility measurements were performed with a Quantum Design susceptometer PPMS-9. The temperature dependences of the magnetization (M) were measured in 1000 and 5000 Oe magnetic fields in the temperature range 2–300 K during cooling, at a cooling rate of 1 K/min. During the AC susceptibility measurements in the frequency range of 10–105 Hz, an alternating magnetic field amplitude was Hac = 1–5 Oe. The measurements were carried out for the samples moistened with mineral oil to prevent any texturizing of the particles in DC magnetic field. The prepared samples were sealed in polyethylene bags. The paramagnetic components of the magnetic susceptibility χ were determined taking into account the diamagnetic contribution evaluated from Pascal’s constants as well as the contributions of the sample holder and mineral oil.
UV-visible diffuse reflectance spectra were recorded on a JASCO V-750 UV-VIS spectrometer with Horizontal Integrating sphere (PIV-756).
Differential scanning calorimetry (DSC) was performed on differential scanning calorimeter, DSC-60 Plus, at a cooling/heating rate of 10 K/min.
3.2. Materials and Synthesis
All manipulations were carried out under an inert atmosphere using vacuumed evacuated glass ampoules accompanied with an argon-filled glovebox. The acetonitrile was dried using the common method: over P2O5, kept on the molecular sieves (4 Å) and withdrawn by condensation just before the synthesis. The cobalt trimethylacetate [Co(Piv)2]n was synthesized with a reaction of cobalt acetate tetrahydrate and an excess of pivalic acid. The Hexamethylenediamine (Aldrich, 98%) was purified by sublimation before use. The dry product 1 is stable to oxygen and air moisture.
Synthesis of [Co2(Piv)2(NH2(CH2)6NH2)]n (1)
Weighed portions of [Co(Piv)2]n (0.260 g, 1.000 mmol) and NH2C6H12NH2 (0.116 g, 1.000 mmol) were placed in a glass ampoule and degassed in a dynamic vacuum for 5 min (ampoule was cooled with liquid nitrogen to prevent diamine evaporation), the acetonitrile (15 mL) was condensed into the ampoule, the latter was fire-sealed and heated in an oil bath (120 °C) for six hours. The color of the reaction mixture changed from violet (initial Co(II) trimethylacetate) to colorless with a formation of block pink crystals precipitate (0.359 g, 95%). Anal. calculated for C16H34CoN2O4 (377.38) C, 50.92; H, 9.08; N, 7.42. Found: C, 50.86; H, 9.04; N, 7.34. IR, ν/cm−1: 3316 w, 3234 w, 3160 w, 2953 m, 2919 m, 2879 w, 2856 m, 1590 m, 1539 vs, 1480 s, 1459 m, 1410 s, 1402 s, 1358 s, 1263 w, 1218 s, 1134 m, 1083 w, 1058 w, 1014 w, 982 m, 940 w, 895 s, 807 m, 792 m, 722 w, 604 s, 535 m, 478 w.
3.3. Cooling Sample 1
Sample 1 (50 mg) were placed in a glass ampoule connected to the vacuum system using a rubber tube, was kept for 5 h in cold bath (173–183 K range, the mixture of liquid nitrogen and methanol; 77 K, liquid nitrogen in a dewar), was taken out and kept at RT to performed powder diffraction.
3.4. PXRD
The XRPD data at room temperature were collected using a Bruker D8 Advance diffractometer (CuKα, λ = 1.54 Å, Ni-filter, LYNXEYE detector, geometry reflection). Low temperature experiments were performed at X-ray structural analysis beamline (XSA) of Kurchatov Synchrotron Radiation Source [71]. Monochromatic radiation with a wavelength of 0.74 Å (photon energy 15,498 eV) was used. The sample was placed in a cryoloop of 300 μm in size and rotated around the horizontal axis during the measurement, which made it possible to average the diffraction patterns according to the orientations of the sample. The diffraction patterns were collected by the 2D Rayonix SX165 detector, which was located at a distance of 150 mm with a 29.5° tilt angle, Debye-Scherrer (transmissional) geometry was used with a 400 μm beam size. The exposure time was 5 min. The two-dimensional diffraction patterns obtained on the detector were further integrated to the standard form of the dependence of the intensity on the scattering angle I (2θ) using Dionis software [72]. The cooling rate was 1–1.4 K/min and 2–2.9 K/min at a measurement step of 10 and 40 K, respectively. The heating rate was 4.5 K/min and 2.9–3.2 K/min at a measurement step of 10 and 40 K, respectively.
The diffraction pattern was described by the Rietveld method in the TOPAS software package. The indexing of the sample at 260 K after cooling was performed used the SVD-Index, as implemented in the TOPAS. Then, the powder pattern was refined using the Pawley method to describe δ-1 lines. The obtained intensity ratio of the peaks in the hkl-phase was further fixed and used in modelling of the patterns at other temperatures, with refined scale factor. To obtain the δ-1 fraction, we compared the obtained scale factors of δ-1 and α-1 at 260 and 300 K. Then, assuming that the sample at these temperatures contained only δ-1 and α-1, based on the values of scale factors, we calculated the ratio of the structural factors and used it in the other modeling.
3.5. Single Crystal X-ray
The X-ray diffraction data for the crystals α-1, β-1 and γ-1 were collected on a Bruker D8 Venture diffractometer equipped with a CCD detector (Mo-Kα, λ = 0.71073 Å, graphite monochromator). Semi-empirical absorption correction was applied by the SADABS program [73]. The structures were solved by direct methods and refined by the full-matrix least squares in the anisotropic approximation for non-hydrogen atoms. The calculations were carried out by the SHELX-2014 program package [74] using Olex2 1.2 [75]. The crystallographic parameters for the investigated crystals and the structure refinement details are given in Table 1. The crystallographic data for the structures reported in this paper have been deposited with the Cambridge Crystallographic Data Center (2190847-2190849).
The experimental data at 150 K were obtained as a result of a multi-temperature experiment, in which a phase transition was observed with a change in the crystal system from a monocline P2/n to a triclinic P-1, as a result of which the crystal was gradually destroyed, including during data collection at 150 K. Thus, the obtained experimental data are not ideal, but more than sufficient for an unambiguous determination of the crystal structure.
3.6. Quantum Chemical Calculation
The Ab initio calculations were performed using the ORCA 5.0.1 computational package [55]. The calculations of the single-ion anisotropy parameters were based on the state-averaged complete-active-space self-consistent field (SA-CASSCF) wave functions [76,77], complemented by the N-electron valence second-order perturbation theory (NEVPT2) [78,79,80]. The active space of the CASSCF calculations was composed of seven electrons in five d-orbitals of Co2+ ions (S = 3/2): CAS(7,5). The state-averaged approach was used, in which all 10 quartet (S = 3/2) and 40 doublets (S = 1/2) states were averaged with equal weights. Both the zero-field splitting parameter (D) and transverse anisotropy (E), based on the dominant spin-orbit coupling contributions from the excited states, were calculated through the quasi-degenerate perturbation theory (QDPT) [81], in which an approximation to the Breit-Pauli form of the spin–orbit coupling operator (SOMF) [82] and the effective Hamiltonian approach [83] was applied. The polarized triple-ӡ-quality basis set def2-TZVP was used for all atoms [84,85]. An auxiliary def2/JK Coulomb fitting basis set was used during the calculation [86]. The splitting of the d-orbitals was analysed within the ab initio ligand field theory (AILFT) [87,88]. All ab initio calculations were performed with the geometry of the experimentally determined X-ray structures. The AILFT d-orbitals are described as linear combinations of the d-orbitals. Splitting is presented based on the largest coefficients for each orbital.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/ijms24010215/s1, Figure S1—IR spectra, Figures S2–S9—PXRD data; Figures S10–S13—Crystal packing; Figure S14—Diffuse reflectance spectra; Figure S15—EPR spectra; Figures S16—AC magnetic data; Table S1—Continuous Shape Measures values.
Author Contributions
Conceptualization, validation, M.A.K. and S.A.N.; methodology, D.S.Y.; formal analysis, M.A.K.; investigation, D.S.Y., J.K.V., A.S.G., R.D.S., N.N.E. and S.L.V.; computational study, A.K.M.; writing—original draft preparation, M.A.K.; writing—review and editing, M.A.K. and I.L.E.; supervision, I.L.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of the Russian Federation, grant number 075-15-2020-779.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The structure parameters of obtained compounds were deposited with the Cambridge Structural Database (CCDC Nos. 2190847 (α-1), 2190848 (β-1) and 2190849 (γ-1); deposit@ccdc.cam.ac.uk or http://www.ccdc.cam.ac.uk/data_request/cif, accessed on 27 November 2022.
Acknowledgments
The compound’s characterization was performed using the equipment at the Center for Collective Use of the Kurnakov Institute RAS (X-ray diffraction analysis, CHN and IR-spectral analyzes, magnetochemical studies) and the Center for molecular composition studies of INEOS RAS (Powder XRD with Rietveld refinement), which operate with the support of the state assignment of the IGIC RAS and INEOS RAS in the field of fundamental scientific research. We are grateful to A. Medvedev and A. Mikhailov for the help with DSC and DSO measurements.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Bogani, L.; Wernsdorfer, W. Molecular Spintronics Using Single-Molecule Magnets. Nat. Mater. 2008, 7, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Cui, Y.; Li, B.; He, H.; Zhou, W.; Chen, B.; Qian, G. Metal–Organic Frameworks as Platforms for Functional Materials. Acc. Chem. Res. 2016, 49, 483–493. [Google Scholar] [CrossRef] [PubMed]
- Westerström, R.; Dreiser, J.; Piamonteze, C.; Muntwiler, M.; Weyeneth, S.; Krämer, K.; Liu, S.-X.; Decurtins, S.; Popov, A.; Yang, S.; et al. Tunneling, Remanence, and Frustration in Dysprosium-Based Endohedral Single-Molecule Magnets. Phys. Rev. B 2014, 89, 60406. [Google Scholar] [CrossRef]
- Sato, O.; Tao, J.; Zhang, Y.-Z. Control of Magnetic Properties through External Stimuli. Angew. Chemie Int. Ed. 2007, 46, 2152–2187. [Google Scholar] [CrossRef] [PubMed]
- Pankratova, Y.; Aleshin, D.; Nikovskiy, I.; Novikov, V.; Nelyubina, Y. In Situ NMR Search for Spin-Crossover in Heteroleptic Cobalt(II) Complexes. Inorg. Chem. 2020, 59, 7700–7709. [Google Scholar] [CrossRef] [PubMed]
- Akiyoshi, R.; Ohtani, R.; Lindoy, L.F.; Hayami, S. Spin Crossover Phenomena in Long Chain Alkylated Complexes. Dalton Trans. 2021, 50, 5065–5079. [Google Scholar] [CrossRef]
- Hayami, S.; Holmes, S.M.; Halcrow, M.A. Spin-State Switches in Molecular Materials Chemistry. J. Mater. Chem. C 2015, 3, 7775–7778. [Google Scholar] [CrossRef]
- Tezgerevska, T.; Alley, K.G.; Boskovic, C. Valence Tautomerism in Metal Complexes: Stimulated and Reversible Intramolecular Electron Transfer between Metal Centers and Organic Ligands. Coord. Chem. Rev. 2014, 268, 23–40. [Google Scholar] [CrossRef]
- Aquino, M.A.S.; Lee, F.L.; Gabe, E.J.; Bensimon, C.; Greedan, J.E.; Crutchley, R.J. Superexchange Metal-Metal Coupling in Dinuclear Pentaammineruthenium Complexes Incorporating a 1,4-Dicyanamidobenzene Dianion Bridging Ligand. J. Am. Chem. Soc. 1992, 114, 5130–5140. [Google Scholar] [CrossRef]
- Sessoli, R.; Gatteschi, D.; Caneschi, A.; Novak, M.A. Magnetic Bistability in a Metal-Ion Cluster. Nature 1993, 365, 141–143. [Google Scholar] [CrossRef]
- Gütlich, P.; Goodwin, H.A. (Eds.) Spin Crossover in Transition Metal Compounds, I–III; Topics in Current Chemistry; Springer: Berlin/Heidelberg, Germany, 2004; Volume 233–235, ISBN 978-3-642-07326-7. [Google Scholar]
- Gaspar, A.B.; Seredyuk, M. Spin Crossover in Soft Matter. Coord. Chem. Rev. 2014, 268, 41–58. [Google Scholar] [CrossRef]
- Frost, M.J.; Harriman, K.; Murugesu, M. The Rise of 3-d Single-Ion Magnets in Molecular Magnetism: Towards Materials from Molecules? Chem. Sci. 2016, 7, 2470–2491. [Google Scholar] [CrossRef] [PubMed]
- Gatteschi, D.; Sessoli, R.; Villain, J. Molecular Nanomagnets; Oxford University Press on Demand: Oxford, UK, 2006; Volume 5, ISBN 0198567537. [Google Scholar]
- Winpenny, R.E.P. (Ed.) Single-Molecule Magnets and Related Phenomena; Springer: New York, NY, USA, 2006; ISBN 3540332391. [Google Scholar]
- Zenno, H.; Akiyoshi, R.; Nakamura, M.; Sekine, Y.; Hayami, S. Crystal Structures and Spin Crossover of Iron(III) Cocrystal Formed via Halogen Bonding. Chem. Lett. 2021, 50, 1259–1262. [Google Scholar] [CrossRef]
- Pfrunder, M.C.; Whittaker, J.J.; Parsons, S.; Moubaraki, B.; Murray, K.S.; Moggach, S.A.; Sharma, N.; Micallef, A.S.; Clegg, J.K.; McMurtrie, J.C. Controlling Spin Switching with Anionic Supramolecular Frameworks. Chem. Mater. 2020, 32, 3229–3234. [Google Scholar] [CrossRef]
- Murata, S.; Takahashi, K.; Mochida, T.; Sakurai, T.; Ohta, H.; Yamamoto, T.; Einaga, Y. Cooperative Spin-Crossover Transition from Three-Dimensional Purely π-Stacking Interactions in a Neutral Heteroleptic Azobisphenolate FeIII Complex with a N3O3 Coordination Sphere. Dalton Trans. 2017, 46, 5786–5789. [Google Scholar] [CrossRef]
- Milocco, F.; de Vries, F.; Siebe, H.S.; Engbers, S.; Demeshko, S.; Meyer, F.; Otten, E. Widening the Window of Spin-Crossover Temperatures in Bis(Formazanate)Iron(II) Complexes via Steric and Noncovalent Interactions. Inorg. Chem. 2021, 60, 2045–2055. [Google Scholar] [CrossRef]
- Zenno, H.; Kobayashi, F.; Nakamura, M.; Sekine, Y.; Lindoy, L.F.; Hayami, S. Hydrogen Bond-Induced Abrupt Spin Crossover Behaviour in 1-D Cobalt(II) Complexes—The Key Role of Solvate Water Molecules. Dalton Trans. 2021, 50, 7843–7853. [Google Scholar] [CrossRef]
- Kanetomo, T.; Ni, Z.; Enomoto, M. Hydrogen-Bonded Cobalt(II)-Organic Framework: Normal and Reverse Spin-Crossover Behaviours. Dalton Trans. 2022, 51, 5034–5040. [Google Scholar] [CrossRef]
- Juhász, G.; Matsuda, R.; Kanegawa, S.; Inoue, K.; Sato, O.; Yoshizawa, K. Bistability of Magnetization without Spin-Transition in a High-Spin Cobalt(II) Complex Due to Angular Momentum Quenching. J. Am. Chem. Soc. 2009, 131, 4560–4561. [Google Scholar] [CrossRef]
- Su, S.-Q.; Wu, S.-Q.; Baker, M.L.; Bencok, P.; Azuma, N.; Miyazaki, Y.; Nakano, M.; Kang, S.; Shiota, Y.; Yoshizawa, K.; et al. Quenching and Restoration of Orbital Angular Momentum through a Dynamic Bond in a Cobalt(II) Complex. J. Am. Chem. Soc. 2020, 142, 11434–11441. [Google Scholar] [CrossRef]
- Baran, E.J.; Piro, O.E.; Zinczuk, J. A New Supramolecular Assembly Obtained by Reaction Between Thiosaccharin and Hexamethylenediamine. Z. Nat. B 2007, 62, 1530–1534. [Google Scholar] [CrossRef][Green Version]
- Stewart, J.E. Vibrational Spectra of Primary and Secondary Aliphatic Amines. J. Chem. Phys. 1959, 30, 1259–1265. [Google Scholar] [CrossRef]
- Nakamoto, K. Recent Progress in Inorganic Vibrational Spectroscopy. J. Spectrosc. Soc. Japan 1981, 30, 437–454. [Google Scholar] [CrossRef]
- Ghosh, I.; Chakraborty, B.; Bera, A.; Paul, S.; Paine, T.K. Selective Oxygenation of C–H and C=C Bonds with H2O2 by High-Spin Cobalt(II)-Carboxylate Complexes. Dalton Trans. 2022, 51, 2480–2492. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Zhang, L.-Y.; Bao, Y.-M.; Zhang, N.; Zhang, J.-Y.; Xing, Y.-Y.; Deng, W.; Liu, Z.-J. Structures and Catalytic Oxidative Coupling Reaction of Four Co-MOFs Modified with R-Isophthalic Acid (R-H, OH and COOH) and Trigonal Ligands. CrystEngComm 2021, 23, 7590–7601. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, J.; Sun, H.X.; He, M.; Li, W.; Du, L.; Xie, M.; Zhao, Q.-H. R-Substituent-Induced Structural Diversity and Single-Crystal to Single-Crystal Transformation of Coordination Polymers: Synthesis, Luminescence, and Magnetic Behaviors. Cryst. Growth Des. 2021, 21, 5086–5099. [Google Scholar] [CrossRef]
- Nikolić, M.A.; Szécsényi, K.M.; Dražić, B.; Rodić, M.V.; Stanić, V.; Tanasković, S. Binuclear Co(II) Complexes with Macrocycle and Carboxylato Ligands: Structure, Cytotoxicity and Thermal Behavior. J. Mol. Struct. 2021, 1236, 130133. [Google Scholar] [CrossRef]
- Chen, K.-J.; Madden, D.G.; Pham, T.; Forrest, K.A.; Kumar, A.; Yang, Q.-Y.; Xue, W.; Space, B.; Perry IV, J.J.; Zhang, J.-P.; et al. Tuning Pore Size in Square-Lattice Coordination Networks for Size-Selective Sieving of CO2. Angew. Chemie Int. Ed. 2016, 55, 10268–10272. [Google Scholar] [CrossRef]
- White, A.H.; Willis, A.C. Structural Studies in Metal–Purpurate Complexes. Part 7. Crystal Structures of Diaquanitratopurpurato-Cobalt(II) and -Zinc(II) Dihydrat. J. Chem. Soc. Dalt. Trans. 1977, 14, 1377–1381. [Google Scholar] [CrossRef]
- Głowiak, T.; Kurdziel, K. Crystal Structure and Physico-Chemical Properties of Hepta-Coordinate Isomorphic Cobalt(II) and Nickel(II) Complexes of 1-Allylimidazole. J. Mol. Struct. 2000, 516, 1–5. [Google Scholar] [CrossRef]
- Pérez-Lourido, P.; Madarasi, E.; Antal, F.; Esteban-Gómez, D.; Wang, G.; Angelovski, G.; Platas-Iglesias, C.; Tircsó, G.; Valencia, L. Stable and Inert Macrocyclic Cobalt(Ii) and Nickel(Ii) Complexes with ParaCEST Response. Dalton Trans. 2022, 51, 1580–1593. [Google Scholar] [CrossRef] [PubMed]
- Stoll, S.; Schweiger, A. EasySpin, a Comprehensive Software Package for Spectral Simulation and Analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef] [PubMed]
- Polunin, R.A.; Kolotilov, S.V.; Kiskin, M.A.; Cador, O.; Mikhalyova, E.A.; Lytvynenko, A.S.; Golhen, S.; Ouahab, L.; Ovcharenko, V.I.; Eremenko, I.L.; et al. Topology Control of Porous Coordination Polymers by Building Block Symmetry. Eur. J. Inorg. Chem. 2010, 2010, 5055–5057. [Google Scholar] [CrossRef]
- Litvinenko, A.S.; Mikhaleva, E.A.; Kolotilov, S.V.; Pavlishchuk, V.V. Effect of Spin–Orbit Coupling on the Magnetic Susceptibility of Polynuclear Complexes of 3d Metals Containing a Co2+ Ion. Theor. Exp. Chem. 2011, 46, 422–428. [Google Scholar] [CrossRef]
- Chilton, N.F.; Anderson, R.P.; Turner, L.D.; Soncini, A.; Murray, K.S. PHI: A Powerful New Program for the Analysis of Anisotropic Monomeric and Exchange-Coupled Polynuclear d- and f-Block Complexes. J. Comput. Chem. 2013, 34, 1164–1175. [Google Scholar] [CrossRef] [PubMed]
- Griffith, J.S. The Theory of Transition-Metal Ions; Cambridge University Press: Cambridge, UK, 1964; ISBN 0521051509. [Google Scholar]
- Lloret, F.; Julve, M.; Cano, J.; Ruiz-García, R.; Pardo, E. Magnetic Properties of Six-Coordinated High-Spin Cobalt(II) Complexes: Theoretical Background and Its Application. Inorg. Chim. Acta 2008, 361, 3432–3445. [Google Scholar] [CrossRef]
- Palii, A.V.; Korchagin, D.V.; Yureva, E.A.; Akimov, A.V.; Misochko, E.Y.; Shilov, G.V.; Talantsev, A.D.; Morgunov, R.B.; Aldoshin, S.M.; Tsukerblat, B.S. Single-Ion Magnet Et4N[CoII(Hfac)3] with Nonuniaxial Anisotropy: Synthesis, Experimental Characterization, and Theoretical Modeling. Inorg. Chem. 2016, 55, 9696–9706. [Google Scholar] [CrossRef]
- Korchagin, D.V.; Gureev, Y.E.; Yureva, E.A.; Shilov, G.V.; Akimov, A.V.; Misochko, E.Y.; Morgunov, R.B.; Zakharov, K.V.; Vasiliev, A.N.; Palii, A.V.; et al. Field-induced single-ion magnet based on a quasi-octahedral Co(II) complex with mixed sulfur–oxygen coordination environment. Dalton Trans. 2021, 50, 13815–13822. [Google Scholar] [CrossRef]
- Palii, A.; Tsukerblat, B.; Klokishner, S.; Dunbar, K.R.; Clemente-Juan, J.M.; Coronado, E. Beyond the Spin Model: Exchange Coupling in Molecular Magnets with Unquenched Orbital Angular Momenta. Chem. Soc. Rev. 2011, 40, 3130–3156. [Google Scholar] [CrossRef]
- Matyukhina, A.K.; Zorina-Tikhonova, E.N.; Goloveshkin, A.S.; Babeshkin, K.A.; Efimov, N.N.; Kiskin, M.A.; Eremenko, I.L. Field-Induced Slow Magnetic Relaxation in CoII Cyclopropane-1,1-Dicarboxylates. Molecules 2022, 27, 6537. [Google Scholar] [CrossRef]
- Zorina-Tikhonova, E.N.; Matyukhina, A.K.; Chistyakov, A.S.; Vologzhanina, A.V.; Korlyukov, A.A.; Gogoleva, N.V.; Novikova, V.A.; Belova, E.V.; Ugolkova, E.A.; Starikova, A.A.; et al. Synthesis, Structure, Magnetic Properties and Thermal Behaviour of Ba–MII (MII = Mn, Co, Cu, and Zn) Allylmalonates. N. J. Chem. 2022, 46, 21245–21256. [Google Scholar] [CrossRef]
- Tupolova, Y.P.; Shcherbakov, I.N.; Popov, L.D.; Lebedev, V.E.; Tkachev, V.V.; Zakharov, K.V.; Vasiliev, A.N.; Korchagin, D.V.; Palii, A.V.; Aldoshin, S.M. Field-Induced Single-Ion Magnet Behaviour of a Hexacoordinated Co(Ii) Complex with Easy-Axis-Type Magnetic Anisotropy. Dalton Trans. 2019, 48, 6960–6970. [Google Scholar] [CrossRef] [PubMed]
- Rigamonti, L.; Bridonneau, N.; Poneti, G.; Tesi, L.; Sorace, L.; Pinkowicz, D.; Jover, J.; Ruiz, E.; Sessoli, R.; Cornia, A. A Pseudo-Octahedral Cobalt(II) Complex with Bispyrazolylpyridine Ligands Acting as a Zero-Field Single-Molecule Magnet with Easy Axis Anisotropy. Chem. Eur. J. 2018, 24, 8857–8868. [Google Scholar] [CrossRef] [PubMed]
- Matos, C.R.M.O.; Sarmiento, C.V.; Silva, H.C.; Ferreira, G.B.; Guedes, G.P.; Nunes, W.C.; Ronconi, C.M. Field-Induced Single-Ion Magnets Exhibiting Tri-Axial Anisotropy in a 1D Co(Ii) Coordination Polymer with a Rigid Ligand 4,4′-(Buta-1,3-Diyne-1,4-Diyl)Dibenzoate. Dalton Trans. 2021, 50, 15003–15014. [Google Scholar] [CrossRef] [PubMed]
- Nemec, I.; Herchel, R.; Trávníček, Z. Two Polymorphic Co(Ii) Field-Induced Single-Ion Magnets with Enormous Angular Distortion from the Ideal Octahedron. Dalton Trans. 2018, 47, 1614–1623. [Google Scholar] [CrossRef] [PubMed]
- Świtlicka, A.; Machura, B.; Penkala, M.; Bieńko, A.; Bieńko, D.C.; Titiš, J.; Rajnák, C.; Boča, R.; Ozarowski, A. Slow Magnetic Relaxation in Hexacoordinated Cobalt(Ii) Field-Induced Single-Ion Magnets. Inorg. Chem. Front. 2020, 7, 2637–2650. [Google Scholar] [CrossRef]
- Huang, X.-C.; Xu, R.; Chen, Y.-Z.; Zhang, Y.-Q.; Shao, D. Two Four-Coordinate and Seven-Coordinate CoII Complexes Based on the Bidentate Ligand 1, 8-Naphthyridine Showing Slow Magnetic Relaxation Behavior. Chem. Asian J. 2020, 15, 279–286. [Google Scholar] [CrossRef]
- Saber, M.R.; Dunbar, K.R. Ligands Effects on the Magnetic Anisotropy of Tetrahedral Cobalt Complexes. Chem. Commun. 2014, 50, 12266–12269. [Google Scholar] [CrossRef]
- Smolko, L.; Černák, J.; Dušek, M.; Miklovič, J.; Titiš, J.; Boča, R. Three Tetracoordinate Co(II) Complexes [Co(Biq)X2] (X = Cl, Br, I) with Easy-Plane Magnetic Anisotropy as Field-Induced Single-Molecule Magnets. Dalton Trans. 2015, 44, 17565–17571. [Google Scholar] [CrossRef]
- Suturina, E.A.; Maganas, D.; Bill, E.; Atanasov, M.; Neese, F. Magneto-Structural Correlations in a Series of Pseudotetrahedral [CoII(XR)4]2– Single Molecule Magnets: An Ab Initio Ligand Field Study. Inorg. Chem. 2015, 54, 9948–9961. [Google Scholar] [CrossRef]
- Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Boča, R. Zero-Field Splitting in Metal Complexes. Coord. Chem. Rev. 2004, 248, 757–815. [Google Scholar] [CrossRef]
- Damgaard-Møller, E.; Krause, L.; Tolborg, K.; Macetti, G.; Genoni, A.; Overgaard, J. Quantification of the Magnetic Anisotropy of a Single-Molecule Magnet from the Experimental Electron Density. Angew. Chemie Int. Ed. 2020, 59, 21203–21209. [Google Scholar] [CrossRef] [PubMed]
- Wu, T.; Zhai, Y.-Q.; Deng, Y.-F.; Chen, W.-P.; Zhang, T.; Zheng, Y.-Z. Correlating Magnetic Anisotropy with the Subtle Coordination Geometry Variation of a Series of Cobalt(Ii)-Sulfonamide Complexes. Dalton Trans. 2019, 48, 15419–15426. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Y.-Q.; Deng, Y.-F.; Zheng, Y.-Z. Pseudotetrahedral Cobalt(Ii) Complexes with PNP-Ligands Showing Uniaxial Magnetic Anisotropy. Dalton Trans. 2018, 47, 8874–8878. [Google Scholar] [CrossRef]
- Lang, L.; Atanasov, M.; Neese, F. Improvement of Ab Initio Ligand Field Theory by Means of Multistate Perturbation Theory. J. Phys. Chem. A 2020, 124, 1025–1037. [Google Scholar] [CrossRef]
- Sertphon, D.; Murray, K.S.; Phonsri, W.; Jover, J.; Ruiz, E.; Telfer, S.G.; Alkaş, A.; Harding, P.; Harding, D.J. Slow Relaxation of Magnetization in a Bis-Mer-Tridentate Octahedral Co(II) Complex. Dalton Trans. 2018, 47, 859–867. [Google Scholar] [CrossRef]
- Nemec, I.; Fellner, O.F.; Indruchová, B.; Herchel, R. Trigonally Distorted Hexacoordinate Co(II) Single-Ion Magnets. Materials 2022, 15, 1064. [Google Scholar] [CrossRef]
- Sundararajan, M.; Ganyushin, D.; Ye, S.; Neese, F. Multireference Ab Initio Studies of Zero-Field Splitting and Magnetic Circular Dichroism Spectra of Tetrahedral Co(II) Complexes. Dalton Trans. 2009, 30, 6021–6036. [Google Scholar] [CrossRef]
- Damgaard-Møller, E.; Krause, L.; Lassen, H.; Malaspina, L.A.; Grabowsky, S.; Bamberger, H.; McGuire, J.; Miras, H.N.; Sproules, S.; Overgaard, J. Investigating Complex Magnetic Anisotropy in a Co(II) Molecular Compound: A Charge Density and Correlated Ab Initio Electronic Structure Study. Inorg. Chem. 2020, 59, 13190–13200. [Google Scholar] [CrossRef]
- Tripathi, S.; Vaidya, S.; Ansari, K.U.; Ahmed, N.; Rivière, E.; Spillecke, L.; Koo, C.; Klingeler, R.; Mallah, T.; Rajaraman, G.; et al. Influence of a Counteranion on the Zero-Field Splitting of Tetrahedral Cobalt(II) Thiourea Complexes. Inorg. Chem. 2019, 58, 9085–9100. [Google Scholar] [CrossRef] [PubMed]
- Vallejo, J.; Castro, I.; Ruiz-García, R.; Cano, J.; Julve, M.; Lloret, F.; De Munno, G.; Wernsdorfer, W.; Pardo, E. Field-Induced Slow Magnetic Relaxation in a Six-Coordinate Mononuclear Cobalt(II) Complex with a Positive Anisotropy. J. Am. Chem. Soc. 2012, 134, 15704–15707. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, S.; Singh, S.K.; Shukla, P.; Ansari, K.; Rajaraman, G.; Shanmugam, M. Role of Halide Ions in the Nature of the Magnetic Anisotropy in Tetrahedral CoII Complexes. Chem. Eur. J. 2017, 23, 9546–9559. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, S.; Upadhyay, A.; Singh, S.K.; Gupta, T.; Tewary, S.; Langley, S.K.; Walsh, J.P.S.; Murray, K.S.; Rajaraman, G.; Shanmugam, M. A Synthetic Strategy for Switching the Single Ion Anisotropy in Tetrahedral Co(Ii) Complexes. Chem. Commun. 2015, 51, 3739–3742. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Liu, J.; Piro, N.A.; Chang, C.J.; Hill, S.; Long, J.R. Slow Magnetic Relaxation in a Pseudotetrahedral Cobalt(Ii) Complex with Easy-Plane Anisotropy. Chem. Commun. 2012, 48, 3927–3929. [Google Scholar] [CrossRef]
- Yambulatov, D.S.; Nikolaevskii, S.A.; Shmelev, M.A.; Babeshkin, K.A.; Korchagin, D.V.; Efimov, N.N.; Goloveshkin, A.S.; Petrov, P.A.; Kiskin, M.A.; Sokolov, M.N.; et al. Heterometallic Coii-Lii Carboxylate Complexes with N-Heterocyclic Carbene, Triphenylphosphine and Pyridine: A Comparative Study of Magnetic Properties. Mendeleev Commun. 2021, 31, 624–627. [Google Scholar] [CrossRef]
- Svetogorov, R.D.; Dorovatovskii, P.V.; Lazarenko, V.A. Belok/XSA Diffraction Beamline for Studying Crystalline Samples at Kurchatov Synchrotron Radiation Source. Cryst. Res. Technol. 2020, 55, 1900184. [Google Scholar] [CrossRef]
- Svetogorov, R.D. Dionis—Diffraction Open Integration Software, Certificate of Registration № 2018660965; State Registration Certificate of a Computer Program; National Research Center “Kurchatov Institute”: Moscow, Russia, 2018.
- Sheldrick, G.M. SADABS. In Program for Empirical Absorption Correction of Area Detector Data; Bruker AXS Inc.: Madiso, WI, USA, 1997. [Google Scholar]
- Sheldrick, G.M. SHELXT Integrated Space-Group and Crystal-Structure Determination. Acta Crystallogr. Sect. A 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A Complete Structure Solution, Refinement and Analysis Program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Malmqvist, P.-Å.; Roos, B.O. The CASSCF State Interaction Method. Chem. Phys. Lett. 1989, 155, 189–194. [Google Scholar] [CrossRef]
- Neese, F. Calculation of the Zero-Field Splitting Tensor on the Basis of Hybrid Density Functional and Hartree-Fock Theory. J. Chem. Phys. 2007, 127, 164112. [Google Scholar] [CrossRef] [PubMed]
- Angeli, C.; Borini, S.; Cestari, M.; Cimiraglia, R. A Quasidegenerate Formulation of the Second Order N-Electron Valence State Perturbation Theory Approach. J. Chem. Phys. 2004, 121, 4043–4049. [Google Scholar] [CrossRef] [PubMed]
- Angeli, C.; Cimiraglia, R.; Evangelisti, S.; Leininger, T.; Malrieu, J.-P. Introduction of N-Electron Valence States for Multireference Perturbation Theory. J. Chem. Phys. 2001, 114, 10252–10264. [Google Scholar] [CrossRef]
- Angeli, C.; Cimiraglia, R.; Malrieu, J.-P. N-Electron Valence State Perturbation Theory: A Spinless Formulation and an Efficient Implementation of the Strongly Contracted and of the Partially Contracted Variants. J. Chem. Phys. 2002, 117, 9138–9153. [Google Scholar] [CrossRef]
- Ganyushin, D.; Neese, F. First-Principles Calculations of Zero-Field Splitting Parameters. J. Chem. Phys. 2006, 125, 24103. [Google Scholar] [CrossRef]
- Neese, F. Efficient and Accurate Approximations to the Molecular Spin-Orbit Coupling Operator and Their Use in Molecular g-Tensor Calculations. J. Chem. Phys. 2005, 122, 34107. [Google Scholar] [CrossRef]
- Maurice, R.; Bastardis, R.; de Graaf, C.; Suaud, N.; Mallah, T.; Guihéry, N. Universal Theoretical Approach to Extract Anisotropic Spin Hamiltonians. J. Chem. Theory Comput. 2009, 5, 2977–2984. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully Optimized Contracted Gaussian Basis Sets of Triple Zeta Valence Quality for Atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Pantazis, D.A.; Chen, X.-Y.; Landis, C.R.; Neese, F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4, 908–919. [Google Scholar] [CrossRef]
- Neese, F. An Improvement of the Resolution of the Identity Approximation for the Formation of the Coulomb Matrix. J. Comput. Chem. 2003, 24, 1740–1747. [Google Scholar] [CrossRef]
- Atanasov, M.; Ganyushin, D.; Sivalingam, K.; Neese, F. A Modern First-Principles View on Ligand Field Theory Through the Eyes of Correlated Multireference Wavefunctions BT. In Molecular Electronic Structures of Transition Metal Complexes II; Mingos, D.M.P., Day, P., Dahl, J.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 149–220. ISBN 978-3-642-27378-0. [Google Scholar]
- Singh, S.K.; Eng, J.; Atanasov, M.; Neese, F. Covalency and Chemical Bonding in Transition Metal Complexes: An Ab Initio Based Ligand Field Perspective. Coord. Chem. Rev. 2017, 344, 2–25. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).