TransPhos: A Deep-Learning Model for General Phosphorylation Site Prediction Based on Transformer-Encoder Architecture
Abstract
:1. Introduction
2. Results
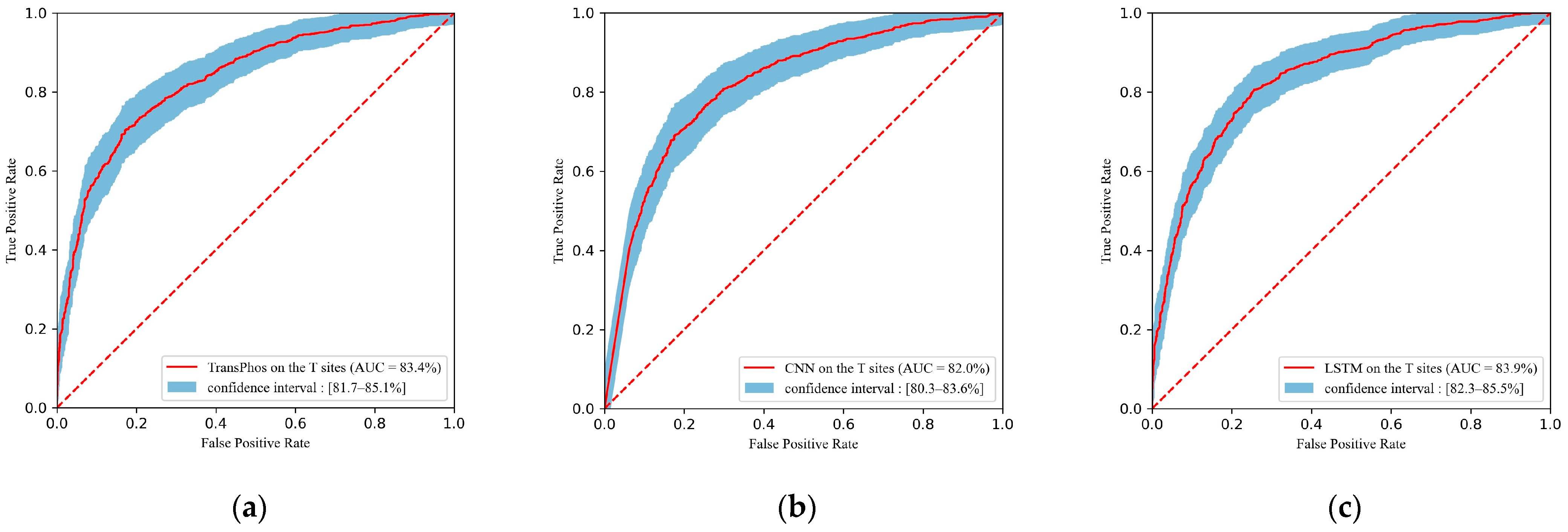
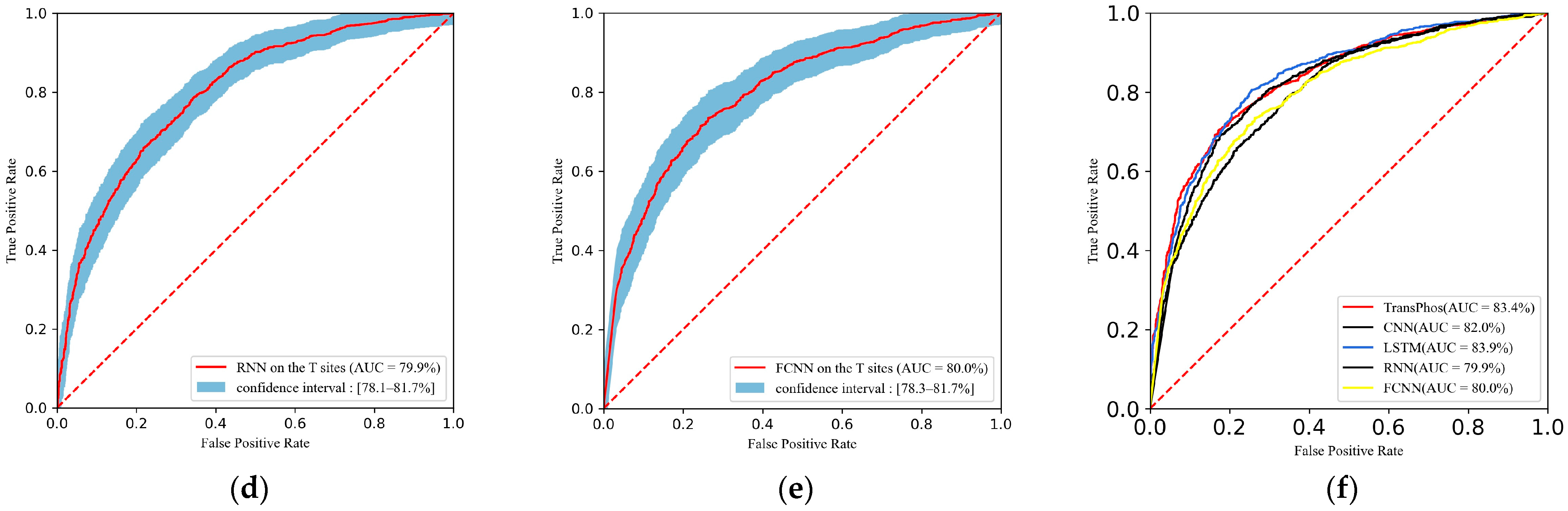
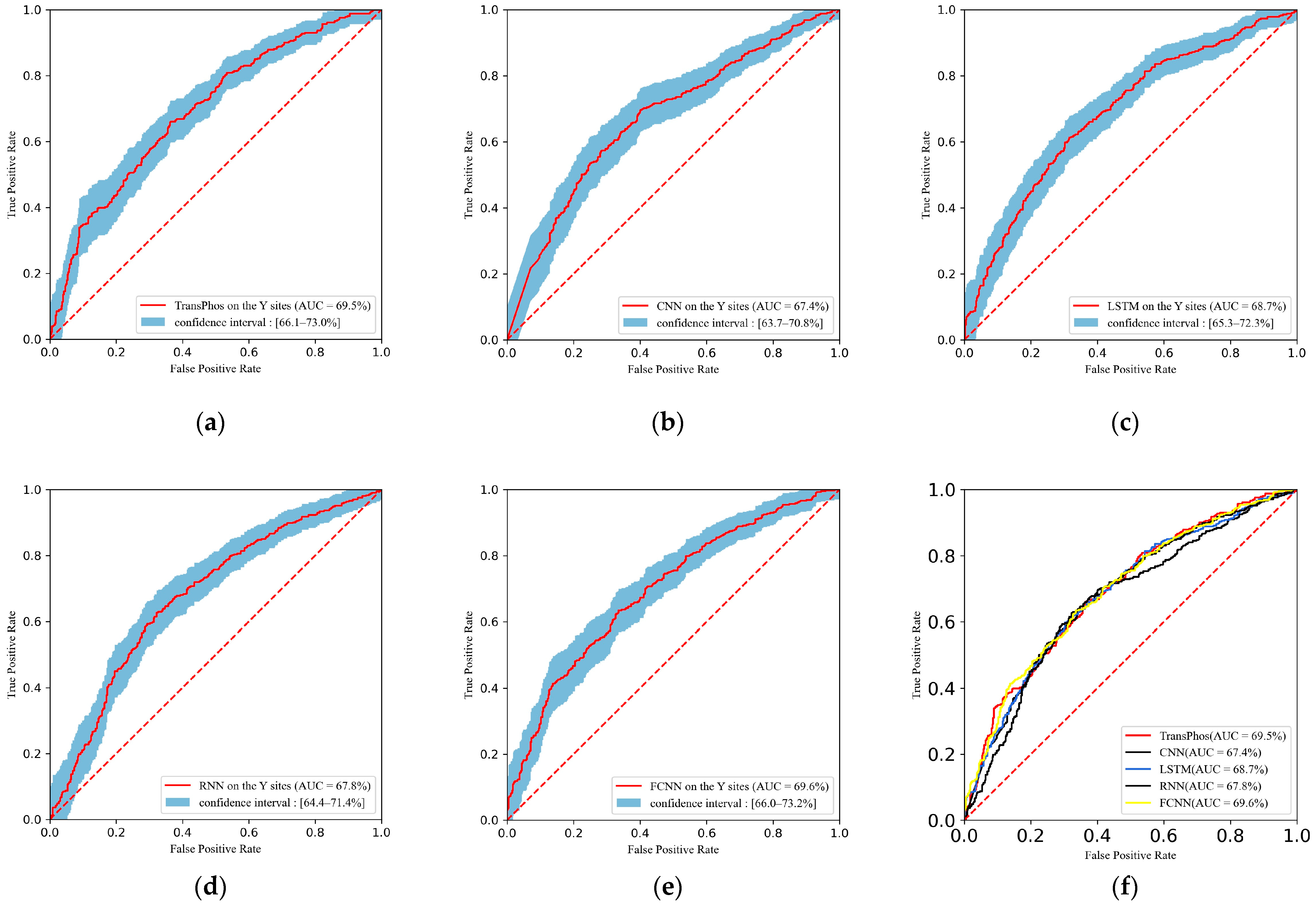
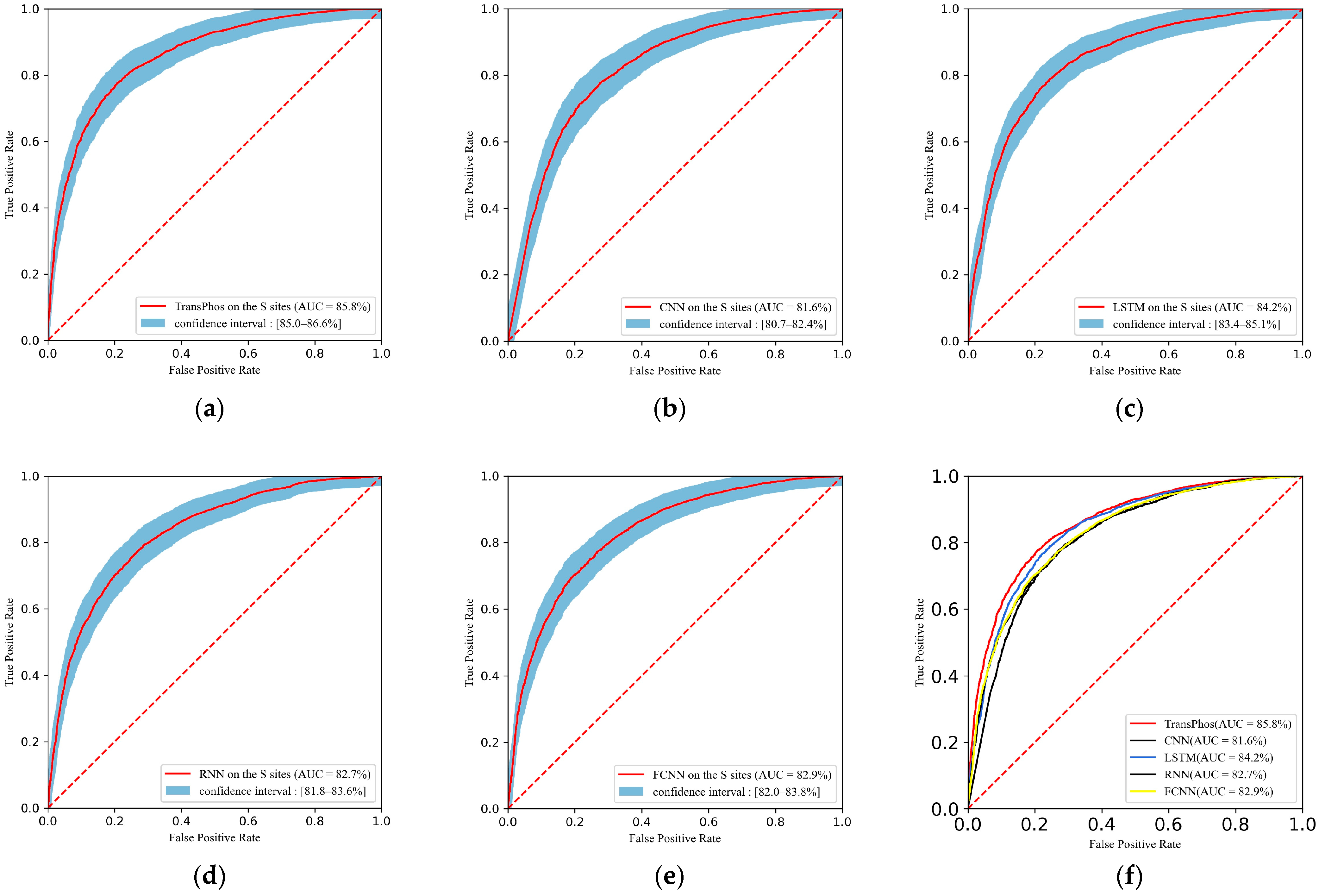
2.1. Comparison with Different Deep Learning Models
2.2. Comparison with Existing Phosphorylation Site Prediction Tools
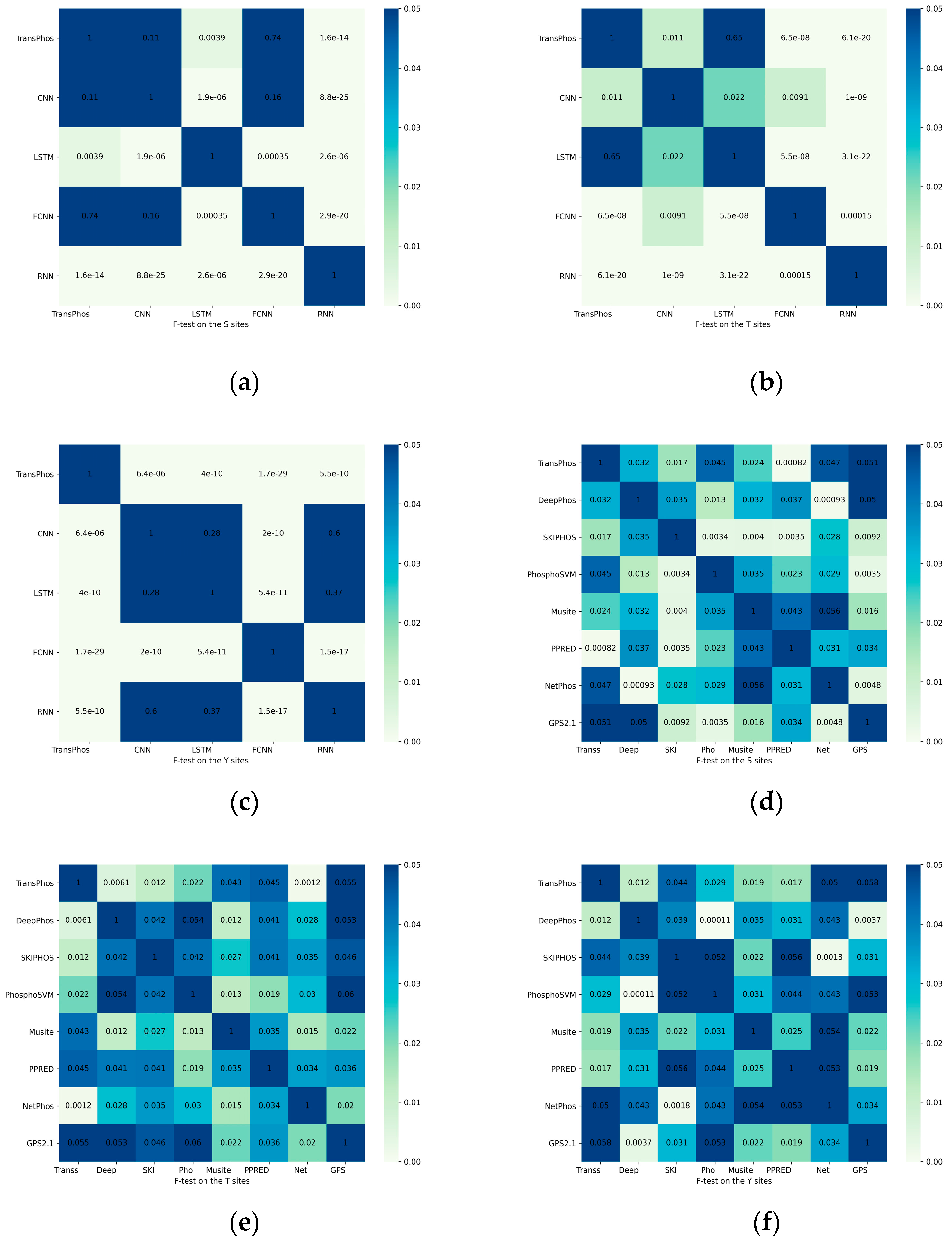
2.3. Significance Test of the Results
3. Discussion
4. Materials and Methods
4.1. Overview
4.2. Dataset Collection and Pre-Processing
4.2.1. Dataset Collection
4.2.2. Data Pre-Processing
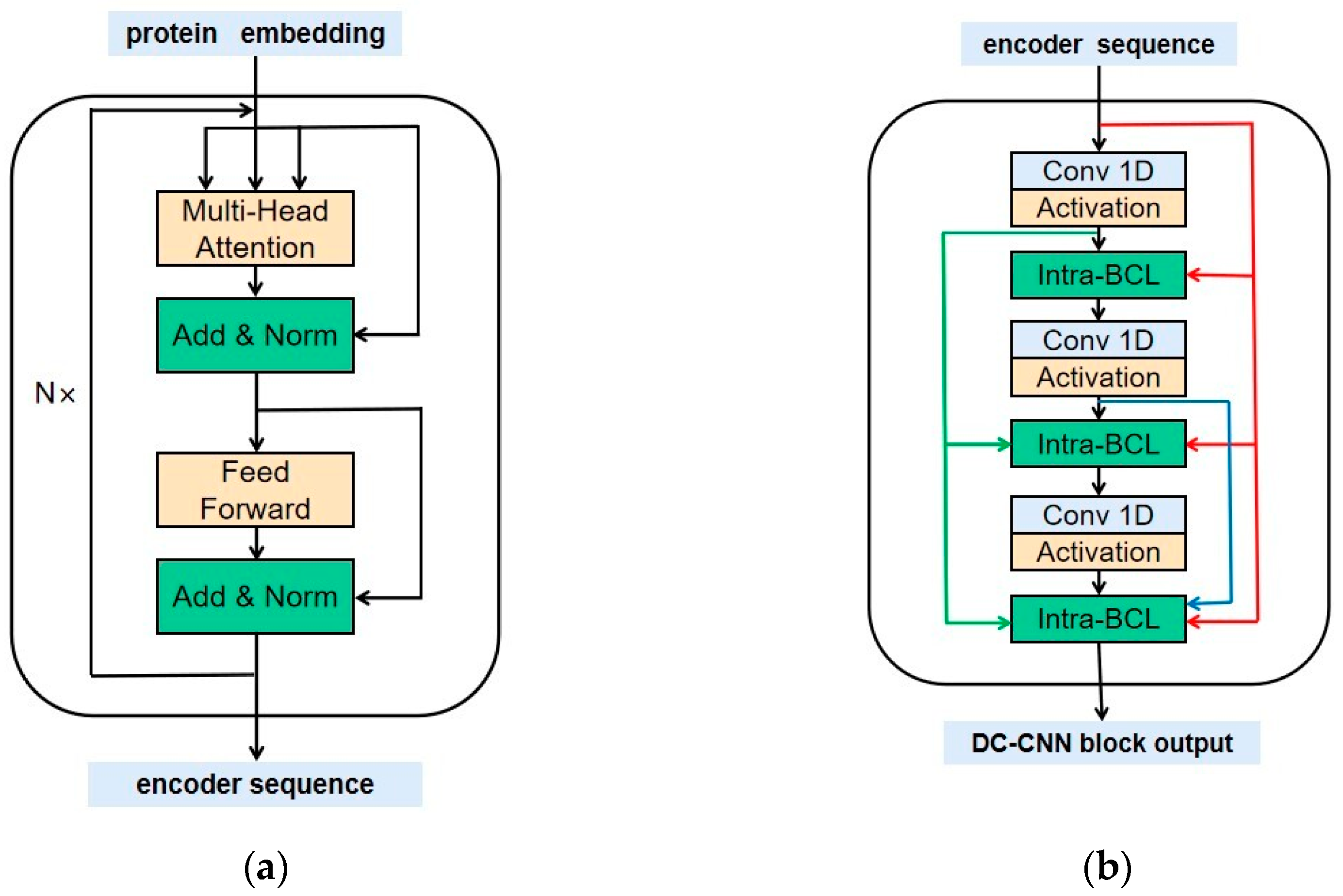
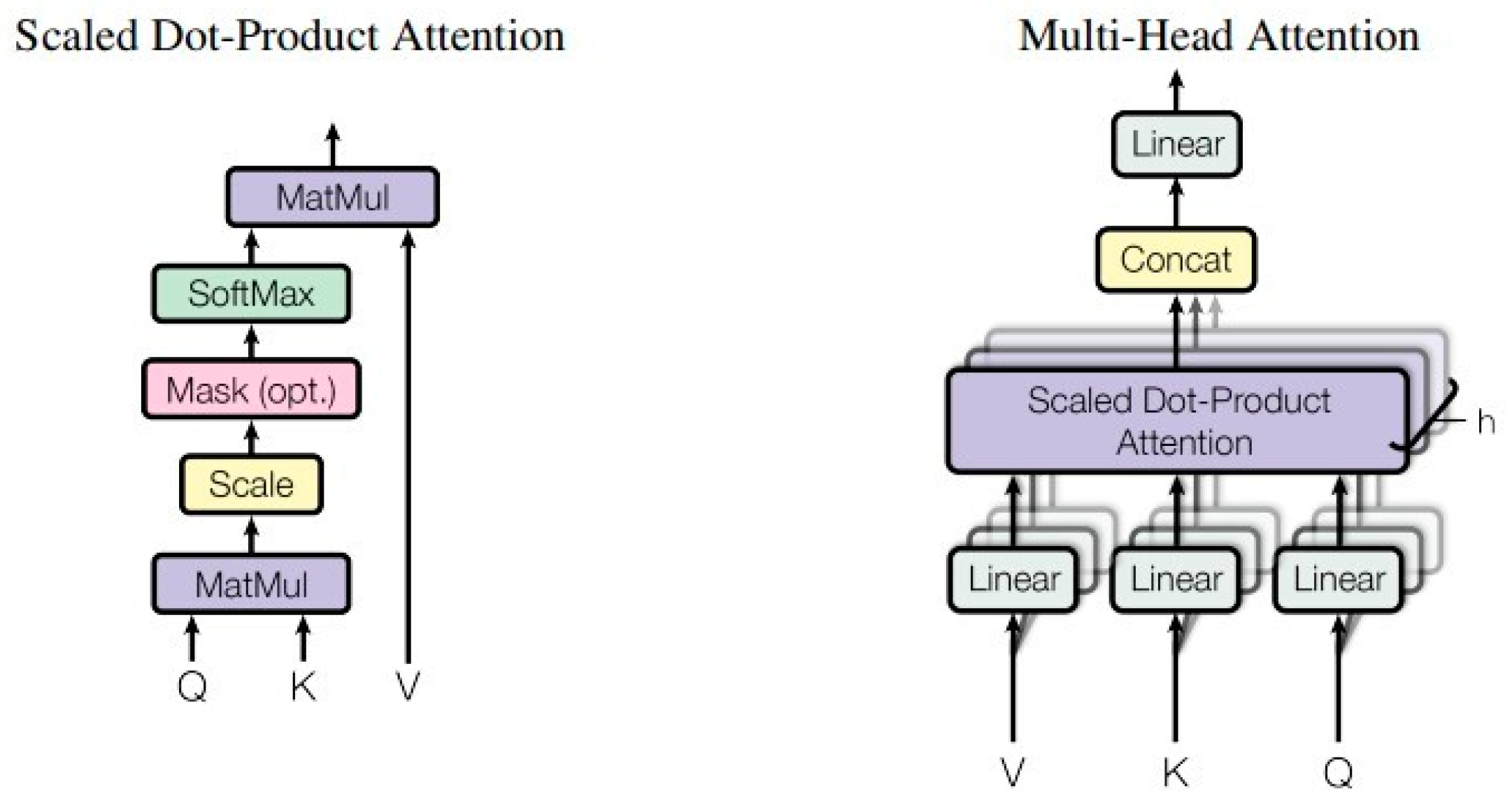
4.3. Methods
4.4. Training of the TransPhos Model
4.5. Performance Evaluation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Audagnotto, M.; Dal Peraro, M. Protein post-translational modifications: In silico prediction tools and molecular modeling. Comput. Struct. Biotechnol. J. 2017, 15, 307–319. [Google Scholar] [CrossRef]
- Khoury, G.A.; Baliban, R.C.; Floudas, C.A. Proteome-wide post-translational modification statistics: Frequency analysis and curation of the swiss-prot database. Sci. Rep. 2011, 1, 90. [Google Scholar] [CrossRef]
- Humphrey, S.J.; James, D.E.; Mann, M. Protein phosphorylation: A major switch mechanism for metabolic regulation. Trends Endocrinol. Metab. 2015, 26, 676–687. [Google Scholar] [CrossRef]
- Trost, B.; Kusalik, A. Computational prediction of eukaryotic phosphorylation sites. Bioinformatics 2011, 27, 2927–2935. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zhang, C.; Zhang, Y.; Meng, X.; Zhang, Z.; Shi, X.; Song, T. IMGG: Integrating Multiple Single-Cell Datasets through Connected Graphs and Generative Adversarial Networks. Int. J. Mol. Sci. 2022, 23, 2082. [Google Scholar] [CrossRef]
- Nishi, H.; Hashimoto, K.; Panchenko, A.R. Phosphorylation in protein-protein binding: Effect on stability and function. Structure 2011, 19, 1807–1815. [Google Scholar] [CrossRef] [Green Version]
- McCubrey, J.; May, W.S.; Duronio, V.; Mufson, A. Serine/threonine phosphorylation in cytokine signal transduction. Leukemia 2000, 14, 9–21. [Google Scholar] [CrossRef]
- Li, T.; Li, F.; Zhang, X. Prediction of kinase-specific phosphorylation sites with sequence features by a log-odds ratio approach. Proteins Struct. Funct. Bioinform. 2008, 70, 404–414. [Google Scholar] [CrossRef]
- Sambataro, F.; Pennuto, M. Post-translational modifications and protein quality control in motor neuron and polyglutamine diseases. Front. Mol. Neurosci. 2017, 10, 82. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Li, C.; Marquez-Lago, T.T.; Leier, A.; Akutsu, T.; Purcell, A.W.; Ian Smith, A.; Lithgow, T.; Daly, R.J.; Song, J. Quokka: A comprehensive tool for rapid and accurate prediction of kinase family-specific phosphorylation sites in the human proteome. Bioinformatics 2018, 34, 4223–4231. [Google Scholar] [CrossRef] [Green Version]
- Cohen, P. The role of protein phosphorylation in human health and disease. The Sir Hans Krebs Medal Lecture. Eur. J. Biochem. 2001, 268, 5001–5010. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Hong, L.; Song, T.; Rodríguez-Patón, A.; Chen, C.; Zhao, H.; Shi, X. Highly biocompatible drug-delivery systems based on DNA nanotechnology. J. Biomed. Nanotechnol. 2017, 13, 747–757. [Google Scholar] [CrossRef]
- Song, T.; Wang, G.; Ding, M.; Rodriguez-Paton, A.; Wang, X.; Wang, S. Network-Based Approaches for Drug Repositioning. Mol. Inform. 2021, 2100200. [Google Scholar] [CrossRef] [PubMed]
- Pang, S.; Zhang, Y.; Song, T.; Zhang, X.; Wang, X.; Rodriguez-Patón, A. AMDE: A novel attention-mechanism-based multidimensional feature encoder for drug–drug interaction prediction. Brief. Bioinform. 2022, 23, bbab545. [Google Scholar] [CrossRef]
- Song, T.; Zhang, X.; Ding, M.; Rodriguez-Paton, A.; Wang, S.; Wang, G. DeepFusion: A Deep Learning Based Multi-Scale Feature Fusion Method for Predicting Drug-Target Interactions. Methods, 2022; in press. [Google Scholar] [CrossRef]
- Rohira, A.D.; Chen, C.-Y.; Allen, J.R.; Johnson, D.L. Covalent small ubiquitin-like modifier (SUMO) modification of Maf1 protein controls RNA polymerase III-dependent transcription repression. J. Biol. Chem. 2013, 288, 19288–19295. [Google Scholar] [CrossRef] [Green Version]
- Aponte, A.M.; Phillips, D.; Harris, R.A.; Blinova, K.; French, S.; Johnson, D.T.; Balaban, R.S. 32P labeling of protein phosphorylation and metabolite association in the mitochondria matrix. Methods Enzymol. 2009, 457, 63–80. [Google Scholar]
- Beausoleil, S.A.; Villén, J.; Gerber, S.A.; Rush, J.; Gygi, S.P. A probability-based approach for high-throughput protein phosphorylation analysis and site localization. Nat. Biotechnol. 2006, 24, 1285–1292. [Google Scholar] [CrossRef]
- Xue, Y.; Li, A.; Wang, L.; Feng, H.; Yao, X. PPSP: Prediction of PK-specific phosphorylation site with Bayesian decision theory. BMC Bioinform. 2006, 7, 163. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.-Y.; Shi, S.-P.; Qiu, J.-D.; Liu, M.-C. Using support vector machines to identify protein phosphorylation sites in viruses. J. Mol. Graph. Model. 2015, 56, 84–90. [Google Scholar] [CrossRef]
- Dou, Y.; Yao, B.; Zhang, C. PhosphoSVM: Prediction of phosphorylation sites by integrating various protein sequence attributes with a support vector machine. Amino Acids 2014, 46, 1459–1469. [Google Scholar] [CrossRef] [PubMed]
- Fan, W.; Xu, X.; Shen, Y.; Feng, H.; Li, A.; Wang, M. Prediction of protein kinase-specific phosphorylation sites in hierarchical structure using functional information and random forest. Amino Acids 2014, 46, 1069–1078. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Thelen, J.J.; Dunker, A.K.; Xu, D. Musite, a tool for global prediction of general and kinase-specific phosphorylation sites. Mol. Cell. Proteom. 2010, 9, 2586–2600. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, L.; Xing, P.; Tang, J.; Zou, Q. PhosPred-RF: A novel sequence-based predictor for phosphorylation sites using sequential information only. IEEE Trans. Nanobioscience 2017, 16, 240–247. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; Morgan Kaufmann: San Francisco, CA, USA, 2017; pp. 5998–6008. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Luo, F.; Wang, M.; Liu, Y.; Zhao, X.-M.; Li, A. DeepPhos: Prediction of protein phosphorylation sites with deep learning. Bioinformatics 2019, 35, 2766–2773. [Google Scholar] [CrossRef] [Green Version]
- Heazlewood, J.L.; Durek, P.; Hummel, J.; Selbig, J.; Weckwerth, W.; Walther, D.; Schulze, W.X. PhosPhAt: A database of phosphorylation sites in Arabidopsis thaliana and a plant-specific phosphorylation site predictor. Nucleic Acids Res. 2007, 36 (Suppl. 1), D1015–D1021. [Google Scholar] [CrossRef]
- Zulawski, M.; Braginets, R.; Schulze, W.X. PhosPhAt goes kinases—searchable protein kinase target information in the plant phosphorylation site database PhosPhAt. Nucleic Acids Res. 2012, 41, D1176–D1184. [Google Scholar] [CrossRef] [Green Version]
- Dinkel, H.; Chica, C.; Via, A.; Gould, C.M.; Jensen, L.J.; Gibson, T.J.; Diella, F. Phospho. ELM: A database of phosphorylation sites—update 2011. Nucleic Acids Res. 2010, 39 (Suppl. 1), D261–D267. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Ren, J.; Gao, X.; Jin, C.; Wen, L.; Yao, X. GPS 2.0, a tool to predict kinase-specific phosphorylation sites in hierarchy. Mol. Cell. Proteom. 2008, 7, 1598–1608. [Google Scholar] [CrossRef] [Green Version]
- Blom, N.; Gammeltoft, S.; Brunak, S. Sequence and structure-based prediction of eukaryotic protein phosphorylation sites. J. Mol. Biol. 1999, 294, 1351–1362. [Google Scholar] [CrossRef]
- Basu, S.; Plewczynski, D. AMS 3.0: Prediction of post-translational modifications. BMC Bioinform. 2010, 11, 210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dang, T.H. SKIPHOS: Non-Kinase Specific Phosphorylation Site Prediction with Random Forests and Amino Acid Skip-Gram Embeddings; VNU University of Engineering and Technology: Hanoi, Vietnam, 2019. [Google Scholar]
- Zar, J.H. Biostatistical Analysis; Pearson Education India: Sholinganallur, India, 1999. [Google Scholar]
- Armaly, M.F.; Krueger, D.E.; Maunder, L.; Becker, B.; Hetherington, J.; Kolker, A.E.; Levene, R.Z.; Maumenee, A.E.; Pollack, I.P.; Shaffer, R.N. Biostatistical analysis of the collaborative glaucoma study: I. Summary report of the risk factors for glaucomatous visual-field defects. Arch. Ophthalmol. 1980, 98, 2163–2171. [Google Scholar] [CrossRef] [PubMed]
- Brownlee, J. Better Deep Learning: Train Faster, Reduce Overfitting, and Make Better Predictions; Machine Learning Mastery: San Francisco, CA, USA, 2018. [Google Scholar]
- Shi, X.; Wu, X.; Song, T.; Li, X. Construction of DNA nanotubes with controllable diameters and patterns using hierarchical DNA sub-tiles. Nanoscale 2016, 8, 14785–14792. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W. Research on the deep learning of the small sample data based on transfer learning. In Proceedings of the AIP Conference Proceedings, Yogyakarta, Indonesia, 9–10 November 2017; AIP Publishing LLC: Melville, NY, USA, 2017; p. 020018. [Google Scholar]
- Ma, J.; Yu, M.K.; Fong, S.; Ono, K.; Sage, E.; Demchak, B.; Sharan, R.; Ideker, T. Using deep learning to model the hierarchical structure and function of a cell. Nat. Methods 2018, 15, 290–298. [Google Scholar] [CrossRef] [PubMed]
- Hornbeck, P.V.; Chabra, I.; Kornhauser, J.M.; Skrzypek, E.; Zhang, B. PhosphoSite: A bioinformatics resource dedicated to physiological protein phosphorylation. Proteomics 2004, 4, 1551–1561. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Song, T.; Chen, Z.; Shi, X.; Chen, C.; Zhang, Z. A universal fast colorimetric method for DNA signal detection with DNA strand displacement and gold nanoparticles. J. Nanomater. 2015, 2015, 365. [Google Scholar] [CrossRef]
- Biswas, A.K.; Noman, N.; Sikder, A.R. Machine learning approach to predict protein phosphorylation sites by incorporating evolutionary information. BMC Bioinform. 2010, 11, 273. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.; Chen, C.; Li, X.; Song, T.; Chen, Z.; Zhang, Z.; Wang, Y. Size-controllable DNA nanoribbons assembled from three types of reusable brick single-strand DNA tiles. Soft Matter 2015, 11, 8484–8492. [Google Scholar] [CrossRef]
- Durek, P.; Schmidt, R.; Heazlewood, J.L.; Jones, A.; MacLean, D.; Nagel, A.; Kersten, B.; Schulze, W.X. PhosPhAt: The Arabidopsis thaliana phosphorylation site database. An update. Nucleic Acids Res. 2010, 38 (Suppl. 1), D828–D834. [Google Scholar] [CrossRef]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [Green Version]
- Blom, N.; Sicheritz-Pontén, T.; Gupta, R.; Gammeltoft, S.; Brunak, S. Prediction of post-translational glycosylation and phosphorylation of proteins from the amino acid sequence. Proteomics 2004, 4, 1633–1649. [Google Scholar] [CrossRef] [PubMed]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar]

| Methods | Residue = S | ||||||
|---|---|---|---|---|---|---|---|
| AUC (%) | Acc (%) | Sn (%) | Sp (%) | Pre (%) | F1 (%) | MCC | |
| TransPhos | 85.79 | 78.18 | 80.56 | 75.80 | 76.83 | 78.65 | 0.564 |
| CNN | 81.56 | 74.96 | 77.12 | 72.80 | 73.85 | 75.45 | 0.500 |
| LSTM | 84.20 | 76.99 | 79.61 | 74.37 | 75.57 | 77.54 | 0.541 |
| RNN | 82.66 | 75.18 | 75.39 | 74.97 | 75.00 | 75.20 | 0.504 |
| FCNN | 82.89 | 75.05 | 72.93 | 77.16 | 76.08 | 74.47 | 0.501 |
| Methods | Residue = T | ||||||
| AUC | Acc | Sn (%) | Sp (%) | Pre (%) | F1 (%) | MCC | |
| TransPhos | 83.35 | 75.59 | 76.54 | 74.70 | 74.12 | 75.31 | 0.512 |
| CNN | 81.99 | 75.50 | 74.82 | 76.16 | 74.82 | 74.82 | 0.510 |
| LSTM | 83.91 | 76.87 | 76.09 | 77.62 | 76.30 | 76.19 | 0.537 |
| RNN | 79.89 | 71.72 | 76.18 | 67.50 | 68.93 | 72.38 | 0.438 |
| FCNN | 80.00 | 73.48 | 73.46 | 73.50 | 72.41 | 72.93 | 0.469 |
| Methods | Residue = Y | ||||||
| AUC | Acc | Sn (%) | Sp (%) | Pre (%) | F1 (%) | MCC | |
| TransPhos | 69.53 | 63.62 | 61.99 | 65.11 | 61.99 | 69.06 | 0.449 |
| CNN | 67.40 | 64.43 | 56.17 | 72.00 | 64.80 | 60.18 | 0.286 |
| LSTM | 68.71 | 63.73 | 66.10 | 61.56 | 61.21 | 63.56 | 0.276 |
| RNN | 67.84 | 62.22 | 75.79 | 49.78 | 58.07 | 65.76 | 0.264 |
| FCNN | 69.55 | 64.31 | 61.02 | 67.33 | 63.16 | 62.07 | 0.284 |
| Methods | Residue = S | ||||||
|---|---|---|---|---|---|---|---|
| AUC (%) | Acc (%) | Sn (%) | Sp (%) | Pre (%) | F1 (%) | MCC | |
| TransPhos | 78.67 | 71.53 | 67.16 | 75.89 | 73.59 | 70.23 | 0.432 |
| CNN | 74.34 | 68.40 | 61.14 | 75.65 | 71.52 | 65.93 | 0.372 |
| LSTM | 77.04 | 70.48 | 65.01 | 75.95 | 72.99 | 68.77 | 0.412 |
| RNN | 75.53 | 68.84 | 61.44 | 76.24 | 72.11 | 66.35 | 0.381 |
| FCNN | 75.30 | 69.14 | 60.68 | 77.61 | 73.04 | 66.29 | 0.388 |
| Methods | Residue = T | ||||||
| AUC | Acc | Sn (%) | Sp (%) | Pre (%) | F1 (%) | MCC | |
| TransPhos | 67.19 | 61.77 | 47.32 | 76.22 | 66.56 | 55.32 | 0.246 |
| CNN | 64.44 | 59.19 | 42.03 | 76.34 | 63.98 | 50.74 | 0.196 |
| LSTM | 66.59 | 60.64 | 41.85 | 79.43 | 67.05 | 51.54 | 0.230 |
| RNN | 66.03 | 61.21 | 48.57 | 73.84 | 65.00 | 55.60 | 0.232 |
| FCNN | 63.94 | 59.63 | 45.30 | 73.96 | 63.50 | 52.88 | 0.201 |
| Methods | Residue = Y | ||||||
| AUC | Acc | Sn (%) | Sp (%) | Pre (%) | F1 (%) | MCC | |
| TransPhos | 60.09 | 55.41 | 38.52 | 72.30 | 58.17 | 46.35 | 0.115 |
| CNN | 59.11 | 54.59 | 34.81 | 74.37 | 57.60 | 43.40 | 0.100 |
| LSTM | 59.49 | 55.56 | 40.74 | 70.37 | 57.89 | 47.83 | 0.116 |
| RNN | 61.71 | 59.48 | 58.96 | 60.00 | 59.58 | 59.27 | 0.190 |
| FCNN | 59.30 | 56.44 | 43.26 | 69.63 | 58.75 | 49.83 | 0.134 |
| Residue | Methods | 10-Fold Cross-Validation Test (P.ELM) | Independent Dataset Test (PPA) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Sn | Sp | MCC | AUC | Sn | Sp | MCC | AUC | ||
| S | GPS 2.1 | 33.07 | 93.29 | 0.201 | 0.741 | 22.20 | 95.26 | 0.135 | 0.670 |
| NetPhos | 34.14 | 86.73 | 0.123 | 0.702 | 28.55 | 87.23 | 0.081 | 0.643 | |
| PPRED | 32.27 | 91.64 | 0.169 | 0.751 | 21.32 | 94.00 | 0.107 | 0.676 | |
| Musite | 41.37 | 93.66 | 0.249 | 0.807 | 28.60 | 95.21 | 0.182 | 0.726 | |
| PhosphoSVM | 44.43 | 94.04 | 0.298 | 0.841 | 34.01 | 95.90 | 0.237 | 0.776 | |
| SKIPHOS | 78.50 | 74.90 | 0.521 | 0.845 | 46.20 | 68.60 | 0.265 | 0.691 | |
| DeepPhos | 81.81 | 75.30 | 0.572 | 0.859 | 66.43 | 75.89 | 0.425 | 0.775 | |
| TransPhos | 80.56 | 75.80 | 0.564 | 0.858 | 67.16 | 75.89 | 0.432 | 0.787 | |
| T | GPS 2.1 | 38.10 | 92.30 | 0.201 | 0.695 | 13.48 | 94.51 | 0.067 | 0.572 |
| NetPhos | 34.32 | 83.65 | 0.090 | 0.655 | 27.02 | 80.66 | 0.038 | 0.554 | |
| PPRED | 30.31 | 90.99 | 0.134 | 0.726 | 26.43 | 83.51 | 0.052 | 0.578 | |
| Musite | 33.84 | 94.76 | 0.221 | 0.785 | 15.56 | 95.36 | 0.098 | 0.622 | |
| PhosphoSVM | 37.31 | 94.99 | 0.251 | 0.818 | 21.79 | 93.41 | 0.115 | 0.665 | |
| SKIPHOS | 74.40 | 78.80 | 0.547 | 0.844 | 65.80 | 58.60 | 0.197 | 0.643 | |
| DeepPhos | 77.63 | 73.58 | 0.512 | 0.826 | 46.02 | 76.04 | 0.231 | 0.674 | |
| TransPhos | 76.54 | 74.70 | 0.512 | 0.834 | 47.32 | 76.22 | 0.246 | 0.672 | |
| Y | GPS 2.1 | 34.49 | 78.86 | 0.083 | 0.611 | 47.93 | 60.83 | 0.043 | 0.552 |
| NetPhos | 34.66 | 84.45 | 0.132 | 0.653 | 63.91 | 46.10 | 0.048 | 0.554 | |
| PPRED | 43.04 | 82.65 | 0.169 | 0.702 | 42.01 | 65.08 | 0.064 | 0.539 | |
| Musite | 38.42 | 86.74 | 0.182 | 0.720 | 28.85 | 81.71 | 0.064 | 0.587 | |
| PhosphoSVM | 41.92 | 87.34 | 0.209 | 0.738 | 28.55 | 84.39 | 0.084 | 0.595 | |
| SKIPHOS | 71.10 | 69.10 | 0.396 | 0.700 | 65.80 | 58.60 | 0.197 | 0.634 | |
| DeepPhos | 69.01 | 64.22 | 0.332 | 0.714 | 49.93 | 66.37 | 0.165 | 0.621 | |
| TransPhos | 61.99 | 65.11 | 0.271 | 0.695 | 38.52 | 72.30 | 0.115 | 0.601 | |
| Dataset | Residue | # of Sequences | # of Sites |
|---|---|---|---|
| P.ELM | S | 6635 | 20,964 |
| T | 3227 | 5685 | |
| Y | 1392 | 2163 | |
| PPA | S | 3037 | 5437 |
| T | 1359 | 1686 | |
| Y | 617 | 676 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zhang, Z.; Zhang, C.; Meng, X.; Shi, X.; Qu, P. TransPhos: A Deep-Learning Model for General Phosphorylation Site Prediction Based on Transformer-Encoder Architecture. Int. J. Mol. Sci. 2022, 23, 4263. https://doi.org/10.3390/ijms23084263
Wang X, Zhang Z, Zhang C, Meng X, Shi X, Qu P. TransPhos: A Deep-Learning Model for General Phosphorylation Site Prediction Based on Transformer-Encoder Architecture. International Journal of Molecular Sciences. 2022; 23(8):4263. https://doi.org/10.3390/ijms23084263
Chicago/Turabian StyleWang, Xun, Zhiyuan Zhang, Chaogang Zhang, Xiangyu Meng, Xin Shi, and Peng Qu. 2022. "TransPhos: A Deep-Learning Model for General Phosphorylation Site Prediction Based on Transformer-Encoder Architecture" International Journal of Molecular Sciences 23, no. 8: 4263. https://doi.org/10.3390/ijms23084263
APA StyleWang, X., Zhang, Z., Zhang, C., Meng, X., Shi, X., & Qu, P. (2022). TransPhos: A Deep-Learning Model for General Phosphorylation Site Prediction Based on Transformer-Encoder Architecture. International Journal of Molecular Sciences, 23(8), 4263. https://doi.org/10.3390/ijms23084263






