Tracing the Primordial Chemical Life of Glycine: A Review from Quantum Chemical Simulations
Abstract
1. Introduction
2. Computational Framework
2.1. Quantum Chemical Methods and Basis Sets
2.2. Potential Energy Surfaces (PESs) and Thermochemical Corrections
2.3. Molecular Dynamics and Metadynamics
2.4. Surface Modeling
3. Gly Formation in the ISM
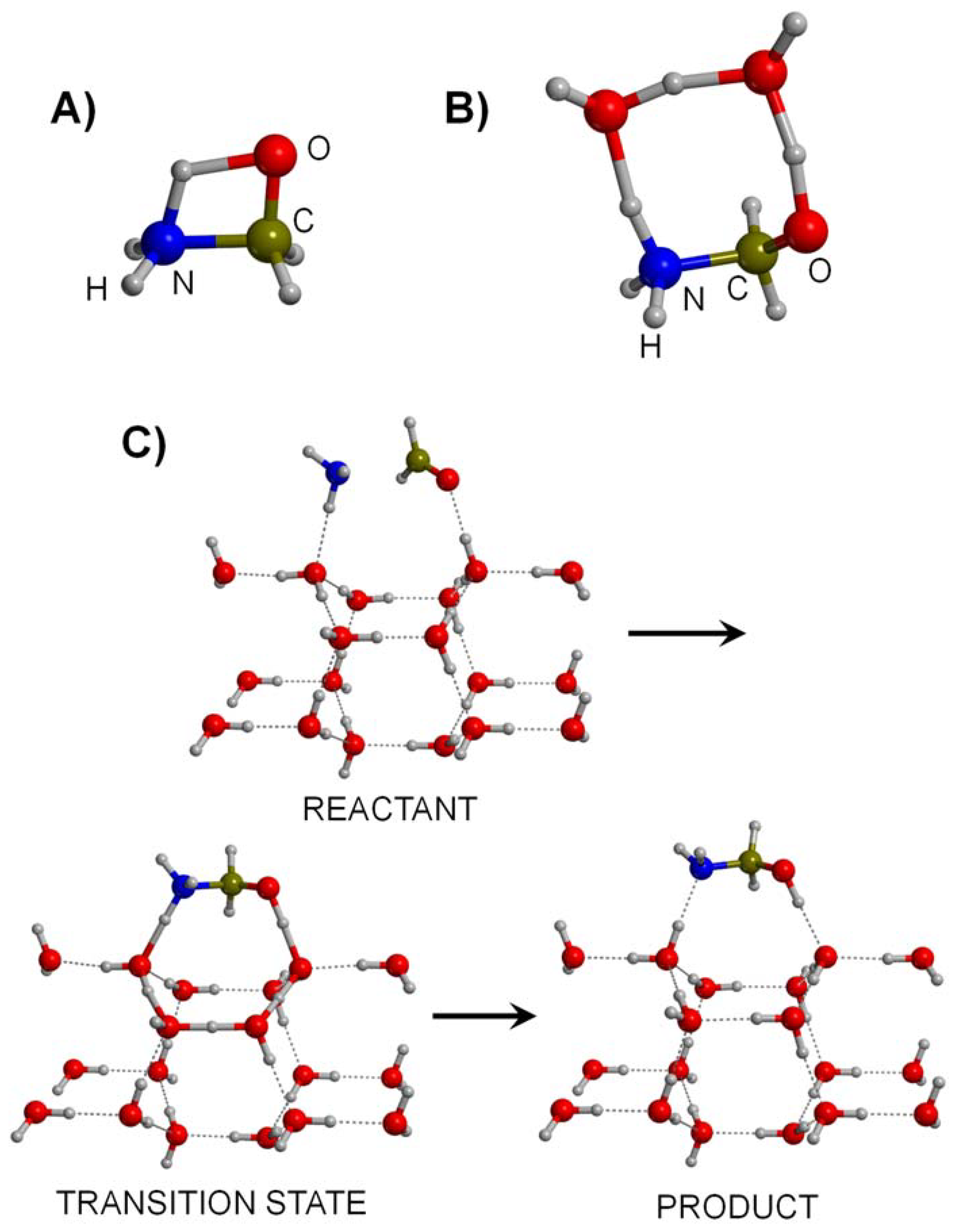
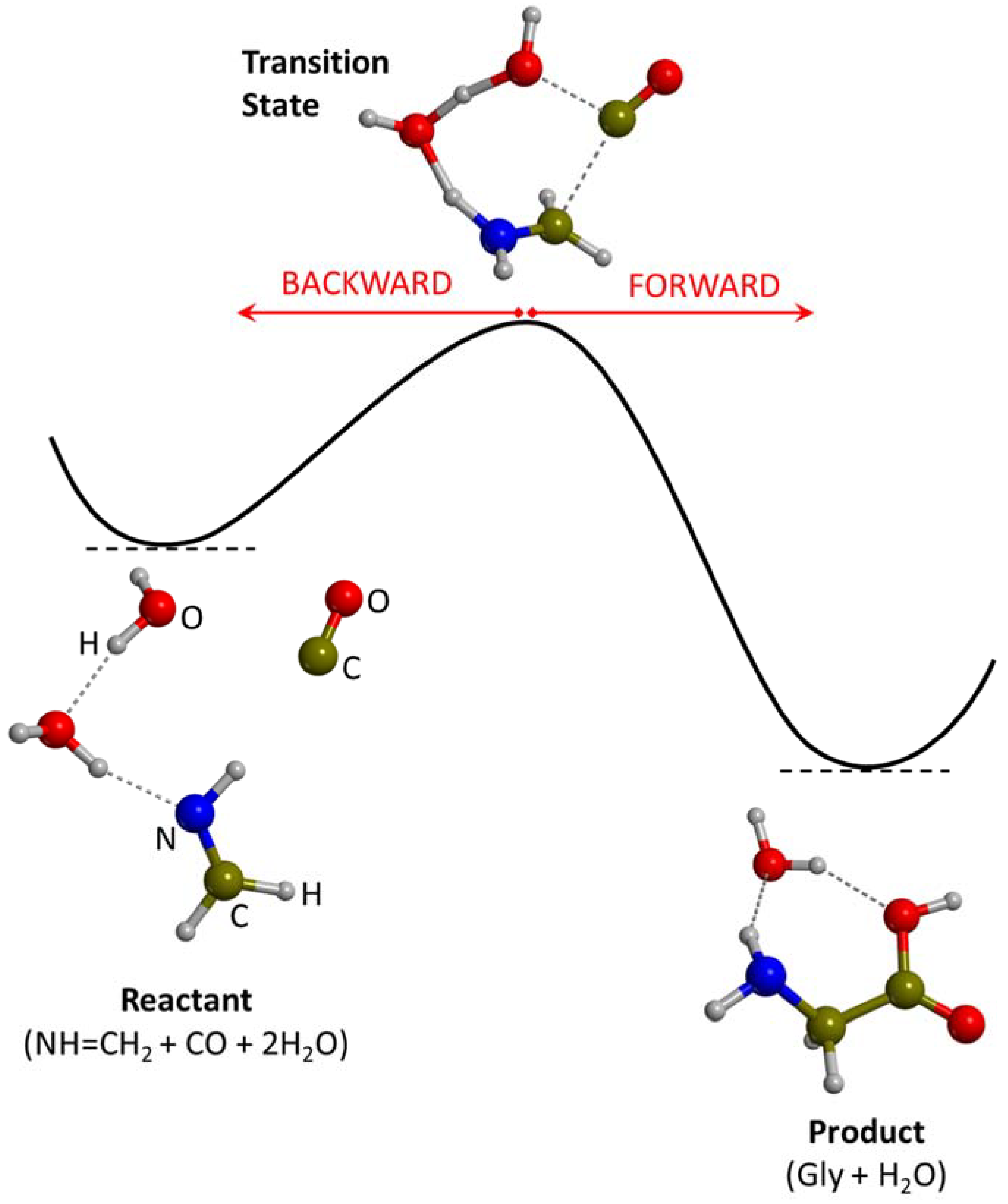
3.1. Gas-Phase Routes
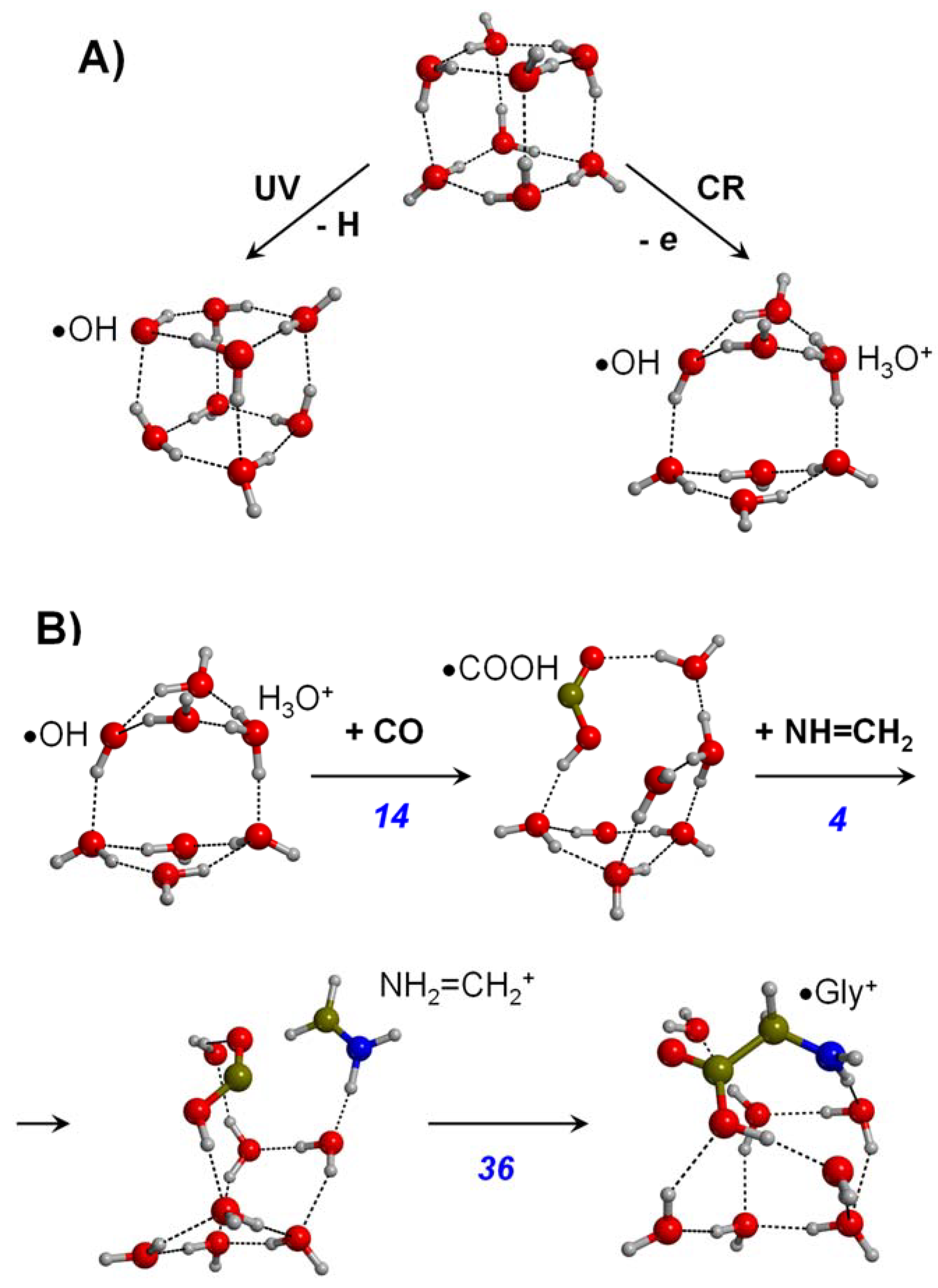
3.2. Grain Surface Routes
- (i)
- H2C=O + NH3 → NH2CH2OH → NH=CH2 + H2O;
- (ii)
- NH=CH2 + HCN → NH2CH2CN;
- (iii)
- NH2CH2CN + 2H2O → NH2CH2COOH + NH3.
4. Gly Transportation and Delivery to Primitive Earth
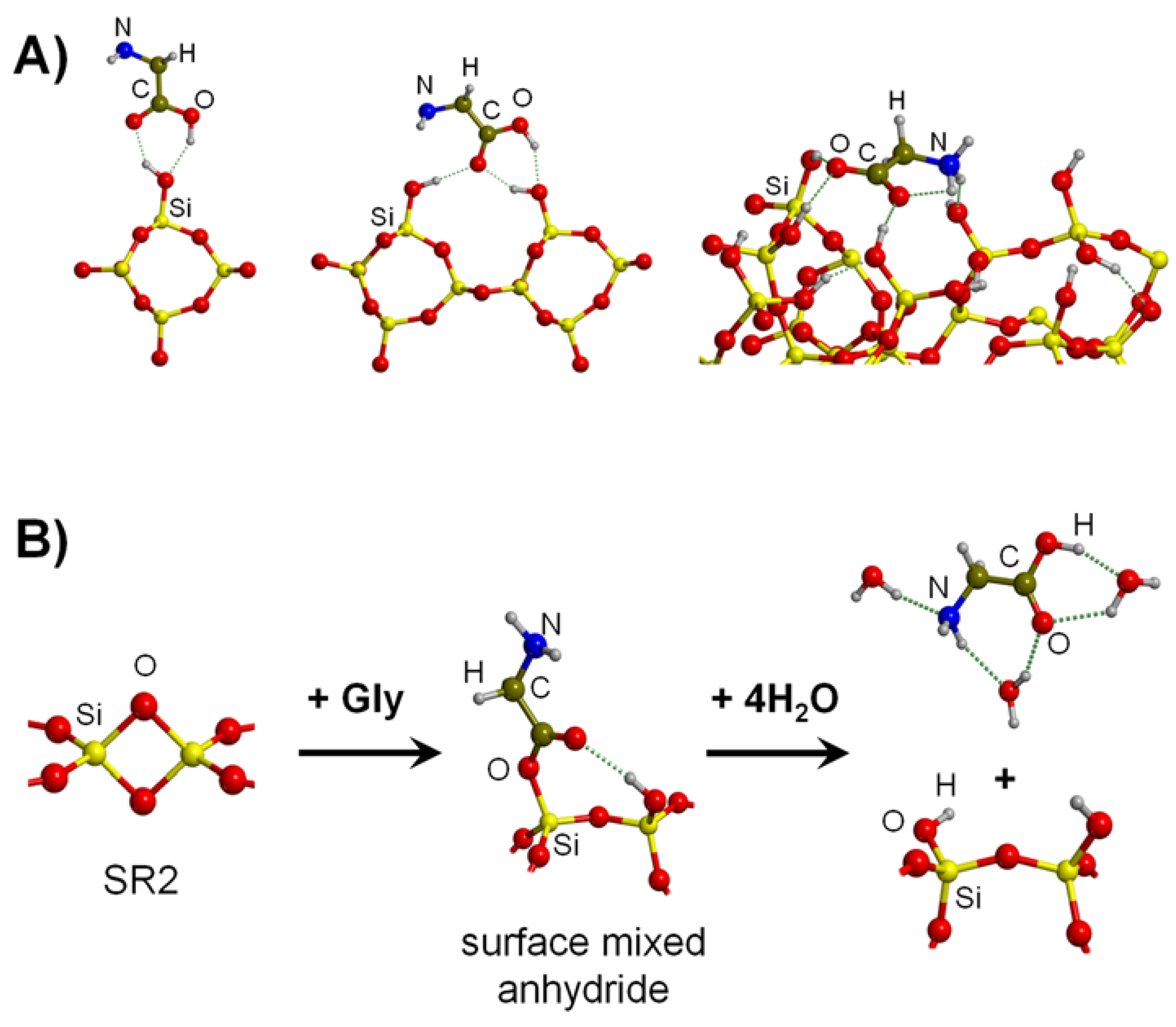
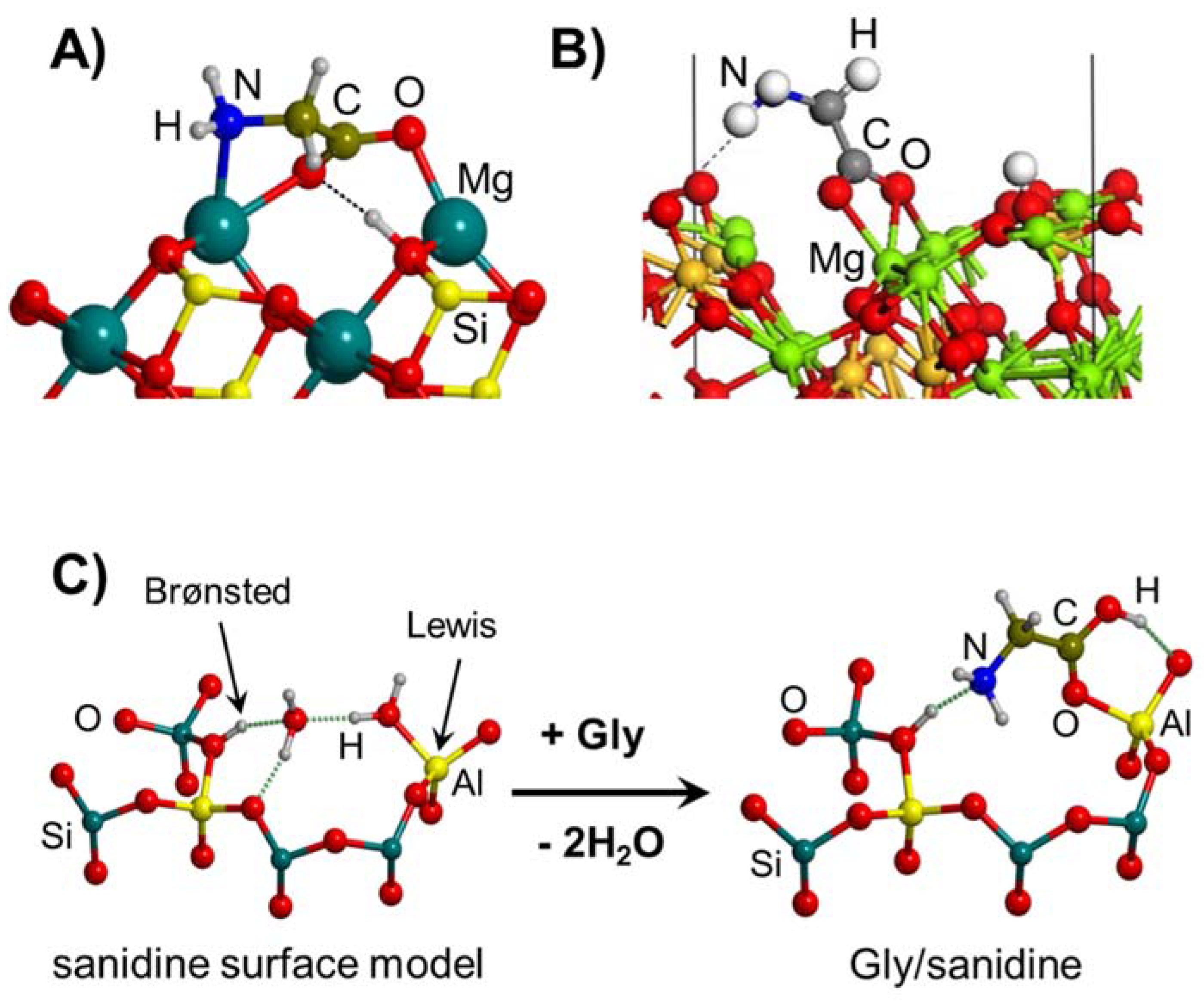
4.1. Gly Interaction with Silica, Silicates and Aluminosilicates
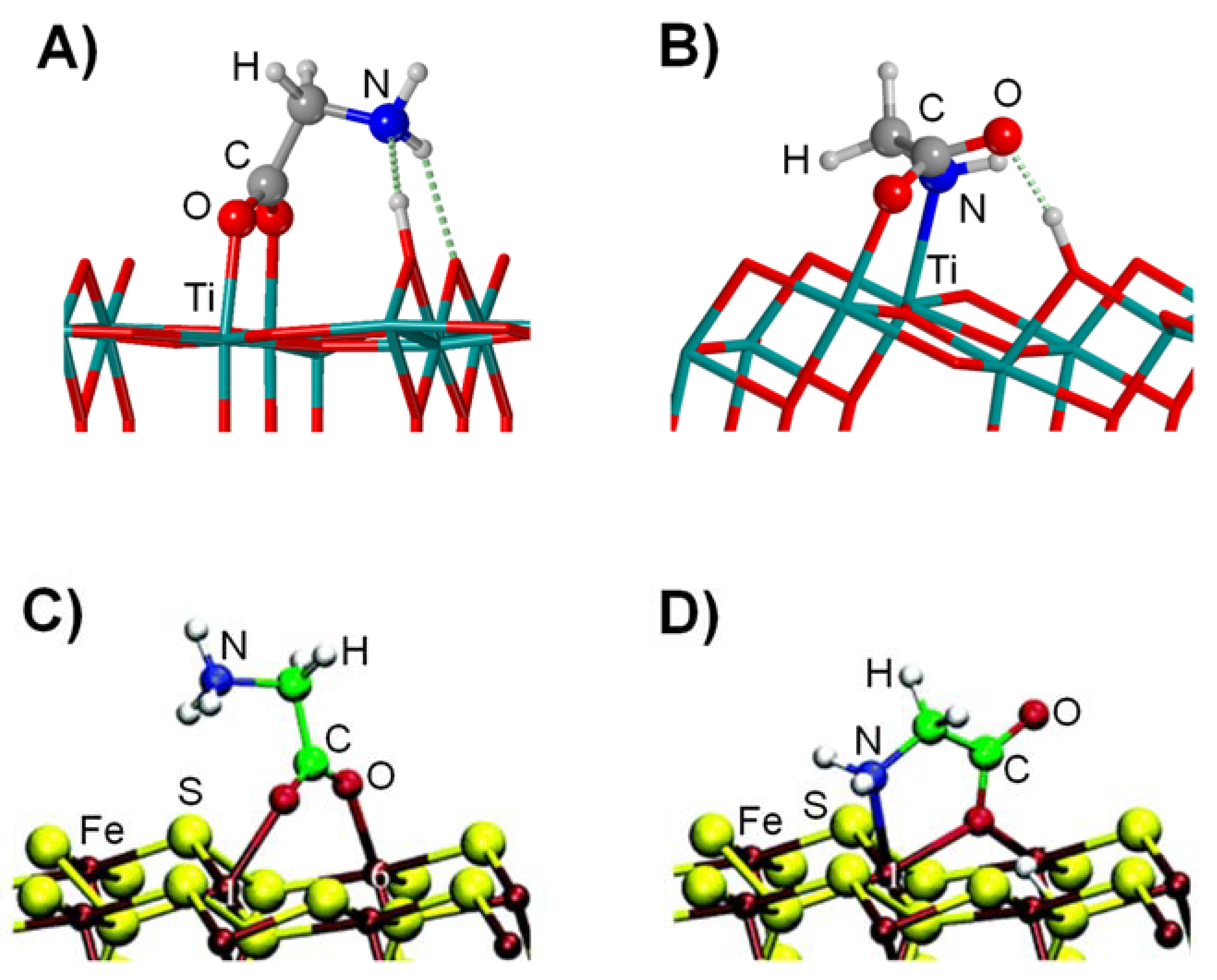
4.2. Gly Interaction with Metal Oxides and Sulphides
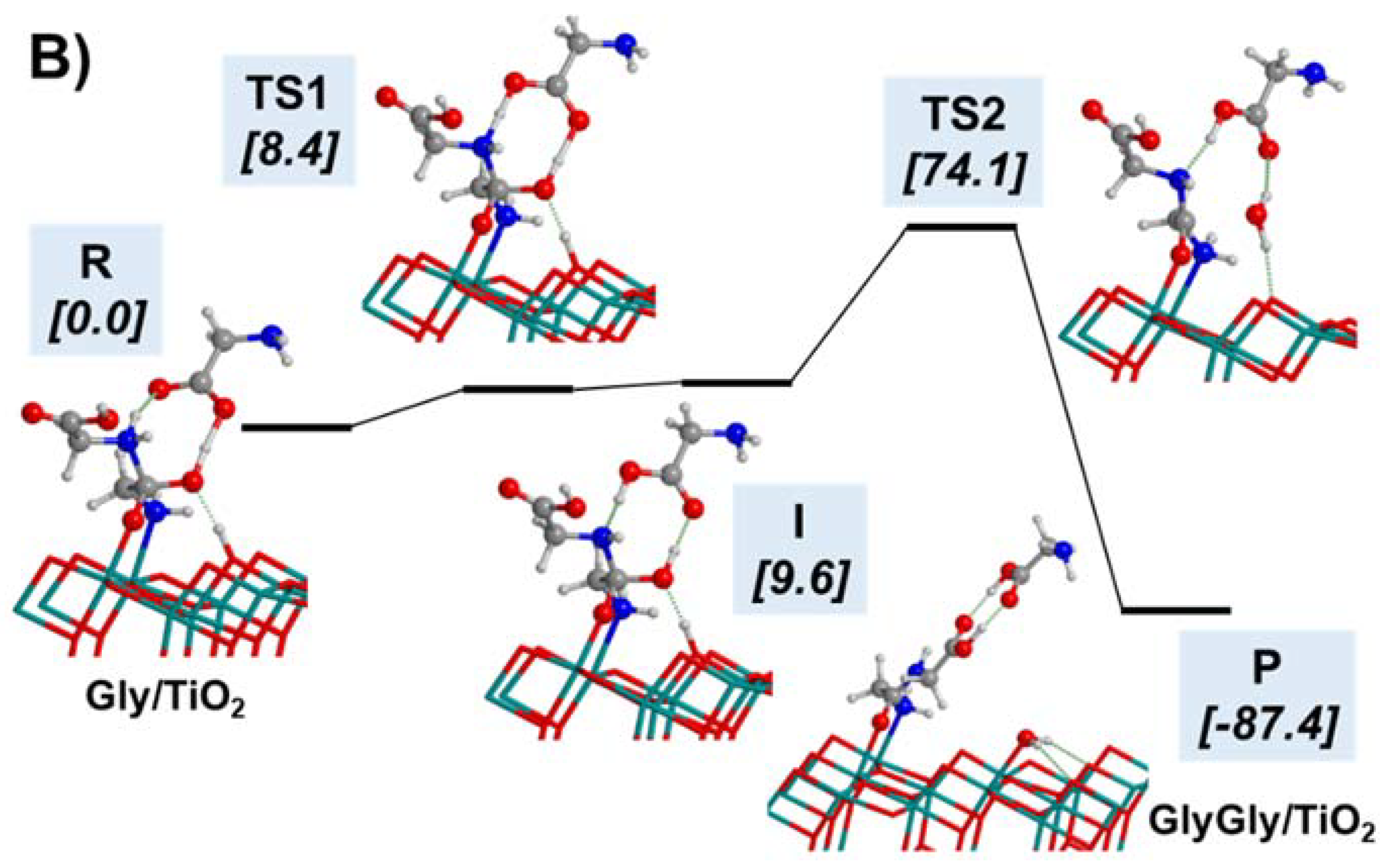
5. Gly Polymerization in the Primitive Earth
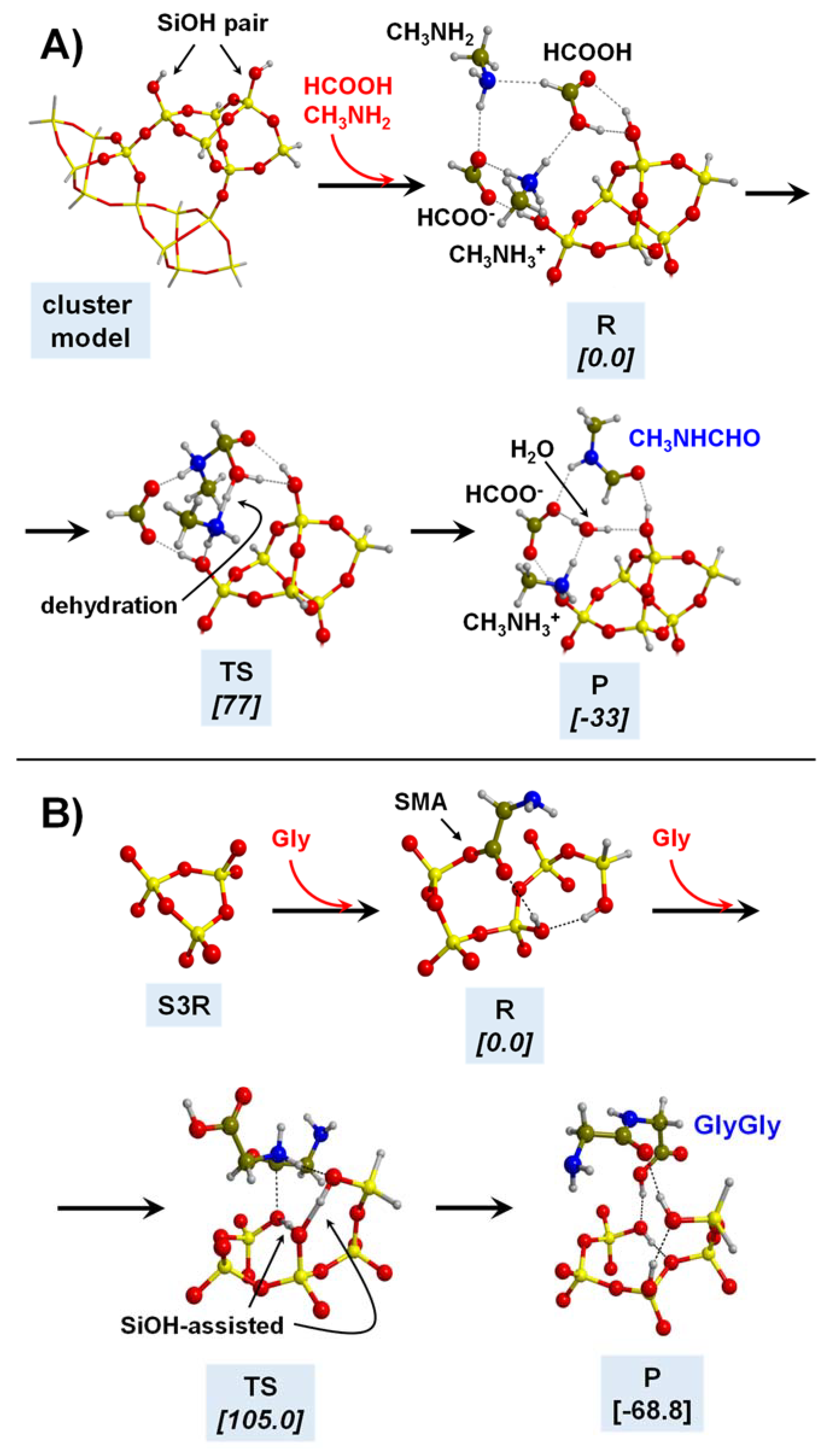
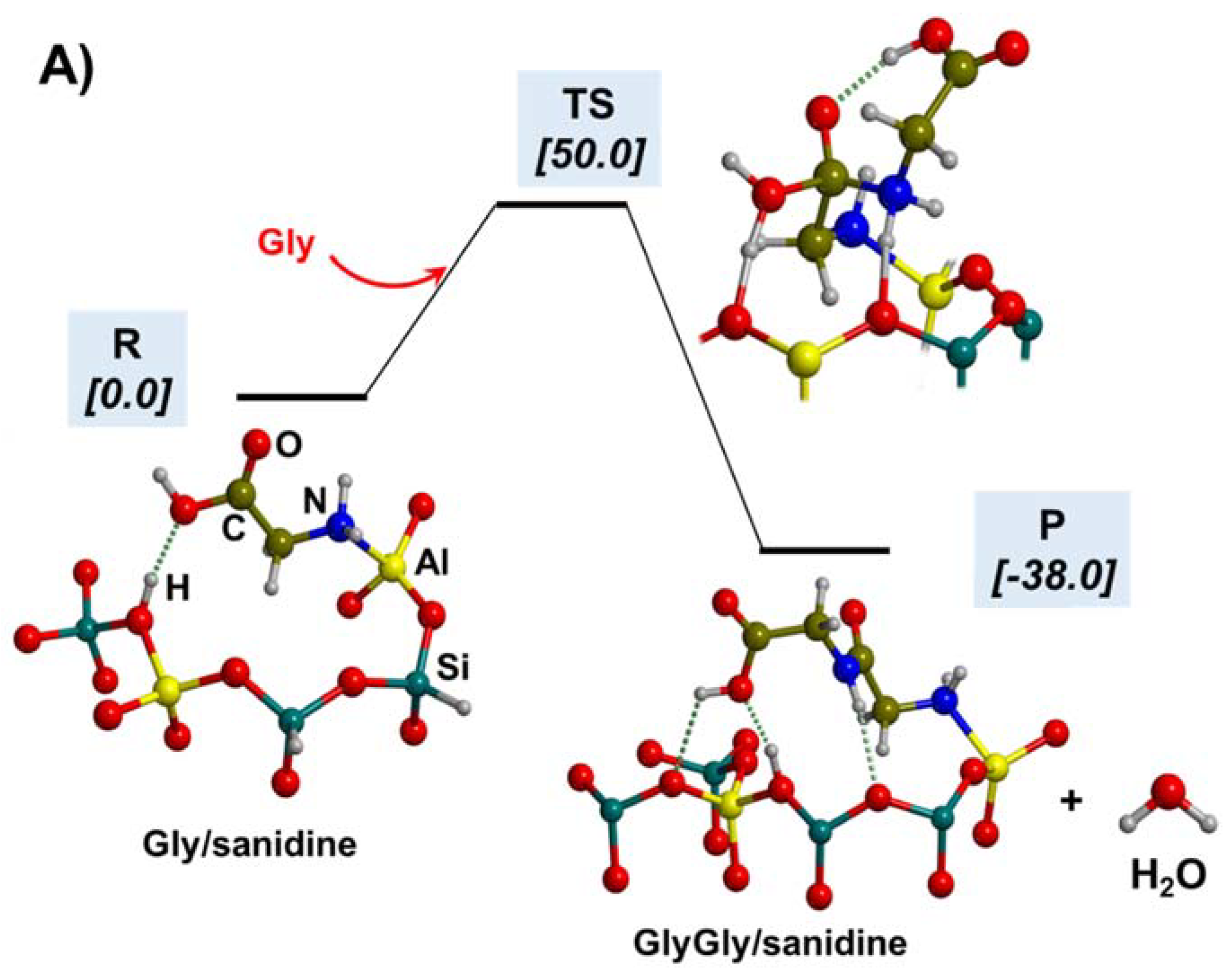
5.1. In the Presence of Mineral Surfaces
5.2. In the Presence of Iron Sulphides under Oceanic Extreme Conditions
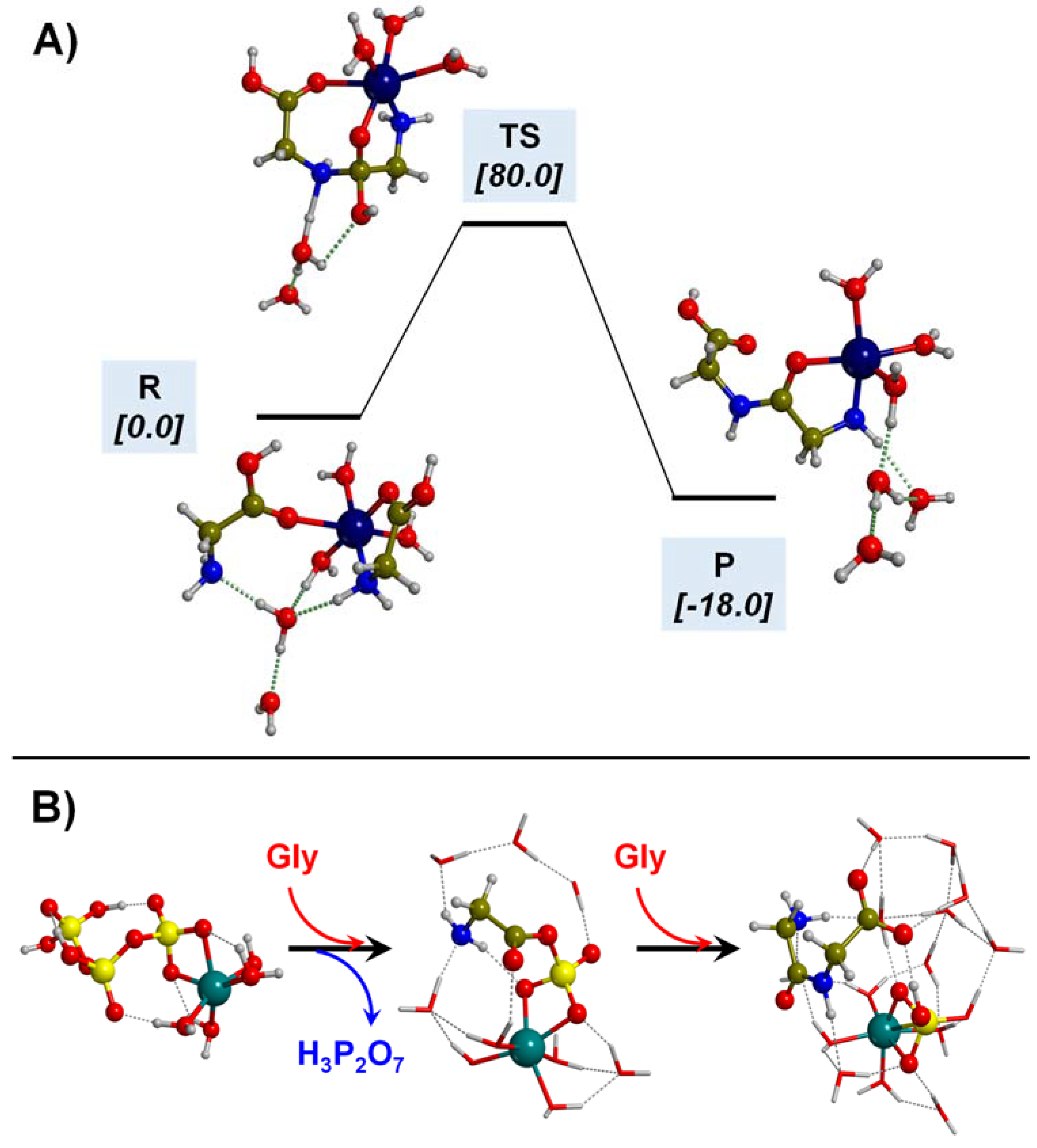
5.3. In the Presence of Metal Cations in Aqueous Solution
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cheung, A.C.; Rank, D.M.; Townes, C.H.; Thornton, D.D.; Welch, W.J. Detection of NH3 Molecules in the Interstellar Medium by Their Microwave Emission. Phys. Rev. Lett. 1968, 21, 1701–1705. [Google Scholar] [CrossRef]
- van Dishoeck, E.F. Astrochemistry of dust, ice and gas: Introduction and overview. Faraday Discuss. 2014, 168, 9–47. [Google Scholar] [CrossRef] [PubMed]
- Tielens, A.G.G.M. The molecular universe. Rev. Modern Phys. 2013, 85, 1021–1081. [Google Scholar] [CrossRef]
- Herbst, E. Three milieux for interstellar chemistry: Gas, dust, and ice. Phys. Chem. Chem. Phys. 2014, 16, 3344–3359. [Google Scholar] [CrossRef]
- McGuire, B.A. 2021 Census of Interstellar, Circumstellar, Extragalactic, Protoplanetary Disk, and Exoplanetary Molecules. Astrophys. J. Suppl. Ser. 2022, 259, 30. [Google Scholar] [CrossRef]
- Henning, T. Cosmic silicates. Annu. Rev. Astron. Astrophys. 2010, 48, 21–46. [Google Scholar] [CrossRef]
- Jones, A.P.; Köhler, M.; Ysard, N.; Bocchio, M.; Verstraete, L.J.A. The global dust modelling framework THEMIS. Astron. Astrophys. 2017, 602, A46. [Google Scholar] [CrossRef]
- Boogert, A.C.A.; Gerakines, P.A.; Whittet, D.C.B. Observations of the icy Universe. Annu. Rev. Astron. Astrophys. 2015, 53, 541–581. [Google Scholar] [CrossRef]
- Caselli, P.; Ceccarelli, C. Our astrochemical heritage. Astron. Astrophys. Rev. 2012, 20, 56. [Google Scholar] [CrossRef]
- Kwok, S. Complex organics in space from Solar System to distant galaxies. Astron. Astrophys. Rev. 2016, 24, 8. [Google Scholar] [CrossRef]
- Kitadai, N.; Maruyama, S. Origins of building blocks of life: A review. Geosci. Front. 2018, 9, 1117–1153. [Google Scholar] [CrossRef]
- Ceccarelli, C.; Caselli, P.; Fontani, F.; Neri, R.; López-Sepulcre, A.; Codella, C.; Feng, S.; Jiménez-Serra, I.; Lefloch, B.; Pineda, J.E.; et al. Seeds Of Life In Space (SOLIS): The Organic Composition Diversity at 300–1000 au Scale in Solar-type Star-forming Regions. Astrophys. J. 2017, 850, 176. [Google Scholar] [CrossRef]
- Ginolfi, M.; Graziani, L.; Schneider, R.; Marassi, S.; Valiante, R.; Dell’Agli, F.; Ventura, P.; Hunt, L.K. Where does galactic dust come from? Mon. Not. R. Astron. Soc. 2017, 473, 4538–4543. [Google Scholar] [CrossRef]
- Ceccarelli, C.; Viti, S.; Balucani, N.; Taquet, V. The evolution of grain mantles and silicate dust growth at high redshift. Mon. Not. R. Astron. Soc. 2018, 476, 1371–1383. [Google Scholar] [CrossRef]
- Duve, C.D. Singularities. Landmarks on the Pathways of Life; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Vidali, G. H2 Formation on Interstellar Grains. Chem. Rev. 2013, 113, 8762–8782. [Google Scholar] [CrossRef]
- Wakelam, V.; Bron, E.; Cazaux, S.; Dulieu, F.; Gry, C.; Guillard, P.; Habart, E.; Hornekær, L.; Morisset, S.; Nyman, G.; et al. H2 formation on interstellar dust grains: The viewpoints of theory, experiments, models and observations. Mol. Astrophys. 2017, 9, 1–36. [Google Scholar] [CrossRef]
- Navarro-Ruiz, J.; Martínez-González, J.Á.; Sodupe, M.; Ugliengo, P.; Rimola, A. Relevance of silicate surface morphology in interstellar H2 formation. Insights from quantum chemical calculations. Mon. Not. R. Astron. Soc. 2015, 453, 914–924. [Google Scholar] [CrossRef]
- Navarro-Ruiz, J.; Sodupe, M.; Ugliengo, P.; Rimola, A. Interstellar H adsorption and H2 formation on the crystalline (010) forsterite surface: A B3LYP-D2* periodic study. Phys. Chem. Chem. Phys. 2014, 16, 17447–17457. [Google Scholar] [CrossRef]
- Navarro-Ruiz, J.; Ugliengo, P.; Sodupe, M.; Rimola, A. Does Fe2+ in olivine-based interstellar grains play any role in the formation of H2? Atomistic insights from DFT periodic simulations. Chem. Commun. 2016, 52, 6873–6876. [Google Scholar] [CrossRef]
- van Dishoeck, E.F.; Herbst, E.; Neufeld, D.A. Interstellar water chemistry: From laboratory to observations. Chem. Rev. 2013, 113, 9043–9085. [Google Scholar] [CrossRef]
- Molpeceres, G.; Rimola, A.; Ceccarelli, C.; Kästner, J.; Ugliengo, P.; Maté, B. Silicate-mediated interstellar water formation: A theoretical study. Mon. Not. R. Astron. Soc. 2019, 482, 5389–5400. [Google Scholar] [CrossRef] [PubMed]
- Dulieu, F.; Amiaud, L.; Congiu, E.; Fillion, J.-H.; Matar, E.; Momeni, A.; Pirronello, V.; Lemaire, J.L. Experimental evidence for water formation on interstellar dust grains by hydrogen and oxygen atoms. Astron. Astrophys. 2010, 512, A30. [Google Scholar] [CrossRef]
- Ioppolo, S.; Cuppen, H.M.; Romanzin, C.; van Dishoeck, E.F.; Linnartz, H. Laboratory Evidence for Efficient Water Formation in Interstellar Ices. Astrophys. J. 2008, 686, 1474–1479. [Google Scholar] [CrossRef]
- Oba, Y.; Watanabe, N.; Kouchi, A.; Hama, T.; Pirronello, V. Experimental studies of surface reactions among OH radicals that yield H2O and CO2 at 40–60 K. Phys. Chem. Chem. Phys. 2011, 13, 15792–15797. [Google Scholar] [CrossRef]
- Romanzin, C.; Ioppolo, S.; Cuppen, H.M.; Dishoeck, E.F.; Linnartz, H. Water formation by surface O3 hydrogenation. J. Chem. Phys. 2011, 134, 084504. [Google Scholar] [CrossRef]
- Hama, T.; Watanabe, N. Surface processes on interstellar amorphous solid water: Adsorption, diffusion, tunneling reactions, and nuclear-spin conversion. Chem. Rev. 2013, 113, 8783–8839. [Google Scholar] [CrossRef]
- Watanabe, N.; Kouchi, A. Ice surface reactions: A key to chemical evolution in space. Prog. Surf. Sci. 2008, 83, 439–489. [Google Scholar] [CrossRef]
- Watanabe, N.; Kouchi, A. Efficient Formation of Formaldehyde and Methanol by the Addition of Hydrogen Atoms to CO in H2O-CO Ice at 10 K. Astrophys. J. 2002, 571, L173–L176. [Google Scholar] [CrossRef]
- Rimola, A.; Taquet, V.; Ugliengo, P.; Balucani, N.; Ceccarelli, C. Combined quantum chemical and modeling study of CO hydrogenation on water ice. Astron. Astrophys. 2014, 572, A70. [Google Scholar] [CrossRef]
- Perrero, J.; Enrique-Romero, J.; Martínez-Bachs, B.; Ceccarelli, C.; Balucani, N.; Ugliengo, P.; Rimola, A. Non-energetic Formation of Ethanol via CCH Reaction with Interstellar H2O Ices. A Computational Chemistry Study. ACS Earth Space Chem. 2022, 6, 496–511. [Google Scholar] [CrossRef]
- Herbst, E. The synthesis of large interstellar molecules. Int. Rev. Phys. Chem. 2017, 36, 287–331. [Google Scholar] [CrossRef]
- Öberg, K.I. Photochemistry and astrochemistry: Photochemical pathways to interstellar complex organic molecules. Chem. Rev. 2016, 116, 9631–9663. [Google Scholar] [CrossRef] [PubMed]
- Linnartz, H.; Ioppolo, S.; Fedoseev, G. Atom addition reactions in interstellar ice analogues. Int. Rev. Phys. Chem. 2015, 34, 205–237. [Google Scholar] [CrossRef]
- Zamirri, L.; Ugliengo, P.; Ceccarelli, C.; Rimola, A. Quantum Mechanical Investigations on the Formation of Complex Organic Molecules on Interstellar Ice Mantles. Review and Perspectives. ACS Earth Space Chem. 2019, 3, 1499–1523. [Google Scholar] [CrossRef]
- Enrique-Romero, J.; Rimola, A.; Ceccarelli, C.; Ugliengo, P.; Balucani, N.; Skouteris, D. Reactivity of HCO with CH3 and NH2 on Water Ice Surfaces. A Comprehensive Accurate Quantum Chemistry Study. ACS Earth Space Chem. 2019, 3, 2158–2170. [Google Scholar] [CrossRef]
- Rimola, A.; Skouteris, D.; Balucani, N.; Ceccarelli, C.; Enrique-Romero, J.; Taquet, V.; Ugliengo, P. Can formamide be formed on interstellar ice? An atomistic perspective. ACS Earth Space Chem. 2018, 2, 720–734. [Google Scholar] [CrossRef]
- Enrique-Romero, J.; Ceccarelli, C.; Rimola, A.; Skouteris, D.; Balucani, N.; Ugliengo, P. Theoretical computations on the efficiency of acetaldehyde formation on interstellar icy grains. Astron. Astrophys. 2021, 655, A9. [Google Scholar] [CrossRef]
- Enrique-Romero, J.; Rimola, A.; Ceccarelli, C.; Ugliengo, P.; Balucani, N.; Skouteris, D. Quantum mechanical simulations of the radical-radical chemistry on icy surfaces. Astrophys. J. Suppl. Ser. 2022, 259, 39. [Google Scholar] [CrossRef]
- Bockelée-Morvan, D.; Biver, N. The composition of cometary ices. Philos. Trans. R. Soc. A 2017, 375, 20160252. [Google Scholar] [CrossRef]
- Pizzarello, S. The Chemistry of Life’s origin: A carbonaceous meteorite perspective. Acc. Chem. Res. 2006, 39, 231–237. [Google Scholar] [CrossRef]
- Trigo-Rodríguez, J.M.; Rimola, A.; Tanbakouei, S.; Soto, V.C.; Lee, M. Accretion of Water in Carbonaceous Chondrites: Current Evidence and Implications for the Delivery of Water to Early Earth. Space Sci. Rev. 2019, 215, 18. [Google Scholar] [CrossRef]
- Le Guillou, C.; Bernard, S.; Brearley, A.J.; Remusat, L. Evolution of organic matter in Orgueil, Murchison and Renazzo during parent body aqueous alteration: In situ investigations. Geochim. Cosmochim. Acta 2014, 131, 368–392. [Google Scholar] [CrossRef]
- Vinogradoff, V.; Bernard, S.; Le Guillou, C.; Remusat, L. Evolution of interstellar organic compounds under asteroidal hydrothermal conditions. Icarus 2018, 305, 358–370. [Google Scholar] [CrossRef]
- Vinogradoff, V.; Le Guillou, C.; Bernard, S.; Binet, L.; Cartigny, P.; Brearley, A.J.; Remusat, L. Paris vs. Murchison: Impact of hydrothermal alteration on organic matter in CM chondrites. Geochim. Cosmochim. Acta 2017, 212, 234–252. [Google Scholar] [CrossRef]
- Rotelli, L.; Trigo-Rodríguez, J.M.; Moyano-Cambero, C.E.; Carota, E.; Botta, L.; Di Mauro, E.; Saladino, R. The key role of meteorites in the formation of relevant prebiotic molecules in a formamide/water environment. Sci. Rep. 2016, 6, 38888. [Google Scholar] [CrossRef] [PubMed]
- Cabedo, V.; Llorca, J.; Trigo-Rodriguez, J.M.; Rimola, A. Study of Fischer–Tropsch-type reactions on chondritic meteorites. Astron. Astrophys. 2021, 650, A160. [Google Scholar] [CrossRef]
- Santalucia, R.; Pazzi, M.; Bonino, F.; Signorile, M.; Scarano, D.; Ugliengo, P.; Spoto, G.; Mino, L. From gaseous HCN to nucleobases at the cosmic silicate dust surface: An experimental insight into the onset of prebiotic chemistry in space. Phys. Chem. Chem. Phys. 2022, 24, 7224–7230. [Google Scholar] [CrossRef]
- Mumma, M.J.; Charnley, S.B. The chemical composition of comets—Emerging taxonomies and natal heritage. Annu. Rev. Astron. Astrophys. 2011, 49, 471–524. [Google Scholar] [CrossRef]
- Wright, I.P.; Sheridan, S.; Barber, S.J.; Morgan, G.H.; Andrews, D.J.; Morse, A.D. CHO-bearing organic compounds at the surface of 67P/Churyumov-Gerasimenko revealed by Ptolemy. Science 2015, 349, aab0673. [Google Scholar] [CrossRef]
- Altwegg, K.; Balsiger, H.; Bar-Nun, A.; Berthelier, J.-J.; Bieler, A.; Bochsler, P.; Briois, C.; Calmonte, U.; Combi, M.R.; Cottin, H.; et al. Prebiotic chemicals-amino acid and phosphorus-in the coma of comet 67P/Churyumov-Gerasimenko. Science 2016, 2, e1600285. [Google Scholar] [CrossRef]
- Elsila, J.E.; Glavin, D.P.; Dworkin, J.P. Cometary glycine detected in samples returned by Stardust. Meteorit. Planet. Sci. 2009, 44, 1323–1330. [Google Scholar] [CrossRef]
- Sandford, S.A.; Aléon, J.; Alexander, C.M.O.D.; Araki, T.; Bajt, S.; Baratta, G.A.; Borg, J.; Bradley, J.P.; Brownlee, D.E.; Brucato, J.R.; et al. Organics captured from comet 81P/Wild 2 by the Stardust spacecraft. Science 2006, 314, 1720–1724. [Google Scholar] [CrossRef] [PubMed]
- Martins, Z. Organic Chemistry of Carbonaceous Meteorites. Elements 2011, 7, 35–40. [Google Scholar] [CrossRef]
- Pizzarello, S.; Huang, Y.; Alexandre, M.R. Molecular asymmetry in extraterrestrial chemistry: Insights from a pristine meteorite. Proc. Natl. Acad. Sci. USA 2008, 105, 3700. [Google Scholar] [CrossRef] [PubMed]
- Aponte, J.C.; Elsila, J.E.; Glavin, D.P.; Milam, S.N.; Charnley, S.B.; Dworkin, J.P. Pathways to Meteoritic Glycine and Methylamine. ACS Earth Space Chem. 2017, 1, 3–13. [Google Scholar] [CrossRef]
- Basiuk, V.A. Formation of Amino Acid Precursors in the Interstellar Medium. A DFT Study of Some Gas-Phase Reactions Starting with Methylenimine. J. Phys. Chem. A 2001, 105, 4252–4258. [Google Scholar] [CrossRef]
- Redondo, P.; Largo, A.; Barrientos, C. Is the reaction between formic acid and protonated aminomethanol a possible source of glycine precursors in the interstellar medium? Astron. Astrophys. 2015, 579, A125. [Google Scholar] [CrossRef][Green Version]
- Bernstein, M.P.; Dworkin, J.P.; Sandford, S.A.; Cooper, G.W.; Allamandola, L.J. Racemic amino acids from the ultraviolet photolysis of interstellar ice analogues. Nature 2002, 416, 401–403. [Google Scholar] [CrossRef]
- Meinert, C.; Filippi, J.-J.; de Marcellus, P.; Le Sergeant d’Hendecourt, L.; Meierhenrich, U.J. N-(2-Aminoethyl)glycine and Amino Acids from Interstellar Ice Analogues. ChemPlusChem 2012, 77, 186–191. [Google Scholar] [CrossRef]
- Meinert, C.; Myrgorodska, I.; de Marcellus, P.; Buhse, T.; Nahon, L.; Hoffmann, S.V.; d’Hendecourt, L.L.S.; Meierhenrich, U.J. Ribose and related sugars from ultraviolet irradiation of interstellar ice analogs. Science 2016, 352, 208. [Google Scholar] [CrossRef]
- Modica, P.; Meinert, C.; de Marcellus, P.; Nahon, L.; Meierhenrich, U.J.; d’Hendecourt, L.L.S. Enantiomeric excesses induced in amino acids by ultraviolet circularly polarized light irradiation of extraterrestrial ice analogs: A possible source of asymmetry for prebiotic chemistry. Astrophys. J. 2014, 788, 79. [Google Scholar] [CrossRef]
- Muñoz-Caro, G.M.; Meierhenrich, U.J.; Schutte, W.A.; Barbier, B.; Segovia, A.A.; Rosenbauer, H.; Thiemann, W.H.-P.; Brack, A.; Greenberg, J.M. Amino acids from ultraviolet irradiation of interstellar ice analogues. Nature 2002, 416, 403–406. [Google Scholar] [CrossRef] [PubMed]
- Nuevo, M.; Auger, G.; Blanot, D.; d’Hendecourt, L. A Detailed Study of the Amino Acids Produced from the Vacuum UV Irradiation of Interstellar Ice Analogs. Orig. Life Evol. Biosph. 2008, 38, 37–56. [Google Scholar] [CrossRef]
- Krasnokutski, S.A.; Jäger, C.; Henning, T. Condensation of Atomic Carbon: Possible Routes toward Glycine. Astrophys. J. 2020, 889, 67. [Google Scholar] [CrossRef]
- Ioppolo, S.; Fedoseev, G.; Chuang, K.J.; Cuppen, H.M.; Clements, A.R.; Jin, M.; Garrod, R.T.; Qasim, D.; Kofman, V.; van Dishoeck, E.F.; et al. A non-energetic mechanism for glycine formation in the interstellar medium. Nat. Astron. 2021, 5, 197–205. [Google Scholar] [CrossRef]
- Ceccarelli, C.; Loinard, L.; Castets, A.; Faure, A.; Lefloch, B. Search for glycine in the solar type protostar IRAS 16293-2422. Astron. Astrophys. 2000, 362, 1122–1126. [Google Scholar]
- Kuan, Y.-J.; Charnley, S.B.; Huang, H.-C.; Tseng, W.-L.; Kisiel, Z. Interstellar Glycine. Astrophys. J. 2004, 593, 848. [Google Scholar] [CrossRef]
- Snyder, L.E. The Search for Interstellar Glycine. Orig. Life Evol. Biosph. 1997, 27, 115–133. [Google Scholar] [CrossRef]
- Snyder, L.E.; Lovas, F.J.; Hollis, J.M.; Friedel, D.N.; Jewell, P.R.; Remijan, A.; Ilyushin, V.V.; Alekseev, E.A.; Dyubko, S.F. A rigorous attempt to verify interstellar glycine. Astrophys. J. 2005, 619, 914–930. [Google Scholar] [CrossRef]
- Maté, B.; Tanarro, I.; Moreno, M.A.; Jiménez-Redondo, M.; Escribano, R.; Herrero, V.J. Stability of carbonaceous dust analogues and glycine under UV irradiation and electron bombardment. Faraday Disc. 2014, 168, 267–285. [Google Scholar] [CrossRef][Green Version]
- Cuppen, H.M.; Walsh, C.; Lamberts, T.; Semenov, D.; Garrod, R.T.; Penteado, E.M.; Ioppolo, S. Grain surface models and data for astrochemistry. Space Sci. Rev. 2017, 212, 1–58. [Google Scholar] [CrossRef]
- Potapov, A.; McCoustra, M. Physics and chemistry on the surface of cosmic dust grains: A laboratory view. Int. Rev. Phys. Chem. 2021, 40, 299–364. [Google Scholar] [CrossRef]
- Rimola, A.; Ferrero, S.; Germain, A.; Corno, M.; Ugliengo, P. Computational Surface Modelling of Ices and Minerals of Interstellar Interest—Insights and Perspectives. Minerals 2021, 11, 26. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Role of Mineral Surfaces in Prebiotic Chemical Evolution. In Silico Quantum Mechanical Studies. Life 2019, 9, 10. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Sherrill, C.D. Frontiers in Electronic Structure Theory. J. Chem. Phys. 2010, 132, 110902. [Google Scholar] [CrossRef] [PubMed]
- Ramabhadran, R.O.; Raghavachari, K. Extrapolation to the Gold-Standard in Quantum Chemistry: Computationally Efficient and Accurate CCSD(T) Energies for Large Molecules Using an Automated Thermochemical Hierarchy. J. Chem. Theory Comput. 2013, 9, 3986–3994. [Google Scholar] [CrossRef]
- Neese, F.; Atanasov, M.; Bistoni, G.; Maganas, D.; Ye, S. Chemistry and Quantum Mechanics in 2019: Give Us Insight and Numbers. J. Am. Chem. Soc. 2019, 141, 2814–2824. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree–Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the Density Functional Ladder: Nonempirical Meta-Generalized Gradient Approximation Designed for Molecules and Solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. A new local density functional for main-group thermochemistry, transition metal bonding, thermochemical kinetics, and noncovalent interactions. J. Chem. Phys. 2006, 125, 194101. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Hao, P.; Sun, J.; Xiao, B.; Ruzsinszky, A.; Csonka, G.I.; Tao, J.; Glindmeyer, S.; Perdew, J.P. Performance of meta-GGA Functionals on General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2013, 9, 355–363. [Google Scholar] [CrossRef]
- Hobza, P.; Šponer, J.; Reschel, T. Density functional theory and molecular clusters. J. Comput. Chem. 1995, 16, 1315–1325. [Google Scholar] [CrossRef]
- Allen, M.J.; Tozer, D.J. Helium dimer dispersion forces and correlation potentials in density functional theory. J. Chem. Phys. 2002, 117, 11113–11120. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-Corrected Mean-Field Electronic Structure Methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar] [CrossRef]
- Dewar, M.J.S.; Thiel, W. Ground states of molecules. 38. The MNDO method. Approximations and parameters. J. Am. Chem. Soc. 1977, 99, 4899–4907. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods I. Method. J. Comput. Chem. 1989, 10, 209–220. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Porezag, D.; Frauenheim, T.; Köhler, T.; Seifert, G.; Kaschner, R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947–12957. [Google Scholar] [CrossRef]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef]
- Pracht, P.; Caldeweyher, E.; Ehlert, S.; Grimme, S. A Robust Non-Self-Consistent Tight-Binding Quantum Chemistry Method for large Molecules. ChemRxiv 2019. [Google Scholar] [CrossRef]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K.; Rassolov, V.; Pople, J.A. Gaussian-3 theory using reduced Mo/ller-Plesset order. J. Chem. Phys. 1999, 110, 4703–4709. [Google Scholar] [CrossRef]
- Montgomery, J.A.; Frisch, M.J.; Ochterski, J.W.; Petersson, G.A. A complete basis set model chemistry. VI. Use of density functional geometries and frequencies. J. Chem. Phys. 1999, 110, 2822–2827. [Google Scholar] [CrossRef]
- Montgomery, J.A.; Frisch, M.J.; Ochterski, J.W.; Petersson, G.A. A complete basis set model chemistry. VII. Use of the minimum population localization method. J. Chem. Phys. 2000, 112, 6532–6542. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- McQuarrie, D.A.; Simon, J.D. Physical Chemistry. A Molecular Approach; University Science Books: Sausalito, CA, USA, 1997. [Google Scholar]
- Iftimie, R.; Minary, P.; Tuckerman, M.E. Ab initio molecular dynamics: Concepts, recent developments, and future trends. Proc. Natl. Acad. Sci. USA 2005, 102, 6654. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bonomi, M.; Parrinello, M. Metadynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 826–843. [Google Scholar] [CrossRef]
- Sutto, L.; Marsili, S.; Gervasio, F.L. New advances in metadynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 771–779. [Google Scholar] [CrossRef]
- Rimola, A.; Costa, D.; Sodupe, M.; Lambert, J.-F.; Ugliengo, P. Silica Surface Features and Their Role in the Adsorption of Biomolecules: Computational Modeling and Experiments. Chem. Rev. 2013, 113, 4216–4313. [Google Scholar] [CrossRef]
- Sauer, J.; Ugliengo, P.; Garrone, E.; Saunders, V.R. Theoretical Study of van der Waals Complexes at Surface Sites in Comparison with the Experiment. Chem. Rev. 1994, 94, 2095–2160. [Google Scholar] [CrossRef]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F.; et al. The ONIOM Method and Its Applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef]
- Germain, A.; Tinacci, L.; Pantaleone, S.; Ceccarelli, C.; Ugliengo, P. Computer Generated Realistic Interstellar Icy Grain Models: Physico-chemical Properties and Interaction with NH3. ACS Earth Space Chem. 2022; submitted. [Google Scholar]
- Sure, R.; Grimme, S. Corrected small basis set Hartree-Fock method for large systems. J. Comput. Chem. 2013, 34, 1672–1685. [Google Scholar] [CrossRef] [PubMed]
- Woon, D.E. Pathways to Glycine and Other Amino Acids in Ultraviolet-irradiated Astrophysical Ices Determined via Quantum Chemical Modeling. Astrophys. J. 2002, 571, L177–L180. [Google Scholar] [CrossRef]
- Pilling, S.; Baptista, L.; Boechat-Roberty, H.M.; Andrade, D.P.P. Formation Routes of Interstellar Glycine Involving Carboxylic Acids: Possible Favoritism Between Gas and Solid Phase. Astrobiology 2011, 11, 883–893. [Google Scholar] [CrossRef] [PubMed]
- Sato, A.; Kitazawa, Y.; Ochi, T.; Shoji, M.; Komatsu, Y.; Kayanuma, M.; Aikawa, Y.; Umemura, M.; Shigeta, Y. First-principles study of the formation of glycine-producing radicals from common interstellar species. Mol. Astrophys. 2018, 10, 11–19. [Google Scholar] [CrossRef]
- Shivani; Singh, A.; Gupta, V.; Misra, A.; Tandon, P. Quantum-chemical approach to serine formation in the interstellar medium: A possible reaction pathway. Astron. Astrophys. 2014, 563, A55. [Google Scholar] [CrossRef][Green Version]
- Jeanvoine, Y.; Largo, A.; Hase, W.L.; Spezia, R. Gas Phase Synthesis of Protonated Glycine by Chemical Dynamics Simulations. J. Phys. Chem. A 2018, 122, 869–877. [Google Scholar] [CrossRef]
- Barrientos, C.; Redondo, P.; Largo, L.; Rayón, V.M.; Largo, A. Gas-phase synthesis of precursors of interstellar glycine: A computational study of the reactions of acetic acid with hydroxylamine and its ionized and protonated derivatives. Astrophys. J. 2012, 748, 99. [Google Scholar] [CrossRef]
- Sanz-Novo, M.; Largo, A.; Redondo, P.; Barrientos, C. Formation of Protonated Glycine Isomers in the Interstellar Medium. ACS Earth Space Chem. 2019, 3, 1170–1181. [Google Scholar] [CrossRef]
- Largo, L.; Redondo, P.; Rayón, V.M.; Largo, A.; Barrientos, C. The reaction between NH3+ and CH3COOH: A possible process for the formation of glycine precursors in the interstellar medium. Astron. Astrophys. 2010, 516, A79. [Google Scholar] [CrossRef]
- Largo, A.; Redondo, P.; Barrientos, C. Theoretical Study of Possible Ion-Molecule Reactions Leading to Precursors of Glycine in the Interstellar Medium. Int. J. Quant. Chem. 2004, 98, 355–360. [Google Scholar] [CrossRef]
- Largo, L.; Rayón, V.M.; Barrientos, C.; Largo, A.; Redondo, P. Gas-Phase Reaction of NH2+ with Acetic Acid: Implications in Astrochemistry. J. Chem. Theory Comput. 2008, 4, 2085–2093. [Google Scholar] [CrossRef] [PubMed]
- Redondo, P.; Barrientos, C.; Largo, A. Complex Organic Molecules Formation in Space Through Gas Phase Reactions: A Theoretical Approach. Astrophys. J. 2017, 836, 240. [Google Scholar] [CrossRef]
- Nhlabatsi, Z.P.; Bhasi, P.; Sitha, S. Possible interstellar formation of glycine through a concerted mechanism: A computational study on the reaction of CH2=NH, CO2 and H2. Phys. Chem. Chem. Phys. 2016, 18, 20109–20117. [Google Scholar] [CrossRef] [PubMed]
- Nhlabatsi, Z.P.; Bhasi, P.; Sitha, S. Possible interstellar formation of glycine from the reaction of CH2=NH, CO and H2O: Catalysis by extra water molecules through the hydrogen relay transport. Phys. Chem. Chem. Phys. 2016, 18, 375–381. [Google Scholar] [CrossRef] [PubMed]
- Thrush, K.L.; Kua, J. Reactions of Glycolonitrile with Ammonia and Water: A Free Energy Map. J. Phys. Chem. A 2018, 122, 6769–6779. [Google Scholar] [CrossRef]
- Maeda, S.; Ohno, K. Generation Mechanisms of Amino Acids in Interstellar Space via Reactions between Closed-Shell Species: Significance of Higher Energy Isomers in Molecular Evolution. Astrophys. J. 2006, 640, 823–828. [Google Scholar] [CrossRef]
- Riffet, V.; Frison, G.; Bouchoux, G. Quantum-Chemical Modeling of the First Steps of the Strecker Synthesis: From the Gas-Phase to Water Solvation. J. Phys. Chem. A 2018, 122, 1643–1657. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Deep-space glycine formation via Strecker-type reactions activated by ice water dust mantles. A computational approach. Phys. Chem. Chem. Phys. 2010, 12, 5285–5294. [Google Scholar] [CrossRef]
- Kayanuma, M.; Kidachi, K.; Shoji, M.; Komatsu, Y.; Sato, A.; Shigeta, Y.; Aikawa, Y.; Umemura, M. A theoretical study of the formation of glycine via hydantoin intermediate in outer space environment. Chem. Phys. Lett. 2017, 687, 178–183. [Google Scholar] [CrossRef]
- Krishnan, Y.; Vincent, A.; Paranjothy, M. Classical dynamics simulations of interstellar glycine formation via CH2 = NH + CO + H2O reaction. J. Chem. Sci. 2017, 129, 1571–1577. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Computational study of interstellar glycine formation occurring at radical surfaces of water-ice dust particles. Astrophys. J. 2012, 754, 24. [Google Scholar] [CrossRef]
- Lee, H.M.; Choe, J.C. Formation of glycine from HCN and H2O: A computational mechanistic study. Chem. Phys. Lett. 2017, 675, 6–10. [Google Scholar] [CrossRef]
- Kayi, H.; Kaiser, R.I.; Head, J.D. A computational study on the structures of methylamine–carbon dioxide–water clusters: Evidence for the barrier free formation of the methylcarbamic acid zwitterion (CH3NH2+COO−) in interstellar water ices. Phys. Chem. Chem. Phys. 2011, 13, 11083–11098. [Google Scholar] [CrossRef] [PubMed]
- Krasnokutski, S.A.; Kuhn, M.; Renzler, M.; Jäger, C.; Henning, T.; Scheier, P. Ultra-low-temperature reactions of carbon atoms with hydrogen molecules. Astrophys. J. Lett. 2016, 818, L31. [Google Scholar] [CrossRef]
- Henning, T.K.; Krasnokutski, S.A. Experimental characterization of the energetics of low-temperature surface reactions. Nat. Astron. 2019, 3, 568–573. [Google Scholar] [CrossRef]
- Singh, A.; Shivani; Misra, A.; Tandon, P. Quantum chemical analysis for the formation of glycine in the interstellar medium. Res. Astron. Astrophys. 2013, 13, 912–920. [Google Scholar] [CrossRef]
- Chyba, C.; Sagan, C. Endogenous production, exogenous delivery and impact-shock synthesis of organic molecules: An inventory for the origins of life. Nature 1992, 355, 125–132. [Google Scholar] [CrossRef]
- Rubin, A.E. Mineralogy of meteorite groups. Meteorit. Planet. Sci. 1997, 32, 231–247. [Google Scholar] [CrossRef]
- Rimola, A.; Ugliengo, P. The role of defective silica surfaces in exogenous delivery of prebiotic compounds: Clues from first principles calculations. Phys. Chem. Chem. Phys. 2009, 11, 2497–2506. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Amide and Peptide Bond Formation: Interplay between Strained Ring Defects and Silanol Groups at Amorphous Silica Surfaces. J. Phys. Chem. C 2016, 120, 24817–24826. [Google Scholar] [CrossRef]
- Rimola, A.; Ugliengo, P.; Sodupe, M. Strained ring motif at silica surfaces: A quantum mechanical study of their reactivity towards protic molecules. Comput. Theor. Chem. 2015, 1074, 168–177. [Google Scholar] [CrossRef]
- Rimola, A.; Trigo-Rodríguez, J.M.; Martins, Z. Interaction of organic compounds with chondritic silicate surfaces. Atomistic insights from quantum chemical periodic simulations. Phys. Chem. Chem. Phys. 2017, 19, 18217–18231. [Google Scholar] [CrossRef] [PubMed]
- Escamilla-Roa, E.; Moreno, F. Adsorption of glycine by cometary dust: Astrobiological implications. Planet. Space Sci. 2012, 70, 1–9. [Google Scholar] [CrossRef]
- Escamilla-Roa, E.; Moreno, F. Adsorption of glycine on cometary dust grains: II—Effect of amorphous water ice. Planet. Space Sci. 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Escamilla-Roa, E.; Sainz-Díaz, C.I. Effect of Amorphous Ammonia–Water Ice onto Adsorption of Glycine on Cometary Dust Grain and IR Spectroscopy. J. Phys. Chem. C 2014, 118, 26080–26090. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M.; Ugliengo, P. Aluminosilicate Surfaces as Promoters for Peptide Bond Formation: An Assessment of Bernal’s Hypothesis by ab Initio Methods. J. Am. Chem. Soc. 2007, 129, 8333–8344. [Google Scholar] [CrossRef] [PubMed]
- Rimola, A.; Ugliengo, P.; Sodupe, M. Formation versus Hydrolysis of the Peptide Bond from a Quantum-mechanical Viewpoint: The Role of Mineral Surfaces and Implications for the Origin of Life. Int. J. Mol. Sci. 2009, 10, 746–760. [Google Scholar] [CrossRef] [PubMed]
- Escamilla-Roa, E.; Huertas, F.J.; Hernández-Laguna, A.; Sainz-Díaz, C.I. A DFT study of the adsorption of glycine in the interlayer space of montmorillonite. Phys. Chem. Chem. Phys. 2017, 19, 14961–14971. [Google Scholar] [CrossRef]
- Hutcheon, I.D.; Huss, G.R.; Fahey, A.J.; Wasserburg, G.J. Extreme 26Mg and 17O Enrichments in an Orgueil Corundum: Identification of a Presolar Oxide Grain. Astrophys. J. 1994, 425, L97. [Google Scholar] [CrossRef]
- Zinner, E.; Amari, S.; Guinness, R.; Nguyen, A.; Stadermann, F.J.; Walker, R.M.; Lewis, R.S. Presolar spinel grains from the Murray and Murchison carbonaceous chondrites. Geochim. Cosmochim. Acta 2003, 67, 5083–5095. [Google Scholar] [CrossRef]
- Ireland, T.R. Presolar isotopic and chemical signatures in hibonite-bearing refractory inclusions from the Murchison carbonaceous chondrite. Geochim. Cosmochim. Acta 1990, 54, 3219–3237. [Google Scholar] [CrossRef]
- Nittler, L.R.; Alexander, C.M.O.D.; Gallino, R.; Hoppe, P.; Nguyen, A.N.; Stadermann, F.J.; Zinner, E.K. Aluminum-, Calcium- and Titanium-rich Oxide Stardust in Ordinary Chondrite Meteorites. Astrophys. J. 2008, 682, 1450–1478. [Google Scholar] [CrossRef]
- Gail, H.-P.; Sedlmayr, E. Inorganic dust formation in astrophysical environments. Faraday Disc. 1998, 109, 303–319. [Google Scholar] [CrossRef]
- Goumans, T.P.M.; Bromley, S.T. Stardust silicate nucleation kick-started by SiO+TiO2. Philos. Trans. R. Soc. A 2013, 371, 20110580. [Google Scholar] [CrossRef] [PubMed]
- Keller, L.P.; Hony, S.; Bradley, J.P.; Molster, F.J.; Waters, L.B.F.M.; Bouwman, J.; de Koter, A.; Brownlee, D.E.; Flynn, G.J.; Henning, T.; et al. Identification of iron sulphide grains in protoplanetary disks. Nature 2002, 417, 148–150. [Google Scholar] [CrossRef]
- Harries, D.; Langenhorst, F. The nanoscale mineralogy of Fe,Ni sulfides in pristine and metamorphosed CM and CM/CI-like chondrites: Tapping a petrogenetic record. Meteorit. Planet. Sci. 2013, 48, 879–903. [Google Scholar] [CrossRef]
- Keller, L.P.; Messenger, S. On the origins of GEMS grains. Geochim. Cosmochim. Acta 2011, 75, 5336–5365. [Google Scholar] [CrossRef]
- Nguyen, A.N.; Keller, L.P.; Messenger, S. Mineralogy of presolar silicate and oxide grains of diverse stellar origins. Astrophys. J. 2016, 818, 51. [Google Scholar] [CrossRef]
- Brownlee, D.; Tsou, P.; Aléon, J.; Alexander Conel, M.O.D.; Araki, T.; Bajt, S.; Baratta Giuseppe, A.; Bastien, R.; Bland, P.; Bleuet, P.; et al. Comet 81P/Wild 2 Under a Microscope. Science 2006, 314, 1711–1716. [Google Scholar] [CrossRef]
- Zolensky Michael, E.; Zega Thomas, J.; Yano, H.; Wirick, S.; Westphal Andrew, J.; Weisberg Mike, K.; Weber, I.; Warren Jack, L.; Velbel Michael, A.; Tsuchiyama, A.; et al. Mineralogy and Petrology of Comet 81P/Wild 2 Nucleus Samples. Science 2006, 314, 1735–1739. [Google Scholar] [CrossRef]
- Hilchenbach, M.; Kissel, J.; Langevin, Y.; Briois, C.; Hoerner, H.v.; Koch, A.; Schulz, R.; Silén, J.; Altwegg, K.; Colangeli, L.; et al. Comet 67p/churyumov–gerasimenko: Close-up on dust particle fragments. Astrophys. J. Lett. 2016, 816, L32. [Google Scholar] [CrossRef]
- Davidsson, B.J.R.; Sierks, H.; Güttler, C.; Marzari, F.; Pajola, M.; Rickman, H.; A’Hearn, M.F.; Auger, A.-T.; El-Maarry, M.R.; Fornasier, S.; et al. The primordial nucleus of comet 67P/Churyumov-Gerasimenko. Astron. Astrophys. 2016, 592, A63. [Google Scholar] [CrossRef]
- Rousseau, B.; Érard, S.; Beck, P.; Quirico, É.; Schmitt, B.; Brissaud, O.; Montes-Hernandez, G.; Capaccioni, F.; Filacchione, G.; Bockelée-Morvan, D.; et al. Laboratory simulations of the Vis-NIR spectra of comet 67P using sub-µm sized cosmochemical analogues. Icarus 2018, 306, 306–318. [Google Scholar] [CrossRef]
- Ojamäe, L.; Aulin, C.; Pedersen, H.; Käll, P.-O. IR and quantum-chemical studies of carboxylic acid and glycine adsorption on rutile TiO2 nanoparticles. J. Colloid Interface Sci. 2006, 296, 71–78. [Google Scholar] [CrossRef]
- Tonner, R. Adsorption of Proline and Glycine on the TiO2(110) Surface: A Density Functional Theory Study. ChemPhysChem 2010, 11, 1053–1061. [Google Scholar] [CrossRef]
- Szieberth, D.; Maria Ferrari, A.; Dong, X. Adsorption of glycine on the anatase (101) surface: An ab initio study. Phys. Chem. Chem. Phys. 2010, 12, 11033–11040. [Google Scholar] [CrossRef]
- Pantaleone, S.; Rimola, A.; Sodupe, M. Canonical, Deprotonated, or Zwitterionic? A Computational Study on Amino Acid Interaction with the TiO2 (101) Anatase Surface. J. Phys. Chem. C 2017, 121, 14156–14165. [Google Scholar] [CrossRef]
- Pantaleone, S.; Rimola, A.; Sodupe, M. Canonical, deprotonated, or zwitterionic? II. A computational study on amino acid interaction with the TiO2(110) rutile surface: Comparison with the anatase (101) surface. Phys. Chem. Chem. Phys. 2020, 22, 16862–16876. [Google Scholar] [CrossRef]
- Nair, N.N.; Schreiner, E.; Marx, D. Glycine at the Pyrite−Water Interface: The Role of Surface Defects. J. Am. Chem. Soc. 2006, 128, 13815–13826. [Google Scholar] [CrossRef]
- Bernal, J.D. The Physical Basis of Life. Proc. Phys. Soc. 1949, 62, 597–618. [Google Scholar] [CrossRef]
- Lambert, J.-F. Adsorption and Polymerization of Amino Acids on Mineral Surfaces: A Review. Orig. Life Evol. Biosph. 2008, 38, 211–242. [Google Scholar] [CrossRef] [PubMed]
- Bujdák, J.; Rode, B.M. Glycine oligomerization on silica and alumina. React. Kinet. Mech. Catal. Lett. 1997, 62, 281–286. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Silica, Alumina, and Clay-Catalyzed Alanine Peptide Bond Formation. J. Mol. Evol. 1997, 45, 457–466. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Silica, Alumina and Clay Catalyzed Peptide Bond Formation: Enhanced Efficiency of Alumina Catalyst. Orig. Life Evol. Biosph. 1999, 29, 451–461. [Google Scholar] [CrossRef] [PubMed]
- Lambert, J.-F.; Jaber, M.; Georgelin, T.; Stievano, L. A Comparative Study of the Catalysis of Peptide Bond Formation by Oxide Surfaces. Phys. Chem. Chem. Phys. 2013, 15, 13371–13380. [Google Scholar] [CrossRef]
- Martra, G.; Deiana, C.; Sakhno, Y.; Barberis, I.; Fabbiani, M.; Pazzi, M.; Vincenti, M. The Formation and Self-Assembly of Long Prebiotic Oligomers Produced by the Condensation of Unactivated Amino Acids on Oxide Surfaces. Angew. Chem. Int. Ed. 2014, 53, 4671–4674. [Google Scholar] [CrossRef]
- Rimola, A.; Fabbiani, M.; Sodupe, M.; Ugliengo, P.; Martra, G. How Does Silica Catalyze the Amide Bond Formation under Dry Conditions? Role of Specific Surface Silanol Pairs. ACS Catal. 2018, 8, 4558–4568. [Google Scholar] [CrossRef]
- Ferris, J.P.; Hill, A.R.; Liu, R.; Orgel, L.E. Synthesis of Long Prebiotic Oligomers on Mineral Surfaces. Nature 1996, 381, 59–61. [Google Scholar] [CrossRef]
- Lahav, N.; White, D.; Chang, S. Peptide formation in the prebiotic era: Thermal condensation of glycine in fluctuating clay environments. Science 1978, 201, 67–69. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Activated alumina as an energy source for peptide bond formation: Consequences for mineral-mediated prebiotic processes. Amino Acids 2001, 21, 281–291. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Preferential amino acid sequences in alumina-catalyzed peptide bond formation. J. Inorg. Biochem. 2002, 90, 1–7. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Peptide Bond Formation on the Surface of Activated Alumina: Peptide Chain Elongation. Catal. Lett. 2003, 91, 149–154. [Google Scholar] [CrossRef]
- Bujdák, J.; Rode, B.M. Alumina catalyzed reactions of amino acids. J. Therm. Anal. Calorim. 2003, 73, 797–805. [Google Scholar] [CrossRef]
- Iqubal, M.A.; Sharma, R.; Jheeta, S.; Kamaluddin. Thermal Condensation of Glycine and Alanine on Metal Ferrite Surface: Primitive Peptide Bond. Life 2017, 7, 15. [Google Scholar] [CrossRef]
- Matrajt, G.; Blanot, D. Properties of synthetic ferrihydrite as an amino acid adsorbent and a promoter of peptide bond formation. Amino Acids 2004, 26, 153–158. [Google Scholar] [CrossRef]
- Deiana, C.; Sakhno, Y.; Fabbiani, M.; Pazzi, M.; Vincenti, M.; Martra, G. Direct Synthesis of Amides from Carboxylic Acids and Amines by Using Heterogeneous Catalysts: Evidence of Surface Carboxylates as Activated Electrophilic Species. ChemCatChem 2013, 5, 2832–2834. [Google Scholar] [CrossRef]
- Leyton, P.; Saladino, R.; Crestini, C.; Campos-Vallette, M.; Paipa, C.; Berríos, A.; Fuentes, S.; Zárate, R.A. Influence of TiO2 on prebiotic thermal synthesis of the Gly-Gln polymer. Amino Acids 2012, 42, 2079–2088. [Google Scholar] [CrossRef]
- Ertem, G.; Ferris, J.P. Synthesis of RNA oligomers on heterogeneous templates. Nature 1996, 379, 238–240. [Google Scholar] [CrossRef]
- Himbert, S.; Chapman, M.; Deamer, D.W.; Rheinstädter, M.C. Organization of Nucleotides in Different Environments and the Formation of Pre-Polymers. Sci. Rep. 2016, 6, 31285. [Google Scholar] [CrossRef]
- Orgel, L.E. Polymerization on the Rocks: Theoretical Introduction. Orig. Life Evol. Biosph. 1998, 28, 227–234. [Google Scholar] [CrossRef]
- Smith, J.V. Biochemical evolution. I. Polymerization on internal, organophilic silica surfaces of dealuminated zeolites and feldspars. Proc. Natl. Acad. Sci. USA 1998, 95, 3370–3375. [Google Scholar] [CrossRef] [PubMed]
- Civiš, S.; Szabla, R.; Szyja, B.M.; Smykowski, D.; Ivanek, O.; Knížek, A.; Kubelík, P.; Šponer, J.; Ferus, M.; Šponer, J.E. TiO2-catalyzed synthesis of sugars from formaldehyde in extraterrestrial impacts on the early Earth. Sci. Rep. 2016, 6, 23199. [Google Scholar] [CrossRef] [PubMed]
- Senanayake, S.D.; Idriss, H. Photocatalysis and the origin of life: Synthesis of nucleoside bases from formamide on TiO2 (001) single surfaces. Proc. Natl. Acad. Sci. USA 2006, 103, 1194. [Google Scholar] [CrossRef] [PubMed]
- Saladino, R.; Ciambecchini, U.; Crestini, C.; Costanzo, G.; Negri, R.; Di Mauro, E. One-Pot TiO2-Catalyzed Synthesis of Nucleic Bases and Acyclonucleosides from Formamide: Implications for the Origin of Life. ChemBioChem 2003, 4, 514–521. [Google Scholar] [CrossRef]
- Pantaleone, S.; Ugliengo, P.; Sodupe, M.; Rimola, A. When the Surface Matters: Prebiotic Peptide-Bond Formation on the TiO2 (101) Anatase Surface through Periodic DFT-D2 Simulations. Chem. Eur. J. 2018, 24, 16292–16301. [Google Scholar] [CrossRef] [PubMed]
- Wächtershäuer, G. Before Enzymes and Templates: Theory of Surface Metabolism. Microbiol. Rev. 1988, 52, 452–484. [Google Scholar] [CrossRef]
- Russell, M.J.; Hall, A.J.; Cairns-Smith, A.G.; Braterman, P.S. Submarine hot springs and the origin of life. Nature 1988, 336, 117. [Google Scholar] [CrossRef]
- Martin, W.; Baross, J.; Kelley, D.; Russell, M.J. Hydrothermal vents and the origin of life. Nat. Rev. Microbiol. 2008, 6, 805. [Google Scholar] [CrossRef]
- Cody, G.D.; Boctor, N.Z.; Filley, T.R.; Hazen, R.M.; Scott, J.H.; Sharma, A.; Yoder, H.S., Jr. Primordial Carbonylated Iron-Sulfur Compounds and the Synthesis of Pyruvate. Science 2000, 289, 1337–1340. [Google Scholar] [CrossRef]
- Huber, C.; Wächtershäuser, G. Activated Acetic Acid by Carbon Fixation on (Fe,Ni)S Under Primordial Conditions. Science 1997, 276, 245–247. [Google Scholar] [CrossRef]
- Huber, C.; Wächtershäuser, G. α-Hydroxy and α-Amino Acids Under Possible Hadean, Volcanic Origin-of-Life Conditions. Science 2006, 314, 630–632. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.; Eisenreich, W.; Hecht, S.; Wächtershäuser, G. A Possible Primordial Peptide Cycle. Science 2003, 301, 938–940. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.; Wächtershäuser, G. Peptides by Activation of Amino Acids with CO on (Ni,Fe)S Surfaces: Implications for the Origin of Life. Science 1998, 281, 670–672. [Google Scholar] [CrossRef]
- Pollet, R.; Boehme, C.; Marx, D. Ab initio Simulations of Desorption and Reactivity of Glycine at a Water-Pyrite Interface at “Iron-Sulfur World” Prebiotic Conditions. Orig. Life Evol. Biosph. 2006, 36, 363–379. [Google Scholar] [CrossRef] [PubMed]
- Boehme, C.; Marx, D. Glycine on a Wet Pyrite Surface at Extreme Conditions. J. Am. Chem. Soc. 2003, 125, 13362–13363. [Google Scholar] [CrossRef] [PubMed]
- Nair, N.N.; Schreiner, E.; Marx, D. Peptide Synthesis in Aqueous Environments: The Role of Extreme Conditions on Amino Acid Activation. J. Am. Chem. Soc. 2008, 130, 14148–14160. [Google Scholar] [CrossRef] [PubMed]
- Schreiner, E.; Nair, N.N.; Marx, D. Influence of Extreme Thermodynamic Conditions and Pyrite Surfaces on Peptide Synthesis in Aqueous Media. J. Am. Chem. Soc. 2008, 130, 2768–2770. [Google Scholar] [CrossRef]
- Schreiner, E.; Nair, N.N.; Wittekindt, C.; Marx, D. Peptide Synthesis in Aqueous Environments: The Role of Extreme Conditions and Pyrite Mineral Surfaces on Formation and Hydrolysis of Peptides. J. Am. Chem. Soc. 2011, 133, 8216–8226. [Google Scholar] [CrossRef]
- Wittekindt, C.; Marx, D. Water confined between sheets of mackinawite FeS minerals. J. Chem. Phys. 2012, 137, 054710. [Google Scholar] [CrossRef]
- Muñoz-Santiburcio, D.; Wittekindt, C.; Marx, D. Nanoconfinement effects on hydrated excess protons in layered materials. Nature 2013, 4, 2349. [Google Scholar] [CrossRef]
- Muñoz-Santiburcio, D.; Marx, D. Chemistry in nanoconfined water. Chem. Sci. 2017, 8, 3444–3452. [Google Scholar] [CrossRef] [PubMed]
- Schwendinger, M.G.; Rode, B.M. Possible Role of Copper and Sodium Chloride in Prebiotic Evolution of Peptides. Anal. Sci. 1989, 5, 411–414. [Google Scholar] [CrossRef]
- Rode, B.M.; Suwannachot, Y. The possible role of Cu(II) for the origin of life. Coord. Chem. Rev. 1999, 190–192, 1085–1099. [Google Scholar] [CrossRef]
- Jakschitz, T.A.E.; Rode, B.M. Chemical evolution from simple inorganic compounds to chiral peptides. Chem. Soc. Rev. 2012, 41, 5484–5489. [Google Scholar] [CrossRef] [PubMed]
- Schwendinger, M.G.; Rode, B.M. Salt-induced formation of mixed peptides under possible prebiotic conditions. Inorg. Chim. Acta 1991, 186, 247–251. [Google Scholar] [CrossRef]
- Rode, B.M.; Son, H.L.; Suwannachot, Y.; Bujdak, J. The Combination of Salt Induced Peptide Formation Reaction and Clay Catalysis: A Way to Higher Peptides under Primitive Earth Conditions. Orig. Life Evol. Biosph. 1999, 29, 273–286. [Google Scholar] [CrossRef]
- Rimola, A.; Rodríguez-Santiago, L.; Ugliengo, P.; Sodupe, M. Is the Peptide Bond Formation Activated by Cu2+ Interactions? Insights from Density Functional Calculations. J. Phys. Chem. B 2007, 111, 5740–5747. [Google Scholar] [CrossRef]
- Martínez-Bachs, B.; Rimola, A. Prebiotic Peptide Bond Formation Through Amino Acid Phosphorylation. Insights from Quantum Chemical Simulations. Life 2019, 9, 75. [Google Scholar] [CrossRef]
- Bottke, W.F.; Norman, M.D. The Late Heavy Bombardment. Annu. Rev. Earth Planet. Sci. 2017, 45, 619–647. [Google Scholar] [CrossRef]
- Martínez-Núñez, E. An automated method to find transition states using chemical dynamics simulations. J. Comput. Chem. 2015, 36, 222–234. [Google Scholar] [CrossRef]
- Martínez-Núñez, E. An automated transition state search using classical trajectories initialized at multiple minima. Phys. Chem. Chem. Phys. 2015, 17, 14912–14921. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Morokuma, K. Communications: A systematic method for locating transition structures of A+B→X type reactions. J. Chem. Phys. 2010, 132, 241102. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Ohno, K.; Morokuma, K. Systematic exploration of the mechanism of chemical reactions: The global reaction route mapping (GRRM) strategy using the ADDF and AFIR methods. Phys. Chem. Chem. Phys. 2013, 15, 3683–3701. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Harabuchi, Y. Exploring paths of chemical transformations in molecular and periodic systems: An approach utilizing force. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, 11, e1538. [Google Scholar] [CrossRef]
- Shemesh, D.; Mullin, J.; Gordon, M.S.; Gerber, R.B. Vibrational spectroscopy for glycine adsorbed on silicon clusters: Harmonic and anharmonic calculations for models of the Si(100)-2×1 surface. Chem. Phys. 2008, 347, 218–228. [Google Scholar] [CrossRef]
- Carnimeo, I.; Biczysko, M.; Bloinoa, J.; Barone, V. Reliable structural, thermodynamic, and spectroscopic properties of organic molecules adsorbed on silicon surfaces from computational modeling: The case of glycine@Si(100). Phys. Chem. Chem. Phys. 2011, 13, 16713–16727. [Google Scholar] [CrossRef]
- Arrabito, G.; Pezzilli, R.; Prestopino, G.; Medaglia, P.G. Layered Double Hydroxides in Bioinspired Nanotechnology. Crystals 2020, 10, 602. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rimola, A.; Balucani, N.; Ceccarelli, C.; Ugliengo, P. Tracing the Primordial Chemical Life of Glycine: A Review from Quantum Chemical Simulations. Int. J. Mol. Sci. 2022, 23, 4252. https://doi.org/10.3390/ijms23084252
Rimola A, Balucani N, Ceccarelli C, Ugliengo P. Tracing the Primordial Chemical Life of Glycine: A Review from Quantum Chemical Simulations. International Journal of Molecular Sciences. 2022; 23(8):4252. https://doi.org/10.3390/ijms23084252
Chicago/Turabian StyleRimola, Albert, Nadia Balucani, Cecilia Ceccarelli, and Piero Ugliengo. 2022. "Tracing the Primordial Chemical Life of Glycine: A Review from Quantum Chemical Simulations" International Journal of Molecular Sciences 23, no. 8: 4252. https://doi.org/10.3390/ijms23084252
APA StyleRimola, A., Balucani, N., Ceccarelli, C., & Ugliengo, P. (2022). Tracing the Primordial Chemical Life of Glycine: A Review from Quantum Chemical Simulations. International Journal of Molecular Sciences, 23(8), 4252. https://doi.org/10.3390/ijms23084252







