1. Introduction
Human beings have the capacity to adapt their choices in a very flexible way in different conditions, depending on the particular scenario in which an action occurs and on previous history of rewards and punishments; a situation described in the literature as reinforcement learning. In particular, in a non-stationary environment, individuals must be able to modify their behavior so that an action previously rewarded can be seen in another scenario as inappropriate and replaced with another choice. In recent years, a large number of studies employed reversal learning paradigms to assess individual variability in reward based tasks. Some of these studies were also aiming to achieve a deeper understanding of cognitive alterations in neurological and neuropsychiatric disorders, such as Parkinson’s disease, schizophrenia, depression, compulsive disorders, or substance abuse.
There is a large consensus in the literature that reversal learning involves at least two main brain structures, the basal ganglia (BG) and the prefrontal cortex, PFC (although amygdala and hippocampus are also involved in several tasks, see [
1]). In particular, cortico-striatal synapses, which represent the initial projections of the BG processing stream linking the cortical structures to the striatum, experiment Hebbian plasticity in response to reward and punishments, a phenomenon mediated by dopamine phasic changes [
2,
3]. Neuroimaging studies illustrate the involvement of the dorsal [
4] and ventral [
5] regions of the striatum during reversal learning. Moreover, reversal learning is impaired in subjects with focal BG lesions [
6] and in parkinsonian subjects [
7,
8]; it is affected by levodopa administration, a dopamine precursor [
9] and by drug manipulation of D1 and D2 receptors [
10,
11,
12].
On the other hand, several studies suggest that the BG is under the control of the PFC (especially the orbito-frontal cortex, OFC) and this influence is essential to correctly perform reversal learning. Neuroimaging studies show increased activity in the OFC in human subjects performing reversal learning [
5,
13,
14], while deficits in reversal learning have been seen after lesions of the OFC [
15,
16]. Moreover, insufficient OFC functioning can determine impaired learning in various psychiatric disorders, such as schizophrenia [
17] and obsessive compulsive disorders [
18]. Furthermore, direct current stimulation over the ventrolateral PFC causes a greater number of perseverative errors, thus impairing reversal learning [
19]. It is generally assumed that the PFC areas exert top-down control on the BG [
20] and this control is especially important to suppress previously learned responses [
14].
A fundamental role in this process is played by dopamine (DA) changes. A traditional point of view is that dopamine neurons, projecting to the striatum, code for reward prediction errors through phasic release, thus mediating information processing in the PFC and the BG [
21,
22,
23]. On the other hand, recent studies [
24,
25,
26,
27,
28] have found the presence of a sustained (tonic) DA response directed towards future rewards, arguing that it may represent a motivational signal. Various recent studies underline the fundamental link existing between flexible learning and dopamine [
29,
30]. Cools et al. [
31] observed that the basal dopamine level, tonic, in the striatum is correlated with the way reversal learning is performed: subjects with high baseline dopamine exhibit relatively better reversal learning from unexpected rewards than from unexpected punishments, whereas subjects with low baseline dopamine showed the opposite behavior.
However, as declared by several authors even in very recent studies [
32], “the precise relationship between dopamine and flexible decision making remains unclear”. Westbroock et al. [
33] suggest that dopamine signaling in distinct cortico-striatal subregions represents a balance between costs and benefits, emphasizing the rich spatiotemporal dynamics of dopamine release in striatal subregions.
The neural mechanisms behind reversal learning in the PFC-BG circuitry and the role of dopamine can be better understood by the use of neurocomputational models, inspired by the biology. Indeed, many such models, based on the classic BG division in Go–NoGo pathways, have been presented in recent years, with important gain of knowledge. Frank developed a model for the BG-dopamine system to provide insights into the BG adaptive choices and the impairments in Parkinson disease (PD) subjects [
34]. In order to overcome previous limitations, a more recent expanded version of their model [
20] includes a module, simulating the OFC, which represents contextual information from previous experiences. With this model, the authors explored conditions when more complex decision-making tasks (including reversal learning) require a top-down control and demonstrate the role of the OFC in these conditions. Berthet et al. [
35] implemented Hebbian Go and NoGo connectivity in a Bayesian network (in which units represent probabilities of stochastic events) and tested the model in several learning paradigms, including reversal learning. An important result of this study is that a flexible strategy for action choices is needed to solve different tasks, hence emphasizing the necessity for an external control. To simulate reversal learning, Moustafa et al. [
36] extended a previous model of the BG, including the role of working memory in the PFC, thus implementing an actor-critic schema. Synapses were trained with Hebbian mechanisms, under the control of the critic by the PFC module, which calculates a temporal difference error signal to affect synapses. The models by Morita et al. [
12,
37,
38] based on a state transition approach, try to understand how dopamine changes are controlled by upstream circuitry and suggest that synapse forgetting and an increase of the reward after dopamine depletion are an essential mechanism to explain the results of many effort-related tasks. Using a mechanistic model of the BG, Mulcahy et al. [
39] observed that after learning, a system becomes biased to the previously rewarded choice; hence, establishing the new choice required a greater number of trials. Moreover, with this model, the authors were able to simulate conditions occurring in PD and Huntington’s diseases.
Although the previous experiments and modeling studies depict a clear basic scenario, some aspects deserve further analysis. In our opinion, most experiments in the literature concerning reversal learning, and most matching neurocomputational simulation results, are based on a quite unnatural paradigm. In the classic probabilistic reversal learning paradigm, it is assumed that one action is more frequently rewarded while another action is more frequently punished. The role of the two actions is then reverted, by exchanging the relative probabilities. However, in our daily life, the significance of actions is more complex than in this previous basic schema. Assuming that many actions can have a function in our life, rewards or punishments generally depend on the context in which an action is performed. An action which is more often rewarded in a given context (that is, in response to a given stimulus), can be rewarded less frequently and should be avoided in a different context (that is, when the input stimulus changes). Humans must establish a kind of hetero-associative relationship between actions and stimuli, and these associations can change in a non-stationary environment. In other terms, it is not possible to assign a value to an action without considering the particular input conditions (stimulus or context) on which an action must be performed. This poses more stringent constraints on the learning rules adopted, and makes the training and reversal learning more complex than in most previous basic experiments.
The aim of the present work is to reconsider the overall problem of probabilistic reversal learning, by investigating a multi-action task, using a biologically inspired model of the human BG we developed in previous years (see
Supplementary Materials SI for a detailed description of the model) [
40,
41]. In this study, we assume that all the selected actions are correct at least in one context, hence, should be selected by the agent when the correct stimulus is present. The task is not to choose only one correct action and refuse all the other actions, but to associate each stimulus to a different action in a random probabilistic environment. Examples are given first in the case of a two-action choice and then for a four-action choice.
As in previous models, we assume that synapses in the striatum are plastic and their changes are governed by Hebbian mechanisms. Moreover, we assume that rewards and punishments (which are now stimulus-dependent) are mimicked via phasic peaks and phasic drops of striatal dopamine.
Two important aspects that, to our best knowledge, were not discussed in previous works are assessed here. First, not all versions of the Hebb rule behave in the same way, assuming that the network starts from a completely naïve condition and must learn different stimulus-action associations. In particular, we show that a Hebb rule which changes synapses only with reference to the post-synaptic winner neuron outperforms the other ones. Second, reverse learning requires that the previous learned action is forgotten, to avoid excessive competition between alternative choices. This requires additional top-down mechanisms allowing a flexible use of dopamine, especially producing a stronger dopamine dip in case of unexpected punishments. The latter aspect is discussed, on the basis of a potential top-down flexible control.
These results are important to achieve a deeper understanding of possible learning rules in the BG and, above all, to develop new concepts on how dopamine could be flexibly modified by an action-critics mechanism, hence providing ideas on a possible role of the PFC. Finally, the present algorithm can find potential application in biologically inspired AI algorithms, devoted to learn flexible stimulus-action associations in a non-stationary probabilistic environment.
3. Discussion
General considerations: in the present work, we simulated probabilistic reinforcement learning and reversal learning in a human BG model, in order to analyze two fundamental problems, not completely solved in previous works:
which learning rule is more suitable in a task where the agent must associate different stimuli S with different actions to maximize rewards;
which reinforcement signal (i.e., phasic dopaminergic change) is more appropriate to perform a reversal learning procedure, when a subject should forget a part of the previous synapses in favor of new synapses, to avoid a conflict between the previous choice and the new choice.
A third problem, which we only partially analyze in the present paper, concerns the effect that pathological modifications can have on learning capacity. Indeed, many indications emerging from the present findings can be applied to the study of neurological and neuropsychiatric disorders associated with alteration in the dopamine reward system.
It is important to stress that the strategy for training we used in the present study differs from many tasks commonly adopted in probabilistic reversal learning paradigms. In classical forced-choice tasks (see for instance [
34,
36,
44,
45]), one stimulus is designated as the correct stimulus, associated with the higher probability of a reward, whereas the other stimulus is associated with a smaller reward probability. The two reward probabilities are then changed during the reversal phase. Hence, on each trial in one phase, the agent must designate only one correct action. Even in studies using a larger number of stimuli (see for instance Peterson et al. [
8], who used four different images) subjects should designate only one stimulus, that is the most likely to be rewarded. Our scenario is much more demanding, since at any phase of the experiment, the model should be able to associate a different stimulus with a different action. We think that our paradigm simulates several important situations in real life, in which different actions can be chosen depending on the particular context, and then flexibly modified as the environment changes.
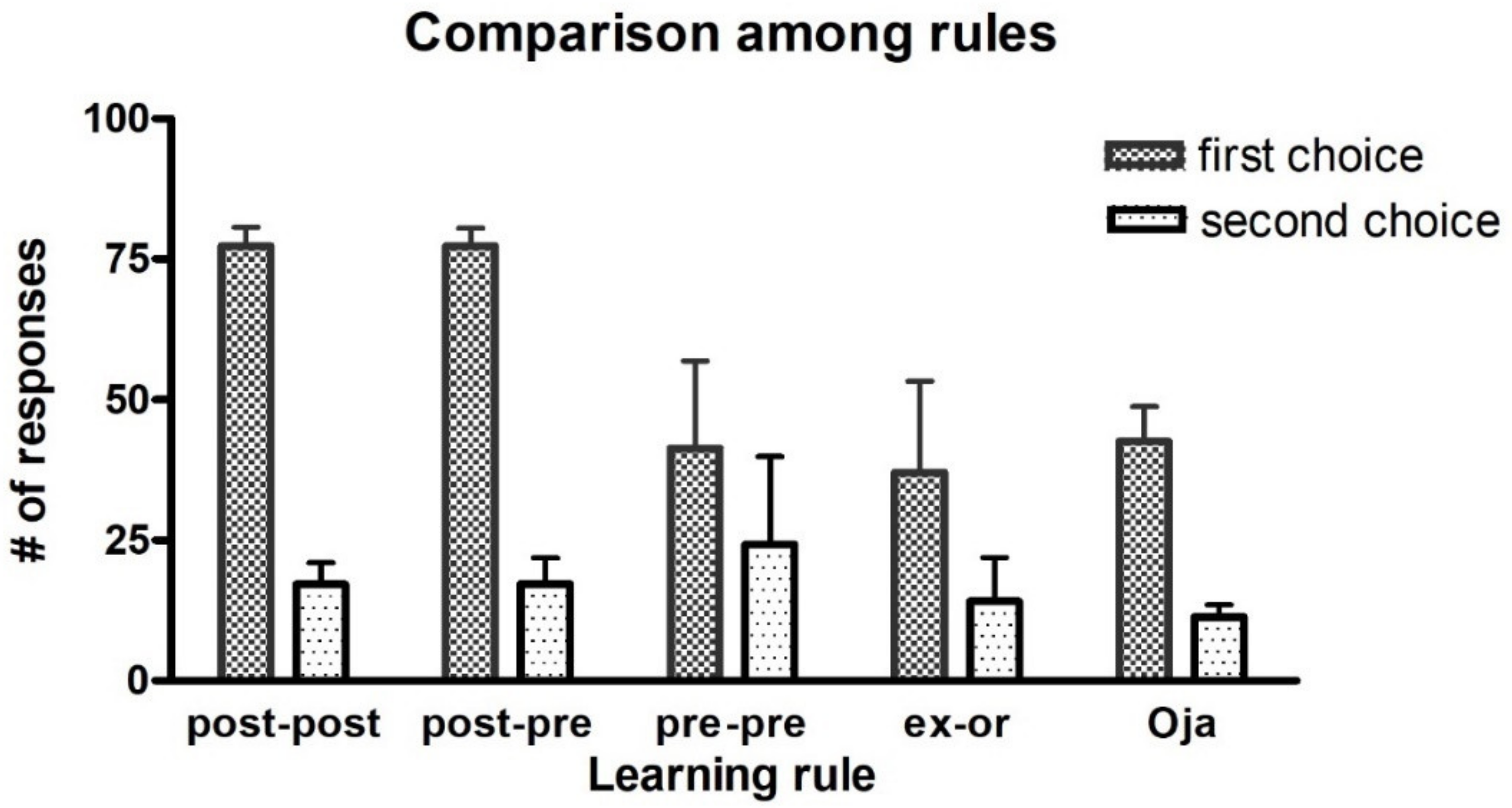
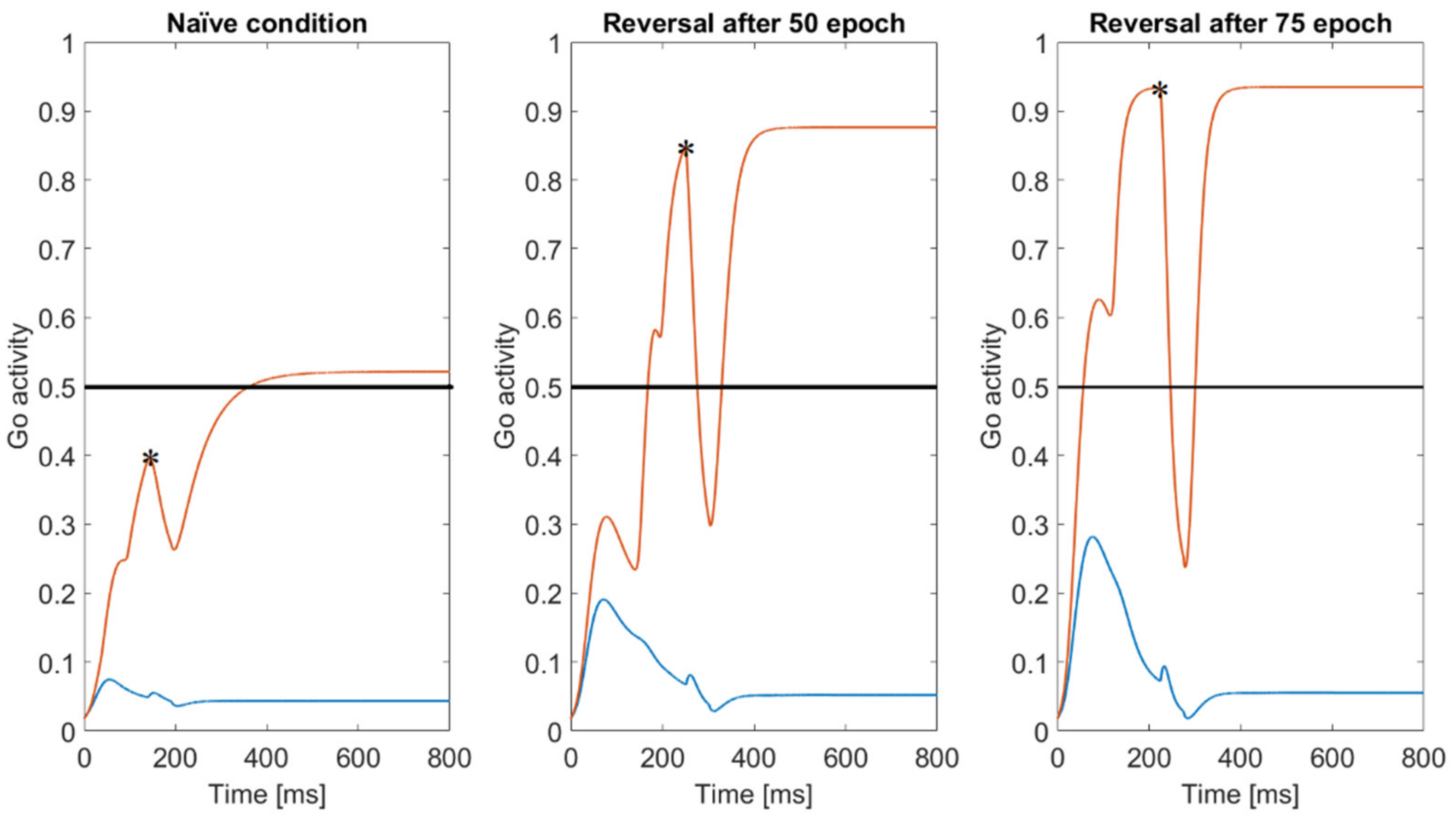
Hebb rule: by simulating this task in a probabilistic environment, a first important result emerged, i.e., that the Hebb rule performs in a largely different way, depending on the choice of the post-synaptic or pre-synaptic terms. In particular, our simulations demonstrate that a rule in which the synaptic changes occur only when the post-synaptic Go neuron is active outperforms the other rules.
It is worth mentioning that, in our previous papers devoted to the analysis of bradykinesia in Parkinson disease [
40,
41] we used a Hebb rule based on the pre-synaptic activity (named
pre-pre in the present work); this rule worked fairly well in a deterministic scenario, as that used in our previous papers, but fails to work in a probabilistic scenario, as the one simulated in the present study.
It is not easy to understand why a rule performs better than another in a probabilistic task. Some examples are given in the
Supplementary Materials SII, to illustrate the reasons for some of the observed differences. Basically, if a network starts from a naïve condition, (and so at the beginning, the number of errors are quite similar as the number of correct choices, in a two-choice task, or greater than the number of correct choices, in a four-choice task), the use of a pre-synaptic positive part results in a more frequent weakening of useful synapses (i.e., those synapses which instead should be reinforced) compared with the use of a post-synaptic positive part. These differences between the Hebb rules are always evident during the basal learning period in a two-choice task (see
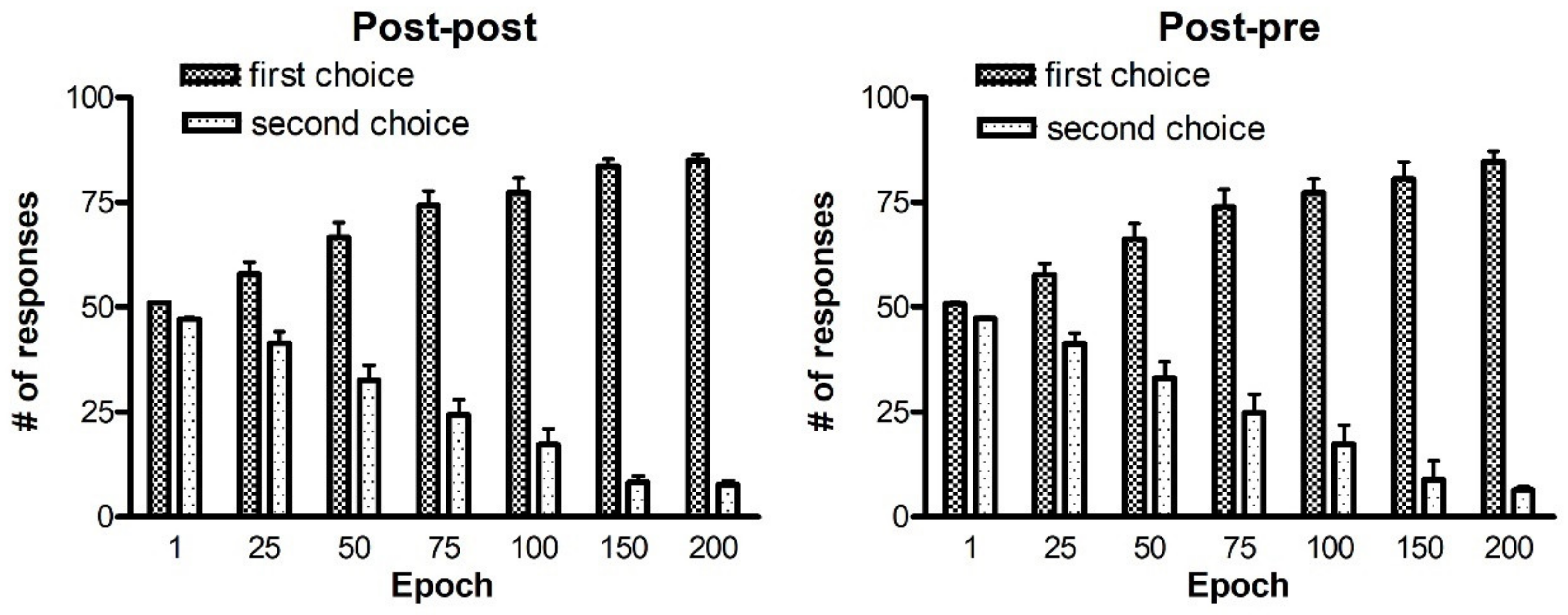
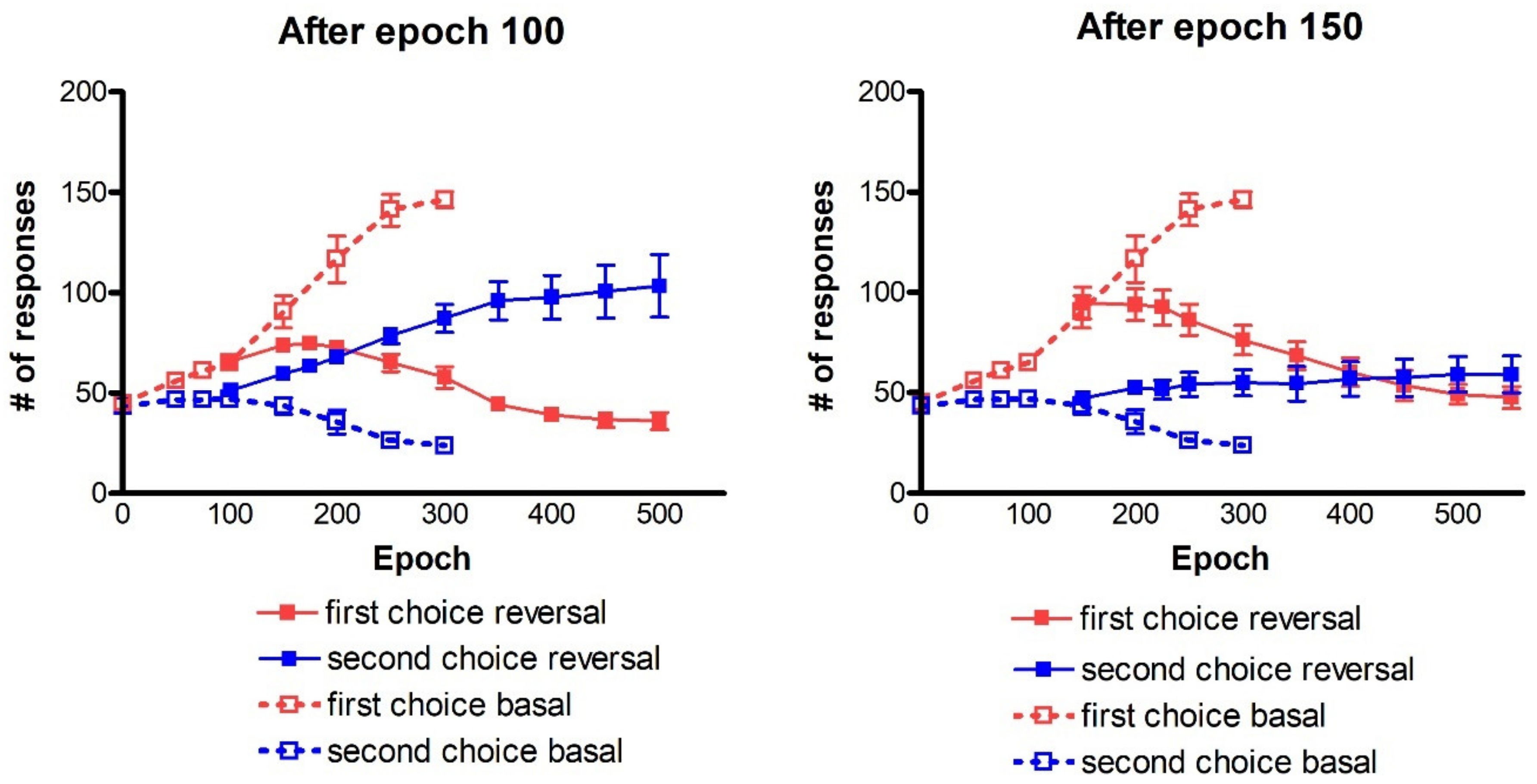
Figure 1) and become even more evident if a four-choice task is performed (see
Figure 8).
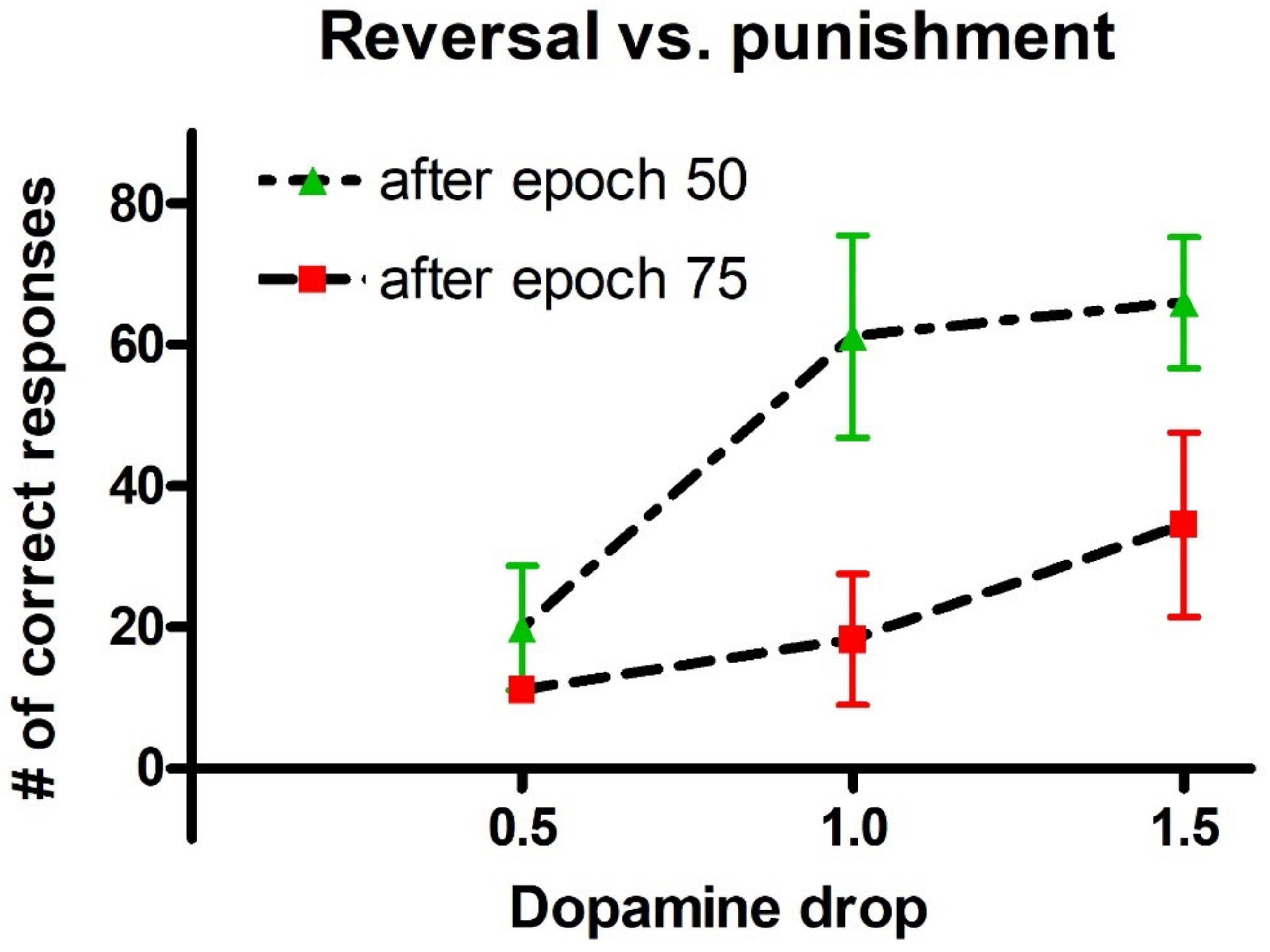
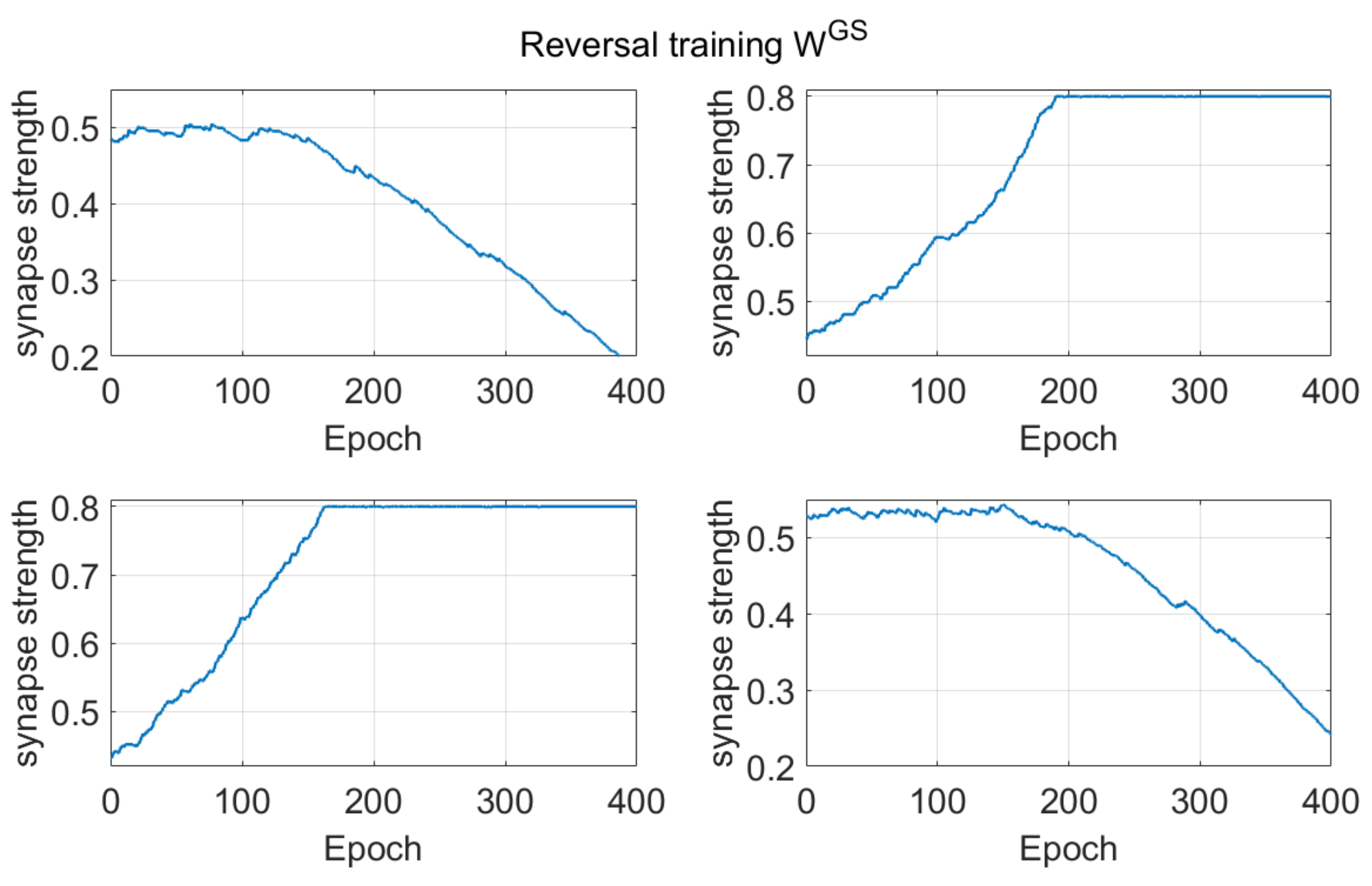
Dopamine changes and reversal learning: simulations concerning the reversal learning show a different aspect. Flexibility requires that a subject partially forgets some of the previous synapses, now associated with a wrong choice, in favor of new synapses, pointing to a more rewarded choice. If previous synapses are not dramatically reduced, an excessive conflict emerges between alternative possible actions, with the effect of either a frequent wrong choice or a frequent no-choice. The importance of forgetting some synapses during reinforcement learning has been stressed by Morita, Kato et al. in a series of modeling papers [
37,
38], although they did not investigate reversal learning specifically. In order to depotentiate previously learned synapses, our simulations point out the necessity for a greater phasic dopaminergic fall during reversal learning, compared with the value used during the initial training; moreover, when the reversal learning becomes more difficult (i.e., in case of a longer previous training and stronger previous habits), a deeper phasic dopaminergic drop is required. This empirical result provides the foundation for the introduction of a top-down control of the dopaminergic input, which should be automatically adjusted to meet the necessity of learning. Actually, as shown in
Figure 7, a decrease in previously learned synapses is the more relevant and more complex target of reversal learning, which can jeopardize the overall process if not sufficiently accomplished.
Top-down dopamine regulation: the necessity of a top-down control of dopamine phasic changes during reinforcement learning is a subject of active research today, a problem which is not completely solved yet and is strictly related with the flexibility of our behavior and with the management of uncertainty (see [
46]). There is large consensus that the striatum plays a pivotal role in this process under the top-down influence of the ventral PFC (especially the OFC) [
17,
47,
48]. Various results suggest a mechanism for an active control of phasic punishment. Ghahremani et al. [
14], through a neuroimaging study, observed an increase in the activity of the OFC and of the dorsal anterior cingulate cortex during reversal learning, and inferred that these regions support an inhibition of learned associations during reversal. Albein-Urios et al. [
19] found that inhibition of the ventro-lateral PFC, achieved via transcranial direct current stimulation, was associated with higher perseverative errors compared to sham conditions. Cools et al. [
5], using functional magnetic resonance imaging, observed signal changes in the right ventrolateral prefrontal cortex on trials when subjects stopped responding to the previously relevant stimulus and shifted responding to the newly relevant stimulus. Recording of single neurons activity in the OFC show that neurons track alterations of reward contingency [
49,
50]. Several studies demonstrated that lesions of the OFC impair reversal learning [
15,
16].
All previous considerations underline that reversal learning paradigms require a dynamic reward representation, including an expectation for the possibility of a change. Soltani and Izquierdo [
1] recently stressed that update of expected rewards necessitate integration of signals among multiple brain areas and suggested that learning must be scaled up when unexpected uncertainty is high. This dynamic representation, in turn, should be converted into dynamic phasic changes in dopamine [
51].
Indeed, many studies suggest that dopamine phasic changes represent the expectancy of a reward, rather than a reward per se (see among the others [
42,
52,
53]) In several previous computational models, this dynamical reward expectancy is simulated using the well-known Sutton and Barto Temporal Difference algorithm [
21,
54]. Moustafa et al. [
36] used this algorithm to implement a critic-actor schema in which the reward prediction is realized through an additional critic node in the network. Conversely, Frank and Claus [
20] adopted a working memory layer to simulate the OFC. A working memory m odule is also used in the model by Deco and Rolls [
55].
The new formulation for phasic dopamine changes: our preliminary simulations clearly demonstrate the need for an ad hoc adjustment in the phasic dopamine signal, in order to adapt this signal to the difficulty of the learning process. Accordingly, in the last part of this work, we propose a new strategy to compute the
expected reward, which is not shared by other models (at least to our knowledge) and does not require any additional computational node. Our suggestion is that information on the
expected reward can be obtained directly from the activity of the winner Go neuron, immediately before the reward/punishment is given (see Equation (1) and
Figure 5). At odd with other models, our rule provides a context dependent reward expectancy. This information can then be directly manipulated by a top-down control, implementing a critic-actor schema, which computes the phasic dopamine changes (i.e., implementing Equations (2) and (3)) in a dynamical way. Of course, our Equations (2) and (3) are empirical, since they simply compute the m-power of the difference between the predicted reward and a naïve prediction (set at 0.5). An important role in our model is given by the parameter
m.
There are two possibilities, which can be tested in future work: either that a single value of m provides adequate reversal learning both in simple and challenging conditions; or that the value of m must be automatically adjusted by a critic. A value m = 2 seems appropriate in a two-action task with probabilities 0.8 and 0.3 and also in the case of simpler tasks (unpublished simulations). An increase in m may be required if the task becomes excessively challenging. This will be the subject of future study.
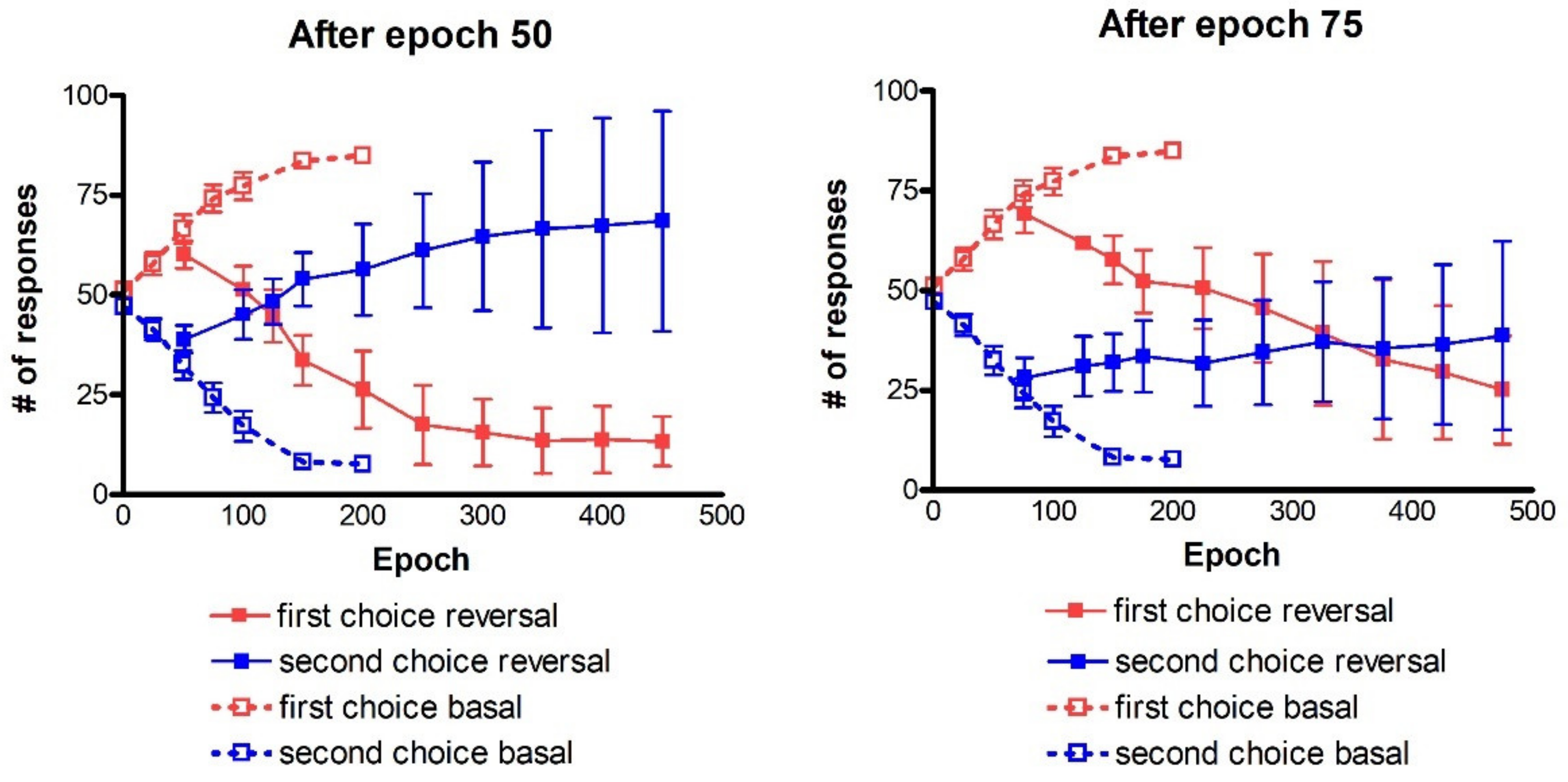
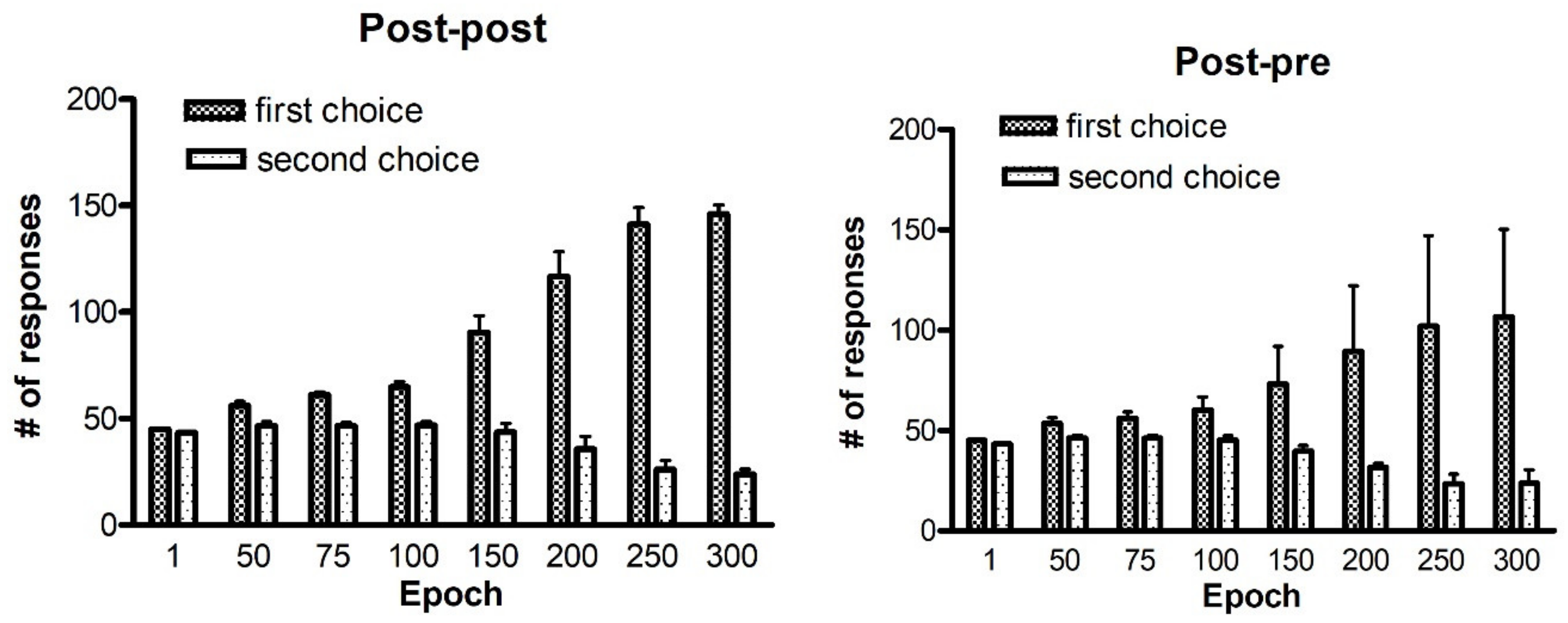
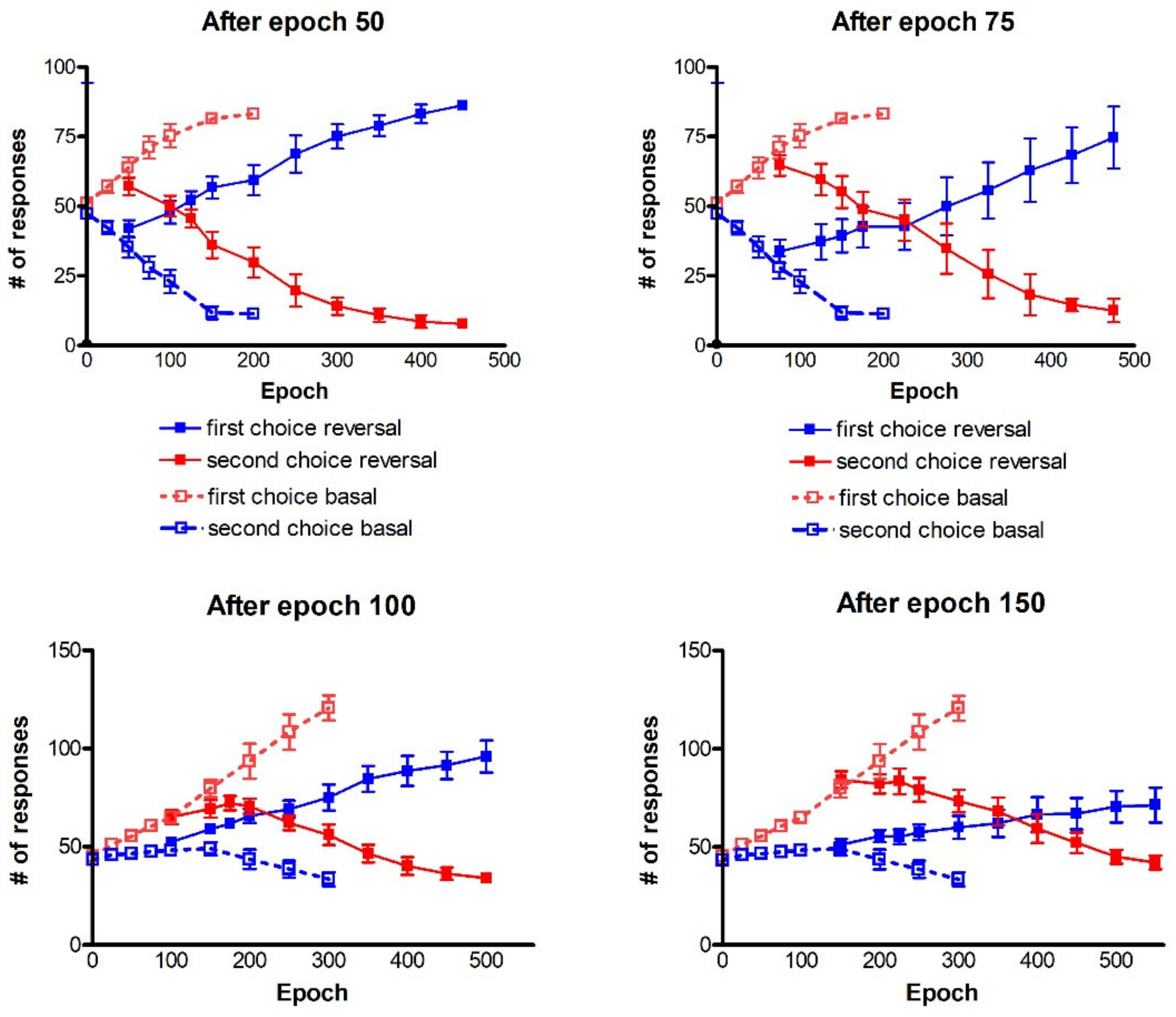
Comparison with existing data: since, as specified above, our task is quite different from the reversal learning tasks found in the literature (which involve one forced choice), we did not make a direct comparison with existing data. However, some considerations can be done, which may represent future testable predictions. Firstly, the reversal learning phase generally requires more time compared with the analogous initial learning phase (see for instance
Figure 11). Moreover, the number of perseverative errors remains higher during the initial period of the reversal. These results are qualitatively in accordance with those of previous experimental tests [
8,
15] and of previous computational results [
36,
39] although, in those works tests were performed in simpler conditions.
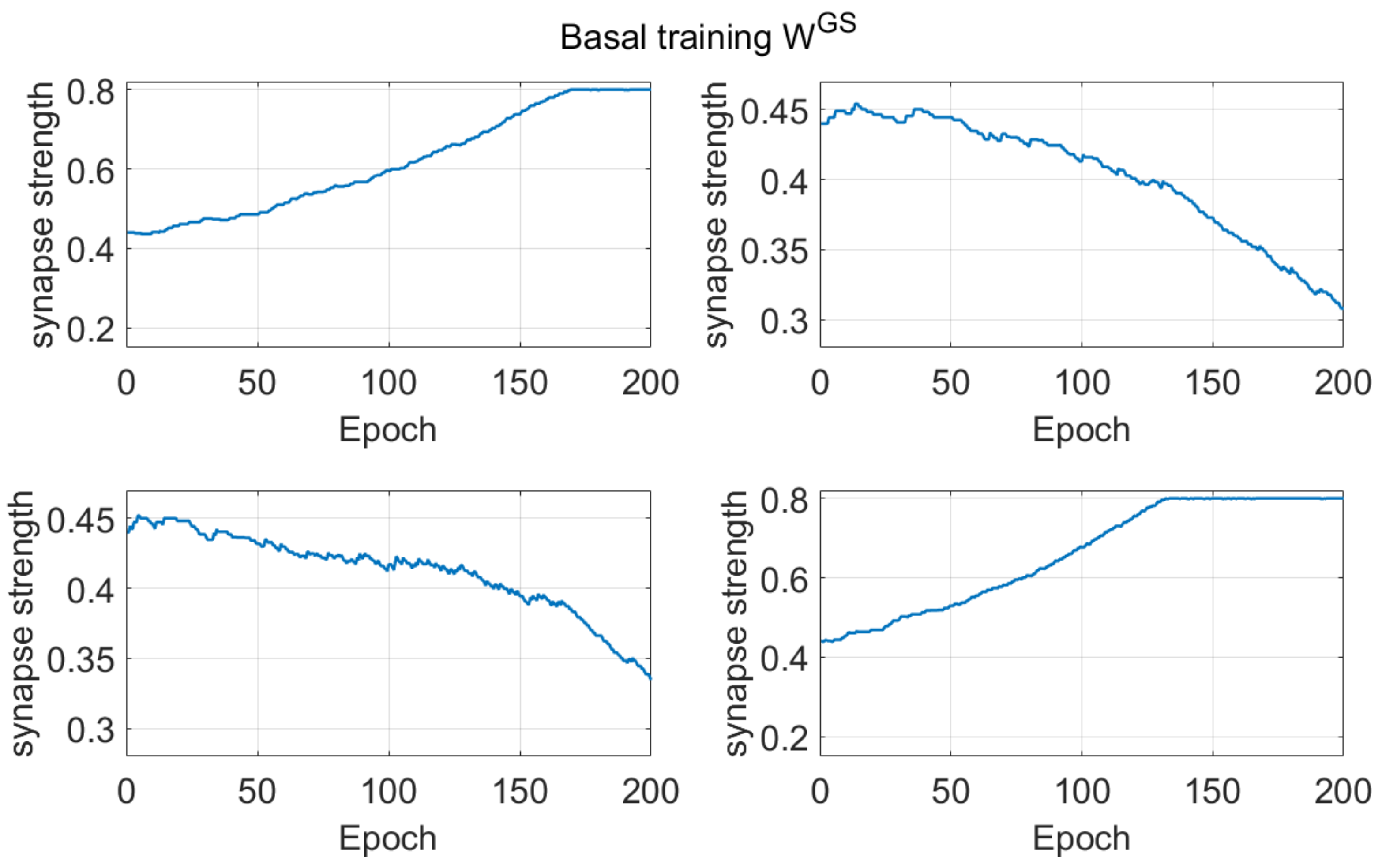
All of these results are quite understandable since, during reversal learning, the agent must forget previous synapses and simultaneously reinforce the new ones. Indeed, looking at the synapse patterns in
Figure 7, one can see that about 150–200 epochs are required before a significant decrease in the previously reinforced synapses.
Another important result that deserves attention is that, after a prolonged reversal learning, the agent sometimes fails to provide any response, especially if reversal occurs in the four-choice task after a long previous learning phase. That is due to an excessive conflict between the previous and the new choice.
Pathological conditions: a notable future application of our model concerns the simulation of learning impairment in neuropsychiatric and neurological diseases. Mukherjee et al. [
56] showed that depressed individuals make fewer optimal choices and adjust more slowly to reversals. Schizophrenic patients perform similarly to control individuals on the initial acquisition of a probabilistic task, but show substantial learning impairments when probabilities are reversed, achieving significantly fewer reversals [
17]. Probabilistic reversal learning is impaired in youths with bipolar disorders compared to healthy control subjects [
57]. Bellebaum et al. [
6] observed that patients with selective BG lesions need more time than control subjects to perform a reversal task. Several of the previous results can be qualitatively simulated with our model by reducing the parameter
m (or more generally by reducing the phasic dopamine drop); this possibility opens interesting perspectives towards future model applications in clinical scenarios.
While the previous deficits seem especially concerned with a malfunctioning of the ventral PFC, learning deficits in patients with Parkinson’s disease (PD) are likely to be connected with a reduction of the baseline dopamine level. Accordingly, reinforcement learning is impaired in PD subjects [
8,
58]. However, dopaminergic therapy improves some cognitive functions and worsens others in patients with PD, an apparently paradoxical result [
9]. In particular, several authors observed that medication worsens reversal learning in PD subjects [
7], although this effect seems to depend on the disease severity [
9,
44].
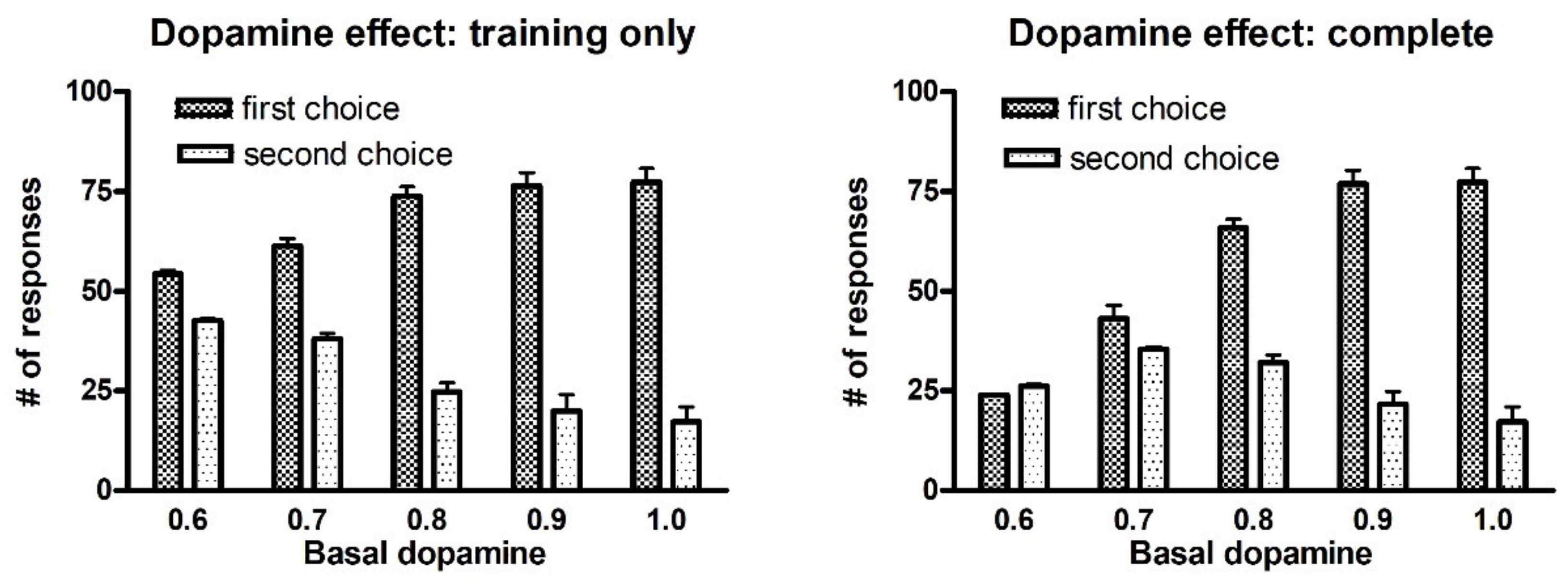
In the present study, we simulated the effect of a change in dopamine basal level (
Figure 10). Our model suggests two concomitant phenomena at the basis of a learning failure in PD subjects, the first related with learning (i.e., a poor adjustment of synaptic changes) and the other related with the strength of the mechanism during the test phase (related to the tonic dopamine level during the test). If the dopamine level is reduced only during the task, but is restored during the test trial, the subject exhibits impaired learning, but with almost 100% of responses. Conversely, if dopamine levels are low both during the training and the test phase, two concurrent phenomena become evident: the incapacity to discriminate between the two choices and a frequent occurrence of no-responses (which corresponds to a typical deficit of PD subjects to start actions, producing symptoms like freezing or bradykinesia). This represents a testable prediction of the model, that may be investigated in future studies, and is in line with the ‘integrative selective gain’ framework proposed by Beeler ([
59,
60], but see also [
41,
61]).
Model limitations: in the present work, we assumed that the unique effect of the PFC top-down control consists in dynamic phasic dopamine changes (especially during punishments). This is the only input to the BG module (besides the external stimulus S). It is possible that other parameters of the model, not only D, are under active control from the PFC (such as the learning rate or the threshold in the Hebb rule). Indeed, Metha et al. [
62] suggested the use of different learning rates for negative and positive prediction errors. Harris et al. [
63] assumed a higher learning rate during reversal learning. An adjustable threshold in the Hebb rule, depending on neural average activity, is typical of the Bienenstock, Cooper, and Munro learning rule, often used in neural network trainings [
64]. However, our model may be seen as more parsimonious, assuming that the entire learning variability depends on the dopaminergic input only. It may be of value to change the learning rate and/or threshold in future works, if the comparison with experimental results should require an improved learning capacity.
Furthermore, the Go pathway plays the more relevant role in our model, while the NoGo synapses increase monotonically (although with a different rate for the different choices, see
Supplementary Materials SIII), signaling a large number of punishments. The choice of a different learning rule for the NoGo portions of the striatum may further improve learning, achieving a better balance between Go and NoGo.
Finally, in future work the model should be tested against human behaviors in the same tasks to compare changes in human performance across training epochs with those predicted by the proposed model. Simulation of experimental results, however, is likely to require an ad hoc fitting of some parameters (for instance the value of the learning rate and the parameter m) to adapt the general network to the particular behavior of individual subjects.
In conclusion, we wish to stress that the present model does not only provide a new step towards a better understanding of dopamine-based reinforcement learning in the PFC-BG complex, but can also represent a tool for future Artificial Intelligence algorithms. This means that it can be applied, in a flexible way, to all conditions where actions must be associated with stimuli in a non-stationary environment.
4. Methods
4.1. Structure of the Network
The overall network is inspired by the human BG. Each neural unit in the model is described using a first-order differential equation, which simulates the integrative properties of the membrane, along with a sigmoidal relationship, which reproduces the presence of lower threshold and upper saturation of neuron activity.
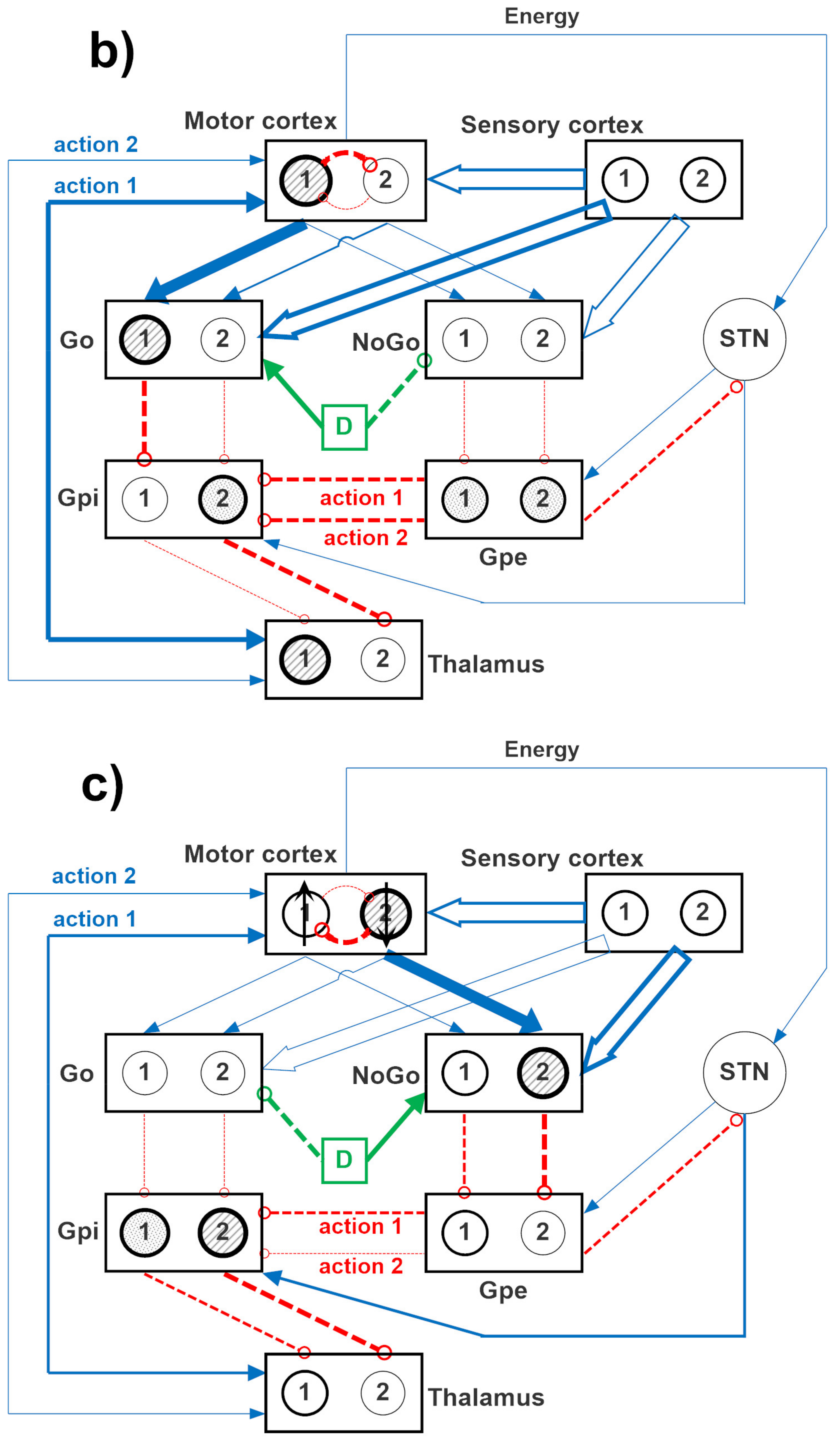
The specific structure of the network is depicted in
Figure 12, where two channels are implemented. A similar structure can be used with four channels, to simulate a four-action choice. The model includes a sensory representation (S) and the corresponding motor representation in the cortex (C). The latter considers several actions in mutual competition, each represented by a segregated channel. The model can be used to simulate several tasks involving reinforcement learning, in which the agent learns to perform a task under the pressure of an environment which rewards or punishes.
In the present study, we focus on probabilistic learning, in which a given action is not always rewarded or punished, but rewards and punishments are delivered per each action with a given probability. Moreover, as specified in the introduction, all actions can be chosen depending on the particular stimulus from the sensory cortex and much focus is given on reversal learning, to study how the network can flexibly change its behavior after a change in the given probabilities.
Downstream the cortex, the model includes the striatum, functionally divided according to dopamine receptor expression (D1: Go, or G, D2: NoGo, or N), the subthalamic nucleus (STN), the globus pallidus pars externa (GPe, or E), the globus pallidus pars interna (GPi, or I), and the thalamus (Th). Accordingly, the model includes the three main neurotransmission pathways (direct, indirect, and hyperdirect) used by the BG. In absence of sufficient stimuli, all actions are inhibited, since the GPi receives a strong basal input and inhibits the thalamus. More particularly, in basal conditions, the cortex, the thalamus, and the striatum are inhibited; conversely, the GPi and GPe exhibit a certain basal activity. We assumed that the basal activity of the GPe is at about half the maximal activity; conversely, the basal activity of the GPi is higher, close to the upper saturation, in agreement with physiological data [
65]. This activity is necessary to maintain the thalamus inhibited, until a significant disinhibition occurs in the GPi as a consequence of the activation of one Go pathway [
40].
In the presence of a sufficient external stimulus, the cortex can select a response based on a competition among cortical neurons. This competition is realized with a winner-takes-all (WTA) process, implemented via lateral inhibition in the cortex. However, in order to win the competition, a neuron in a WTA circuit must receive a strong self-excitation: this is an essential mechanism to trigger the instability that is typical of WTA dynamics. In the model, this self-excitation becomes operative only when the corresponding neuron in the thalamus is activated: this thalamic neuron sends excitation to the cortex and closes a self-excitatory loop (see
Figure 12). Selection of an active neuron in the thalamus, in turn, is a consequence of a prevalence of the Go pathway on the NoGo pathway for a specific action channel. Hence, the final decision actually occurs in the BG, and this choice becomes operative when the corresponding neuron in the thalamus overcomes a certain excitation threshold.
In the model, the hyperdirect pathway (from the cortex to the STN and then to the GPi) is used to excite the GPi (and so to inhibit the thalamus) in the presence of several conflicting actions in the cortex. This is used to prevent many simultaneous cortical winners, and let the cortex have more time to solve the conflict.
In the following we will use the symbol Wlk to represent the array of all synapses entering into a downstream layer, l, from an upstream layer, k. Hence, the lower case symbol, , is used to represent an individual synapse in the previous array, namely the synapse from neuron at position j in the upstream layer k, to a neuron at position i in the downstream layer l. These arrays have dimension Nc × Nc, where Nc represents the number of channels used in the simulation, equal to the number of possible selected actions (2 or 4). It is worth noting that all these arrays are diagonal, since all channels are segregated (hence, ), with the only exception of the arrays originating from the sensory cortex (i.e., the array WGS from the sensory cortex to the Go neurons, and the array WNS from the sensory cortex to the NoGo neurons), which are fully connected.
4.2. The Effect of Dopamine on the Go and NoGo Pathways
According to the literature, we assumed that dopamine exerts a different effect on neurons in the Go pathway (which express D1 receptors) and neurons in the NoGo pathway (D2 receptor expression). In particular, dopamine has an excitatory influence on active neurons in the Go pathway, and an inhibitory effect on the inactive neurons, thus realizing a kind of contrast enhancement mechanism [
66], which favors the selection of the winner action only. Conversely, dopamine has an inhibitory effect on all neurons in the NoGo pathway. Furthermore, we assumed that the action of dopamine is potentiated by cholinergic influences, through a kind of push-pull mechanism: an increase in dopamine reduces the cholinergic activity, thus introducing a disinhibition on the Go pathway and further inhibition in the NoGo. In fact, cholinergic activity is inhibitory on the Go and excitatory on the NoGo, while cholinergic changes are always specular to dopamine changes [
67].
The effects of dopamine changes in the model are represented through a quantity, named
dopaminergic input,
D. The latter exhibits a constant (tonic) level (
) at rest, a transient phasic (
) increase (
) during rewards and a transient phasic decrease (
) during punishments. As expressed in the following Equations (4)–(6):
It is worth noting that, in some of the subsequent simulations, the value of the dopaminergic input can become negative during a phasic dopaminergic drop. This is not a contradiction since, in the model, the quantity D does not represent dopamine concentration per se, but rather an external input, which accounts for the effect that dopamine concentration changes can have on the neurons in the striatum, mediated via D1 and D2 receptors.
According to Equation (5), following a reward, the dopaminergic input is increased to a value twofold the basal one () and maintained for a time sufficient for the network to reach a new steady state condition, characterized by a high value of the winner Go neuron and a low value for the other Go and NoGo neurons. Similarly, after a punishment, the dopaminergic input is decreased by a factor Ddrop, causing a fall in the activity of the winner Go neuron and an increase in the activity of the NoGo neurons (especially in the winning channel). Finally, in the steady state condition after a reward or a punishment, the Hebb rule described below is applied.
In the last simulations, as described in the
Section 2, Equations (5) and (6) are replaced with new expressions (see Equations (2) and (3)), to account for
expected reward changes.
4.3. Synapse Learning
We assumed that synapses entering into the striatum (i.e., from the sensory cortex into the Go and NoGo layers, named WGS and WNS, and from the motor cortex to the Go and NoGo layers, WGC and WNC, respectively) are plastic and can be trained using Hebbian mechanisms. In order to implement these mechanisms, we assumed that the activity of the post-synaptic neuron (say to denote the activity of neuron i in the layer A) and the activity of the presynaptic neuron (say to denote the activity of neuron j in the layer B) are compared with a threshold and multiplied. In this way, both long term potentiation can be simulated, when activity of both neurons is above the threshold, and long term depression, when one neuron activity is above the threshold and the other is below the threshold. Furthermore, the synaptic change is applied only after a reward or a punishment, when a dopamine change occurs.
However, in order to avoid that, a synapse is reinforced when both the pre-synaptic and post-synaptic activities are below the threshold (i.e., when both neurons are scarcely active, a condition which should not produce any synaptic change), we introduced a function “positive part” either to the post-synaptic or pre-synaptic term in the Hebb rule (see Equations (7)–(9)): this signifies that, the Hebb rule should be applied only when the corresponding neuron is active. In this way, different alternative forms of the Hebb rule can be simulated and tested. Asdemonstrated in the
Section 2, these different rules have different behavior in the hetero-associative paradigm used in this work.
In previous papers, we used the following version of the Hebb rule, that is similar to a rule used in [
40], assuming that the activity of the presynaptic neuron must be above the threshold to have a synaptic change. We can write:
where
represents the variation of the synapse between the pre-synaptic neuron
in layer B (B = S or C) and the post-synaptic neuron
in layer A (A = G or N) and the ()
+ represents the function “positive part”, that is: (
x)
+ =
x if
x > 0; otherwise (
x)
+ = 0.
Since the function “positive part” is applied to the presynaptic neurons (both in the Sensory cortex S and in the motor Cortex, C), this rule (Equation (7)) will be named the pre-pre synaptic rule.
However, as shown in the
Section 2, and further illustrated in the
Supplementary Materials SII, we observed that the previous rule, when applied to a probabilistic hetero-associative problem, does not work properly. Hence, we tested different rules.
In a rule named post-post synaptic rule (Equation (8)), we assumed that the function “positive part” applies to the post-synaptic neurons, both in Go and NoGo pathways:
Hence, the synapse change is applied only if the post synaptic neuron is active.
As analyzed in the
Supplementary Materials SII of this work, the previous equations may have advantages and disadvantages when applied to the schema in
Figure 12. So, we considered also the possibility that the postsynaptic rule applies to synapses connecting the sensory cortex to the striatum, while the pre-synaptic rule applies to synapses connecting the motor cortex to the striatum. Hence, two alternative rules have been applied depending on the upstream region:
where the post-synaptic neuron
belongs to layer A (A = G or N). In the following, Equations (9) are named the post-pre synaptic rule.
Finally, we also tested two additional more traditional rules. In the first, we applied the covariance Hebb rule, which only excludes the possibility of potentiation when both neurons are below threshold (as in the exclusive or operation). This rule, named the ex-or covariance rule (Equation (10)):
Finally, we also tested the Oja rule (Equation (11)), which is a classic Hebb rule (without threshold) with the inclusion of a forgetting factor to have depotentiation:
Finally, for any of the previous rules, we assumed that synapse cannot decrease below zero nor can increase above a maximum value (say,
wmax). That is, after any learning step, we checked:
4.4. Training the Network
The network was trained using a probabilistic reinforcement learning paradigm, in which a combination of inputs is given to the network in the sensory cortex and the chosen action is rewarded or punished with a pre-assigned probability. If the stimulus changes, the chosen action also changes. This is a more difficult protocol compared with a case in which an action is always rewarded or always punished following a given stimulus-response combination. It is also a more realistic paradigm, compared with the case when only one forced choice is implemented (i.e., a choice which does not depend on the context or stimulus S). Moreover, after a learning period, we modified the probability associated with rewards and punishments, to simulate a reversal learning paradigm; hence, the preliminary choices are necessarily modified on the basis of a new experience in a non-stationary environment.
Since the BG are especially involved in a slow learning of positive and negative outcomes, resulting in motor habits [
20,
68], we used a slow value for the learning factor (
σ in Equations (7)–(11)); as a consequence, the training required different epochs to reach a clear discrimination between responses.
It is worth noting that, while the number of elements in the motor cortex always corresponds to the number of possible actions, the dimension of the sensory representation S can be independent of the number of selected actions and can be chosen to simulate inputs with different complexity. In this work, we used a vector S with dimension 2 × 1 and 4 × 1, for 2 and 4 channels, respectively, just for the sake of simplicity, to facilitate the analysis of synapses.
4.4.1. Two-Choice Experiment
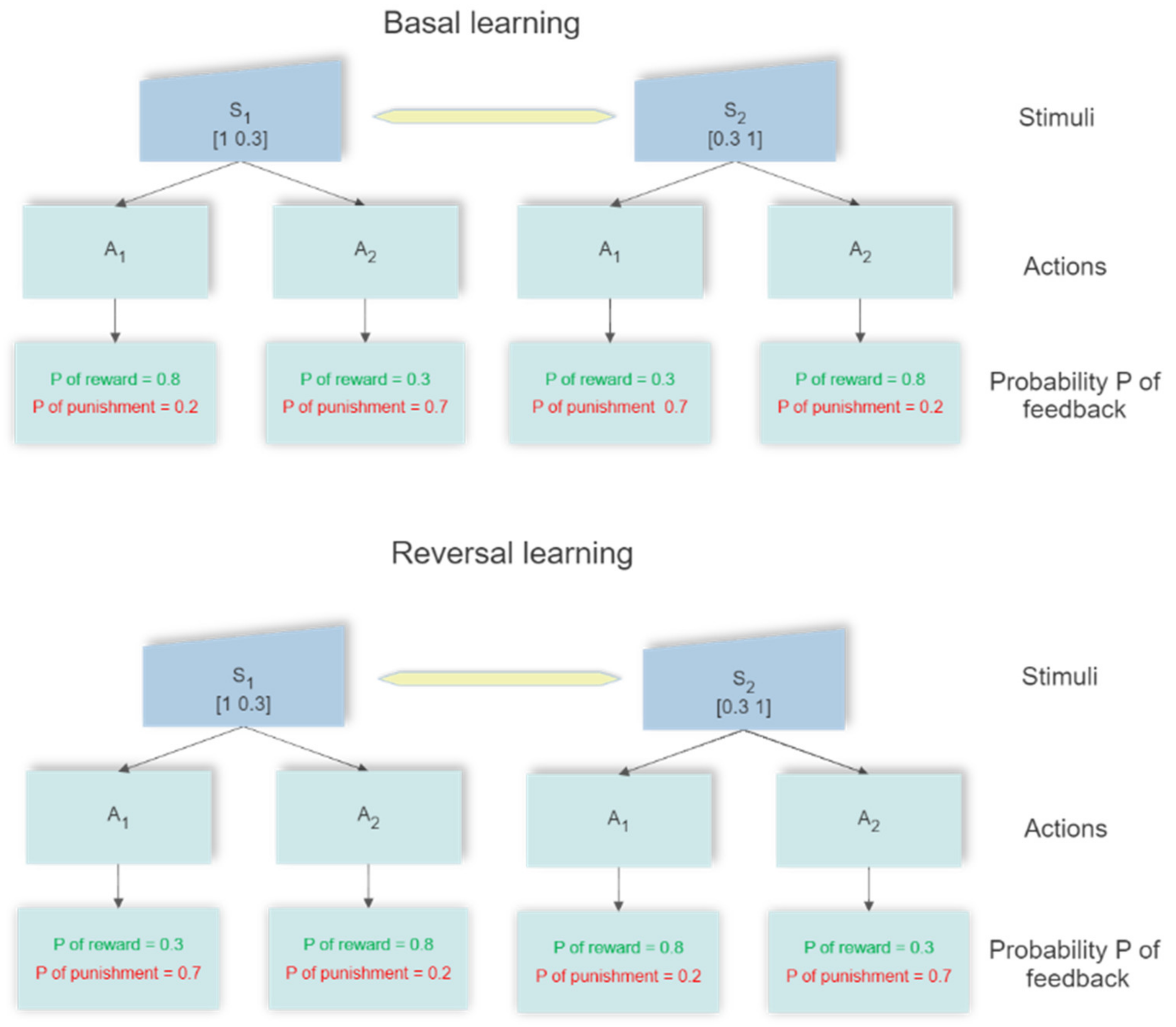
In a first paradigm, we simulated a two-choice experiment, where one of two actions (described through channels 1 and channels 2 in the model) in response to two alternative stimuli must be selected. A schematic representation of the experiment is shown in
Figure 13. The network starts from a naïve condition, in which all synapses have the same values for each channel (hence no action is preferentially selected) and the synapses from each element of the input stimulus are identical (hence the stimuli in the vector S have initially an identical meaning). The values of these initial synapses have been given so that the activity of the Go and the NoGo neurons in the winner channel, before any reward or punishment, settle at a value as high as 0.5 (which is the middle since the activity is scaled between 0 and 1). Rewards increase the activation of the winner Go neuron well above 0.5, while punishments decrease activation to a small value. The opposite occurs for the NoGo neuron in the winner channel. A Gaussian white noise was added to all neurons in the motor cortex (zero mean value, standard deviation 0.2) to have a different response at each trial.
Each training procedure consisted of 200 epochs. Each epoch consists of the two stimuli, S1 = [1 0.3] and S2 = [0.3 1], permuted in a random fashion. A total of 10 independent learning procedures (each with 200 epochs starting from the naïve network and different noise realizations, with different seed of noise) were performed, to simulate 10 different networks independently trained.
At each trial, a reward or punishment is given whenever the network performs a single choice. This occurs if one neuron in the motor cortex reaches a value higher than 0.9 in the final steady state condition, while all other neurons in the motor cortex have activity close to zero (thanks to the winner takes all dynamics). The cases in which no neuron reaches the value 0.9 (absence of a response), or more than one neuron overcomes the value 0.9 (multiple responses) are considered as no-response, and neither a reward nor a punishment is assigned.
During the basic learning phase, in response to the first stimulus, S
1, the first action is randomly rewarded with a probability as high as 0.8 (otherwise the action is punished), while the second action is randomly rewarded with a probability as low as 0.3 (otherwise punished). When a second stimulus S
2 is given the reward probabilities are 0.3 for the first choice and 0.8 for the second one. We also tested different values for the probabilities to implement a simpler task (probabilities 0.9 and 0.2) or a more challenging task (probabilities 0.7 and 0.4). As seen in the
Section 2, we presented the results for the intermediate task only, which represents a sufficient level of complexity. A few details on the other tasks have been given at the end of the
Section 2.
Reversal learning can theoretically be initiated after any epoch during the basal learning. However, the longer the previous learning period (i.e., the greater the number of epochs used for learning), the more difficult is the reversal. For this reason, reversal learning was attempted at different moments, namely after 50 epochs and after 75 epochs of previous learning. Reversal consists in the same inputs S1 and S2, randomly permuted at each epoch, but with the opposite associated reward probabilities: action 1 is associated with 0.3 reward probability after presentation of the stimulus S1 and with 0.8 reward probability after S2; action 2 is associated with 0.8 and 0.3 reward probabilities after S1 and S2, respectively.
The capacity of the network to learn the more probable reward, still maintaining the capacity to explore different possibilities, is tested via a testing procedure. In total, 100 trials are executed, by using the inputs S1 and S2 50 times each, but without rewards or punishments, and the number of responses (either the reinforced action or the unreinforced action) is counted. Correct learning is characterized by a greater percentage number of the reinforced responses, and a smaller number of unreinforced ones. This testing procedure has been performed starting from the network obtained after different epochs of learning (1, 25, 50, 75, 100, 150, 200) to assess the effect of a longer learning on the network behavior. During the test, random Gaussian noise was applied not only to cortical neurons, but also to the input stimuli (simulating a noisy environment).
4.4.2. Four-Choice Experiment
The simulations were then repeated using a more complex 4-actions paradigm. In this case we used the stimuli indicated below, associated with the reward probabilities for the four actions
S1 = [1.0 0.3 0.1 0.1] associated with the reward probabilities: P1 = [ 0.8 0.3 0.1 0.1]
S2 = [0.3 1.0 0.1 0.1] associated with the reward probabilities P2 = [ 0.3 0.8 0.1 0.1]
S3 = [0.1 0.1 1.0 0.3] associated with the reward probabilities: P3 = [ 0.1 0.1 0.8 0.3]
S4 = [0.1 0.1 0.3 0.1] associated with the reward probabilities: P4 = [ 0.1 0.1 0.3 0.8]
During reversal learning, the probabilities P1 and P2 were inverted for the stimuli S1 and S2, and the probabilities P3 and P4 were inverted for the stimuli S3 and S4. Each epoch consists of each four possible inputs, given in a randomly permuted order. The test phase consisted of 200 trials, and each input is used 50 times.
4.5. Sensitivity Analysis
In order to better understand the role of some parameters in the model, a sensitivity analysis was performed. Indeed, the most important parameters in the model are the tonic dopaminergic input,
Dtonic, and the dopamine fall during punishments,
Ddrop (we remind that the dopaminergic increase after a reward (
) was always equal to +
Dtonic, i.e., a twofold increase in the dopaminergic input). The parameter
Ddrop was essential to control learning, especially in the reversal phase, hence its role was tested carefully by repeating learning with different values of
Ddrop. We assume that this parameter must be under control of top-down regulating mechanisms (see
Section 3).
Different values of D (tonic condition) were tested, to analyze how learning can be affected by dopamine imbalances, as those occurring in Parkinsonian subjects, or after medication.
4.6. Active Control of the Phasic Dopamine
The simulation results suggest that a different phasic dopamine should be used during reversal learning compared with the basic learning, to avoid excessive competition between a previously learned choice and a new choice (in particular unexpected punishments should have a strong impact during a reverse choice, to depotentiate the synapses). Hence, in the last series of simulations shown in the
Section 2, we repeated the basic learning procedure and the reversal learning procedure assuming that the phasic dopamine changes are
controlled by the activity of the winner Go neuron. Briefly, we can consider that the value of the winner Go neuron, at the instant of the reward/punishment,
signals the expected probability of a reward. This quantity is automatically updated by the network, on the basis of a previous history of rewards and punishments, and also depends on the input stimulus (hence on the context). Consequently, we decided that the higher the Go activity, the smaller the phasic dopamine reward (in case the action is rewarded) or the higher the phasic dopamine punishment (in case the action is punished).