Atomistic Simulations of Functionalized Nano-Materials for Biosensors Applications
Abstract
:1. Introduction
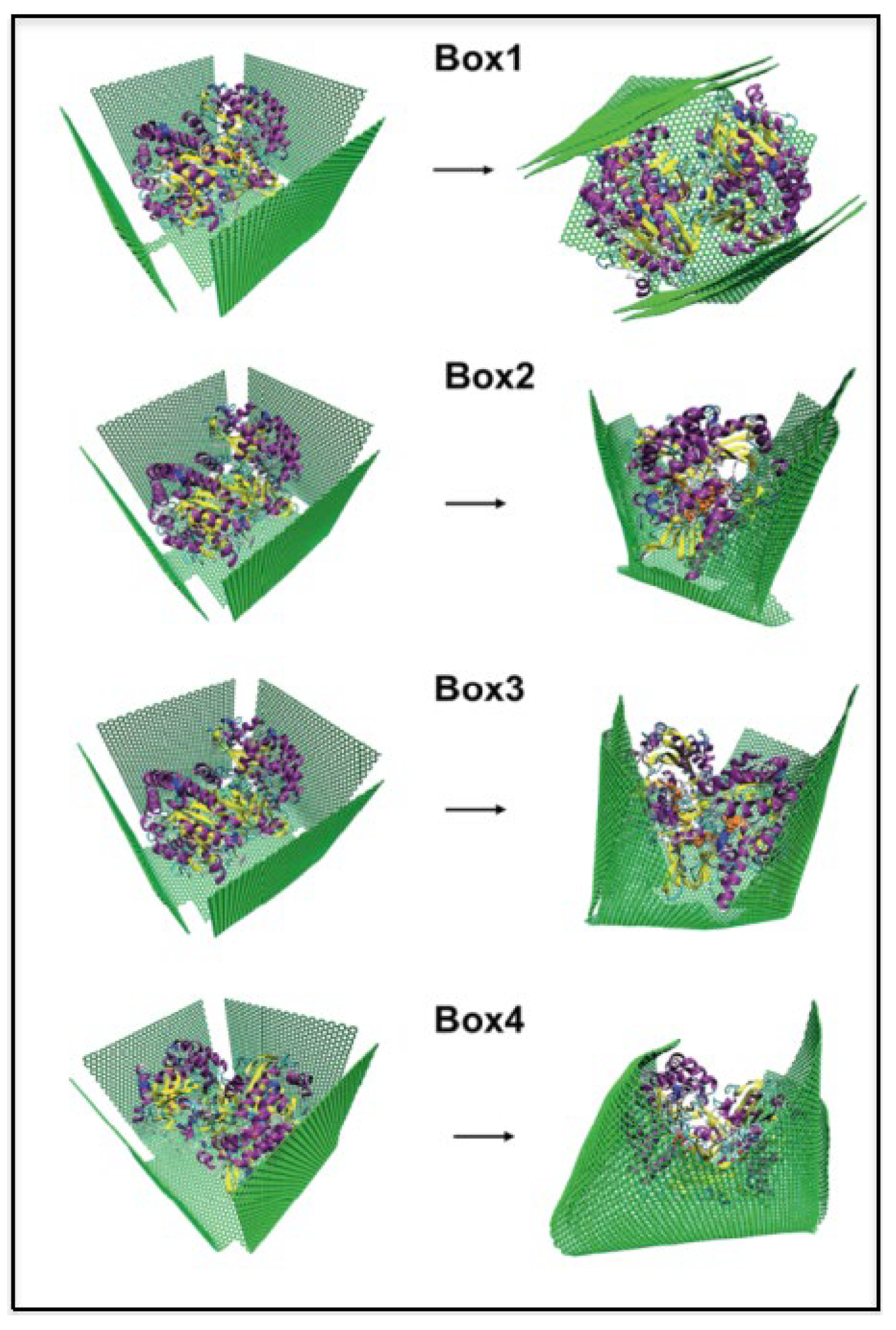
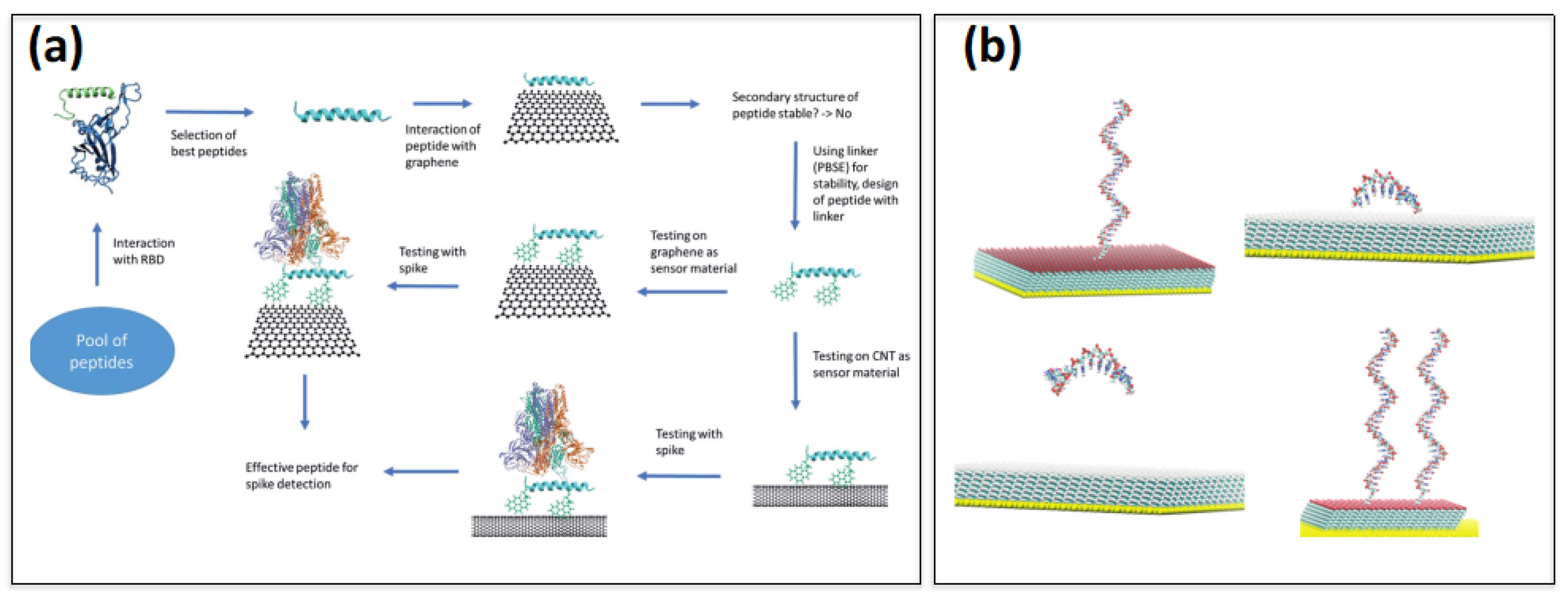
2. Graphene-Based Biosensors
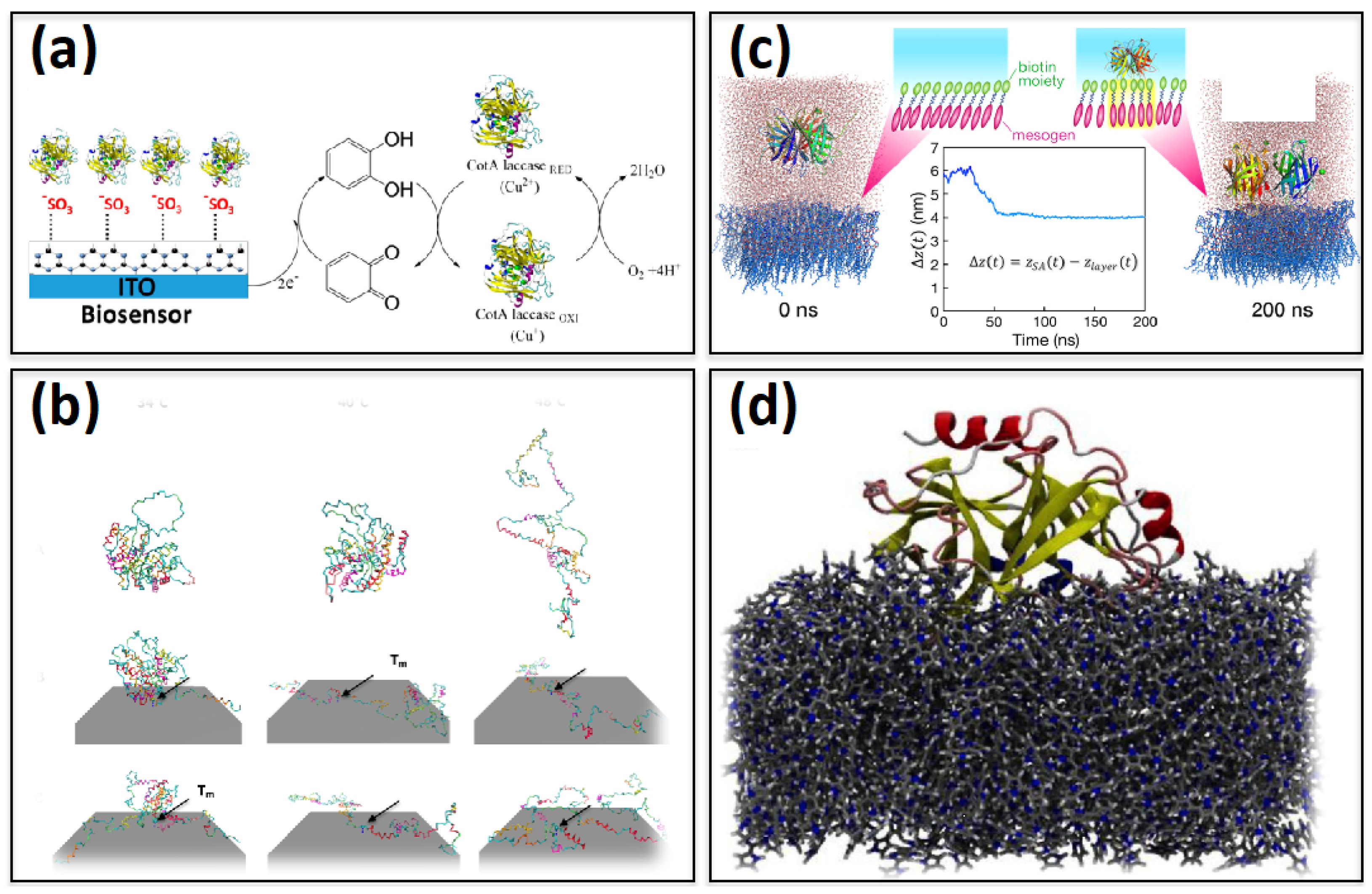
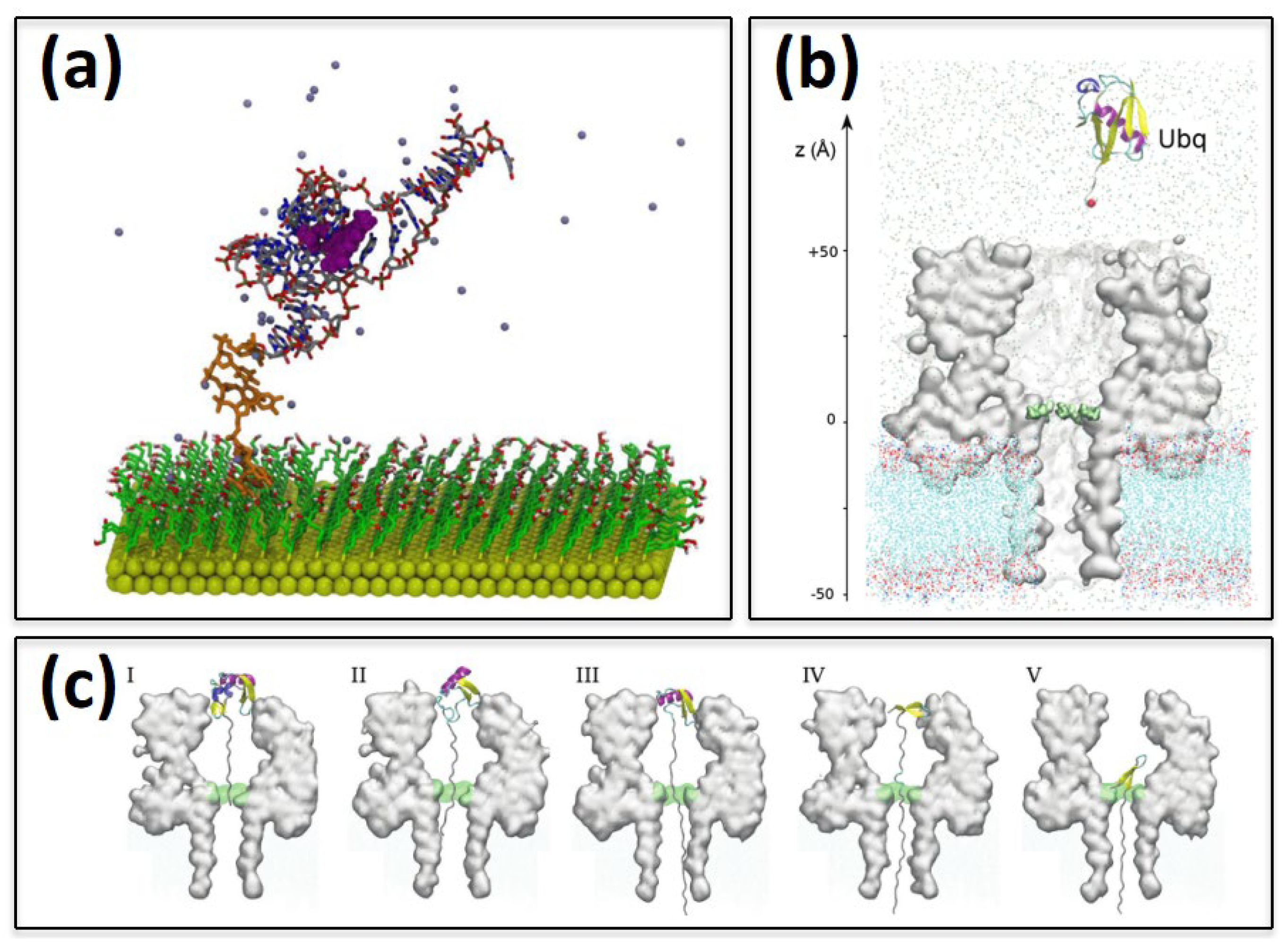
Self-Assembled Monolayer-Based Biosensors
3. Polymer-Based Biosensors
3.1. Aptasensors
3.2. Nanopore Based Biosensors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mittal, S.; Kaur, H.; Gautam, N.; Mantha, A.K. Biosensors for breast cancer diagnosis: A review of bioreceptors, biotransducers and signal amplification strategies. Biosens. Bioelectron. 2017, 88, 217–231. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, N.; Jolly, P.; Formisano, N.; Estrela, P. Introduction to Biosensors. Essays Biochem. 2016, 60, 1–8. [Google Scholar] [PubMed] [Green Version]
- Mikuła, E. Recent Advancements in Electrochemical Biosensors for Alzheimer’s Disease Biomarkers Detection. Curr. Med. Chem. 2021, 28, 4049–4073. [Google Scholar] [CrossRef] [PubMed]
- Shui, B.; Tao, D.; Florea, A.; Cheng, J.; Zhao, Q.; Gu, Y.; Li, W.; Jaffrezic-Renault, N.; Mei, Y.; Guo, Z. Biosensors for Alzheimer’s disease biomarker detection: A review. Biochimie 2018, 147, 13–24. [Google Scholar] [CrossRef]
- Li, Z.; Mohamed, M.A.; Mohan, A.M.V.; Zhu, Z.; Sharma, V.; Mishra, G.K.; Mishra, R.K. Application of electrochemical aptasensors toward clinical diagnostics, food, and environmental monitoring. Sensors 2019, 19, 5435. [Google Scholar] [CrossRef] [Green Version]
- Saha, K.; Agasti, S.S.; Kim, C.; Li, X.; Rotello, V.M. Gold nanoparticles in chemical and biological sensing. Chem. Rev. 2012, 112, 2739–2779. [Google Scholar] [CrossRef] [Green Version]
- Eissa, S.; Zourob, M. Development of a Low-Cost Cotton-Tipped Electrochemical Immunosensor for the Detection of SARS-CoV-2. Anal. Chem. 2021, 93, 1826–1833. [Google Scholar] [CrossRef]
- Sin, M.L.; Mach, K.E.; Wong, P.K.; Liao, J.C. Advances and challenges in biosensor-based diagnosis of infectious diseases. Expert. Rev. Mol. Diagn. 2014, 14, 225–244. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.; Tilley, R.D.; Gooding, J.J. Challenges and Solutions in Developing Ultrasensitive Biosensors. J. Am. Chem. Soc. 2019, 141, 1162–1170. [Google Scholar] [CrossRef]
- Lowe, B.M.; Skylaris, C.K.; Green, N.G.; Shibuta, Y.; Sakata, T. Molecular dynamics simulation of potentiometric sensor response: The effect of biomolecules, surface morphology and surface charge. Nanoscale 2018, 10, 8650–8666. [Google Scholar] [CrossRef] [Green Version]
- Kucherenko, I.S.; Soldatkin, O.O.; Kucherenko, D.Y.; Soldatkina, O.V.; Dzyadevych, S.V. A Novel Amperometric Glutamate Biosensor Based on Glutamate Oxidase Adsorbed on Silicalite. Nanoscale Adv. 2019, 1, 4560–4577. [Google Scholar] [CrossRef] [Green Version]
- Jurado-Sanchez, B. Nanoscale Biosensors Based on Self-Propelled Objects. Biosensors 2018, 8, 59. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Guo, Q.; Cui, D. Recent advances in nanotechnology applied to biosensors. Sensors 2009, 9, 1033–1053. [Google Scholar] [CrossRef] [Green Version]
- Hong, P.T.K.; Jang, C.-H. Sensitive and label-free liquid crystal-based optical sensor for the detection of malathion. Anal Biochem. 2020, 593, 113589. [Google Scholar] [CrossRef] [PubMed]
- Bhalla, N.; Pan, Y.; Yang, Z.; Payam, A.F. Opportunities and Challenges for Biosensors and Nanoscale Analytical Tools for Pandemics: COVID-19. ACS Nano 2020, 14, 7783–7807. [Google Scholar] [CrossRef] [PubMed]
- Vidotti, M.; Carvalhal, R.F.; Mendes, R.K.; Ferreira, D.C.M.; Kubota, L.T. Biosensors based on gold nanostructures. J. Braz. Chem. Soc. 2011, 22, 3–20. [Google Scholar] [CrossRef] [Green Version]
- Ozboyaci, M.; Kokh, D.B.; Corni, S.; Wade, R.C. Modeling and simulation of protein-surface interactions: Achievements and challenges. Q. Rev. Biophys. 2016, 49, e4. [Google Scholar] [CrossRef] [Green Version]
- Reimhult, E.; Hook, F. Design of surface modifications for nanoscale sensor applications. Sensors 2015, 15, 1635–1675. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.; Li, N.; Zhang, R.; Yin, P.; Zhang, C.; Yang, N.; Liang, K.; Kong, B. Carbon-based SERS biosensor: From substrate design to sensing and bioapplication. NPG Asia Mater. 2021, 13. [Google Scholar] [CrossRef]
- Wang, Z.; Dai, Z. Carbon nanomaterial-based electrochemical biosensors: An overview. Nanoscale 2015, 7, 6420–6431. [Google Scholar] [CrossRef]
- Maiti, D.; Tong, X.; Mou, X.; Yang, K. Carbon-Based Nanomaterials for Biomedical Applications: A Recent Study. Front. Pharmacol. 2018, 9, 1401. [Google Scholar] [CrossRef] [PubMed]
- Holzinger, M.; Le Goff, A.; Cosnier, S. Nanomaterials for biosensing applications: A review. Front. Chem. 2014, 2, 63. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aldewachi, H.; Chalati, T.; Woodroofe, M.N.; Bricklebank, N.; Sharrack, B.; Gardiner, P. Gold nanoparticle-based colorimetric biosensors. Nanoscale 2017, 10, 18–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hutter, E.; Maysinger, D. Gold-nanoparticle-based biosensors for detection of enzyme activity. Trends Pharmacol. Sci. 2013, 34, 497–507. [Google Scholar] [CrossRef] [Green Version]
- Lakard, B. Electrochemical Biosensors Based on Conducting Polymers: A Review. Appl. Sci. 2020, 10, 6614. [Google Scholar] [CrossRef]
- Aydemir, N.; Malmstrom, J.; Travas-Sejdic, J. Conducting polymer based electrochemical biosensors. Phys. Chem. Chem. Phys. 2016, 18, 8264–8277. [Google Scholar] [CrossRef]
- Zhao, Y.; Cao, L.; Li, L.; Cheng, W.; Xu, L.; Ping, X.; Pan, L.; Shi, Y. Conducting Polymers and Their Applications in Diabetes Management. Sensors 2016, 16, 1787. [Google Scholar] [CrossRef] [Green Version]
- Tomczykowa, M.; Plonska-Brzezinska, M.E. Conducting Polymers, Hydrogels and Their Composites: Preparation, Properties and Bioapplications. Polymers 2019, 11, 350. [Google Scholar] [CrossRef] [Green Version]
- Mok, W.; Li, Y. Recent Progress in Nucleic Acid Aptamer-Based Biosensors and Bioassays. Sensors 2008, 8, 7050–7084. [Google Scholar] [CrossRef]
- Wang, R.E.; Zhang, Y.; Cai, J.; Cai, W.; Gao, T. Aptamer-based fluorescent biosensors. Curr. Med. Chem. 2011, 18, 4175–4184. [Google Scholar] [CrossRef]
- Walter, J.-G.; Heilkenbrinker, A.; Austerjost, J.; Timur, S.; Stahl, F.; Scheper, T. Aptasensors for Small Molecule Detection. Curr. Opin. Biotechnol. 2012, 67, 976–986. [Google Scholar] [CrossRef] [Green Version]
- Varongchayakul, N.; Song, J.; Meller, A.; Grinstaff, M.W. Single-molecule protein sensing in a nanopore: A tutorial. Chem. Soc. Rev. 2018, 47, 8512–8524. [Google Scholar] [CrossRef] [PubMed]
- Spitzberg, J.D.; Zrehen, A.; van Kooten, X.F.; Meller, A. Single Plasmonic Nanostructures for Biomedical Diagnosis. Adv. Mater. 2019, 31, e1900422. [Google Scholar] [CrossRef] [PubMed]
- Thangamuthu, M.; Hsieh, K.Y.; Kumar, P.V.; Chen, G.Y. Graphene- and Graphene Oxide-Based Nanocomposite Platforms for Electrochemical Biosensing Applications. Int. J. Mol. Sci. 2019, 20, 2975. [Google Scholar] [CrossRef] [Green Version]
- Beitollahi, H.; Safaei, M.; Tajik, S. Application of Graphene and Graphene Oxide for modification of electrochemical sensors and biosensors: A review. Int. J. Nano Dimens. 2019, 10, 125–140. [Google Scholar]
- Pena-Bahamonde, J.; Nguyen, H.N.; Fanourakis, S.K.; Rodrigues, D.F. Fast, accurate, point-of-care COVID-19 pandemic diagnosis enabled through advanced lab-on-chip optical biosensors: Opportunities and challenges. J. Nanobiotechnol. 2018, 16, 75. [Google Scholar]
- Bai, Y.; Xu, T.; Zhang, X. Graphene-Based Biosensors for Detection of Biomarkers. Micromachines 2020, 11, 60. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, S.K.; Singh, E.; Singh, P.; Meyyappan, M.; Nalwa, H.S. A review on graphene-based nanocomposites for electrochemical and fluorescent biosensors. RSC Adv. 2019, 9, 8778–8881. [Google Scholar] [CrossRef]
- Szunerits, S.; Boukherroub, R. Graphene-based biosensors. Interface Focus 2018, 8, 20160132. [Google Scholar] [CrossRef]
- Tyagi, A.; Chu, K.L.; Abidi, I.H.; Cagang, A.A.; Zhang, Q.; Leung, N.L.C.; Zhao, E.; Tang, B.Z.; Luo, Z. Single-probe multistate detection of DNA via aggregation-induced emission on a graphene oxide platform. Acta Biomater. 2017, 50, 334–343. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L., 3rd; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Tao, L.; Lu, X.; Yang, Q.; Pachauri, V.; Wang, Z.; Ingebrandt, S.; Chen, X. Photothermal effects induced by surface plasmon resonance at graphene/gold nanointerfaces: A multiscale modeling study. Biosens. Bioelectron. 2019, 126, 470–477. [Google Scholar] [CrossRef] [PubMed]
- Foiles, S.M.; Baskes, M.I.; Daw, M.S. Embedded-atom-method functions for the fcc metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys. Phys. Rev. B Condens. Matter 1986, 33, 7983–7991. [Google Scholar] [CrossRef]
- Harper, A.; Anderson, M.R. Electrochemical Glucose Sensors—Developments Using Electrostatic Assembly and Carbon Nanotubes for Biosensor Construction. Sensors 2010, 10, 8248–8274. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghoshdastider, U.; Wu, R.; Trzaskowski, B.; Mlynarczyk, K.; Miszta, P.; Gurusaran, M.; Viswanathan, S.; Renugopalakrishnan, V.; Filipek, S. Molecular effects of encapsulation of glucose oxidase dimer by graphene. RSC Adv. 2015, 5, 13570. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Maxwell, D.S.; TiradoRives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Badhe, Y.; Gupta, R.; Rai, B. In silico design of peptides with binding to the receptor binding domain (RBD) of the SARS-CoV-2 and their utility in bio-sensor development for SARS-CoV-2 detection. RSC Adv. 2021, 11, 3816–3826. [Google Scholar] [CrossRef]
- Cholko, T.; Kaushik, S.; Chang, C.A. Dynamics and molecular interactions of single-stranded DNA in nucleic acid biosensors with varied surface properties. Phys. Chem. Chem. Phys. 2019, 21, 16367–16380. [Google Scholar] [CrossRef]
- Zhou, Y.; Chiu, C.W.; Liang, H. Interfacial Structures and Properties of Organic Materials for Biosensors: An Overview. Sensors 2012, 12, 15036–15062. [Google Scholar] [CrossRef] [Green Version]
- Singh, M.; Kaur, N.; Comini, E. The role of self-assembled monolayers in electronic devices. J. Mater. Chem. C 2020, 8, 3938–3955. [Google Scholar] [CrossRef]
- Gooding, J.J.; Darwish, N. The rise of self-assembled monolayers for fabricating electrochemical biosensors—An interfacial perspective. Chem. Rec. 2012, 12, 92–105. [Google Scholar] [CrossRef] [PubMed]
- Brothers, M.C.; Moore, D.; Lawrence, M.S.; Harris, J.; Joseph, R.M.; Ratcliff, E.; Ruiz, O.N.; Glavin, N.; Kim, S.S. Impact of Self-Assembled Monolayer Design and Electrochemical Factors on Impedance-Based Biosensing. Sensors 2020, 20, 2246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.S.; Yau, S.; Chau, L.K.; Mohamed, A.; Huang, C.J. Functional Biointerfaces Based on Mixed Zwitterionic Self-Assembled Monolayers for Biosensing Applications. Langmuir ACS J. Surf. Colloids 2019, 35, 1652–1661. [Google Scholar] [CrossRef] [PubMed]
- Stine, K.J. Biosensor Applications of Electrodeposited Nanostructures. Appl. Sci. 2019, 9, 797. [Google Scholar] [CrossRef] [Green Version]
- Bhattarai, J.K.; Neupane, D.; Nepal, B.; Mikhaylov, V.; Demchenko, A.V.; Stine, K.J. Nanoporous Gold and Other Related Materials. Nanomaterials 2018, 8, 1080. [Google Scholar]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Puente-Santiago, A.R.; Rodríguez-Padrón, D.; Quan, X.; Batista, M.J.M.O.; Martins, L.O.; Verma, S.; Varma, R.S.; Zhou, J.; Luque, R. Unprecedent wiring efficiency of sulfonated carbon nitride materials: Towards high-performance amperometric recombinant CotA-laccase biosensors. ACS Sustain Chem. Eng. 2019, 7, 1474–1484. [Google Scholar] [CrossRef]
- Earl, D.J.; Deem, M.W. Parallel tempering: Theory, applications, and new perspectives. Phys. Chem. Chem. Phys. 2005, 7, 3910–3916. [Google Scholar] [CrossRef] [Green Version]
- Rozada, I.; Aramon, M.; Machta, J.; Katzgraber, H.G. Effects of setting temperatures in the parallel tempering Monte Carlo algorithm. Phys. Rev. E 2019, 100, 043311. [Google Scholar] [CrossRef] [Green Version]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. Effects of setting temperatures in the parallel tempering Monte Carlo algorithm. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ogorzalek, T.L.; Wei, S.; Liu, Y.; Wang, Q.; Brooks, C.L., 3rd; Chen, Z.; Marsh, E.N. Molecular-Level Insights into Orientation-Dependent Changes in the Thermal Stability of Enzymes Covalently Immobilized on Surfaces. Langmuir ACS J. Surf. Colloids 2015, 31, 6145–6153. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, G.; Eimura, H.; Abbott, N.L.; Kato, T. Biomolecular Binding at Aqueous Interfaces of Langmuir Monolayers of Bioconjugated Amphiphilic Mesogenic Molecules: A Molecular Dynamics Study. Langmuir ACS J. Surf. Colloids 2020, 36, 12281–12287. [Google Scholar] [CrossRef] [PubMed]
- Mazouz, Z.; Mokni, M.; Fourati, N.; Zerrouki, C.; Barbault, F.; Seydou, M.; Kalfat, R.; Yaakoubi, N.; Omezzine, A.; Bouslema, A.; et al. Computational approach and electrochemical measurements for protein detection with MIP-based sensor. Biosens. Bioelectron. 2020, 151, 111978. [Google Scholar] [CrossRef]
- Karanicolas, J.; Brooks, C.L., 3rd. The structural basis for biphasic kinetics in the folding of the WW domain from a formin-binding protein: Lessons for protein design? Proc. Natl. Acad. Sci. USA 2003, 100, 3954–3959. [Google Scholar] [CrossRef] [Green Version]
- Karanicolas, J.; Brooks, C.L., 3rd. Integrating folding kinetics and protein function: Biphasic kinetics and dual binding specificity in a WW domain. Proc. Natl. Acad. Sci. USA 2004, 101, 3432–3437. [Google Scholar] [CrossRef] [Green Version]
- Wei, S.; Knotts, T.A.T. A coarse grain model for protein-surface interactions. J. Chem. Phys. 2013, 139, 095102. [Google Scholar] [CrossRef]
- Qi, R.; Wei, G.; Ma, B.; Nussinov, R. Replica Exchange Molecular Dynamics: A Practical Application Protocol with Solutions to Common Problems and a Peptide Aggregation and Self-Assembly Example. Methods Mol. Biol. 2018, 1777, 101–119. [Google Scholar]
- Nagpal, P.; Jamal, S.; Singh, H.; Ali, W.; Tanweer, S.; Sharma, R.; Grover, A.; Grover, S. Long-range replica exchange molecular dynamics guided drug repurposing against tyrosine kinase PtkA of Mycobacterium tuberculosis. Sci. Rep. 2020, 10, 4413. [Google Scholar] [CrossRef]
- Liang, F.; Guo, Y.; Hou, S.; Quan, Q. Photonic-plasmonic hybrid single-molecule nanosensor measures the effect of fluorescent labels on DNA-protein dynamics. Sci. Adv. 2017, 3, e1602991. [Google Scholar] [CrossRef] [Green Version]
- Le Trong, I.; Wang, Z.; Hyre, D.E.; Lybrand, T.P.; Stayton, P.S.; Stenkamp, R.E. Streptavidin and its biotin complex at atomic resolution. Acta Crystallogr. D Biol. Crystallogr. 2011, 67, 813–821. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vanquelef, E.; Simon, S.; Marquant, G.; Garcia, E.; Klimerak, G.; Delepine, J.C.; Cieplak, P.; Dupradeau, F.Y. RED Server: A web service for deriving RESP and ESP charges and building force field libraries for new molecules and molecular fragments. Nucleic Acids Res. 2011, 39, W511–W517. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian Inc. Wallingford CT. 2009. Available online: https://gaussian.com/g09citation/ (accessed on 10 December 2021).
- Dutta, S.; Bellucci, L.; Agostini, M.; Gagliardi, M.; Corni, S.; Cecchini, M.; Brancolini, G. Atomistic simulations of gold surface functionalization for nanoscale biosensors applications. Nanotechnology 2021, 32, 095702. [Google Scholar] [CrossRef] [PubMed]
- Iori, F.; di Felice, R.; Molinari, E.; Corni, S. GolP: An atomistic force-field to describe the interaction of proteins with Au(111) surfaces in water. J. Comput. Chem. 2009, 30, 1465–1476. [Google Scholar] [CrossRef] [PubMed]
- Holguín, M.; Álvarez, O.E.R.; Arizabaleta, C.A.; Torresb, W. Molecular dynamics of the interaction of l-tryptophan with polypyrrole oligomers. Comput. Theor. Chem. 2019, 1147, 29–34. [Google Scholar] [CrossRef]
- Kleinjung, J.; Fraternali, F. Design and application of implicit solvent models in biomolecular simulations. Curr. Opin. Struct. Biol. 2014, 25, 126–134. [Google Scholar] [CrossRef] [Green Version]
- Mackerell, A.D., Jr.; Feig, M.; Brooks, C.L., 3rd. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [Green Version]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E.; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Ghoreishi, D.; Gilson, M.K.; et al. AMBER 2018 University of California, San Francisco. 2018. Available online: https://ambermd.org/CiteAmber.php (accessed on 10 December 2021).
- Martinez, L.; Andrade, R.; Birgin, E.G.; Martinez, J.M. Packmol: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef]
- Putri, A.D.; Murti, B.T.; Kanchi, S.; Sabela, M.I.; Bisetty, K.; Tiwari, A.; Inamuddin; Asiri, A.M. Computational studies on the molecular insights of aptamer induced poly(N-isopropylacrylamide)-graft-graphene oxide for on/off-switchable whole-cell cancer diagnostics. Sci. Rep. 2019, 9, 7873. [Google Scholar] [CrossRef] [Green Version]
- Vovusha, H.; Sanyal, S.; Sanyal, B. Interaction of Nucleobases and Aromatic Amino Acids with Graphene Oxide and Graphene Flakes. J. Phys. Chem. Lett. 2013, 4, 3710–3718. [Google Scholar] [CrossRef]
- Rosas, J.J.H.; Gutierrez, R.E.R.; Escobedo-Morales, A.; Anota, E.C. First principles calculations of the electronic and chemical properties of graphene, graphane, and graphene oxide. J. Mol. Model. 2011, 17, 1133–1139. [Google Scholar] [CrossRef] [PubMed]
- Matsuzawa, N.; Ata, M.; Dixon, D.A. Density functional theory prediction of the second-order hyperpolarizability of metalloporphines. J. Phys. Chem. 1995, 99, 7698–7706. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.L.; Ma, Y.; Ma, Y.; Li, Y.; Chen, X.B.; Dong, W.L.; Wang, R.L. The design of novel inhibitors for treating cancer by targeting CDC25B through disruption of CDC25B-CDK2/Cyclin A interaction using computational approaches. Oncotarget 2017, 8, 33225–33240. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Boroznjak, R.; Reut, J.; Tretjakov, A.; Lomaka, A.; Opik, A.; Syritski, V. A computational approach to study functional monomer-protein molecular interactions to optimize protein molecular imprinting. J. Mol. Recognit. 2017, 30. [Google Scholar] [CrossRef]
- Cho, A.E.; Guallar, V.; Berne, B.J.; Friesner, R. Importance of accurate charges in molecular docking: Quantum mechanical/molecular mechanical (QM/MM) approach. J. Comput. Chem. 2005, 26, 915–931. [Google Scholar] [CrossRef] [Green Version]
- Friesner, R.A.; Banks, J.L.; Murphy, R.B.; Halgren, T.A.; Klicic, J.J.; Mainz, D.T.; Repasky, M.P.; Knoll, E.H.; Shelley, M.; Perry, J.K.; et al. Glide: A New Approach for Rapid, Accurate Docking and Scoring. 1. Method and Assessment of Docking Accuracy. J. Med. Chem. 2004, 47, 1739–1749. [Google Scholar] [CrossRef]
- Zanuy, D.; Fabregat, G.; Ferreira, C.A.; Aleman, C. A molecular dynamics study on glucose molecular recognition by a non-enzymatic selective sensor based on a conducting polymer. Phys. Chem. Chem. Phys. 2019, 21, 8099–8107. [Google Scholar] [CrossRef]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Gould, I.R.; Merz, K.M.; Ferguson, D.M.; Spellmeyer, D.C.; Fox, T.; Caldwell, J.W.; Kollman, P.A. A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules. J. Am. Chem. Soc. 1995, 117, 5179–5197. [Google Scholar] [CrossRef] [Green Version]
- Buglak, A.A.; Samokhvalov, A.V.; Zherdev, A.V.; Dzantiev, B.B. Methods and Applications of In Silico Aptamer Design and Modeling. Int. J. Mol. Sci. 2020, 21, 8420. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chung, L.W.; Li, G. Multiscale Simulations on Spectral Tuning and the Photoisomerization Mechanism in Fluorescent RNA Spinach. J. Chem. Theory Comput. 2016, 12, 5453–5464. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Kumar, A. Nucleobase sequence based building up of reliable QSAR models with the index of ideality correlation using Monte Carlo method. J. Biomol. Struct. Dyn. 2020, 38, 3296–3306. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Zheng, Y.; Huang, M.; Wu, L.; Wang, W.; Zhu, Z.; Song, Y.; Yang, C. A Sequential Multidimensional Analysis Algorithm for Aptamer Identification based on Structure Analysis and Machine Learning. Anal. Chem. 2020, 92, 3307–3314. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Huang, Y.; Dong, Y.; Han, X.; Wang, S.; Liang, X. AbobotulinumtoxinA (Dysport®), OnabotulinumtoxinA (Botox®), and IncobotulinumtoxinA (Xeomin®) Neurotoxin Content and Potential Implications for Duration of Response in Patients. Toxins 2018, 10, 535. [Google Scholar]
- Ruan, M.; Seydou, M.; Noel, V.; Piro, B.; Maurel, F.; Barbault, F. Molecular Dynamics Simulation of a RNA Aptasensor. J. Phys. Chem. B 2017, 121, 4071–4080. [Google Scholar] [CrossRef]
- Case, D.A.; Darden, T.A.; Cheatham, T.E.; Simmerling, C.L.; Wang, J.; Duke, R.E.; Luo, R.; Walker, R.; Zhang, W.; Merz, K.M.e.a. AMBER 12.0 Univ. Calif. San Fr. 2012. Available online: https://ambermd.org/doc12/Amber12.pdf (accessed on 10 December 2021).
- Bonome, E.L.; Cecconi, F.; Chinappi, M. Translocation intermediates of ubiquitin through an α-hemolysin nanopore: Implications for detection of post-translational modifications. Nanoscale 2019, 11, 9920–9930. [Google Scholar] [CrossRef]
- Rhinehardt, K.L.; Srinivas, G.; Mohan, R.V. Molecular Dynamics Simulation Analysis of Anti-MUC1 Aptamer and Mucin 1 Peptide Binding. J. Phys. Chem. B 2015, 119, 6571–6583. [Google Scholar] [CrossRef]
- Phanchai, W.; Srikulwong, U.; Chompoosor, A.; Sakonsinsiri, C.; Puangmali, T. Insight into the Molecular Mechanisms of AuNP-Based Aptasensor for Colorimetric Detection: A Molecular Dynamics Approach. Langmuir ACS J. Surf. Colloids 2018, 34, 6161–6169. [Google Scholar] [CrossRef]
- Hills, R.D., Jr.; Brooks, C.L., 3rd. Insights from Coarse-Grained Gō Models for Protein Folding and Dynamics. Int. J. Mol. Sci. 2009, 10, 889–905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramachandran, A.; Guo, Q.; Iqbal, S.M.; Liu, Y. Coarse-Grained Molecular Dynamics Simulation of DNA Translocation in Chemically Modified Nanopores. J. Phys. Chem. B 2011, 115, 6138–6148. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutta, S.; Corni, S.; Brancolini, G. Atomistic Simulations of Functionalized Nano-Materials for Biosensors Applications. Int. J. Mol. Sci. 2022, 23, 1484. https://doi.org/10.3390/ijms23031484
Dutta S, Corni S, Brancolini G. Atomistic Simulations of Functionalized Nano-Materials for Biosensors Applications. International Journal of Molecular Sciences. 2022; 23(3):1484. https://doi.org/10.3390/ijms23031484
Chicago/Turabian StyleDutta, Sutapa, Stefano Corni, and Giorgia Brancolini. 2022. "Atomistic Simulations of Functionalized Nano-Materials for Biosensors Applications" International Journal of Molecular Sciences 23, no. 3: 1484. https://doi.org/10.3390/ijms23031484
APA StyleDutta, S., Corni, S., & Brancolini, G. (2022). Atomistic Simulations of Functionalized Nano-Materials for Biosensors Applications. International Journal of Molecular Sciences, 23(3), 1484. https://doi.org/10.3390/ijms23031484






