An Agent-Based Model of Radiation-Induced Lung Fibrosis
Abstract
1. Introduction
2. Results
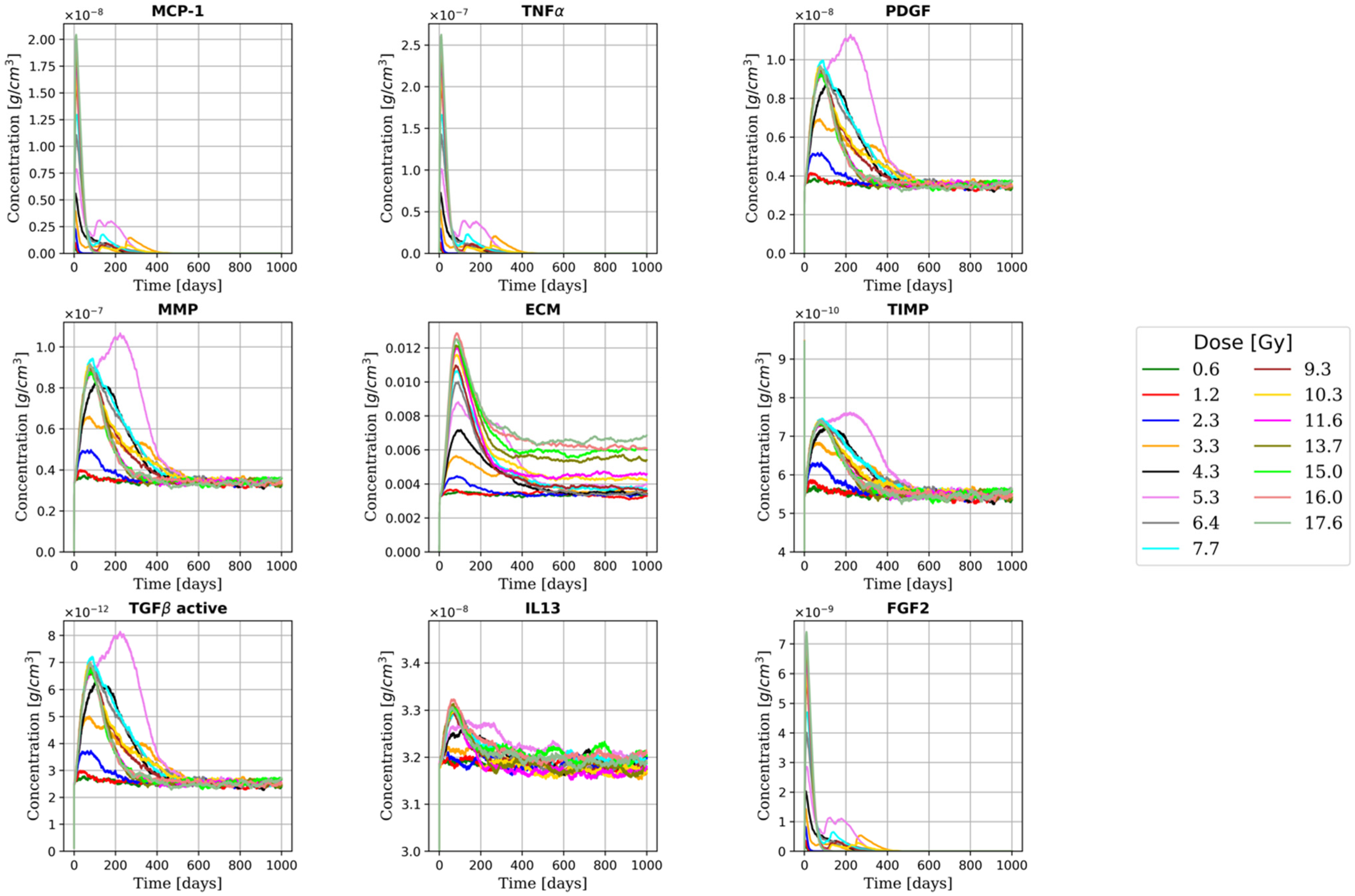
2.1. Early and Late Fibrotic Response
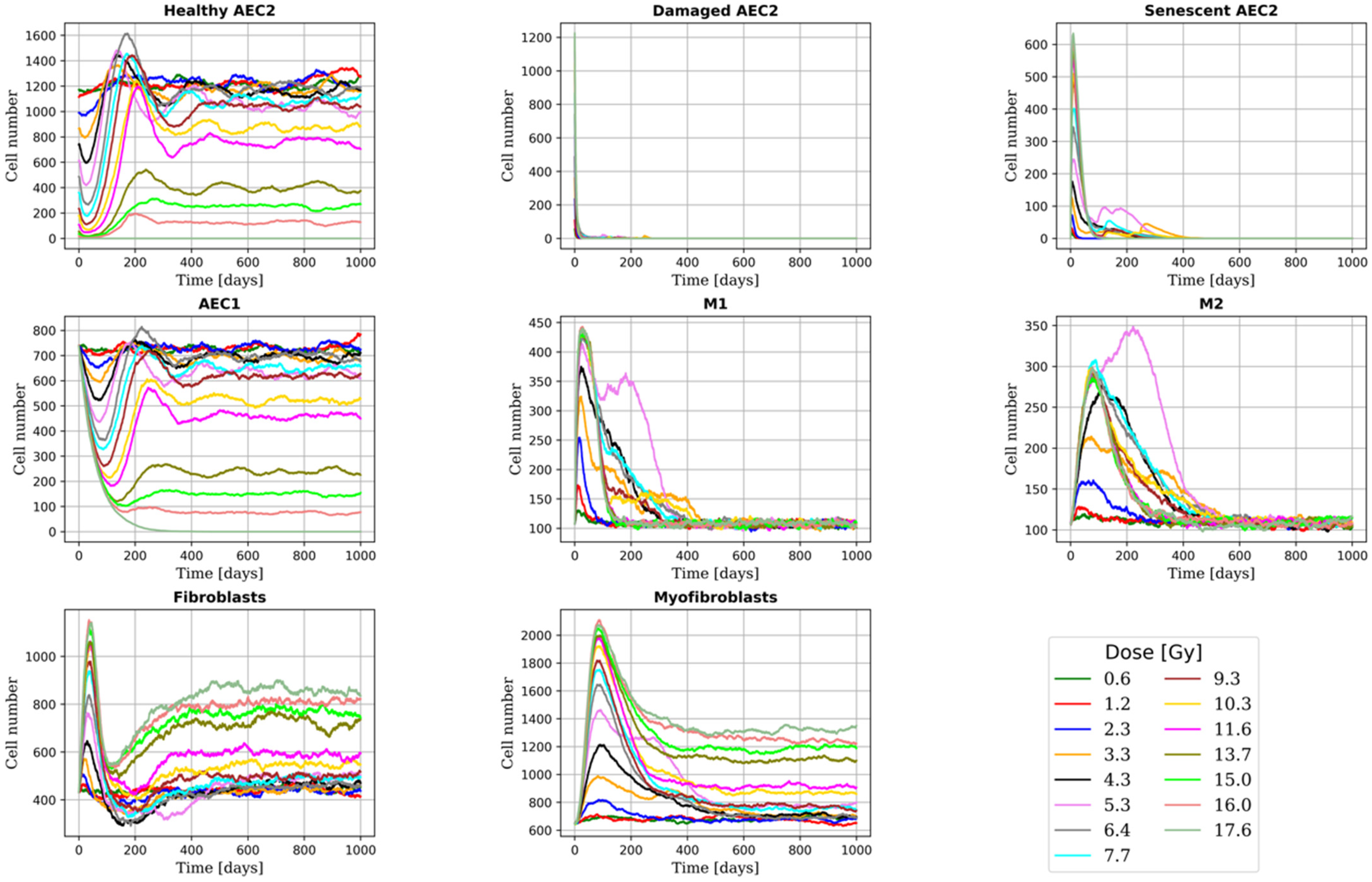
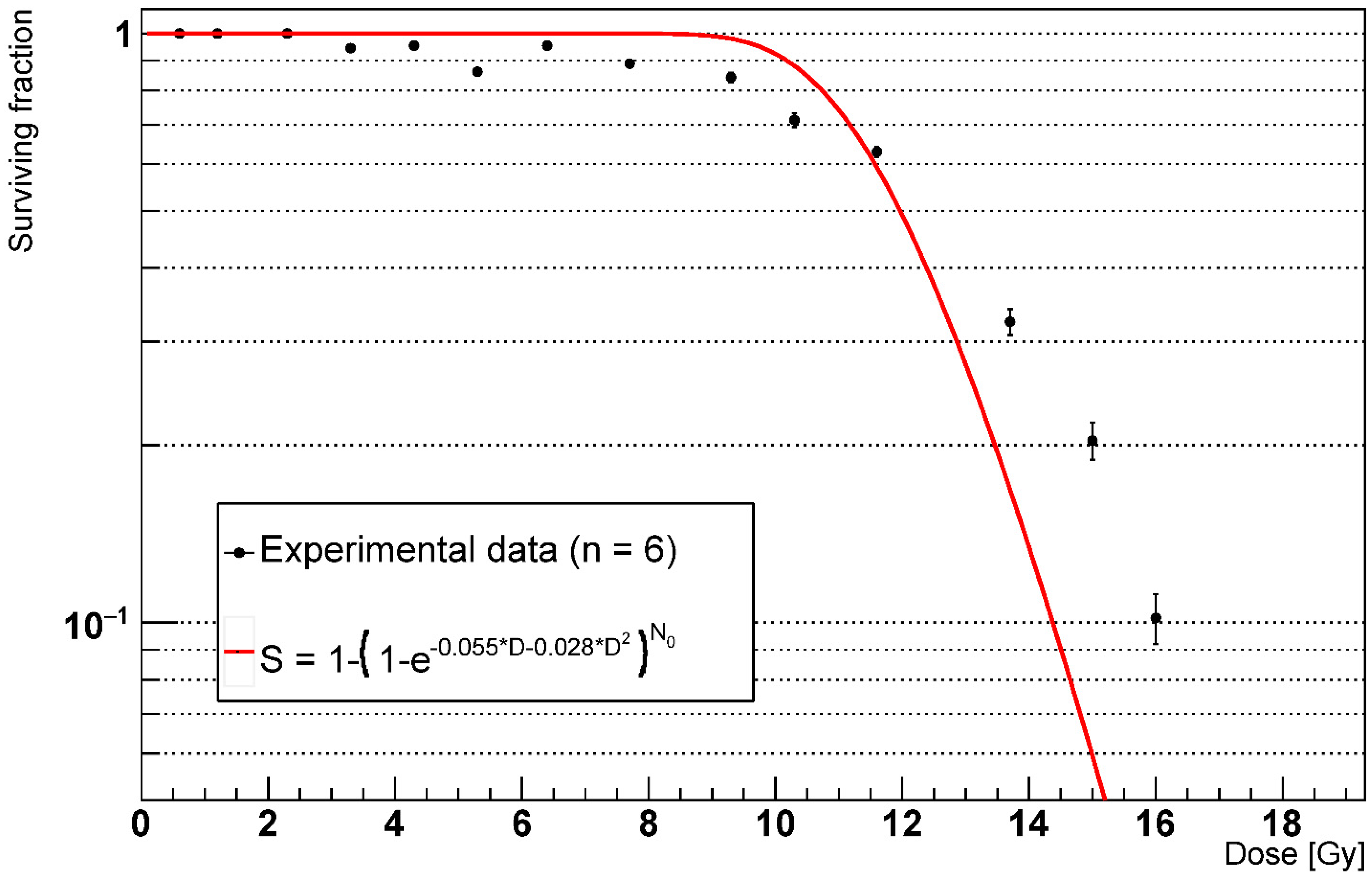
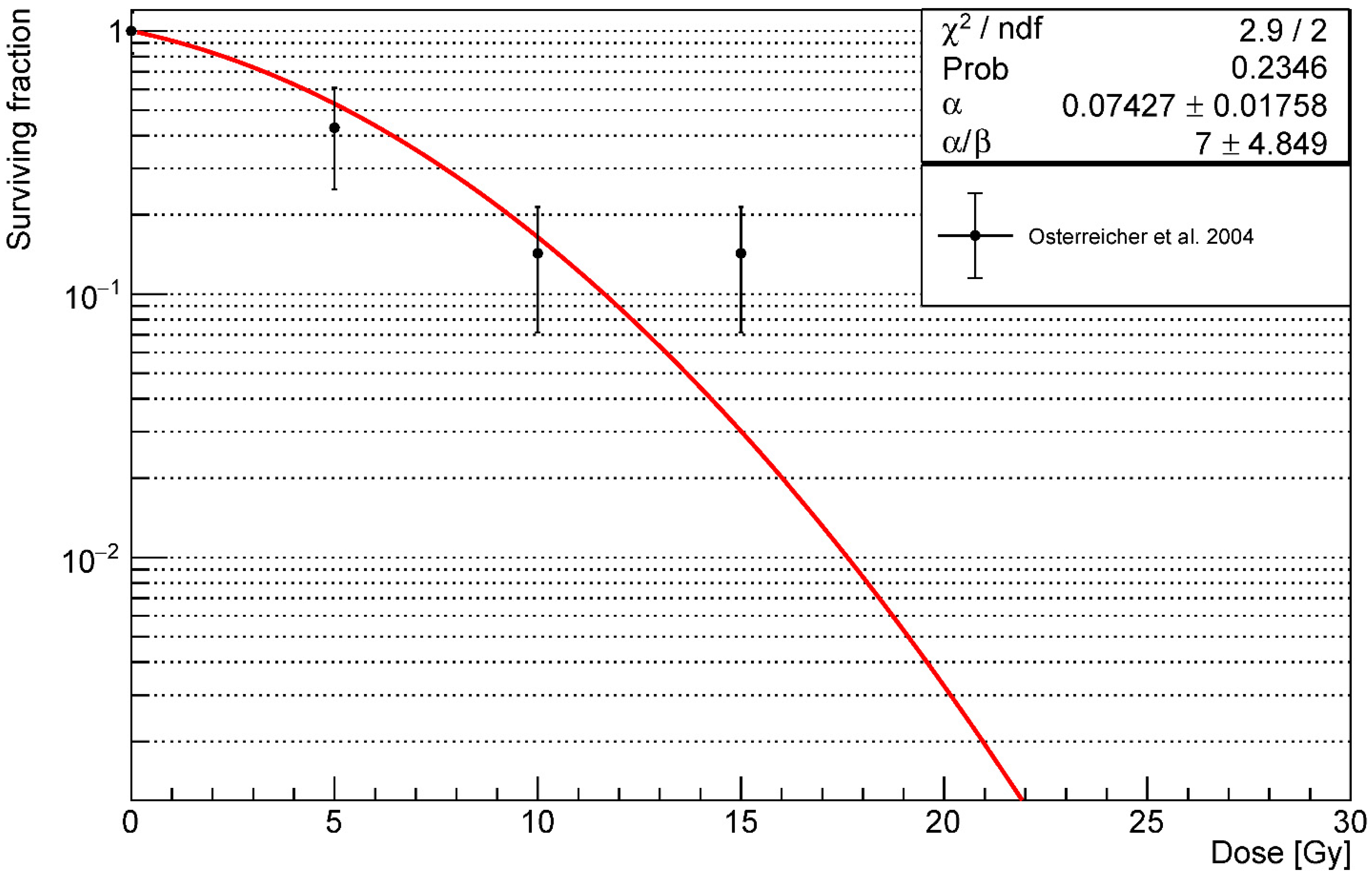
2.2. Alveoli Survival
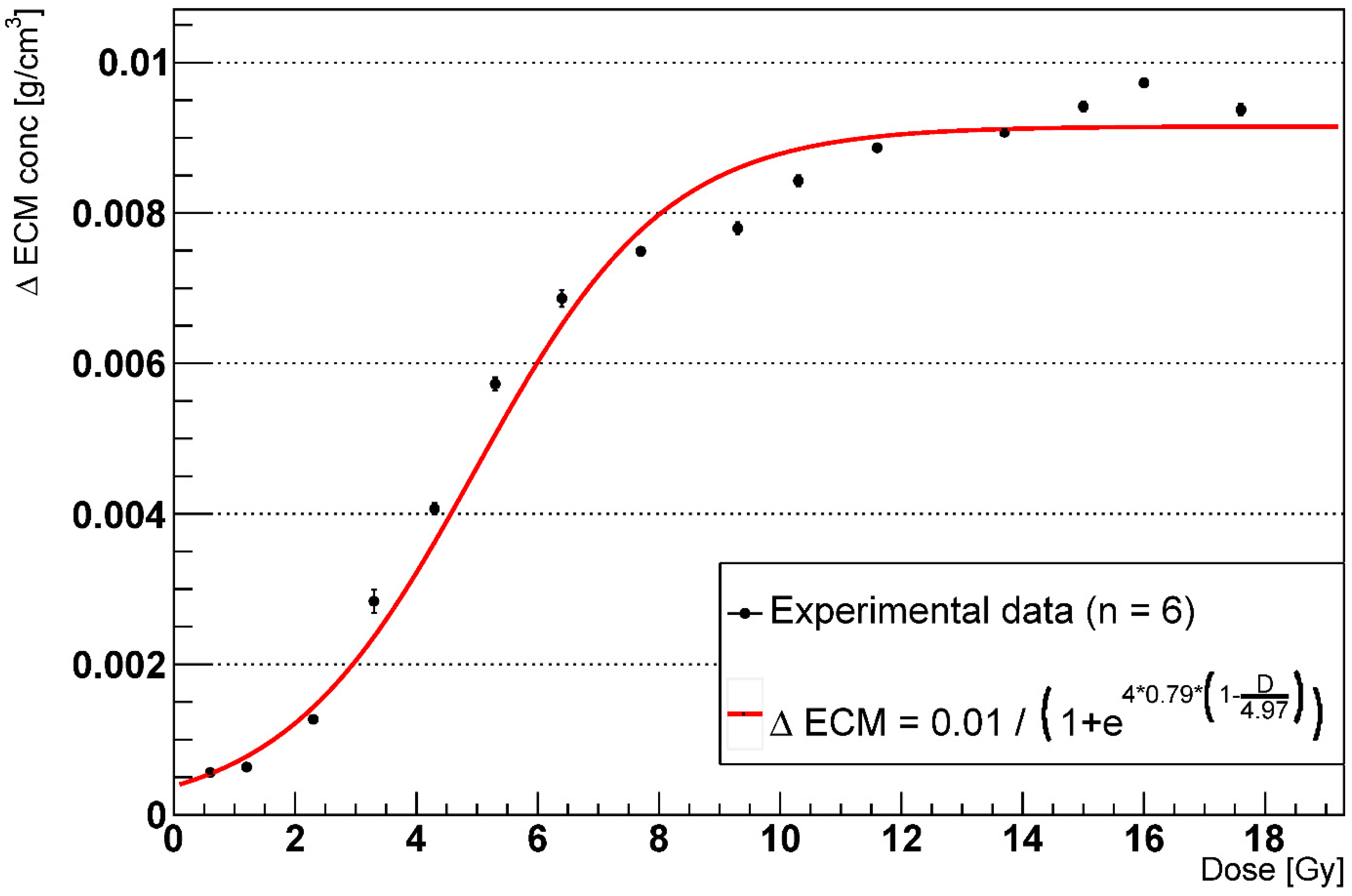
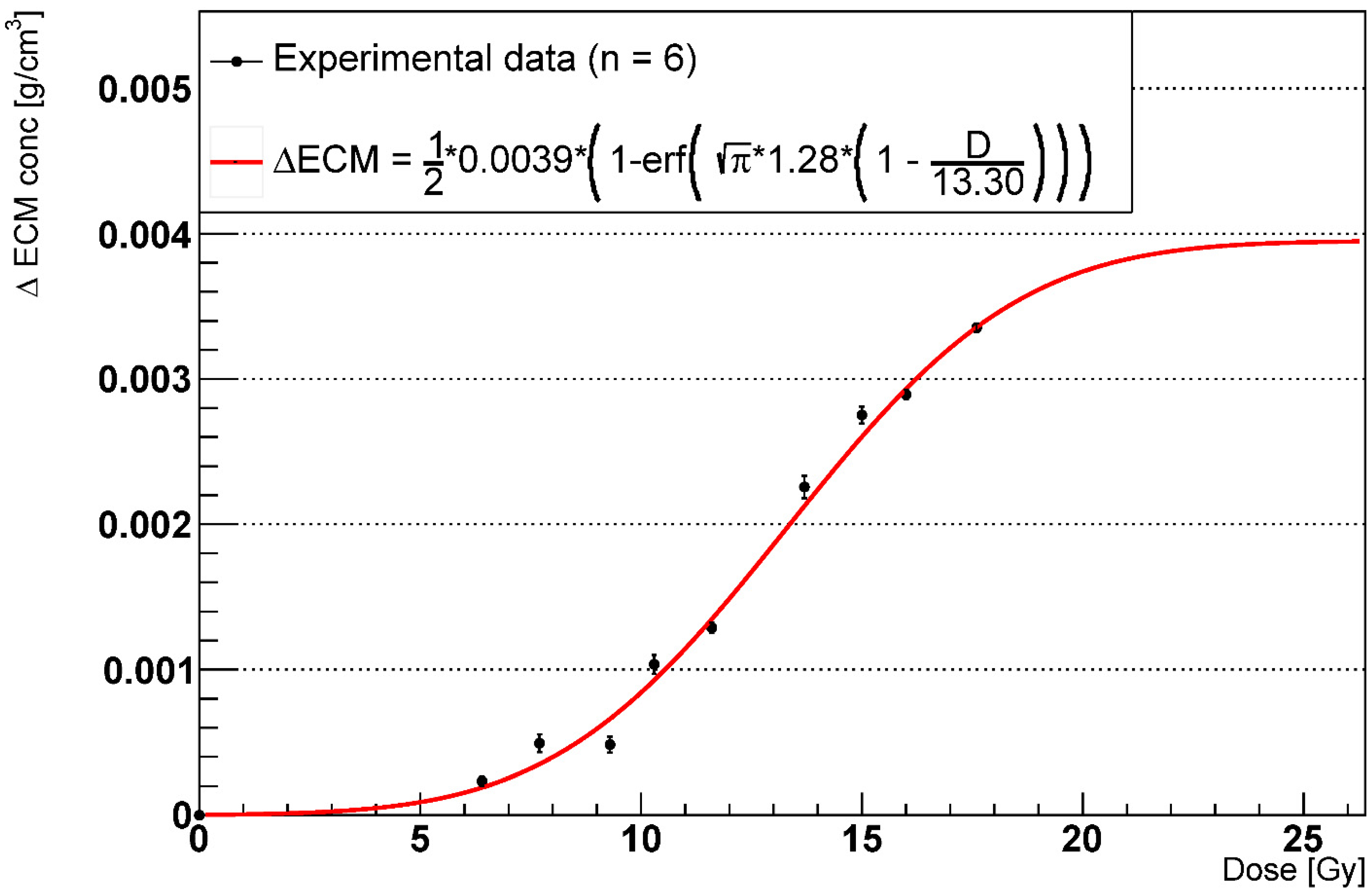
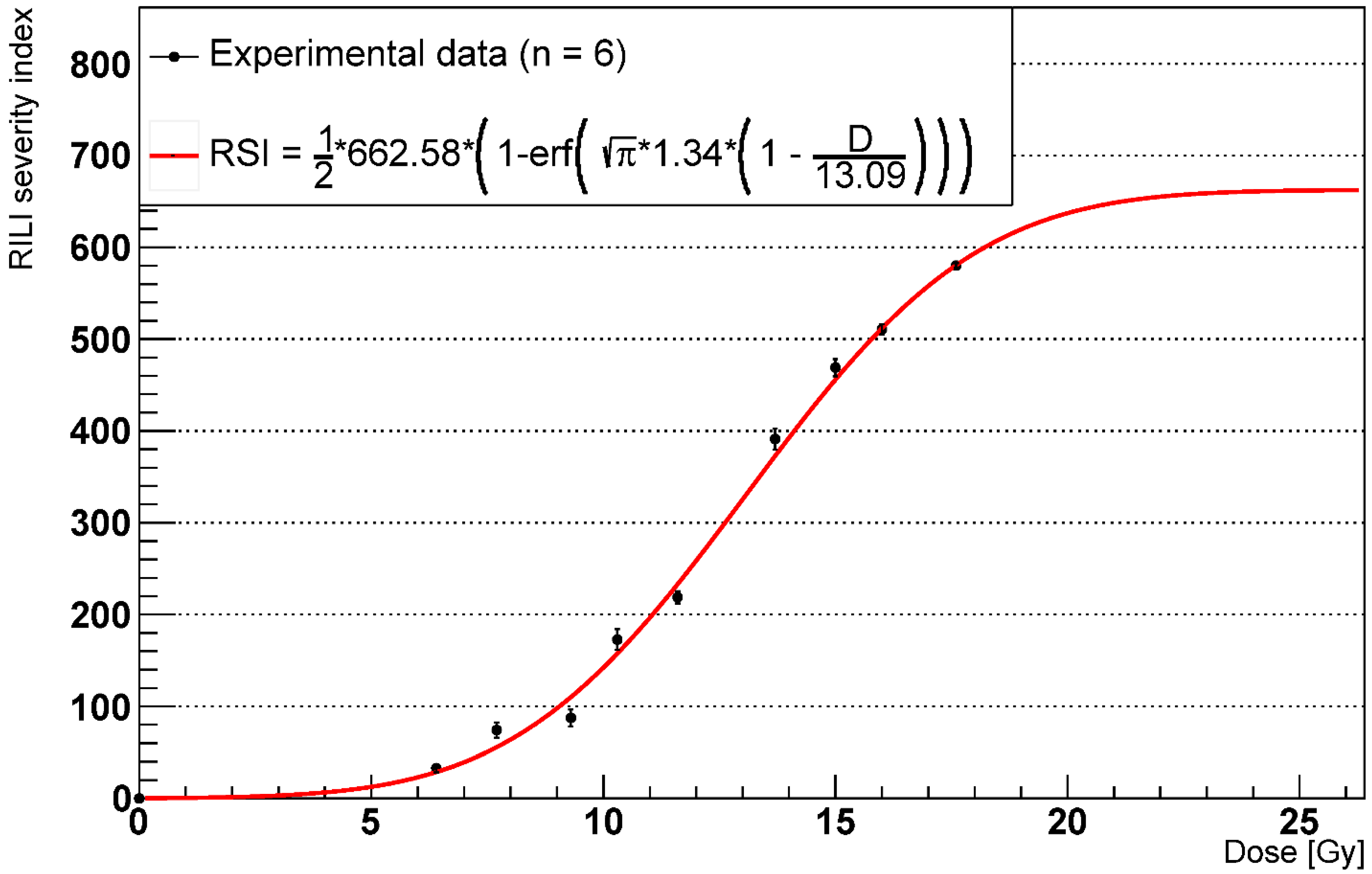
2.3. RILF Severity Index
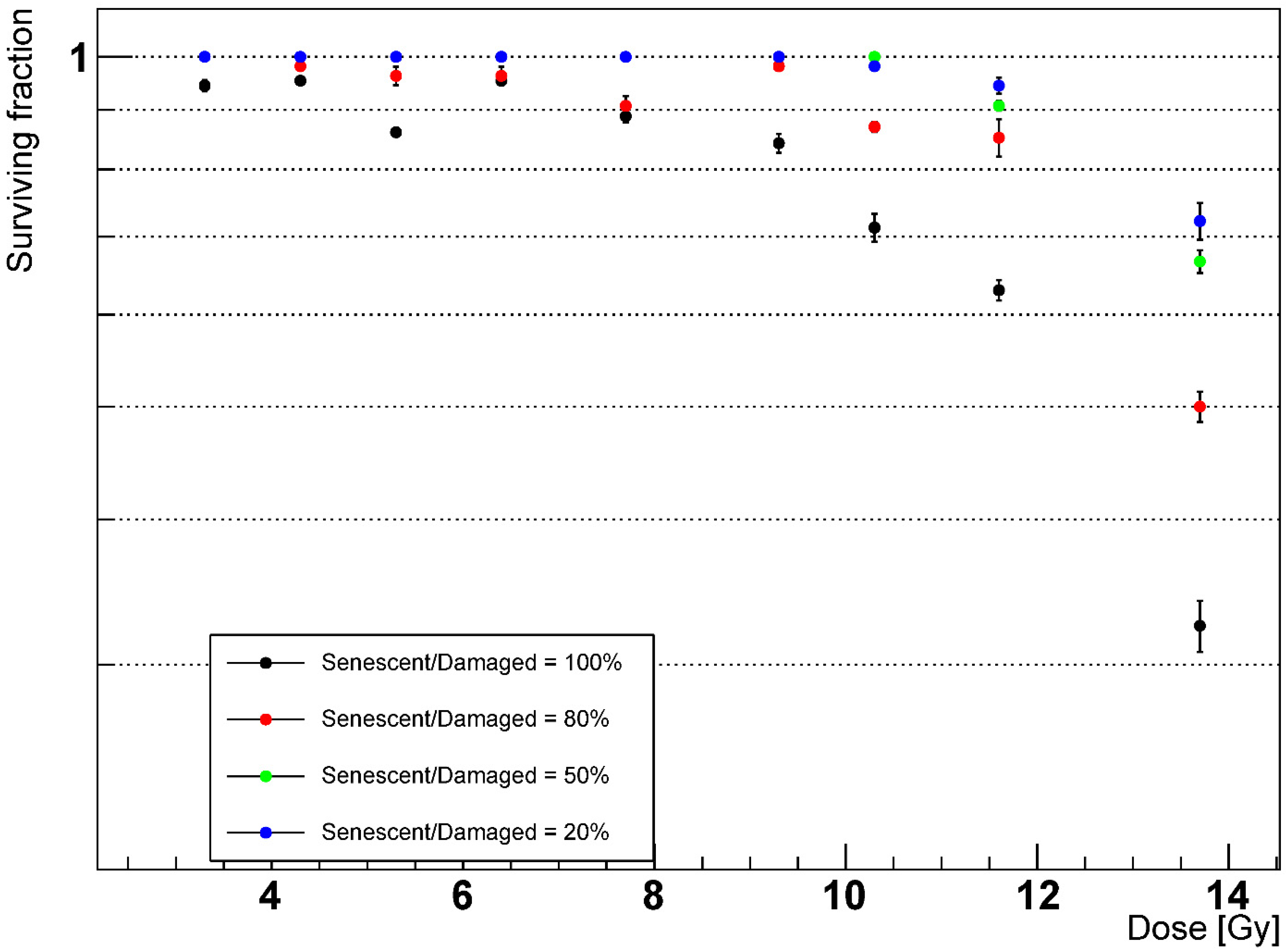
2.4. Effects of AEC2 Apoptotic to Senescent Ratio
3. Discussion
4. Materials and Methods
4.1. Software Platform and Modelling Environment
4.2. Geometric Frame and Operations
- determine the number of surviving alveoli;
- simulate the secretion of IL13 from lymphocytes (which, for simplicity, are not included in the model) at the centre of each alveolus [61];
- simulate the inflow of fibroblasts in the interstitial space with a rate that depends on the number of AEC2 per alveolus. According to the literature [62,63], prostaglandin E2 secreted by AEC2 inhibits fibroblasts’ chemotaxis and proliferation. We modelled this phenomenon using a reverse Hill function with coefficient 1 (to avoid abrupt changes in the fibroblasts’ flow) multiplied by a constant rate. We assumed the Hill constant to be equal to the initial number of AEC2 per alveolus to reduce the number of unknown parameters and tuned the constant influx rate to keep the number of fibroblasts in homeostatic conditions constant;
4.3. Cell Behaviours
4.3.1. Secretion
- M2: PDGF (constant rate), MMP (constant rate), TIMP (constant rate), IL13 (constant rate), TGFβactive (rate is positively affected by IL13 concentration);
- M1: TNFα (constant rate);
- F: TGFβinactive (constant rate), ECM (rate is affected with inverse proportionality by ECM concentration; no secretion if the concentration exceeds a saturation threshold);
- MF: ECM (rate is positively affected by TGFβactive concentration);
- Senescent AEC2: TNFα (constant rate), MCP1 (constant rate), FGF2 (rate is positively affected by TGFβactive concentration).
4.3.2. Damage Spreading and Clearance
4.3.3. Migration
- The epithelial cell detects all its neighbours within an alveolar radius distance in the alveolus it belongs to (AEC1 detect other only AEC1, while AEC2 detect both AEC1 and AEC2);
- For each of the detected neighbours, the distance from the acting cell is measured;
- Using the distances from the step above, the cell determines the centre of mass of its neighbours, where each distance is weighted with the inverse of its squared normalized value;
- The cell migrates in the opposite direction from the location of the centre of mass, given a constant migration speed and the length of the simulation step.
4.3.4. Proliferation
4.3.5. Differentiation
4.3.6. Apoptosis
4.4. Initial Conditions
4.4.1. Homeostasis
4.4.2. Radiation-Induced Damage
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richeldi, L.; Collard, H.R.; Jones, M.G. Idiopathic pulmonary fibrosis. Lancet 2017, 389, 1941–1952. [Google Scholar] [CrossRef]
- Giuranno, L.; Ient, J.; De Ruysscher, D.; Vooijs, M.A. Radiation-Induced Lung Injury (RILI). Front. Oncol. 2019, 9, 877. [Google Scholar] [CrossRef] [PubMed]
- Arroyo-Hernández, M.; Maldonado, F.; Lozano-Ruiz, F.; Muñoz-Montaño, W.; Nuñez-Baez, M.; Arrieta, O. Radiation-induced lung injury: Current evidence. BMC Pulm. Med. 2021, 21, 9. [Google Scholar] [CrossRef] [PubMed]
- Martinez, F.J.; Collard, H.R.; Pardo, A.; Raghu, G.; Richeldi, L.; Selman, M.; Swigris, J.J.; Taniguchi, H.; Wells, A.U. Idiopathic pulmonary fibrosis. Nat. Rev. Dis. Prim. 2017, 3, 17074. [Google Scholar] [CrossRef] [PubMed]
- Citrin, D.E.; Shankavaram, U.; Horton, J.A.; Shield, W.; Zhao, S.; Asano, H.; White, A.; Sowers, A.; Thetford, A.; Chung, E.J. Role of type II pneumocyte senescence in radiation-induced lung fibrosis. J. Natl. Cancer Inst. 2013, 105, 1474–1484. [Google Scholar] [CrossRef]
- Sisson, T.H.; Mendez, M.; Choi, K.; Subbotina, N.; Courey, A.; Cunningham, A.; Dave, A.; Engelhardt, J.F.; Liu, X.; White, E.S.; et al. Targeted injury of type II alveolar epithelial cells induces pulmonary fibrosis. Am. J. Respir. Crit. Care Med. 2010, 181, 254–263. [Google Scholar] [CrossRef]
- Jin, H.; Yoo, Y.; Kim, Y.; Kim, Y.; Cho, J.; Lee, Y.S. Radiation-induced lung fibrosis: Preclinical animal models and therapeutic strategies. Cancers 2020, 12, 1561. [Google Scholar] [CrossRef] [PubMed]
- Citrin, D.E.; Prasanna, P.G.S.; Walker, A.J.; Freeman, M.L.; Eke, I.; Barcellos-Hoff, M.H.; Arankalayil, M.J.; Cohen, E.P.; Wilkins, R.C.; Ahmed, M.M.; et al. Radiation-Induced Fibrosis: Mechanisms and Opportunities to Mitigate. Report of an NCI Workshop, September 19, 2016. Radiat. Res. 2017, 188, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Türkkan, G.; Willems, Y.; Hendriks, L.E.L.; Mostard, R.; Conemans, L.; Gietema, H.A.; Mitea, C.; Peeters, S.; De Ruysscher, D. Idiopathic pulmonary fibrosis: Current knowledge, future perspectives and its importance in radiation oncology. Radiother. Oncol. 2021, 155, 269–277. [Google Scholar] [CrossRef]
- Hong, X.; Wang, L.; Zhang, K.; Liu, J.-P.; Liu, J.-P. Molecular Mechanisms of Alveolar Epithelial Stem Cell Senescence and Senescence-Associated Differentiation Disorders in Pulmonary Fibrosis. Cells 2022, 11, 877. [Google Scholar] [CrossRef]
- Yao, C.; Guan, X.; Carraro, G.; Parimon, T.; Liu, X.; Huang, G.; Mulay, A.; Soukiasian, H.J.; David, G.; Weigt, S.S.; et al. Senescence of Alveolar Type 2 Cells Drives Progressive Pulmonary Fibrosis. Am. J. Respir. Crit. Care Med. 2021, 203, 707–717. [Google Scholar] [CrossRef] [PubMed]
- Parimon, T.; Yao, C.; Stripp, B.R.; Noble, P.W.; Chen, P. Alveolar epithelial type II cells as drivers of lung fibrosis in idiopathic pulmonary fibrosis. Int. J. Mol. Sci. 2020, 21, 2269. [Google Scholar] [CrossRef] [PubMed]
- Weibel, E.R. Lung morphometry: The link between structure and function. Cell Tissue Res. 2017, 367, 413–426. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.; Salerno, K.E.; Citrin, D.E. Biology of Radiation-Induced Lung Injury. Semin. Radiat. Oncol. 2021, 31, 155–161. [Google Scholar] [CrossRef]
- Broekelmann, T.J.; Limper, A.H.; Colby, T.V.; McDonald, J.A. Transforming growth factor β1 is present at sites of extracellular matrix gene expression in human pulmonary fibrosis. Proc. Natl. Acad. Sci. USA 1991, 88, 6642–6646. [Google Scholar] [CrossRef]
- Khalil, N.; Whitman, C.; Zuo, L.; Danielpour, D.; Greenberg, A. Regulation of alveolar macrophage transforming growth factor-β secretion by corticosteroids in bleomycin-induced pulmonary inflammation in the rat. J. Clin. Investig. 1993, 92, 1812–1818. [Google Scholar] [CrossRef]
- Nagaoka, I.; Trapnell, B.C.; Crystal, R.G. Upregulation of platelet-derived growth factor-A and -B gene expression in alveolar macrophages of individuals with idiopathic pulmonary fibrosis. J. Clin. Investig. 1990, 85, 2023–2027. [Google Scholar] [CrossRef]
- Hancock, A.; Armstrong, L.; Gama, R.; Millar, A. Production of interleukin 13 by alveolar macrophages from normal and fibrotic lung. Am. J. Respir. Cell Mol. Biol. 1998, 18, 60–65. [Google Scholar] [CrossRef]
- Zhang, K.; Rekhter, M.D.; Gordon, D.; Phan, S.H. Myofibroblasts and their role in lung collagen gene expression during pulmonary fibrosis: A combined immunohistochemical and in situ hybridization study. Am. J. Pathol. 1994, 145, 114–125. [Google Scholar]
- Raghu, G.; Masta, S.; Meyers, D.; Narayanan, A.S. Collagen synthesis by normal and fibrotic human lung fibroblasts and the effect of transforming growth factor-beta. Am. Rev. Respir. Dis. 1989, 140, 95–100. [Google Scholar] [CrossRef]
- Cogno, N.; Bauer, R.; Durante, M. A 3D Agent-Based Model of Lung Fibrosis. Symmetry 2022, 14, 90. [Google Scholar] [CrossRef]
- Phernambucq, E.C.J.; Spoelstra, F.O.B.; Verbakel, W.F.A.R.; Postmus, P.E.; Melissant, C.F.; Maassen van den Brink, K.I.; Frings, V.; van de Ven, P.M.; Smit, E.F.; Senan, S. Outcomes of concurrent chemoradiotherapy in patients with stage III non-small-cell lung cancer and significant comorbidity. Ann. Oncol. 2011, 22, 132–138. [Google Scholar] [CrossRef] [PubMed]
- Barriger, R.B.; Fakiris, A.J.; Hanna, N.; Yu, M.; Mantravadi, P.; McGarry, R.C. Dose-volume analysis of radiation pneumonitis in non-small-cell lung cancer patients treated with concurrent cisplatinum and etoposide with or without consolidation docetaxel. Int. J. Radiat. Oncol. Biol. Phys. 2010, 78, 1381–1386. [Google Scholar] [CrossRef] [PubMed]
- Palma, D.A.; Senan, S.; Tsujino, K.; Barriger, R.B.; Rengan, R.; Moreno, M.; Bradley, J.D.; Kim, T.H.; Ramella, S.; Marks, L.B.; et al. Predicting radiation pneumonitis after chemoradiation therapy for lung cancer: An international individual patient data meta-analysis. Int. J. Radiat. Oncol. Biol. Phys. 2013, 85, 444–450. [Google Scholar] [CrossRef] [PubMed]
- Palma, G.; Monti, S.; Conson, M.; Pacelli, R.; Cella, L. Normal tissue complication probability (NTCP) models for modern radiation therapy. Semin. Oncol. 2019, 46, 210–218. [Google Scholar] [CrossRef]
- Stavrev, P.; Stavreva, N.; Sharplin, J.; Fallone, B.G.; Franko, A. Critical volume model analysis of lung complication data from different strains of mice. Int. J. Radiat. Biol. 2005, 81, 77–88. [Google Scholar] [CrossRef]
- Niemierko, A.; Goitein, M. Modeling of normal tissue response to radiation: The critical volume model. Int. J. Radiat. Oncol. Biol. Phys. 1993, 25, 135–145. [Google Scholar] [CrossRef]
- Adamus-Górka, M.; Mavroidis, P.; Lind, B.K.; Brahme, A. Comparison of dose response models for predicting normal tissue complications from cancer radiotherapy: Application in rat spinal cord. Cancers 2011, 3, 2421–2443. [Google Scholar] [CrossRef]
- Wilensky, U.; Rand, W. An Introduction to Agent-Based Modeling; MIT Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Figueredo, G.P.; Siebers, P.O.; Owen, M.R.; Reps, J.; Aickelin, U. Comparing stochastic differential equations and agent-based modelling and simulation for early-stage cancer. PLoS ONE 2014, 9, e95150. [Google Scholar] [CrossRef]
- Nelson, G.; Wordsworth, J.; Wang, C.; Jurk, D.; Lawless, C.; Martin-Ruiz, C.; von Zglinicki, T. A senescent cell bystander effect: Senescence-induced senescence. Aging Cell 2012, 11, 345–349. [Google Scholar] [CrossRef]
- Prata, L.G.P.L.; Ovsyannikova, I.G.; Tchkonia, T.; Kirkland, J.L. Senescent cell clearance by the immune system: Emerging therapeutic opportunities. Semin. Immunol. 2018, 40, 101275. [Google Scholar] [CrossRef] [PubMed]
- Elder, S.S.; Emmerson, E. Senescent cells and macrophages: Key players for regeneration?: Senescent cells and macrophages. Open Biol. 2020, 10, 200309. [Google Scholar] [CrossRef] [PubMed]
- Bernchou, U.; Schytte, T.; Bertelsen, A.; Bentzen, S.M.; Hansen, O.; Brink, C. Time evolution of regional CT density changes in normal lung after IMRT for NSCLC. Radiother. Oncol. 2013, 109, 89–94. [Google Scholar] [CrossRef] [PubMed]
- Defraene, G.; La Fontaine, M.; van Kranen, S.; Reymen, B.; Belderbos, J.; Sonke, J.; De Ruysscher, D. Radiation-Induced Lung Density Changes on CT Scan for NSCLC: No Impact of Dose-Escalation Level or Volume. Int. J. Radiat. Oncol. Biol. Phys. 2018, 102, 642–650. [Google Scholar] [CrossRef] [PubMed]
- Konkol, M.; Bryl, M.; Fechner, M.; Matuszewski, K.; Śniatała, P.; Milecki, P. Normal Lung Tissue CT Density Changes after Volumetric-Arc Radiotherapy (VMAT) for Lung Cancer. J. Pers. Med. 2022, 12, 485. [Google Scholar] [CrossRef]
- Zhou, C.; Jones, B.; Moustafa, M.; Schwager, C.; Bauer, J.; Yang, B.; Cao, L.; Jia, M.; Mairani, A.; Chen, M.; et al. Quantitative assessment of radiation dose and fractionation effects on normal tissue by utilizing a novel lung fibrosis index model. Radiat. Oncol. 2017, 12, 172. [Google Scholar] [CrossRef]
- Wiesemann, A.; Ketteler, J.; Slama, A.; Wirsdörfer, F.; Hager, T.; Röck, K.; Engel, D.R.; Fischer, J.W.; Aigner, C.; Jendrossek, V.; et al. Inhibition of Radiation-Induced Ccl2 Signaling Protects Lungs from Vascular Dysfunction and Endothelial Cell Loss. Antioxid. Redox Signal. 2019, 30, 213–231. [Google Scholar] [CrossRef]
- Rübe, C.E.; Uthe, D.; Schmid, K.W.; Richter, K.D.; Wessel, J.; Schuck, A.; Willich, N.; Rübe, C. Dose-dependent induction of transforming growth factor β (TGF-β) in the lung tissue of fibrosis-prone mice after thoracic irradiation. Int. J. Radiat. Oncol. Biol. Phys. 2000, 47, 1033–1042. [Google Scholar] [CrossRef]
- Franko, A.J.; Sharplin, J. Development of fibrosis after lung irradiation in relation to inflammation and lung function in a mouse strain prone to fibrosis. Radiat. Res. 1994, 140, 347–355. [Google Scholar] [CrossRef]
- Misharin, A.V.; Morales-Nebreda, L.; Reyfman, P.A.; Cuda, C.M.; Walter, J.M.; McQuattie-Pimentel, A.C.; Chen, C.I.; Anekalla, K.R.; Joshi, N.; Williams, K.J.N.; et al. Monocyte-derived alveolar macrophages drive lung fibrosis and persist in the lung over the life span. J. Exp. Med. 2017, 214, 2387–2404. [Google Scholar] [CrossRef]
- Defraene, G.; Van Elmpt, W.; De Ruysscher, D. Regional lung avoidance by CT numbers to reduce radiation-induced lung damage risk in non- small—Cell lung cancer: A simulation study. Acta Oncol. 2020, 59, 201–207. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Dykstra, M.; Best, T.D.; Pursley, J.; Chopra, N.; Keane, F.K.; Khandekar, M.J.; Sharp, G.C.; Paganetti, H.; Willers, H.; et al. Differential inflammatory response dynamics in normal lung following stereotactic body radiation therapy with protons versus photons. Radiother. Oncol. 2019, 136, 169–175. [Google Scholar] [CrossRef] [PubMed]
- Kligerman, S.J.; Franks, T.J.; Galvin, J.R. From the Radiologic Pathology Archives: Organization and fibrosis as a response to lung injury in diffuse alveolar damage, organizing pneumonia, and acute fibrinous and organizing pneumonia. Radiographics 2013, 33, 1951–1975. [Google Scholar] [CrossRef] [PubMed]
- Meiners, S.; Lehmann, M. Senescent Cells in IPF: Locked in Repair? Front. Med. 2020, 7, 606330. [Google Scholar] [CrossRef] [PubMed]
- Hao, W.; Marsh, C.; Friedman, A. A mathematical model of idiopathic pulmonary fibrosis. PLoS ONE 2015, 10, e0135097. [Google Scholar] [CrossRef] [PubMed]
- Österreicher, J.; Pejchal, J.; Škopek, J.; Mokrỳ, J.; Vilasová, Z.; Psutka, J.; Vávrová, J.; Mazurová, Y. Role of type II pneumocytes in pathogenesis of radiation pneumonitis: Dose response of radiation-induced long changes in the transient high vascular permeability period. Exp. Toxicol. Pathol. 2004, 56, 181–187. [Google Scholar] [CrossRef]
- Vinogradskiy, Y.; Diot, Q.; Kavanagh, B.; Schefter, T.; Gaspar, L.; Miften, M. Spatial and dose-response analysis of fibrotic lung changes after stereotactic body radiation therapy. Med. Phys. 2013, 40, 081712. [Google Scholar] [CrossRef][Green Version]
- Pan, J.; Li, D.; Xu, Y.; Zhang, J.; Wang, Y.; Chen, M.; Lin, S.; Huang, L.; Chung, E.J.; Citrin, D.E.; et al. Inhibition of Bcl-2/xl With ABT-263 Selectively Kills Senescent Type II Pneumocytes and Reverses Persistent Pulmonary Fibrosis Induced by Ionizing Radiation in Mice. Int. J. Radiat. Oncol. Biol. Phys. 2017, 99, 353–361. [Google Scholar] [CrossRef]
- Lehmann, M.; Korfei, M.; Mutze, K.; Klee, S.; Skronska-Wasek, W.; Alsafadi, H.N.; Ota, C.; Costa, R.; Schiller, H.B.; Lindner, M.; et al. Senolytic drugs target alveolar epithelial cell function and attenuate experimental lung fibrosis ex vivo. Eur. Respir. J. 2017, 50, 1602367. [Google Scholar] [CrossRef]
- Chung, E.J.; McKay-Corkum, G.; Chung, S.; White, A.; Scroggins, B.T.; Mitchell, J.B.; Mulligan-Kehoe, M.J.; Citrin, D. Truncated Plasminogen Activator Inhibitor-1 Protein Protects from Pulmonary Fibrosis Mediated by Irradiation in a Murine Model. Int. J. Radiat. Oncol. Biol. Phys. 2016, 94, 1163–1172. [Google Scholar] [CrossRef]
- Parikh, P.; Wicher, S.; Khandalavala, K.; Pabelick, C.M.; Britt, R.D.; Prakash, Y.S. Cellular senescence in the lung across the age spectrum. Am. J. Physiol.—Lung Cell Mol. Physiol. 2019, 316, L826–L842. [Google Scholar] [CrossRef] [PubMed]
- Campisi, J. Cellular senescence and lung function during aging: Yin and Yang. Ann. Am. Thorac. Soc. 2016, 13, S402–S406. [Google Scholar] [CrossRef]
- Dehing-Oberije, C.; De Ruysscher, D.; van Baardwijk, A.; Yu, S.; Rao, B.; Lambin, P. The importance of patient characteristics for the prediction of radiation-induced lung toxicity. Radiother. Oncol. 2009, 91, 421–426. [Google Scholar] [CrossRef] [PubMed]
- Vogelius, I.R.; Bentzen, S.M. A literature-based meta-analysis of clinical risk factors for development of radiation induced pneumonitis. Acta Oncol. 2012, 51, 975–983. [Google Scholar] [CrossRef] [PubMed]
- Demetriades, M.; Zivanovic, M.; Hadjicharalambous, M.; Ioannou, E.; Ljujic, B.; Vucicevic, K.; Ivosevic, Z.; Dagovic, A.; Milivojevic, N.; Kokkinos, O.; et al. Interrogating and Quantifying In Vitro Cancer Drug Pharmacodynamics via Agent-Based and Bayesian Monte Carlo Modelling. Pharmaceutics 2022, 14, 749. [Google Scholar] [CrossRef] [PubMed]
- Breitwieser, L.; Hesam, A.; de Montigny, J.; Vavourakis, V.; Iosif, A.; Jennings, J.; Kaiser, M.; Manca, M.; Di Meglio, A.; Al-Ars, Z.; et al. BioDynaMo: A modular platform for high-performance agent-based simulation. Bioinformatics 2021, 38, 453–460. [Google Scholar] [CrossRef] [PubMed]
- PyROOT Tutorial. Available online: https://indico.cern.ch/event/704163/contributions/2936719/attachments/1693833/2726445/Tutorial-PyROOT.pdf (accessed on 10 October 2022).
- Weibel, E.R. Morphometry of the Human Lung, 1st ed.; Springer: Berlin/Heidelberg, Germany, 1963. [Google Scholar] [CrossRef]
- Stone, K.C.; Mercer, R.R.; Gehr, P.; Stockstill, B.; Crapo, J.D. Allometric relationships of cell numbers and size in the mammalian lung. Am. J. Respir. Cell Mol. Biol. 1992, 6, 235–243. [Google Scholar] [CrossRef]
- Pahl, A.; Zhang, M.; Kuss, H.; Szelenyi, I.; Brune, K. Regulation of IL-13 synthesis in human lymphocytes: Implications for asthma therapy. Br. J. Pharmacol. 2002, 135, 1915–1926. [Google Scholar] [CrossRef]
- Lama, V.; Moore, B.B.; Christensen, P.; Toews, G.B.; Peters-Golden, M. Prostaglandin E2 synthesis and suppression of fibroblast proliferation by alveolar epithelial cells is cyclooxygenase-2-dependent. Am. J. Respir. Cell Mol. Biol. 2002, 27, 752–758. [Google Scholar] [CrossRef]
- Kohyama, T.; Ertl, R.F.; Valenti, V.; Spurzem, J.; Kawamoto, M.; Nakamura, Y.; Veys, T.; Allegra, L.; Romberger, D.; Rennard, S.I. Prostaglandin E2 inhibits fibroblast chemotaxis. Am. J. Physiol.—Lung Cell Mol. Physiol. 2001, 281, 1257–1263. [Google Scholar] [CrossRef]
- Selman, M.; Pardo, A. Role of epithelial cells in idiopathic pulmonary fibrosis: From innocent targets to serial killers. Proc. Am. Thorac. Soc. 2006, 3, 364–372. [Google Scholar] [CrossRef] [PubMed]
- Jansing, N.L.; McClendon, J.; Henson, P.M.; Tuder, R.M.; Hyde, D.M.; Zemans, R.L. Unbiased quantitation of alveolar type II to alveolar type i cell transdifferentiation during repair after lung injury in mice. Am. J. Respir. Cell Mol. Biol. 2017, 57, 519–526. [Google Scholar] [CrossRef] [PubMed]
- McMahon, S.J.; Butterworth, K.T.; Trainor, C.; McGarry, C.K.; O’Sullivan, J.M.; Schettino, G.; Hounsell, A.R.; Prise, K.M. A Kinetic-Based Model of Radiation-Induced Intercellular Signalling. PLoS ONE 2013, 8, 15–18. [Google Scholar] [CrossRef] [PubMed]
- Hubackova, S.; Krejcikova, K.; Bartek, J.; Hodny, Z. IL1-and TGFβ-Nox4 signaling, oxidative stress and DNA damage response are shared features of replicative, oncogene-induced, and drug-induced paracrine “Bystander senescence”. Aging 2012, 4, 932–951. [Google Scholar] [CrossRef]
- Shao, C.; Folkard, M.; Prise, K.M. Role of TGF-Β1 and nitric oxide in the bystander response of irradiated glioma cells. Oncogene 2008, 27, 434–440. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, X.; Tian, W.; Yin, X.; Wang, J.; Yang, H. The role of TGF-β1-miR-21-ROS pathway in bystander responses induced by irradiated non-small-cell lung cancer cells. Br. J. Cancer 2014, 111, 772–780. [Google Scholar] [CrossRef]
- Acosta, J.C.; Banito, A.; Wuestefeld, T.; Georgilis, A.; Janich, P.; Morton, J.P.; Athineos, D.; Kang, T.W.; Lasitschka, F.; Andrulis, M.; et al. A complex secretory program orchestrated by the inflammasome controls paracrine senescence. Nat. Cell Biol. 2013, 15, 978–990. [Google Scholar] [CrossRef]
- Chung, E.J.; Kwon, S.; Shankavaram, U.; White, A.O.; Das, S.; Citrin, D.E. Natural variation in macrophage polarization and function impact pneumocyte senescence and susceptibility to fibrosis. Aging 2022, 14, 7692. [Google Scholar] [CrossRef]
- Nagre, N.; Cong, X.; Pearson, A.C.; Zhao, X. Alveolar Macrophage Phagocytosis and Bacteria Clearance in Mice. J. Vis. Exp. 2019, 145, e59088. [Google Scholar] [CrossRef]
- Janssen, W.J.; McPhillips, K.A.; Dickinson, M.G.; Linderman, D.J.; Morimoto, K.; Xiao, Y.Q.; Oldham, K.M.; Vandivier, R.W.; Henson, P.M.; Gardai, S.J. Surfactant Proteins A and D Suppress Alveolar Macrophage Phagocytosis via Interaction with SIRPα. Am. J. Respir. Crit. Care Med. 2008, 178, 158–167. [Google Scholar] [CrossRef]
- Hu, B.; Sonstein, J.; Christensen, P.J.; Punturieri, A.; Curtis, J.L. Deficient In Vitro and In Vivo Phagocytosis of Apoptotic T Cells by Resident Murine Alveolar Macrophages. J. Immunol. 2000, 165, 2124–2133. [Google Scholar] [CrossRef] [PubMed]
- Fehrenbach, H.; Kasper, M.; Tschernig, T.; Pan, T.; Schuh, D.; Shannon, J.M.; Müller, M.; Masor, R.J. Keratinocyte growth factor-induced hyperplasia of rat alveolar type II cells in vivo is resolved by differentiation into type I cells and by apoptosis. Eur. Respir. J. 1999, 14, 534–544. [Google Scholar] [CrossRef][Green Version]
- Crosby, L.M.; Luellen, C.; Zhang, Z.; Tague, L.L.; Sinclair, S.E.; Waters, C.M. Balance of life and death in alveolar epithelial type II cells: Proliferation, apoptosis, and the effects of cyclic stretch on wound healing. Am. J. Physiol.—Lung Cell Mol. Physiol. 2011, 301, 536–546. [Google Scholar] [CrossRef]
- Madas, B.G. Radon induced hyperplasia: Effective adaptation reducing the local doses in the bronchial epithelium. J. Radiol. Prot. 2016, 36, 653–666. [Google Scholar] [CrossRef] [PubMed]
- Saito, A.; Okazaki, H.; Sugawara, I.; Yamamoto, K.; Takizawa, H. Potential action of IL-4 and IL-13 as fibrogenic factors on lung fibroblasts in vitro. Int. Arch. Allergy Immunol. 2003, 132, 168–176. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L. TGF-beta 1 induced fibroblast proliferation is mediated by the FGF-2/ERK pathway. Front. Biosci. 2012, 17, 2667. [Google Scholar] [CrossRef] [PubMed]
- Li, C.M.; Khosla, J.; Pagan, I.; Hoyle, P.; Sannes, P.L. TGF-β1 and fibroblast growth factor-1 modify fibroblast growth factor-2 production in type II cells. Am. J. Physiol.—Lung Cell Mol. Physiol. 2000, 279, 1038–1046. [Google Scholar] [CrossRef]
- Groves, A.M.; Johnston, C.J.; Williams, J.P.; Finkelstein, J.N. Role of Infiltrating Monocytes in the Development of Radiation-Induced Pulmonary Fibrosis. Radiat. Res. 2018, 189, 300–311. [Google Scholar] [CrossRef]
- Redente, E.F.; Keith, R.C.; Janssen, W.; Henson, P.M.; Ortiz, L.A.; Downey, G.P.; Bratton, D.L.; Riches, D.W.H. Tumor necrosis factor-α accelerates the resolution of established pulmonary fibrosis in mice by targeting profibrotic lung macrophages. Am. J. Respir. Cell Mol. Biol. 2014, 50, 825–837. [Google Scholar] [CrossRef]
- Gu, L.; Zhu, Y.J.; Yang, X.; Guo, Z.J.; Xu, W.B.; Tian, X.L. Effect of TGF-β/Smad signaling pathway on lung myofibroblast differentiation. Acta Pharmacol. Sin. 2007, 28, 382–391. [Google Scholar] [CrossRef]
- Boström, H.; Willetts, K.; Pekny, M.; Levéen, P.; Lindahl, P.; Hedstrand, H.; Pekna, M.; Hellström, M.; Gebre-Medhin, S.; Schalling, M.; et al. PDGF-A signaling is a critical event in lung alveolar myofibroblast development and alveogenesis. Cell 1996, 85, 863–873. [Google Scholar] [CrossRef]
- Childs, B.G.; Baker, D.J.; Kirkland, J.L.; Campisi, J.; Deursen, J.M. Senescence and apoptosis: Dueling or complementary cell fates? EMBO Rep. 2014, 15, 1139–1153. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, J.P.; Brenner, D.J.; Orton, C.G. The linear-quadratic model is inappropriate to model high dose per fraction effects in radiosurgery. Med. Phys. 2009, 36, 3381–3384. [Google Scholar] [CrossRef] [PubMed]
- McMahon, S.J. The linear quadratic model: Usage, interpretation and challenges. Phys. Med. Biol. 2018, 64, 01TR01. [Google Scholar] [CrossRef] [PubMed]
- Kołodziej, M.; Sauer, D.G.; Beck, J.; Marek, W.K.; Hahn, R.; Jungbauer, A.; Dürauer, A.; Piątkowski, W.; Antos, D. Scale up of a chromatographic capture step for a clarified bacterial homogenate—Influence of mass transport limitation and competitive adsorption of impurities. J. Chromatogr. A 2020, 1618, 460856. [Google Scholar] [CrossRef] [PubMed]
- Dvorak, P.; Bednar, D.; Vanacek, P.; Balek, L.; Eiselleova, L.; Stepankova, V.; Sebestova, E.; Kunova Bosakova, M.; Konecna, Z.; Mazurenko, S.; et al. Computer-assisted engineering of hyperstable fibroblast growth factor 2. Biotechnol. Bioeng. 2018, 115, 850–862. [Google Scholar] [CrossRef] [PubMed]
- Grazul-Bilska, A.T.; Luthra, G.; Reynolds, L.P.; Bilski, J.J.; Johnson, M.L.; Adbullah, S.A.; Redmer, D.A.; Abdullah, K.M. Effects of basic fibroblast growth factor (FGF-2) on proliferation of human skin fibroblasts in type II diabetes mellitus. Exp. Clin. Endocrinol. Diabetes 2002, 110, 176–181. [Google Scholar] [CrossRef] [PubMed]
- Rikard, S.M.; Athey, T.L.; Nelson, A.R.; Christiansen, S.L.; Lee, J.J.; Holmes, J.W.; Peirce, S.M.; Saucerman, J.J. Multiscale Coupling of an Agent-Based Model of Tissue Fibrosis and a Logic-Based Model of Intracellular Signaling. Front. Physiol. 2019, 10, 1481. [Google Scholar] [CrossRef] [PubMed]
- Pollmächer, J.; Figge, M.T. Agent-based model of human alveoli predicts chemotactic signaling by epithelial cells during early Aspergillus fumigatus infection. PLoS ONE 2014, 9, e111630. [Google Scholar] [CrossRef]
- Legrand, C.; Gilles, C.; Zahm, J.M.; Polette, M.; Buisson, A.C.; Kaplan, H.; Birembaut, P.; Tournier, J.M. Airway epithelial cell migration dynamics: MMP-9 role in cell- extracellular matrix remodeling. J. Cell Biol. 1999, 146, 517–529. [Google Scholar] [CrossRef]
- Ochs, M.; Nyengaard, J.R.; Jung, A.; Knudsen, L.; Voigt, M.; Wahlers, T.; Richter, J.; Gundersen, H.J. The Number of Alveoli in the Human Lung. Am. J. Respir. Crit. Care Med. 2004, 169, 120–124. [Google Scholar] [CrossRef] [PubMed]
- Fathi, M.; Johansson, A.; Lundborg, M.; Orre, L.; Sköld, C.M.; Camner, P. Functional and morphological differences between human alveolar and interstitial macrophages. Exp. Mol. Pathol. 2001, 70, 77–82. [Google Scholar] [CrossRef] [PubMed]

| Category | Type | Initial Number per Alveolus | Source |
|---|---|---|---|
| Epithelial | AEC1 | 41 | [60] |
| AEC2 healthy | 69 | [60] | |
| AEC2 damaged | 0 | ||
| AEC2 senescent | 0 | ||
| Macrophage | Macrophage M1 | 6 1 | [60] |
| Macrophage M2 | 6 1 | [60] | |
| Mesenchymal | Fibroblast | 24 2 | [46,60] |
| Myofibroblast | 36 2 | [46,60] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cogno, N.; Bauer, R.; Durante, M. An Agent-Based Model of Radiation-Induced Lung Fibrosis. Int. J. Mol. Sci. 2022, 23, 13920. https://doi.org/10.3390/ijms232213920
Cogno N, Bauer R, Durante M. An Agent-Based Model of Radiation-Induced Lung Fibrosis. International Journal of Molecular Sciences. 2022; 23(22):13920. https://doi.org/10.3390/ijms232213920
Chicago/Turabian StyleCogno, Nicolò, Roman Bauer, and Marco Durante. 2022. "An Agent-Based Model of Radiation-Induced Lung Fibrosis" International Journal of Molecular Sciences 23, no. 22: 13920. https://doi.org/10.3390/ijms232213920
APA StyleCogno, N., Bauer, R., & Durante, M. (2022). An Agent-Based Model of Radiation-Induced Lung Fibrosis. International Journal of Molecular Sciences, 23(22), 13920. https://doi.org/10.3390/ijms232213920








