Nanobody Paratope Ensembles in Solution Characterized by MD Simulations and NMR
Abstract
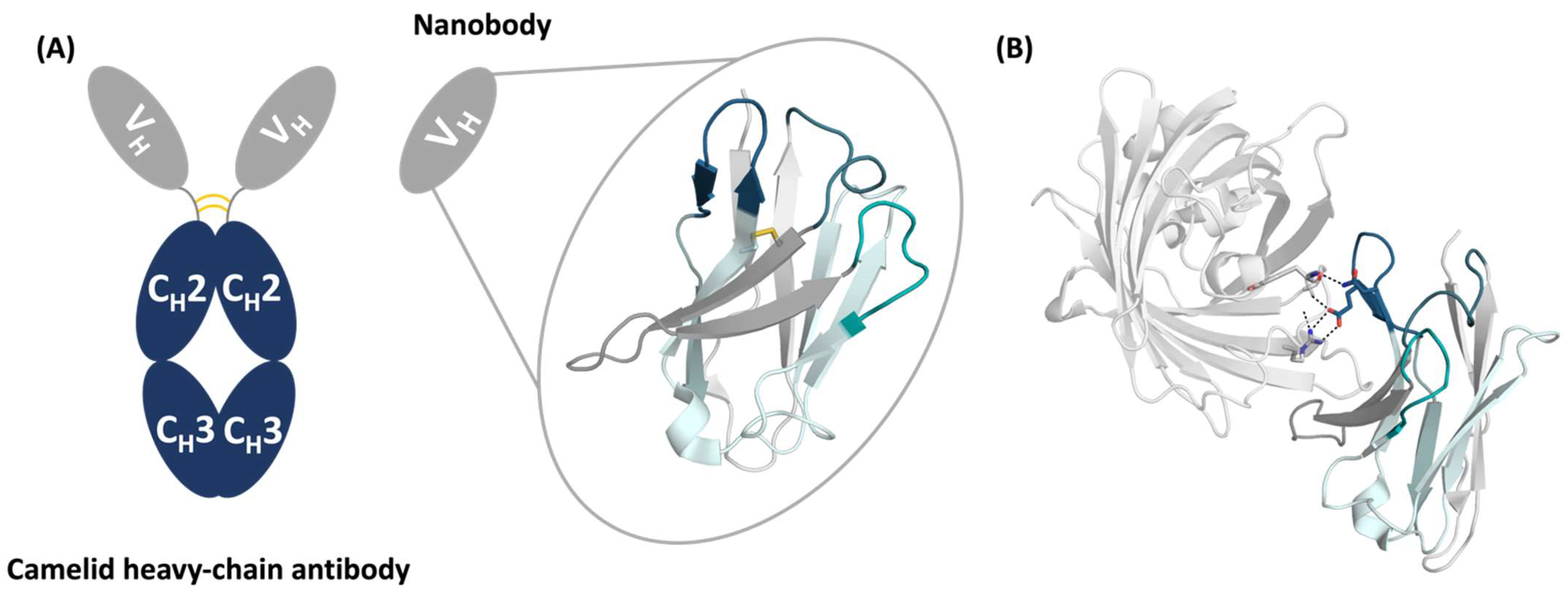
:1. Introduction
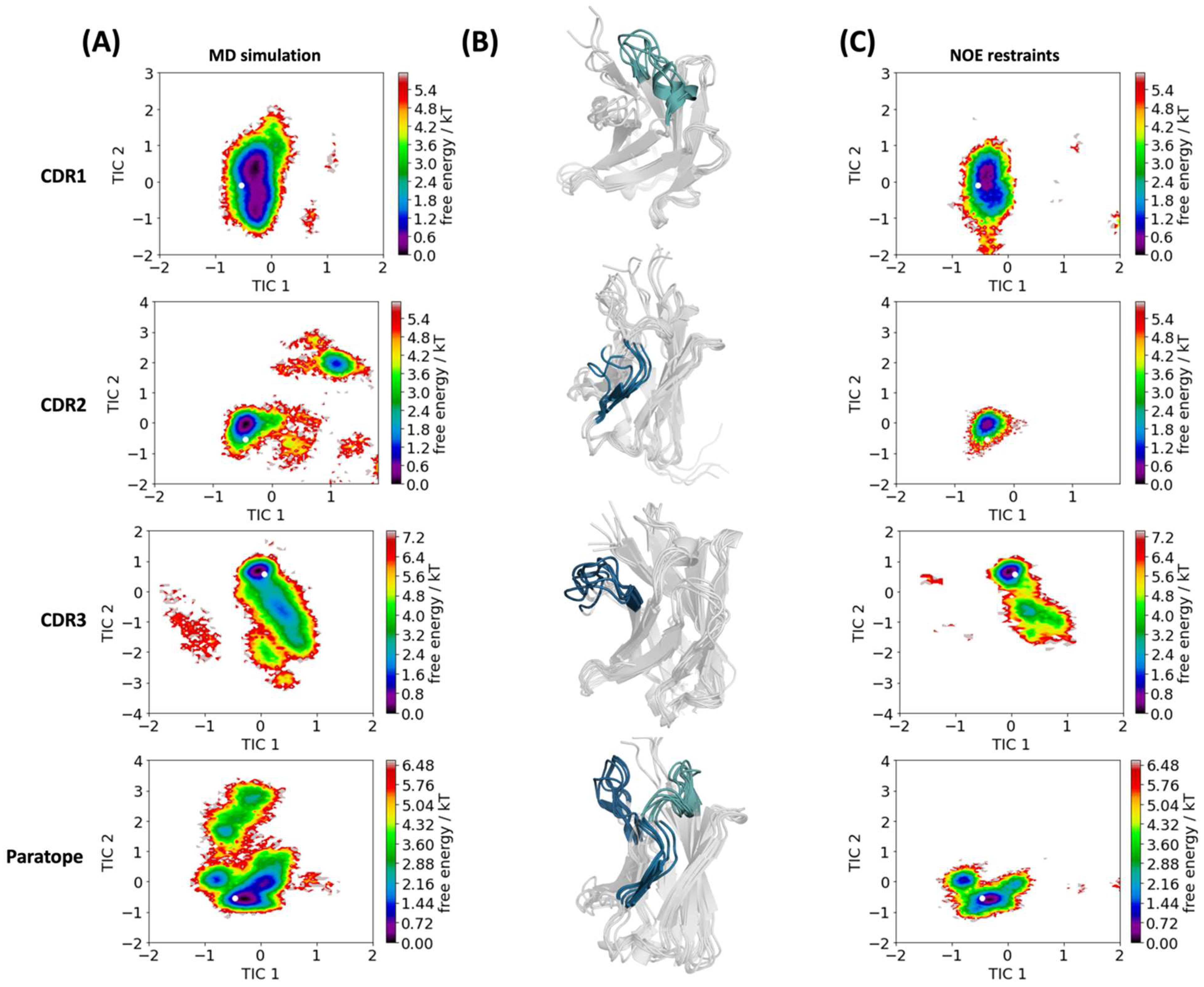
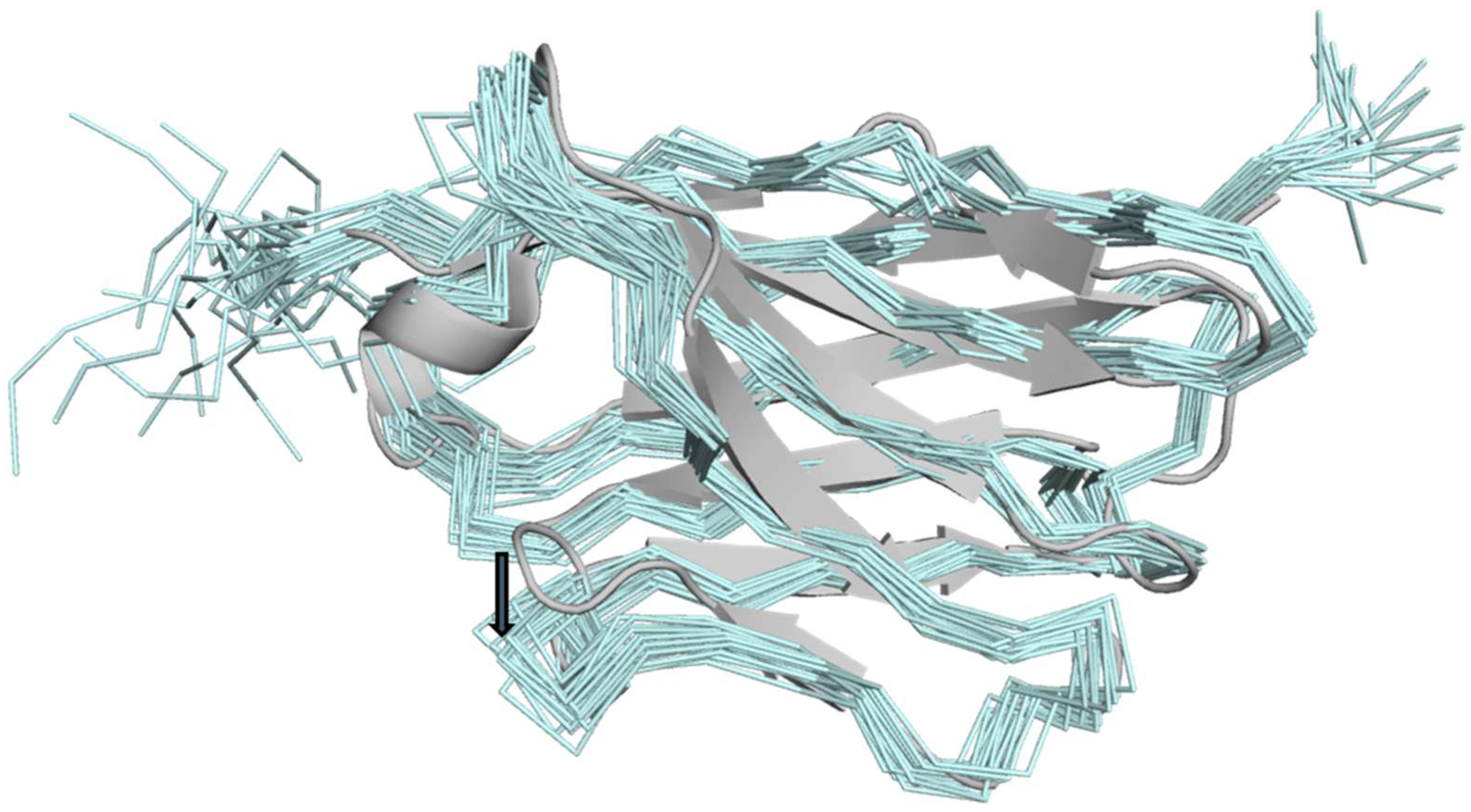
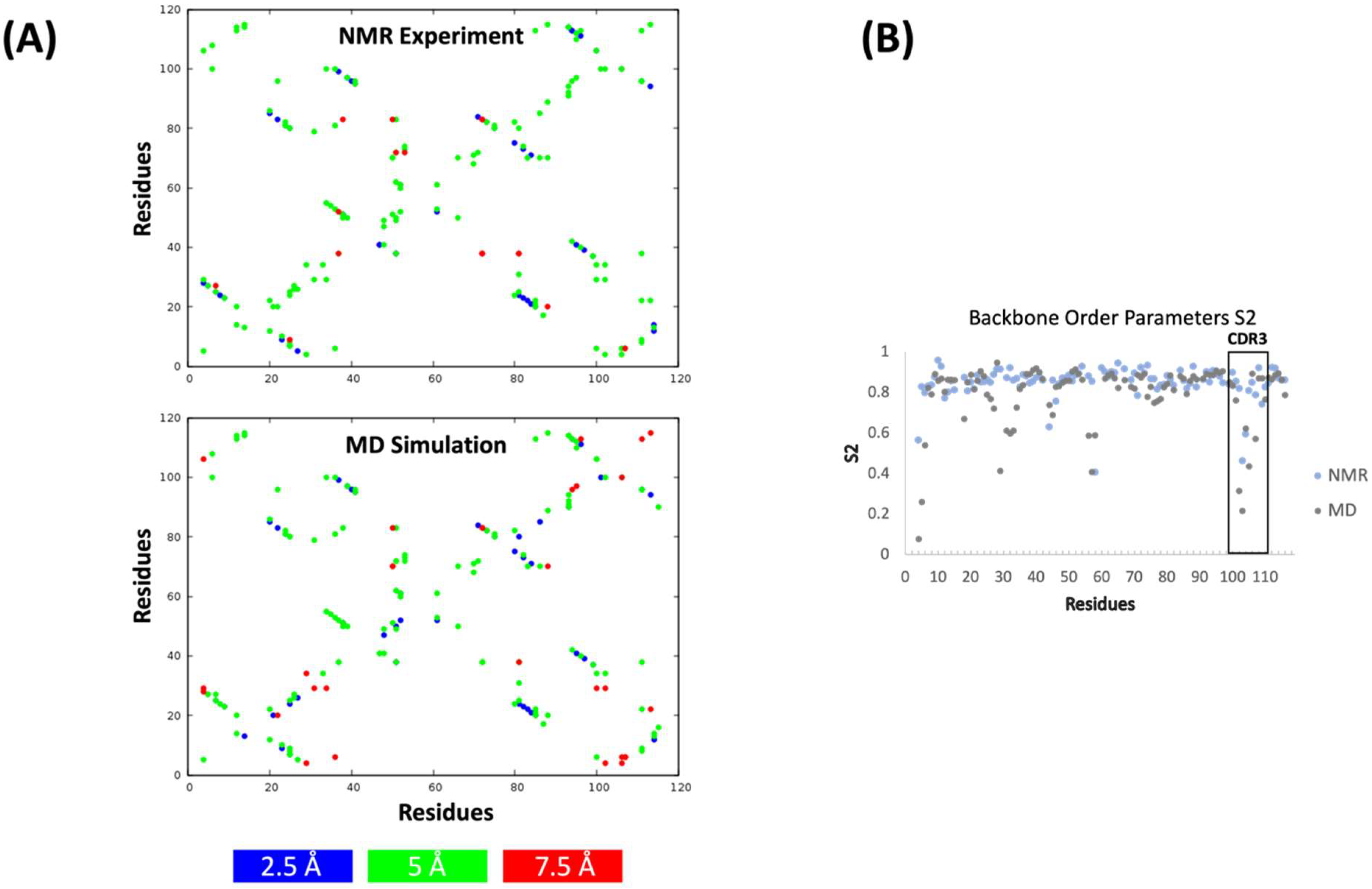
2. Results
3. Discussion
4. Methods
4.1. Structure Preparation
4.2. Metadynamics Simulations
4.3. Molecular Dynamics Simulations
4.4. NOE Restraints Simulations—NMR Ensemble
4.5. Expression
4.6. Purification
4.7. NMR Data Acquisition
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hamers-Casterman, C.; Atarhouch, T.; Muyldermans, S.; Robinson, G.; Hammers, C.; Songa, E.B.; Bendahman, N.; Hammers, R. Naturally Occurring Antibodies Devoid of Light Chains. Nature 1993, 363, 446–448. [Google Scholar] [CrossRef] [PubMed]
- Vincke, C.; Muyldermans, S. Introduction to Heavy Chain Antibodies and Derived Nanobodies. In Single Domain Antibodies: Methods and Protocols; Saerens, D., Muyldermans, S., Eds.; Humana Press: Totowa, NJ, USA, 2012; pp. 15–26. ISBN 978-1-61779-968-6. [Google Scholar]
- Muyldermans, S. Nanobodies: Natural Single-Domain Antibodies. Annu. Rev. Biochem. 2013, 82, 775–797. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Revets, H.; De Baetselier, P.; Muyldermans, S. Nanobodies as Novel Agents for Cancer Therapy. Expert Opin. Biol. Ther. 2005, 5, 111–124. [Google Scholar] [CrossRef] [PubMed]
- Bannas, P.; Hambach, J.; Koch-Nolte, F. Nanobodies and Nanobody-Based Human Heavy Chain Antibodies As Antitumor Therapeutics. Front. Immunol. 2017, 8, 1603. [Google Scholar] [CrossRef]
- Wolfson, W. Ablynx Makes Nanobodies from Llama Bodies. Chem. Biol. 2006, 13, 1243–1244. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steeland, S.; Vandenbroucke, R.E.; Libert, C. Nanobodies as Therapeutics: Big Opportunities for Small Antibodies. Drug Discov. Today 2016, 21, 1076–1113. [Google Scholar] [CrossRef]
- Harmsen, M.M.; De Haard, H.J. Properties, Production, and Applications of Camelid Single-Domain Antibody Fragments. Appl. Microbiol. Biotechnol. 2007, 77, 13–22. [Google Scholar] [CrossRef] [Green Version]
- Muyldermans, S.; Atarhouch, T.; Saldanha, J.; Barbosa, J.A.R.G.; Hamers, R. Sequence and Structure of VH Domain from Naturally Occurring Camel Heavy Chain Immunoglobulins Lacking Light Chains. Protein Eng. Des. Sel. 1994, 7, 1129–1135. [Google Scholar] [CrossRef]
- Kabat, E.A.; National Institutes of Health (U.S.); Columbia University. Sequences of Proteins of Immunological Interest; U.S. Department of Health and Human Services, Public Health Service, National Institutes of Health: Bethesda, MD, USA, 1991.
- Chiu, M.L.; Goulet, D.R.; Teplyakov, A.; Gilliland, G.L. Antibody Structure and Function: The Basis for Engineering Therapeutics. Antibodies 2019, 8, 55. [Google Scholar] [CrossRef] [Green Version]
- Hoey, R.J.; Eom, H.; Horn, J.R. Structure and Development of Single Domain Antibodies as Modules for Therapeutics and Diagnostics. Exp. Biol. Med. 2019, 244, 1568–1576. [Google Scholar] [CrossRef]
- Lesk, A.M.; Chothia, C. Evolution of Proteins Formed by β-Sheets: II. The Core of the Immunoglobulin Domains. J. Mol. Biol. 1982, 160, 325–342. [Google Scholar] [CrossRef]
- Chothia, C.; Gelfand, I.; Kister, A. Structural Determinants in the Sequences of Immunoglobulin Variable Domain. J. Mol. Biol. 1998, 278, 457–479. [Google Scholar] [CrossRef] [PubMed]
- Zavrtanik, U.; Lukan, J.; Loris, R.; Lah, J.; Hadži, S. Structural Basis of Epitope Recognition by Heavy-Chain Camelid Antibodies. J. Mol. Biol. 2018, 430, 4369–4386. [Google Scholar] [CrossRef] [PubMed]
- Akiba, H.; Tamura, H.; Kiyoshi, M.; Yanaka, S.; Sugase, K.; Caaveiro, J.M.M.; Tsumoto, K. Structural and Thermodynamic Basis for the Recognition of the Substrate-Binding Cleft on Hen Egg Lysozyme by a Single-Domain Antibody. Sci. Rep. 2019, 9, 15481. [Google Scholar] [CrossRef]
- Regep, C.; Georges, G.; Shi, J.; Popovic, B.; Deane, C.M. The H3 Loop of Antibodies Shows Unique Structural Characteristics. Proteins Struct. Funct. Bioinforma. 2017, 85, 1311–1318. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Quintero, M.L.; Pomarici, N.D.; Math, B.A.; Kroell, K.B.; Waibl, F.; Bujotzek, A.; Georges, G.; Liedl, K.R. Antibodies Exhibit Multiple Paratope States Influencing VH–VL Domain Orientations. Commun. Biol. 2020, 3, 589. [Google Scholar] [CrossRef]
- Fernández-Quintero, M.L.; Georges, G.; Varga, J.M.; Liedl, K.R. Ensembles in Solution as a New Paradigm for Antibody Structure Prediction and Design. mAbs 2021, 13, 1923122. [Google Scholar] [CrossRef]
- Fernández-Quintero, M.L.; Kroell, K.B.; Hofer, F.; Riccabona, J.R.; Liedl, K.R. Mutation of Framework Residue H71 Results in Different Antibody Paratope States in Solution. Front. Immunol. 2021, 12, 243. [Google Scholar] [CrossRef]
- Fernández-Quintero, M.L.; Kraml, J.; Georges, G.; Liedl, K.R. CDR-H3 Loop Ensemble in Solution—Conformational Selection upon Antibody Binding. mAbs 2019, 11, 1077–1088. [Google Scholar] [CrossRef]
- Allison, J.R. Assessing and Refining Molecular Dynamics Simulations of Proteins with Nuclear Magnetic Resonance Data. Biophys. Rev. 2012, 4, 189–203. [Google Scholar] [CrossRef] [Green Version]
- Papaleo, E.; Camilloni, C.; Teilum, K.; Vendruscolo, M.; Lindorff-Larsen, K. Molecular Dynamics Ensemble Refinement of the Heterogeneous Native State of NCBD Using Chemical Shifts and NOEs. PeerJ 2018, 6, e5125. [Google Scholar] [CrossRef] [PubMed]
- Kümmerer, F.; Orioli, S.; Harding-Larsen, D.; Hoffmann, F.; Gavrilov, Y.; Teilum, K.; Lindorff-Larsen, K. Fitting Side-Chain NMR Relaxation Data Using Molecular Simulations. J. Chem. Theory Comput. 2021, 17, 5262–5275. [Google Scholar] [CrossRef] [PubMed]
- Maragakis, P.; Lindorff-Larsen, K.; Eastwood, M.P.; Dror, R.O.; Klepeis, J.L.; Arkin, I.T.; Jensen, M.Ø.; Xu, H.; Trbovic, N.; Friesner, R.A.; et al. Microsecond Molecular Dynamics Simulation Shows Effect of Slow Loop Dynamics on Backbone Amide Order Parameters of Proteins. J. Phys. Chem. B 2008, 112, 6155–6158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Charlier, C.; Khan, S.N.; Marquardsen, T.; Pelupessy, P.; Reiss, V.; Sakellariou, D.; Bodenhausen, G.; Engelke, F.; Ferrage, F. Nanosecond Time Scale Motions in Proteins Revealed by High-Resolution NMR Relaxometry. J. Am. Chem. Soc. 2013, 135, 18665–18672. [Google Scholar] [CrossRef] [PubMed]
- Kleckner, I.R.; Foster, M.P. An Introduction to NMR-Based Approaches for Measuring Protein Dynamics. Biochim. Biophys. Acta 2011, 1814, 942–968. [Google Scholar] [CrossRef] [Green Version]
- Kubala, M.H.; Kovtun, O.; Alexandrov, K.; Collins, B.M. Structural and Thermodynamic Analysis of the GFP:GFP-Nanobody Complex. Protein Sci. 2010, 19, 2389–2401. [Google Scholar] [CrossRef] [Green Version]
- Kirchhofer, A.; Helma, J.; Schmidthals, K.; Frauer, C.; Cui, S.; Karcher, A.; Pellis, M.; Muyldermans, S.; Casas-Delucchi, C.S.; Cardoso, M.C.; et al. Modulation of Protein Properties in Living Cells Using Nanobodies. Nat. Struct. Mol. Biol. 2010, 17, 133–138. [Google Scholar] [CrossRef]
- Biswas, M.; Lickert, B.; Stock, G. Metadynamics Enhanced Markov Modeling of Protein Dynamics. J. Phys. Chem. B 2018, 122, 5508–5514. [Google Scholar] [CrossRef]
- Fernández-Quintero, M.L.; Seidler, C.A.; Liedl, K.R. T-Cell Receptor Variable β Domains Rigidify During Affinity Maturation. Sci. Rep. 2020, 10, 4472. [Google Scholar] [CrossRef]
- Pérez-Hernández, G.; Noé, F. Hierarchical Time-Lagged Independent Component Analysis: Computing Slow Modes and Reaction Coordinates for Large Molecular Systems. J. Chem. Theory Comput. 2016, 12, 6118–6129. [Google Scholar] [CrossRef]
- Chodera, J.D.; Noé, F. Markov State Models of Biomolecular Conformational Dynamics. Curr. Opin. Struct. Biol. 2014, 25, 135–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- David, A.; Case, H.N.; Daniel, R.; Roe, J.S. PYTRAJ: Interactive Data Analysis for Molecular Dynamics Simulations; Rutgers University: New Brunswick, NJ, USA, 2016. [Google Scholar]
- Nichols, P.J.; Born, A.; Henen, M.A.; Strotz, D.; Celestine, C.N.; Güntert, P.; Vögeli, B. Extending the Applicability of Exact Nuclear Overhauser Enhancements to Large Proteins and RNA. ChemBioChem 2018, 19, 1695–1701. [Google Scholar] [CrossRef] [PubMed]
- Nichols, P.J.; Born, A.; Henen, M.A.; Strotz, D.; Orts, J.; Olsson, S.; Güntert, P.; Chi, C.N.; Vögeli, B. The Exact Nuclear Overhauser Enhancement: Recent Advances. Molecules 2017, 22, 1176. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Quintero, M.L.; Kroell, K.B.; Bacher, L.M.; Loeffler, J.R.; Quoika, P.K.; Georges, G.; Bujotzek, A.; Kettenberger, H.; Liedl, K.R. Germline-Dependent Antibody Paratope States and Pairing Specific VH-VL Interface Dynamics. Front. Immunol. 2021, 12, 2741. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Quintero, M.L.; Seidler, C.A.; Quoika, P.K.; Liedl, K.R. Shark Antibody Variable Domains Rigidify Upon Affinity Maturation—Understanding the Potential of Shark Immunoglobulins as Therapeutics. Front. Mol. Biosci. 2021, 8, 226. [Google Scholar] [CrossRef]
- Fernández-Quintero, M.L.; Loeffler, J.R.; Kraml, J.; Kahler, U.; Kamenik, A.S.; Liedl, K.R. Characterizing the Diversity of the CDR-H3 Loop Conformational Ensembles in Relationship to Antibody Binding Properties. Front. Immunol. 2019, 9, 3065. [Google Scholar] [CrossRef]
- Fernández-Quintero, M.L.; Loeffler, J.R.; Bacher, L.M.; Waibl, F.; Seidler, C.A.; Liedl, K.R. Local and Global Rigidification Upon Antibody Affinity Maturation. Front. Mol. Biosci. 2020, 7, 182. [Google Scholar] [CrossRef]
- Mulder, F.A.A.; Skrynnikov, N.R.; Hon, B.; Dahlquist, F.W.; Kay, L.E. Measurement of Slow (Μs−ms) Time Scale Dynamics in Protein Side Chains by 15N Relaxation Dispersion NMR Spectroscopy: Application to Asn and Gln Residues in a Cavity Mutant of T4 Lysozyme. J. Am. Chem. Soc. 2001, 123, 967–975. [Google Scholar] [CrossRef]
- Sharp, K.A. Chapter One-Companion Simulations and Modeling to NMR-Based Dynamical Studies of Proteins. In Methods in Enzymology; Wand, A.J., Ed.; Academic Press: Cambridge, MA, USA, 2019; Volume 615, pp. 1–41. ISBN 0076-6879. [Google Scholar]
- Gu, Y.; Li, D.-W.; Brüschweiler, R. NMR Order Parameter Determination from Long Molecular Dynamics Trajectories for Objective Comparison with Experiment. J. Chem. Theory Comput. 2014, 10, 2599–2607. [Google Scholar] [CrossRef]
- Mitchell, L.S.; Colwell, L.J. Comparative Analysis of Nanobody Sequence and Structure Data. Proteins Struct. Funct. Bioinforma. 2018, 86, 697–706. [Google Scholar] [CrossRef]
- Labute, P. Protonate3D: Assignment of Ionization States and Hydrogen Coordinates to Macromolecular Structures. Proteins 2009, 75, 187–205. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Molecular Operating Environment (MOE); 1010 Sherbrooke St. West, Suite #910; MOE: Montreal, QC, Canada, 2020.
- Case, D.A.; Belfon, K.; Ben-Shalom, I.Y.; Brozell, S.R.; Cerutti, D.S.; Cheatham, T.E., III; Cruzeiro, V.W.D.; Darden, T.A.; Duke, R.E.; Giambasu, G.; et al. AMBER 2020; University of California, San Francisco: San Francisco, CA, USA, 2020. [Google Scholar]
- Hub, J.S.; de Groot, B.L.; Grubmüller, H.; Groenhof, G. Quantifying Artifacts in Ewald Simulations of Inhomogeneous Systems with a Net Charge. J. Chem. Theory Comput. 2014, 10, 381–390. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- El Hage, K.; Hédin, F.; Gupta, P.K.; Meuwly, M.; Karplus, M. Valid Molecular Dynamics Simulations of Human Hemoglobin Require a Surprisingly Large Box Size. eLife 2018, 7, e35560. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Gapsys, V.; de Groot, B.L. Comment on “Valid Molecular Dynamics Simulations of Human Hemoglobin Require a Surprisingly Large Box Size”. eLife 2019, 8, e44718. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. Ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from Ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef] [Green Version]
- Wallnoefer, H.G.; Handschuh, S.; Liedl, K.R.; Fox, T. Stabilizing of a Globular Protein by a Highly Complex Water Network: A Molecular Dynamics Simulation Study on Factor Xa. J. Phys. Chem. B 2010, 114, 7405–7412. [Google Scholar] [CrossRef]
- Wallnoefer, H.G.; Liedl, K.R.; Fox, T. A Challenging System: Free Energy Prediction for Factor Xa. J. Comput. Chem. 2011, 32, 1743–1752. [Google Scholar] [CrossRef]
- Tribello, G.A.; Bonomi, M.; Branduardi, D.; Camilloni, C.; Bussi, G. PLUMED 2: New Feathers for an Old Bird. Comput. Phys. Commun. 2014, 185, 604–613. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Domene, C.; Barbini, P.; Furini, S. Bias-Exchange Metadynamics Simulations: An Efficient Strategy for the Analysis of Conduction and Selectivity in Ion Channels. J. Chem. Theory Comput. 2015, 11, 1896–1906. [Google Scholar] [CrossRef] [PubMed]
- Barducci, A.; Bussi, G.; Parrinello, M. Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method. Phys. Rev. Lett. 2008, 100, 020603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Laio, A.; Gervasio, F.L. Metadynamics: A Method to Simulate Rare Events and Reconstruct the Free Energy in Biophysics, Chemistry and Material Science. Rep. Prog. Phys. 2008, 71, 126601. [Google Scholar] [CrossRef]
- Fernández-Quintero, M.L.; Pomarici, N.D.; Loeffler, J.R.; Seidler, C.A.; Liedl, K.R. T-Cell Receptor CDR3 Loop Conformations in Solution Shift the Relative Vα-Vβ Domain Distributions. Front. Immunol. 2020, 11, 1440. [Google Scholar] [CrossRef]
- Ramachandran, G.N.; Ramakrishnan, C.; Sasisekharan, V. Stereochemistry of Polypeptide Chain Configurations. J. Mol. Biol. 1963, 7, 95–99. [Google Scholar] [CrossRef]
- Roe, D.R.; Cheatham, T.E. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Götz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine Microsecond Molecular Dynamics Simulations with AMBER on GPUs. 2. Explicit Solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Berendsen, H.; van Postma, J.P.M.; van Gunsteren, W.; DiNola, A.; Haak, J.R. Molecular-Dynamics with Coupling to An External Bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Doll, J.D.; Myers, L.E.; Adelman, S.A. Generalized Langevin Equation Approach for Atom/Solid-Surface Scattering: Inelastic Studies. J. Chem. Phys. 1975, 63, 4908–4914. [Google Scholar] [CrossRef]
- Adelman, S.A.; Doll, J.D. Generalized Langevin Equation Approach for Atom/Solid-surface Scattering: General Formulation for Classical Scattering off Harmonic Solids. J. Chem. Phys. 1976, 64, 2375–2388. [Google Scholar] [CrossRef]
- Scherer, M.; Trendelkamp-Schroer, B.; Paul, F.; Pérez-Hernández, G.; Hoffmann, M.; Plattner, N.; Wehmeyer, C.; Prinz, J.-H.; Noé, F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015, 11, 5525–5542. [Google Scholar] [CrossRef] [PubMed]
- Zagrovic, B.; van Gunsteren, W.F. Comparing Atomistic Simulation Data with the NMR Experiment: How Much Can NOEs Actually Tell Us? Proteins Struct. Funct. Bioinforma. 2006, 63, 210–218. [Google Scholar] [CrossRef] [Green Version]
- Palmer, A.G. NMR Characterization of the Dynamics of Biomacromolecules. Chem. Rev. 2004, 104, 3623–3640. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, D.; Mueller, G.A.; Schramm, G.; Edwards, L.L.; Petersen, A.; London, R.E.; Haas, H.; Gupta Bhattacharya, S. Primary Identification, Biochemical Characterization, and Immunologic Properties of the Allergenic Pollen Cyclophilin Cat R 1. J. Biol. Chem. 2014, 289, 21374–21385. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, T.; Güntert, P.; Wüthrich, K. Protein NMR Structure Determination with Automated NOE Assignment Using the New Software CANDID and the Torsion Angle Dynamics Algorithm DYANA. J. Mol. Biol. 2002, 319, 209–227. [Google Scholar] [CrossRef] [Green Version]
- Mueller, G.A.; Pari, K.; DeRose, E.F.; Kirby, T.W.; London, R.E. Backbone Dynamics of the RNase H Domain of HIV-1 Reverse Transcriptase. Biochemistry 2004, 43, 9332–9342. [Google Scholar] [CrossRef]
- Farrow, N.A.; Muhandiram, R.; Singer, A.U.; Pascal, S.M.; Kay, C.M.; Gish, G.; Shoelson, S.E.; Pawson, T.; Forman-Kay, J.D.; Kay, L.E. Backbone Dynamics of a Free and a Phosphopeptide-Complexed Src Homology 2 Domain Studied by 15N NMR Relaxation. Biochemistry 1994, 33, 5984–6003. [Google Scholar] [CrossRef]
- d’Auvergne, E.J.; Gooley, P.R. The Use of Model Selection in the Model-Free Analysis of Protein Dynamics. J. Biomol. NMR 2003, 25, 25–39. [Google Scholar] [CrossRef]
- Bieri, M.; d’Auvergne, E.J.; Gooley, P.R. RelaxGUI: A New Software for Fast and Simple NMR Relaxation Data Analysis and Calculation of Ps-Ns and Μs Motion of Proteins. J. Biomol. NMR 2011, 50, 147–155. [Google Scholar] [CrossRef]
- Kleckner, I.R.; Foster, M.P. GUARDD: User-Friendly MATLAB Software for Rigorous Analysis of CPMG RD NMR Data. J. Biomol. NMR 2012, 52, 11–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
| NOE Assigned by CYANA | 1194 |
|---|---|
| Manually assigned NOEs | 171 |
| H-Bond restraints | 38 |
| Dihedral restraints | 194 |
| Backbone RMSD (residues 3–113) | 1.5 Å |
| Ramachandran Space | |
| Most Favored | 80.3 % |
| Additionally Allowed | 19.2 % |
| Generously Allowed | 0.5 % |
| Disallowed | 0 |
| Violations | |
| NOE (<0.2 Å) | 19 |
| Dihedrals | 3 |
| VDW close contacts | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Quintero, M.L.; DeRose, E.F.; Gabel, S.A.; Mueller, G.A.; Liedl, K.R. Nanobody Paratope Ensembles in Solution Characterized by MD Simulations and NMR. Int. J. Mol. Sci. 2022, 23, 5419. https://doi.org/10.3390/ijms23105419
Fernández-Quintero ML, DeRose EF, Gabel SA, Mueller GA, Liedl KR. Nanobody Paratope Ensembles in Solution Characterized by MD Simulations and NMR. International Journal of Molecular Sciences. 2022; 23(10):5419. https://doi.org/10.3390/ijms23105419
Chicago/Turabian StyleFernández-Quintero, Monica L., Eugene F. DeRose, Scott A. Gabel, Geoffrey A. Mueller, and Klaus R. Liedl. 2022. "Nanobody Paratope Ensembles in Solution Characterized by MD Simulations and NMR" International Journal of Molecular Sciences 23, no. 10: 5419. https://doi.org/10.3390/ijms23105419
APA StyleFernández-Quintero, M. L., DeRose, E. F., Gabel, S. A., Mueller, G. A., & Liedl, K. R. (2022). Nanobody Paratope Ensembles in Solution Characterized by MD Simulations and NMR. International Journal of Molecular Sciences, 23(10), 5419. https://doi.org/10.3390/ijms23105419






