The Interplay between the Theories of Mode Coupling and of Percolation Transition in Attractive Colloidal Systems
Abstract
1. Introduction
2. Schematic Models
2.1. Ideal MCT
2.2. Basic PT
3. Revised MCT Including Hopping Processes and Fragile to Strong Dynamic Crossover (FSC)
3.1. Hopping in the Memory Kernel
3.2. Hopping in the Correlator
4. The Interplay between Percolation and MCT
4.1. Kinetic Facilitated Models and Bootstrap Percolation
4.1.1. Decay to the Plateau by Using the Cluster Approach
4.1.2. Departure from the Plateau Using the Damage Spreading Mechanism
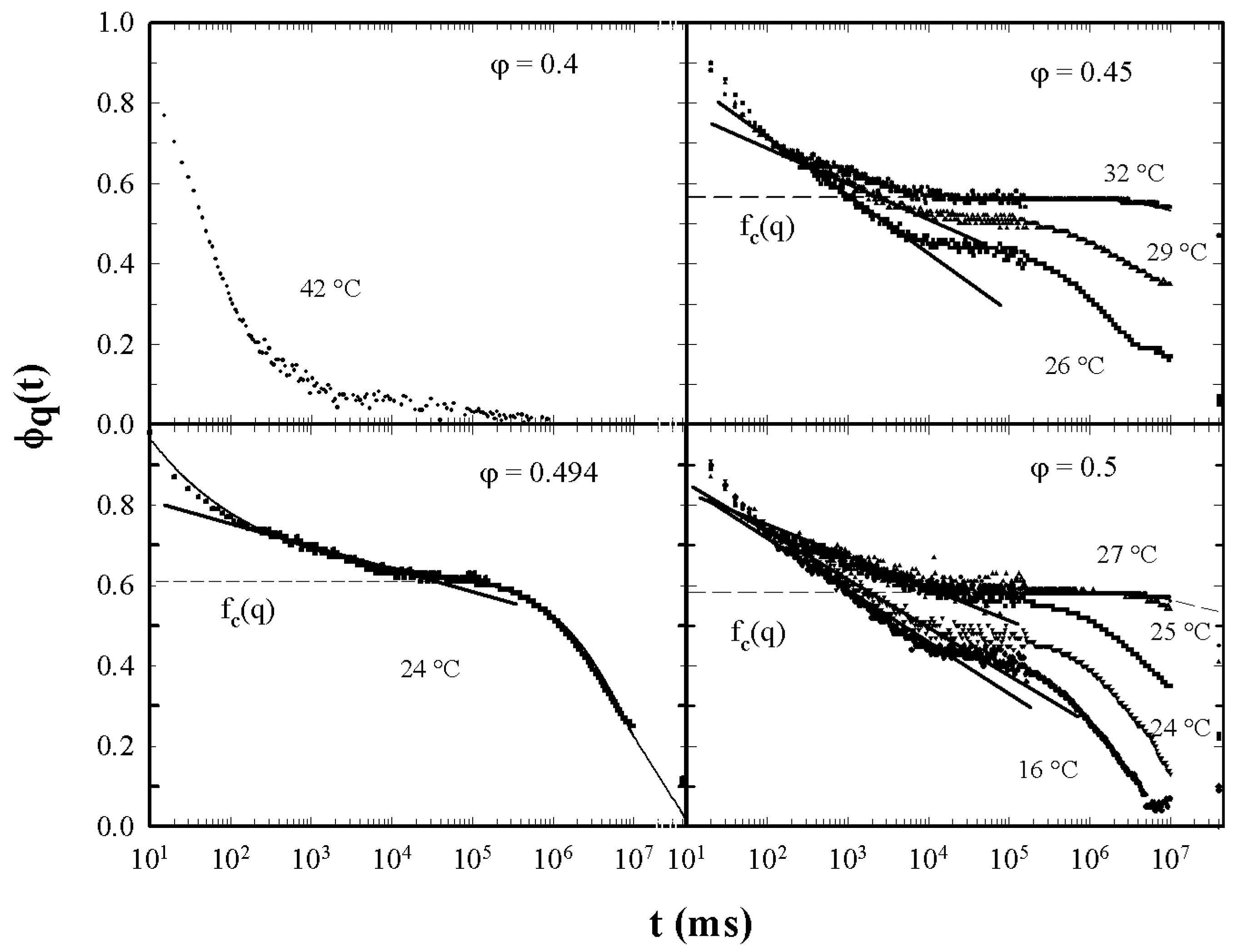
4.2. Comparison with Discontinuous MCT Model B
4.2.1. Fluctuations of the Order Parameter
4.2.2. Comparison with MCT
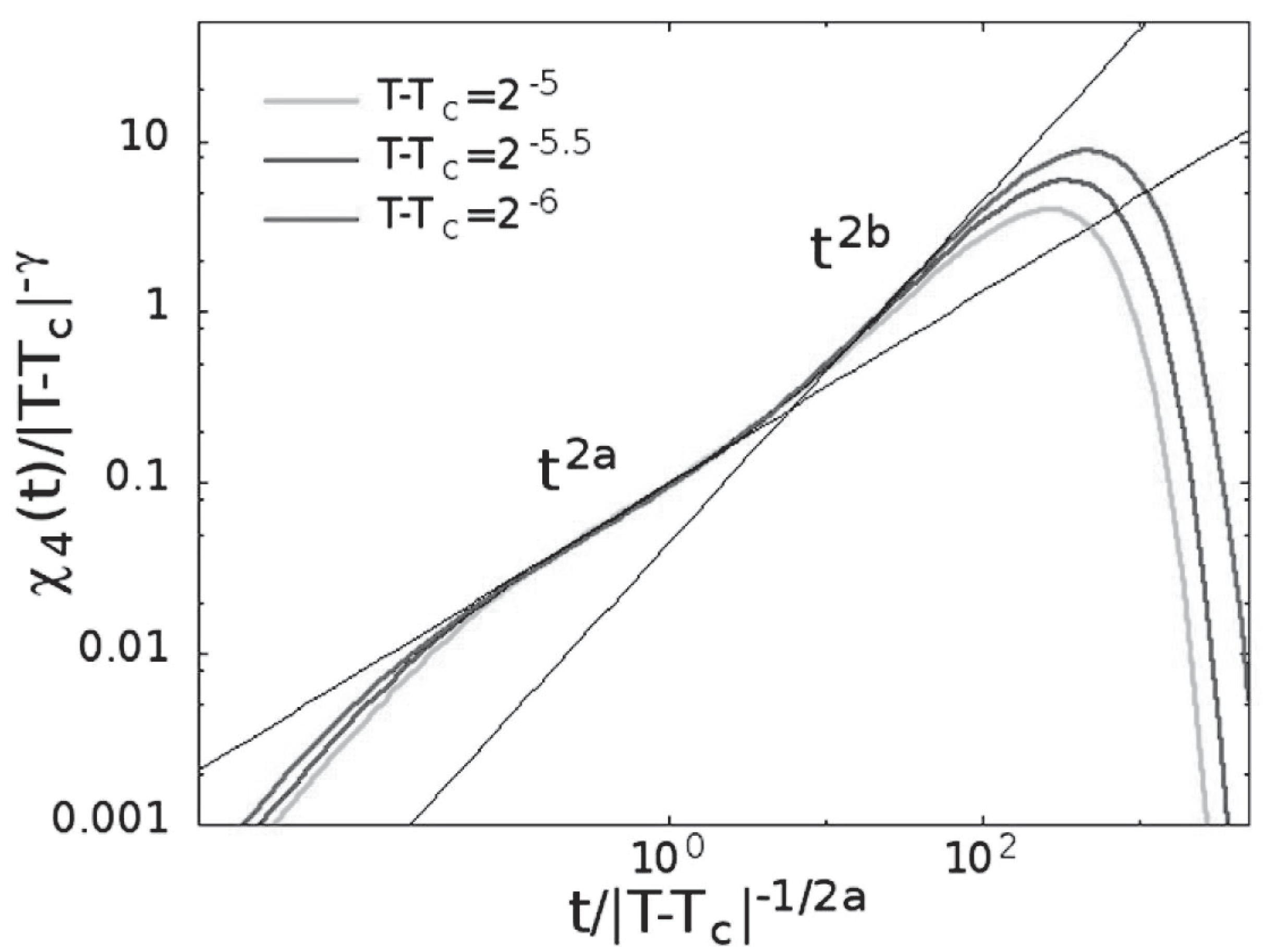
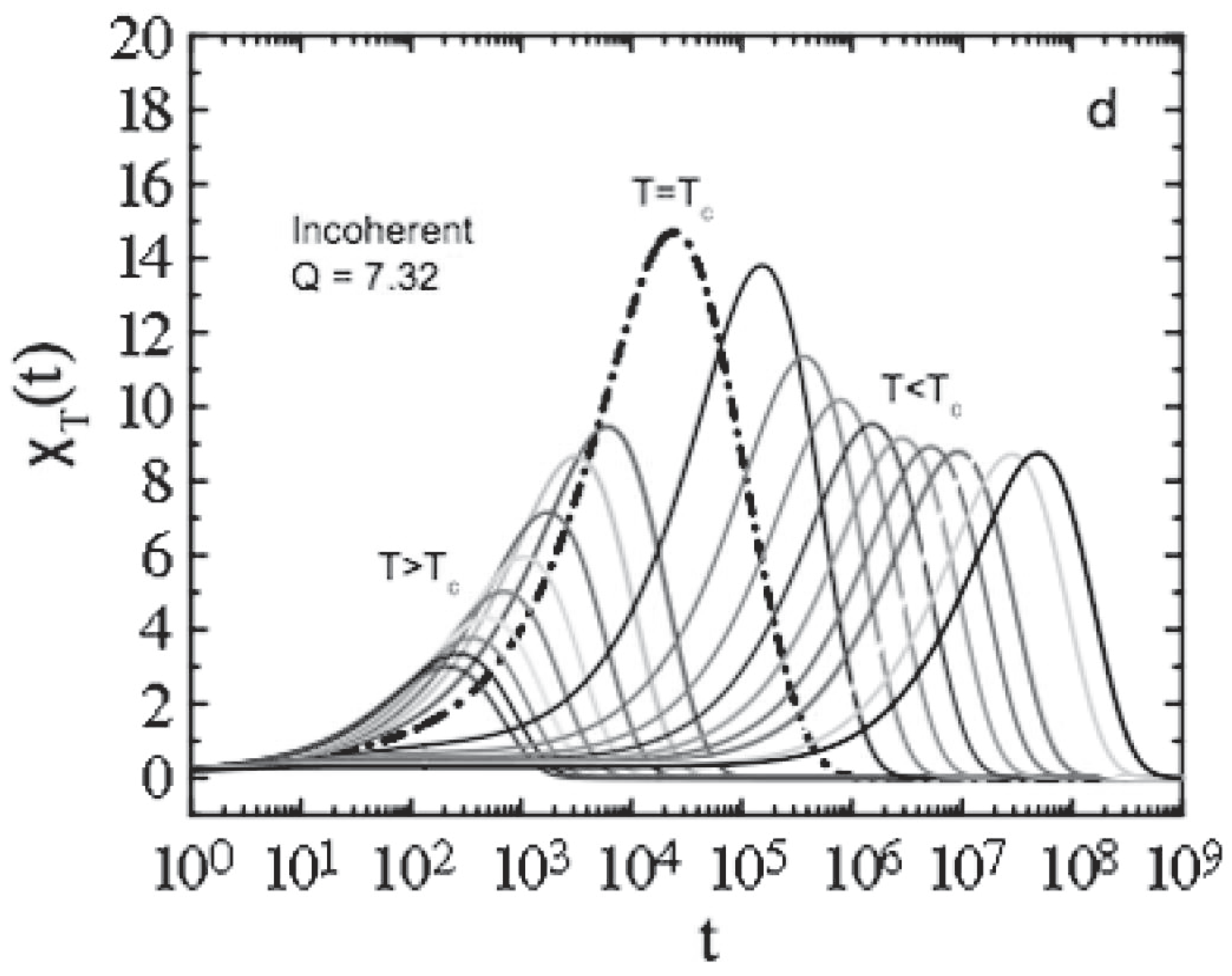
4.3. The Related Main Findings
4.3.1. From Theory and MD Simulations
4.3.2. From Experimental Data (a) Hopping in the Memory Kernel
4.3.3. From Experimental Data (b) Hopping in the Correlator
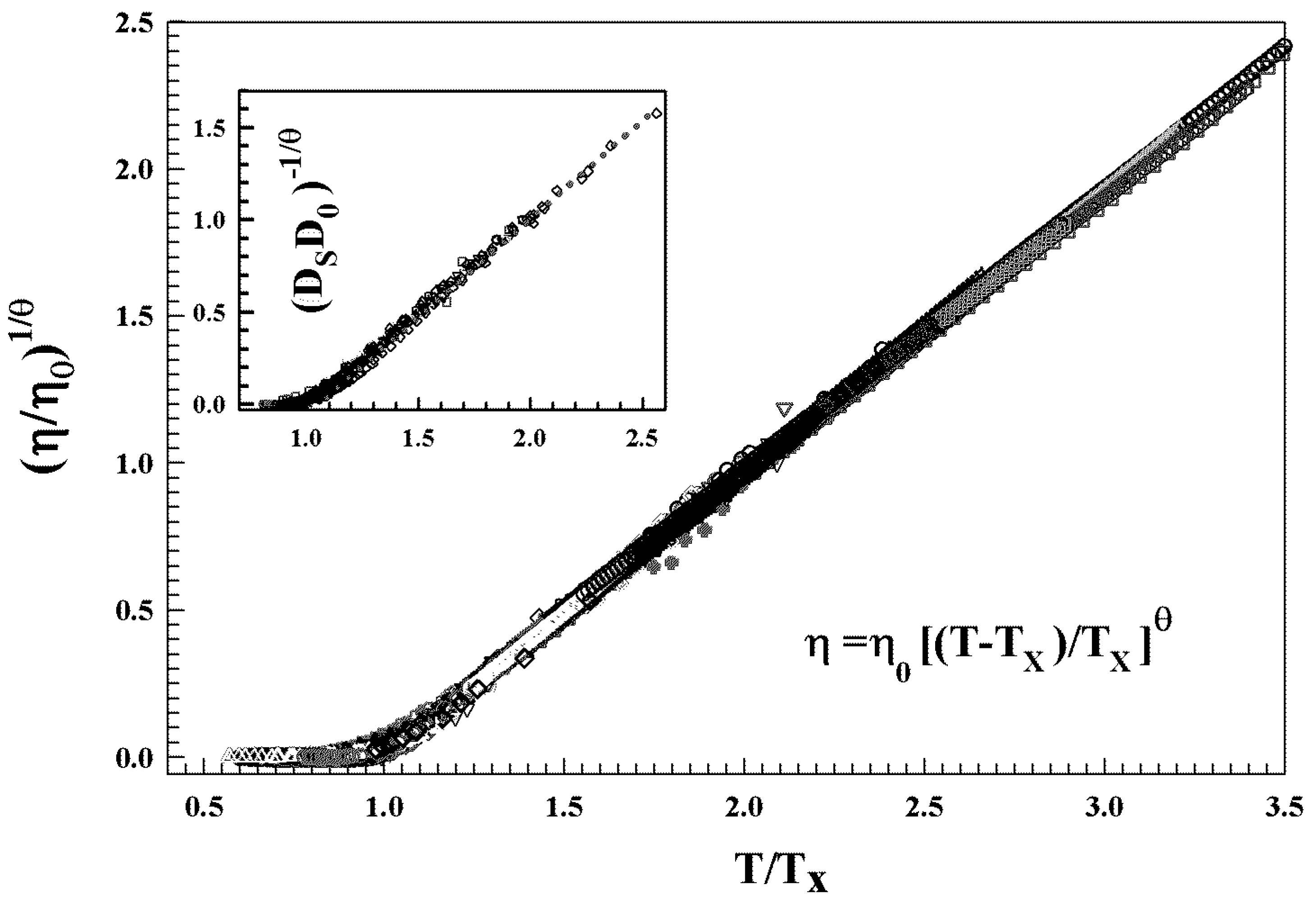
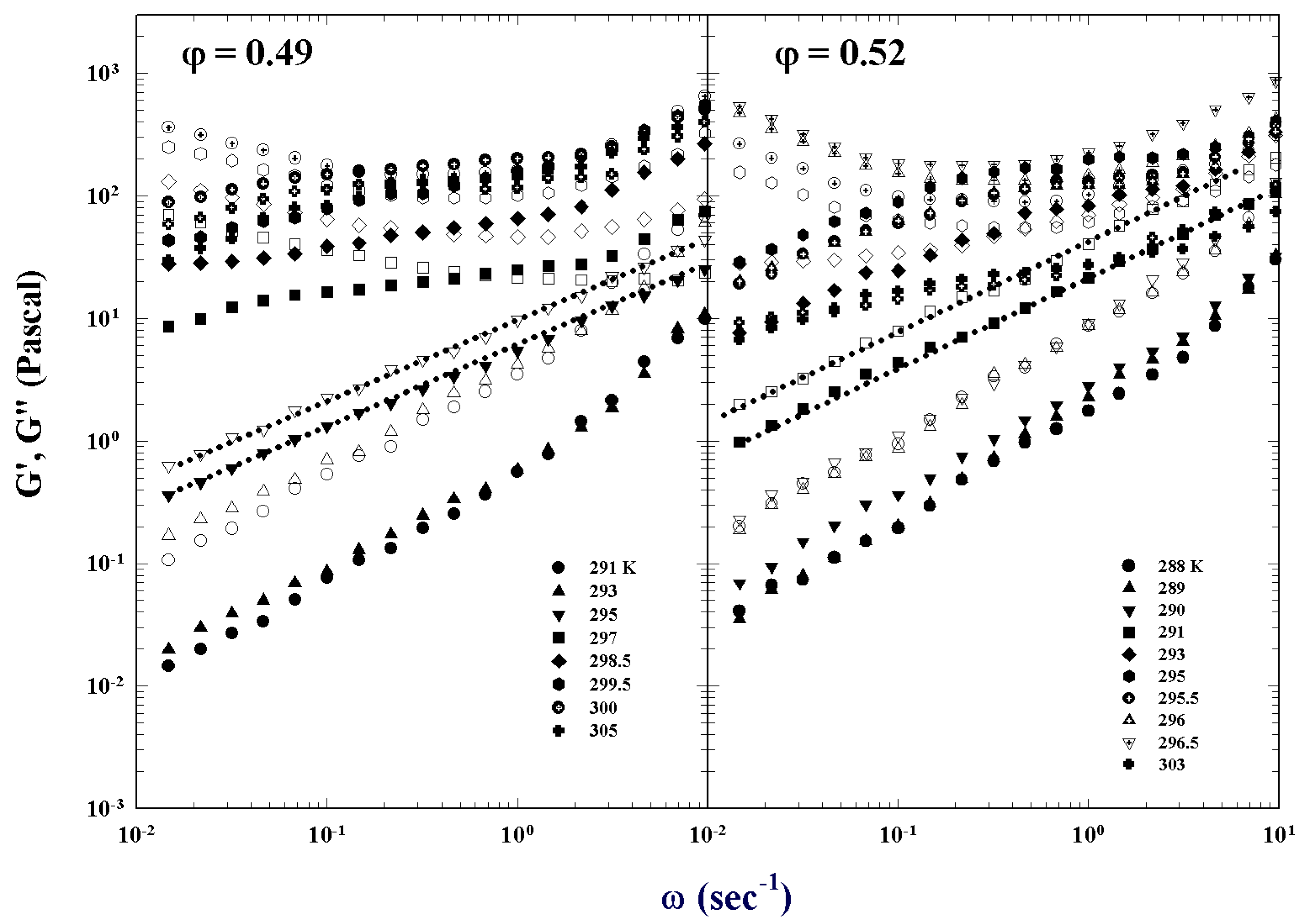
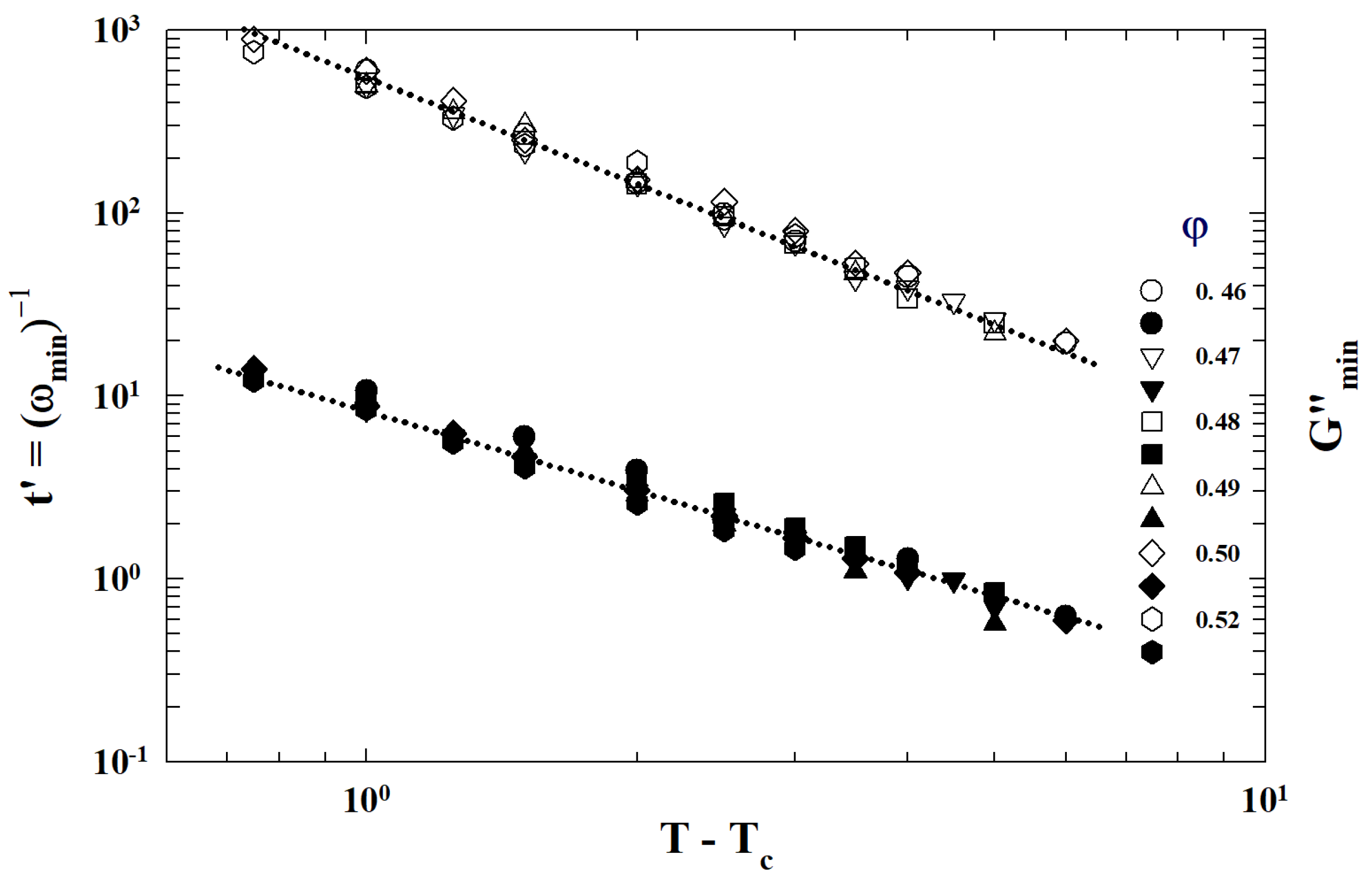
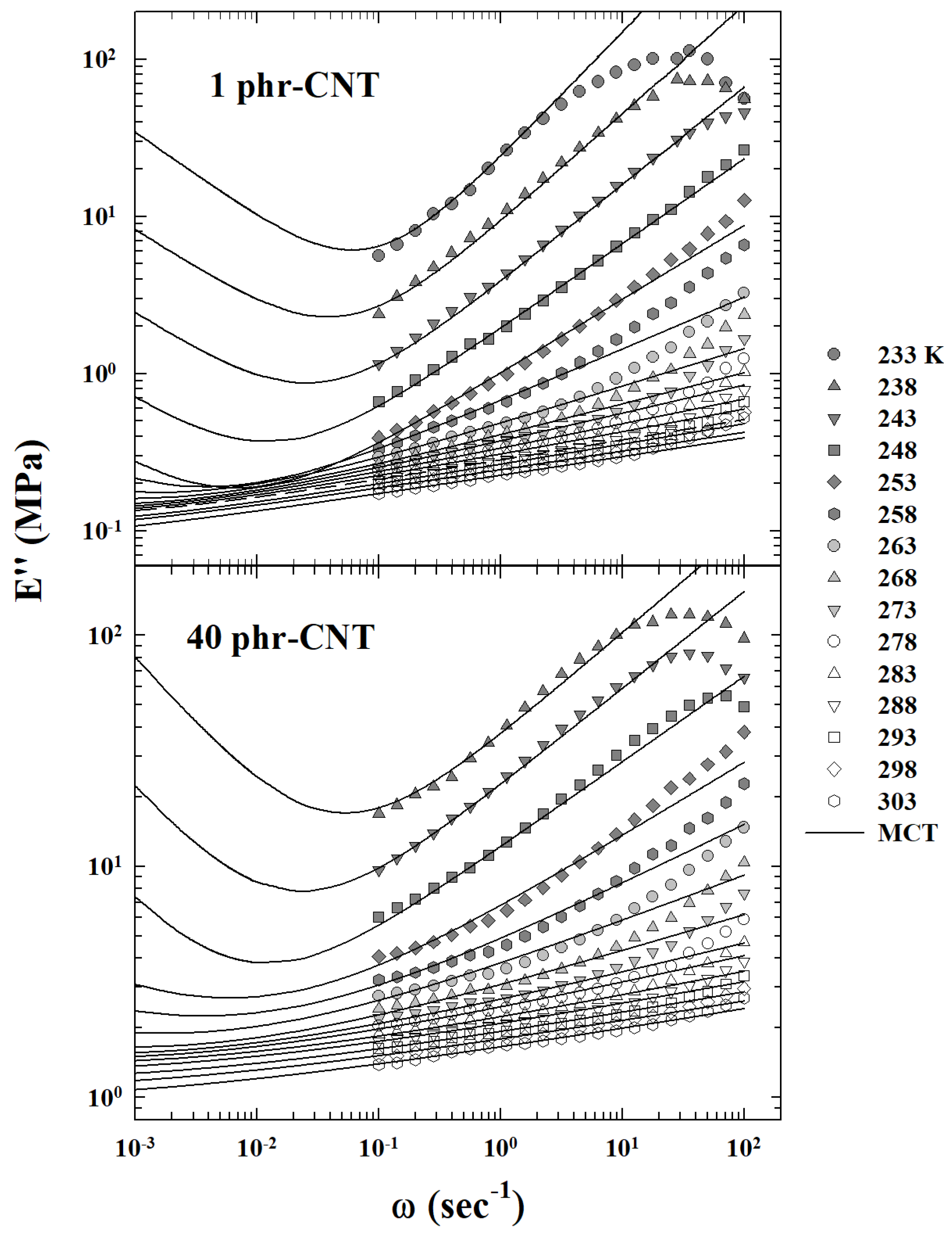
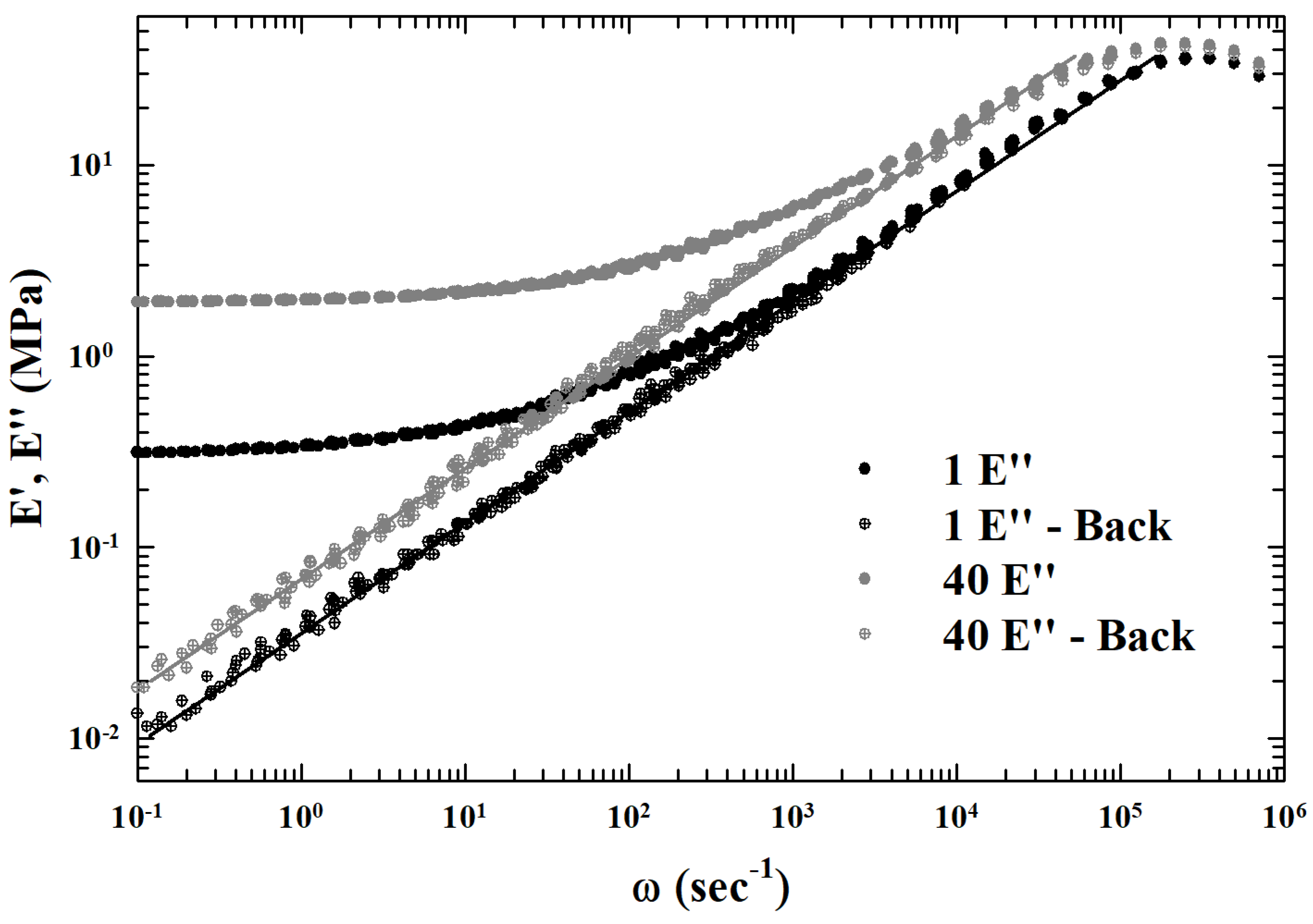
5. Viscoelasticity
5.1. MCT
5.2. Percolation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stanley, H.E. Introduction to Phase Transition and Critical Phenomena; Oxford University Press: Oxford, UK, 1971. [Google Scholar]
- Kawasaki, K. Kinetic equations and time correlation functions of critical fluctuations. Ann. Phys. 1970, 61, 1–56. [Google Scholar] [CrossRef]
- Kadanoff, L.P.; Swift, J. Transport coefficients near the critical point: A master-equation approach. Phys. Rev. 1968, 165, 310–322. [Google Scholar] [CrossRef]
- Halperin, B.I.; Hohemberg, P.C. Generalization of scaling laws to dynamical properties of a system near its critical point. Phys. Rev. Lett. 1967, 19, 700–703. [Google Scholar] [CrossRef]
- Flory, P.J. Principles of Polymer Chemistry; Cornell University Press: Ithaca, NY, USA, 1953. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon: Oxford, UK, 1986. [Google Scholar]
- de Gennes, P.G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1993. [Google Scholar]
- Fixman, M. Viscosity of critical mixtures. J. Chem. Phys. 1962, 36, 310–318. [Google Scholar] [CrossRef]
- Keyes, T. Statistical Mechanics, Part B: Time-Dependent Processes; Berne, B.J., Ed.; Plenum Press: New York, NY, USA, 1977; p. 59. [Google Scholar]
- Götze, W. Complex Dynamics of Glass-Forming Liquids; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Boon, J.P.; Yip, S. Molecular Hydrodynamics; Mc-Graw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Bengtzelius, U.; Götze, W.; Sjolander, A. Dynamics of supercooled liquids and the glass transition. J. Phys. C 1984, 17, 5915–5934. [Google Scholar] [CrossRef]
- Leutheusser, E. Dynamical model of the liquid-glass transition. Phys. Rev. A 1984, 29, 2765–2773. [Google Scholar] [CrossRef]
- Anderson, P.W. Through the glass lightly. Science 1995, 267, 1615. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J.H. On the Temperature Dependence of Cooperative Relaxation Properties in Glass-Forming Liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef]
- Angell, C.A. Perspective on the glass-transition. J. Phys. Chem. Solids 1988, 49, 863–871. [Google Scholar] [CrossRef]
- Stillinger, F.H. Supercooled liquids, glass transitions, and the Kauzmann paradox. J. Chem. Phys. 1988, 88, 7818–7825. [Google Scholar] [CrossRef]
- Stillinger, F.H.; Debenedetti, P.G. Energy landscape diversity and supercooled liquid properties. J. Chem. Phys. 2002, 116, 3353. [Google Scholar] [CrossRef]
- Yip, S.; Short, M.P. Multiscale materials modelling at the mesoscale. Nat. Mat. 2013, 12, 774. [Google Scholar] [CrossRef] [PubMed]
- Liao, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
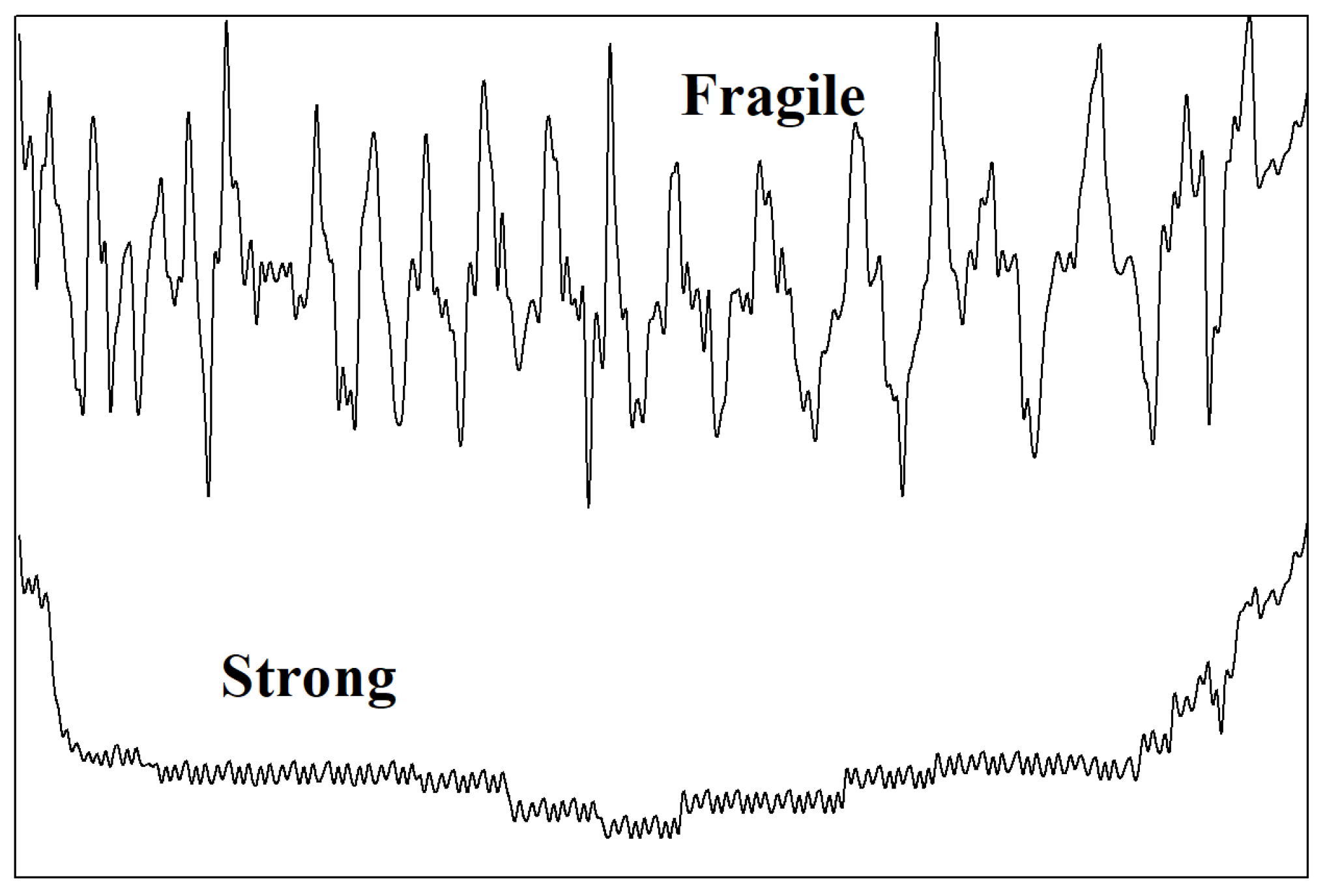
- Mallamace, F.; Branca, C.; Corsaro, C.; Leone, N.; Spooren, J.; Chen, S.-H.; Stanley, H.E. Transport properties of glass-forming liquids suggest that dynamic crossover temperature is as important as the glass transition temperature. Proc. Natl Acad. Sci. USA 2010, 28, 22457–22462. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Osetsky, Y.; Yip, S.; Yildiz, B. Onset mechanism of strain-rate-induced flow stress upturn. Phys. Rev. Lett. 2012, 109, 135503. [Google Scholar] [CrossRef]
- Götze, W.; Sjögren, L. The glass transition singularity. Z. Phys. B 1987, 65, 415–427. [Google Scholar] [CrossRef]
- Götze, W.; Voigtmann, T. Universal and nonuniversal features of glassy relaxation in propylene carbonate. Phys. Rev. E 2000, 61, 4133–4147. [Google Scholar] [CrossRef]
- Chong, S.H. Connections of activated hopping processes with the breakdown of the Stokes-Einstein relation and with aspects of dynamical heterogeneities. Phys. Rev. E 2008, 78, 041501. [Google Scholar] [CrossRef]
- Arenzon, J.J.; Coniglio, A.; Fierro, A.; Sellitto, M. Percolation approach to glassy dynamics with continuously broken ergodicity. Phys. Rev. E 2014, 90, 020301. [Google Scholar] [CrossRef]
- Cicerone, M.T.; Ediger, M.D. Enhanced translation of probe molecules in supercooled o-terphenyl: Signature of spatially heterogeneous dynamics? J. Chem. Phys. 1996, 104, 7210–7218. [Google Scholar] [CrossRef]
- Cicerone, M.T.; Blackburn, F.R.; Ediger, M.D. Anomalous diffusion of probe molecules in polystyrene: Evidence for spatially heterogeneous segmental dynamics. Macromolecules 1995, 28, 8224. [Google Scholar] [CrossRef]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor & Francis: Abingdon, UK, 1992; p. 192. [Google Scholar]
- Fierro, A.; Abete, T.; Coniglio, A. Static and Dynamic Heterogeneities in a Model for Irreversible Gelation. J. Chem. Phys. 2009, 131, 194906. [Google Scholar] [CrossRef]
- Götze, W.; Sjogren, L. Relaxation processes in supercooled liquids. Rep. Prog. Phys. 1992, 55, 241. [Google Scholar] [CrossRef]
- Pusey, P.N.; van Megen, W. Observation of a glass transition in suspensions of spherical colloidal particles. Phys. Rev. Lett. 1987, 59, 2083. [Google Scholar] [CrossRef]
- Kob, W.; Andersen, H.C. Testing mode-coupling theory for a supercooled binary Lennard-Jones mixture. II. Intermediate scattering function and dynamic susceptibility. Phys. Rev. E 1995, 51, 4134. [Google Scholar] [CrossRef] [PubMed]
- Dawson, K.; Foffi, G.; Fuchs, M.; Götze, W.; Sciortino, F.; Sperl, M.; Tartaglia, P.; Voigtmann, T.; Zaccarelli, E. Higher-order glass-transition singularities in colloidal systems with attractive interactions. Phys. Rev. E 2000, 63, 011401. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F.; Gambadauro, P.; Micali, N.; Tartaglia, P.; Liao, C.; Chen, S.H. Kinetic Glass Transition in a Micellar System with Short-Range Attractive Interaction. Phys. Rev. Lett. 2000, 84, 5431–5434. [Google Scholar] [CrossRef]
- Pham, K.N.; Puertas, A.M.; Bergenholtz, J.; Egelhaaf, S.U.; Moussaid, A.; Pusey, P.N.; Schofield, A.B.; Cates, M.E.; Fuchs, M.; Poon, W.C.K. Multiple Glassy States in a Simple Model System. Science 2002, 296, 104. [Google Scholar] [CrossRef]
- Chen, S.H.; Chen, W.R.; Mallamace, F. The Glass-to-Glass Transition and Its End Point in a Copolymer Micellar System. Science 2003, 300, 619. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Stanley, H.E.; Mallamace, D.; Chen, S.H. The dynamical crossover in attractive colloidal systems. J. Chem. Phys. 2013, 193, 214502. [Google Scholar] [CrossRef]
- Stevenson, J.D.; Walczak, A.; Hall, R.W.; Wolynes, P.G. Constructing explicit magnetic analogies for the dynamics of glass forming liquids. J. Chem. Phys. 2008, 129, 194505. [Google Scholar] [CrossRef] [PubMed]
- Biroli, G.; Cammarota, C.; Tarjus, G.; Tarzia, M. Random-field-like criticality in glass-forming liquids. Phys. Rev. Lett. 2014, 112, 175701. [Google Scholar] [CrossRef]
- Fuchs, M.; Hofacker, I. Latz, Primary relaxation in a hard-sphere system A. Phys. Rev. A 1992, 45, 898–912. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R. Memory Effects in Irreversible Thermodynamics. Phys. Rev. 1961, 124, 983. [Google Scholar] [CrossRef]
- Mori, H. A Continued-Fraction Representation of the Time-Correlation Functions. Prog. Theor. Phys. 1965, 34, 399–416. [Google Scholar] [CrossRef]
- Götze, W.; Sperl, M. Logarithmic relaxation in glass-forming systems. Phys. Rev. E 2002, 66, 011405. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Andersen, H.C. Kinetic Ising model of the glass transition. Phys. Rev. Lett. 1984, 53, 1244–1247. [Google Scholar] [CrossRef]
- Sellitto, M.; Biroli, G.; Toninelli, C. Facilitated spin models on Bethe lattice: Bootstrap percolation, mode-coupling transition and glassy dynamics. Europhys. Lett. 2005, 69, 496–502. [Google Scholar] [CrossRef]
- de Candia, A.; Fierro, A.; Coniglio, A. Scaling and universality in glass transition. Sci. Rep. 2016, 6, 26481. [Google Scholar] [CrossRef]
- Lobry, L.; Micali, N.; Mallamace, F.; Liao, C.; Chen, S.H. Interaction and percolation in the L64 triblock copolymer micellar system. Phys. Rev. E 1999, 60, 7076–7087. [Google Scholar] [CrossRef]
- Chen, W.R.; Mallamace, F.; Glinka, C.J.; Fratini, E.; Chen, S.H. Neutron- and light-scattering studies of the liquid-to-glass and glass-to-glass transitions in dense copolymer micellar solutions. Phys. Rev. E 2003, 68, 041402. [Google Scholar] [CrossRef]
- Fisher, M.E. Magnetic Critical Point Exponents–Their Interrelations and Meaning. J. Appl. Phys. 1967, 38, 981. [Google Scholar] [CrossRef]
- Fisher, M.E.; Widom, B. Decay of Correlations in Linear Systems. J. Chem. Phys. 1969, 50, 3756. [Google Scholar] [CrossRef]
- Stauffer, D. Scaling theory of percolation clusters. Phys. Rep. 1979, 54, 1–74. [Google Scholar] [CrossRef]
- Franosch, T.; Fuchs, M.; Götze, W.; Mayr, M.R.; Singh, A.P. Theory for the reorientational dynamics in glass-forming liquids. Phys. Rev. E 1997, 56, 5659–5674. [Google Scholar] [CrossRef]
- Chong, S.H.; Götze, W.; Singh, A.P. Mode-coupling theory for the glassy dynamics of a diatomic probe molecule immersed in a simple liquid. Phys. Rev. E 2000, 63, 011206. [Google Scholar] [CrossRef]
- Ritter von Schweidler, E. Studien über die Anomalien im Verhalten der Dielektrika. Ann. Phys. 1907, 24, 711–770. [Google Scholar] [CrossRef]
- Blochowicz, T.; Rössler, E.A. Beta relaxation versus high frequency wing in the dielectric spectra of a binary molecular glass former. Phys. Rev. Lett. 2004, 92, 225701. [Google Scholar] [CrossRef]
- Dreyfus, C.; Lebon, M.J.; Cummins, H.Z.; Toulouse, J.; Bonello, B.; Pick, R.M. Brillouin scattering in salol: Determining Tc of the mode coupling theory. Phys. Rev. Lett. 1992, 69, 3666–3669. [Google Scholar] [CrossRef]
- Yang, Y.; Nelson, K.A. Impulsive stimulated thermal anomaly in Ca0.4K0.6(NO3)1.4. J. Chem. Phys. 1996, 104, 5429. [Google Scholar] [CrossRef]
- Wiedersich, J.; Surovtsev, N.V.; Rössler, E. A comprehensive light scattering study of the glass former toluene. J. Chem. Phys. 2000, 113, 1143–1153. [Google Scholar] [CrossRef]
- Adichtchev, S.V.; Benkhof, S.; Blochowicz, T.; Novikov, V.N.; Rössler, E.A.; Tschirwitz, C.; Wiedersich, J. Anomaly of the nonergodicity parameter and crossover to white noise in the fast relaxation spectrum of a simple glass former. Phys. Rev. Lett. 2002, 88, 055703. [Google Scholar] [CrossRef] [PubMed]
- Götze, W.; Mayr, M.R. Evolution of vibrational excitations in glassy systems. Phys. Rev. E 2000, 61, 587–606. [Google Scholar] [CrossRef] [PubMed]
- Bartsch, A.; Rätzke, K.; Meyer, A.; Faupel, F. Dynamic arrest in multicomponent glass-forming alloys. Phys. Rev. Lett. 2010, 104, 195901. [Google Scholar] [CrossRef] [PubMed]
- Du, W.M.; Li, G.; Cummins, H.Z.; Fuchs, M.; Toulouse, J.; Knauss, L.A. Light-scattering study of the liquid-glass transition in propylene carbonate. Phys. Rev. E 1994, 49, 2192–2205. [Google Scholar] [CrossRef] [PubMed]
- Hinze, G.; Brace, D.D.; Gottke, S.D.; Fayer, M.D. A detailed test of mode-coupling theory on all time scales: Time domain studies of structural relaxation in a supercooled liquid. J. Chem. Phys. 2000, 113, 3723–3733. [Google Scholar] [CrossRef][Green Version]
- Krakoviack, V.; Alba-Simionesco, C. What can be learned from the schematic mode-coupling approach to experimental data? J. Chem. Phys. 2002, 117, 2161–2171. [Google Scholar] [CrossRef]
- Bhattacharyya, S.M.; Bagchi, B.; Wolynes, P.G. Bridging the gap between the mode coupling and the random first order transition theories of structural relaxation in liquids. Phys. Rev. E 2005, 72, 031509. [Google Scholar] [CrossRef]
- Chong, S.H.; Chen, S.H.; Mallamace, F. A possible scenario for the fragile-to-strong dynamic crossover predicted by the extended mode-coupling theory for glass transition. J. Phys. Cond. Matter 2009, 21, 504101. [Google Scholar] [CrossRef]
- Chen, S.H.; Zhang, Y.; Lagi, M.; Chong, S.H.; Baglioni, P.; Mallamace, F. Evidence of dynamic crossover phenomena in water and other glass-forming liquids: Experiments, MD simulations and theory. J. Phys. Cond. Matter 2009, 21, 504102. [Google Scholar] [CrossRef]
- Cates, M.E.; Ramaswamy, S. Do current-density nonlinearities cut off the glass transition? Phys. Rev. Lett. 2006, 96, 135701. [Google Scholar] [CrossRef] [PubMed]
- Greenall, M.; Cates, M.E. Crossover behavior and multistep relaxation in a schematic model of the cut-off glass transition. Phys. Rev. E 2007, 75, 051503. [Google Scholar] [CrossRef] [PubMed]
- Mayer, P.; Miyazaki, K.; Reichman, D.R. Cooperativity beyond caging: Generalized mode-coupling theory. Phys. Rev. Lett. 2006, 97, 095702. [Google Scholar] [CrossRef]
- Domschke, M.; Marsilius, M.; Blochowicz, T.; Voigtmann, T. Glassy relaxation and excess wing in mode-coupling theory: The dynamic susceptibility of propylene carbonate above and below. Phys. Rev. E 2011, 84, 031506. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Chen, S.H.; Faraone, A.; Yen, C.W.; Mou, C.Y. Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water. Phys. Rev. Lett. 2005, 95, 117802. [Google Scholar] [CrossRef] [PubMed]
- Mallamace, F.; Broccio, M.; Corsaro, C.; Faraone, A.; Wanderlingh, U.; Liu, L.; Mou, C.Y.; Chen, S.H. The fragile-to-strong dynamic crossover transition in confined water: Nuclear magnetic resonance results. J. Chem. Phys. 2006, 124, 161102. [Google Scholar] [CrossRef]
- Taborek, P.; Kleiman, R.N.; Bishop, D.J. Power-law behavior in the viscosity of supercooled liquids. J. Phys. Rev. B 1986, 34, 1835–1840. [Google Scholar] [CrossRef]
- Rössler, E. Corresponding states analysis for viscosity and nuclear magnetic resonance data in the glass transition regime. J. Chem. Phys. 1990, 92, 3725–3735. [Google Scholar] [CrossRef]
- Zöllmer, V.; Rätzke, K.; Faupel, F.; Meyer, A. Diffusion in a metallic melt at the critical temperature of mode coupling theory. Phys. Rev. Lett. 2003, 90, 195502. [Google Scholar] [CrossRef]
- Faupel, F.; Frank, W.; Macht, M.P.; Mehrer, H.; Naundorf, V.; Rätzke, K.; Schober, H.R.; Sharma, S.K.; Teichler, H. Diffusion in metallic glasses and supercooled melts. Rev. Mod. Phys. 2003, 75, 237. [Google Scholar] [CrossRef]
- Angell, C.A. Mechanical stress relaxation in inorganic glasses studied by a step-strain technique. J. Non-Cryst. Solids 1991, 131–133, 13. [Google Scholar] [CrossRef]
- Fuchs, M. The Kohlrausch law as a limit solution to mode coupling equations. J. Non-Cryst. Solids 1994, 172–174, 241–247. [Google Scholar] [CrossRef]
- Williams, G.; Fournier, J. The determination of apparent memory functions from dielectric relaxation data for amorphous polymers and glass-forming liquids: Theory and experiment. J. Chem. Phys. 1996, 104, 5690. [Google Scholar] [CrossRef]
- Sjörgen, L. Regenerative processes in supercooled liquids and glasses. Physica A 2003, 322, 81–117. [Google Scholar]
- Tokuyama, M.; Mori, H. Statistical-Mechanical Theory of Random Frequency Modulations and Generalized Brownian Motions. Prog. Theor. Phys. 1976, 55, 411–429. [Google Scholar] [CrossRef]
- Götze, W.; Voigtmann, T. Effect of composition changes on the structural relaxation of a binary mixture. Phys. Rev. E 2003, 67, 021502. [Google Scholar] [CrossRef]
- Schweizer, K.S.; Saltzman, E.J. Entropic barriers, activated hopping, and the glass transition in colloidal suspensions. J. Chem. Phys. 2003, 119, 1181–1196. [Google Scholar] [CrossRef]
- Brambilla, G.; El Masri, D.; Pierno, M.; Berthier, L.; Cipelletti, L.; Petekidis, G.; Schofield, A.B. Probing the equilibrium dynamics of colloidal hard spheres above the mode-coupling glass transition. Phys. Rev. Lett. 2009, 102, 085703. [Google Scholar] [CrossRef]
- Sjögren, L. Diffusion of impurities in a dense fluid near the glass transition. Phys. Rev. A 1986, 33, 1254–1260. [Google Scholar] [CrossRef]
- Heesemann, A.; Zöllmer, V.; Rätzke, K.; Faupel, F. Evidence of highly collective co diffusion in the whole stability range of co-zr glasses. Phys. Rev. Lett. 2000, 84, 1467–1470. [Google Scholar] [CrossRef]
- Gapiński, J.; Steffen, W.; Patkowski, A.; Sokolov, A.P.; Kisliuk, A.; Buchenau, U.; Russina, M.; Mezei, F.; Schober, H. Spectrum of fast dynamics in glass forming liquids: Does the “knee” exist? J. Chem. Phys. 1999, 110, 2312. [Google Scholar] [CrossRef][Green Version]
- Kohlrausch, R. Theorie des elektrischen Rü ckstandes in der Leidener Flasche. Ann. Physik 1854, 164, 56. [Google Scholar] [CrossRef]
- Schneider, U.; Lunkenheimer, P.; Brand, R.; Loidl, A. Broadband dielectric spectroscopy on glass-forming propylene carbonate. Phys. Rev. E 1999, 59, 6924–6936. [Google Scholar] [CrossRef] [PubMed]
- de Candia, A.; Fierro, A.; Pastore, R.; Pica Ciamarra, M.; Coniglio, A. Relaxation functions and dynamical heterogeneities in a model of chemical gel interfering with glass transition. Eur. Phys. J. Spec. Top. 2017, 226, 323–329. [Google Scholar] [CrossRef][Green Version]
- Toninelli, C.; Wyart, M.; Berthier, L.; Biroli, G.; Bouchaud, J.P. Dynamical susceptibility of glass formers: Contrasting the predictions of theoretical scenarios. Phys. Rev. E 2005, 71, 041505. [Google Scholar] [CrossRef] [PubMed]
- Pastore, R.; Coniglio, A.; Pica Ciamarra, M. Dynamical Correlation Length and Relaxation Processes in a Glass Former. Phys. Rev. Lett. 2011, 107, 065703. [Google Scholar] [CrossRef]
- Baxter, G.J.; Dorogovtsev, S.N.; Goltsev, A.V.; Mendes, J.F.F. Heterogeneous k-core versus bootstrap percolation on complex networks. Phys. Rev. E 2011, 83, 051134. [Google Scholar] [CrossRef]
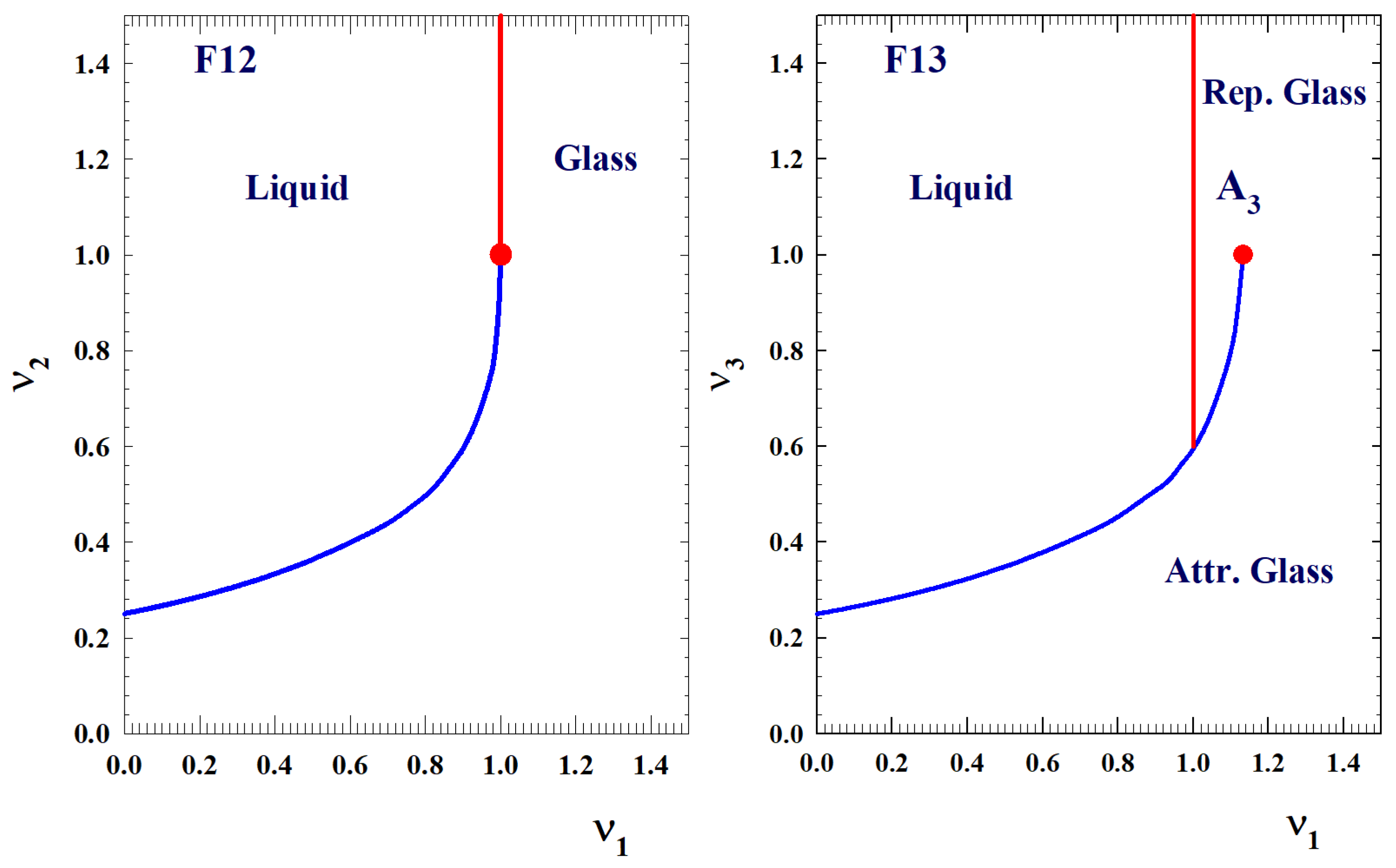
- Arenzon, J.J.; Sellitto, M. Microscopic models of mode-coupling theory: The F12 scenario. J. Chem. Phys. 2012, 137, 084501. [Google Scholar] [CrossRef]
- Sellitto, M. Crossover from beta to alpha Relaxation in Cooperative Facilitation Dynamics. Phys. Rev. Lett. 2015, 115, 225701. [Google Scholar] [CrossRef]
- Dorogovtsev, S.N.; Goltsev, A.V.; Mendes, J.F.F. Critical phenomena in complex networks. Rev. Mod. Phys. 2008, 80, 1275–1335. [Google Scholar] [CrossRef]
- Baxter, G.J.; Dorogovtsev, S.N.; Lee, K.E.; Mendes, J.F.F.; Goltsev, A.V. Critical dynamics of the k–core pruning process. Phys. Rev. X 2015, 5, 031017. [Google Scholar]
- Bennemann, C.; Donati, C.; Baschnagel, J.; Glotzer, S.C. Growing range of correlated motion in a polymer melt on cooling towards the glass transition. Nature 1999, 399, 246. [Google Scholar] [CrossRef]
- Berthier, L.; Biroli, G.; Bouchaud, J.P.; Cipelletti, L.; El Masrid, D.; L’Hotef, D.; Ladiem, F.; Pierno, M. Direct experimental evidence of a growing length scale accompanying the glass transition. Science 2005, 310, 1797. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, P.; Berthier, L.; Kob, W. Universal nature of particle displacements close to glass and jamming transitions. Phys. Rev. Lett. 2007, 99, 060604. [Google Scholar] [CrossRef] [PubMed]
- Pan, A.C.; Garrahan, J.P.; Chandler, D. Heterogeneity and growing length scales in the dynamics of kinetically constrained lattice gases in two dimensions. Phys. Rev. E 2005, 72, 041106. [Google Scholar] [CrossRef] [PubMed]
- Biroli, G.; Bouchaud, J.P. Diverging length scale and upper critical dimension in the Mode-Coupling Theory of the glass transition. Europhys. Lett. 2004, 67, 21. [Google Scholar] [CrossRef]
- Berthier, L.; Biroli, G.; Bouchaud, J.P.; Kob, W.; Miyazaki, K.; Reichman, D.R. Spontaneous and induced dynamic correlations in glass formers. II. Model calculations and comparison to numerical simulations. J. Chem. Phys. 2007, 126, 184504. [Google Scholar] [CrossRef]
- Fierro, A.; de Candia, A.; Coniglio, A. Interplay between the glass and the gel transition. Sci. China-Phys. Mech. Astron. 2019, 62, 107007. [Google Scholar] [CrossRef]
- de Candia, A.; Del Gado, E.; Fierro, A.; Sator, N.; Coniglio, A. Colloidal gelation, percolation and structural arrest. Physica A 2005, 358, 239–249. [Google Scholar] [CrossRef]
- Fierro, A.; Del Gado, E.; de Candia, A.; Coniglio, A. Dynamical heterogeneities in attractive colloids. J. Stat. Mech. 2008, 4, L04002. [Google Scholar] [CrossRef]
- Pastore, R.; de Candia, A.; Fierro, A.; Pica Ciamarra, M.; Coniglio, A. Cluster structure and dynamics in gels and glasses. J. Stat. Mech. 2016, 7, 074011. [Google Scholar] [CrossRef][Green Version]
- Sciortino, F.; Tartaglia, P.; Zaccarelli, E. One-dimensional cluster growth and branching gels in colloidal systems with short-range depletion attraction and screened electrostatic repulsion. J. Phys. Chem. B 2005, 109, 21942–21953. [Google Scholar] [CrossRef] [PubMed]
- Crocker, J.C.; Grier, D.G. Microscopic measurement of the pair interaction potential of charge-stabilized colloid. Phys. Rev. Lett. 1994, 73, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Campbell, A.I.; Anderson, V.J.; van Duijneveldt, J.S.; Bartlett, P. Dynamical Arrest in Attractive Colloids: The Effect of Long-Range Repulsion. Phys. Rev. Lett. 2005, 94, 208301. [Google Scholar] [CrossRef] [PubMed]
- Khalil, N.; de Candia, A.; Fierro, A.; Pica Ciamarra, M.; Coniglio, A. Dynamical arrest: Interplay of glass and gel transitions. Soft Matter 2014, 10, 4800–4805. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Abete, T.; de Candia, A.; Del Gado, E.; Fierro, A.; Coniglio, A. Static and dynamic heterogeneities in a model for irreversible gelation. Phys. Rev. Lett. 2007, 98, 088301. [Google Scholar] [CrossRef]
- Mallamace, F.; Corsaro, C.; Vasi, S.; Mallamace, D.; Chen, S.H. The dynamical fragile-to-strong crossover in attractive colloidal systems. J. Non-Cryst. Solids 2015, 407, 355–360. [Google Scholar] [CrossRef]
- Mallamace, F.; Chen, S.H.; Coniglio, A.; de Arcangelis, L.; Del Gado, E.; Fierro, A. Complex viscosity behavior and cluster formation in attractive colloidal systems. Phys. Rev. E 2006, 73, 020402. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids, 2nd ed.; London Academic: London, UK, 1968. [Google Scholar]
- Flynn, C.P. Atomic migration in monatomic crystals. Phys. Rev. 1968, 171, 682–698. [Google Scholar]
- Swallen, S.F.; Bonvallet, P.A.; McMahon, R.J.; Ediger, M.D. Self-Diffusion of tris-Naphthylbenzene near the Glass Transition Temperature. Phys. Rev. Lett. 2003, 90, 015901. [Google Scholar] [CrossRef]
- Mapes, M.K.; Swallen, S.F.; Ediger, M.D. Self-diffusion of supercooled o-terphenyl near the glass transition temperature. J. Phys. Chem. B 2006, 110, 507–511. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.H.; Mallamace, F.; Mou, C.Y.; Broccio, M.; Corsaro, C.; Faraone, A.; Liu, L. The violation of the Stokes-Einstein relation in supercooled water. Proc. Natl Acad. Sci. USA 2006, 103, 12974–12978. [Google Scholar] [CrossRef] [PubMed]
- Jung, Y.J.; Garrahan, J.P.; Chandler, D. Excitation lines and the breakdown of Stokes-Einstein relations in supercooled liquids. Phys. Rev. E 2004, 69, 061205. [Google Scholar] [CrossRef] [PubMed]
- Angell, C.A.; Boehm, L.; Oguni, M.; Smith, D.L. Far IR spectra and heat capacities for propylene carbonate and propylene glycol, and the connection to the dielectric response function. J. Mol. Liq. 1993, 56, 275–286. [Google Scholar] [CrossRef]
- Brodin, A.; Rössler, E.A. Universal and non-universal features of the dynamic susceptibility of supercooled liquids. J. Phys. Condens. Matter 2006, 18, 8481–8492. [Google Scholar] [CrossRef]
- Brodin, A.; Bergman, R.; Mattsson, J.; Rössler, E.A. Light scattering and dielectric manifestations of secondary relaxations in molecular glassformers. Eur. Phys. J. B 2003, 36, 349–357. [Google Scholar] [CrossRef]
- Szamel, G.; Flenner, E. Independence of the relaxation of a supercooled fluid from its microscopic dynamics: Need for yet another extension of the mode-coupling theory. Europhys. Lett. 2004, 67, 779–785. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Mason, T.G.; Weitz, D.A. Linear Viscoelasticity of Colloidal Hard Sphere Suspensions near the Glass Transition. Phys. Rev. Lett. 1995, 75, 2770–2773. [Google Scholar] [CrossRef]
- Brader, J.M.; Voigtmann, T.; Fuchs, M.; Larsonc, R.G.; Cates, M.E. Glass rheology: From mode-coupling theory to a dynamical yield criterion. Proc. Natl. Acad. Sci. USA 2009, 106, 15186–15191. [Google Scholar] [CrossRef]
- Suzuki, K.; Hayakawa, H. Nonequilibrium mode-coupling theory for uniformly sheared underdamped systems. Phys. Rev. E 2013, 87, 012304. [Google Scholar] [CrossRef]
- Zakani, B.; Ansari, M.; Grecov, D. Dynamic rheological properties of a fumed silica grease. Rheol. Acta 2018, 57, 83–94. [Google Scholar] [CrossRef]
- Ciarella, S.; Biezemansa, A.R.A.; Janssen, L.M.C. Understanding, predicting, and tuning the fragility of vitrimeric polymers. Proc. Natl. Acad. Sci. USA 2019, 116, 25013–25022. [Google Scholar] [CrossRef] [PubMed]
- Berntsen, P.; Ericsson, T.; Swenson, J.; Sjögren, L. Complex modulus and compliance for airway smooth muscle cells. Phys. Rev. E 2020, 101, 032410. [Google Scholar] [CrossRef] [PubMed]
- Roy, P.; Menon, S.; Sengupta, N. Dynamical Manifestations of Supercooling in Amyloid Hydration. J. Phys. Chem. B 2022, 126, 44–53. [Google Scholar] [CrossRef]
- Reichert, J.; Mandal, S.; Voigtmann, T. Mode-coupling theory for tagged-particle motion of active Brownian particles. Phys. Rev. E 2021, 104, 044608. [Google Scholar] [CrossRef]
- Lionberger, R.A.; Russel, W.B. High frequency modulus of hard sphere colloids. J. Rheol. 1994, 38, 1885–1908. [Google Scholar] [CrossRef]
- de Schepper, I.M.; Smorenburg, H.E.; Cohen, E.G.D. Viscoelasticity in dense hard sphere colloids. Phys. Rev. Lett. 1993, 70, 2178–2181. [Google Scholar] [CrossRef]
- Woodcock, L.V. Glass transition in hard-sphere model and Kauzmann’s paradox. Ann. N. Y. Acad. Sci. 1981, 371, 274–298. [Google Scholar] [CrossRef]
- Mallamace, F.; Tartaglia, P.; Chen, W.R.; Faraone, A.; Chen, S.H. A mode coupling theory analysis of viscoelasticity near the kinetic glass transition of a copolymer micellar system. J. Phys. Condens. Matter 2004, 16, S4975–S4986. [Google Scholar] [CrossRef]
- Essam, J. Percolation theory. Rep. Prog. Phys. 1980, 43, 833–912. [Google Scholar] [CrossRef]
- de Gennes, F. On a relation between percolation theory and the elasticity of gels. J. Phys. Lett. 1976, 37, L1. [Google Scholar] [CrossRef]
- Efros, A.L.; Shkolovskii, B.I. Critical Behaviour of Conductivity and Dielectric Constant near the Metal-Non-Metal Transition Threshold. Phys. Status Solidi B 1976, 76, 475–485. [Google Scholar] [CrossRef]
- Herrmann, H.J.; Derrida, B.; Vannimenus, J. Superconductivity exponents in two- and three-dimensional percolation. J. Phys. Rev. B 1984, 30, 4080–4082. [Google Scholar] [CrossRef]
- Mallamace, F.; Stanley, H.E.; Chen, S.H. The role of the dynamic crossover temperature and the arrest in glass-forming fluids. Eur. Phys. J. E 2011, 34, 94. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Ceram. Soc. 1953, 77, 3701–3707. [Google Scholar] [CrossRef]
- Götze, W. Recent tests of the mode-coupling theory for glassy dynamics. J. Phys. Condens. Matter 1999, 11, A1. [Google Scholar] [CrossRef]
- Olsen, N.B.; Christensen, T.; Dyre, J.C. Time-Temperature Superposition in Viscous Liquids. Phys. Rev. Lett. 2001, 86, 1271. [Google Scholar] [CrossRef]
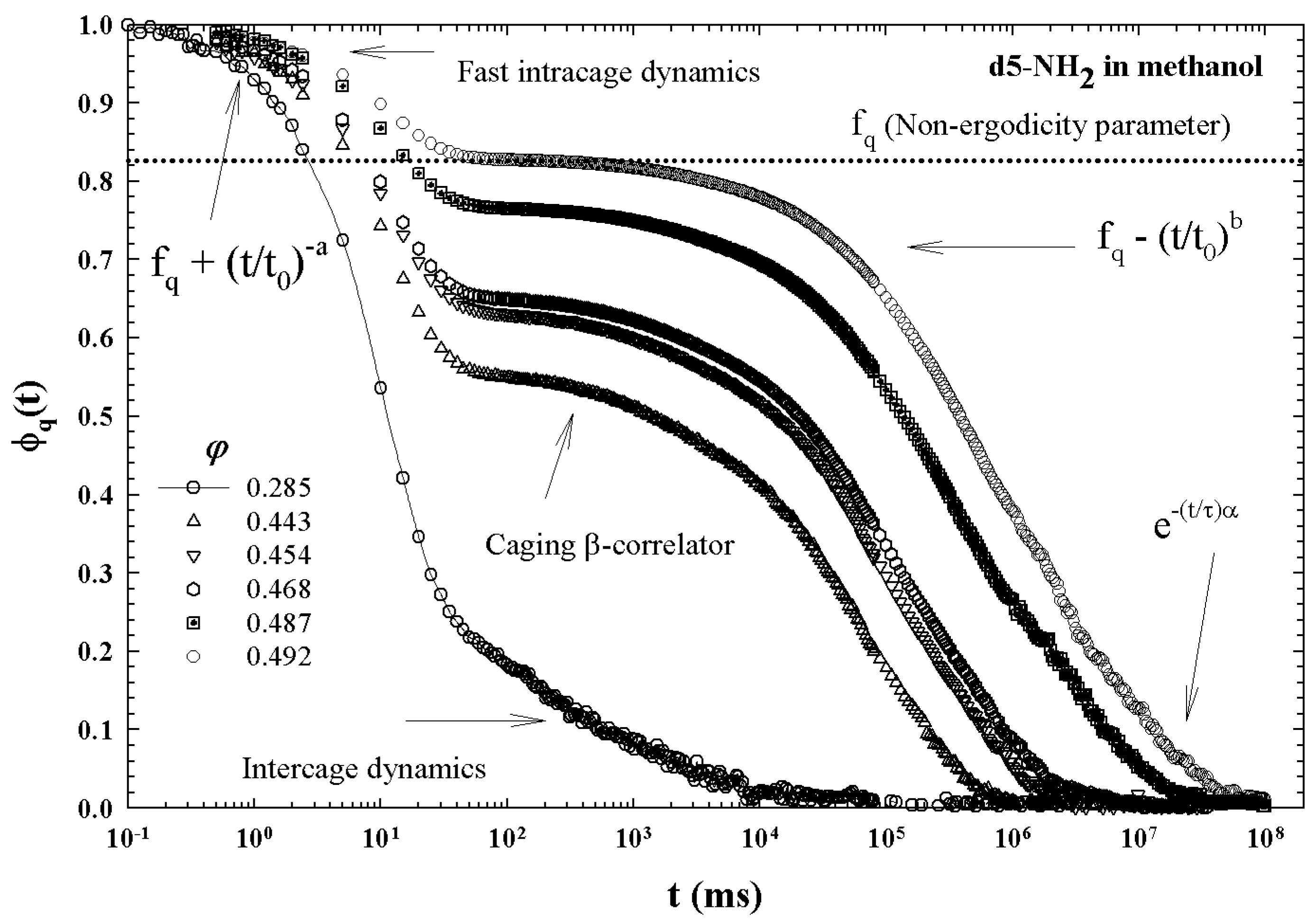

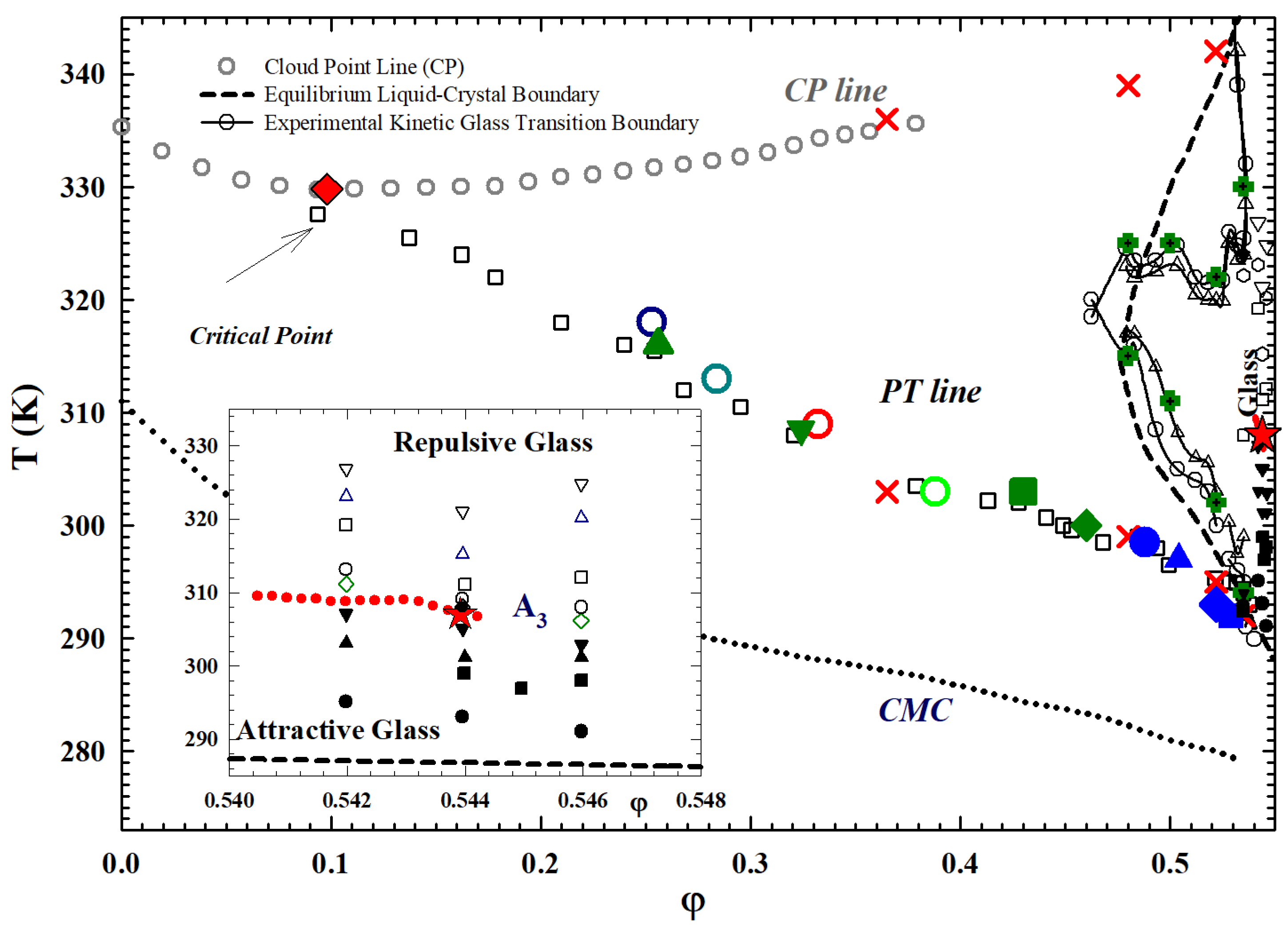
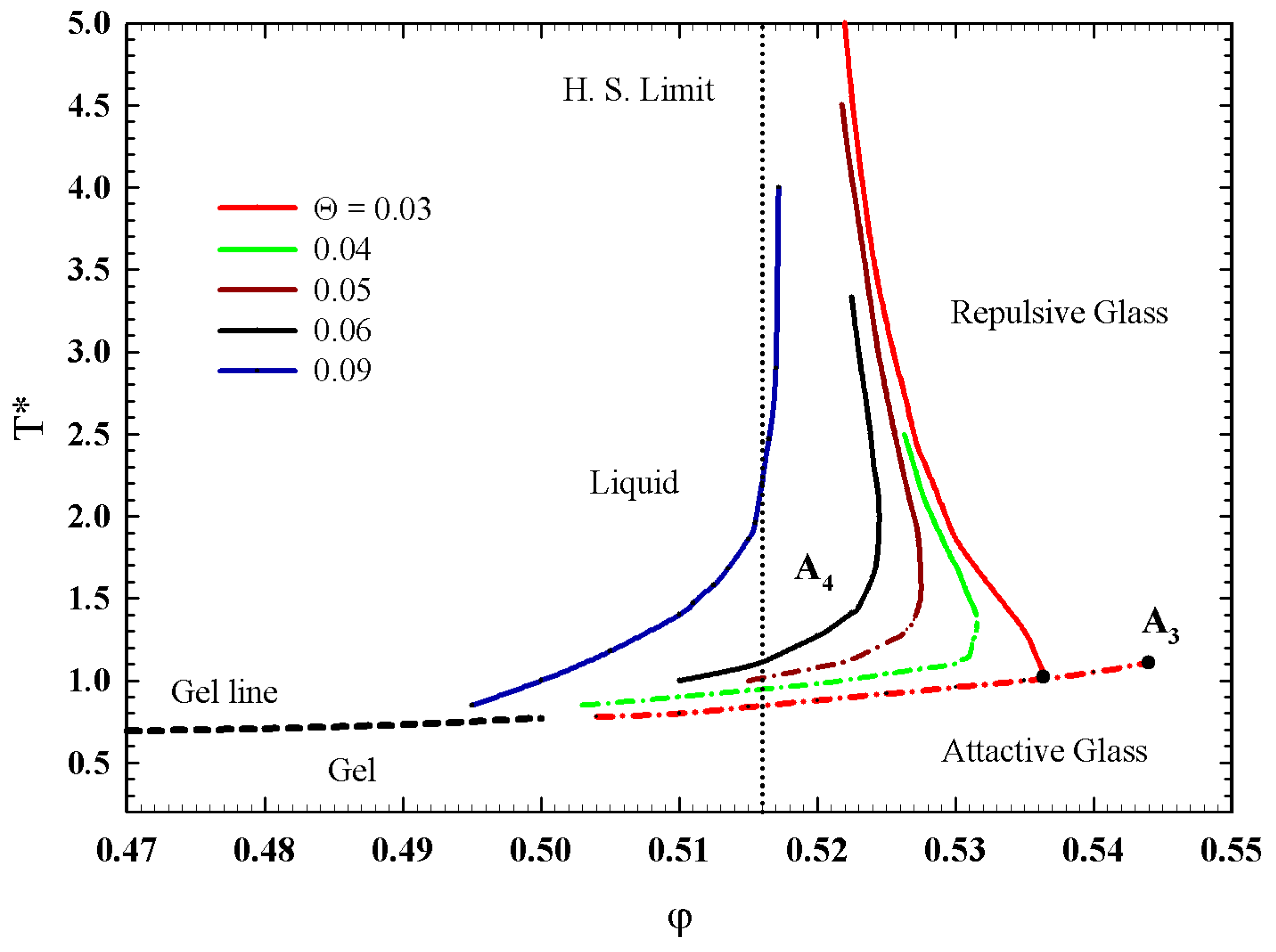
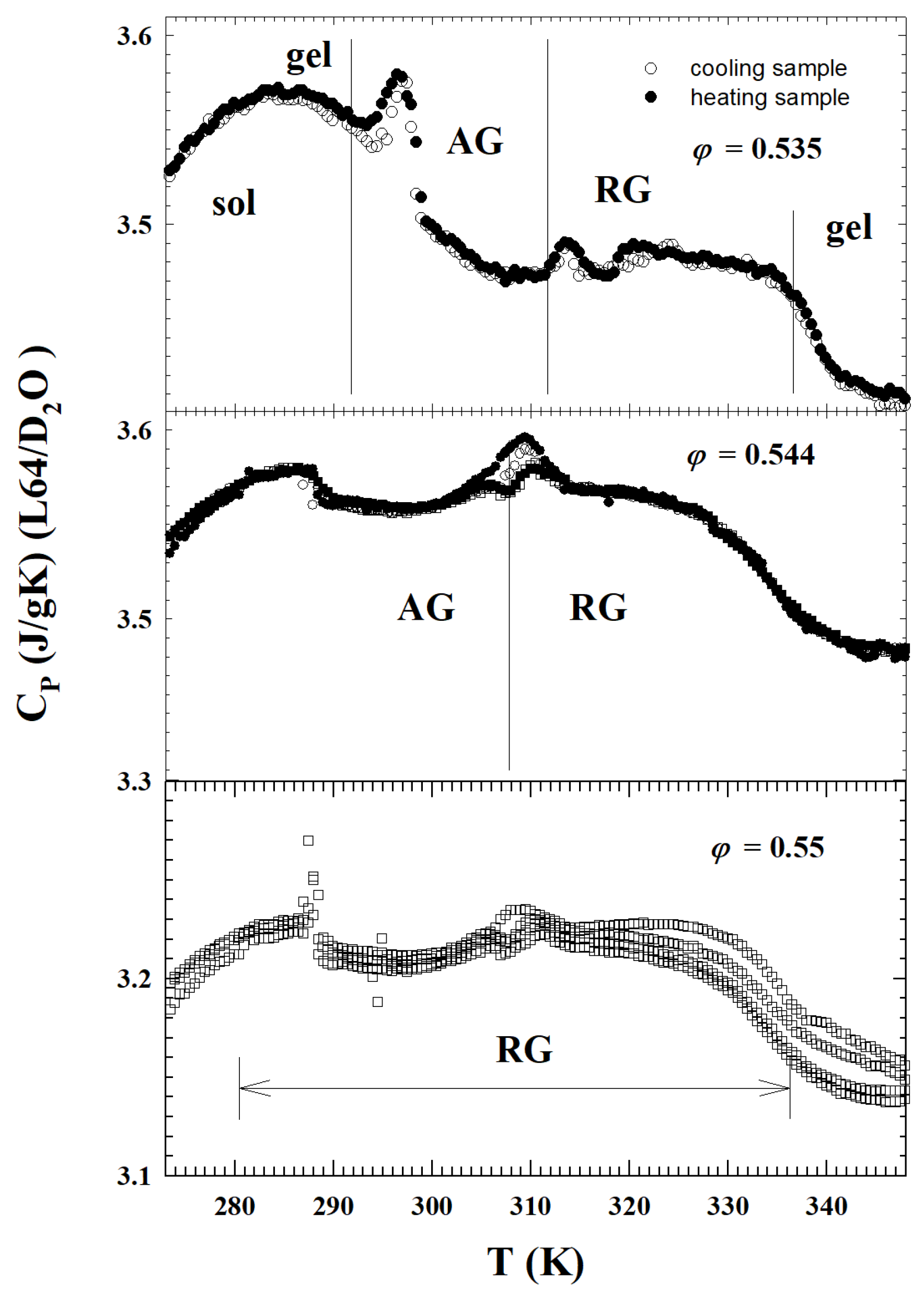
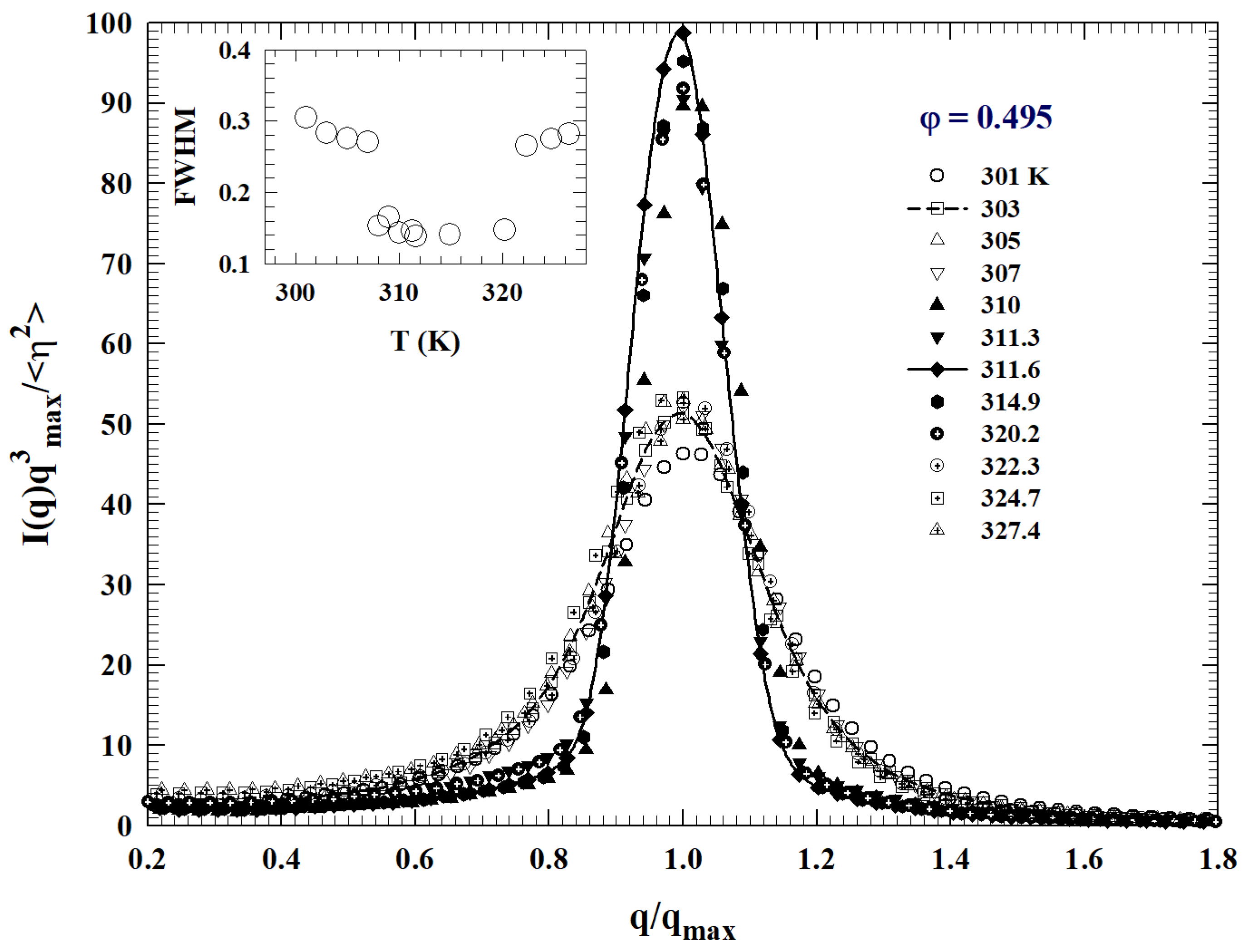
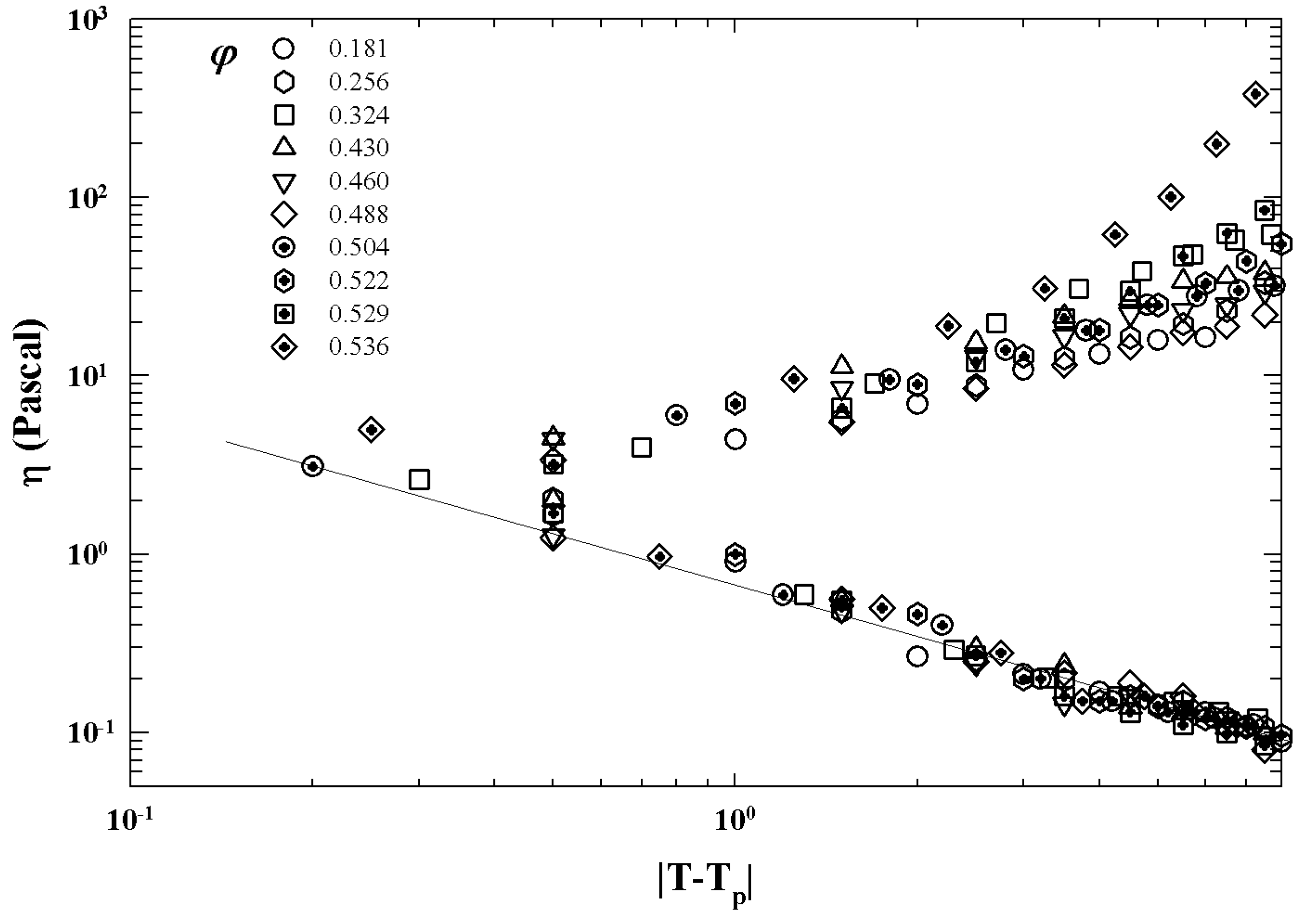
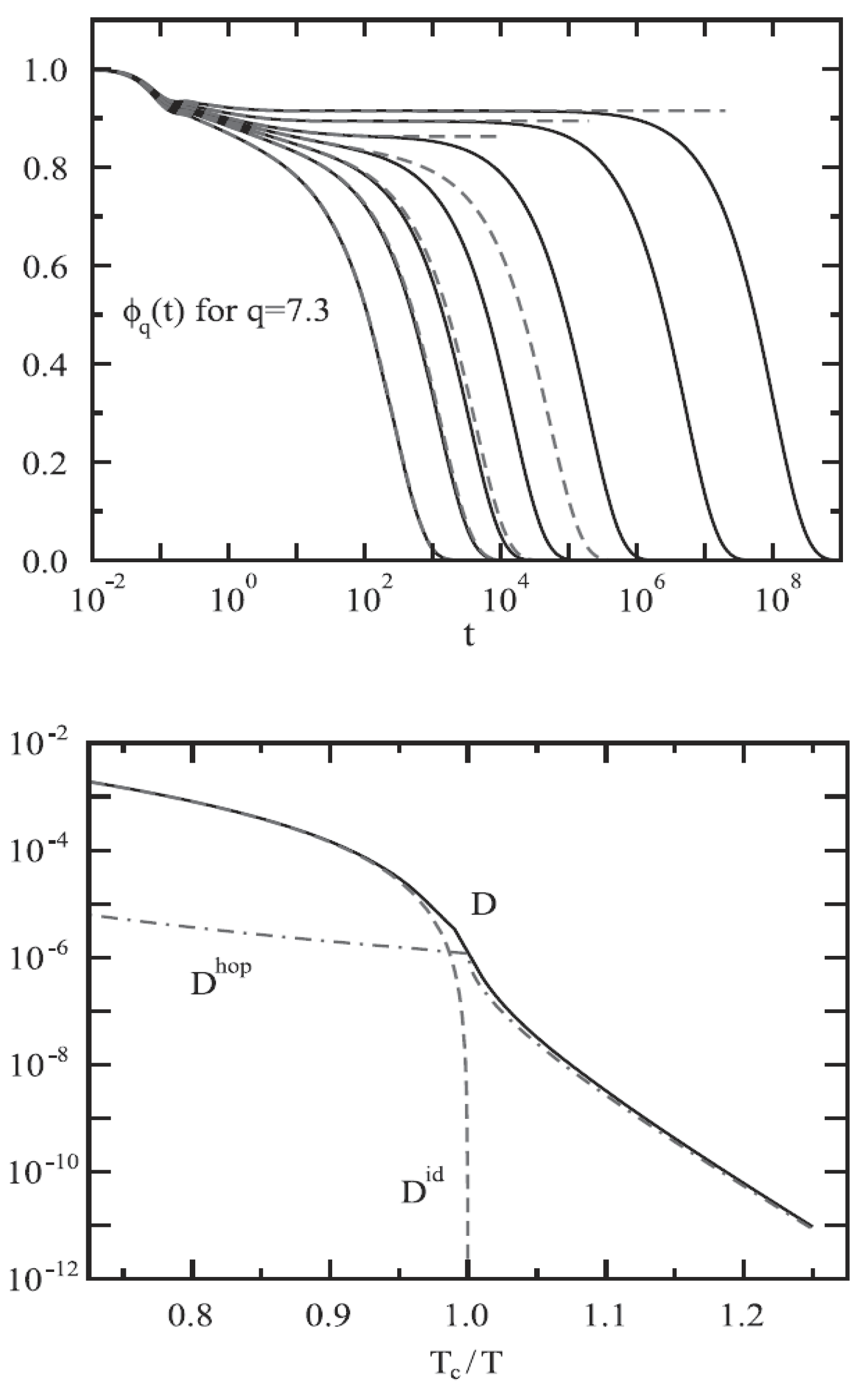
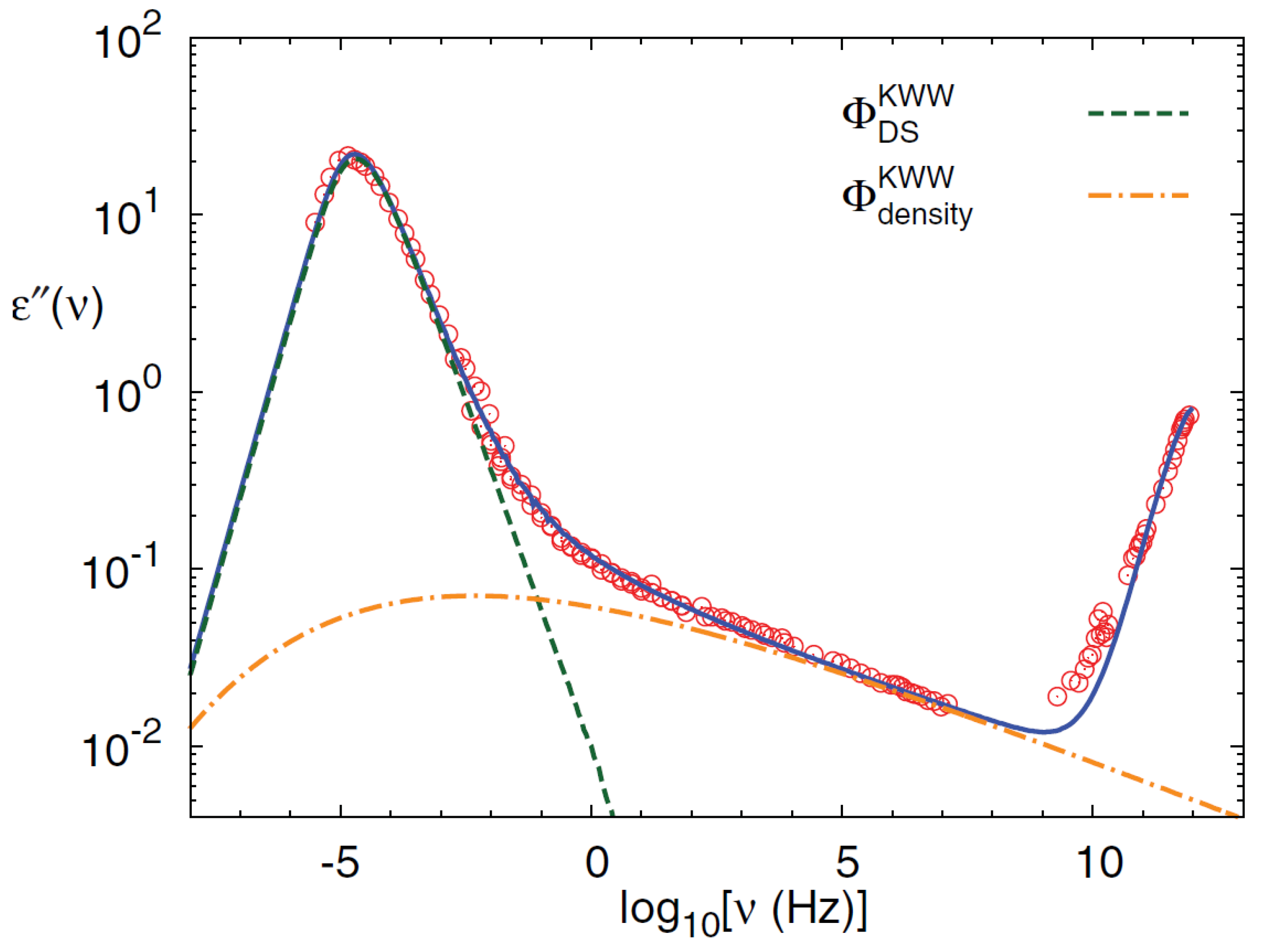



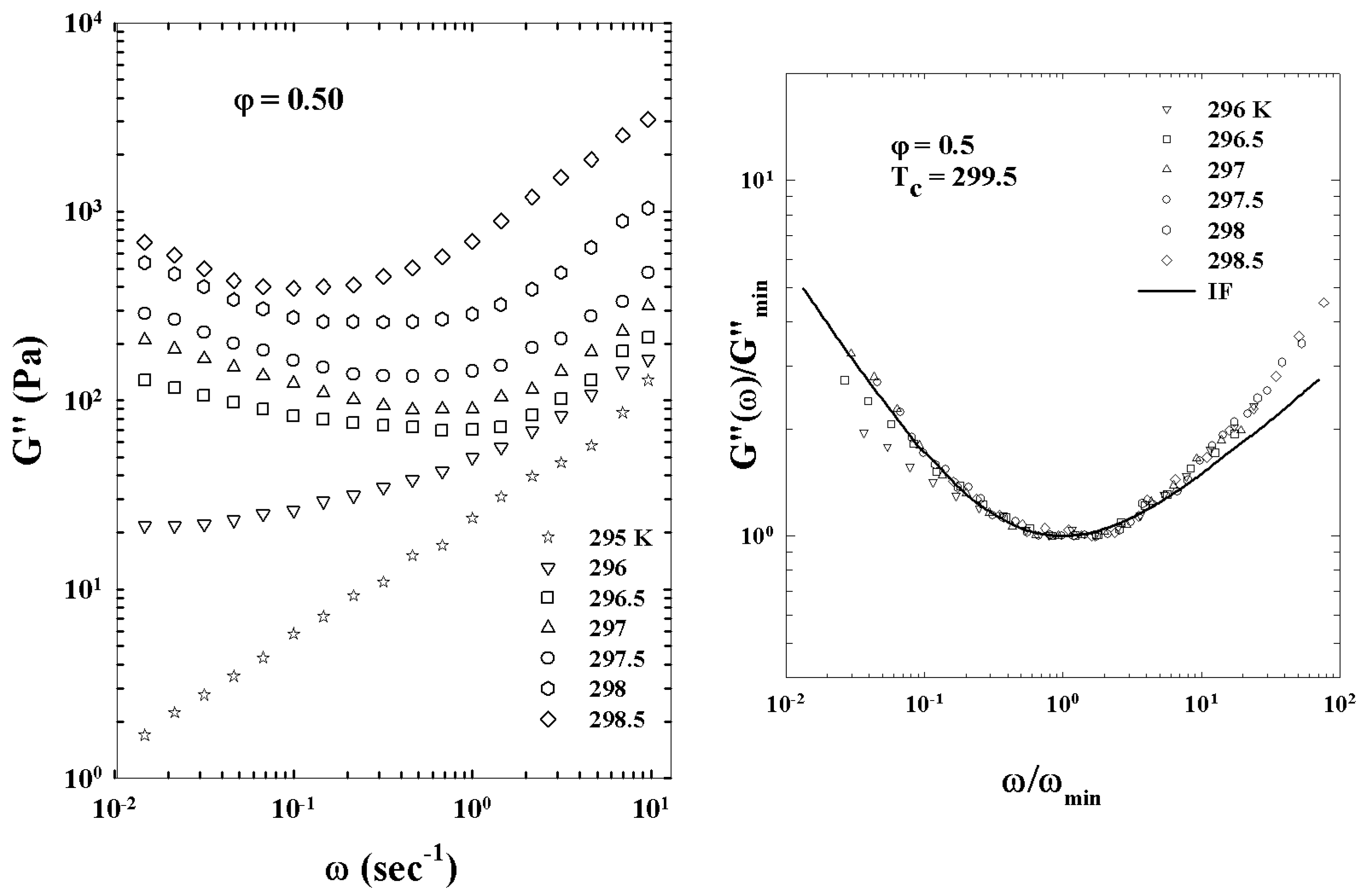
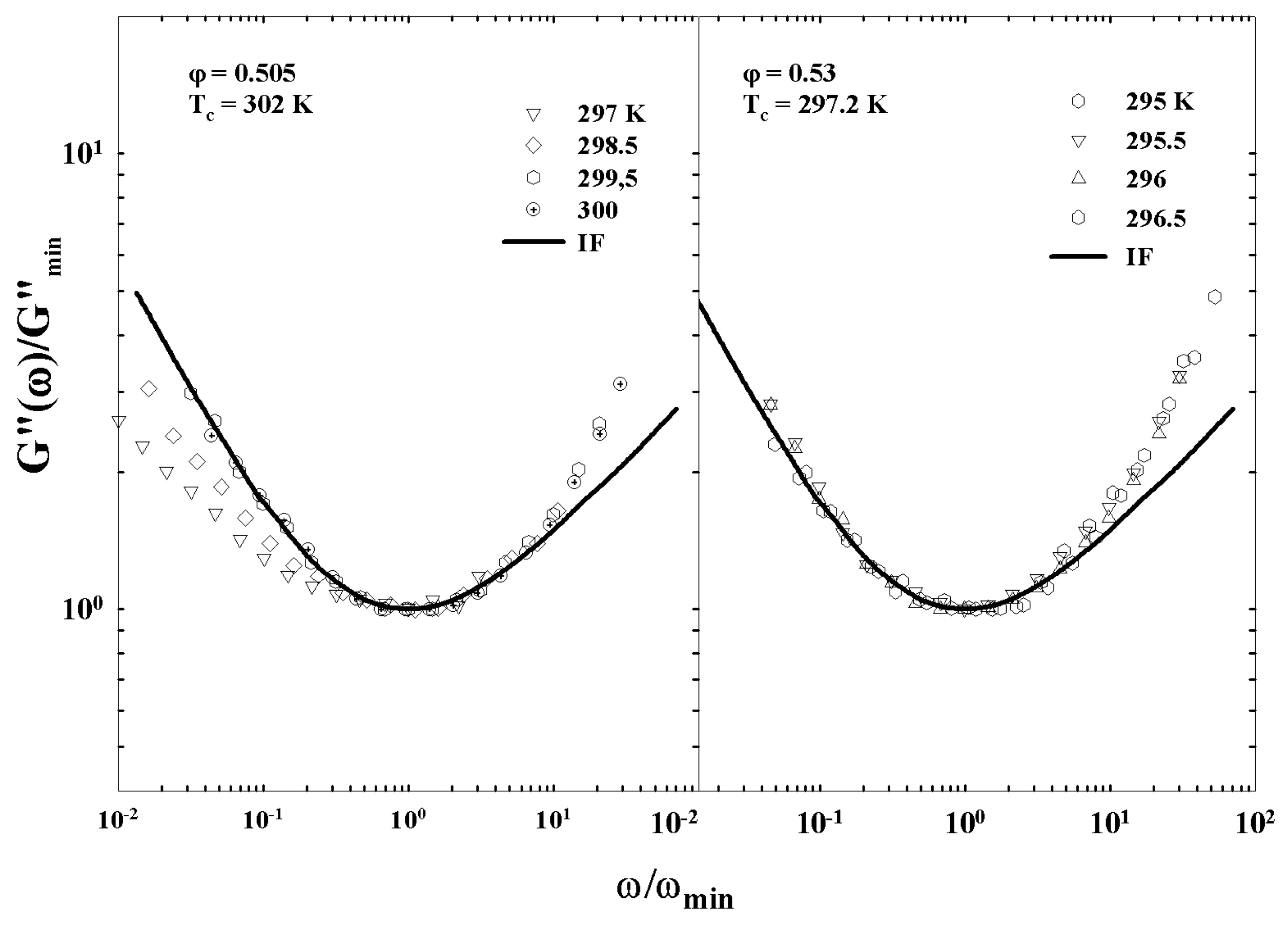
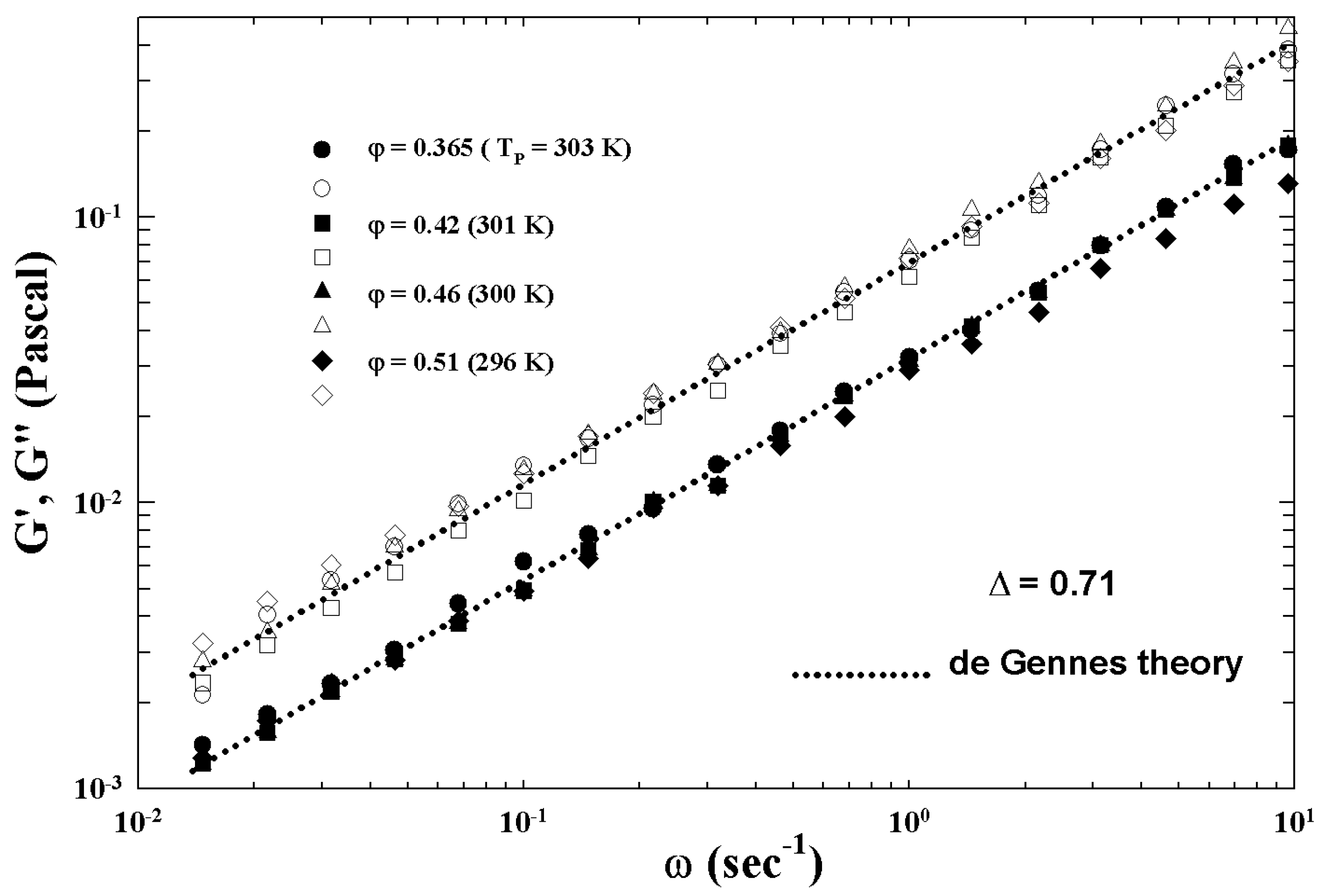
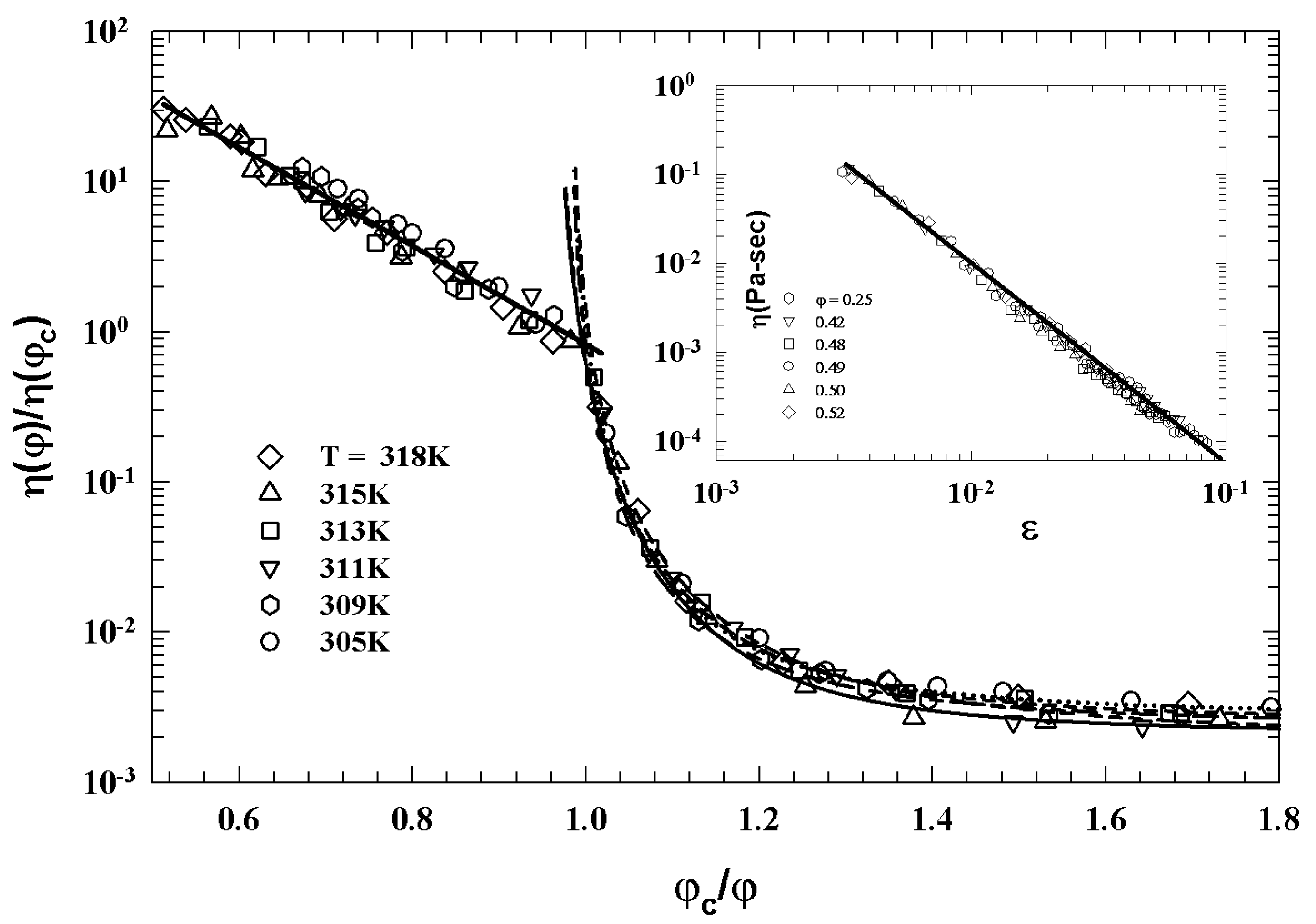
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mallamace, F.; Mensitieri, G.; Salzano de Luna, M.; Lanzafame, P.; Papanikolaou, G.; Mallamace, D. The Interplay between the Theories of Mode Coupling and of Percolation Transition in Attractive Colloidal Systems. Int. J. Mol. Sci. 2022, 23, 5316. https://doi.org/10.3390/ijms23105316
Mallamace F, Mensitieri G, Salzano de Luna M, Lanzafame P, Papanikolaou G, Mallamace D. The Interplay between the Theories of Mode Coupling and of Percolation Transition in Attractive Colloidal Systems. International Journal of Molecular Sciences. 2022; 23(10):5316. https://doi.org/10.3390/ijms23105316
Chicago/Turabian StyleMallamace, Francesco, Giuseppe Mensitieri, Martina Salzano de Luna, Paola Lanzafame, Georgia Papanikolaou, and Domenico Mallamace. 2022. "The Interplay between the Theories of Mode Coupling and of Percolation Transition in Attractive Colloidal Systems" International Journal of Molecular Sciences 23, no. 10: 5316. https://doi.org/10.3390/ijms23105316
APA StyleMallamace, F., Mensitieri, G., Salzano de Luna, M., Lanzafame, P., Papanikolaou, G., & Mallamace, D. (2022). The Interplay between the Theories of Mode Coupling and of Percolation Transition in Attractive Colloidal Systems. International Journal of Molecular Sciences, 23(10), 5316. https://doi.org/10.3390/ijms23105316








