The Interplay of Conjugation and Metal Coordination in Tuning the Electron Transfer Abilities of NTA-Graphene Based Interfaces
Abstract
1. Introduction
2. Results and Discussion
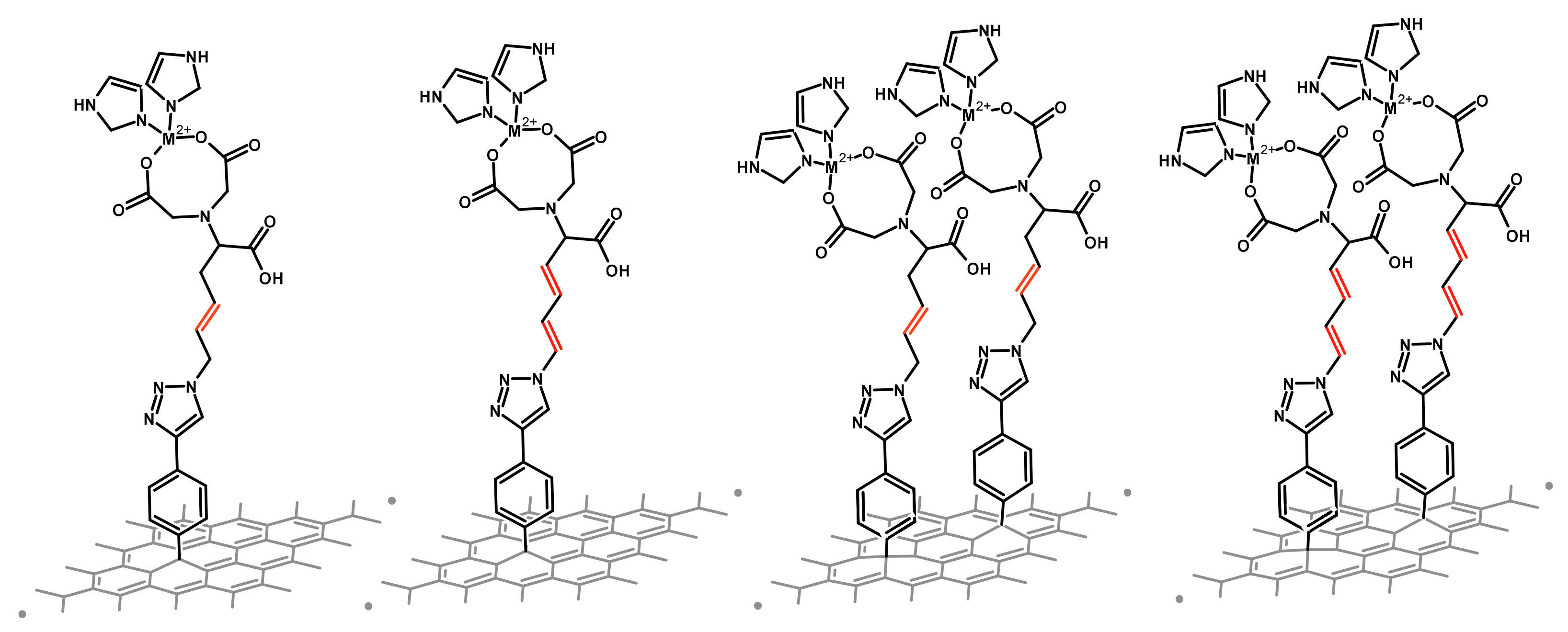
2.1. Effect of Different Chain’s Saturation
2.1.1. Interfaces without a Metal
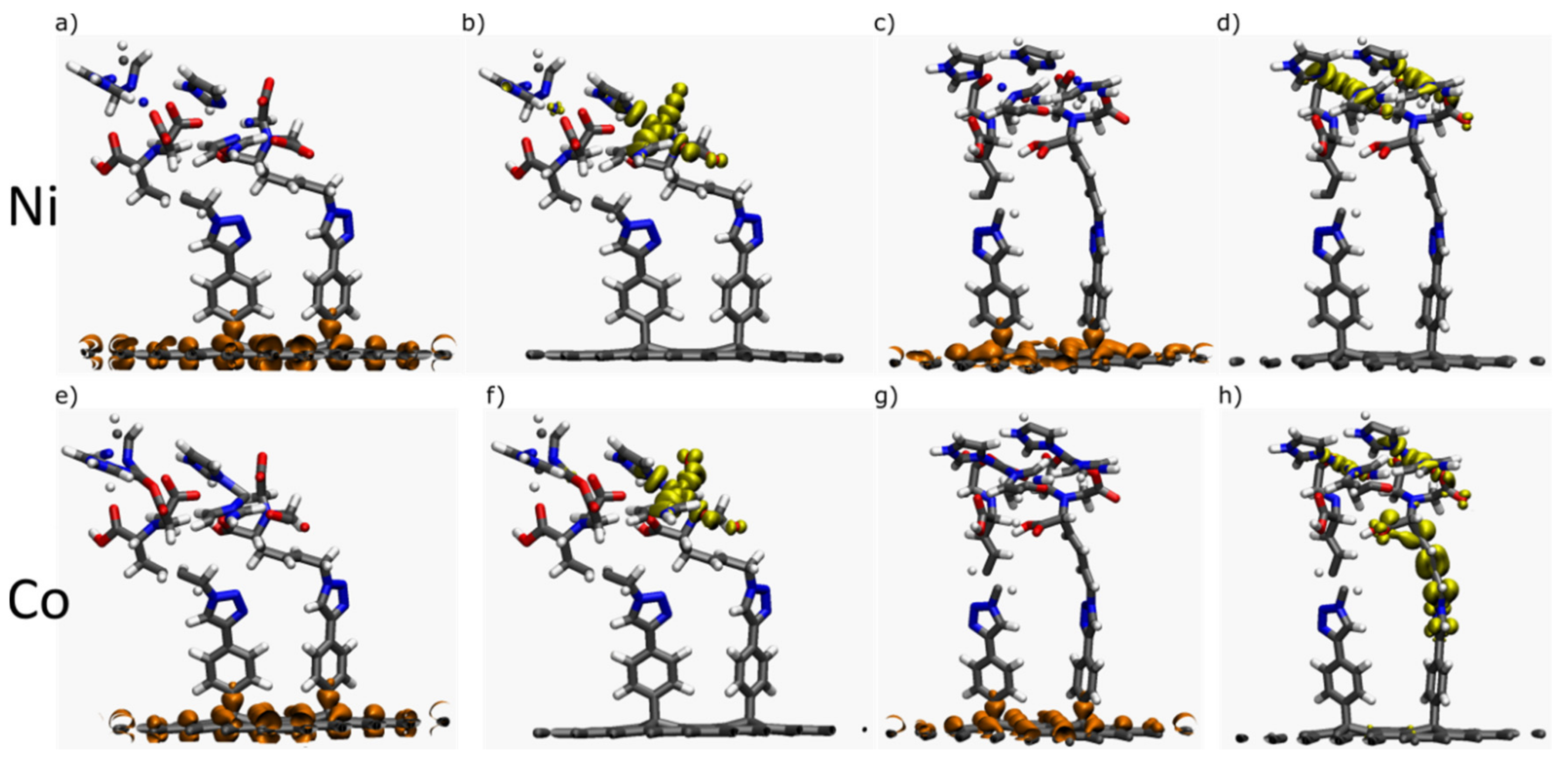
2.1.2. Interfaces with a Metal—One Double Bond
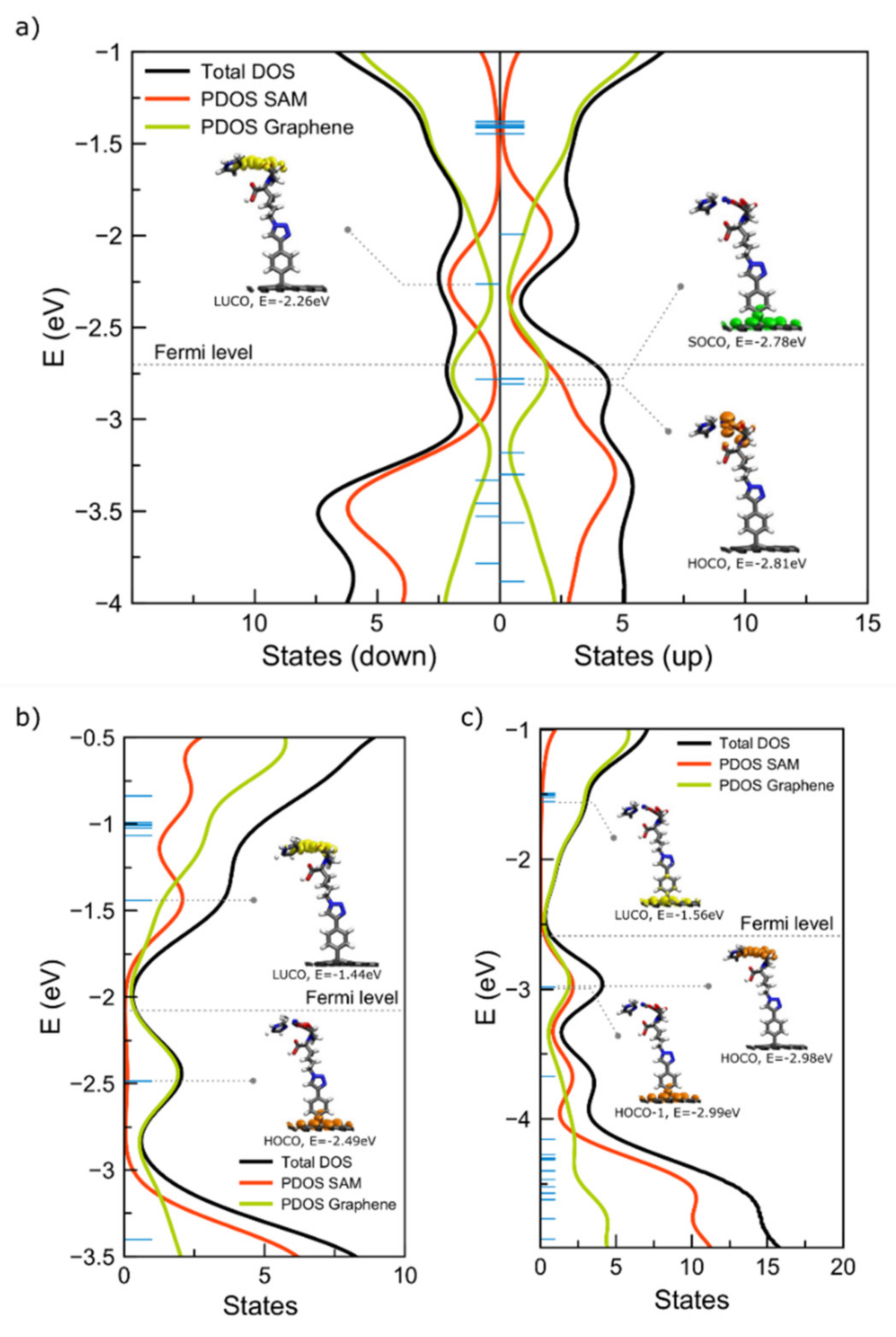
2.1.3. Interfaces with a Metal—Two Double Bonds
2.2. Effect of Surface Coverage Density
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Osella, S.; Kargul, J.; Izzo, M.; Trzaskowski, B. Architecture and Function of Biohybrid Solar Cell and Solar-to-Fuel Nanodevices. In Theory and Simulation in Physics for Materials Applications; Springer: Cham, Switzerland, 2020; Volume 296, pp. 227–274. [Google Scholar] [CrossRef]
- Badu, S.; Melnik, R.; Singh, S. Analysis of photosynthetic systems and their applications with mathematical and computational models. Appl. Sci. 2020, 10, 6821. [Google Scholar] [CrossRef]
- Janna Olmos, J.D.; Kargul, J. A quest for the artificial leaf. Int. J. Biochem. Cell Biol. 2015, 66, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Cao, R.; Lai, W.; Du, P. Catalytic water oxidation at single metal sites. Energy Environ. Sci. 2012, 5, 8134–8157. [Google Scholar] [CrossRef]
- Walter, M.G.; Warren, E.I.; McKone, J.R.; Boettcher, S.W.; Mi, Q.; Santori, E.A.; Lewis, N.S. Solar water splitting cells. Chem. Rev. 2010, 110, 6446–6473. [Google Scholar] [CrossRef]
- Chaki, N.K.; Vijayamohanan, K. Self-assembled monolayers as a tunable platform for biosensor applications. Biosens. Bioelectron. 2002, 17, 1–12. [Google Scholar] [CrossRef]
- Singh, M.; Kaur, N.; Comini, E. The role of self-assembled monolayers in electronic devices. J. Mater. Chem. C 2020, 8, 3938–3955. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Pumera, M. Graphene-based nanomaterials and their electrochemistry. Chem. Soc. Rev. 2010, 39, 4146–4157. [Google Scholar] [CrossRef]
- Krishnan, S.K.; Singh, E.; Singh, P.; Meyyappan, M.; Singh Nalwa, H. A review on graphene-based nanocomposites for electrochemical and fluorescent biosensors. RSC Adv. 2019, 9, 8778–8781. [Google Scholar] [CrossRef]
- Kaplan, A.; Yuan, Z.; Benck, J.D.; Rajan, A.G.; Chu, X.S.; Wang, Q.H.; Strano, M.S. Current and future directions in electron transfer chemistry of graphene. Chem. Soc. Rev. 2017, 46, 4530–4571. [Google Scholar] [CrossRef]
- Brownson, D.A.C.; Banks, C.E. Graphene electrochemistry: An overview of potential applications. Analyst 2010, 135, 2768–2778. [Google Scholar] [CrossRef]
- Brownson, D.; Kampouris, D.; Banks, C.E. An overview of graphene in energy production and storage applications. J. Power Sources 2011, 196, 4873–4885. [Google Scholar] [CrossRef]
- Nöll, T.; Nöll, G. Strategies for “wiring” redox-active proteins to electrodes and applications in biosensors, biofuel cells, and nanotechnology. Chem. Soc. Rev. 2011, 40, 3564–3576. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Holzinger, M.; Tabrizian, M.; Winters, S.; Berner, N.; Cosnier, S.; Duesberg, G.S. Noncovalently functionalized monolayer graphene for sensitivity enhancement of surface plasmon resonance immunosensors. J. Am. Chem. Soc. 2015, 137, 2800–2803. [Google Scholar] [CrossRef] [PubMed]
- Hinnemo, M.; Zhao, J.; Ahlberg, P.; Hägglund, C.; Djurberg, V.; Scheicher, R.H.; Zhang, S.-L.; Zhang, Z.-B. On Monolayer Formation of Pyrenebutyric Acid on Graphene. Langmuir 2017, 33, 3588–3593. [Google Scholar] [CrossRef] [PubMed]
- Bosch-Navarro, C.; Laker, Z.P.; Marsden, A.J.; Wilson, N.R.; Rourke, J.P. Non-covalent functionalization of graphene with a hydrophilic self-limiting monolayer for macro-molecule immobilization. FlatChem 2017, 1, 52–56. [Google Scholar] [CrossRef]
- Ersu, G.; Gokpek, Y.; Can, M.; Zafer, C.; Demic, S. Applications of Graphene Modified by Self-Assembled Monolayers. In Advances in Condensed-Matter and Materials Physics-Rudimentary Research to Topical Technology; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Wang, C.-F.; Sun, X.-Y.; Su, M.; Wang, Y.-P.; Lv, Y.-K. Electrochemical biosensors based on antibody, nucleic acid and enzyme functionalized graphene for the detection of disease-related biomolecules. Analyst 2020, 145, 1550–1562. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; Wang, E. Electrochemical biosensors on platforms of graphene. Chem. Commun. 2013, 49, 9526–9539. [Google Scholar] [CrossRef]
- Vashist, S.K.; Luong, J.H. Recent advances in electrochemical biosensing schemes using graphene and graphene-based nanocomposites. Carbon 2015, 84, 519–550. [Google Scholar] [CrossRef]
- Song, Y.; Luo, Y.; Zhu, C.; Li, H.; Du, D.; Lin, Y. Recent advances in electrochemical biosensors based on graphene two-dimensional nanomaterials. Biosens. Bioelectron. 2016, 76, 195–212. [Google Scholar] [CrossRef]
- Karimi, A.; Othman, A.; Uzunoglu, A.; Stanciu, L.; Andreescu, S. Graphene based enzymatic bioelectrodes and biofuel cells. Nanoscale 2015, 7, 6909–6923. [Google Scholar] [CrossRef]
- Babadi, A.A.; Bagheri, S.; Hamid, S.B.A. Progress on implantable biofuel cell: Nano-carbon functionalization for enzyme immobilization enhancement. Biosens. Bioelectron. 2016, 79, 850–860. [Google Scholar] [CrossRef] [PubMed]
- Diez-Cabanes, V.; Morales, D.C.; Souto, M.; Paradinas, M.; Delchiaro, F.; Painelli, A.; Ocal, C.; Cornil, D.; Cornil, J.; Veciana, J.; et al. Effect of the Molecular Polarizability of SAMs on the Work Function Modification of Gold: Closed- versus Open-Shell Donor–Acceptor SAMs. Adv. Mater. Technol. 2019, 4, 1–7. [Google Scholar] [CrossRef]
- Heimel, G.; Romaner, L.; Zojer, E.; Bredas, J.-L. The interface energetics of self-assembled monolayers on metals. Acc. Chem. Res. 2008, 41, 721–729. [Google Scholar] [CrossRef] [PubMed]
- Osella, S.; Kiliszek, M.; Harputlu, E.; Unlu, C.G.; Ocakoglu, K.; Kargul, J.; Trzaskowski, B. Controlling the charge transfer flow at the graphene/pyrene-nitrilotriacetic acid interface. J. Mater. Chem. C 2018, 6, 5046–5054. [Google Scholar] [CrossRef]
- Osella, S.; Kiliszek, M.; Harputlu, E.; Unlu, C.G.; Ocakoglu, K.; Trzaskowski, B.; Kargul, J. Role of Metal Centers in Tuning the Electronic Properties of Graphene-Based Conductive Interfaces. J. Phys. Chem. C 2019, 123, 8623–8632. [Google Scholar] [CrossRef]
- Huang, Z.; Hwang, P.; Watson, D.S.; Cao, L.; Szoka, J.F.C. Tris-nitrilotriacetic acids of subnanomolar affinity toward hexahistidine tagged molecules. Bioconjug. Chem. 2009, 20, 1667–1672. [Google Scholar] [CrossRef][Green Version]
- Shen, W.; Zhong, H.; Neff, D.; Norton, M.L. NTA directed protein nanopatterning on DNA origami nanoconstructs. J. Am. Chem. Soc. 2009, 131, 6660–6661. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Holzinger, M.; Biloivan, O.; Cosnier, S. 3D-nanostructured scaffold electrodes based on single-walled carbon nanotubes and nanodiamonds for high performance biosensors. Carbon 2013, 61, 349–356. [Google Scholar] [CrossRef]
- Auer, S.; Azizi, L.; Faschinger, F.; Blazevic, V.; Vesikari, T.; Gruber, H.J.; Hytönen, V.P. Stable immobilisation of His-tagged proteins on BLI biosensor surface using cobalt. Sens. Actuators B Chem. 2017, 243, 104–113. [Google Scholar] [CrossRef]
- Conzuelo, F.; Gamella, M.; Campuzano, S.; Martínez-Ruiz, P.; Esteban-Torres, M.; Rivas, B.D.L.; Reviejo, A.J.; Muñoz, R.; Pingarrón, J.M.; Ruiz, S.C. Integrated Amperometric Affinity Biosensors Using Co2+–Tetradentate Nitrilotriacetic Acid Modified Disposable Carbon Electrodes: Application to the Determination of. Anal. Chem. 2013, 85, 3246–3254. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafé, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.Y.; Dumitrică, T.; Dominguez, A.; et al. DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef]
- Porezag, D.; Frauenheim, T.; Köhler, T.; Seifert, G.; Kaschner, R. Construction of tight-binding-like potentials on the basis of density-functional theory: Application to carbon. Phys. Rev. B 1995, 51, 12947–12957. [Google Scholar] [CrossRef]
- Katsnelson, M.I. Graphene: Carbon in Two Dimensions; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Yuan, S.; Rösner, M.; Schulz, A.; Wehling, T.O.; Katsnelson, M.I. Electronic structures and optical properties of partially and fully fluorinated graphene. Phys. Rev. Lett. 2015, 114, 047403. [Google Scholar] [CrossRef]
- Fiori, G.; Lebègue, S.; Betti, A.; Michetti, P.; Klintenberg, M.; Eriksson, O.; Iannaccone, G. Simulation of hydrogenated graphene field-effect transistors through a multiscale approach. Phys. Rev. B-Condens. Matter Mater. Phys. 2010, 82, 153404. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. Quantum Espresso: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef]
- Hamann, D.R. Optimized norm-conserving Vanderbilt pseudopotentials. Phys. Rev. B-Condens. Matter Mater. Phys. 2013, 88, 1–10. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Heimel, G.; Salzmann, I.; Duhm, S.; Koch, N. Design of organic semiconductors from molecular electrostatics. Chem. Mater. 2011, 23, 359–377. [Google Scholar] [CrossRef]
- Cahen, D.; Kahn, A. Electron energetics at surfaces and interfaces: Concepts and experiments. Adv. Mater. 2003, 15, 271–277. [Google Scholar] [CrossRef]
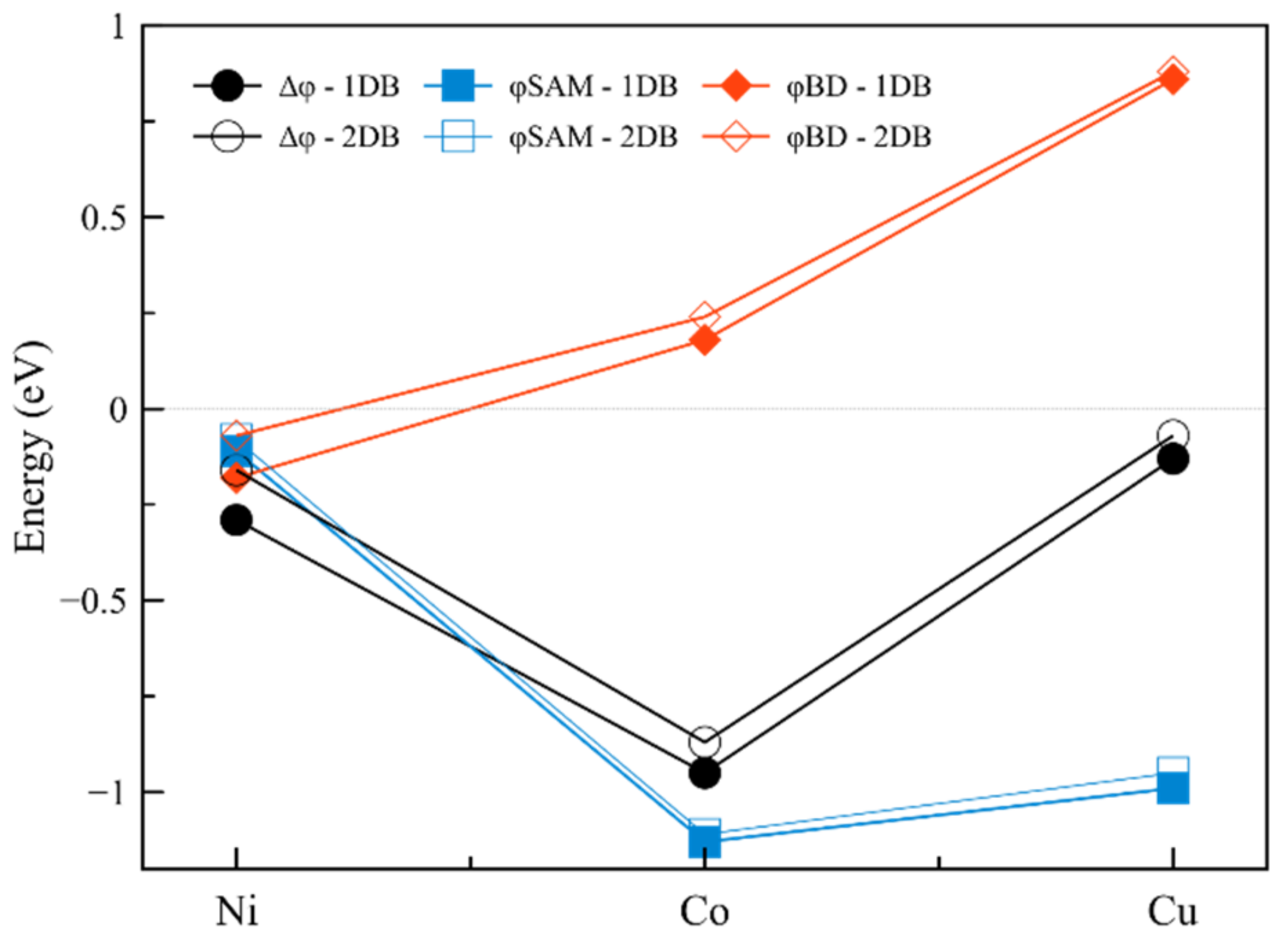
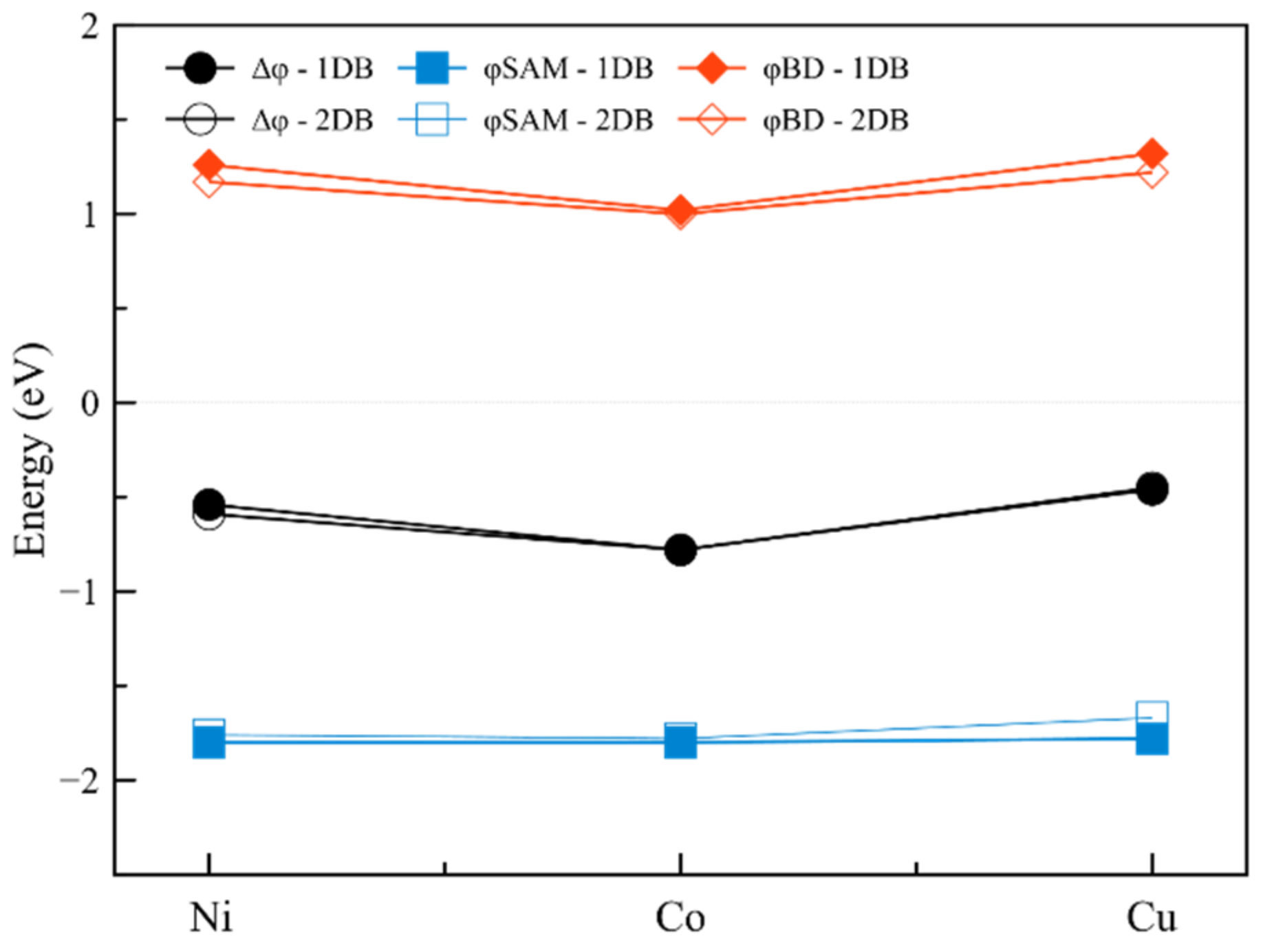
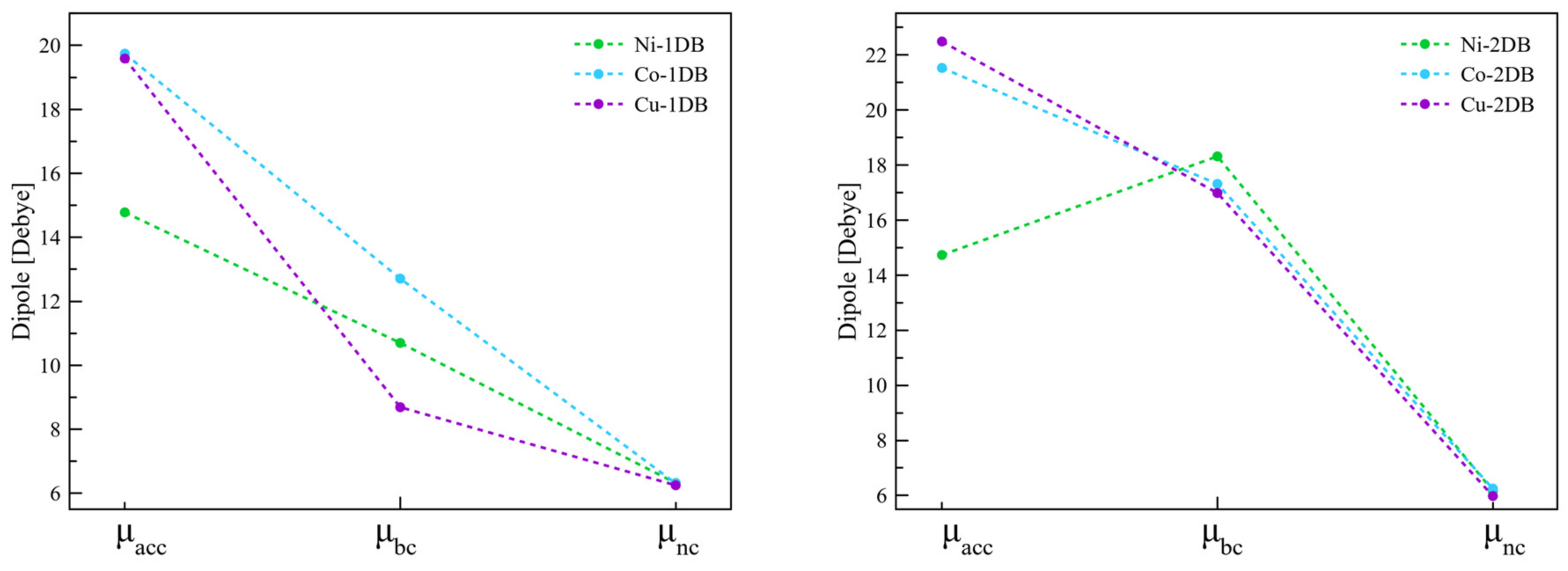
| Interface | Dipole Moment of SAM [Debye] | Dipole Moment of the Interface [Debye] | Δφ [meV] | φSAM [meV] | φBD [meV] | |
|---|---|---|---|---|---|---|
| 1 | Ni-1DB | 0.38 | 1.01 | −290 | −110 | −180 |
| 2 | Co-1DB | 3.97 | 3.34 | −950 | −1130 | 180 |
| 3 | Cu-1DB | 3.47 | 0.45 | −130 | −990 | 860 |
| Interface | Dipole Moment of the Interface [Debye] | Dipole Moment of SAM [Debye] | Δφ [meV] | φSAM [meV] | φBD [meV] | |
|---|---|---|---|---|---|---|
| 1 | Ni-2DB | 0.54 | 0.29 | −160 | −80 | −70 |
| 2 | Co-2DB | 3.04 | 3.88 | −870 | −1110 | 240 |
| 3 | Cu-2DB | 0.24 | 3.32 | −70 | −950 | 880 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaźmierczak, M.; Trzaskowski, B.; Osella, S. The Interplay of Conjugation and Metal Coordination in Tuning the Electron Transfer Abilities of NTA-Graphene Based Interfaces. Int. J. Mol. Sci. 2022, 23, 543. https://doi.org/10.3390/ijms23010543
Kaźmierczak M, Trzaskowski B, Osella S. The Interplay of Conjugation and Metal Coordination in Tuning the Electron Transfer Abilities of NTA-Graphene Based Interfaces. International Journal of Molecular Sciences. 2022; 23(1):543. https://doi.org/10.3390/ijms23010543
Chicago/Turabian StyleKaźmierczak, Magdalena, Bartosz Trzaskowski, and Silvio Osella. 2022. "The Interplay of Conjugation and Metal Coordination in Tuning the Electron Transfer Abilities of NTA-Graphene Based Interfaces" International Journal of Molecular Sciences 23, no. 1: 543. https://doi.org/10.3390/ijms23010543
APA StyleKaźmierczak, M., Trzaskowski, B., & Osella, S. (2022). The Interplay of Conjugation and Metal Coordination in Tuning the Electron Transfer Abilities of NTA-Graphene Based Interfaces. International Journal of Molecular Sciences, 23(1), 543. https://doi.org/10.3390/ijms23010543








