In Silico Logical Modelling to Uncover Cooperative Interactions in Cancer
Abstract
1. Oncogenesis: A Dynamic Process of Multifactorial Nature
1.1. Cooperative Oncogenesis
1.2. Experimental Assessment of Cooperative Oncogenesis and Current Limitations
2. Computational Modelling Approaches to Pinpoint Cooperative Interactions in Oncogenesis
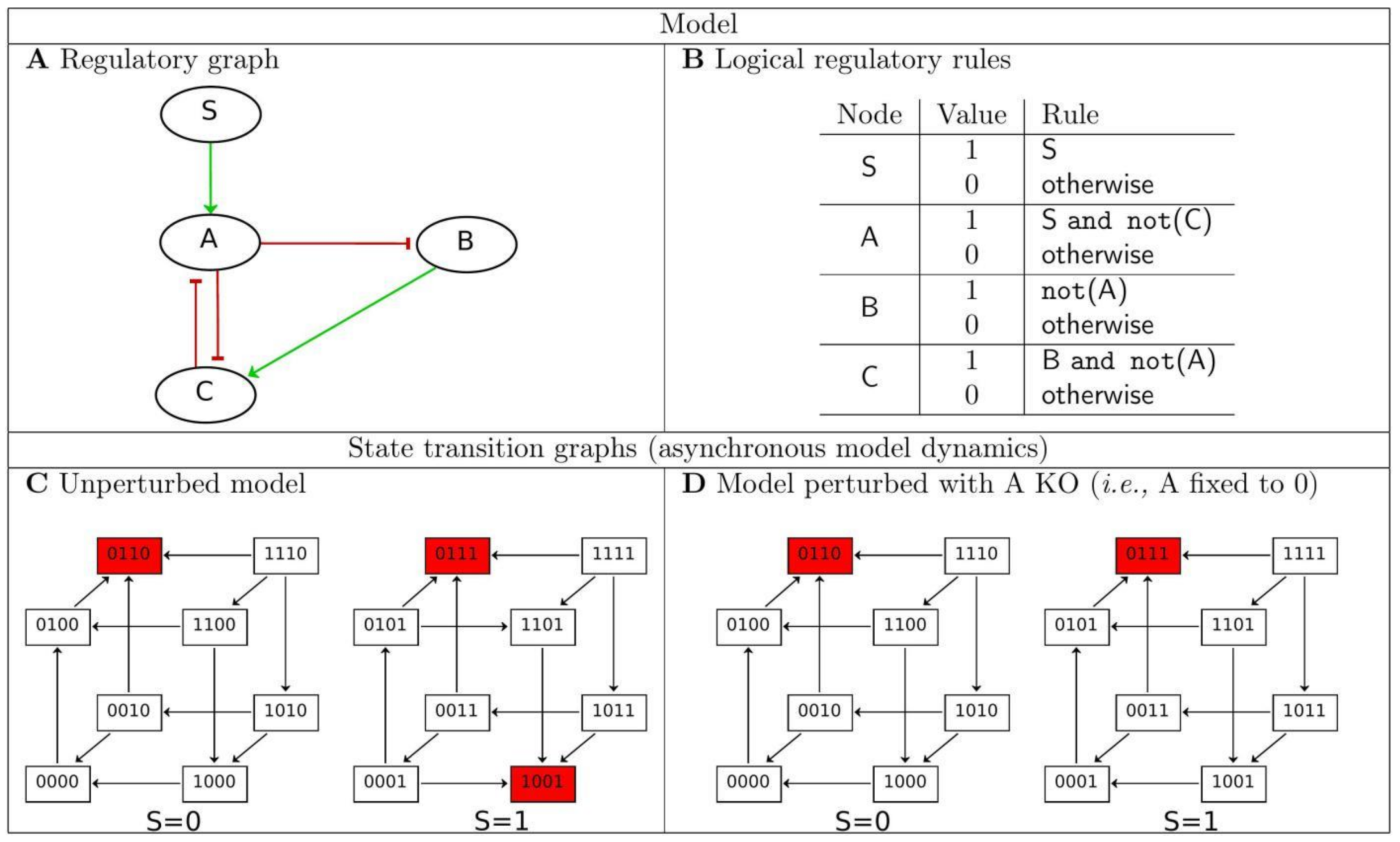
2.1. Basics of Logical Modelling
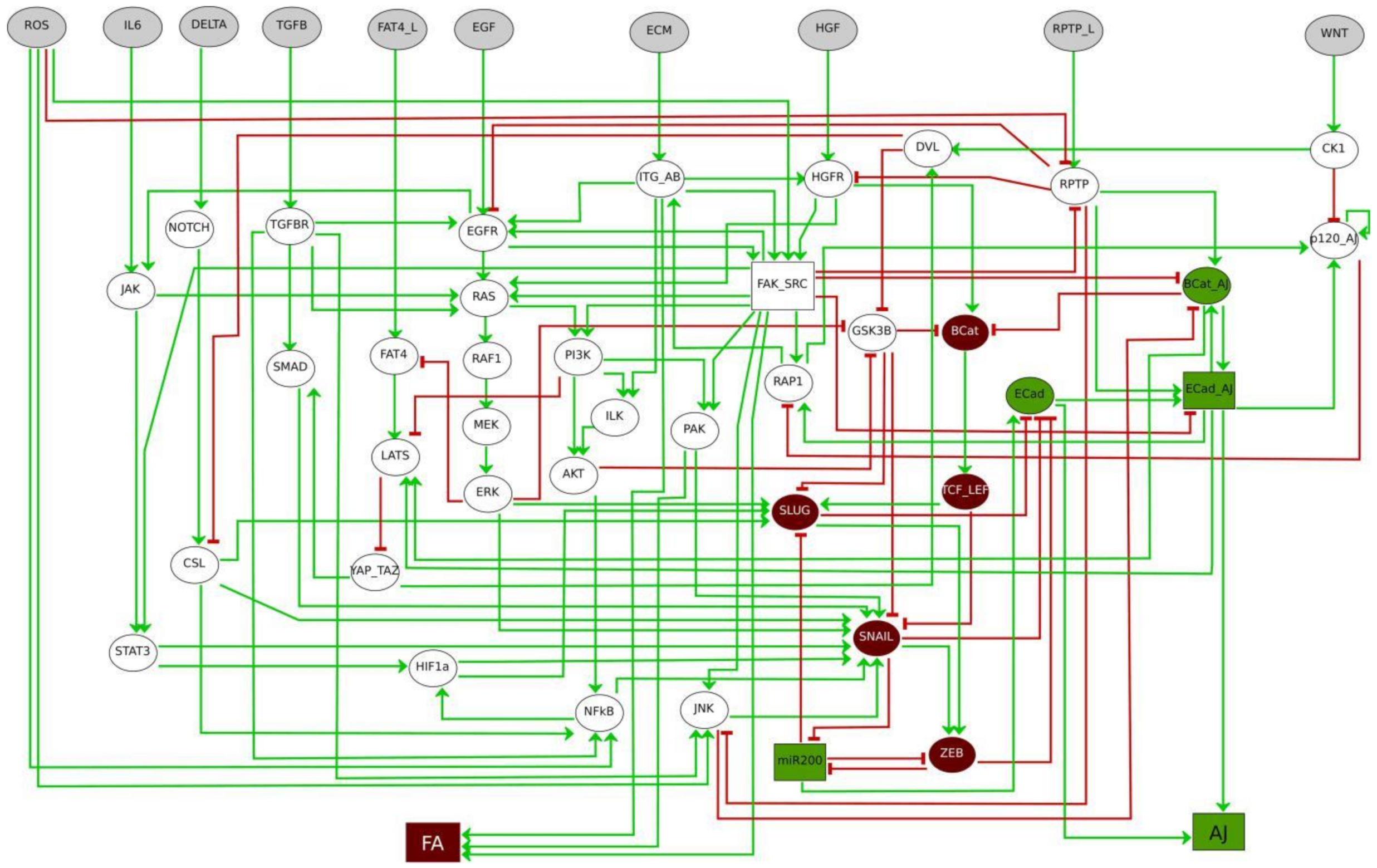
2.2. Logical Models and Their Contribution to Cooperative Oncogenesis
3. Logical Modelling Predicts Cooperative Signals Governing Phenotypes Amid the EMT Continuum
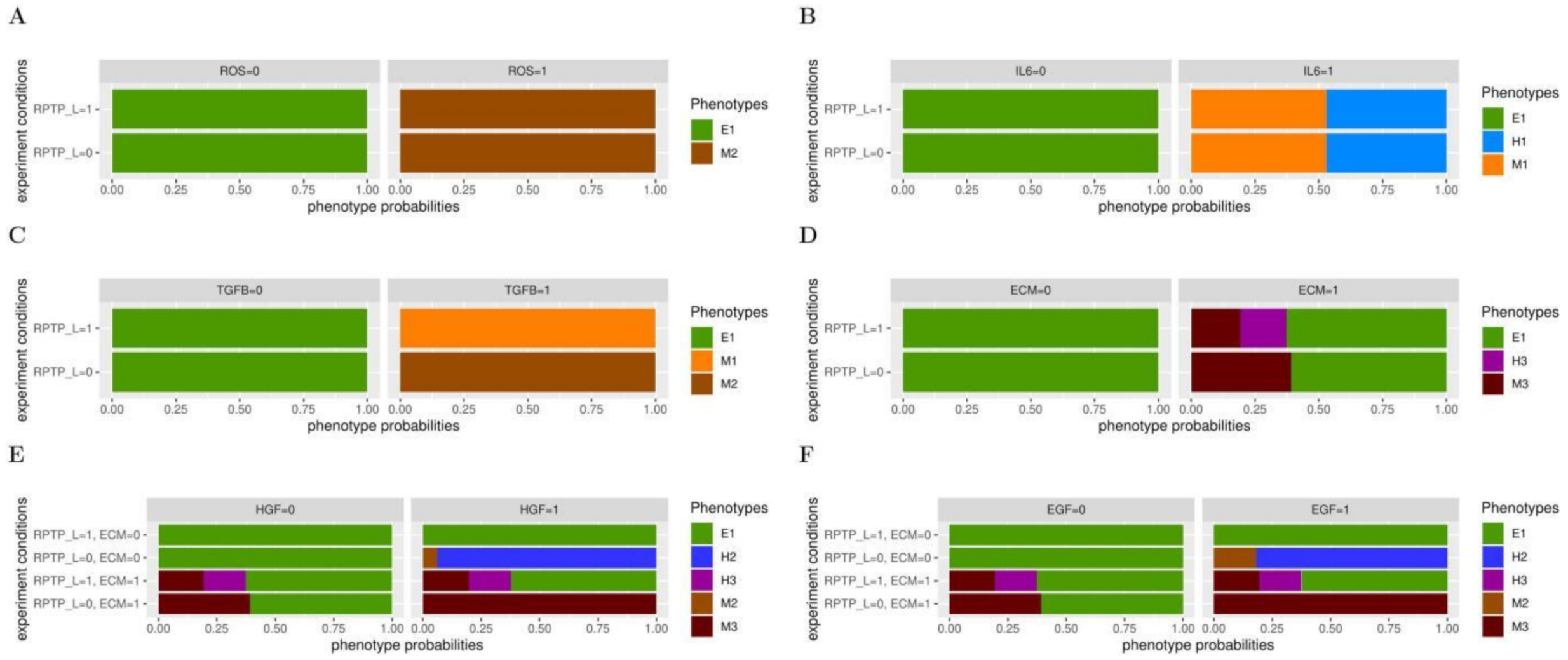
3.1. RPTP_L Cooperates with Inputs from the Microenvironment in EMT
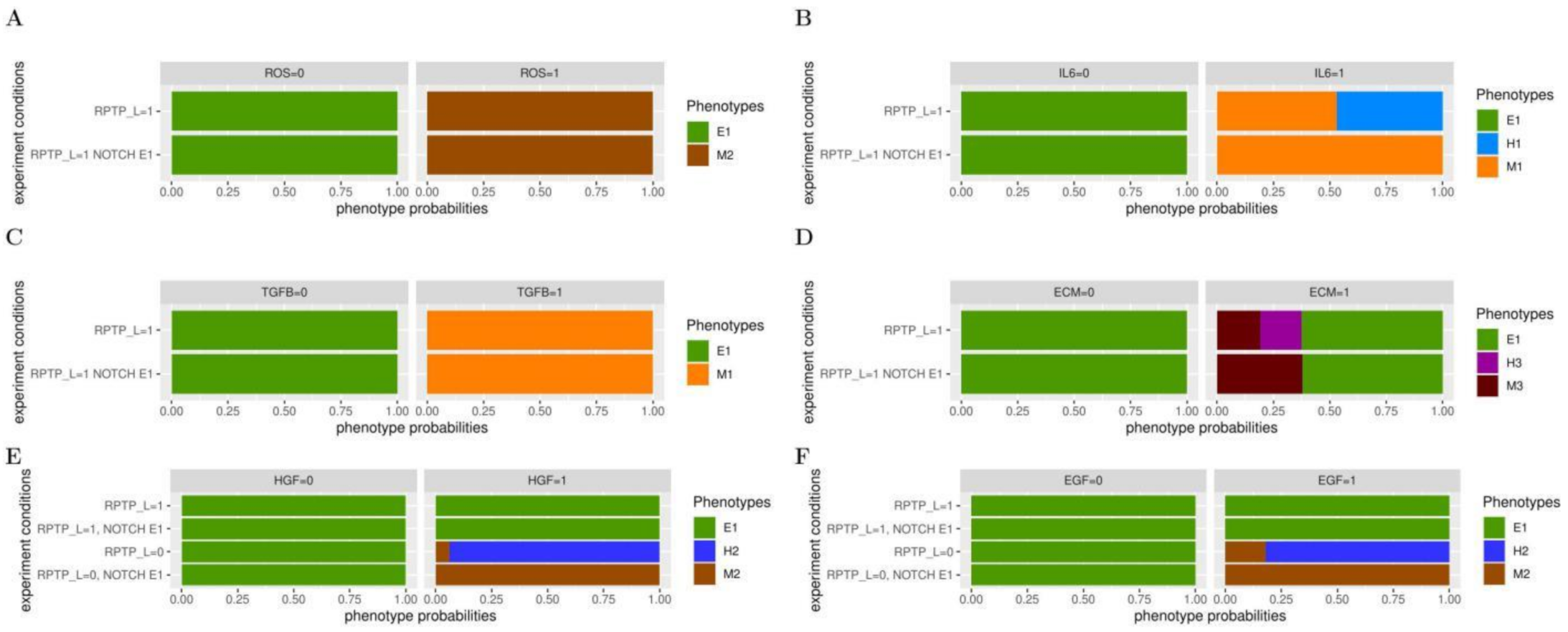
3.2. NOTCH Cooperates with Inputs from the Tumour Microenvironment in EMT
3.3. NOTCH Cooperates with Secondary Mutations in EMT
4. Conclusions and Prospects
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AJ | Adherens Junction |
| AKT | Protein kinase B |
| BCat | Catenin beta-1 |
| CDKN2A | Cyclin-Dependent Kinase inhibitor 2A |
| CK1 | Casein Kinase 1 |
| CRC | Colorectal Cancer |
| CRISPR | Clustered Regularly Interspaced Short Palindromic Repeats |
| CSC | Cancer Stem-like Cell |
| DELTA | Delta-like protein |
| DVL | Segment polarity protein dishevelled homolog |
| E2F | Transcription factor E2F |
| ECad | E-cadherin |
| ECM | Extracellular Matrix |
| EGF | Epidermal Growth Factor |
| EGFR | Epidermal Growth Factor Receptor |
| EMT | Epithelial-to-Mesenchymal Transition |
| ERK | Extracellular-signal-Regulated Kinase |
| FA | Focal Adhesion |
| FAK | Focal Adhesion Kinase |
| FAT4 | Protocadherin Fat 4 |
| FAT4_L | Protocadherin Fat 4 ligand |
| FGFR3 | Fibroblast Growth Factor Receptor 3 |
| GoF | Gain of Function |
| HCC | Hepatocellular Carcinoma |
| HGF | Hepatocyte Growth Factor |
| IL6 | Interleukin 6 |
| JAK | Janus Kinase |
| LATS | Large Tumour Suppressor kinase |
| LEF | Lymphoid enhancer-binding factor |
| LoF | Loss of Function |
| MAPK | Mitogen-Activated Protein Kinase |
| MDCK | Madin-Darby Canine Kidney |
| miR200 | miR-200 superfamily of miRNAs |
| p14 | ARF tumour suppressor |
| p21CIP | Cyclin–Dependent Kinase Inhibitors p21 |
| p38MAPK | p38 Mitogen-Activated Protein Kinases |
| p53 | Tumour protein P53 |
| PI3K | PhosphoInositide 3-Kinase |
| ROS | Reactive oxygen species |
| RPTP | Receptor-type tyrosine-protein phosphatase |
| RPTP_L | Receptor-type tyrosine-protein phosphatase ligand |
| RPTP-kappa | Receptor-type tyrosine-protein phosphatase kappa |
| SHH | Sonic hedgehog |
| SLUG | Zinc finger protein SNAI2 |
| SNAIL | Zinc finger protein SNAI1 |
| SRC | Proto-oncogene tyrosine-protein kinase |
| STAT | Signal Transducer and Activator of Transcription |
| TAZ | Transcriptional co-activator with PDZ binding motif |
| TCF | Transcription Factor 7 |
| TCGA | The Cancer Genome Atlas |
| TGFB | Transforming growth factor beta |
| TME | Tumour Microenvironment |
| WNT | Protein Wnt |
| YAP | Yes-Associated Protein |
| ZEB | Zinc finger E-box-binding homeobox |
References
- Olivier, M.; Asmis, R.; Hawkins, G.A.; Howard, T.D.; Cox, L.A. The Need for Multi-Omics Biomarker Signatures in Precision Medicine. Int. J. Mol. Sci. 2019, 20, 4781. [Google Scholar] [CrossRef] [PubMed]
- Shanmuganathan, N.; Branford, S. The Hidden Pathogenesis of CML: Is BCR-ABL1 the First Event? Curr. Hematol. Malig. Rep. 2019, 14, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Armitage, P.; Doll, R. The age distribution of cancer and a multi-stage theory of carcinogenesis. Br. J. Cancer 1954, 8, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Bowler, E.H.; Wang, Z.; Ewing, R.M. How do oncoprotein mutations rewire protein-protein interaction networks? Expert Rev. Proteomics 2015, 12, 449–455. [Google Scholar] [CrossRef][Green Version]
- Merlo, L.M.F.; Pepper, J.W.; Reid, B.J.; Maley, C.C. Cancer as an evolutionary and ecological process. Nat. Rev. Cancer 2006, 6, 924–935. [Google Scholar] [CrossRef]
- Di Giorgio, E.; Paluvai, H.; Picco, R.; Brancolini, C. Genetic Programs Driving Oncogenic Transformation: Lessons from In Vitro Models. Int. J. Mol. Sci. 2019, 20, 6283. [Google Scholar] [CrossRef]
- Knudson, A.G. Two genetic hits (more or less) to cancer. Nat. Rev. Cancer 2001, 1, 157–162. [Google Scholar] [CrossRef]
- Land, H.; Parada, L.F.; Weinberg, R.A. Tumorigenic conversion of primary embryo fibroblasts requires at least two cooperating oncogenes. Nature 1983, 304, 596–602. [Google Scholar] [CrossRef]
- Hahn, W.C.; Counter, C.M.; Lundberg, A.S.; Beijersbergen, R.L.; Brooks, M.W.; Weinberg, R.A. Creation of human tumour cells with defined genetic elements. Nature 1999, 400, 464–468. [Google Scholar] [CrossRef]
- Richardson, H.E.; Portela, M. Modelling Cooperative Tumorigenesis in Drosophila. Biomed Res. Int. 2018, 2018. [Google Scholar] [CrossRef]
- Wang, M.; Zhao, J.; Zhang, L.; Wei, F.; Lian, Y.; Wu, Y.; Gong, Z.; Zhang, S.; Zhou, J.; Cao, K.; et al. Role of tumor microenvironment in tumorigenesis. J. Cancer 2017, 8, 761–773. [Google Scholar] [CrossRef]
- Wu, M.; Pastor-Pareja, J.C.; Xu, T. Interaction between Ras V12 and scribbled clones induces tumour growth and invasion. Nature 2010, 463, 545–548. [Google Scholar] [CrossRef]
- Cleary, A.S.; Leonard, T.L.; Gestl, S.A.; Gunther, E.J. Tumour cell heterogeneity maintained by cooperating subclones in Wnt-driven mammary cancers. Nature 2014, 508, 113–117. [Google Scholar] [CrossRef]
- Zhang, M.; Tsimelzon, A.; Chang, C.-H.; Fan, C.; Wolff, A.; Perou, C.M.; Hilsenbeck, S.G.; Rosen, J.M. Intratumoral Heterogeneity in a Trp53-Null Mouse Model of Human Breast Cancer. Cancer Discov. 2015, 5, 520–533. [Google Scholar] [CrossRef]
- Neelakantan, D.; Zhou, H.; Oliphant, M.U.J.; Zhang, X.; Simon, L.M.; Henke, D.M.; Shaw, C.A.; Wu, M.-F.; Hilsenbeck, S.G.; White, L.D.; et al. EMT cells increase breast cancer metastasis via paracrine GLI activation in neighbouring tumour cells. Nat. Commun. 2017, 8, 15773. [Google Scholar] [CrossRef]
- Alexandrov, L.B.; Nik-Zainal, S.; Wedge, D.C.; Aparicio, S.A.J.R.; Behjati, S.; Biankin, A.V.; Bignell, G.R.; Bolli, N.; Borg, A.; Børresen-Dale, A.L.; et al. Signatures of mutational processes in human cancer. Nature 2013, 500, 415–421. [Google Scholar] [CrossRef]
- Kim, J.E.; Stones, C.; Joseph, W.R.; Leung, E.; Finlay, G.J.; Shelling, A.N.; Phillips, W.A.; Shepherd, P.R.; Baguley, B.C. Comparison of growth factor signalling pathway utilisation in cultured normal melanocytes and melanoma cell lines. BMC Cancer 2012, 12. [Google Scholar] [CrossRef]
- Stepanenko, A.A.; Vassetzky, Y.S.; Kavsan, V.M. Antagonistic functional duality of cancer genes. Gene 2013, 529, 199–207. [Google Scholar] [CrossRef]
- Caroli, J.; Dori, M.; Bicciato, S. Computational Methods for the Integrative Analysis of Genomics and Pharmacological Data. Front. Oncol. 2020, 10. [Google Scholar] [CrossRef]
- Onaciu, A.; Munteanu, R.; Munteanu, V.C.; Gulei, D.; Raduly, L.; Feder, R.I.; Pirlog, R.; Atanasov, A.G.; Korban, S.S.; Irimie, A.; et al. Spontaneous and Induced Animal Models for Cancer Research. Diagnostics 2020, 10, 660. [Google Scholar] [CrossRef]
- Bangi, E. Strategies for Functional Interrogation of Big Cancer Data Using Drosophila Cancer Models. Int. J. Mol. Sci. 2020, 21, 3754. [Google Scholar] [CrossRef]
- Kholodenko, B.; Yaffe, M.B.; Kolch, W. Computational approaches for analyzing information flow in biological networks. Sci. Signal. 2012, 5. [Google Scholar] [CrossRef]
- Samaga, R.; Klamt, S. Modeling approaches for qualitative and semi-quantitative analysis of cellular signaling networks. Cell Commun. Signal. 2013, 11. [Google Scholar] [CrossRef]
- Le Novère, N. Quantitative and logic modelling of molecular and gene networks. Nat. Rev. Genet. 2015, 16, 146–158. [Google Scholar] [CrossRef]
- Mendes, N.D.; Henriques, R.; Remy, E.; Carneiro, J.; Monteiro, P.T.; Chaouiya, C. Estimating Attractor Reachability in Asynchronous Logical Models. Front Physiol 2018, 9, 1161. [Google Scholar] [CrossRef]
- Abou-Jaoudé, W.; Traynard, P.; Monteiro, P.T.; Saez-Rodriguez, J.; Helikar, T.; Thieffry, D.; Chaouiya, C. Logical Modeling and Dynamical Analysis of Cellular Networks. Front. Genet. 2016, 7, 94. [Google Scholar] [CrossRef]
- Kauffman, S. Differentiation of malignant to benign cells. J. Theor. Biol. 1971, 31, 429–451. [Google Scholar] [CrossRef]
- Huang, S. Gene expression profiling, genetic networks, and cellular states: An integrating concept for tumorigenesis and drug discovery. J. Mol. Med. 1999, 77, 469–480. [Google Scholar] [CrossRef]
- Thomas, R.; D’Ari, R. Biological Feedback; CRC Press: Boca Raton, FL, USA, 1990; ISBN 9780849367663. [Google Scholar]
- Albert, R.; Thakar, J. Boolean modeling: A logic-based dynamic approach for understanding signaling and regulatory networks and for making useful predictions. Wiley Interdiscip. Rev. Syst. Biol. Med. 2014, 6, 353–369. [Google Scholar] [CrossRef]
- Traynard, P.; Tobalina, L.; Eduati, F.; Calzone, L.; Saez-Rodriguez, J. Logic modeling in quantitative systems pharmacology. CPT Pharmacometrics Syst. Pharmacol. 2017, 6, 499–511. [Google Scholar] [CrossRef]
- Zañudo, G.T.J.; Steinway, S.N.; Albert, R. Discrete dynamic network modeling of oncogenic signaling: Mechanistic insights for personalized treatment of cancer. Curr. Opin. Syst. Biol. 2018, 9, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Beal, J.; Montagud, A.; Traynard, P.; Barillot, E.; Calzone, L. Personalization of logical models with multi-omics data allows clinical stratification of patients. Front. Physiol. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Gjerga, E.; Trairatphisan, P.; Gabor, A.; Koch, H.; Chevalier, C.; Ceccarelli, F.; Dugourd, A.; Mitsos, A.; Saez-Rodriguez, J. Converting networks to predictive logic models from perturbation signalling data with CellNOpt. Bioinformatics 2020, 36, 4523–4524. [Google Scholar] [CrossRef] [PubMed]
- Grieco, L.; Calzone, L.; Bernard-Pierrot, I.; Radvanyi, F.; Kahn-Perlès, B.; Thieffry, D. Integrative Modelling of the Influence of MAPK Network on Cancer Cell Fate Decision. PLoS Comput. Biol. 2013, 9. [Google Scholar] [CrossRef]
- Remy, E.; Rebouissou, S.; Chaouiya, C.; Zinovyev, A.; Radvanyi, F.; Calzone, L. A Modeling Approach to Explain Mutually Exclusive and Co-Occurring Genetic Alterations in Bladder Tumorigenesis. Cancer Res. 2015, 75, 4042–4052. [Google Scholar] [CrossRef]
- Rossato, V.V.; Silveira, D.A.; Gupta, S.; Mombach, J.C.M. Towards the contribution of the p38MAPK pathway to the dual role of TGFβ in cancer: A boolean model approach. Comput. Biol. Med. 2019, 104, 235–240. [Google Scholar] [CrossRef]
- Gómez Tejeda Zañudo, J.; Guinn, M.T.; Farquhar, K.; Szenk, M.; Steinway, S.N.; Balázsi, G.; Albert, R. Towards control of cellular decision-making networks in the epithelial-to-mesenchymal transition. Phys. Biol. 2019, 16, 031002. [Google Scholar] [CrossRef]
- Jolly, M.K.; Somarelli, J.A.; Sheth, M.; Biddle, A.; Tripathi, S.C.; Armstrong, A.J.; Hanash, S.M.; Bapat, S.A.; Rangarajan, A.; Levine, H. Hybrid epithelial/mesenchymal phenotypes promote metastasis and therapy resistance across carcinomas. Pharmacol. Ther. 2019, 194, 161–184. [Google Scholar] [CrossRef]
- Steinway, S.N.; Zañudo, J.G.T.; Ding, W.; Rountree, C.B.; Feith, D.J.; Loughran Jr, T.P.; Albert, R. Network modeling of TGFβ signaling in hepatocellular carcinoma epithelial-to-mesenchymal transition reveals joint sonic hedgehog and Wnt pathway activation. Cancer Res 2014, 74, 5963–5977. [Google Scholar] [CrossRef]
- Steinway, S.N.; Zañudo, J.G.T.; Michel, P.J.; Feith, D.J.; Loughran, T.P.; Albert, R. Combinatorial interventions inhibit TGFβ-driven epithelial-to-mesenchymal transition and support hybrid cellular phenotypes. npj Syst. Biol. Appl. 2015, 1, 15014. [Google Scholar] [CrossRef]
- Cohen, D.P.A.; Martignetti, L.; Robine, S.; Barillot, E.; Zinovyev, A.; Calzone, L. Mathematical Modelling of Molecular Pathways Enabling Tumour Cell Invasion and Migration. PLoS Comput. Biol. 2015, 11, e1004571. [Google Scholar] [CrossRef]
- Méndez-López, L.F.; Davila-Velderrain, J.; Domínguez-Hüttinger, E.; Enríquez-Olguín, C.; Martínez-García, J.C.; Alvarez-Buylla, E.R. Gene regulatory network underlying the immortalization of epithelial cells. BMC Syst. Biol. 2017, 11, 1–15. [Google Scholar] [CrossRef]
- Selvaggio, G.; Canato, S.; Pawar, A.; Monteiro, P.T.; Guerreiro, P.S.; Brás, M.M.; Janody, F.; Chaouiya, C. Hybrid Epithelial-Mesenchymal Phenotypes Are Controlled by Microenvironmental Factors. Cancer Res. 2020, 80, 2407–2420. [Google Scholar] [CrossRef]
- Flobak, Å.; Baudot, A.; Remy, E.; Thommesen, L.; Thieffry, D.; Kuiper, M.; Lægreid, A. Discovery of Drug Synergies in Gastric Cancer Cells Predicted by Logical Modeling. PLoS Comput. Biol. 2015, 11. [Google Scholar] [CrossRef]
- Terfve, C.; Cokelaer, T.; Henriques, D.; MacNamara, A.; Goncalves, E.; Morris, M.K.; van Iersel, M.; Lauffenburger, D.A.; Saez-Rodriguez, J. CellNOptR: a flexible toolkit to train protein signaling networks to data using multiple logic formalisms. BMC Syst Biol 2012, 6, 133. [Google Scholar] [CrossRef]
- Rodriguez, A.; Crespo, I.; Androsova, G.; Del Sol, A. Discrete logic modelling optimization to contextualize prior knowledge networks using PRUNET. PLoS ONE 2015, 10. [Google Scholar] [CrossRef]
- Fumiã, H.F.; Martins, M.L. Boolean Network Model for Cancer Pathways: Predicting Carcinogenesis and Targeted Therapy Outcomes. PLoS ONE 2013, 8. [Google Scholar] [CrossRef]
- Curtis, C.; Shah, S.P.; Chin, S.F.; Turashvili, G.; Rueda, O.M.; Dunning, M.J.; Speed, D.; Lynch, A.G.; Samarajiwa, S.; Yuan, Y.; et al. The genomic and transcriptomic architecture of 2,000 breast tumours reveals novel subgroups. Nature 2012, 486, 346–352. [Google Scholar] [CrossRef]
- Pereira, B.; Chin, S.F.; Rueda, O.M.; Vollan, H.K.M.; Provenzano, E.; Bardwell, H.A.; Pugh, M.; Jones, L.; Russell, R.; Sammut, S.J.; et al. The somatic mutation profiles of 2,433 breast cancers refines their genomic and transcriptomic landscapes. Nat. Commun. 2016, 7. [Google Scholar] [CrossRef]
- Keating, S.M.; Waltemath, D.; König, M.; Zhang, F.; Dräger, A.; Chaouiya, C.; Bergmann, F.T.; Finney, A.; Gillespie, C.S.; Helikar, T.; et al. SBML Level 3: an extensible format for the exchange and reuse of biological models. Mol. Syst. Biol. 2020, 16. [Google Scholar] [CrossRef]
- Naldi, A.; Monteiro, P.T.; Müssel, C.; Kestler, H.A.; Thieffry, D.; Xenarios, I.; Saez-Rodriguez, J.; Helikar, T.; Chaouiya, C.; Albert, R.; et al. Cooperative development of logical modelling standards and tools with CoLoMoTo. Bioinformatics 2015, 31, 1154–1159. [Google Scholar] [CrossRef]
- Naldi, A.; Hernandez, C.; Levy, N.; Stoll, G.; Monteiro, P.T.; Chaouiya, C.; Helikar, T.; Zinovyev, A.; Calzone, L.; Cohen-Boulakia, S.; et al. The CoLoMoTo interactive notebook: Accessible and reproducible computational analyses for qualitative biological networks. Front. Physiol. 2018, 9. [Google Scholar] [CrossRef]
- Naldi, A.; Hernandez, C.; Levy, N.; Stoll, G.; Monteiro, P.T.; Chaouiya, C.; Helikar, T.; Zinovyev, A.; Calzone, L.; Cohen-Boulakia, S.; et al. Prediction of Mutations to Control Pathways Enabling Tumor Cell Invasion with the CoLoMoTo Interactive Notebook (Tutorial). Front. Physiol. 2018, 9. [Google Scholar] [CrossRef]
- Naldi, A.; Berenguier, D.; Fauré, A.; Lopez, F.; Thieffry, D.; Chaouiya, C. Logical modelling of regulatory networks with GINsim 2.3. Biosystems 2009, 97, 134–139. [Google Scholar] [CrossRef]
- Craig, S.E.L.; Brady-Kalnay, S.M. Regulation of development and cancer by the R2B subfamily of RPTPs and the implications of proteolysis. Semin. Cell Dev. Biol. 2015, 37, 108–118. [Google Scholar] [CrossRef]
- Kwon, O.-J.; Valdez, J.M.; Zhang, L.; Zhang, B.; Wei, X.; Su, Q.; Ittmann, M.M.; Creighton, C.J.; Xin, L. Increased Notch signalling inhibits anoikis and stimulates proliferation of prostate luminal epithelial cells. Nat. Commun. 2014, 5, 4416. [Google Scholar] [CrossRef]
- Mori, K.; Shibanuma, M.; Nose, K. Invasive potential induced under long-term oxidative stress in mammary epithelial cells. Cancer Res. 2004, 64, 7464–7472. [Google Scholar] [CrossRef]
- Peinado, H.; Quintanilla, M.; Cano, A. Transforming growth factor β-1 induces Snail transcription factor in epithelial cell lines. Mechanisms for epithelial mesenchymal transitions. J. Biol. Chem. 2003, 278, 21113–21123. [Google Scholar] [CrossRef]
- Wei, S.C.; Fattet, L.; Tsai, J.H.; Guo, Y.; Pai, V.H.; Majeski, H.E.; Chen, A.C.; Sah, R.L.; Taylor, S.S.; Engler, A.J.; et al. Matrix stiffness drives epithelial–mesenchymal transition and tumour metastasis through a TWIST1–G3BP2 mechanotransduction pathway. Nat. Cell Biol. 2015, 17, 678–688. [Google Scholar] [CrossRef]
- Farrell, J.; Kelly, C.; Rauch, J.; Kida, K.; García-Muñoz, A.; Monsefi, N.; Turriziani, B.; Doherty, C.; Mehta, J.P.; Matallanas, D.; et al. HGF induces epithelial-to-mesenchymal transition by modulating the mammalian Hippo/MST2 and ISG15 pathways. J. Proteome Res. 2014, 13, 2874–2886. [Google Scholar] [CrossRef] [PubMed]
- Ogunwobi, O.O.; Liu, C. Hepatocyte growth factor upregulation promotes carcinogenesis and epithelial-mesenchymal transition in hepatocellular carcinoma via Akt and COX-2 pathways. Clin. Exp. Metastasis 2011, 28, 721–731. [Google Scholar] [CrossRef] [PubMed]
- Mittal, S.; Subramanyam, D.; Dey, D.; Kumar, R.V.; Rangarajan, A. Cooperation of Notch and Ras/MAPK signaling pathways in human breast carcinogenesis. Mol. Cancer 2009, 8, 128. [Google Scholar] [CrossRef] [PubMed]
- Katoh, M.; Katoh, M. Precision medicine for human cancers with Notch signaling dysregulation (Review). Int. J. Mol. Med. 2020, 45, 279–297. [Google Scholar] [CrossRef] [PubMed]
- Dongre, A.; Weinberg, R.A. New insights into the mechanisms of epithelial–mesenchymal transition and implications for cancer. Nat. Rev. Mol. Cell Biol. 2019, 20, 69–84. [Google Scholar] [CrossRef]
- Naldi, A. BioLQM: a java toolkit for the manipulation and conversion of Logical Qualitative Models of biological networks. Front. Physiol. 2018, 9, 1605. [Google Scholar] [CrossRef]
- Liu, Z.; Li, H.; Fan, S.; Lin, H.; Lian, W. STAT3-induced upregulation of long noncoding RNA HNF1A-AS1 promotes the progression of oral squamous cell carcinoma via activating Notch signaling pathway. Cancer Biol. Ther. 2019, 20, 444–453. [Google Scholar] [CrossRef]
- Bui, Q.T.; Im, J.H.; Jeong, S.B.; Kim, Y.M.; Lim, S.C.; Kim, B.; Kang, K.W. Essential role of Notch4/STAT3 signaling in epithelial–mesenchymal transition of tamoxifen-resistant human breast cancer. Cancer Lett. 2017, 390, 115–125. [Google Scholar] [CrossRef]
- Kwon, O.J.; Zhang, L.; Wang, J.; Su, Q.; Feng, Q.; Zhang, X.H.F.; Mani, S.A.; Paulter, R.; Creighton, C.J.; Ittmann, M.M.; et al. Notch promotes tumor metastasis in a prostate-specific Pten-null mouse model. J. Clin. Investig. 2016, 126, 2626–2641. [Google Scholar] [CrossRef]
- Pannuti, A.; Foreman, K.; Rizzo, P.; Osipo, C.; Golde, T.; Osborne, B.; Miele, L. Targeting Notch to target cancer stem cells. Clin. Cancer Res. 2010, 16, 3141–3152. [Google Scholar] [CrossRef]
- Rayon, T.; Menchero, S.; Nieto, A.; Xenopoulos, P.; Crespo, M.; Cockburn, K.; Cañon, S.; Sasaki, H.; Hadjantonakis, A.K.; de la Pompa, J.L.; et al. Notch and Hippo Converge on Cdx2 to Specify the Trophectoderm Lineage in the Mouse Blastocyst. Dev. Cell 2014, 30, 410–422. [Google Scholar] [CrossRef]
- Watanabe, Y.; Miyasaka, K.Y.; Kubo, A.; Kida, Y.S.; Nakagawa, O.; Hirate, Y.; Sasaki, H.; Ogura, T. Notch and Hippo signaling converge on Strawberry Notch 1 (Sbno1) to synergistically activate Cdx2 during specification of the trophectoderm. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Yamamizu, K.; Matsunaga, T.; Uosaki, H.; Fukushima, H.; Katayama, S.; Hiraoka-Kanie, M.; Mitani, K.; Yamashita, J.K. Convergence of Notch and β-catenin signaling induces arterial fate in vascular progenitors. J. Cell Biol. 2010, 189, 325–338. [Google Scholar] [CrossRef]
- Bedard, P.L.; Hyman, D.M.; Davids, M.S.; Siu, L.L. Small molecules, big impact: 20 years of targeted therapy in oncology. Lancet 2020, 395, 1078–1088. [Google Scholar] [CrossRef]
- Wong, C.H.; Siah, K.W.; Lo, A.W. Estimation of clinical trial success rates and related parameters. Biostatistics 2019, 20, 273–286. [Google Scholar] [CrossRef]
- Janiszewska, M.; Primi, M.C.; Izard, T. Cell adhesion in cancer: Beyond the migration of single cells. J. Biol. Chem. 2020, 295, 2495–2505. [Google Scholar] [CrossRef]
- Hardy, S.G.; Julien, S.L.; Tremblay, M. Impact of Oncogenic Protein Tyrosine Phosphatases in Cancer. Anticancer. Agents Med. Chem. 2012, 12, 4–18. [Google Scholar] [CrossRef]
- Comte, B.; Baumbach, J.; Benis, A.; Basílio, J.; Debeljak, N.; Flobak, Å.; Franken, C.; Harel, N.; He, F.; Kuiper, M.; et al. Network and Systems Medicine: Position Paper of the European Collaboration on Science and Technology Action on Open Multiscale Systems Medicine. Netw. Syst. Med. 2020, 3, 67–90. [Google Scholar] [CrossRef]
- De Jong, H. Modeling and simulation of genetic regulatory systems: A literature review. J. Comput. Biol. 2002, 9, 67–103. [Google Scholar] [CrossRef]
- Varela, P.L.; Ramos, C.V.; Monteiro, P.T.; Chaouiya, C. EpiLog: A software for the logical modelling of epithelial dynamics (version 2; referees: 3 approved). F1000Research 2018, 7. [Google Scholar] [CrossRef]
- Letort, G.; Montagud, A.; Stoll, G.; Heiland, R.; Barillot, E.; Macklin, P.; Zinovyev, A.; Calzone, L. PhysiBoSS: A multi-scale agent-based modelling framework integrating physical dimension and cell signalling. Bioinformatics 2018. [Google Scholar] [CrossRef]
- Malik-Sheriff, R.S.; Glont, M.; Nguyen, T.V.N.; Tiwari, K.; Roberts, M.G.; Xavier, A.; Vu, M.T.; Men, J.; Maire, M.; Kananathan, S.; et al. BioModels-15 years of sharing computational models in life science. Nucleic Acids Res. 2020, 48, D407–D415. [Google Scholar] [CrossRef] [PubMed]
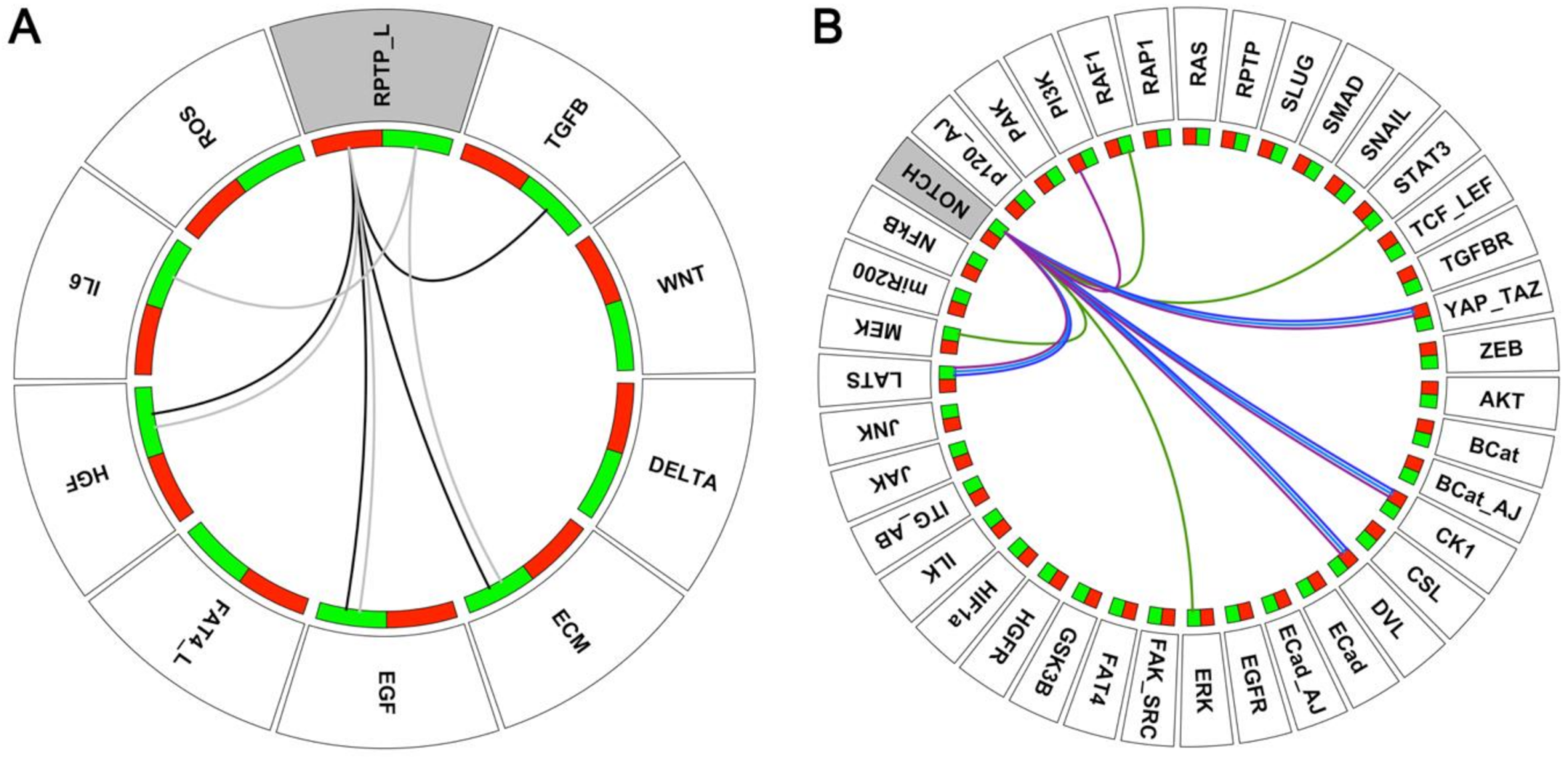
| Phenotypes | Adherens Junctions (AJs) | Focal Adhesions (FAs) | Description | |
|---|---|---|---|---|
 | Epithelial | 2 | 0 | AJ assembly due to ECad-BCat interaction at the membrane |
 | Hybrid | 2 | 1 | AJ assembly due to ECad-BCat interaction at the membrane, combined with a weak ability to recycle FAs |
 | 1 | 2 | Failure to assemble AJs while maintaining ECad expression, combined with an intermediate ability to recycle FAs | |
 | 2 | 3 | AJ assembly due to Ecad-Bcat interaction at the membrane, combined with a high ability to recycle FAs | |
 | Unknown | 0 | 0 | Lack of either epithelial or mesenchymal markers, undefined phenotype |
 | Mesenchymal | 0 | 1 | Failure to assemble AJs and to express epithelial markers, combined with the expression of mesenchymal markers and a weak ability to recycle FAs |
 | 0 | 2 | Failure to assemble AJs and to express epithelial markers, combined with the expression of mesenchymal markers and an intermediate ability to recycle FAs | |
 | 0 | 3 | Failure to assemble AJs and to express epithelial markers, combined with the expression of mesenchymal markers and a high ability to recycle FAs | |
| Phenotypes | AJ stability | FA recycling | Unperturbed model | NOTCH E1 | RAF E1 | NOTCH E1 RAF E1 | MEK E1 | MEK E1 NOTCH E1 | ERK E1 | ERK E1 NOTCH E1 | STAT3 E1 | STAT3 E1 NOTCH E1 | PI3K KO | PI3K KO NOTCH E1 | LATS E1 | LATS E1 NOTCH E1 | YAP_TAZ KO | YAP_TAZ KO NOTCH E1 | DVL KO | DVL KO NOTCH E1 | CK1 KO | CK1 KO NOTCH E1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | Epithelial | 2 | 0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||
 | Hybrid | 2 | 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
 | 1 | 2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||
 | 2 | 3 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
 | Unknown | 0 | 0 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
 | Mesenchymal | 0 | 1 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
 | 0 | 2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
 | 0 | 3 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selvaggio, G.; Chaouiya, C.; Janody, F. In Silico Logical Modelling to Uncover Cooperative Interactions in Cancer. Int. J. Mol. Sci. 2021, 22, 4897. https://doi.org/10.3390/ijms22094897
Selvaggio G, Chaouiya C, Janody F. In Silico Logical Modelling to Uncover Cooperative Interactions in Cancer. International Journal of Molecular Sciences. 2021; 22(9):4897. https://doi.org/10.3390/ijms22094897
Chicago/Turabian StyleSelvaggio, Gianluca, Claudine Chaouiya, and Florence Janody. 2021. "In Silico Logical Modelling to Uncover Cooperative Interactions in Cancer" International Journal of Molecular Sciences 22, no. 9: 4897. https://doi.org/10.3390/ijms22094897
APA StyleSelvaggio, G., Chaouiya, C., & Janody, F. (2021). In Silico Logical Modelling to Uncover Cooperative Interactions in Cancer. International Journal of Molecular Sciences, 22(9), 4897. https://doi.org/10.3390/ijms22094897







