On the Role of Curved Membrane Nanodomains and Passive and Active Skeleton Forces in the Determination of Cell Shape and Membrane Budding
Abstract
1. Introduction
2. Modeling of Closed Membrane Shapes
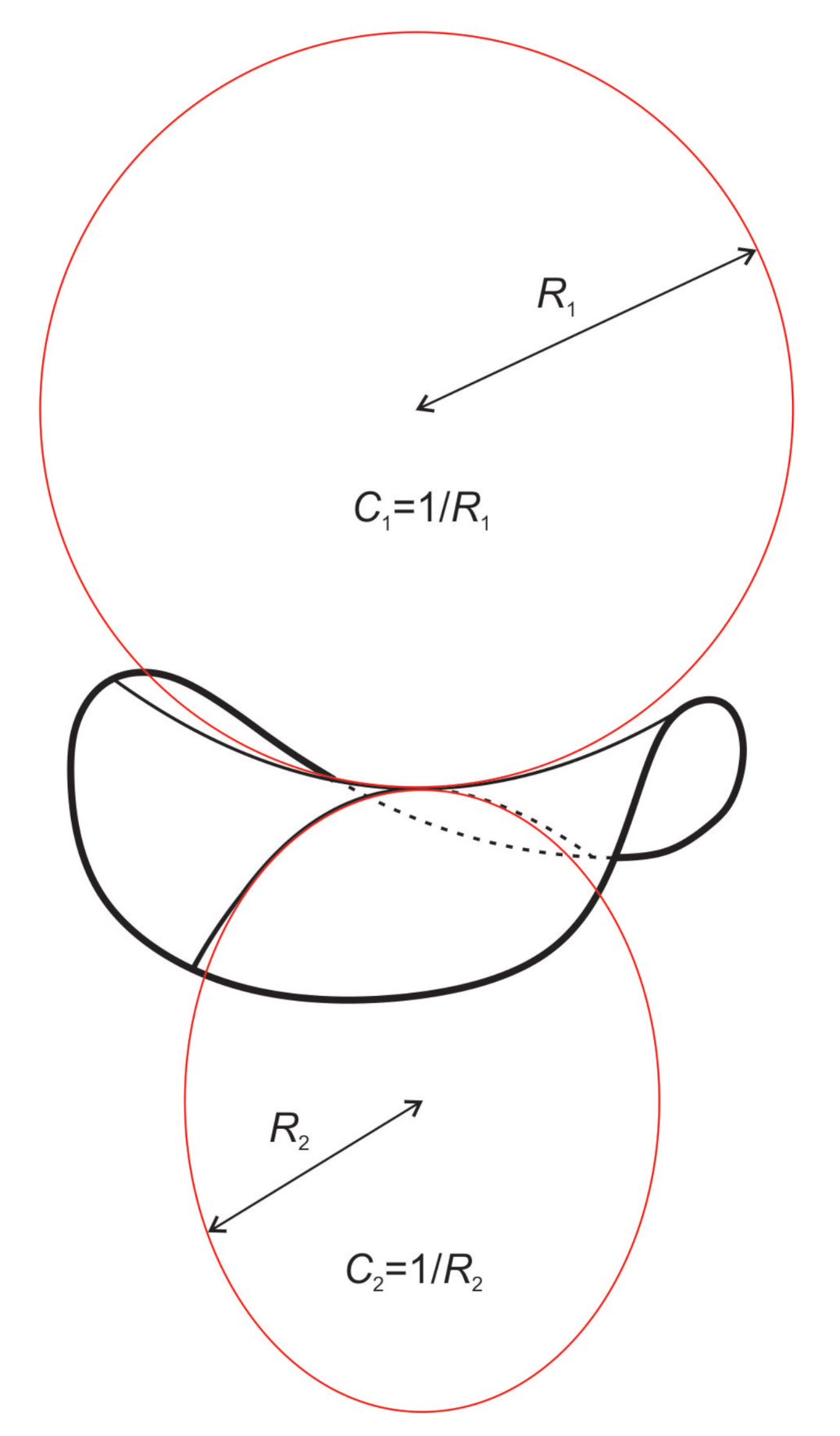
2.1. Deviatoric Elasticity Model
2.2. Elastic Constants and Intrinsic Curvatures of Protein-Induced Nanodomain as a Function of Lipid and Protein Properties
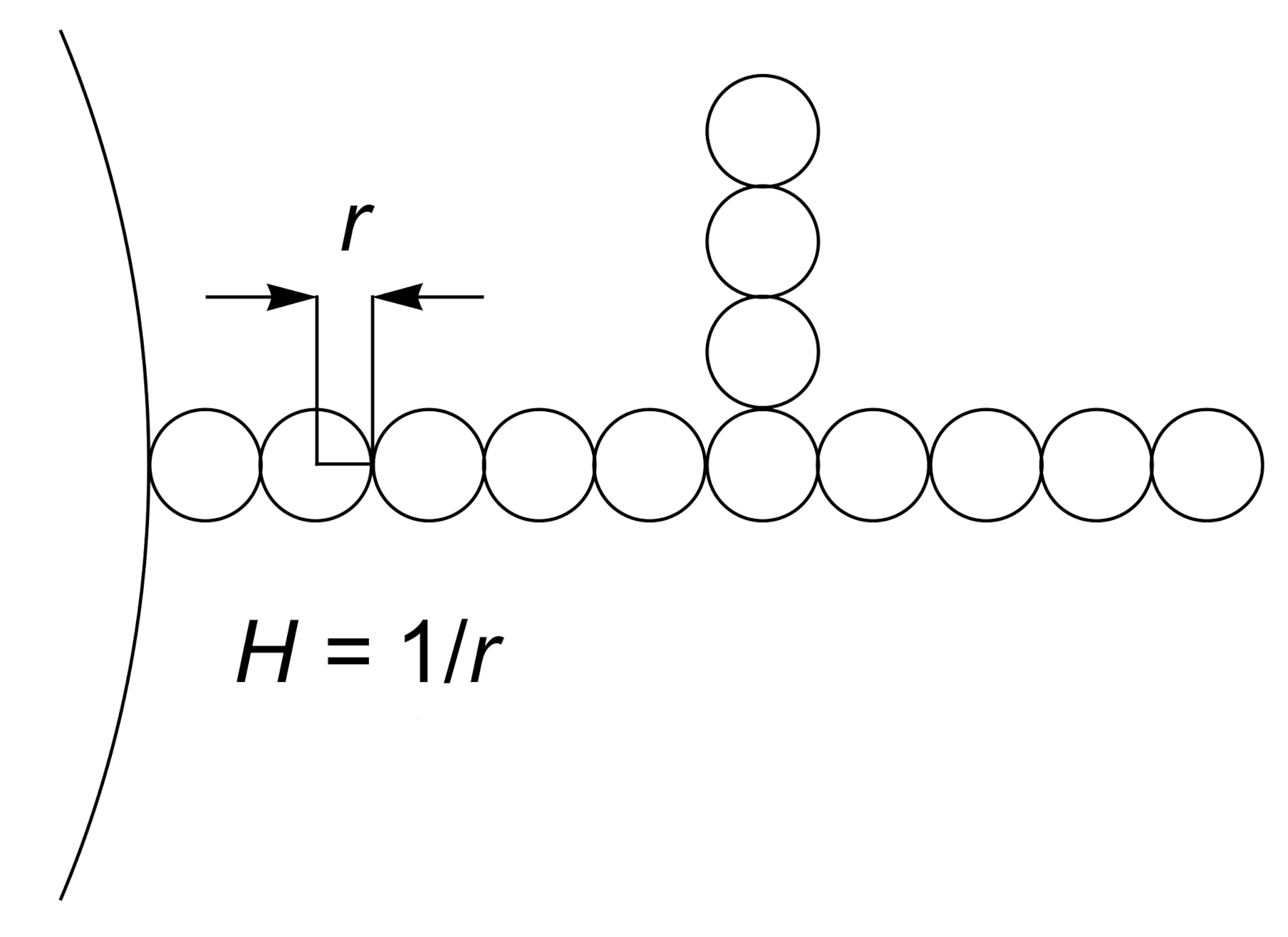
2.3. Isotropic Limit and Helfrich Model
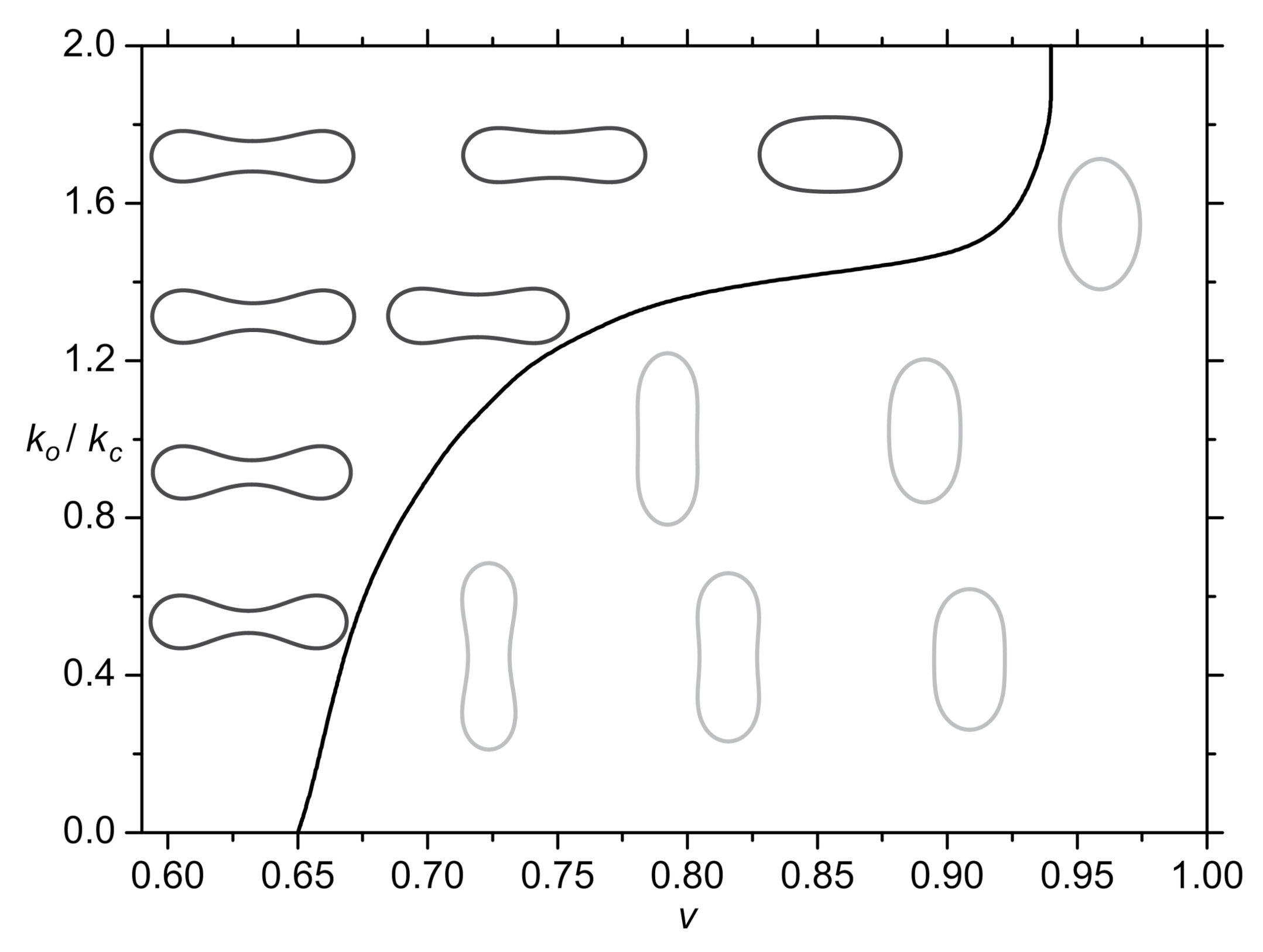
2.4. Cell Shape Changes Driven by Nematic Orientational Ordering
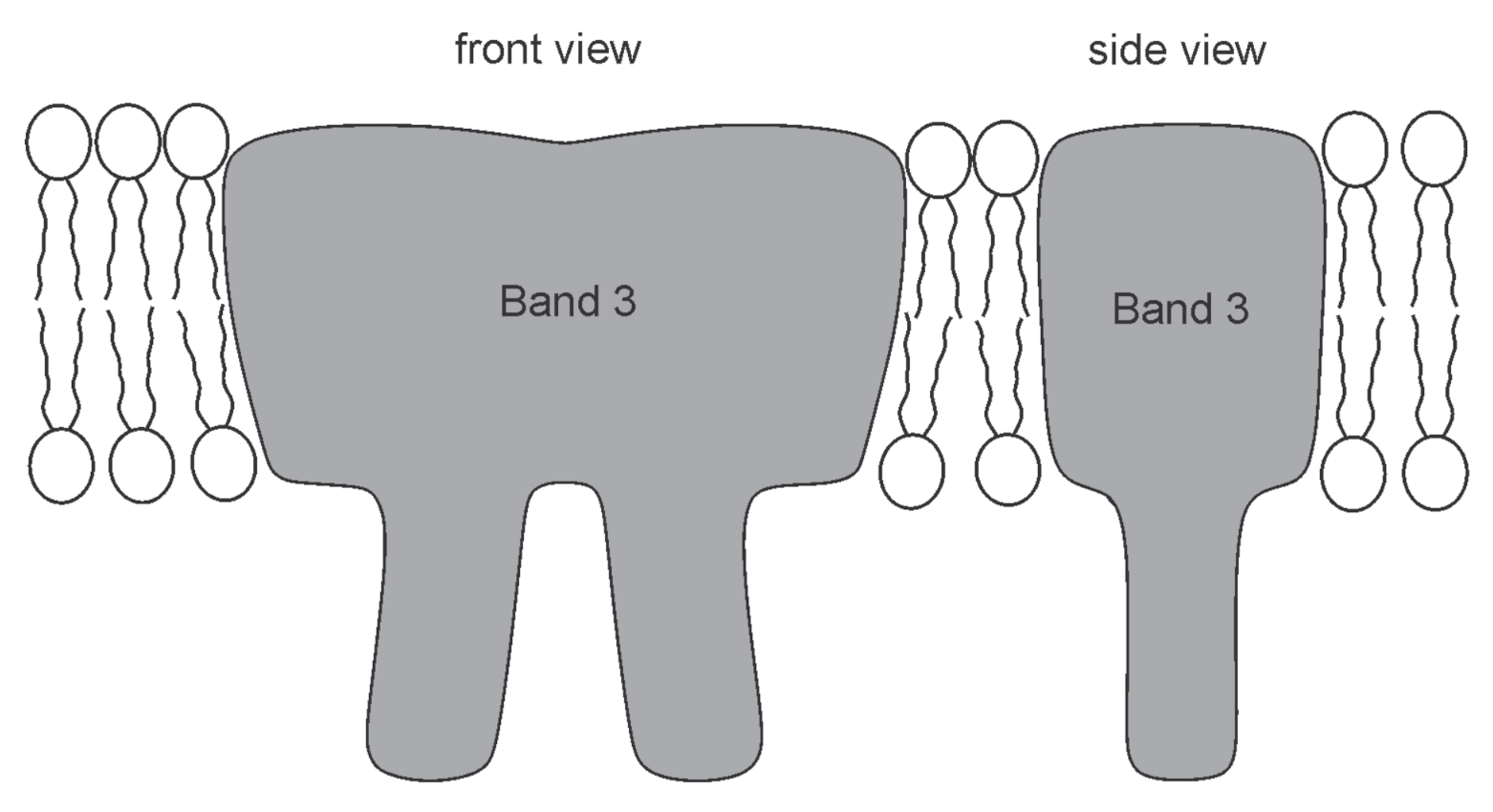
2.5. Influence of Membrane Skeleton
2.5.1. Shear Deformation of Membrane Skeleton and Echinocyte Shape of Red Blood Cells
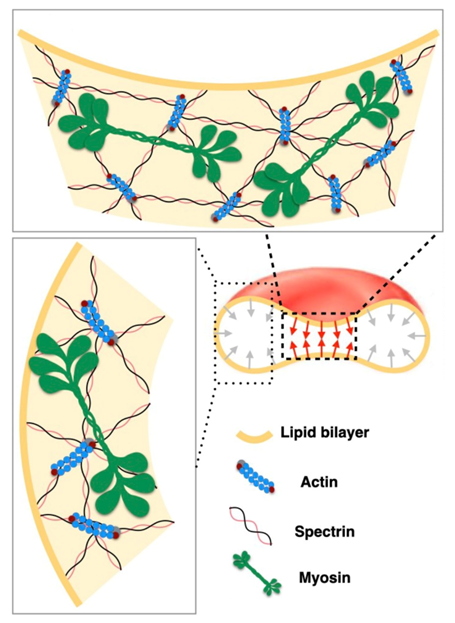
2.5.2. Membrane-Myosin Interactions in Red Blood Cells
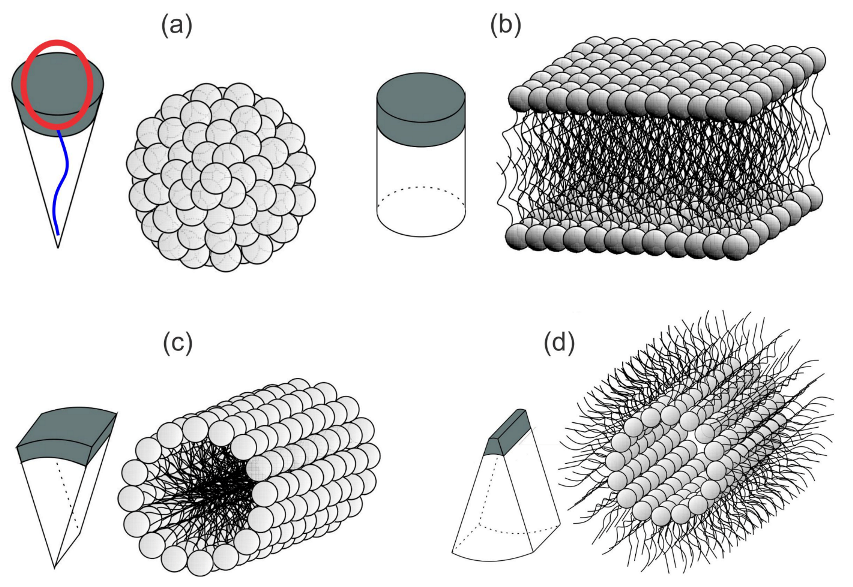
2.6. Theory of Self-Assembly of Isotropic Curved Membrane Components into Larger Domains
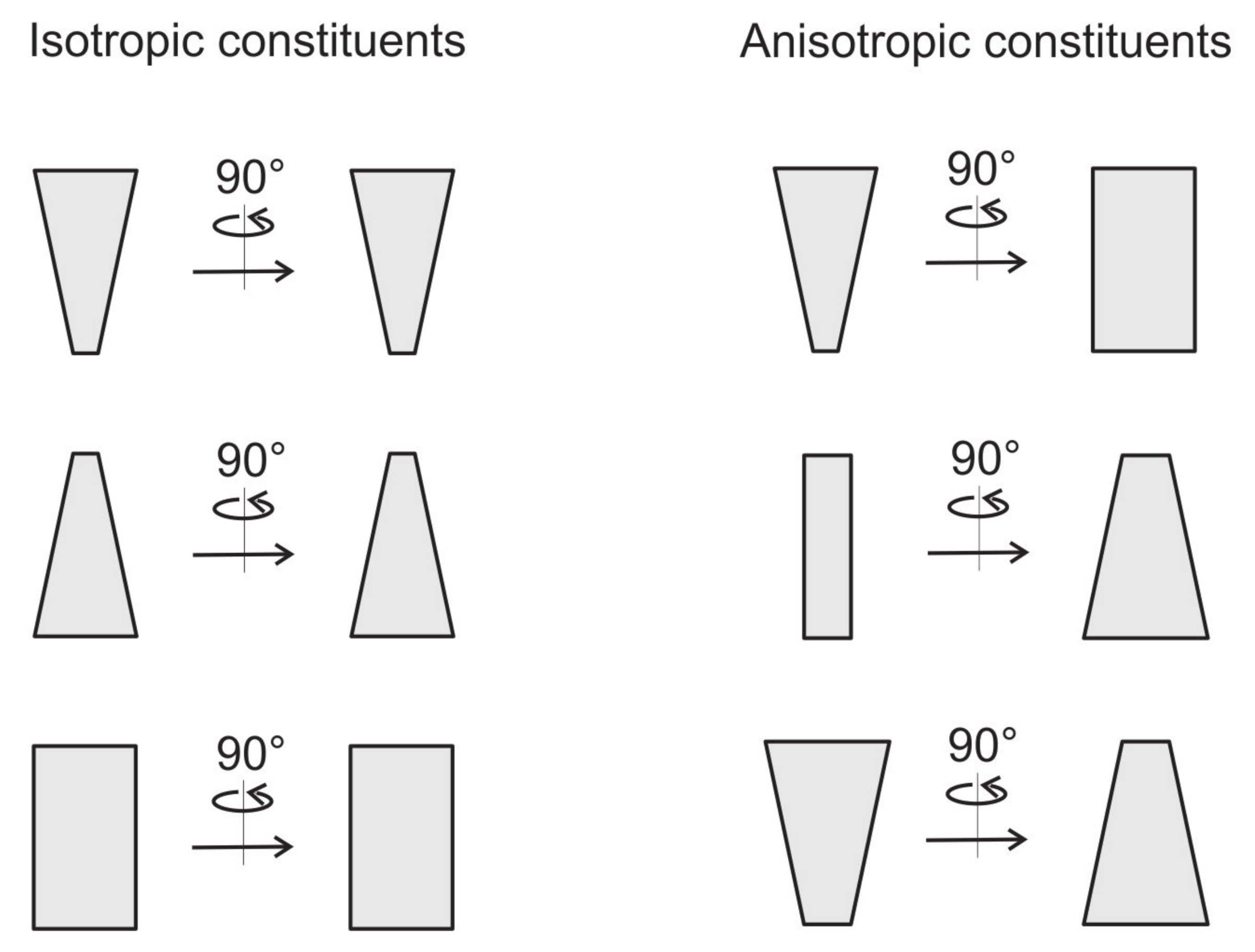
2.7. Free Energy of Two-Component Anisotropic Membrane: An Approximative Approach
3. Cytoskeleton and Cell Shape
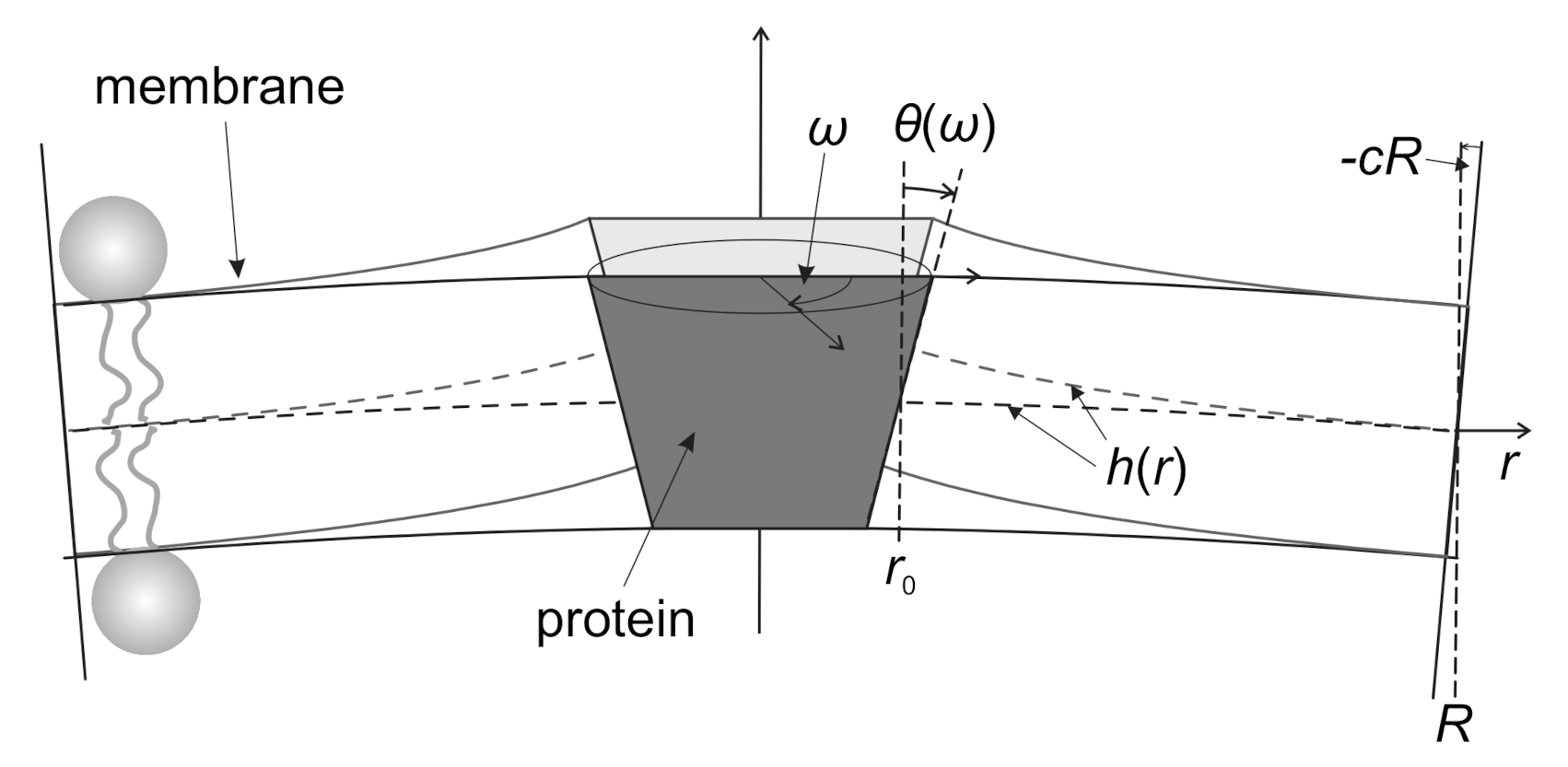
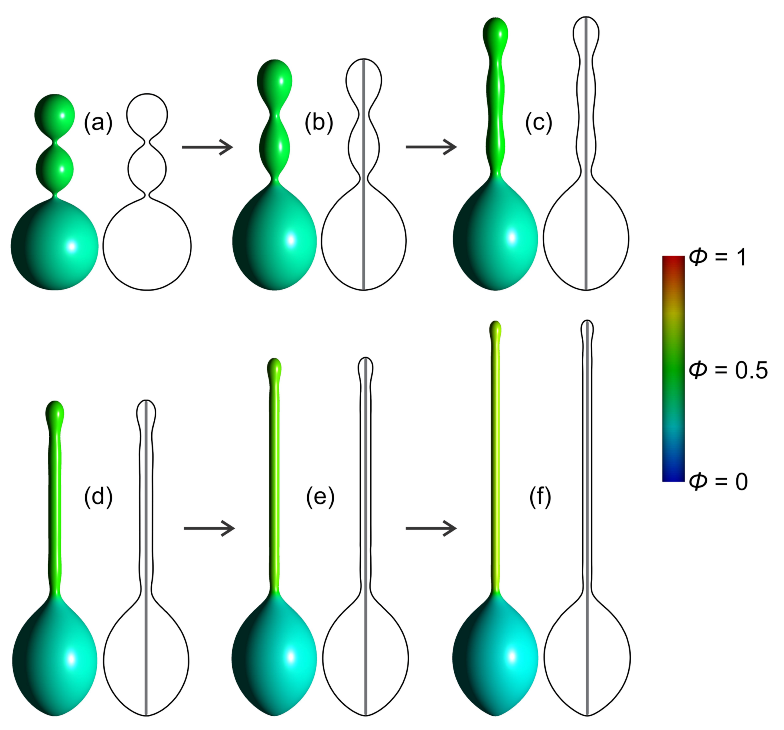
3.1. Interplay between Cytoskeleton Force and Distribution of Curved Membrane Nanodomains in Membrane Protrusive Growth
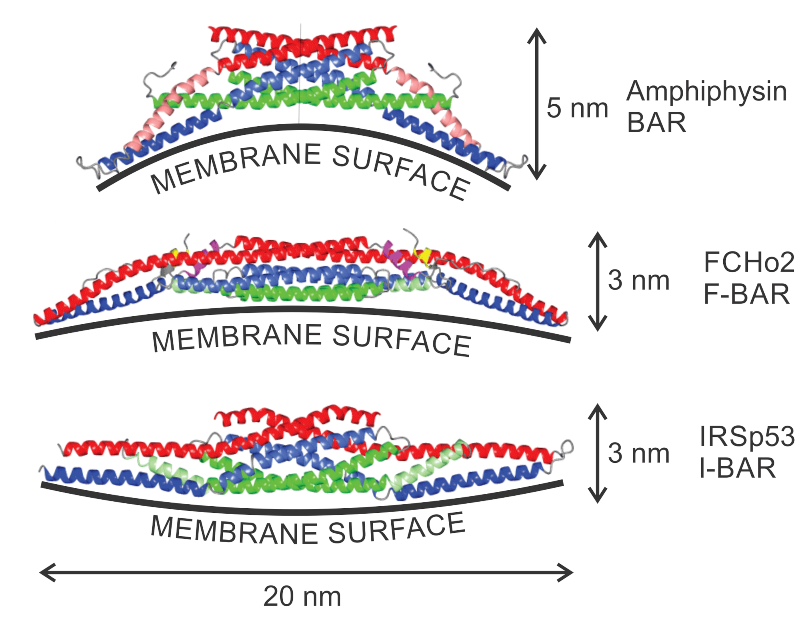
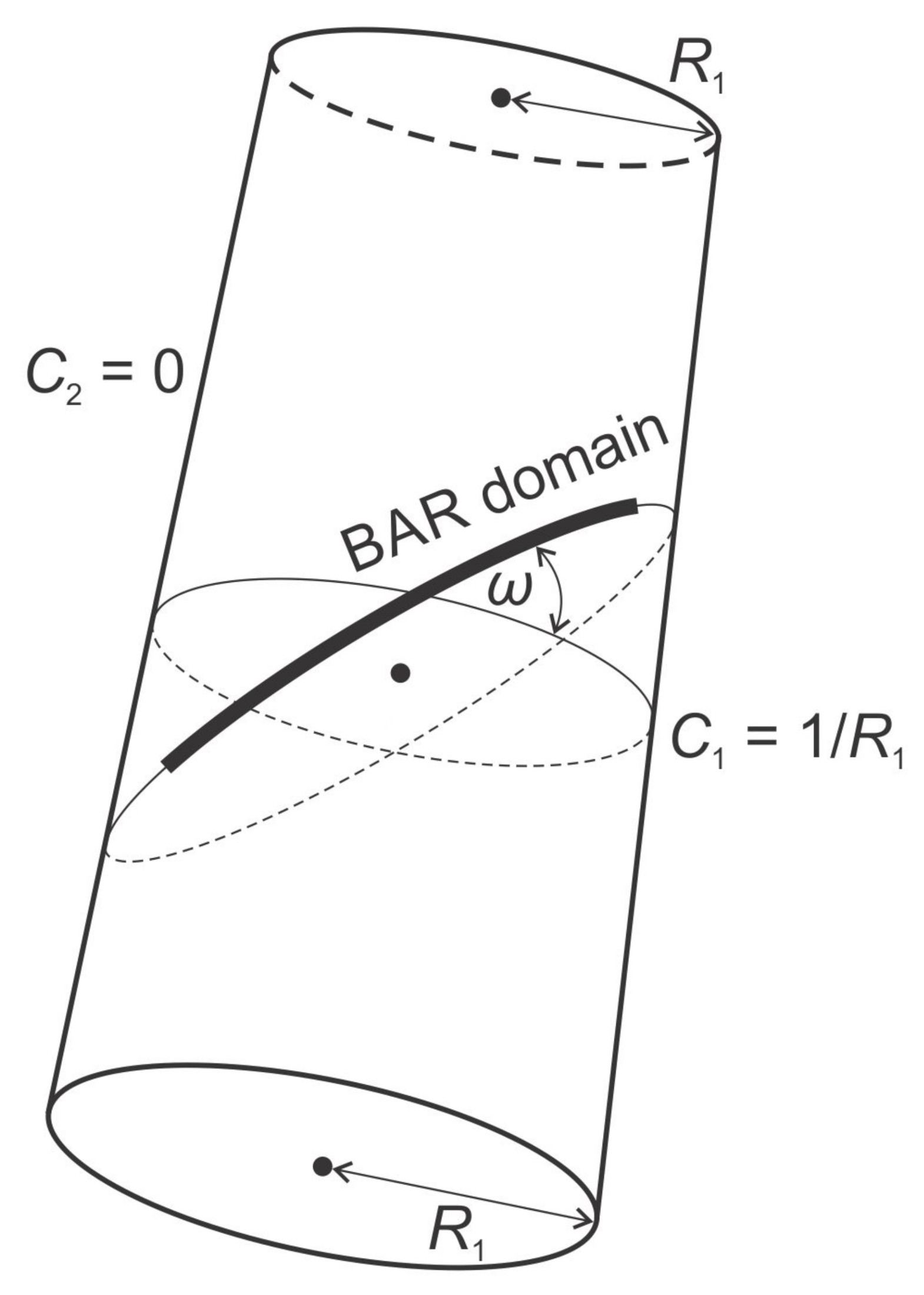
3.2. Orientational Ordering of Membrane Attached Bar Domains and the Force of Cytoskeleton
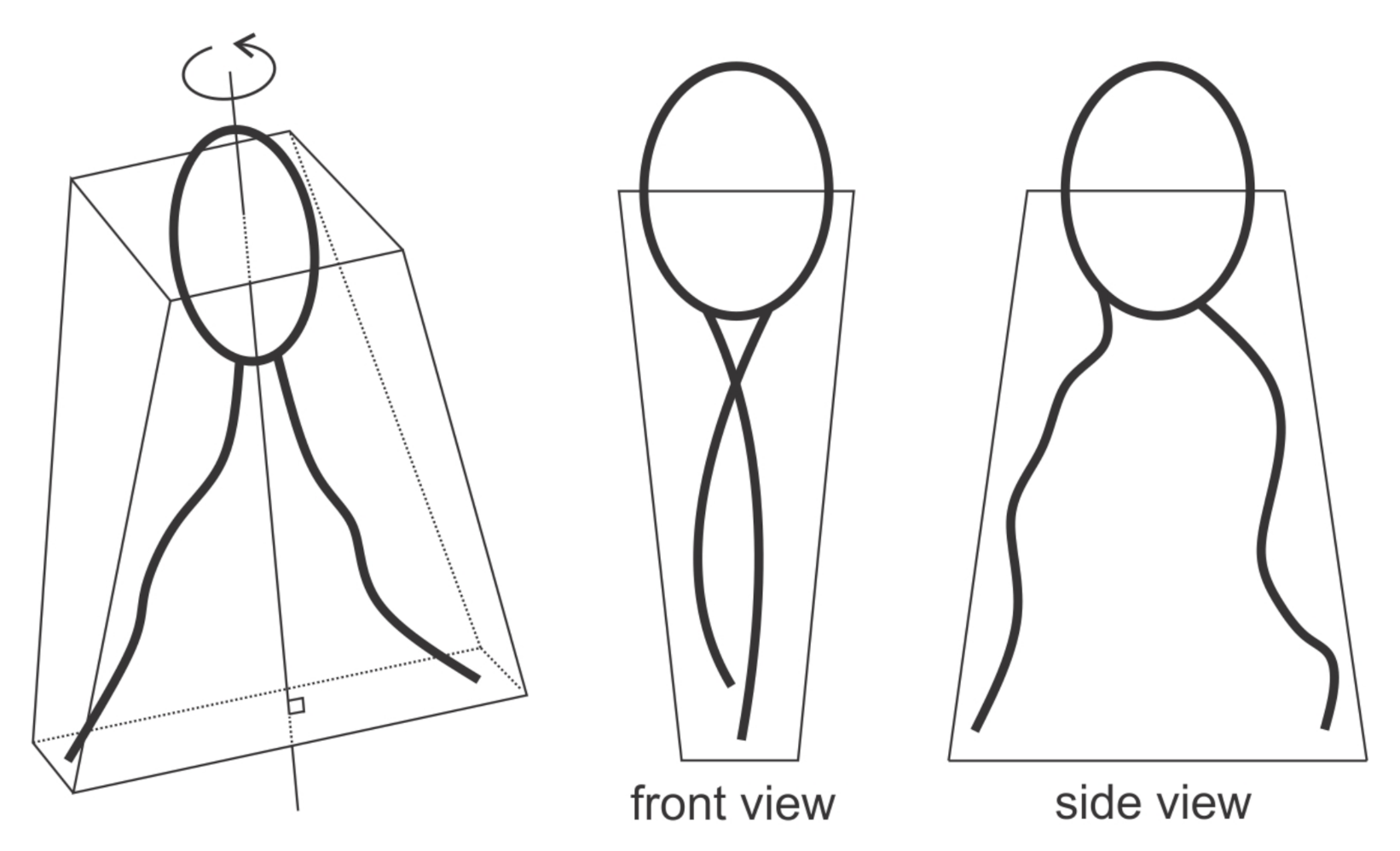
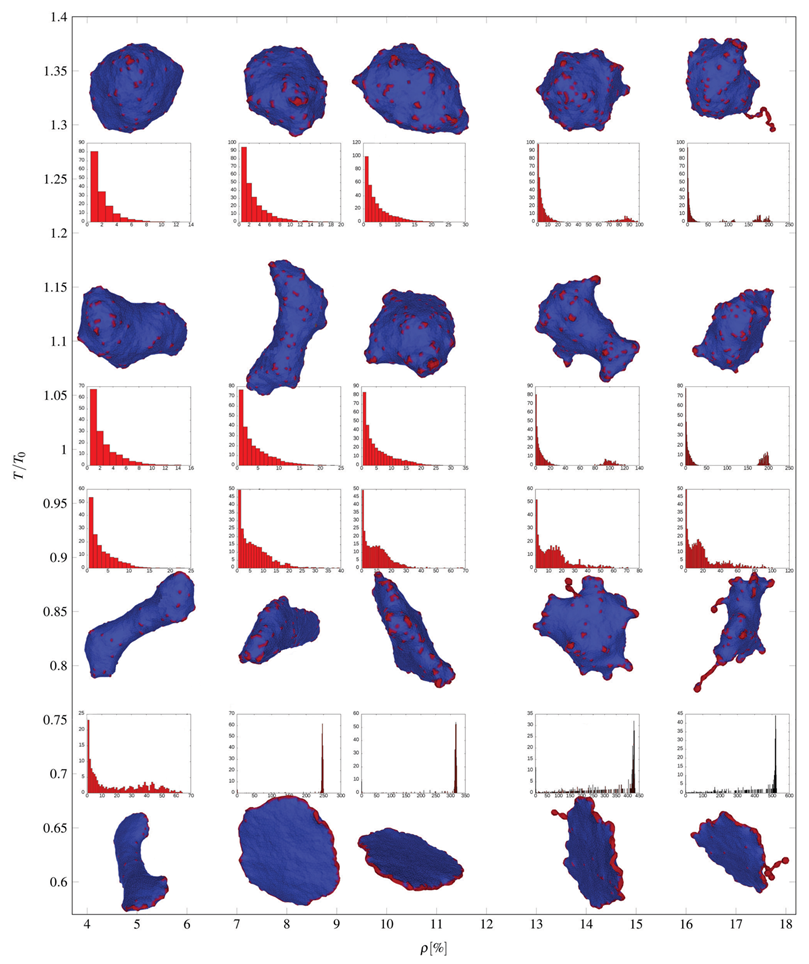
3.3. Active Protrusive Force
4. Discussion and Conclusions
5. Materials and Methods
5.1. Calculation of Axisymmetric Closed Membrane Shapes
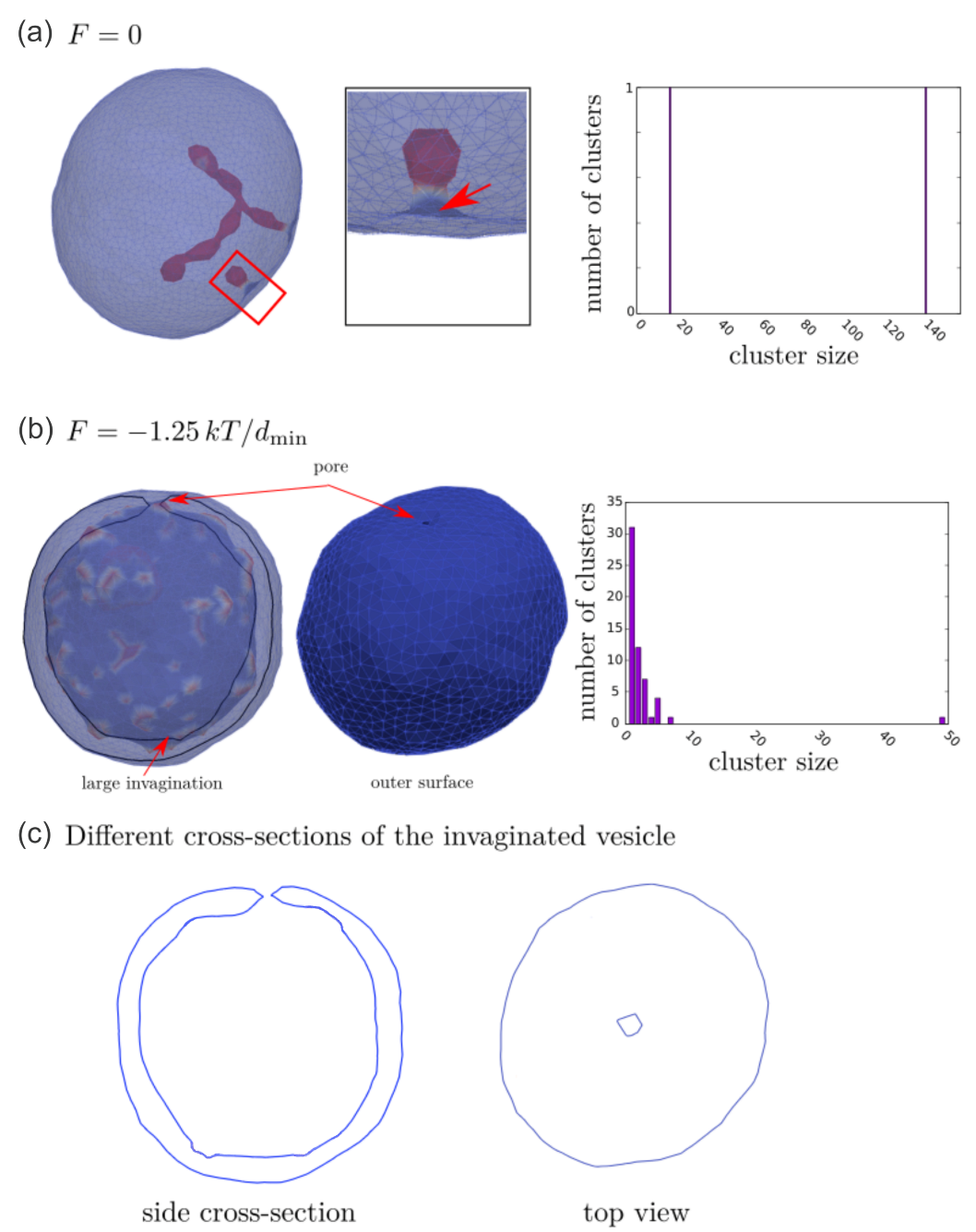
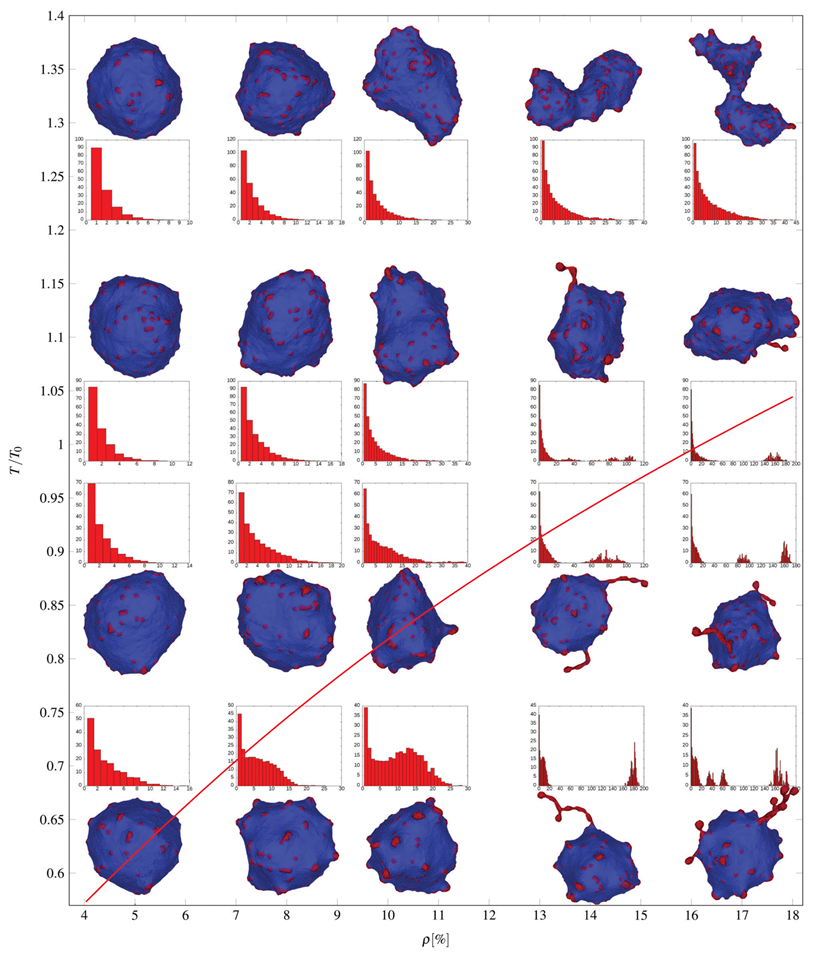
5.2. Monte-Carlo Simulations of Closed Membrane Shapes
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ATP | Adenosine triphosphate |
| RBC | Red blood cell |
| NMIIA | Non-muscle myosin IIA |
| DE | Deviatoric elasticity |
| BAR | Bin/Amphiphysin/Rvs |
| MC | Monte-Carlo |
References
- Cevc, G.; Marsh, D. Phospholipid Bilayers: Physical Principles and Models; Wiley: Hoboken, NJ, USA, 1987. [Google Scholar]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Biochemistry, 5th ed.; W.H. Freeman: New York, NY, USA, 2002. [Google Scholar]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Perutková, Š.; Daniel, M.; Dolinar, G.; Rappolt, M.; Kralj-Iglič, V.; Iglič, A. Stability of the inverted hexagonal phase. Adv. Planar Lipid Bilayers Liposomes 2009, 9, 237–278. [Google Scholar]
- Gao, H.J.; Shi, W.D.; Freund, L.B. Mechanics of receptor-mediated endocytosis. Proc. Natl. Acad. Sci. USA 2005, 102, 9469–9474. [Google Scholar] [CrossRef] [PubMed]
- Doherty, G.J.; McMahon, H.T. Mechanisms of endocytosis. Annu. Rev. Biochem. 2009, 78, 857–902. [Google Scholar] [CrossRef] [PubMed]
- Baumgart, T.; Capraro, B.R.; Zhu, C.; Das, S.L. Thermodynamics and mechanics of membrane curvature generation and sensing by proteins and lipids. Annu. Rev. Phys. Chem. 2011, 62, 483–506. [Google Scholar] [CrossRef]
- Sackmann, E. Molecular and global structure and dynamics of membranes and lipid bilayers. Can. J. Phys. 1990, 68, 999–1012. [Google Scholar] [CrossRef]
- Szleifer, I.; Kramer, D.; Ben-Shaul, A.; Gelbart, W.M.; Safran, S.A. Molecular theory of curvature elasticity in surfactant films. J. Chem. Phys. 1990, 92, 6800–6817. [Google Scholar] [CrossRef]
- Nielsen, C.; Goulian, M.; Andersen, O.S. Energetics of inclusion-induced bilayer deformations. Biophys. J. 1998, 74, 1966–1983. [Google Scholar] [CrossRef]
- Fošnarič, M.; Bohinc, K.; Gauger, D.R.; Iglič, A.; Kralj-Iglič, V.; May, S. The influence of anisotropic membrane inclusions on curvature elastic properties of lipid membranes. J. Chem. Inf. Model. 2005, 45, 1652–1661. [Google Scholar] [CrossRef]
- Markin, V. Lateral organization of membranes and cell shapes. Biophys. J. 1981, 36, 1–19. [Google Scholar] [CrossRef]
- Leibler, S. Curvature instability in membranes. J. Phys. 1986, 47, 507–516. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Heinrich, V.; Svetina, S.; Žekš, B. Free energy of closed membrane with anisotropic inclusions. Eur. Phys. J. B-Condens. Matter Complex Syst. 1999, 10, 5–8. [Google Scholar] [CrossRef]
- Iglič, A.; Babnik, B.; Bohinc, K.; Fošnarič, M.; Hägerstrand, H.; Kralj-Iglič, V. On the role of anisotropy of membrane constituents in formation of a membrane neck during budding of a multicomponent membrane. J. Biomech. 2007, 40, 579–585. [Google Scholar] [CrossRef] [PubMed]
- Walani, N.; Torres, J.; Agrawal, A. Endocytic proteins drive vesicle growth via instability in high membrane tension environment. Proc. Natl. Acad. Sci. USA 2015, 112, E1423–E1432. [Google Scholar] [CrossRef] [PubMed]
- Mesarec, L.; Góźdź, W.; Iglič, V.K.; Kralj, S.; Iglič, A. Closed membrane shapes with attached BAR domains subject to external force of actin filaments. Colloids Surf. Biointerfaces 2016, 141, 132–140. [Google Scholar] [CrossRef] [PubMed]
- Gov, N. Guided by curvature: Shaping cells by coupling curved membrane proteins and cytoskeletal forces. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20170115. [Google Scholar] [CrossRef]
- Discher, D.E. Biomembrane Mechanical Properties Direct Diverse Cell Functions. In Physics of Biological Membranes; Springer: Berlin/Heidelberg, Germany, 2018; pp. 263–285. [Google Scholar]
- Iglič, A.; Drobne, D.; Kralj-Iglic, V. Nanostructures in Biological Systems: Theory and Applications; Jenny Stanford Publishing: Singapore, 2015. [Google Scholar]
- Fošnarič, M.; Iglič, A.; May, S. Influence of rigid inclusions on the bending elasticity of a lipid membrane. Phys. Rev. E 2006, 74, 051503. [Google Scholar] [CrossRef]
- Mesarec, L.; Góźdź, W.; Kralj, S.; Fošnarič, M.; Penič, S.; Kralj-Iglič, V.; Iglič, A. On the role of external force of actin filaments in the formation of tubular protrusions of closed membrane shapes with anisotropic membrane components. Eur. Biophys. J. 2017, 46, 705–718. [Google Scholar] [CrossRef]
- Fošnarič, M.; Penič, S.; Iglič, A.; Kralj-Iglič, V.; Drab, M.; Gov, N. Theoretical study of vesicle shapes driven by coupling curved proteins and active cytoskeletal forces. Soft Matter 2019, 15, 5319–5330. [Google Scholar] [CrossRef]
- Hägerstrand, H.; Mrowczynska, L.; Salzer, U.; Prohaska, R.; Michelsen, K.A.; Kralj-Iglič, V.; Iglič, A. Curvature-dependent lateral distribution of raft markers in the human erythrocyte membrane. Mol. Membr. Biol. 2006, 23, 277–288. [Google Scholar] [CrossRef]
- Iglič, A.; Lokar, M.; Babnik, B.; Slivnik, T.; Veranič, P.; Hägerstrand, H.; Kralj-Iglič, V. Possible role of flexible red blood cell membrane nanodomains in the growth and stability of membrane nanotubes. Blood Cells Mol. Dis. 2007, 39, 14–23. [Google Scholar] [CrossRef] [PubMed]
- Veksler, A.; Gov, N.S. Phase transitions of the coupled membrane-cytoskeleton modify cellular shape. Biophys. J. 2007, 93, 3798–3810. [Google Scholar] [CrossRef] [PubMed]
- Božič, B.; Kralj-Iglič, V.; Svetina, S. Coupling between vesicle shape and lateral distribution of mobile membrane inclusions. Phys. Rev. E 2006, 73, 041915. [Google Scholar] [CrossRef]
- Drab, M.; Stopar, D.; Kralj-Iglič, V.; Iglič, A. Inception mechanisms of tunneling nanotubes. Cells 2019, 8, 626. [Google Scholar] [CrossRef] [PubMed]
- Umeda, T.; Nakajima, H.; Hotani, H. Theoretical analysis of shape transformations of liposomes caused by microtubule assembly. J. Phys. Soc. Jpn. 1998, 67, 682–688. [Google Scholar] [CrossRef]
- Singer, S.J.; Nicolson, G.L. The fluid mosaic model of the structure of cell membranes. Science 1972, 175, 720–731. [Google Scholar] [CrossRef] [PubMed]
- McMahon, H.T.; Gallop, J.L. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature 2005, 438, 590–596. [Google Scholar] [CrossRef]
- Peter, B.J.; Kent, H.M.; Mills, I.G.; Vallis, Y.; Butler, P.J.G.; Evans, P.R.; McMahon, H.T. BAR domains as sensors of membrane curvature: The amphiphysin BAR structure. Science 2004, 303, 495–499. [Google Scholar] [CrossRef] [PubMed]
- Saarikangas, J.; Zhao, H.; Pykäläinen, A.; Laurinmäki, P.; Mattila, P.K.; Kinnunen, P.K.; Butcher, S.J.; Lappalainen, P. Molecular mechanisms of membrane deformation by I-BAR domain proteins. Curr. Biol. 2009, 19, 95–107. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Llobregat, J.; Elías-Wolff, F.; Lindén, M. Anisotropic membrane curvature sensing by amphipathic peptides. Biophys. J. 2016, 110, 197–204. [Google Scholar] [CrossRef] [PubMed]
- Simons, K.; Sampaio, J.L. Membrane organization and lipid rafts. Cold Spring Harb. Perspect. Biol. 2011, 3, a004697. [Google Scholar] [CrossRef]
- Perutková, Š.; Daniel, M.; Rappolt, M.; Pabst, G.; Dolinar, G.; Kralj-Iglič, V.; Iglič, A. Elastic deformations in hexagonal phases studied by small-angle X-ray diffraction and simulations. Phys. Chem. Chem. Phys. 2011, 13, 3100–3107. [Google Scholar] [CrossRef] [PubMed]
- Rappolt, M.; Hodzic, A.; Sartori, B.; Ollivon, M.; Laggner, P. Conformational and hydrational properties during the-to-and-to HII-phase transition in phosphatidylethanolamine. Chem. Phys. Lipids 2008, 154, 46–55. [Google Scholar] [CrossRef]
- Kulkarni, C.V. Lipid crystallization: From self-assembly to hierarchical and biological ordering. Nanoscale 2012, 4, 5779–5791. [Google Scholar] [CrossRef]
- Kozlov, M.M.; Campelo, F.; Liska, N.; Chernomordik, L.V.; Marrink, S.J.; McMahon, H.T. Mechanisms shaping cell membranes. Curr. Opin. Cell Biol. 2014, 29, 53–60. [Google Scholar] [CrossRef]
- Boulbitch, A. Deflection of a cell membrane under application of a local force. Phys. Rev. E 1998, 57, 2123. [Google Scholar] [CrossRef]
- Evans, E.; Skalak, R. Mechanics and Thermodynamics of Biomembranes; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Mohandas, N.; Evans, E. Mechanical properties of the red cell membrane in relation to molecular structure and genetic defects. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 787–818. [Google Scholar] [CrossRef] [PubMed]
- Iglič, A. A possible mechanism determining the stability of spiculated red blood cells. J. Biomech. 1997, 30, 35–40. [Google Scholar] [CrossRef]
- Iglič, A.; Kralj-Iglič, V.; Hägerstrand, H. Amphiphile induced echinocyte-spheroechinocyte transformation of red blood cell shape. Eur. Biophys. J. 1998, 27, 335–339. [Google Scholar] [CrossRef]
- Lim H.W., G.; Wortis, M.; Mukhopadhyay, R. Stomatocyte-discocyte-echinocyte sequence of the human red blood cell: Evidence for the bilayer-couple hypothesis from membrane mechanics. Proc. Natl. Acad. Sci. USA 2002, 99, 16766–16769. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-García, R.; López-Montero, I.; Mell, M.; Egea, G.; Gov, N.S.; Monroy, F. Direct cytoskeleton forces cause membrane softening in red blood cells. Biophys. J. 2015, 108, 2794–2806. [Google Scholar] [CrossRef]
- Smith, A.S.; Nowak, R.B.; Zhou, S.; Giannetto, M.; Gokhin, D.S.; Papoin, J.; Ghiran, I.C.; Blanc, L.; Wan, J.; Fowler, V.M. Myosin IIA interacts with the spectrin-actin membrane skeleton to control red blood cell membrane curvature and deformability. Proc. Natl. Acad. Sci. USA 2018, 115, E4377–E4385. [Google Scholar] [CrossRef] [PubMed]
- Alimohamadi, H.; Smith, A.S.; Nowak, R.B.; Fowler, V.M.; Rangamani, P. Non-uniform distribution of myosin-mediated forces governs red blood cell membrane curvature through tension modulation. PLoS Comput. Biol. 2020, 16, e1007890. [Google Scholar] [CrossRef]
- Penič, S.; Fošnarič, M.; Mesarec, L.; Iglič, A.; Kralj-Iglič, V. Active forces of myosin motors may control endovesiculation of red blood cells. Acta Chim. Slov. 2020, 67, 674–681. [Google Scholar] [CrossRef]
- Graziano, B.R.; Town, J.P.; Sitarska, E.; Nagy, T.L.; Fošnarič, M.; Penič, S.; Iglič, A.; Kralj-Iglič, V.; Gov, N.S.; Diz-Muñoz, A.; et al. Cell confinement reveals a branched-actin independent circuit for neutrophil polarity. PLoS Biol. 2019, 17, e3000457. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, R.; Lim, H.G.; Wortis, M. Echinocyte shapes: Bending, stretching, and shear determine spicule shape and spacing. Biophys. J. 2002, 82, 1756–1772. [Google Scholar] [CrossRef]
- Sheetz, M.P.; Singer, S. Biological membranes as bilayer couples. A molecular mechanism of drug-erythrocyte interactions. Proc. Natl. Acad. Sci. USA 1974, 71, 4457–4461. [Google Scholar] [CrossRef] [PubMed]
- Hägerstrand, H.; Isomaa, B. Morphological characterization of exovesicles and endovesicles released from human erythrocytes following treatment with amphiphiles. Biochim. Biophys. Acta (BBA) Biomembr. 1992, 1109, 117–126. [Google Scholar] [CrossRef]
- Hägerstrand, H.; Isomaa, B. Vesiculation induced by amphiphiles in erythrocytes. Biochim. Biophys. Acta (BBA) Biomembr. 1989, 982, 179–186. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Hägerstrand, H.; Veranič, P.; Jezernik, K.; Babnik, B.; Gauger, D.R.; Iglič, A. Amphiphile-induced tubular budding of the bilayer membrane. Eur. Biophys. J. 2005, 34, 1066–1070. [Google Scholar] [CrossRef]
- Deuticke, B. Transformation and restoration of biconcave shape of human erythrocytes induced by amphiphilic agents and changes of ionic environment. Biochim. Biophys. Acta (BBA) Biomembr. 1968, 163, 494–500. [Google Scholar] [CrossRef]
- Helfrich, W. Blocked lipid exchange in bilayers and its possible influence on the shape of vesicles. Z. Naturforschung C 1974, 29, 510–515. [Google Scholar] [CrossRef] [PubMed]
- Stokke, B.; Mikkelsen, A.; Elgsaeter, A. The human erythrocyte membrane skeleton may be an ionic gel. Eur. Biophys. J. 1986, 13, 203–218. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.A. Bending resistance and chemically induced moments in membrane bilayers. Biophys. J. 1974, 14, 923–931. [Google Scholar] [CrossRef]
- Brochard, F.; Lennon, J. Frequency spectrum of the flicker phenomenon in erythrocytes. J. Phys. 1975, 36, 1035–1047. [Google Scholar] [CrossRef]
- Miao, L.; Seifert, U.; Wortis, M.; Döbereiner, H.G. Budding transitions of fluid-bilayer vesicles: The effect of area-difference elasticity. Phys. Rev. E 1994, 49, 5389. [Google Scholar] [CrossRef] [PubMed]
- Deuling, H.; Helfrich, W. The curvature elasticity of fluid membranes: A catalogue of vesicle shapes. J. Phys. 1976, 37, 1335–1345. [Google Scholar] [CrossRef]
- Evans, E. Bending elastic modulus of red blood cell membrane derived from buckling instability in micropipet aspiration tests. Biophys. J. 1983, 43, 27. [Google Scholar] [CrossRef]
- Geekiyanage, N.M.; Balanant, M.A.; Sauret, E.; Saha, S.; Flower, R.; Lim, C.T.; Gu, Y. A coarse-grained red blood cell membrane model to study stomatocyte-discocyte-echinocyte morphologies. PLoS ONE 2019, 14, e0215447. [Google Scholar] [CrossRef]
- Muñoz, S.; Sebastián, J.; Sancho, M.; Álvarez, G. Elastic energy of the discocyte–stomatocyte transformation. Biochim. Biophys. Acta (BBA) Biomembr. 2014, 1838, 950–956. [Google Scholar] [CrossRef] [PubMed]
- Veranič, P.; Lokar, M.; Schütz, G.J.; Weghuber, J.; Wieser, S.; Hägerstrand, H.; Kralj-Iglič, V.; Iglič, A. Different types of cell-to-cell connections mediated by nanotubular structures. Biophys. J. 2008, 95, 4416–4425. [Google Scholar] [CrossRef]
- Liese, S.; Carlson, A. Membrane Shape Remodeling by Protein Crowding. bioRxiv 2020. [Google Scholar] [CrossRef]
- Iglič, A.; Hägerstrand, H.; Bobrowska-Hägerstrand, M.; Arrigler, V.; Kralj-Iglič, V. Possible role of phospholipid nanotubes in directed transport of membrane vesicles. Phys. Lett. A 2003, 310, 493–497. [Google Scholar] [CrossRef]
- Hurtig, J.; Chiu, D.T.; Önfelt, B. Intercellular nanotubes: Insights from imaging studies and beyond. Wiley Interdiscip. Rev. Nanomed. Nanobiotechnol. 2010, 2, 260–276. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Lokar, M.; Kralj-Iglič, V.; Veranič, P.; Iglič, A. Temperature and cholera toxin B are factors that influence formation of membrane nanotubes in RT4 and T24 urothelial cancer cell lines. Int. J. Nanomed. 2011, 6, 495. [Google Scholar] [CrossRef] [PubMed]
- Canham, P.B. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. J. Theor. Biol. 1970, 26, 61–81. [Google Scholar] [CrossRef]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Naturforschung C 1973, 28, 693–703. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Iglič, A.; Hägerstrand, H.; Peterlin, P. Stable tubular microexovesicles of the erythrocyte membrane induced by dimeric amphiphiles. Phys. Rev. E 2000, 61, 4230. [Google Scholar] [CrossRef]
- Kralj-Iglic, V.; Iglic, A.; Gomiscek, G.; Sevsek, F.; Arrigler, V.; Hägerstrand, H. Microtubes and nanotubes of a phospholipid bilayer membrane. J. Phys. A Math. Gen. 2002, 35, 1533. [Google Scholar] [CrossRef]
- Seifert, U. Configurations of fluid membranes and vesicles. Adv. Phys. 1997, 46, 13–137. [Google Scholar] [CrossRef]
- Fischer, T.M. Bending stiffness of lipid bilayers. II. Spontaneous curvature of the monolayers. J. Phys. II 1992, 2, 327–336. [Google Scholar] [CrossRef][Green Version]
- Fischer, T.M. Bending stiffness of lipid bilayers. V. Comparison of two formulations. J. Phys. II 1993, 3, 1795–1805. [Google Scholar] [CrossRef][Green Version]
- Kralj-Iglič, V.; Svetina, S.; Žekž, B. Shapes of bilayer vesicles with membrane embedded molecules. Eur. Biophys. J. 1996, 24, 311–321. [Google Scholar] [CrossRef] [PubMed]
- Fournier, J. Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions. Phys. Rev. Lett. 1996, 76, 4436–4439. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Babnik, B.; Gauger, D.R.; May, S.; Iglič, A. Quadrupolar ordering of phospholipid molecules in narrow necks of phospholipid vesicles. J. Stat. Phys. 2006, 125, 727–752. [Google Scholar] [CrossRef]
- Helfrich, W.; Prost, J. Intrinsic bending force in anisotropic membranes made of chiral molecules. Phys. Rev. A 1988, 38, 3065. [Google Scholar] [CrossRef] [PubMed]
- Walani, N.; Torres, J.; Agrawal, A. Anisotropic spontaneous curvatures in lipid membranes. Phys. Rev. E 2014, 89, 062715. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Remškar, M.; Vidmar, G.; Fošnarič, M.; Iglič, A. Deviatoric elasticity as a possible physical mechanism explaining collapse of inorganic micro and nanotubes. Phys. Lett. A 2002, 296, 151–155. [Google Scholar] [CrossRef]
- Iglič, A.; Hägerstrand, H.; Veranič, P.; Plemenitaš, A.; Kralj-Iglič, V. Curvature-induced accumulation of anisotropic membrane components and raft formation in cylindrical membrane protrusions. J. Theor. Biol. 2006, 240, 368–373. [Google Scholar] [CrossRef]
- Perutková, Š.; Kralj-Iglič, V.; Frank, M.; Iglič, A. Mechanical stability of membrane nanotubular protrusions influenced by attachment of flexible rod-like proteins. J. Biomech. 2010, 43, 1612–1617. [Google Scholar] [CrossRef]
- Kabaso, D.; Bobrovska, N.; Góźdź, W.; Gov, N.; Kralj-Iglič, V.; Veranič, P.; Iglič, A. On the role of membrane anisotropy and BAR proteins in the stability of tubular membrane structures. J. Biomech. 2012, 45, 231–238. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Bobrovska, N.; Góźdź, W.; Gongadze, E.; Kralj-Iglič, V.; Zorec, R.; Iglič, A. The transport along membrane nanotubes driven by the spontaneous curvature of membrane components. Bioelectrochemistry 2012, 87, 204–210. [Google Scholar] [CrossRef] [PubMed]
- Bobrovska, N.; Góźdź, W.; Kralj-Iglič, V.; Iglič, A. On the role of anisotropy of membrane components in formation and stabilization of tubular structures in multicomponent membranes. PLoS ONE 2013, 8, e73941. [Google Scholar]
- Iglič, A.; Babnik, B.; Gimsa, U.; Kralj-Iglič, V. On the role of membrane anisotropy in the beading transition of undulated tubular membrane structures. J. Phys. A Math. Gen. 2005, 38, 8527. [Google Scholar] [CrossRef]
- Kralj-Iglič, V. Stability of membranous nanostructures: A possible key mechanism in cancer progression. Int. J. Nanomed. 2012, 7, 3579. [Google Scholar] [CrossRef] [PubMed]
- Morris, A.M.; Watzky, M.A.; Finke, R.G. Protein aggregation kinetics, mechanism, and curve-fitting: A review of the literature. Biochim. Biophys. Acta (BBA) Proteins Proteom. 2009, 1794, 375–397. [Google Scholar] [CrossRef]
- Yang, C.; Hoelzle, M.; Disanza, A.; Scita, G.; Svitkina, T. Coordination of membrane and actin cytoskeleton dynamics during filopodia protrusion. PLoS ONE 2009, 4, e5678. [Google Scholar] [CrossRef]
- Zhao, H.; Pykäläinen, A.; Lappalainen, P. I-BAR domain proteins: Linking actin and plasma membrane dynamics. Curr. Opin. Cell Biol. 2011, 23, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Tsafrir, I.; Caspi, Y.; Guedeau-Boudeville, M.A.; Arzi, T.; Stavans, J. Budding and Tubulation in Highly Oblate Vesicles by Anchored Amphiphilic Molecules. Phys. Rev. Lett. 2003, 91, 138102. [Google Scholar] [CrossRef] [PubMed]
- Koster, G.; VanDuijn, M.; Hofs, B.; Dogterom, M. Membrane tube formation from giant vesicles by dyanmic association of motor proteins. Proc. Natl. Acad. Sci. USA 2003, 100, 15583–15588. [Google Scholar] [CrossRef] [PubMed]
- Roux, A.; Cuvelier, D.; Nassoy, P.; Prost, J.; Bassereau, P.; Goud, B. Role of curvature and phase transition in lipid sorting and fission of membrane tubules. EMBO J. 2005, 24, 1537–1545. [Google Scholar] [CrossRef]
- Huttner, W.; Schmidt, A. Membrane curvature: A case of endofilin. Trends Cell Biol. 2002, 12, 155–158. [Google Scholar] [CrossRef]
- Davis, D.; Sowinski, S. Membrane nanotubes: Dynamic long-distance connections between animal cells. Nat. Rev. Mol. Cell Biol. 2008, 9, 431–436. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.B.; Bu, W.; Goh, W.I.; Koh, E.; Ong, S.H.; Pawson, T.; Sudhaharan, T.; Ahmed, S. The Cdc42 effector IRSp53 generates filopodia by coupling membrane protrusion with actin dynamics. J. Biol. Chem. 2008, 283, 20454–20472. [Google Scholar] [CrossRef]
- Tian, A.; Baumgart, T. Sorting of lipids and proteins in membrane curvature gradients. Biophys. J. 2009, 96, 2676–2688. [Google Scholar] [CrossRef]
- Shlomovitz, R.; Gov, N.; Roux, A. Membrane-mediated interactions and the dynamics of dynamin oligomers on membrane tubes. New J. Phys. 2011, 13, 065008. [Google Scholar] [CrossRef]
- Zimmerberg, J.; McLaughlin, S. Membrane curvature: How BAR domains bend bilayers. Curr. Biol. 2004, 14, R250–R252. [Google Scholar] [CrossRef]
- Angulo-Urarte, A.; van der Wal, T.; Huveneers, S. Cell-cell junctions as sensors and transducers of mechanical forces. Biochim. Biophys. Acta (BBA) Biomembr. 2020, 183316. [Google Scholar] [CrossRef] [PubMed]
- Simunovic, M.; Evergren, E.; Callan-Jones, A.; Bassereau, P. Curving cells inside and out: Roles of BAR domain proteins in membrane shaping and its cellular implications. Annu. Rev. Cell Dev. Biol. 2019, 35, 111–129. [Google Scholar] [CrossRef] [PubMed]
- Hayer, A.; Shao, L.; Chung, M.; Joubert, L.M.; Yang, H.W.; Tsai, F.C.; Bisaria, A.; Betzig, E.; Meyer, T. Engulfed cadherin fingers are polarized junctional structures between collectively migrating endothelial cells. Nat. Cell Biol. 2016, 18, 1311–1323. [Google Scholar] [CrossRef] [PubMed]
- Dorland, Y.L.; Malinova, T.S.; Van Stalborch, A.M.D.; Grieve, A.G.; Van Geemen, D.; Jansen, N.S.; de Kreuk, B.J.; Nawaz, K.; Kole, J.; Geerts, D.; et al. The F-BAR protein pacsin2 inhibits asymmetric VE-cadherin internalization from tensile adherens junctions. Nat. Commun. 2016, 7, 1–18. [Google Scholar] [CrossRef] [PubMed]
- BAR Superfamily Home Page. Available online: http://bar-superfamily.org/ (accessed on 17 March 2015).
- Kessels, M.M.; Qualmann, B. Syndapin oligomers interconnect the machineries for endocytic vesicle formation and actin polymerization. J. Biol. Chem. 2006, 281, 13285–13299. [Google Scholar] [CrossRef] [PubMed]
- Frost, A.; Unger, V.M.; De Camilli, P. The BAR domain superfamily: Membrane-molding macromolecules. Cell 2009, 137, 191–196. [Google Scholar] [CrossRef] [PubMed]
- Ayton, G.S.; Voth, G.A. Multiscale Simulation of Protein Mediated Membrane Remodeling. In Seminars in Cell and Developmental Biology; Elsevier: Amsterdam, The Netherlands, 2010; Volume 21, pp. 357–362. [Google Scholar]
- Davtyan, A.; Simunovic, M.; Voth, G.A. Multiscale simulations of protein-facilitated membrane remodeling. J. Struct. Biol. 2016, 196, 57–63. [Google Scholar] [CrossRef] [PubMed]
- Ayton, G.S.; Lyman, E.; Krishna, V.; Swenson, R.D.; Mim, C.; Unger, V.M.; Voth, G.A. New insights into BAR domain-induced membrane remodeling. Biophys. J. 2009, 97, 1616–1625. [Google Scholar] [CrossRef]
- Suetsugu, S. The proposed functions of membrane curvatures mediated by the BAR domain superfamily proteins. J. Biochem. 2010, 148, 1–12. [Google Scholar] [CrossRef]
- Lee, S.H.; Kerff, F.; Chereau, D.; Ferron, F.; Klug, A.; Dominguez, R. Structural basis for the actin-binding function of missing-in-metastasis. Structure 2007, 15, 145–155. [Google Scholar] [CrossRef]
- Chial, H.J.; Lenart, P.; Chen, Y.Q. APPL proteins FRET at the BAR: Direct observation of APPL1 and APPL2 BAR domain-mediated interactions on cell membranes using FRET microscopy. PLoS ONE 2010, 5, e12471. [Google Scholar] [CrossRef] [PubMed]
- Kabaso, D.; Gongadze, E.; Elter, P.; Van Rienen, U.; Gimsa, J.; Kralj-Iglič, V.; Iglič, A. Attachment of rod-like (BAR) proteins and membrane shape. Mini Rev. Med. Chem. 2011, 11, 272–282. [Google Scholar] [CrossRef]
- Khelashvili, G.; Harries, D.; Weinstein, H. Modeling membrane deformations and lipid demixing upon protein-membrane interaction: The BAR dimer adsorption. Biophys. J. 2009, 97, 1626–1635. [Google Scholar] [CrossRef]
- Takei, K.; Slepnev, V.I.; Haucke, V.; De Camilli, P. Functional partnership between amphiphysin and dynamin in clathrin-mediated endocytosis. Nat. Cell Biol. 1999, 1, 33–39. [Google Scholar] [CrossRef] [PubMed]
- Shimada, A.; Takano, K.; Shirouzu, M.; Hanawa-Suetsugu, K.; Terada, T.; Toyooka, K.; Umehara, T.; Yamamoto, M.; Yokoyama, S.; Suetsugu, S. Mapping of the basic amino-acid residues responsible for tubulation and cellular protrusion by the EFC/F-BAR domain of pacsin2/Syndapin II. FEBS Lett. 2010, 584, 1111–1118. [Google Scholar] [CrossRef] [PubMed]
- Prévost, C.; Zhao, H.; Manzi, J.; Lemichez, E.; Lappalainen, P.; Callan-Jones, A.; Bassereau, P. IRSp53 senses negative membrane curvature and phase separates along membrane tubules. Nat. Commun. 2015, 6, 1–11. [Google Scholar] [CrossRef]
- Mattila, P.K.; Pykalainen, A.; Saarikangas, J.; Paavilainen, V.O.; Vihinen, H.; Jokitalo, E.; Lappalainen, P. Missing-in-metastasis and IRSp53 deform PI (4, 5) P2-rich membranes by an inverse BAR domain–like mechanism. J. Cell Biol. 2007, 176, 953–964. [Google Scholar] [CrossRef]
- Krugmann, S.; Jordens, I.; Gevaert, K.; Driessens, M.; Vandekerckhove, J.; Hall, A. Cdc42 induces filopodia by promoting the formation of an IRSp53: Mena complex. Curr. Biol. 2001, 11, 1645–1655. [Google Scholar] [CrossRef]
- Miyata, H.; Nishiyama, S.; Akashi, K.I.; Kinosita, K. Protrusive growth from giant liposomes driven by actin polymerization. Proc. Natl. Acad. Sci. USA 1999, 96, 2048–2053. [Google Scholar] [CrossRef]
- Jelerčič, U.; Gov, N.S. Pearling instability of membrane tubes driven by curved proteins and actin polymerization. Phys. Biol. 2015, 12, 066022. [Google Scholar] [CrossRef] [PubMed]
- Häckl, W.; Bärmann, M.; Sackmann, E. Shape Changes of Self-Assembled Actin Bilayer Composite Membranes. Phys. Rev. Lett. 1998, 80, 1786–1789. [Google Scholar] [CrossRef]
- Noguchi, H. Membrane tubule formation by banana-shaped proteins with or without transient network structure. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef]
- Simunovic, M.; Voth, G.A.; Callan-Jones, A.; Bassereau, P. When physics takes over: BAR proteins and membrane curvature. Trends Cell Biol. 2015, 25, 780–792. [Google Scholar] [CrossRef] [PubMed]
- Yochelis, A.; Ebrahim, S.; Millis, B.; Cui, R.; Kachar, B.; Naoz, M.; Gov, N.S. Self-organization of waves and pulse trains by molecular motors in cellular protrusions. Sci. Rep. 2015, 5, 1–15. [Google Scholar] [CrossRef]
- Liu, A.P.; Richmond, D.L.; Maibaum, L.; Pronk, S.; Geissler, P.L.; Fletcher, D.A. Membrane-induced bundling of actin filaments. Nat. Phys. 2008, 4, 789–793. [Google Scholar] [CrossRef]
- Shlomovitz, R.; Gov, N.S. Physical model of contractile ring initiation in dividing cells. Biophys. J. 2008, 94, 1155–1168. [Google Scholar] [CrossRef] [PubMed]
- Jarin, Z.; Pak, A.J.; Bassereau, P.; Voth, G.A. Lipid-Composition-Mediated Forces Can Stabilize Tubular Assemblies of I-BAR Proteins. Biophys. J. 2021, 120, 46–54. [Google Scholar] [CrossRef]
- Alimohamadi, H.; Vasan, R.; Hassinger, J.E.; Stachowiak, J.C.; Rangamani, P. The role of traction in membrane curvature generation. Mol. Biol. Cell 2018, 29, 2024–2035. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.; Sirota, E.; Safinya, C.; Clark, N.A. Structure of the L β phases in a hydrated phosphatidylcholine multimembrane. Phys. Rev. Lett. 1988, 60, 813. [Google Scholar] [CrossRef]
- Lubensky, T.; Prost, J. Orientational order and vesicle shape. J. Phys. II 1992, 2, 371–382. [Google Scholar] [CrossRef]
- Bernchou, U.; Brewer, J.; Midtiby, H.S.; Ipsen, J.H.; Bagatolli, L.A.; Simonsen, A.C. Texture of lipid bilayer domains. J. Am. Chem. Soc. 2009, 131, 14130–14131. [Google Scholar] [CrossRef]
- Mesarec, L.; Góźdź, W.; Iglič, A.; Kralj-Iglič, V.; Virga, E.; Kralj, S. Normal red blood cells’ shape stabilized by membrane’s in-plane ordering. Sci. Rep. 2019, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- May, S. Membrane perturbations induced by integral proteins: Role of conformational restrictions of the lipid chains. Langmuir 2002, 18, 6356–6364. [Google Scholar] [CrossRef]
- Dan, N.; Safran, S. Effect of lipid characteristics on the structure of transmembrane proteins. Biophys. J. 1998, 75, 1410–1414. [Google Scholar] [CrossRef]
- Deuling, H.J.; Helfrich, W. Red blood cell shapes as explained on the basis of curvature elasticity. Biophys. J. 1976, 16, 861–868. [Google Scholar] [CrossRef]
- Shi, Z.; Baumgart, T. Dynamics and instabilities of lipid bilayer membrane shapes. Adv. Colloid Interface Sci. 2014, 208, 76–88. [Google Scholar] [CrossRef] [PubMed]
- Boulbitch, A.; Simson, R.; Simson, D.; Merkel, R.; Häckl, W.; Bärmann, M.; Sackmann, E. Shape instability of a biomembrane driven by a local softening of the underlying actin cortex. Phys. Rev. E 2000, 62, 3974. [Google Scholar] [CrossRef] [PubMed]
- Lipowsky, R.; Sackmann, E. Structure and Dynamics of Membranes: I. From Cells to Vesicles/II. Generic and Specific Interactions; Elsevier: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Wang, D.N. Band 3 protein: Structure, flexibility and function. FEBS Lett. 1994, 346, 26–31. [Google Scholar] [CrossRef]
- Delaunay, J. The molecular basis of hereditary red cell membrane disorders. Blood Rev. 2007, 21, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Reithmeier, R.A.; Casey, J.R.; Kalli, A.C.; Sansom, M.S.; Alguel, Y.; Iwata, S. Band 3, the human red cell chloride/bicarbonate anion exchanger (AE1, SLC4A1), in a structural context. Biochim. Biophys. Acta (BBA) Biomembr. 2016, 1858, 1507–1532. [Google Scholar] [CrossRef]
- Bohinc, K.; Kralj-Iglič, V.; May, S. Interaction between two cylindrical inclusions in a symmetric lipid bilayer. J. Chem. Phys. 2003, 119, 7435–7444. [Google Scholar] [CrossRef]
- Marčelja, S. Lipid-mediated protein interaction in membranes. Biochim. Biophys. Acta (BBA) Biomembr. 1976, 455, 1–7. [Google Scholar] [CrossRef]
- Sintes, T.; Baumgärtner, A. Protein attraction in membranes induced by lipid fluctuations. Biophys. J. 1997, 73, 2251–2259. [Google Scholar] [CrossRef]
- Canham, P.; Burton, A.C. Distribution of size and shape in populations of normal human red cells. Circ. Res. 1968, 22, 405–422. [Google Scholar] [CrossRef]
- Fung, Y.; Tsang, W.C.; Patitucci, P. High-resolution data on the geometry of red blood cells. Biorheology 1981, 18, 369–385. [Google Scholar] [CrossRef]
- Gruber, W.; Deuticke, B. Comparative aspects of phosphate transfer across mammalian erythrocyte membranes. J. Membr. Biol. 1973, 13, 19–36. [Google Scholar] [CrossRef] [PubMed]
- Emmons, W.F. The interrelation of number, volume, diameter and area of mammalian erythrocytes. J. Physiol. 1927, 64, 215. [Google Scholar] [CrossRef]
- Seifert, U.; Berndl, K.; Lipowsky, R. Shape transformations of vesicles: Phase diagram for spontaneous-curvature and bilayer-coupling models. Phys. Rev. A 1991, 44, 1182. [Google Scholar] [CrossRef] [PubMed]
- Mesarec, L.; Góźdź, W.; Iglič, A.; Kralj, S. Effective topological charge cancelation mechanism. Sci. Rep. 2016, 6, 27117. [Google Scholar] [CrossRef]
- Selinger, R.L.B.; Konya, A.; Travesset, A.; Selinger, J.V. Monte Carlo studies of the XY model on two-dimensional curved surfaces. J. Phys. Chem. B 2011, 115, 13989–13993. [Google Scholar] [CrossRef]
- Napoli, G.; Vergori, L. Extrinsic curvature effects on nematic shells. Phys. Rev. Lett. 2012, 108, 207803. [Google Scholar] [CrossRef] [PubMed]
- Discher, D.; Mohandas, N.; Evans, E. Molecular maps of red cell deformation: Hidden elasticity and in situ connectivity. Science 1994, 266, 1032–1035. [Google Scholar] [CrossRef]
- Discher, D.E.; Mohandas, N. Kinematics of red cell aspiration by fluorescence-imaged microdeformation. Biophys. J. 1996, 71, 1680–1694. [Google Scholar] [CrossRef]
- Iglič, A.; Svetina, S.; Žekš, B. Depletion of membrane skeleton in red blood cell vesicles. Biophys. J. 1995, 69, 274–279. [Google Scholar] [CrossRef]
- Evans, E.; Skalak, R. Mechanics and thermodynamics of biomembranes: Part 2. CRC Crit. Rev. Bioeng. 1979, 3, 331. [Google Scholar]
- Waugh, R.E. Elastic energy of curvature-driven bump formation on red blood cell membrane. Biophys. J. 1996, 70, 1027–1035. [Google Scholar] [CrossRef]
- Urbanija, J.; Babnik, B.; Frank, M.; Tomšič, N.; Rozman, B.; Kralj-Iglič, V.; Iglič, A. Attachment of β 2-glycoprotein I to negatively charged liposomes may prevent the release of daughter vesicles from the parent membrane. Eur. Biophys. J. 2008, 37, 1085–1095. [Google Scholar] [CrossRef]
- Iglič, A.; Veranič, P.; Jezernik, K.; Fošnarič, M.; Kamin, B.; Hägerstrand, H.; Kralj-Iglič, V. Spherocyte shape transformation and release of tubular nanovesicles in human erythrocytes. Bioelectrochemistry 2004, 62, 159–161. [Google Scholar] [CrossRef] [PubMed]
- Hägerstrand, H.; Danieluk, M.; Bobrowska-Hägerstrand, M.; Iglič, A.; Wróbel, A.; Isomaa, B.; Nikinmaa, M. Influence of band 3 protein absence and skeletal structures on amphiphile-and Ca2+-induced shape alterations in erythrocytes: A study with lamprey (Lampetra fluviatilis), trout (Onchorhynchus mykiss) and human erythrocytes. Biochim. Biophys. Acta (BBA) Biomembr. 2000, 1466, 125–138. [Google Scholar] [CrossRef]
- Hwang, W.C.; Waugh, R.E. Energy of dissociation of lipid bilayer from the membrane skeleton of red blood cells. Biophys. J. 1997, 72, 2669. [Google Scholar] [CrossRef]
- Hägerstrand, H.; Kralj-Iglič, V.; Bobrowska-Hägerstrand, M.; Iglič, A. Membrane skeleton detachment in spherical and cylindrical microexovesicles. Bull. Math. Biol. 1999, 61, 1019–1030. [Google Scholar] [CrossRef] [PubMed]
- Penič, S.; Mesarec, L.; Fošnarič, M.; Mrówczyńska, L.; Hägerstrand, H.; Kralj-Iglič, V.; Iglič, A. Budding and fission of membrane vesicles: A mini review. Front. Phys. 2020, 8, 342. [Google Scholar] [CrossRef]
- Fischer, T.M. Mechanisms for determining the time scales in vesicle budding. Phys. Rev. E 1994, 50, 4156. [Google Scholar] [CrossRef]
- Kralj-Iglič, V.; Pocsfalvi, G.; Mesarec, L.; Šuštar, V.; Hägerstrand, H.; Iglič, A. Minimizing isotropic and deviatoric membrane energy—An unifying formation mechanism of different cellular membrane nanovesicle types. PLoS ONE 2020, 15, 1–25. [Google Scholar] [CrossRef]
- Jesenek, D.; Perutková, Š.; Góźdź, W.; Kralj-Iglič, V.; Iglič, A.; Kralj, S. Vesiculation of biological membrane driven by curvature induced frustrations in membrane orientational ordering. Int. J. Nanomed. 2013, 8, 677–687. [Google Scholar] [CrossRef]
- Bobrowska-Hägerstrand, M.; Kralj-Iglič, V.; Iglič, A.; Bialkowska, K.; Isomaa, B.; Hägerstrand, H. Torocyte membrane endovesicles induced by octaethyleneglycol dodecylether in human erythrocytes. Biophys. J. 1999, 77, 3356–3362. [Google Scholar] [CrossRef][Green Version]
- Bouvrais, H. Bending rigidities of lipid bilayers: Their determination and main inputs in biophysical studies. In Advances in Planar Lipid Bilayers and Liposomes; Elsevier: Amsterdam, The Netherlands, 2012; Volume 15, pp. 1–75. [Google Scholar]
- Dimova, R. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci. 2014, 208, 225–234. [Google Scholar] [CrossRef]
- Strey, H.; Peterson, M.; Sackmann, E. Measurement of erythrocyte membrane elasticity by flicker eigenmode decomposition. Biophys. J. 1995, 69, 478–488. [Google Scholar] [CrossRef]
- Betz, T.; Lenz, M.; Joanny, J.F.; Sykes, C. ATP-dependent mechanics of red blood cells. Proc. Natl. Acad. Sci. USA 2009, 106, 15320–15325. [Google Scholar] [CrossRef]
- Yoon, Y.Z.; Hong, H.; Brown, A.; Kim, D.C.; Kang, D.J.; Lew, V.L.; Cicuta, P. Flickering analysis of erythrocyte mechanical properties: Dependence on oxygenation level, cell shape, and hydration level. Biophys. J. 2009, 97, 1606–1615. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Best, C.A.; Auth, T.; Gov, N.S.; Safran, S.A.; Popescu, G.; Suresh, S.; Feld, M.S. Metabolic remodeling of the human red blood cell membrane. Proc. Natl. Acad. Sci. USA 2010, 107, 1289–1294. [Google Scholar] [CrossRef] [PubMed]
- Gimsa, U.; Iglič, A.; Fiedler, S.; Zwanzig, M.; Kralj-Iglič, V.; Jonas, L.; Gimsa, J. Actin is not required for nanotubular protrusions of primary astrocytes grown on metal nano-lawn. Mol. Membr. Biol. 2007, 24, 243–255. [Google Scholar] [CrossRef]
- Fošnarič, M.; Iglič, A.; Slivnik, T.; Kralj-Iglič, V. Flexible membrane inclusions and membrane inclusions induced by rigid globular proteins. Adv. Planar Lipid Bilayers Liposomes 2008, 7, 143–168. [Google Scholar]
- Millard, T.H.; Bompard, G.; Heung, M.Y.; Dafforn, T.R.; Scott, D.J.; Machesky, L.M.; Fütterer, K. Structural basis of filopodia formation induced by the IRSp53/MIM homology domain of human IRSp53. EMBO J. 2005, 24, 240–250. [Google Scholar] [CrossRef]
- Scita, G.; Confalonieri, S.; Lappalainen, P.; Suetsugu, S. IRSp53: Crossing the road of membrane and actin dynamics in the formation of membrane protrusions. Trends Cell Biol. 2008, 18, 52–60. [Google Scholar] [CrossRef]
- Emsellem, V.; Cardoso, O.; Tabeling, P. Vesicle deformation by microtubules: A phase diagram. Phys. Rev. E 1998, 58, 4807. [Google Scholar] [CrossRef]
- Tsai, F.C.; Roth, S.; Dogterom, M.; Koenderink, G.H. Biomimetic Liposome Model Systems to Study Cell Shape Control by the Cytoskeleton. In Advances in Planar Lipid Bilayers and Liposomes; Elsevier: Amsterdam, The Netherlands, 2014; Volume 19, pp. 139–173. [Google Scholar]
- Fygenson, D.K.; Elbaum, M.; Shraiman, B.; Libchaber, A. Microtubules and vesicles under controlled tension. Phys. Rev. E 1997, 55, 850. [Google Scholar] [CrossRef]
- Tsai, F.C.; Koenderink, G.H. Shape control of lipid bilayer membranes by confined actin bundles. Soft Matter 2015, 11, 8834–8847. [Google Scholar] [CrossRef] [PubMed]
- Fygenson, D.K.; Marko, J.F.; Libchaber, A. Mechanics of microtubule-based membrane extension. Phys. Rev. Lett. 1997, 79, 4497. [Google Scholar] [CrossRef]
- Iglič, A.; Slivnik, T.; Kralj-Iglič, V. Elastic properties of biological membranes influenced by attached proteins. J. Biomech. 2007, 40, 2492–2500. [Google Scholar] [CrossRef]
- Iglič, A.; Tzaphlidou, M.; Remškar, M.; Babnik, B.; Daniel, M.; Kralj-Iglič, V. Stable Shapes of Thin Anisotropic Nano-strips. Fullerenes Nanotub. Carbon Nonstruct. 2005, 13, 183–192. [Google Scholar] [CrossRef]
- Ziserman, L.; Lee, H.Y.; Raghavan, S.R.; Mor, A.; Danino, D. Unraveling the mechanism of nanotube formation by chiral self-assembly of amphiphiles. J. Am. Chem. Soc. 2011, 133, 2511–2517. [Google Scholar] [CrossRef]
- Danino, D. Cryo-TEM of soft molecular assemblies. Curr. Opin. Colloid Interface Sci. 2012, 17, 316–329. [Google Scholar] [CrossRef]
- Saha, S.; Nagy, T.L.; Weiner, O.D. Joining forces: Crosstalk between biochemical signalling and physical forces orchestrates cellular polarity and dynamics. Philos. Trans. R. Soc. B Biol. Sci. 2018, 373, 20170145. [Google Scholar] [CrossRef]
- Girard, P.; Prost, J.; Bassereau, P. Passive or active fluctuations in membranes containing proteins. Phys. Rev. Lett. 2005, 94, 088102. [Google Scholar] [CrossRef] [PubMed]
- Gov, N. Membrane undulations driven by force fluctuations of active proteins. Phys. Rev. Lett. 2004, 93, 268104. [Google Scholar] [CrossRef]
- Gladnikoff, M.; Shimoni, E.; Gov, N.S.; Rousso, I. Retroviral assembly and budding occur through an actin-driven mechanism. Biophys. J. 2009, 97, 2419–2428. [Google Scholar] [CrossRef] [PubMed]
- Votteler, J.; Sundquist, W.I. Virus budding and the ESCRT pathway. Cell Host Microbe 2013, 14, 232–241. [Google Scholar] [CrossRef] [PubMed]
- Góźdź, W.T. Spontaneous curvature induced shape transformation of tubular polymersomes. Langmuir 2004, 20, 7385–7391. [Google Scholar] [CrossRef]
- Góźdź, W.T. Influence of spontaneous curvature and microtubules on the conformations of lipid vesicles. J. Phys. Chem. B 2005, 109, 21145–21149. [Google Scholar] [CrossRef]
- Góźdź, W.T. The interface width of separated two-component lipid membranes. J. Phys. Chem. B 2006, 110, 21981–21986. [Google Scholar] [CrossRef]
- Góźdź, W.T.; Bobrovska, N.; Ciach, A. Separation of components in lipid membranes induced by shape transformation. J. Chem. Phys. 2012, 137, 015101. [Google Scholar] [CrossRef]
- Penič, S.; Iglič, A.; Bivas, I.; Fošnarič, M. Bending elasticity of vesicle membranes studied by Monte Carlo simulations of vesicle thermal shape fluctuations. Soft Matter 2015, 11, 5004–5009. [Google Scholar] [CrossRef]
- Penič, S.; Perutková, Š.; Fošnarič, M.; Iglič, A. Monte Carlo methods used in inverted hexagonal lipid phase and in simulations of thermally fluctuating lipid vesicles. Int. J. Adv. Eng. Sci. Appl. Math. 2016, 8, 147–161. [Google Scholar] [CrossRef]
- Noguchi, H. Membrane simulation models from nanometer to micrometer scale. J. Phys. Soc. Jpn. 2009, 78, 1007. [Google Scholar] [CrossRef]






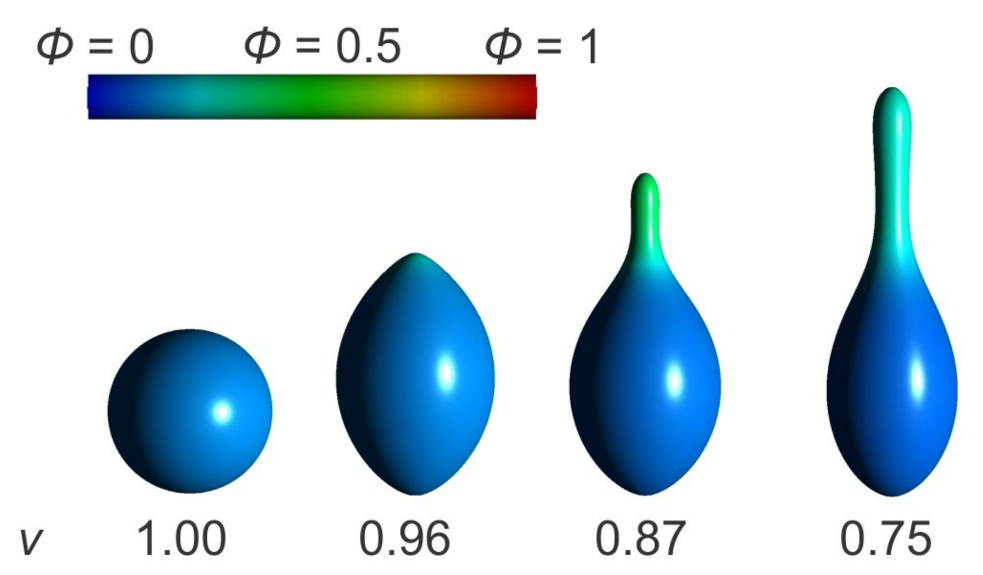
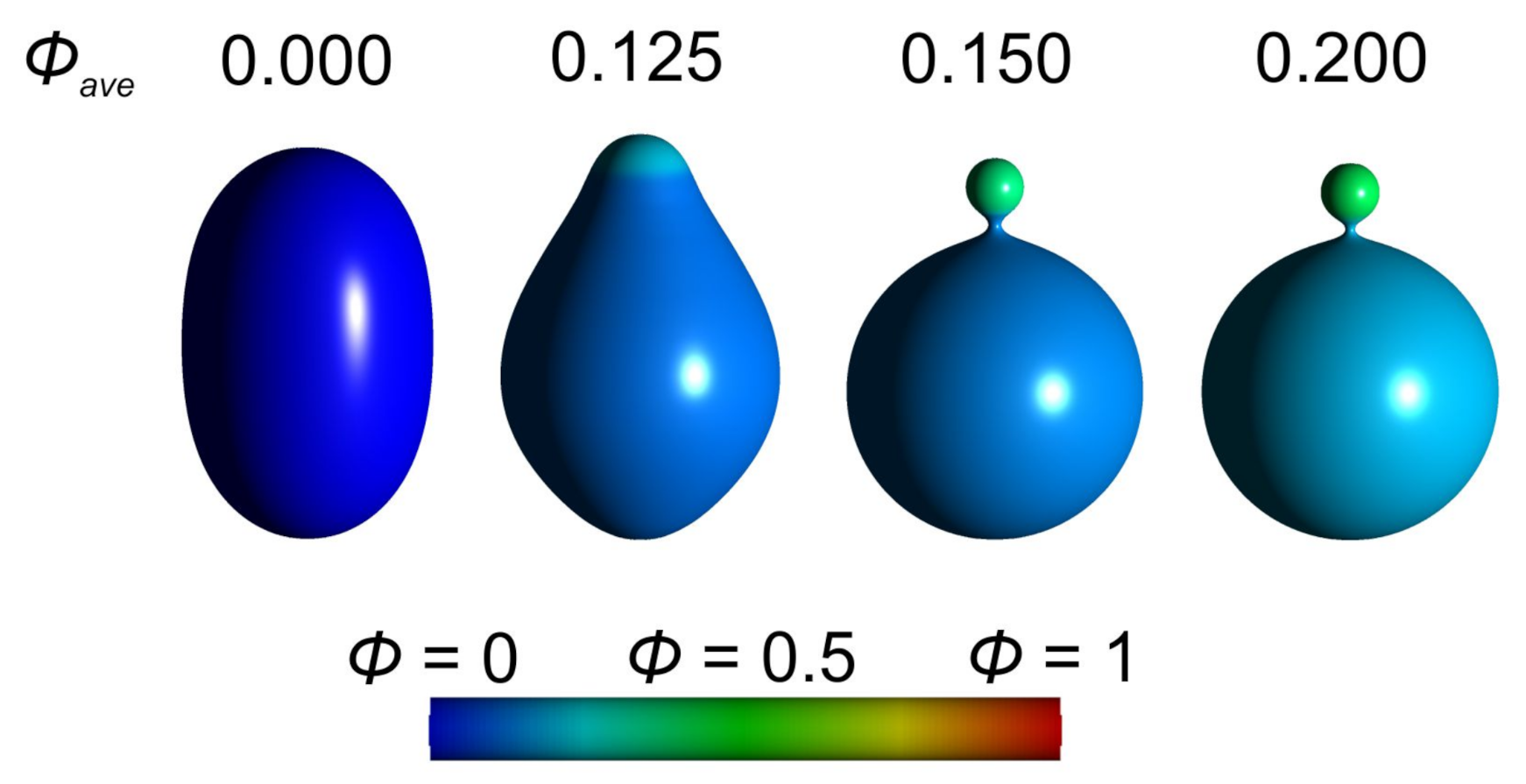
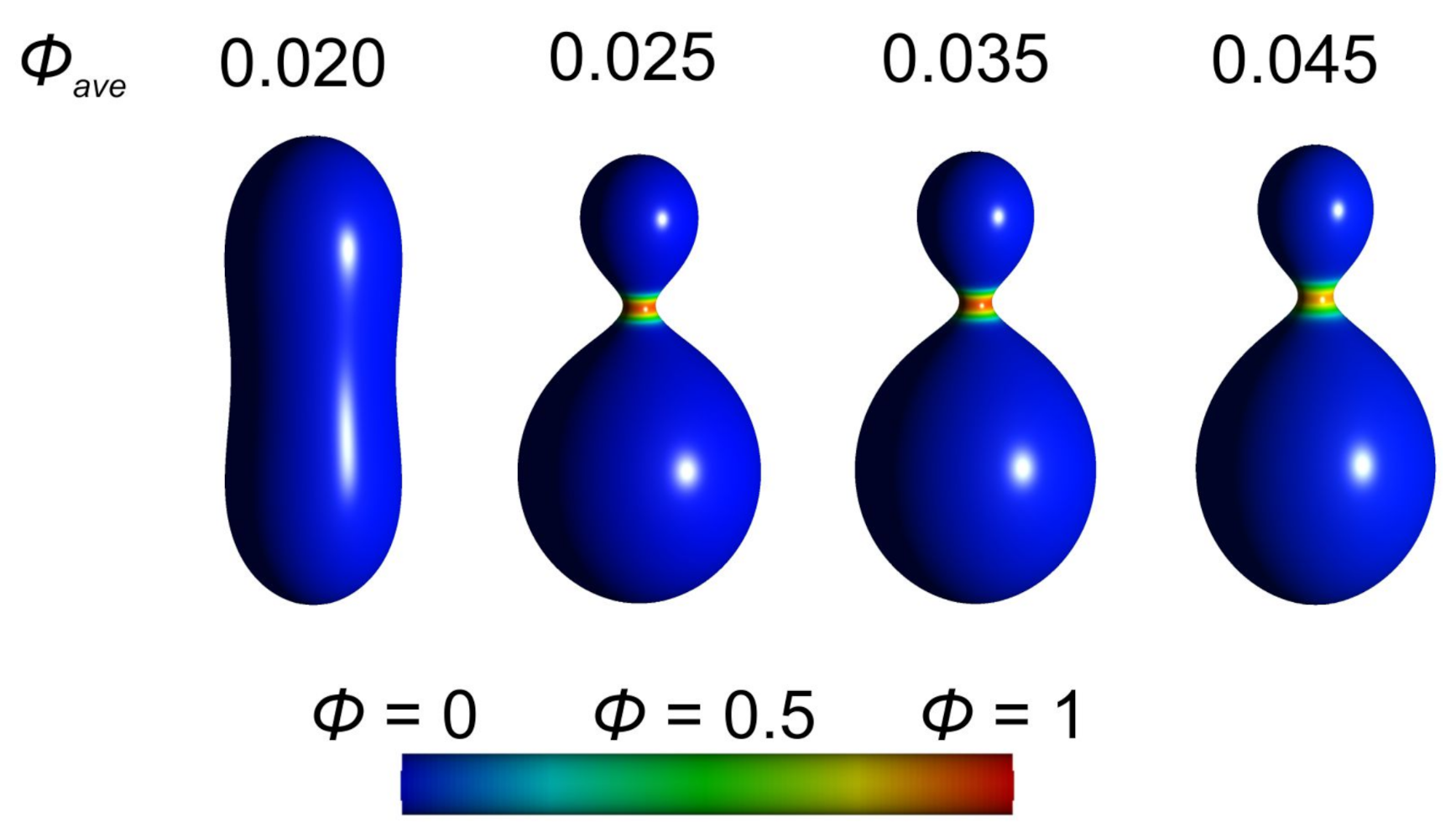
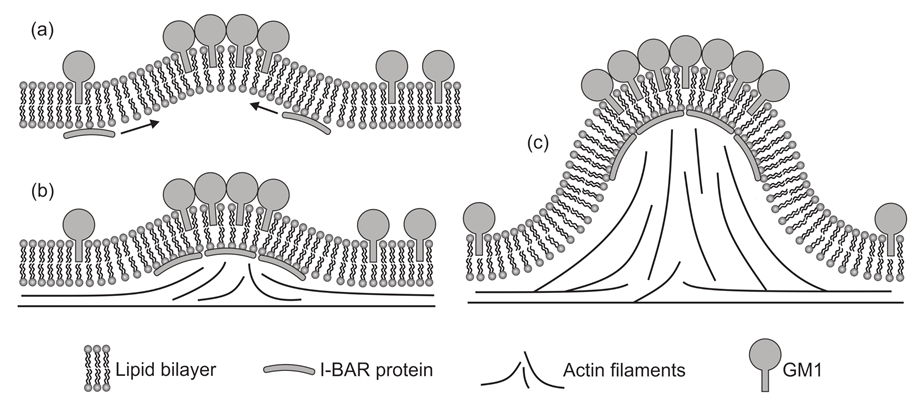


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mesarec, L.; Drab, M.; Penič, S.; Kralj-Iglič, V.; Iglič, A. On the Role of Curved Membrane Nanodomains and Passive and Active Skeleton Forces in the Determination of Cell Shape and Membrane Budding. Int. J. Mol. Sci. 2021, 22, 2348. https://doi.org/10.3390/ijms22052348
Mesarec L, Drab M, Penič S, Kralj-Iglič V, Iglič A. On the Role of Curved Membrane Nanodomains and Passive and Active Skeleton Forces in the Determination of Cell Shape and Membrane Budding. International Journal of Molecular Sciences. 2021; 22(5):2348. https://doi.org/10.3390/ijms22052348
Chicago/Turabian StyleMesarec, Luka, Mitja Drab, Samo Penič, Veronika Kralj-Iglič, and Aleš Iglič. 2021. "On the Role of Curved Membrane Nanodomains and Passive and Active Skeleton Forces in the Determination of Cell Shape and Membrane Budding" International Journal of Molecular Sciences 22, no. 5: 2348. https://doi.org/10.3390/ijms22052348
APA StyleMesarec, L., Drab, M., Penič, S., Kralj-Iglič, V., & Iglič, A. (2021). On the Role of Curved Membrane Nanodomains and Passive and Active Skeleton Forces in the Determination of Cell Shape and Membrane Budding. International Journal of Molecular Sciences, 22(5), 2348. https://doi.org/10.3390/ijms22052348








