SSnet: A Deep Learning Approach for Protein-Ligand Interaction Prediction
Abstract
1. Introduction
2. Methods and Rationale
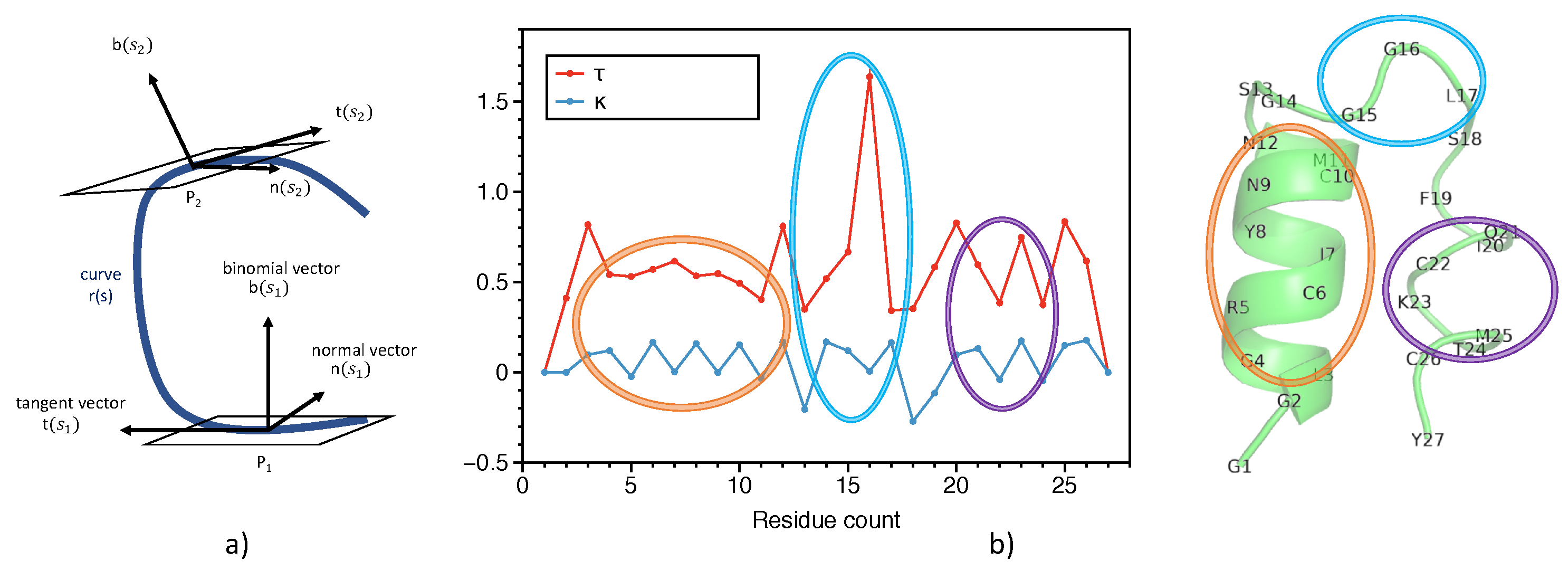
2.1. Representation of Proteins
2.2. Representation of Ligands
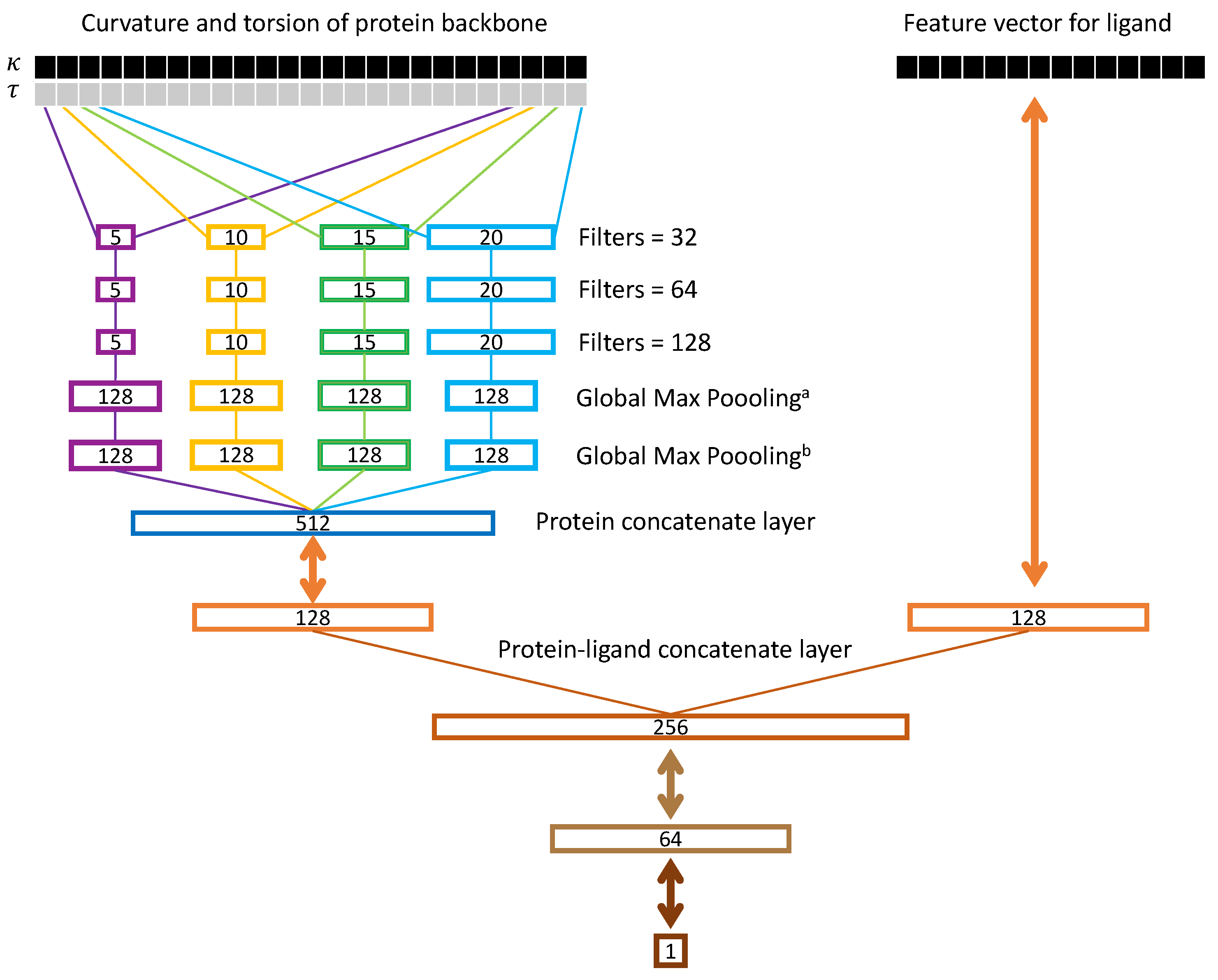
2.3. Ssnet Model
2.4. Grad-CAM Method for Heatmap Generation
2.5. Evaluation Criteria
2.6. Datasets
- (1)
- The target has PDB ID cross-referenced as 3D structure. The first annotated structure is taken as reference PDB file.
- (2)
- The ligand has SMILES representation in the entry.
- (3)
- Record has IC50 value (a measure of strength of binding) and is either less than x (active) or greater than y (inactive).
3. Results
3.1. Selection of Ligand Representation
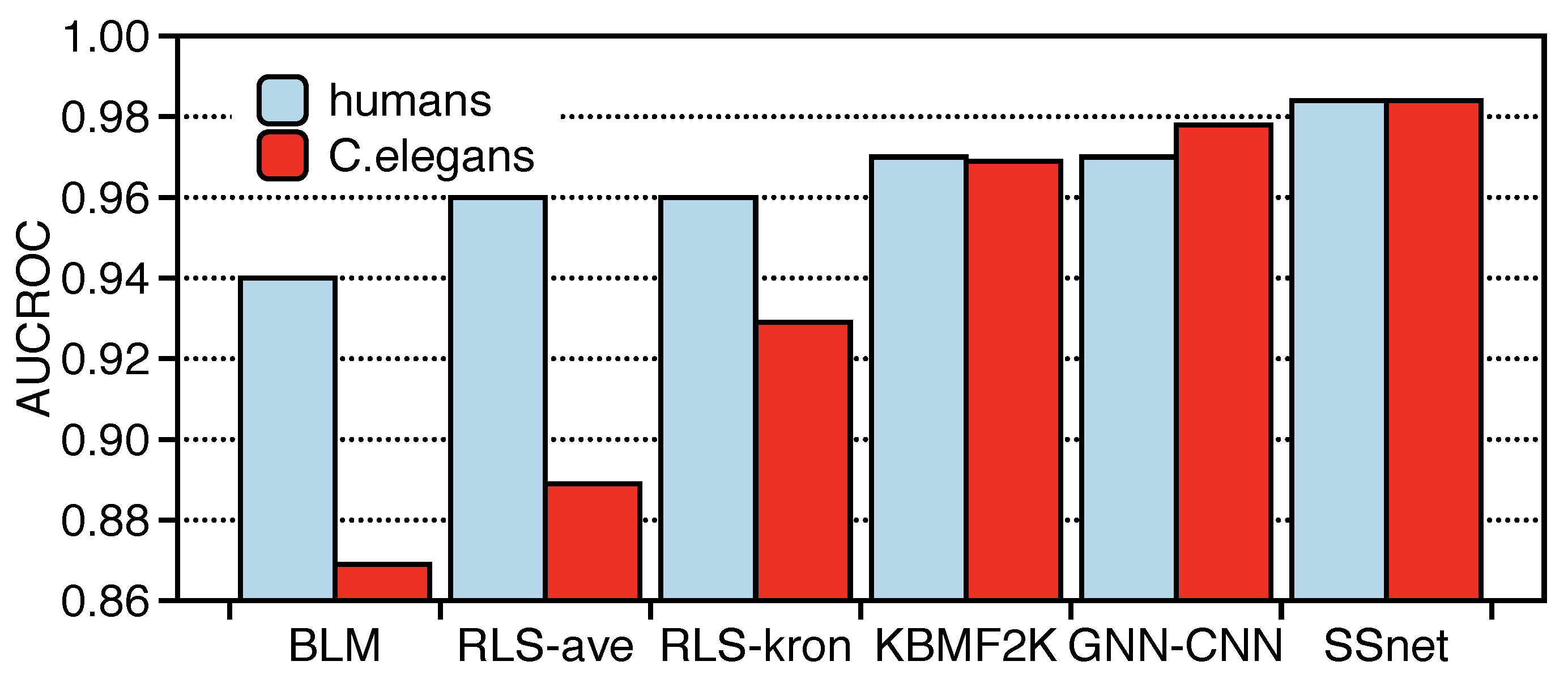
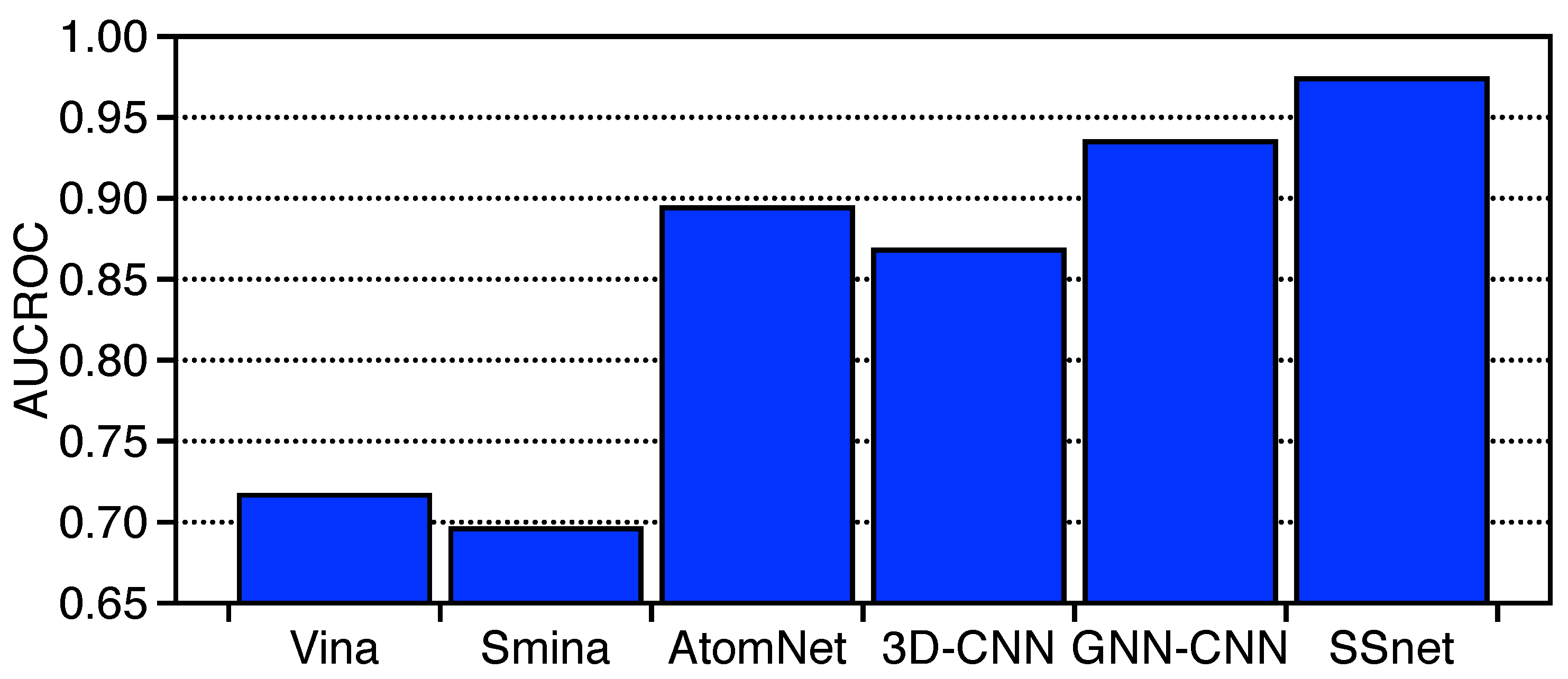
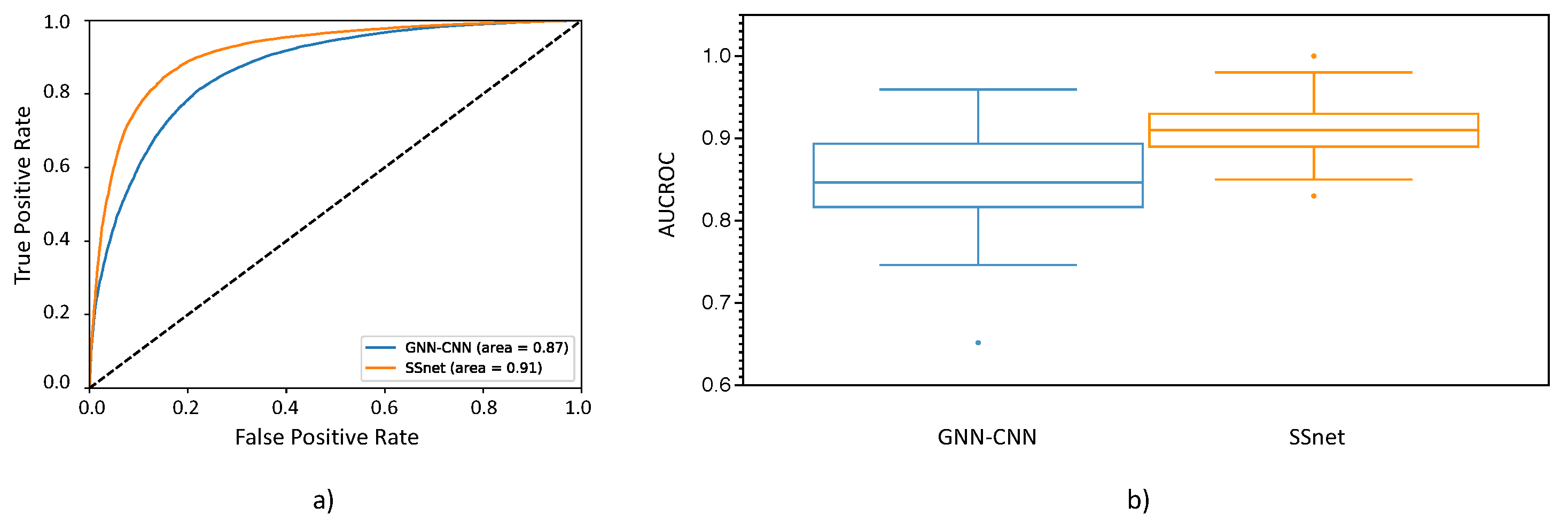
3.2. SSnet Compared on Computational Datasets
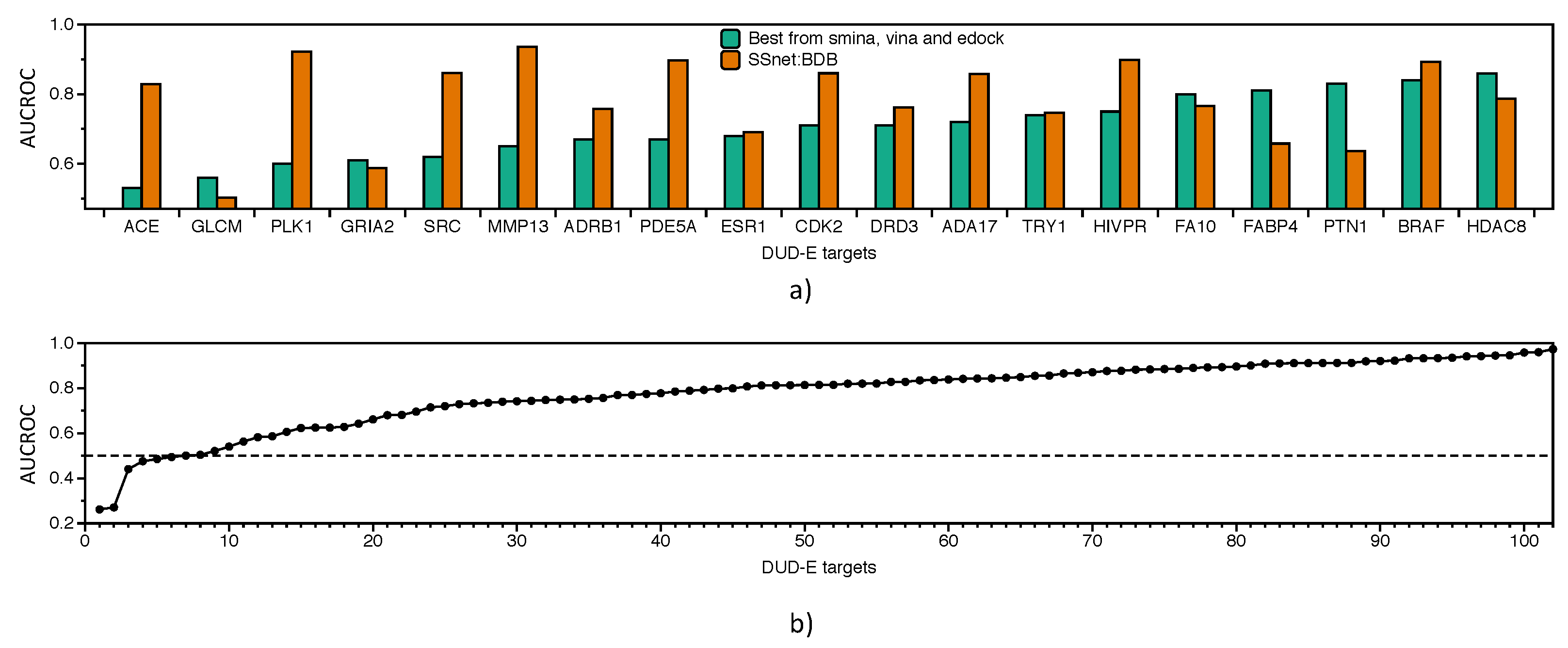
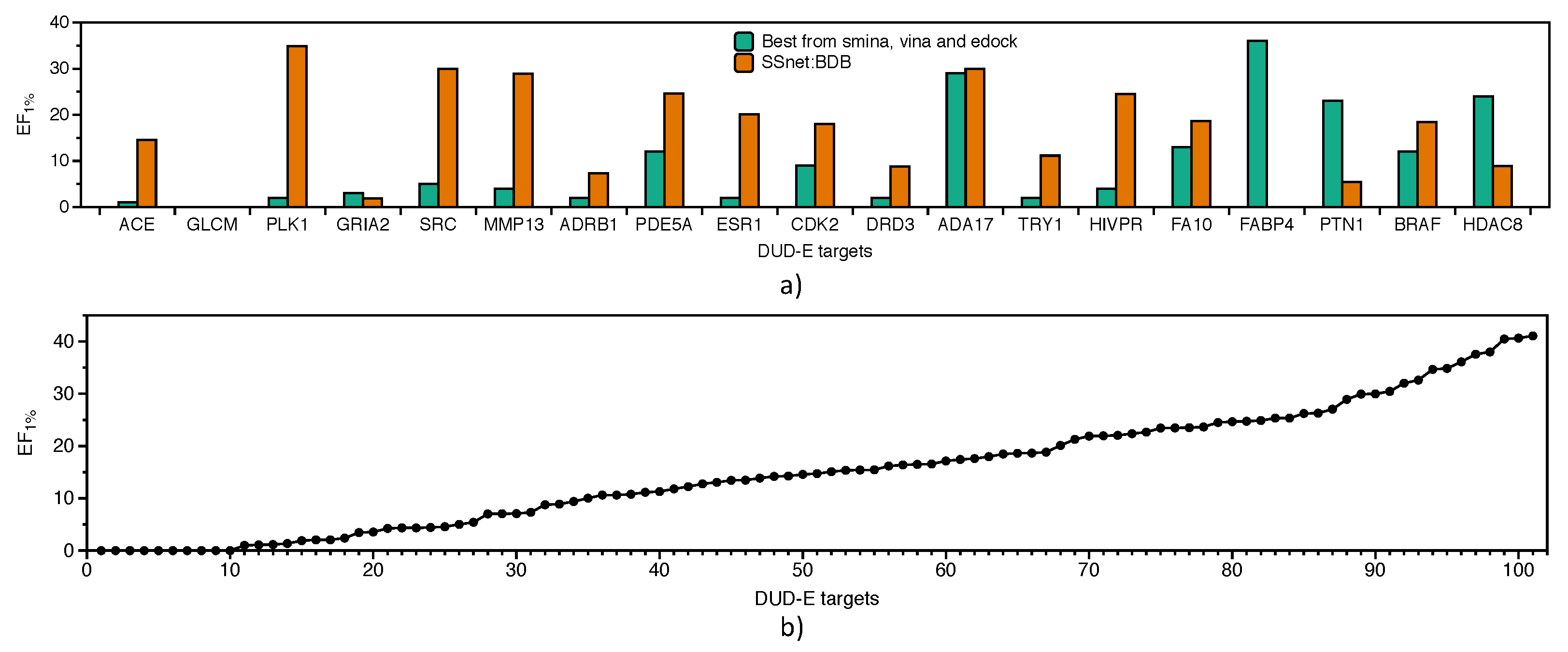
3.3. Benchmarking SSnet
- Check for ligand similarity by comparing Tanimoto Coefficient (TC) score [78] for each ligand in the BDB train dataset to all ligands of the DUD-E dataset.
- Boosting consensus score (BCS) is a gradient-based decision tree framework which is trained on binary labels (actives and decoys) on an individual decision tree for each target where the input is composed of docking scores obtained from each docking method. For each target, the docking scores were provided to other off-targets for boosting the model performance.
- Mean-variance consensus (MVC) is a parameterized function based on gaussian distribution of the scores.
- Mean, median (Med), maximum (Max), and minimum (Min) are the statistics obtained from normalized scores across the docking methods.
3.4. Applicability of SSnet
3.4.1. Latent Space for Proteins
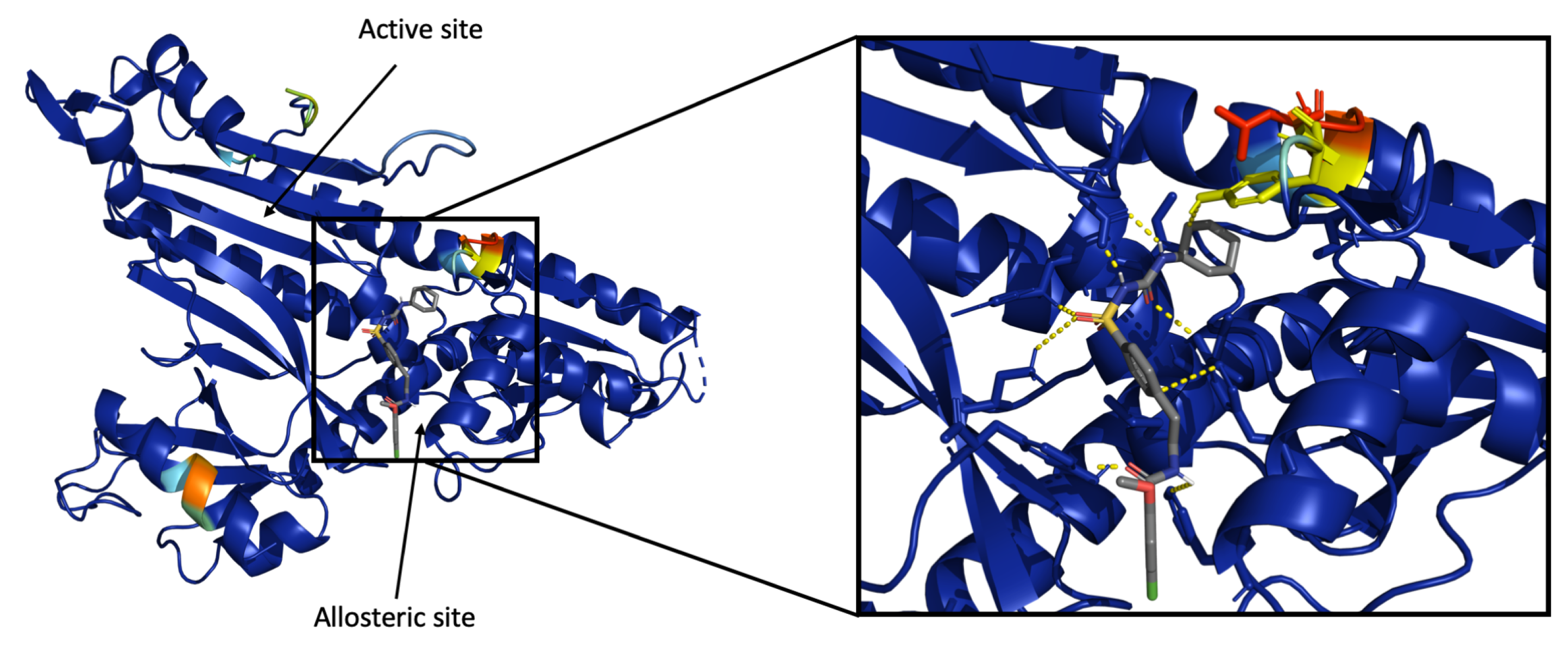
3.4.2. Visualization of Heatmap Using Grad-CAM
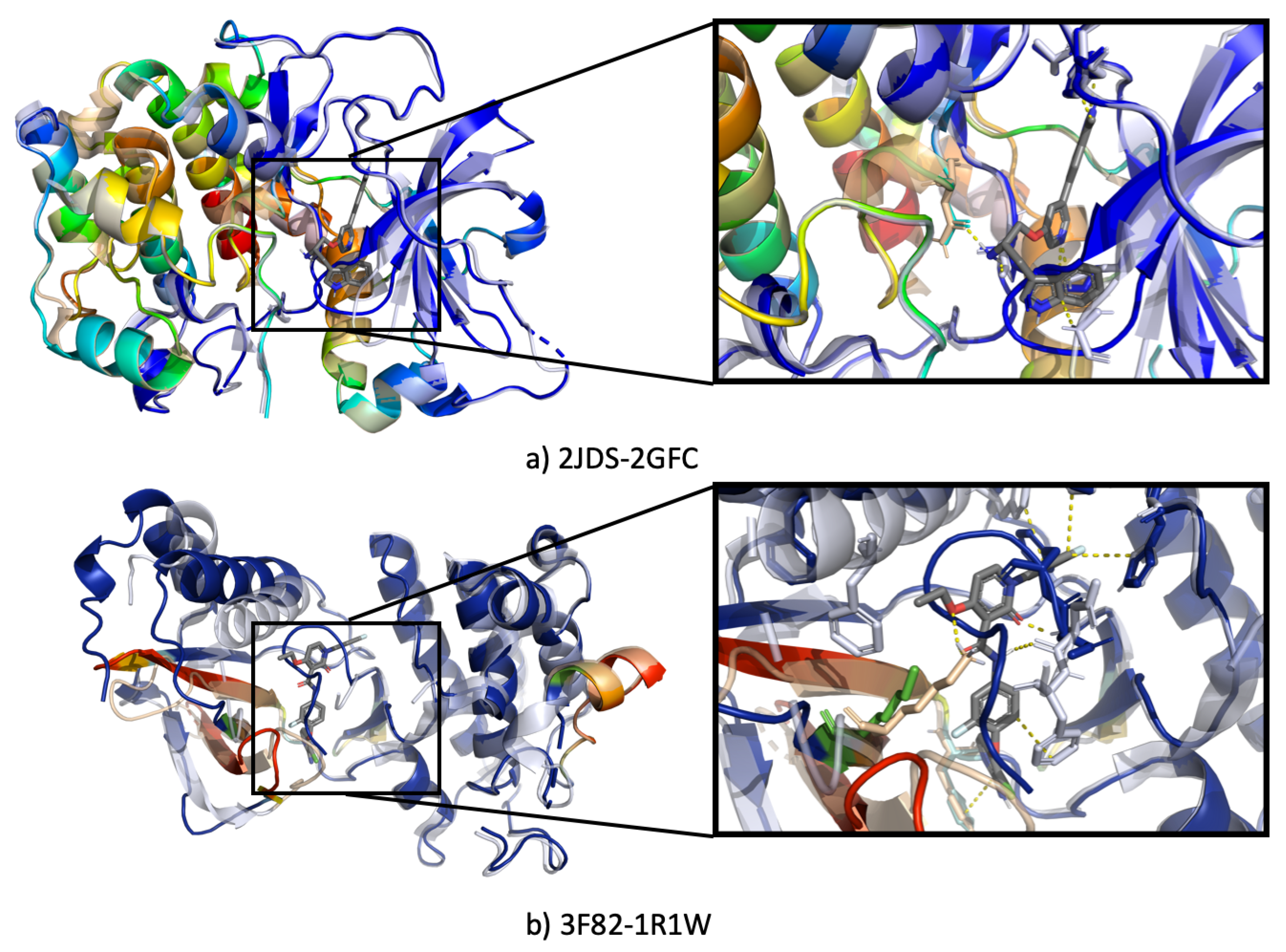
3.4.3. Ssnet Is Conformation Blind
- Can SSnet predict the same results using an unbound protein structure or a different conformation of the same protein?
- Can SSnet detect cryptic sites based on unbound protein structures?
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, D.; Oezguen, N.; Urvil, P.; Ferguson, C.; Dann, S.M.; Savidge, T.C. Regulation of Protein-Ligand Binding Affinity by Hydrogen Bond Pairing. Sci. Adv. 2016, 2, e1501240. [Google Scholar] [CrossRef]
- Itoh, Y.; Nakashima, Y.; Tsukamoto, S.; Kurohara, T.; Suzuki, M.; Sakae, Y.; Oda, M.; Okamoto, Y.; Suzuki, T. N+-C-H⋯O Hydrogen Bonds in Protein-ligand Complexes. Sci. Rep. 2019, 9. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.; Woo, S.M.; Siu, T.; Cortopassi, W.A.; Duarte, F.; Paton, R.S. Cation-π Interactions in Protein–ligand Binding: Theory and Data-mining reveal Different Roles for Lysine and Arginine. Chem. Sci. 2018, 9, 2655–2665. [Google Scholar] [CrossRef] [PubMed]
- Patil, R.; Das, S.; Stanley, A.; Yadav, L.; Sudhakar, A.; Varma, A.K. Optimized Hydrophobic Interactions and Hydrogen Bonding at the Target-Ligand Interface Leads the Pathways of Drug-Designing. PLoS ONE 2010, 5, e12029. [Google Scholar] [CrossRef]
- Kitchen, D.B.; Decornez, H.; Furr, J.R.; Bajorath, J. Docking and Scoring in Virtual Screening for Drug Discovery: Methods and Applications. Nat. Rev. Drug Discov. 2004, 3, 935–949. [Google Scholar] [CrossRef]
- Sliwoski, G.; Kothiwale, S.; Meiler, J.; Lowe, E.W. Computational Methods in Drug Discovery. Pharmacol. Rev. 2013, 66, 334–395. [Google Scholar] [CrossRef] [PubMed]
- Lyne, P.D. Structure-based Virtual Screening: An Overview. Drug Discov. Today 2002, 7, 1047–1055. [Google Scholar] [CrossRef]
- Pagadala, N.S.; Syed, K.; Tuszynski, J. Software for Molecular Docking: A Review. Biophys. Rev. 2017, 9, 91–102. [Google Scholar] [CrossRef]
- McGann, M. FRED and HYBRID docking performance on standardized datasets. J. Comput. Aided Mol. Des. 2012, 26, 897–906. [Google Scholar] [CrossRef] [PubMed]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.; Žídek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, K.; Lin, D.; Zhu, Y.; Chen, C.; He, L.; Guo, X.; Chen, K.; Wang, R.; Liu, Z.; et al. Artificial intelligence deciphers codes for color and odor perceptions based on large-scale chemoinformatic data. GigaScience 2020, 9, giaa011. [Google Scholar] [CrossRef] [PubMed]
- Manzhos, S. Machine learning for the solution of the Schrödinger equation. Mach. Learn. Sci. Technol. 2020, 1, 013002. [Google Scholar] [CrossRef]
- Baskin, I.I.; Madzhidov, T.I.; Antipin, I.S.; Varnek, A.A. Artificial intelligence in synthetic chemistry: Achievements and prospects. Russ. Chem. Rev. 2017, 86, 1127–1156. [Google Scholar] [CrossRef]
- Holzinger, A.; Langs, G.; Denk, H.; Zatloukal, K.; Müller, H. Causability and explainability of artificial intelligence in medicine. WIREs Data Min. Knowl. Discov. 2019, 9, e1312. [Google Scholar] [CrossRef]
- Le, N.Q.K. Fertility-GRU: Identifying Fertility-Related Proteins by Incorporating Deep-Gated Recurrent Units and Original Position-Specific Scoring Matrix Profiles. J. Proteome Res. 2019, 18, 3503–3511. [Google Scholar] [CrossRef]
- Do, D.T.; Le, T.Q.T.; Le, N.Q.K. Using deep neural networks and biological subwords to detect protein S-sulfenylation sites. Brief. Bioinform. 2020. [Google Scholar] [CrossRef]
- Le, N.Q.K.; Do, D.T.; Hung, T.N.K.; Lam, L.H.T.; Huynh, T.T.; Nguyen, N.T.K. A Computational Framework Based on Ensemble Deep Neural Networks for Essential Genes Identification. Int. J. Mol. Sci. 2020, 21, 9070. [Google Scholar] [CrossRef]
- Rifaioglu, A.S.; Atas, H.; Martin, M.J.; Cetin-Atalay, R.; Atalay, V.; Doğan, T. Recent applications of deep learning and machine intelligence on in silico drug discovery: Methods, tools and databases. Brief. Bioinform. 2019, 20, 1878–1912. [Google Scholar] [CrossRef] [PubMed]
- Dana, D.; Gadhiya, S.; Surin, L.S.; Li, D.; Naaz, F.; Ali, Q.; Paka, L.; Yamin, M.; Narayan, M.; Goldberg, I.; et al. Deep Learning in Drug Discovery and Medicine; Scratching the Surface. Molecules 2018, 23, 2384. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Ding, J.; Wang, Z.; Cao, D.; Ding, X.; Hou, T. From Machine Learning to Deep Learning: Advances in Scoring Functions for Protein–ligand Docking. WIREs Comput. Mol. Sci. 2019, 10, e1429. [Google Scholar] [CrossRef]
- Hong, Y.; Hou, B.; Jiang, H.; Zhang, J. Machine Learning and Artificial Neural Network Accelerated Computational Discoveries in Materials Science. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2019, 10, e1450. [Google Scholar] [CrossRef]
- Kulik, H.J. Making Machine Learning a Useful Tool in the Accelerated Discovery of Transition Metal Complexes. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2019, 10, e1439. [Google Scholar] [CrossRef]
- Bredel, M.; Jacoby, E. Chemogenomics: An Emerging Strategy for Rapid Target and Drug Discovery. Nat. Rev. Genet. 2004, 5, 262–275. [Google Scholar] [CrossRef]
- Jacob, L.; Vert, J.P. Protein-ligand Interaction Prediction: An Improved Chemogenomics Approach. Bioinformatics 2008, 24, 2149–2156. [Google Scholar] [CrossRef]
- Yamanishi, Y.; Araki, M.; Gutteridge, A.; Honda, W.; Kanehisa, M. Prediction of Drug-target Interaction Networks from the Integration of Chemical and Genomic Spaces. Bioinformatics 2008, 24, i232–i240. [Google Scholar] [CrossRef]
- Wallach, I.; Dzamba, M.; Heifets, A. AtomNet: A Deep Convolutional Neural Network for Bioactivity Prediction in Structure-based Drug Discovery. arXiv 2015, arXiv:1510.02855. [Google Scholar]
- Tsubaki, M.; Tomii, K.; Sese, J. Compound–protein Interaction Prediction with End-to-end Learning of Neural Networks for Graphs and Sequences. Bioinformatics 2018, 35, 309–318. [Google Scholar] [CrossRef]
- Li, L.; Koh, C.C.; Reker, D.; Brown, J.B.; Wang, H.; Lee, N.K.; Liow, H.H.; Dai, H.; Fan, H.M.; Chen, L.; et al. Predicting Protein-Ligand Interactions based on Bow-Pharmacological Space and Bayesian Additive Regression Trees. Sci. Rep. 2019, 9, 7703. [Google Scholar] [CrossRef] [PubMed]
- Lee, I.; Keum, J.; Nam, H. DeepConv-DTI: Prediction of Drug-target Interactions via Deep Learning with Convolution on Protein Sequences. PLoS Comput. Biol. 2019, 15, e1007129. [Google Scholar] [CrossRef]
- Ekins, S.; Puhl, A.C.; Zorn, K.M.; Lane, T.R.; Russo, D.P.; Klein, J.J.; Hickey, A.J.; Clark, A.M. Exploiting Machine Learning for End-to-end Drug Discovery and Development. Nat. Mater. 2019, 18, 435–441. [Google Scholar] [CrossRef]
- Gómez-Bombarelli, R.; Wei, J.N.; Duvenaud, D.; Hernández-Lobato, J.M.; Sánchez-Lengeling, B.; Sheberla, D.; Aguilera-Iparraguirre, J.; Hirzel, T.D.; Adams, R.P.; Aspuru-Guzik, A. Automatic Chemical Design Using a Data-Driven Continuous Representation of Molecules. ACS Cent. Sci. 2018, 4, 268–276. [Google Scholar] [CrossRef]
- Riniker, S.; Landrum, G.A. Open-source Platform to Benchmark Fingerprints for Ligand-based Virtual Screening. J. Cheminf. 2013, 5, 26. [Google Scholar] [CrossRef] [PubMed]
- Rogers, D.; Hahn, M. Extended-Connectivity Fingerprints. J. Chem. Inf. Model. 2010, 50, 742–754. [Google Scholar] [CrossRef] [PubMed]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
- Ranganathan, S.; Izotov, D.; Kraka, E.; Cremer, D. Description and Recognition of Regular and Distorted Secondary Structures in Proteins using the Automated Protein Structure Analysis Method. Proteins 2009, 76, 418–438. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization. arXiv 2016, arXiv:1610.02391. [Google Scholar]
- Mysinger, M.M.; Carchia, M.; Irwin, J.J.; Shoichet, B.K. Directory of Useful Decoys, Enhanced (DUD-E): Better Ligands and Decoys for Better Benchmarking. J. Med. Chem. 2012, 55, 6582–6594. [Google Scholar] [CrossRef] [PubMed]
- Gilson, M.K.; Liu, T.; Baitaluk, M.; Nicola, G.; Hwang, L.; Chong, J. BindingDB in 2015: A public Database for Medicinal Chemistry, Computational Chemistry and Systems Pharmacology. Nucleic Acids Res. 2015, 44, D1045–D1053. [Google Scholar] [CrossRef]
- Murzin, A. SCOP: A Structural Classification of Proteins Database for the Investigation of Sequences and Structures. J. Mol. Biol. 1995, 247, 536–540. [Google Scholar] [CrossRef]
- Orengo, C.; Michie, A.; Jones, S.; Jones, D.; Swindells, M.; Thornton, J. CATH—A Hierarchic Classification of Protein Domain Structures. Structure 1997, 5, 1093–1109. [Google Scholar] [CrossRef]
- Dietmann, S.; Holm, L. Identification of Homology in Protein Structure Classification. Nat. Struct. Biol. 2001, 8, 953–957. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of Protein Secondary Structure: Pattern Recognition of Hydrogen-bonded and Geometrical Features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Frishman, D.; Argos, P. Knowledge-based Protein Secondary Structure Assignment. Proteins 1995, 23, 566–579. [Google Scholar] [CrossRef] [PubMed]
- Richards, F.M.; Kundrot, C.E. Identification of Structural Motifs from Protein Coordinate Data: Secondary Structure and First-level Supersecondary Structure. Proteins 1988, 3, 71–84. [Google Scholar] [CrossRef]
- Martin, J.; Letellier, G.; Marin, A.; Taly, J.F.; de Brevern, A.G.; Gibrat, J.F. Protein Secondary Structure Assignment Revisited: A Detailed Analysis of Different Assignment Methods. BMC Struct. Biol. 2005, 5, 17. [Google Scholar] [CrossRef]
- Day, R.; Beck, D.A.; Armen, R.S.; Daggett, V. A Consensus View of Fold Space: Combining SCOP, CATH, and the Dali Domain Dictionary. Protein Sci. 2003, 12, 2150–2160. [Google Scholar] [CrossRef]
- Guo, Z.; Cremer, D. Methods for a Rapid and Automated Description of Proteins. In Reviews in Computational Chemistry; Lipkowics, K., Boyd, D., Eds.; John Wiley & Sons: New York, NY, USA, 2016; pp. 369–438. [Google Scholar]
- Kraka, E.; Zou, W.; Tao, Y.; Freindorf, M. Exploring the Mechanism of Catalysis with the Unified Reaction Valley Approach (URVA)—A Review. Catalysts 2020, 10, 691. [Google Scholar] [CrossRef]
- Venkatachalam, C.M. Stereochemical Criteria for Polypeptides and Proteins. V. Conformation of a System of three linked Peptide Units. Biopolymers 1968, 6, 1425–1436. [Google Scholar] [CrossRef]
- Landrum, G. RDKit: Open-Source Cheminformatics. 2020. Available online: http://www.rdkit.org (accessed on 30 January 2021).
- Variani, E.; Lei, X.; McDermott, E.; Moreno, I.L.; Gonzalez-Dominguez, J. Deep Neural Networks for Small Footprint Text-dependent Speaker Verification. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 4052–4056. [Google Scholar]
- Snyder, D.; Garcia-Romero, D.; Sell, G.; Povey, D.; Khudanpur, S. X-vectors: Robust dnn embeddings for speaker recognition. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 5329–5333. [Google Scholar]
- Triballeau, N.; Acher, F.; Brabet, I.; Pin, J.P.; Bertrand, H.O. Virtual Screening Workflow Development Guided by the “Receiver Operating Characteristic” Curve Approach. Application to High-Throughput Docking on Metabotropic Glutamate Receptor Subtype 4. J. Med. Chem. 2005, 48, 2534–2547. [Google Scholar] [CrossRef] [PubMed]
- Empereur-mot, C.; Guillemain, H.; Latouche, A.; Zagury, J.F.; Viallon, V.; Montes, M. Predictiveness Curves in Virtual Screening. J. Cheminf. 2015, 7, 52. [Google Scholar] [CrossRef]
- Pearlman, D.A.; Charifson, P.S. Improved Scoring of Ligand-Protein Interactions Using OWFEG Free Energy Grids. J. Med. Chem. 2001, 44, 502–511. [Google Scholar] [CrossRef] [PubMed]
- Truchon, J.F.; Bayly, C.I. Evaluating Virtual Screening Methods: Good and Bad Metrics for the “Early Recognition” Problem. J. Chem. Inf. Model. 2007, 47, 488–508. [Google Scholar] [CrossRef] [PubMed]
- Masters, L.; Eagon, S.; Heying, M. Evaluation of consensus scoring methods for AutoDock Vina, smina and idock. J. Mol. Graph. Model. 2020, 96, 107532. [Google Scholar] [CrossRef]
- Ericksen, S.S.; Wu, H.; Zhang, H.; Michael, L.A.; Newton, M.A.; Hoffmann, F.M.; Wildman, S.A. Machine Learning Consensus Scoring Improves Performance Across Targets in Structure-Based Virtual Screening. J. Chem. Inf. Model. 2017, 57, 1579–1590. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Sun, J.; Guan, J.; Zheng, J.; Zhou, S. Improving Compound–protein Interaction Prediction by Building up Highly Credible Negative Samples. Bioinformatics 2015, 31, i221–i229. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S.; Knox, C.; Guo, A.C.; Cheng, D.; Shrivastava, S.; Tzur, D.; Gautam, B.; Hassanali, M. DrugBank: A Knowledgebase for Drugs, Drug Actions and Drug Targets. Nucleic Acids Res. 2007, 36, D901–D906. [Google Scholar] [CrossRef] [PubMed]
- Gunther, S.; Kuhn, M.; Dunkel, M.; Campillos, M.; Senger, C.; Petsalaki, E.; Ahmed, J.; Urdiales, E.G.; Gewiess, A.; Jensen, L.J.; et al. SuperTarget and Matador: Resources for Exploring Drug-target Relationships. Nucleic Acids Res. 2007, 36, D919–D922. [Google Scholar] [CrossRef]
- Tabei, Y.; Yamanishi, Y. Scalable Prediction of Compound-protein Interactions using Minwise Hashing. BMC Syst. Biol. 2013, 7, S3. [Google Scholar] [CrossRef]
- Ragoza, M.; Hochuli, J.; Idrobo, E.; Sunseri, J.; Koes, D.R. Protein–Ligand Scoring with Convolutional Neural Networks. J. Chem. Inf. Model. 2017, 57, 942–957. [Google Scholar] [CrossRef]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Bleakley, K.; Yamanishi, Y. Supervised Prediction of Drug–target Interactions Using Bipartite Local Models. Bioinformatics 2009, 25, 2397–2403. [Google Scholar] [CrossRef]
- van Laarhoven, T.; Nabuurs, S.B.; Marchiori, E. Gaussian Interaction Profile Kernels for Predicting Drug–target Interaction. Bioinformatics 2011, 27, 3036–3043. [Google Scholar] [CrossRef] [PubMed]
- Gonen, M. Predicting Drug-target Interactions from Chemical and Genomic Kernels using Bayesian Matrix Factorization. Bioinformatics 2012, 28, 2304–2310. [Google Scholar] [CrossRef] [PubMed]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the Speed and Accuracy of Docking with a New Scoring Function, Efficient Optimization, and Multithreading. J. Comput. Chem. 2009, 31, 455–461. [Google Scholar] [CrossRef]
- Koes, D.R.; Baumgartner, M.P.; Camacho, C.J. Lessons Learned in Empirical Scoring with Smina from the CSAR 2011 Benchmarking Exercise. J. Chem. Inf. Model. 2013, 53, 1893–1904. [Google Scholar] [CrossRef]
- Yang, J.; Shen, C.; Huang, N. Predicting or Pretending: Artificial Intelligence for Protein-Ligand Interactions Lack of Sufficiently Large and Unbiased Datasets. Front. Pharmacol. 2020, 11, 69. [Google Scholar] [CrossRef] [PubMed]
- Sieg, J.; Flachsenberg, F.; Rarey, M. In Need of Bias Control: Evaluating Chemical Data for Machine Learning in Structure-Based Virtual Screening. J. Chem. Inf. Model. 2019, 59, 947–961. [Google Scholar] [CrossRef]
- von Korff, M.; Freyss, J.; Sander, T. Comparison of Ligand- and Structure-Based Virtual Screening on the DUD Data Set. J. Chem. Inf. Model. 2009, 49, 209–231. [Google Scholar] [CrossRef] [PubMed]
- Kearnes, S.; McCloskey, K.; Berndl, M.; Pande, V.; Riley, P. Molecular graph convolutions: Moving beyond fingerprints. J. Comput. Aided Mol. Des. 2016, 30, 595–608. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, V.; Pérez-Nueno, V.I.; Mavridis, L.; Ritchie, D.W. Comprehensive Comparison of Ligand-Based Virtual Screening Tools Against the DUD Data set Reveals Limitations of Current 3D Methods. J. Chem. Inf. Model. 2010, 50, 2079–2093. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.N.; Nicholls, A. Recommendations for evaluation of computational methods. J. Comput. Aided Mol. Des. 2008, 22, 133–139. [Google Scholar] [CrossRef]
- Nicholls, A. What do we know and when do we know it? J. Comput. Aided Mol. Des. 2008, 22, 239–255. [Google Scholar] [CrossRef]
- McGann, M.; Nicholls, A.; Enyedy, I. The statistics of virtual screening and lead optimization. J. Comput. Aided Mol. Des. 2015, 29, 923–936. [Google Scholar] [CrossRef]
- Raymond, J.W.; Willett, P. Effectiveness of graph-based and fingerprint-based similarity measures for virtual screening of 2D chemical structure databases. J. Comput. Aided Mol. Des. 2002, 16, 59–71. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Skolnick, J. Scoring Function for Automated Assessment of Protein Structure Template Quality. Proteins 2004, 57, 702–710. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Zhang, Y. How Significant is a Protein Structure Similarity with TM-Score = 0.5? Bioinformatics 2010, 26, 889–895. [Google Scholar] [CrossRef] [PubMed]
- Cross, J.B.; Thompson, D.C.; Rai, B.K.; Baber, J.C.; Fan, K.Y.; Hu, Y.; Humblet, C. Comparison of Several Molecular Docking Programs: Pose Prediction and Virtual Screening Accuracy. J. Chem. Inf. Model. 2009, 49, 1455–1474. [Google Scholar] [CrossRef]
- Kolb, P.; Irwin, J. Docking Screens: Right for the Right Reasons? Curr. Top. Med. Chem. 2009, 9, 755–770. [Google Scholar] [CrossRef]
- Scior, T.; Bender, A.; Tresadern, G.; Medina-Franco, J.L.; Martínez-Mayorga, K.; Langer, T.; Cuanalo-Contreras, K.; Agrafiotis, D.K. Recognizing Pitfalls in Virtual Screening: A Critical Review. J. Chem. Inf. Model. 2012, 52, 867–881. [Google Scholar] [CrossRef]
- Hewitt, S.N.; Dranow, D.M.; Horst, B.G.; Abendroth, J.A.; Forte, B.; Hallyburton, I.; Jansen, C.; Baragaña, B.; Choi, R.; Rivas, K.L.; et al. Biochemical and Structural Characterization of Selective Allosteric Inhibitors of the Plasmodium falciparum Drug Target, Prolyl-tRNA-synthetase. ACS Infect. Dis. 2016, 3, 34–44. [Google Scholar] [CrossRef]
- Furnham, N.; Holliday, G.L.; de Beer, T.A.P.; Jacobsen, J.O.B.; Pearson, W.R.; Thornton, J.M. The Catalytic Site Atlas 2.0: Cataloging catalytic sites and residues identified in enzymes. Nucleic Acids Res. 2013, 42, D485–D489. [Google Scholar] [CrossRef] [PubMed]
- Cimermancic, P.; Weinkam, P.; Rettenmaier, T.J.; Bichmann, L.; Keedy, D.A.; Woldeyes, R.A.; Schneidman-Duhovny, D.; Demerdash, O.N.; Mitchell, J.C.; Wells, J.A.; et al. CryptoSite: Expanding the Druggable Proteome by Characterization and Prediction of Cryptic Binding Sites. J. Mol. Biol. 2016, 428, 709–719. [Google Scholar] [CrossRef]
- Laskowski, R.A.; Gerick, F.; Thornton, J.M. The Structural Basis of Allosteric Regulation in Proteins. FEBS Lett. 2009, 583, 1692–1698. [Google Scholar] [CrossRef]
- Beglov, D.; Hall, D.R.; Wakefield, A.E.; Luo, L.; Allen, K.N.; Kozakov, D.; Whitty, A.; Vajda, S. Exploring the Structural Origins of Cryptic Sites on Proteins. Proc. Natl. Acad. Sci. USA 2018, 115, E3416–E3425. [Google Scholar] [CrossRef] [PubMed]
- Lipinski, C.A. Lead- and drug-like compounds: The rule-of-five revolution. Drug Discov. Today Technol. 2004, 1, 337–341. [Google Scholar] [CrossRef] [PubMed]
| Ligand Descriptor | AUCROC | |
|---|---|---|
| Human | DUD-E | |
| Avalon | 0.982 | 0.968 |
| ECF | 0.982 | 0.974 |
| CLP | 0.966 | 0.905 |
| GNN | 0.944 | 0.972 |
| Dataset | k-NN | RF | L2 | SVM | GNN-CNN | SSnet |
|---|---|---|---|---|---|---|
| humans (1:1) | 0.860 | 0.940 | 0.911 | 0.910 | 0.970 | 0.984 |
| humans (1:3) | 0.904 | 0.954 | 0.920 | 0.942 | 0.950 | 0.978 |
| humans (1:5) | 0.913 | 0.967 | 0.920 | 0.951 | 0.970 | 0.976 |
| C. elegans (1:1) | 0.858 | 0.902 | 0.892 | 0.894 | 0.978 | 0.984 |
| C. elegans (1:3) | 0.892 | 0.926 | 0.896 | 0.901 | 0.971 | 0.983 |
| C. elegans (1:5) | 0.897 | 0.928 | 0.906 | 0.907 | 0.971 | 0.983 |
| Target | AD4 | DOCK6 | FRED | HYBRID | PLANTS | rDock | Smina | Surflex | SSnet:BDB | BEST |
|---|---|---|---|---|---|---|---|---|---|---|
| ADRB1 | 0.68 | 0.78 | 0.77 | 0.65 | 0.86 | 0.81 | 0.79 | 0.8 | 0.71 | 0.86 |
| DRD3 | 0.69 | 0.59 | 0.79 | 0.81 | 0.69 | 0.66 | 0.68 | 0.71 | 0.73 | 0.81 |
| ESR1 | 0.82 | 0.54 | 0.88 | 0.81 | 0.77 | 0.87 | 0.86 | 0.74 | 0.83 | 0.88 |
| ESR2 | 0.77 | 0.48 | 0.89 | 0.89 | 0.69 | 0.8 | 0.79 | 0.68 | 0.82 | 0.89 |
| ACE | 0.78 | 0.72 | 0.8 | 0.84 | 0.84 | 0.62 | 0.61 | 0.76 | 0.89 | 0.89 |
| HIVINT | 0.54 | 0.65 | 0.74 | 0.6 | 0.76 | 0.67 | 0.81 | 0.66 | 0.50 | 0.81 |
| ADA17 | 0.51 | 0.4 | 0.59 | 0.69 | 0.58 | 0.58 | 0.54 | 0.7 | 0.91 | 0.91 |
| FA10 | 0.86 | 0.81 | 0.79 | 0.82 | 0.8 | 0.9 | 0.84 | 0.76 | 0.90 | 0.90 |
| MMP13 | 0.67 | 0.6 | 0.77 | 0.87 | 0.71 | 0.67 | 0.67 | 0.76 | 0.96 | 0.96 |
| TRY1 | 0.79 | 0.82 | 0.8 | 0.83 | 0.81 | 0.74 | 0.75 | 0.93 | 0.84 | 0.93 |
| mean | 0.71 | 0.64 | 0.78 | 0.78 | 0.75 | 0.73 | 0.73 | 0.75 | 0.81 | 0.88 |
| std. dev. | 0.12 | 0.14 | 0.08 | 0.10 | 0.08 | 0.11 | 0.11 | 0.08 | 0.13 | 0.05 |
| Target | Best | BCS | MVC | Mean | Med | Max | Min | SSnet:BDB |
|---|---|---|---|---|---|---|---|---|
| ADRB1 | 0.86 | 0.92 | 0.92 | 0.91 | 0.89 | 0.9 | 0.79 | 0.71 |
| DRD3 | 0.81 | 0.81 | 0.75 | 0.79 | 0.78 | 0.74 | 0.73 | 0.73 |
| ESR1 | 0.88 | 0.88 | 0.9 | 0.87 | 0.86 | 0.89 | 0.74 | 0.83 |
| ESR2 | 0.89 | 0.91 | 0.89 | 0.85 | 0.82 | 0.89 | 0.68 | 0.82 |
| ACE | 0.89 | 0.85 | 0.83 | 0.83 | 0.83 | 0.81 | 0.78 | 0.89 |
| HIVINT | 0.81 | 0.81 | 0.82 | 0.82 | 0.8 | 0.8 | 0.68 | 0.50 |
| ADA17 | 0.91 | 0.74 | 0.69 | 0.62 | 0.6 | 0.71 | 0.52 | 0.91 |
| FA10 | 0.90 | 0.91 | 0.95 | 0.93 | 0.92 | 0.93 | 0.8 | 0.90 |
| MMP13 | 0.96 | 0.88 | 0.84 | 0.81 | 0.78 | 0.84 | 0.72 | 0.96 |
| TRY1 | 0.93 | 0.93 | 0.93 | 0.93 | 0.91 | 0.92 | 0.82 | 0.84 |
| mean | 0.87 | 0.86 | 0.85 | 0.84 | 0.82 | 0.84 | 0.73 | 0.81 |
| std. dev. | 0.04 | 0.06 | 0.08 | 0.09 | 0.09 | 0.08 | 0.09 | 0.13 |
| Target | AD4 | DOCK6 | FRED | HYBRID | PLANTS | rDock | Smina | Surflex | SSnet:BDB | BEST |
|---|---|---|---|---|---|---|---|---|---|---|
| ADRB1 | 5 | 25 | 7 | 19 | 19 | 13 | 6 | 13 | 7 | 25 |
| DRD3 | 4 | 1 | 10 | 10 | 3 | 1 | 2 | 3 | 9 | 10 |
| ESR1 | 32 | 8 | 37 | 36 | 17 | 29 | 23 | 20 | 20 | 37 |
| ESR2 | 21 | 9 | 40 | 40 | 12 | 22 | 20 | 12 | 19 | 40 |
| ACE | 14 | 12 | 18 | 20 | 24 | 3 | 3 | 9 | 15 | 24 |
| HIVINT | 0 | 11 | 8 | 10 | 15 | 7 | 8 | 5 | 10 | 15 |
| ADA17 | 0 | 0 | 8 | 17 | 6 | 10 | 14 | 10 | 30 | 30 |
| FA10 | 26 | 16 | 17 | 19 | 12 | 27 | 18 | 8 | 19 | 27 |
| MMP13 | 12 | 6 | 18 | 30 | 15 | 3 | 4 | 11 | 29 | 30 |
| TRY1 | 7 | 16 | 17 | 20 | 17 | 14 | 3 | 39 | 11 | 39 |
| mean | 12 | 10 | 18 | 22 | 14 | 13 | 10 | 13 | 17 | 28 |
| std. dev. | 11 | 7 | 12 | 10 | 6 | 10 | 8 | 10 | 8 | 10 |
| Target | Best | BCS | MVC | Mean | Med | Max | Min | SSnet:BDB |
|---|---|---|---|---|---|---|---|---|
| ADRB1 | 25 | 31 | 27 | 28 | 24 | 21 | 19 | 7 |
| DRD3 | 10 | 13 | 7 | 12 | 11 | 4 | 11 | 9 |
| ESR1 | 37 | 38 | 37 | 34 | 34 | 32 | 16 | 20 |
| ESR2 | 40 | 35 | 34 | 31 | 28 | 26 | 9 | 19 |
| ACE | 24 | 33 | 30 | 30 | 26 | 19 | 13 | 15 |
| HIVINT | 15 | 19 | 21 | 17 | 11 | 13 | 10 | 10 |
| ADA17 | 30 | 19 | 17 | 16 | 17 | 11 | 4 | 30 |
| FA10 | 27 | 26 | 30 | 33 | 30 | 23 | 19 | 19 |
| MMP13 | 30 | 34 | 25 | 26 | 24 | 20 | 18 | 29 |
| TRY1 | 39 | 33 | 31 | 28 | 27 | 24 | 18 | 11 |
| mean | 30 | 28 | 26 | 26 | 23 | 19 | 14 | 17 |
| std. dev. | 8 | 8 | 9 | 8 | 8 | 8 | 5 | 8 |
| Cutoff ( in Å ) | Truly Detected Residue | Covalently Involved | Electrostatically Involved | Hydrogen Bond Involved | Metal Ligand |
|---|---|---|---|---|---|
| 0 | 50.4 | 38.1 | 51.2 | 45.1 | 67.2 |
| 4 | 69.0 | 57.9 | 70.0 | 64.8 | 82.5 |
| 6 | 81.7 | 78.5 | 80.1 | 80.3 | 88.6 |
| 8 | 89.1 | 93.2 | 88.3 | 88.0 | 93.0 |
| # of annotated residues | 11936 | 354 | 2867 | 3436 | 1665 |
| PLC | DC | State | RMSD | Actives | Inactives | Error e | ||
|---|---|---|---|---|---|---|---|---|
| PLC | DC | PLC | DC | |||||
| 1B9V | 1B9S | Bound | 0.267 | 22,518 | 22,518 | 23,091 | 22,518 | 0.00% |
| 1C8K | 8GPB | Bound | 0.279 | 22,505 | 22,498 | 23,104 | 23,111 | 0.03% |
| 1MV9 | 1MVC | Bound | 0.175 | 22,434 | 22,436 | 23,175 | 23,173 | 0.01% |
| 1Q4X | 2J4A | Bound | 0.463 | 22,507 | 22,509 | 23,102 | 23,100 | 0.01% |
| 1QW6 | 1QWC | Bound | 0.237 | 22,507 | 22,509 | 23,102 | 23,100 | 0.01% |
| 1BCD | 2FNM | Unbound | 0.270 | 22,518 | 22,518 | 23,091 | 23,091 | 0.00% |
| 1H00 | 4EK3 | Unbound | 0.178 | 22,518 | 22,518 | 23,091 | 23,091 | 0.00% |
| 1J4H | 5HT1 | Unbound | 0.666 | 22,518 | 22,518 | 23,091 | 23,091 | 0.00% |
| 1KVO | 1MF4 | Unbound | 0.565 | 22,517 | 22,521 | 23,092 | 23,088 | 0.01% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, N.; Qu, X.; Trozzi, F.; Elsaied, M.; Karki, N.; Tao, Y.; Zoltowski, B.; Larson, E.C.; Kraka, E. SSnet: A Deep Learning Approach for Protein-Ligand Interaction Prediction. Int. J. Mol. Sci. 2021, 22, 1392. https://doi.org/10.3390/ijms22031392
Verma N, Qu X, Trozzi F, Elsaied M, Karki N, Tao Y, Zoltowski B, Larson EC, Kraka E. SSnet: A Deep Learning Approach for Protein-Ligand Interaction Prediction. International Journal of Molecular Sciences. 2021; 22(3):1392. https://doi.org/10.3390/ijms22031392
Chicago/Turabian StyleVerma, Niraj, Xingming Qu, Francesco Trozzi, Mohamed Elsaied, Nischal Karki, Yunwen Tao, Brian Zoltowski, Eric C. Larson, and Elfi Kraka. 2021. "SSnet: A Deep Learning Approach for Protein-Ligand Interaction Prediction" International Journal of Molecular Sciences 22, no. 3: 1392. https://doi.org/10.3390/ijms22031392
APA StyleVerma, N., Qu, X., Trozzi, F., Elsaied, M., Karki, N., Tao, Y., Zoltowski, B., Larson, E. C., & Kraka, E. (2021). SSnet: A Deep Learning Approach for Protein-Ligand Interaction Prediction. International Journal of Molecular Sciences, 22(3), 1392. https://doi.org/10.3390/ijms22031392








