Signal Deconvolution and Generative Topographic Mapping Regression for Solid-State NMR of Multi-Component Materials
Abstract
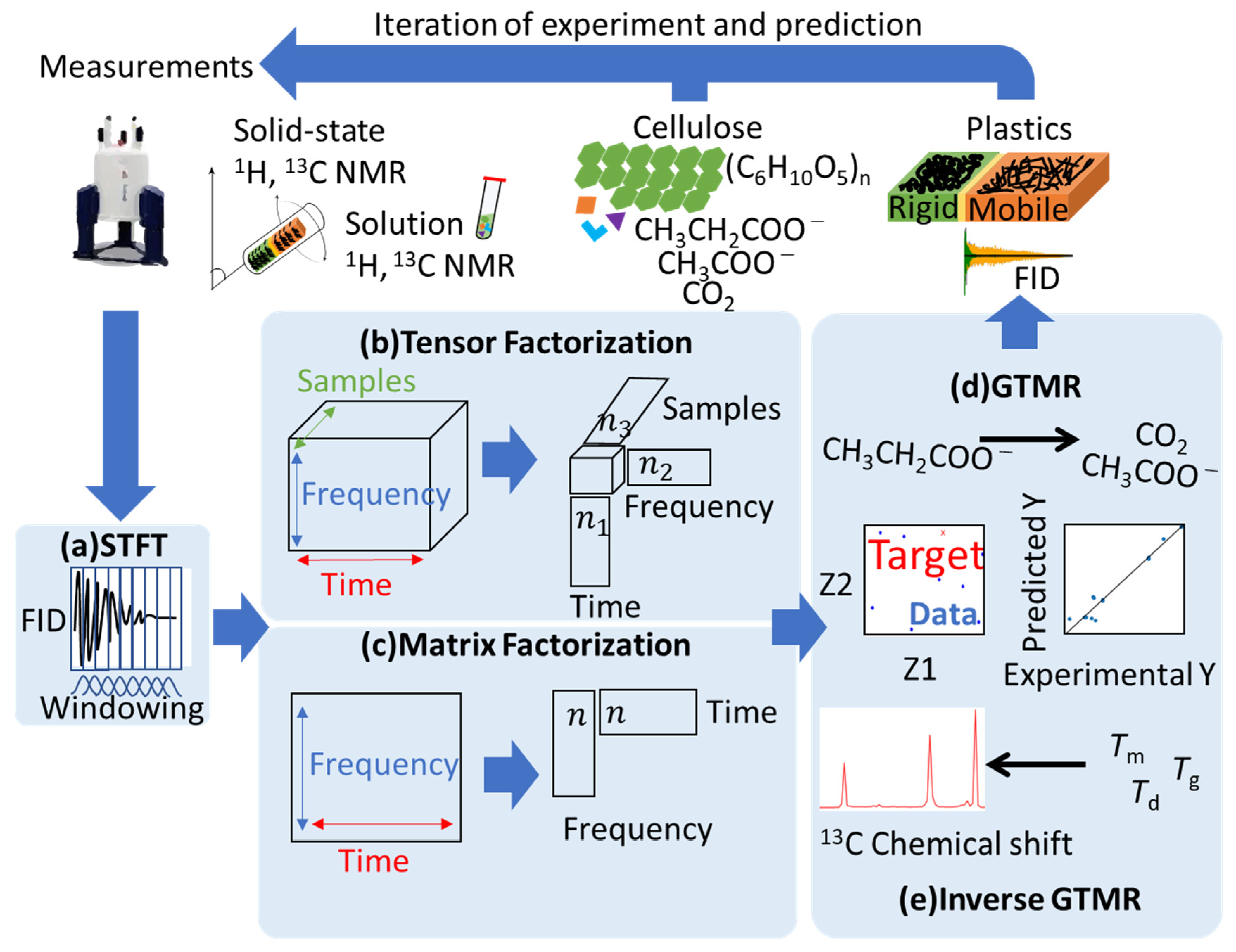
1. Introduction
2. Results and Discussion
2.1. Signal Deconvolution and Prediction for Solid-State NMR of Multi-Component Materials
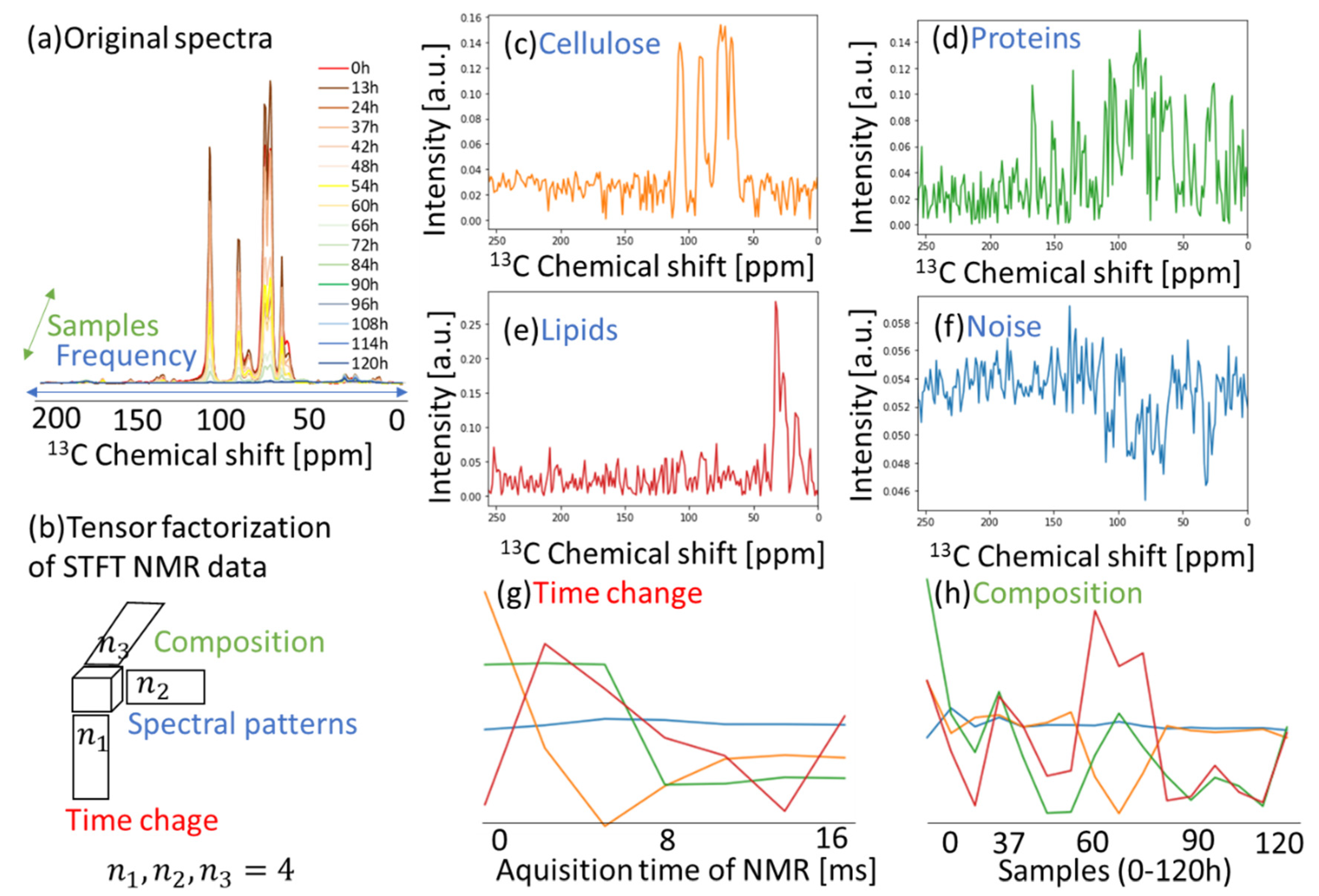
2.2. Non-Negative Tucker Decomposition to 13C CP-MAS in Cellulose Degradation Process
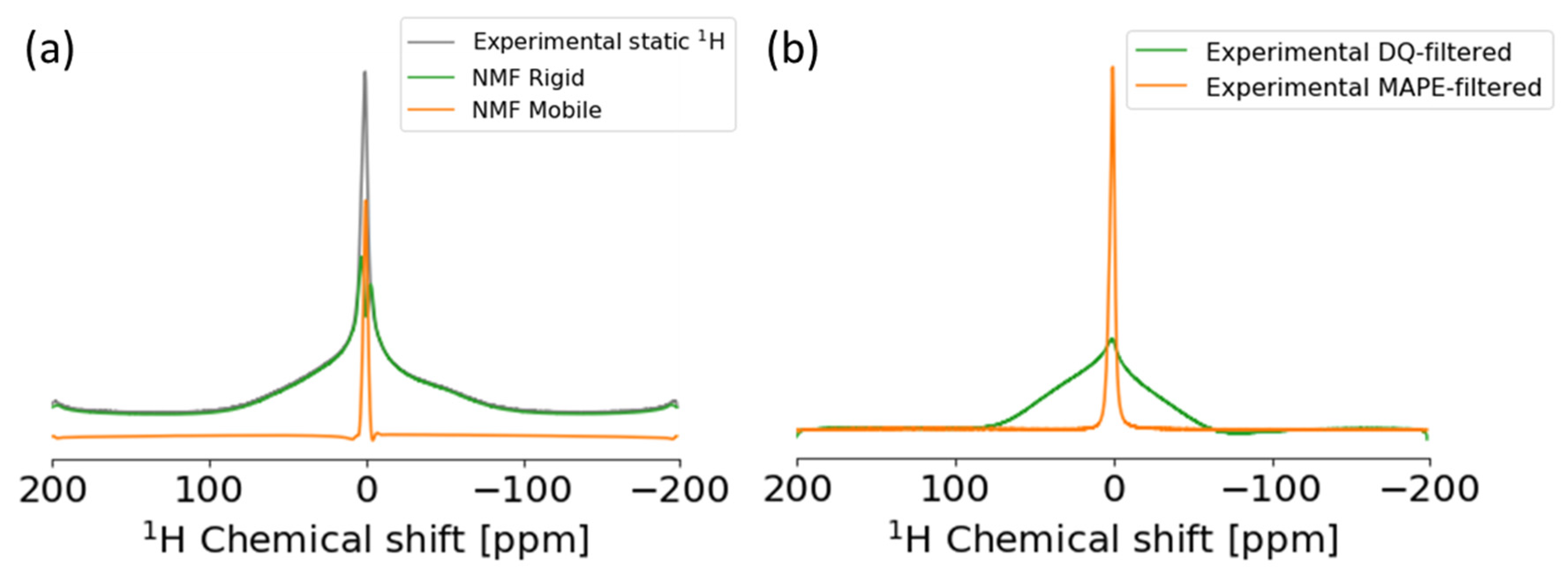
2.3. Non-Negative Matrix Factorization to Static 1H ssNMR in PCL and E. gracilis Samples
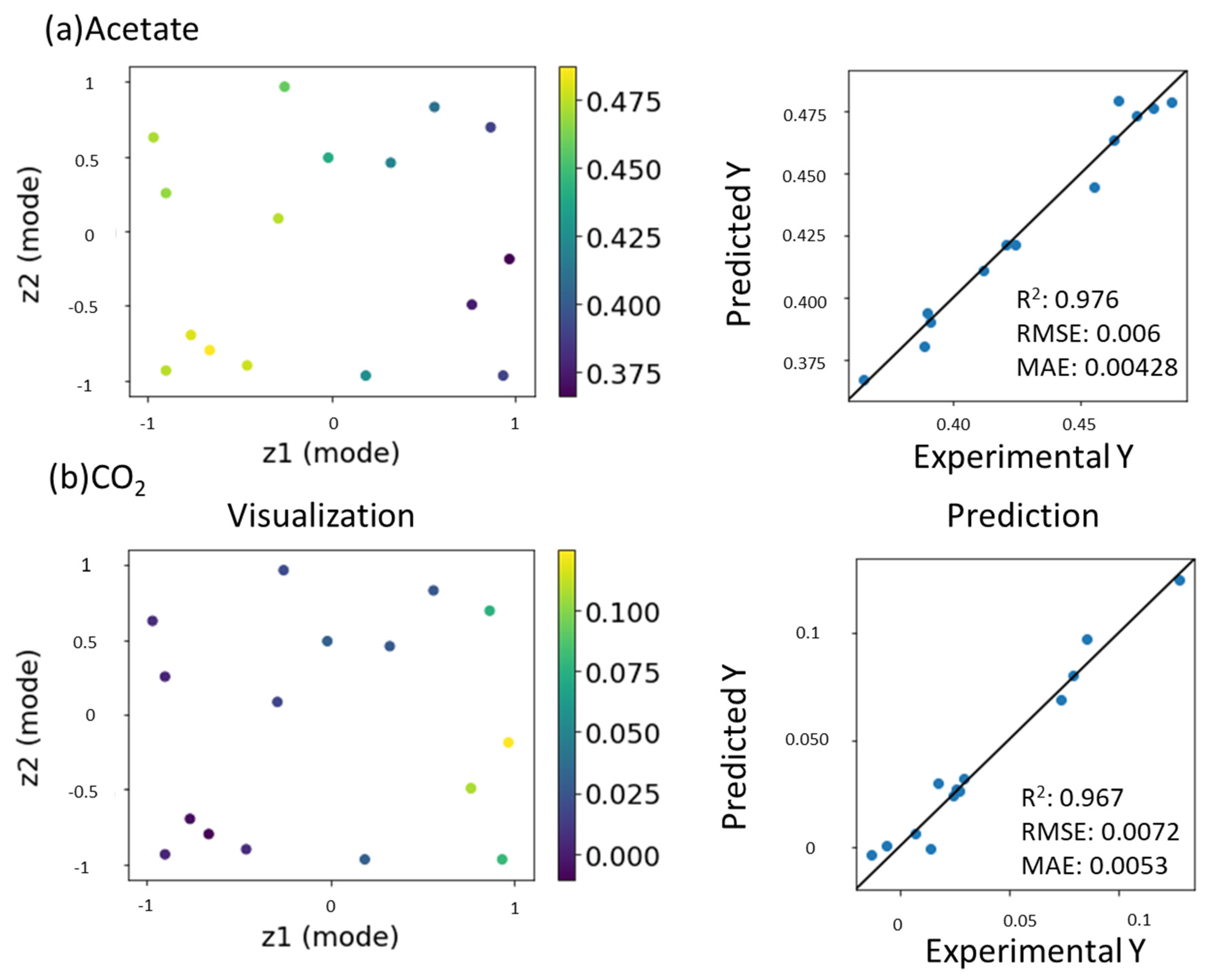
2.4. Prediction of Concentration of Products in the Cellulose Degradation Process
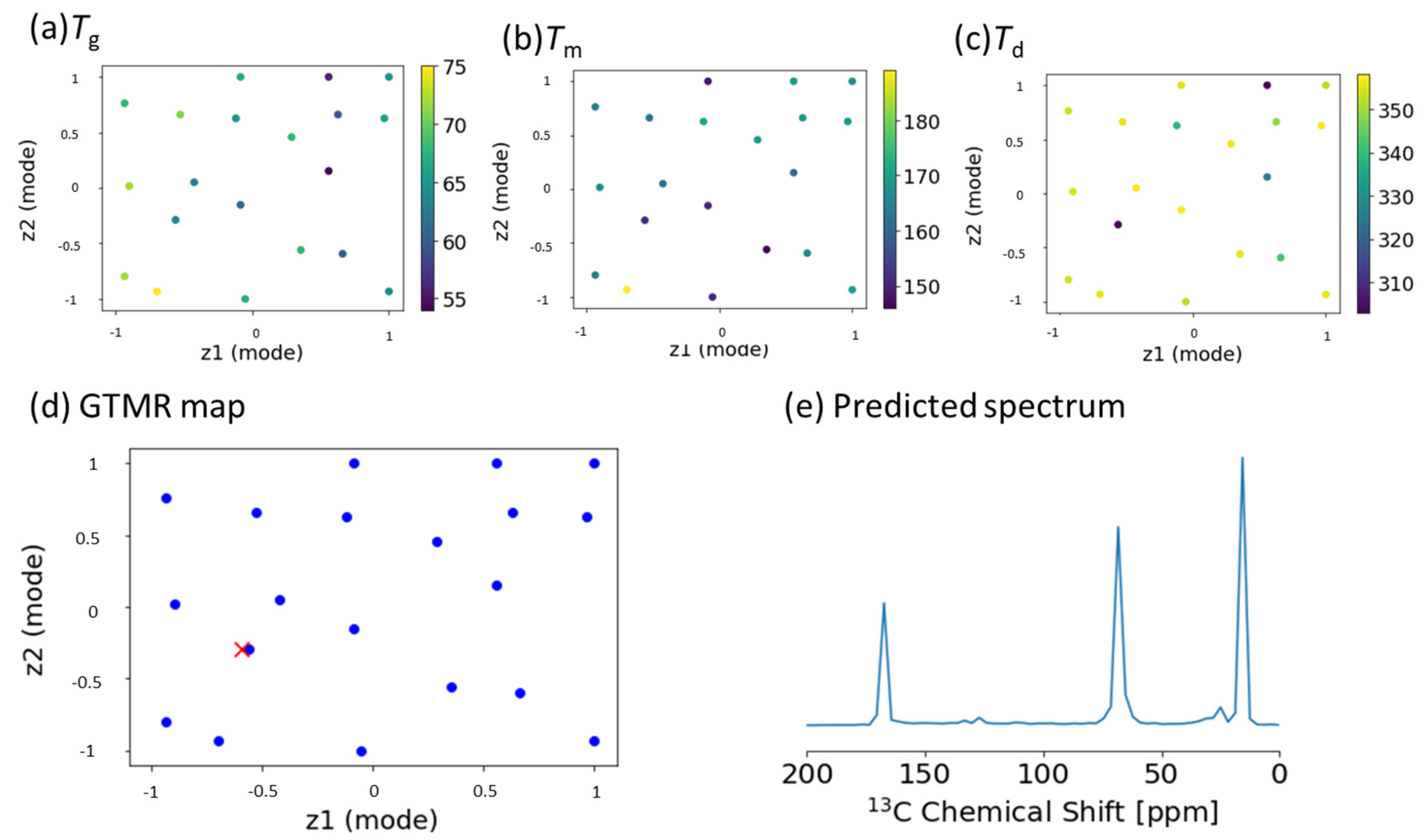
2.5. Prediction of NMR Signals from Thermal Properties in Plastics
3. Materials and Methods
3.1. NMR Analysis
3.2. Thermal Analysis of Plastics
3.3. Signal Deconvolution Methods
3.4. Prediction Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hepburn, C.; Adlen, E.; Beddington, J.; Carter, E.A.; Fuss, S.; Mac Dowell, N.; Minx, J.C.; Smith, P.; Williams, C.K. The technological and economic prospects for CO. Nature 2019, 575, 87–97. [Google Scholar] [CrossRef]
- Zhu, Y.; Romain, C.; Williams, C.K. Sustainable polymers from renewable resources. Nature 2016, 540, 354–362. [Google Scholar] [CrossRef]
- Inkinen, S.; Hakkarainen, M.; Albertsson, A.; Sodergard, A. From Lactic Acid to Poly(lactic acid) (PLA): Characterization and Analysis of PLA and Its Precursors. Biomacromolecules 2011, 12, 523–532. [Google Scholar] [CrossRef]
- Schaler, K.; Achilles, A.; Barenwald, R.; Hackel, C.; Saalwachter, K. Dynamics in Crystallites of Poly(epsilon-caprolactone) As Investigated by Solid-State NMR. Macromolecules 2013, 46, 7818–7825. [Google Scholar] [CrossRef]
- Foston, M. Advances in solid-state NMR of cellulose. Curr. Opin. Biotechnol. 2014, 27, 176–184. [Google Scholar] [CrossRef]
- Okushita, K.; Chikayama, E.; Kikuchi, J. Solubilization mechanism and characterization of the structural change of bacterial cellulose in regenerated states through ionic liquid treatment. Biomacromolecules 2012, 13, 1323–1330. [Google Scholar] [CrossRef]
- Mori, T.; Chikayama, E.; Tsuboi, Y.; Ishida, N.; Shisa, N.; Noritake, Y.; Moriya, S.; Kikuchi, J. Exploring the conformational space of amorphous cellulose using NMR chemical shifts. Carbohydr. Polym. 2012, 90, 1197–1203. [Google Scholar] [CrossRef]
- Komatsu, T.; Kikuchi, J. Selective Signal Detection in Solid-State NMR Using Rotor-Synchronized Dipolar Dephasing for the Analysis of Hemicellulose in Lignocellulosic Biomass. J. Phys. Chem. Lett. 2013, 4, 2279–2283. [Google Scholar] [CrossRef]
- Okushita, K.; Komatsu, T.; Chikayama, E.; Kikuchi, J. Statistical approach for solid-state NMR spectra of cellulose derived from a series of variable parameters. Polym. J. 2012, 44, 895–900. [Google Scholar] [CrossRef]
- Yamazawa, A.; Iikura, T.; Shino, A.; Date, Y.; Kikuchi, J. Solid-, Solution-, and Gas-state NMR Monitoring of C-13-Cellulose Degradation in an Anaerobic Microbial Ecosystem. Molecules 2013, 18, 9021–9033. [Google Scholar] [CrossRef]
- Komatsu, T.; Kikuchi, J. Comprehensive signal assignment of 13C-labeled lignocellulose using multidimensional solution NMR and 13C chemical shift comparison with solid-state NMR. Anal. Chem. 2013, 85, 8857–8865. [Google Scholar] [CrossRef]
- Yamazawa, A.; Iikura, T.; Morioka, Y.; Shino, A.; Ogata, Y.; Date, Y.; Kikuchi, J. Cellulose digestion and metabolism induced biocatalytic transitions in anaerobic microbial ecosystems. Metabolites 2013, 4, 36–52. [Google Scholar] [CrossRef]
- Eden, M. Editorial for the Special Issue on Solid-State NMR Spectroscopy in Materials Chemistry. Molecules 2020, 25, 2720. [Google Scholar] [CrossRef]
- Kikuchi, J.; Ito, K.; Date, Y. Environmental metabolomics with data science for investigating ecosystem homeostasis. Prog. Nucl. Magn. Reson. Spectrosc. 2018, 104, 56–88. [Google Scholar] [CrossRef]
- Wang, Z.; Hanrahan, M.; Kobayashi, T.; Perras, F.; Chen, Y.; Engelke, F.; Reiter, C.; Purea, A.; Rossini, A.; Pruski, M. Combining fast magic angle spinning dynamic nuclear polarization with indirect detection to further enhance the sensitivity of solid-state NMR spectroscopy. Solid State Nucl. Magn. Reson. 2020, 109. [Google Scholar] [CrossRef]
- Pustovalova, Y.; Hoch, J. Sensetivity Gain in Nonuniformly Sampled NMR Experiments. Biophys. J. 2020, 118, 612A. [Google Scholar] [CrossRef]
- Sugishita, T.; Matsuki, Y.; Fujiwara, T. Absolute H-1 polarization measurement with a spin-correlated component of magnetization by hyperpolarized MAS-DNP solid-state NMR. Solid State Nucl. Magn. Reson. 2019, 99, 20–26. [Google Scholar] [CrossRef]
- Plainchont, B.; Berruyer, P.; Dumez, J.; Tannin, S.; Giraudeau, P. Dynamic Nuclear Polarization Opens New Perspectives for NMR Spectroscopy in Analytical Chemistry. Anal. Chem. 2018, 90, 3639–3650. [Google Scholar] [CrossRef]
- Chen, K. A Practical Review of NMR Lineshapes for Spin-1/2 and Quadrupolar Nuclei in Disordered Materials. Int. J. Mol. Sci. 2020, 21, 5666. [Google Scholar] [CrossRef]
- Sekiyama, Y.; Chikayama, E.; Kikuchi, J. Profiling polar and semipolar plant metabolites throughout extraction processes using a combined solution-state and high-resolution magic angle spinning NMR approach. Anal. Chem. 2010, 82, 1643–1652. [Google Scholar] [CrossRef]
- Mori, T.; Tsuboi, Y.; Ishida, N.; Nishikubo, N.; Demura, T.; Kikuchi, J. Multidimensional High-Resolution Magic Angle Spinning and Solution-State NMR Characterization of 13C-labeled Plant Metabolites and Lignocellulose. Sci. Rep. 2015, 5, 11848. [Google Scholar] [CrossRef]
- Komatsu, T.; Kobayashi, T.; Hatanaka, M.; Kikuchi, J. Profiling Planktonic Biomass Using Element-Specific, Multicomponent Nuclear Magnetic Resonance Spectroscopy. Env. Sci. Technol. 2015, 49, 7056–7062. [Google Scholar] [CrossRef]
- Demco, D.; Johansson, A.; Tegenfeldt, J. Proton spin-diffusion for spatial heterogeneity and morphology investigations of polymers. Solid State Nucl. Magn. Reson. 1995, 4, 13–38. [Google Scholar] [CrossRef]
- Buda, A.; Demco, D.; Bertmer, M.; Blumich, B.; Reining, B.; Keul, H.; Hocker, H. Domain sizes in heterogeneous polymers by spin diffusion using single-quantum and double-quantum dipolar filters. Solid State Nucl. Magn. Reson. 2003, 24, 39–67. [Google Scholar] [CrossRef]
- Masuda, K.; Kaji, H.; Horii, F. Solid-state C-13 NMR and H-1 CRAMPS investigations of the hydration process and hydrogen bonding for poly(vinyl alcohol) films. Polym. J. 2001, 33, 356–363. [Google Scholar] [CrossRef]
- Struppe, J.; Quinn, C.; Lu, M.; Wang, M.; Hou, G.; Lu, X.; Kraus, J.; Andreas, L.; Stanek, J.; Lalli, D.; et al. Expanding the horizons for structural analysis of fully protonated protein assemblies by NMR spectroscopy at MAS frequencies above 100 kHz. Solid State Nucl. Magn. Reson. 2017, 87, 117–125. [Google Scholar] [CrossRef]
- Schlagnitweit, J.; Tang, M.; Baias, M.; Richardson, S.; Schantz, S.; Emsley, L. A solid-state NMR method to determine domain sizes in multi-component polymer formulations. J. Magn. Reson. 2015, 261, 43–48. [Google Scholar] [CrossRef]
- Besghini, D.; Mauri, M.; Simonutti, R. Time Domain NMR in Polymer Science: From the Laboratory to the Industry. Appl. Sci. 2019, 9, 1801. [Google Scholar] [CrossRef]
- Ogura, T.; Date, Y.; Kikuchi, J. Differences in Cellulosic Supramolecular Structure of Compositionally Similar Rice Straw Affect Biomass Metabolism by Paddy Soil Microbiota. PLoS ONE 2013, 8, e66919. [Google Scholar] [CrossRef]
- Mileo, P.; Yuan, S.; Ayala, S.; Duan, P.; Semino, R.; Cohen, S.; Schmidt-Rohr, K.; Maurin, G. Structure of the Polymer Backbones in polyMOF Materials. J. Am. Chem. Soc. 2020, 142, 10863–10868. [Google Scholar] [CrossRef]
- Schaler, K.; Roos, M.; Micke, P.; Golitsyn, Y.; Seidlitz, A.; Thurn-Albrecht, T.; Schneider, H.; Hempel, G.; Saalwachter, K. Basic principles of static proton low-resolution spin diffusion NMR in nanophase-separated materials with mobility contrast. Solid State Nucl. Magn. Reson. 2015, 72, 50–63. [Google Scholar] [CrossRef] [PubMed]
- Yamada, S.; Ito, K.; Kurotani, A.; Yamada, Y.; Chikayama, E.; Kikuchi, J. InterSpin: Integrated Supportive Webtools for Low- and High-Field NMR Analyses Toward Molecular Complexity. ACS Omega 2019, 4, 3361–3369. [Google Scholar] [CrossRef] [PubMed]
- Schneider, H.; Saalwachter, K.; Roos, M. Complex Morphology of the Intermediate Phase in Block Copolymers and Semicrystalline Polymers As Revealed by H-1 NMR Spin Diffusion Experiments. Macromolecules 2017, 50, 8598–8610. [Google Scholar] [CrossRef]
- Weingarth, M.; Tekely, P.; Bruschweiler, R.; Bodenhausen, G. Improving the quality of 2D solid-state NMR spectra of microcrystalline proteins by covariance analysis. Chem. Commun. 2010, 46, 952–954. [Google Scholar] [CrossRef] [PubMed]
- Bak, M.; Rasmussen, J.; Nielsen, N. SIMPSON: A general simulation program for solid-state NMR spectroscopy. J. Magn. Reson. 2000, 147, 296–330. [Google Scholar] [CrossRef] [PubMed]
- Veshtort, M.; Griffin, R. SPINEVOLUTION: A powerful tool for the simulation of solid and liquid state NMR experiments. J. Magn. Reson. 2006, 178, 248–282. [Google Scholar] [CrossRef]
- Massiot, D.; Fayon, F.; Capron, M.; King, I.; Le Calve, S.; Alonso, B.; Durand, J.; Bujoli, B.; Gan, Z.; Hoatson, G. Modelling one- and two-dimensional solid-state NMR spectra. Magn. Reson. Chem. 2002, 40, 70–76. [Google Scholar] [CrossRef]
- Grimminck, D.; van Meerten, B.; Verkuijlen, M.; van Eck, E.; Meerts, W.; Kentgens, A. EASY-GOING deconvolution: Automated MQMAS NMR spectrum on a model with analytical crystallite excitation efficiencies. J. Magn. Reson. 2013, 228, 116–124. [Google Scholar] [CrossRef]
- Smith, A. INFOS: Spectrum fitting software for NMR analysis. J. Biomol. NMR 2017, 67, 77–94. [Google Scholar] [CrossRef]
- Wojdyr, M. Fityk: A general-purpose peak fitting program. J. Appl. Crystallogr. 2010, 43, 1126–1128. [Google Scholar] [CrossRef]
- van Meerten, S.; Franssen, W.; Kentgens, A. ssNake: A cross-platform open-source NMR data processing and fitting application. J. Magn. Reson. 2019, 301, 56–66. [Google Scholar] [CrossRef] [PubMed]
- Kusaka, Y.; Hasegawa, T.; Kaji, H. Noise Reduction in Solid-State NMR Spectra Using Principal Component Analysis. J. Phys. Chem. A 2019, 123, 10333–10338. [Google Scholar] [CrossRef] [PubMed]
- Yamada, S.; Kurotani, A.; Chikayama, E.; Kikuchi, J. Signal Deconvolution and Noise Factor Analysis Based on a Combination of Time-Frequency Analysis and Probabilistic Sparse Matrix Factorization. Int. J. Mol. Sci. 2020, 21, 2978. [Google Scholar] [CrossRef] [PubMed]
- Kaneko, H. Data Visualization, Regression, Applicability Domains and Inverse Analysis Based on Generative Topographic Mapping. Mol. Inform. 2019, 38. [Google Scholar] [CrossRef] [PubMed]
- Kossaifi, J.; Panagakis, Y.; Anandkumar, A.; Pantic, M. TensorLy: Tensor Learning in Python. J. Mach. Learn. Res. 2019, 20, 925–930. [Google Scholar]
- Dal Poggetto, G.; Castanar, L.; Adams, R.; Morris, G.; Nilsson, M. Dissect and Divide: Putting NMR Spectra of Mixtures under the Knife. J. Am. Chem. Soc. 2019, 141, 5766–5771. [Google Scholar] [CrossRef]
- Kasai, T.; Ono, S.; Koshiba, S.; Yamamoto, M.; Tanaka, T.; Ikeda, S.; Kigawa, T. Amino-acid selective isotope labeling enables simultaneous overlapping signal decomposition and information extraction from NMR spectra. J. Biomol. NMR 2020, 74, 125–137. [Google Scholar] [CrossRef]
- Ito, K.; Obuchi, Y.; Chikayama, E.; Date, Y.; Kikuchi, J. Exploratory machine-learned theoretical chemical shifts can closely predict metabolic mixture signals. Chem. Sci. 2018, in press. [Google Scholar] [CrossRef]
- Chen, G.; Shen, Z.; Iyer, A.; Ghumman, U.; Tang, S.; Bi, J.; Chen, W.; Li, Y. Machine-Learning-Assisted De Novo Design of Organic Molecules and Polymers: Opportunities and Challenges. Polymers 2020, 12, 163. [Google Scholar] [CrossRef]
- Miyao, T.; Kaneko, H.; Funatsu, K. Inverse QSPR/QSAR Analysis for Chemical Structure Generation (from y to x). J. Chem. Inf. Model. 2016, 56, 286–299. [Google Scholar] [CrossRef]
- Aursand, M.; Standal, I.; Axelson, D. High-resolution 13C nuclear magnetic resonance spectroscopy pattern recognition of fish oil capsules. J. Agric. Food Chem. 2007, 55, 38–47. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Terayama, K.; Sumita, M.; Yoshizoe, K.; Ito, K.; Kikuchi, J.; Tsuda, K. NMR-TS: De novo molecule identification from NMR spectra. Sci. Technol. Adv. Mater. 2020, 21, 552–561. [Google Scholar] [CrossRef] [PubMed]
- Aguilera-Saez, L.; Arrabal-Campos, F.; Callejon-Ferre, A.; Medina, M.; Fernandez, I. Use of multivariate NMR analysis in the content prediction of hemicellulose, cellulose and lignin in greenhouse crop residues. Phytochemistry 2019, 158, 110–119. [Google Scholar] [CrossRef] [PubMed]
- Tang, Q.; Chen, Y.; Yang, H.; Liu, M.; Xiao, H.; Wu, Z.; Chen, H.; Naqvi, S. Prediction of Bio-oil Yield and Hydrogen Contents Based on Machine Learning Method: Effect of Biomass Compositions and Pyrolysis Conditions. Energy Fuels 2020, 34, 11050–11060. [Google Scholar] [CrossRef]
- Kasmuri, N.; Kamarudin, S.; Abdullah, S.; Hasan, H.; Som, A. Integrated advanced nonlinear neural network-simulink control system for production of bio-methanol from sugar cane bagasse via pyrolysis. Energy 2019, 168, 261–272. [Google Scholar] [CrossRef]
- Yucel, O.; Aydin, E.; Sadikoglu, H. Comparison of the different artificial neural networks in prediction of biomass gasification products. Int. J. Energy Res. 2019, 43, 5992–6003. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, H.; Song, Y.; Xiao, R. Prediction of product distribution and bio-oil heating value of biomass fast pyrolysis. Chem. Eng. Process.-Process Intensif. 2018, 130, 36–42. [Google Scholar] [CrossRef]
- Verma, R.P.; Hansch, C. Use of 13C NMR chemical shift as QSAR/QSPR descriptor. Chem. Rev. 2011, 111, 2865–2899. [Google Scholar] [CrossRef]
- Himanen, L.; Geurts, A.; Foster, A.; Rinke, P. Data-Driven Materials Science: Status, Challenges, and Perspectives (vol 6, 1900808, 2019). Adv. Sci. 2020, 7, 1903667. [Google Scholar] [CrossRef]
- Ma, R.; Luo, T. PI1M: A Benchmark Database for Polymer Informatics. J. Chem. Inf. Model. 2020, 60, 4684–4690. [Google Scholar] [CrossRef]
- Granda, J.M.; Donina, L.; Dragone, V.; Long, D.L.; Cronin, L. Controlling an organic synthesis robot with machine learning to search for new reactivity. Nature 2018, 559, 377–381. [Google Scholar] [CrossRef]
- Ito, K.; Sakata, K.; Date, Y.; Kikuchi, J. Integrated Analysis of Seaweed Components during Seasonal Fluctuation by Data Mining Across Heterogeneous Chemical Measurements with Network Visualization. Anal. Chem. 2014, 86, 1098–1105. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Pu, Y.; Chen, F.; Ragauskas, A.J. Synthesis and Characterization of Lignin-grafted-poly(ε-caprolactone) from Different Biomass Sources. New Biotechnol. 2021, 60, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Zitnik, M.; Zupan, B. NIMFA: A Python Library for Nonnegative Matrix Factorization. J. Mach. Learn. Res. 2012, 13, 849–853. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamada, S.; Chikayama, E.; Kikuchi, J. Signal Deconvolution and Generative Topographic Mapping Regression for Solid-State NMR of Multi-Component Materials. Int. J. Mol. Sci. 2021, 22, 1086. https://doi.org/10.3390/ijms22031086
Yamada S, Chikayama E, Kikuchi J. Signal Deconvolution and Generative Topographic Mapping Regression for Solid-State NMR of Multi-Component Materials. International Journal of Molecular Sciences. 2021; 22(3):1086. https://doi.org/10.3390/ijms22031086
Chicago/Turabian StyleYamada, Shunji, Eisuke Chikayama, and Jun Kikuchi. 2021. "Signal Deconvolution and Generative Topographic Mapping Regression for Solid-State NMR of Multi-Component Materials" International Journal of Molecular Sciences 22, no. 3: 1086. https://doi.org/10.3390/ijms22031086
APA StyleYamada, S., Chikayama, E., & Kikuchi, J. (2021). Signal Deconvolution and Generative Topographic Mapping Regression for Solid-State NMR of Multi-Component Materials. International Journal of Molecular Sciences, 22(3), 1086. https://doi.org/10.3390/ijms22031086





