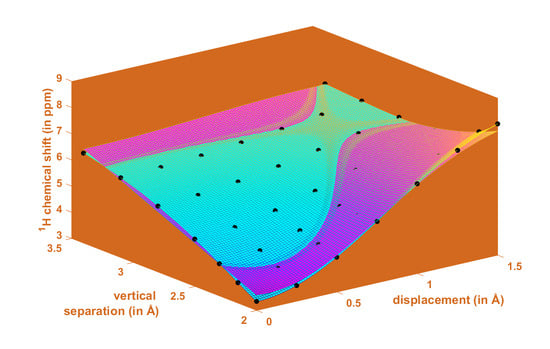
Parametrizing the Spatial Dependence of 1H NMR Chemical Shifts in π-Stacked Molecular Fragments
Abstract
:1. Introduction
2. Results
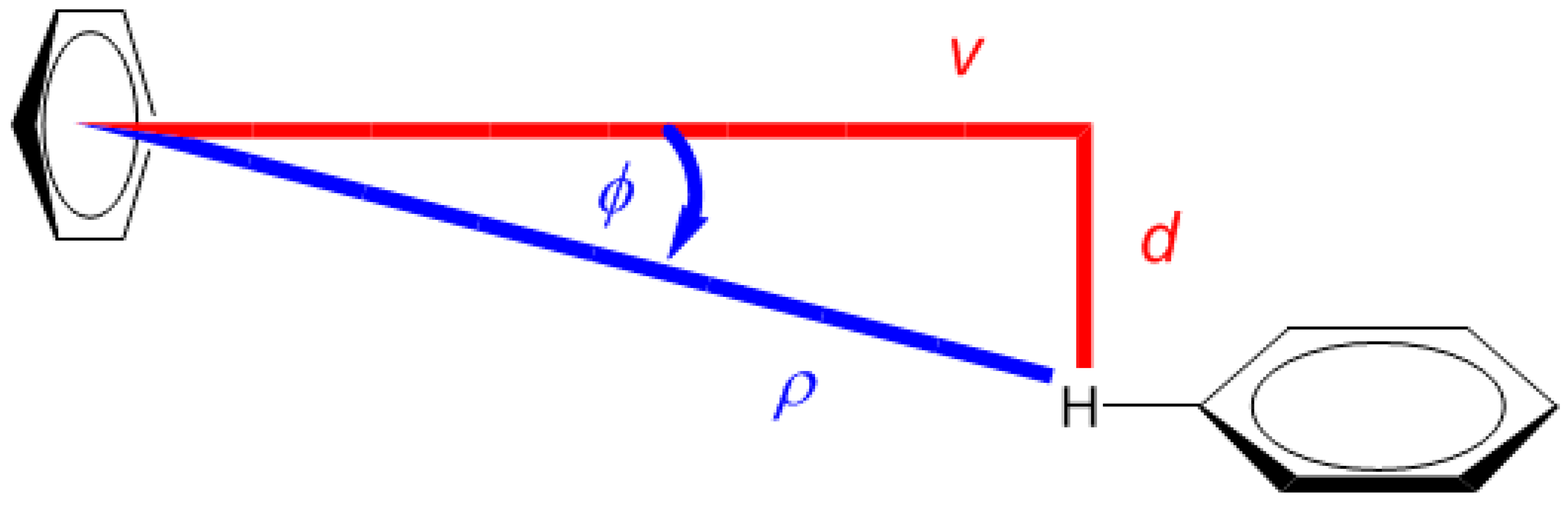
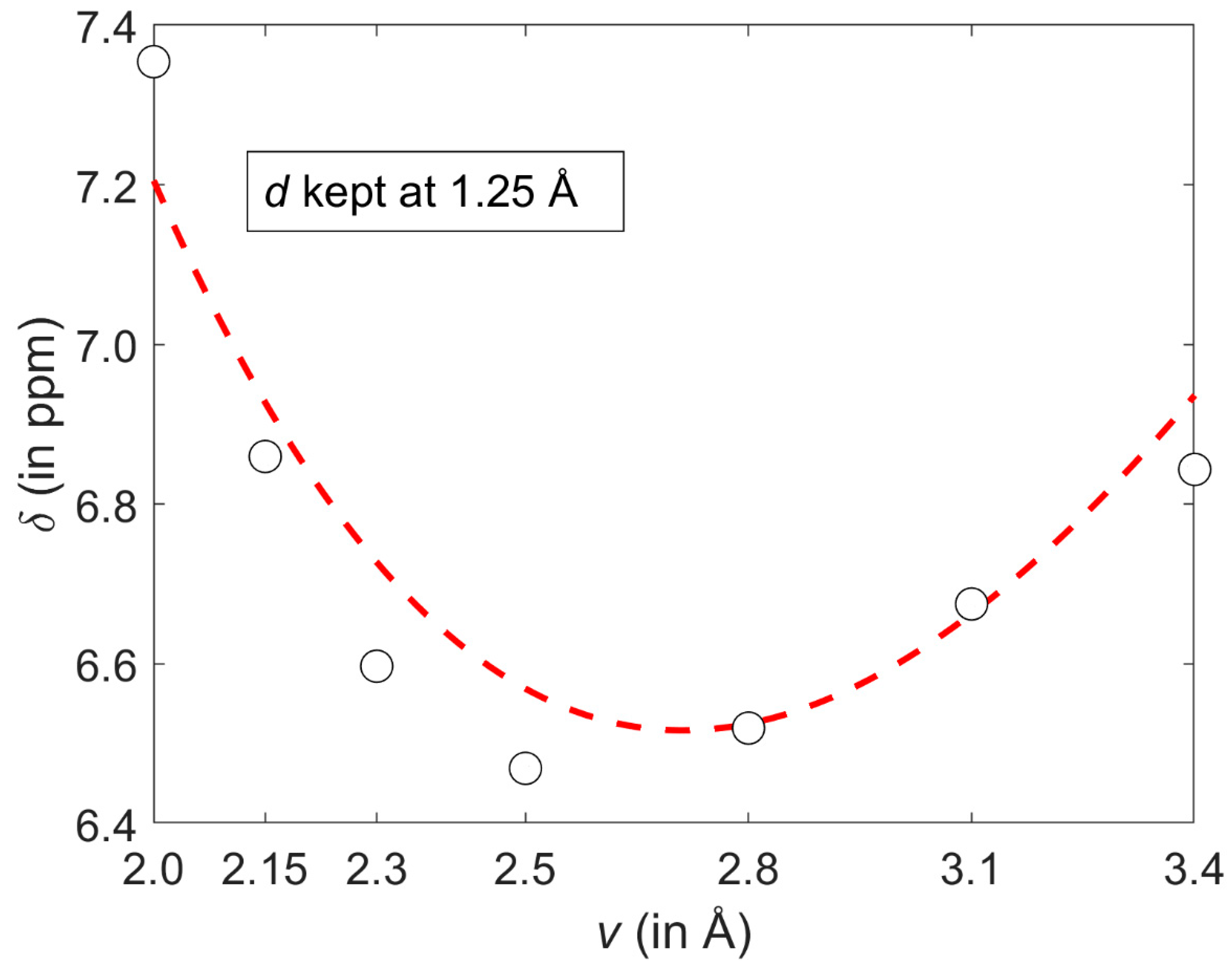
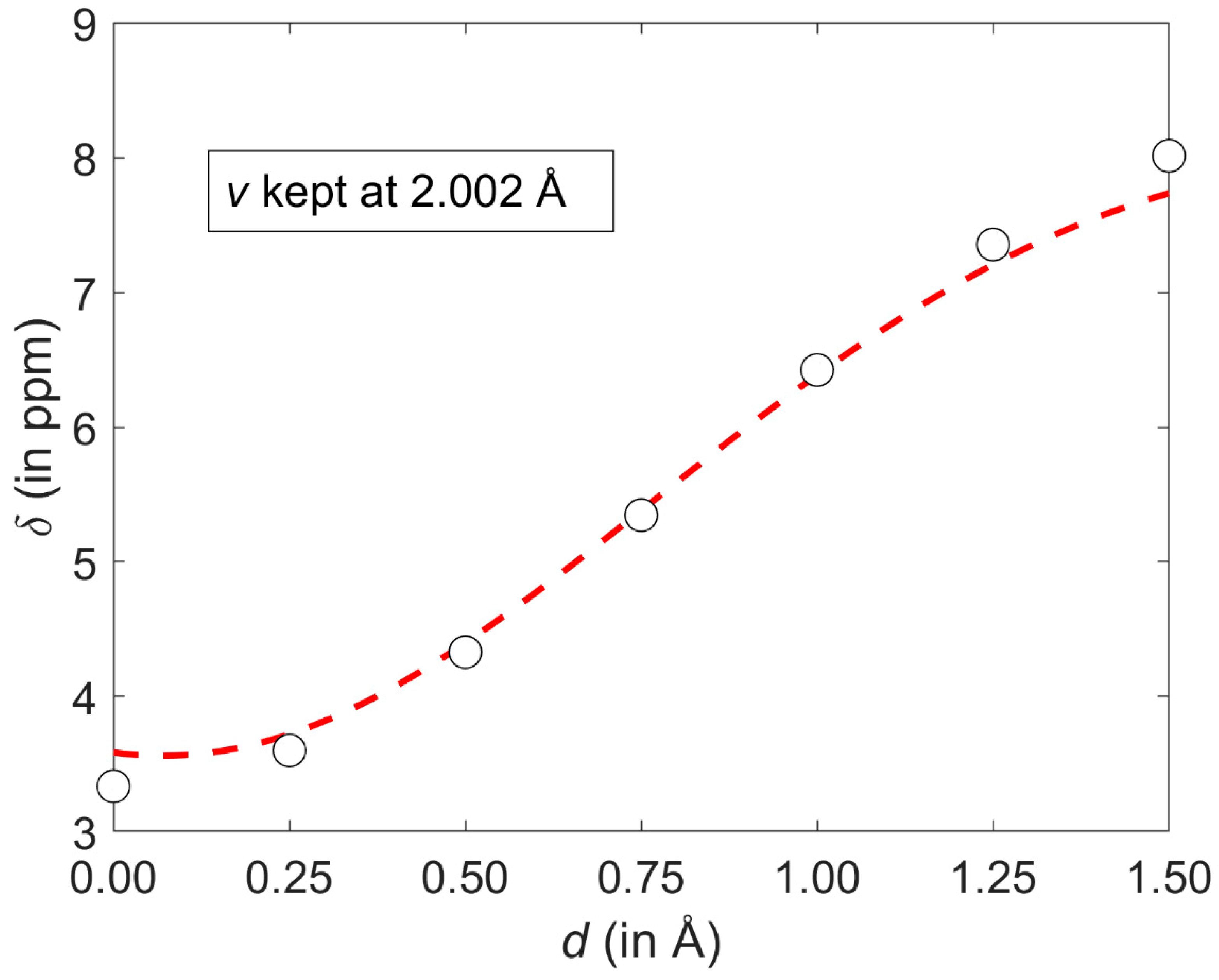
2.1. Development of the Proton Chemical Shift (1H CS) Surface
2.2. Validation of the Dimer Model
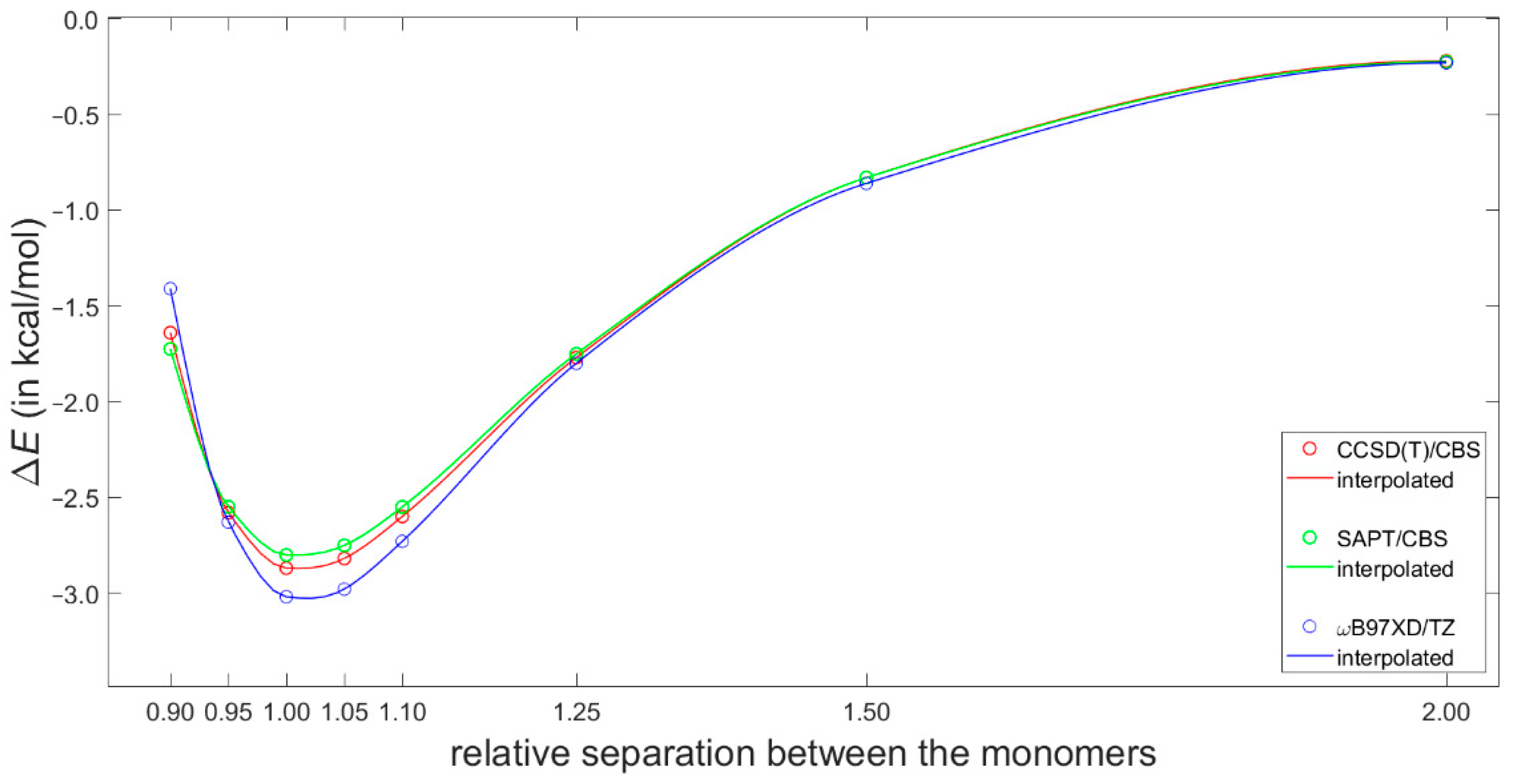
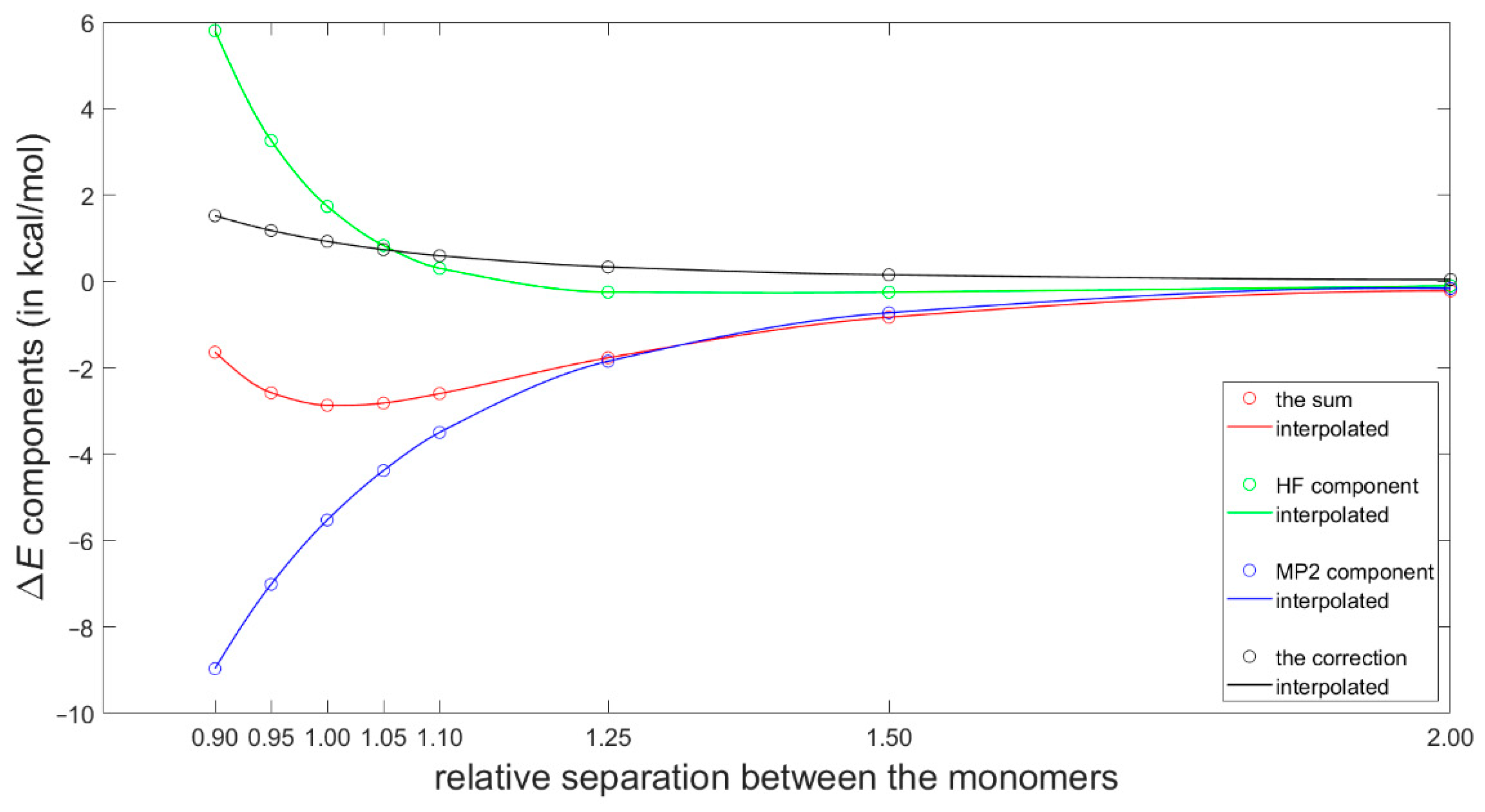
2.3. Dimerization Energy Considerations
3. Discussion
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Larive, C.K.; Barding, G.A.; Dinges, M.N. NMR spectroscopy for metabolomics and metabolic profiling. Anal. Chem. 2015, 87, 133–146. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Mroue, K.H.; Sun, P.; Ramamoorthy, A. High-Resolution Proton NMR Spectroscopy of Polymers and Biological Solids. In Modern Magnetic Resonance, 2nd ed.; Webb, G.A., Ed.; Springer: Cham, Switzerland, 2018; pp. 521–536. [Google Scholar]
- Stone, A.J. The Theory of Intermolecular Forces, 1st ed.; Clarendon Press: Oxford, UK, 2002; pp. 56–63. [Google Scholar]
- Kudisch, B.; Maiuri, M.; Moretti, L.; Oviedo, M.B.; Wang, L.; Oblinsky, D.G.; Prud’homme, R.K.; Wong, B.M.; McGill, S.A.; Scholes, G.D. Ring currents modulate optoelectronic properties of aromatic chromophores at 25 T. Proc. Natl. Acad. Sci. USA 2020, 117, 11289–11298. [Google Scholar] [CrossRef] [PubMed]
- Platzer, G.; Mayer, M.; Beier, A.; Brüschweiler, S.; Fuchs, J.E.; Engelhardt, H.; Geist, L.; Bader, G.; Schörghuber, J.; Lichtenecker, R.; et al. PI by NMR: Probing CH–π Interactions in Protein–Ligand Complexes by NMR Spectroscopy. Angew. Chem. Int. Ed. 2020, 59, 14861–14868. [Google Scholar] [CrossRef] [PubMed]
- Rickhaus, M.; Jirasek, M.; Tejerina, L.; Gotfredsen, H.; Peeks, M.D.; Haver, R.; Jiang, H.-W.; Claridge, T.D.W.; Anderson, H.L. Global aromaticity at the nanoscale. Nat. Chem. 2020, 12, 236–241. [Google Scholar] [CrossRef]
- Gabryelczyk, B.; Cai, H.; Shi, X.; Sun, Y.; Swinkels, P.J.M.; Salentinig, S.; Pervushin, K.; Miserez, A. Hydrogen bond guidance and aromatic stacking drive liquid-liquid phase separation of intrinsically disordered histidine-rich peptides. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef] [Green Version]
- Chaudhari, S.R.; Griffin, J.M.; Broch, K.; Lesage, A.; Lemaur, V.; Dudenko, D.; Olivier, Y.; Sirringhaus, H.; Emsley, L.; Grey, C.P. Donor–acceptor stacking arrangements in bulk and thin-film high-mobility conjugated polymers characterized using molecular modelling and MAS and surface-enhanced solid-state NMR spectroscopy. Chem. Sci. 2017, 8, 3126–3136. [Google Scholar] [CrossRef] [Green Version]
- Bass, T.M.; Carr, C.R.; Sherbow, T.J.; Fettinger, J.C.; Berben, L.A. Syntheses of Square Planar Galluim Complexes and a Proton NMR Correlation Probing Metalloaromaticity. Inor. Chem. 2020, 59, 13517–13523. [Google Scholar] [CrossRef]
- Lampkin, B.J.; Karadakov, P.B.; VanVeller, B. Detailed Visualization of Aromaticity Using Isotropic Magnetic Shielding. Angew. Chem. Int. Ed. 2020, 59, 2–9. [Google Scholar] [CrossRef]
- Kilymis, D.; Bartók, A.P.; Pickard, C.J.; Forse, A.C.; Merlet, C. Efficient prediction of nucleus independent chemical shifts for polycyclic aromatic hydrocarbons. Phys. Chem. Chem. Phys. 2020, 22, 13746–13755. [Google Scholar] [CrossRef]
- Pöppler, A.-C.; Corlett, E.K.; Pearce, H.; Seymour, M.P.; Reid, M.; Montgomery, M.G.; Brown, S.P. Single-crystal X-ray diffraction and NMR crystallography of a 1:1 cocrystal of dithianon and pyrimethanil. Acta Cryst. C 2017, 73, 149–156. [Google Scholar] [CrossRef]
- Schwartz, E.; Lim, E.; Gowda, C.M.; Liscio, A.; Fenwick, O.; Tu, G.; Palermo, V.; de Gelder, R.; Cornelissen, J.J.L.M.; Van Eck, E.R.H.; et al. Synthesis, Characterization, and Surface Initiated Polymerization of Carbazole Functionalized Isocyanides. Chem. Mater. 2010, 8, 2597–2607. [Google Scholar] [CrossRef]
- Gowda, C.M.; Vasconcelos, F.; Schwartz, E.; Van Eck, E.R.H.; Marsman, M.; Cornelissen, J.J.L.M.; Rowan, A.E.; De Wijs, G.A.; Kentgens, A.P.M. Hydrogen bonding and chemical shifts assignments in carbazole functionalized isocyanides from solid-state NMR and first-principles calculations. Phys. Chem. Chem. Phys. 2011, 13, 13082–13095. [Google Scholar] [CrossRef] [PubMed]
- Bonhomme, C.; Gervais, C.; Babonneau, F.; Coelho, C.; Pourpoint, F.; Azais, T.; Asbrook, S.E.; Griffin, J.M.; Yates, J.R.; Pickard, J.C. First-Principles Calculation of NMR Parameters Using the Gauge Including Projector Augmented Wave Method: A Chemist’s Point of View. Chem. Rev. 2012, 112, 5733–5779. [Google Scholar] [CrossRef] [PubMed]
- Bootsma, A.N.; Doney, A.C.; Wheeler, S.E. Predicting the Strength of Stacking Interactions between Heterocycles and Aromatic Amino Acid Side Chain. J. Am. Chem. Soc. 2019, 141, 11027–11035. [Google Scholar] [CrossRef]
- D’Ischia, M.; Napolitano, A.; Pezzella, A.; Meredith, P.; Buehler, M. Melanin biopolymers: Tailoring chemical complexity for materials design. Angew. Chem. Int. Ed. 2020, 59, 11196–11205. [Google Scholar] [CrossRef]
- Lyu, Q.; Hsueh, N.; Chai, C.L.L. Unravelling the polydopamine mystery: Is the end in sight? Polym. Chem. 2019, 10, 5771–5777. [Google Scholar] [CrossRef]
- Proks, V.; Brus, J.; Pop-Georgievski, O.; Večerníková, E.; Wiśniewski, W.; Kotek, J.; Urbanová, M.; Rypáček, F. Thermal-Induced Transformation of Polydopamine Structures: An Efficient Route for the Stabilization of the Polydopamine Surfaces. Macromol. Chem. Phys. 2013, 214, 499–507. [Google Scholar] [CrossRef]
- Circu, M.; Filip, C. Closer to the polydopamine structure: New insights from a combined 13C/1H/2H solid-state NMR study on deuterated samples. Polym. Chem. 2018, 9, 3379–3387. [Google Scholar] [CrossRef]
- Loeffler, J.R.; Fernández-Quintero, M.L.; Schauperl, M.; Liedl, K.R. STACKED – Solvation Theory of Aromatic Complexes as Key for Estimating Drug Binding. J. Chem. Inf. Model. 2020, 60, 2304–2313. [Google Scholar] [CrossRef] [Green Version]
- Bartolomei, M.; Pirani, F.; Marques, J.M.C. Low-energy structures of benzene clusters with a novel accurate potential surface. J. Comput. Chem. 2015, 36, 2291–2301. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, M.R.; McDonald, A.R.; DePrince, A.E., III; Marshall, M.S.; Podeszwa, R.; Sherrill, C.D. Resolving the three-body contribution to the lattice energy of crystalline benzene: Benchmark results from coupled-cluster theory. J. Chem. Phys. 2014, 140. [Google Scholar] [CrossRef]
- Miliordos, E.; Apra, E.; Xantheas, S.S. Benchmark Theoretical Study of the π−π Binding Energy in the Benzene Dimer. J. Phys. Chem. A 2014, 118, 7568–7578. [Google Scholar] [CrossRef]
- DiStasio, R.A., Jr.; Von Helden, G.; Steele, R.P.; Head-Gordon, M. On the T-shaped structures of the benzene dimer. Chem. Phys. Lett. 2007, 437, 277–283. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J. Exploring Accuracy Limits of Predictions of the 1H NMR Chemical Shielding Anisotropy in the Solid State. Molecules 2019, 24, 1731. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Czernek, J.; Brus, J. Monitoring the Site-Specific Solid-State NMR Data in Oligopeptides. Int. J. Mol. Sci. 2020, 21, 2700. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J. Polymorphic Forms of Valinomycin Investigated by NMR Crystallography. Int. J. Mol. Sci. 2020, 21, 4907. [Google Scholar] [CrossRef]
- Řezáč, J.; Riley, K.E.; Hobza, P. S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures. J. Chem. Theory Comput. 2011, 7, 2427–2438. [Google Scholar] [CrossRef]
- Řezáč, J.; Jurečka, P.; Riley, K.E.; Černý, J.; Valdes, H.; Pluháčková, K.; Berka, K.; Řezáč, T.; Pitoňák, M.; Vondrášek, J.; et al. Quantum Chemical Benchmark Energy and Geometry Database for Molecular Clusters and Complex Molecular Systems (www.begdb.com): A Users Manual and Examples. Collect. Czech. Chem. Commun. 2008, 73, 1261–1270. [Google Scholar] [CrossRef] [Green Version]
- Brown, S.P. Applications of high-resolution 1H solid-state NMR. Solid State Nucl. Magn. Reson. 2012, 41, 1–27. [Google Scholar] [CrossRef]
- Dudenko, D.V.; Yates, J.R.; Harris, K.D.M.; Brown, S.P. An NMR crystallography DFT-D approach to analyse the role of intermolecular hydrogen bonding and π–π interactions in driving cocrystallisation of indomethacin and nicotinamide. CrystEngComm 2013, 15, 8797–8807. [Google Scholar] [CrossRef]
- Dudenko, D.V.; Williams, P.A.; Hughes, C.E.; Antzutkin, O.N.; Velaga, S.P.; Brown, S.P.; Harris, K.D.M. Exploiting the Synergy of Powder X-ray Diffraction and Solid-State NMR Spectroscopy in Structure Determination of Organic Molecular Solids. J. Phys. Chem. C 2013, 117, 12258–12265. [Google Scholar] [CrossRef] [PubMed]
- Czernek, J.; Brus, J. The covariance of the differences between experimental and theoretical chemical shifts as an aid for assigning two-dimensional heteronuclear correlation solid-state NMR spectra. Chem. Phys. Lett. 2014, 608, 334–339. [Google Scholar] [CrossRef]
- Carignani, E.; Borsacchi, S.; Bradley, J.P.; Brown, S.P.; Geppi, M. Strong Intermolecular Ring Current Influence on 1H Chemical Shifts in Two Crystalline Forms of Naproxen: A Combined Solid-State NMR and DFT Study. J. Phys. Chem. C 2013, 117, 17731–17740. [Google Scholar] [CrossRef]
- Czernek, J. On the solid-state NMR spectra of naproxen. Chem. Phys. Lett. 2015, 619, 230–235. [Google Scholar] [CrossRef]
- Corlett, E.K.; Blade, H.; Hughes, L.P.; Sidebottom, P.J.; Walker, D.; Walton, R.I.; Brown, S.P. Investigating discrepancies between experimental solid-state NMR and GIPAW calculation: N=C–N 13C and OH⋯O 1H chemical shifts in pyridinium fumarates and their cocrystals. Solid State Nucl. Magn. Reson. 2020, 108. [Google Scholar] [CrossRef]
- Hušák, M.; Jegorov, A.; Rohlíček, J.; Fitch, A.; Czernek, J.; Kobera, L.; Brus, J. Determining the Crystal Structures of Peptide Analogs of Boronic Acid in the Absence of Single Crystals: Intricate Motifs of Ixazomib Citrate Revealed by XRPD Guided by ss-NMR. Cryst. Growth Des. 2018, 18, 3616–3625. [Google Scholar] [CrossRef]
- Harris, R.K.; Hodgkinson, P.; Zorin, V.; Dumez, J.N.; Elena-Herrmann, B.; Emsley, L.; Salager, E.; Stein, R.S. Computation and NMR crystallography of terbutaline sulfate. Magn. Reson. Chem. 2010, 48, S103–S112. [Google Scholar] [CrossRef]
- Kerr, H.E.; Softley, L.K.; Suresh, K.; Nangia, A.; Hodgkinson, P.; Radosavjlevic Evans, I. A furosemide–isonicotinamide cocrystal: An investigation of properties and extensive structural disorder. CrystEngComm 2015, 17, 6707–6715. [Google Scholar] [CrossRef] [Green Version]
- Frantsuzov, I.; Ford, S.J.; Radosavjlevic Evans, I.; Horsewill, A.J.; Trommsdorff, H.P.; Johnson, M.R. Measurement of Proton Tunneling in Short Hydrogen Bonds in Single Crystals of 3,5 Pyridinedicarboxylic Acid Using Nuclear Magnetic Resonance Spectroscopy. Phys. Rev. Lett. 2014, 113. [Google Scholar] [CrossRef] [Green Version]
- Dračínský, M.; Hodgkinson, P. A molecular dynamics study of the effects of fast molecular motions on solid-state NMR parameters. CrystEngComm 2013, 15, 8705–8712. [Google Scholar] [CrossRef] [Green Version]
- Nishiyama, Y.; Malon, M.; Potrzebowski, M.J.; Paluch, P.; Amoreux, J.P. Accurate NMR determination of C–H or N–H distances for unlabeled molecules. Solid State Nucl. Magn. Reson. 2016, 73, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Mroue, K.H.; Ramamoorthy, A. Proton-Based Ultrafast Magic Angle Spinning Solid-State NMR Spectroscopy. Acc. Chem. Res. 2017, 50, 1105–1113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, M.; Lu, X.; Xu, W.; Troup, G.M.; McNevin, M.J.; Nie, H.; Su, Y. Quantifying Pharmaceutical Formulations from Proton Detected Solid-State NMR under Ultrafast Magic Angle Spinning. J. Pharm. Sci. 2020, 109, 3045–3053. [Google Scholar] [CrossRef] [PubMed]
- Huber, R.G.; Margreiter, M.A.; Fuchs, J.E.; Von Grefenstein, S.; Tuatermann, C.S.; Liedl, K.R.; Fox, T. Heteroaromatic π-Stacking Energy Landscapes. J. Chem. Inf. Model. 2014, 54, 1371–1379. [Google Scholar] [CrossRef]
- Gyevy-Nagy, L.; Kállay, M.; Nagy, P.R. Integral-Direct and Parallel Implementation of the CCSD(T) Method: Algorithmic Developments and Large-Scale Applications. J. Chem. Theory Comput. 2020, 16, 366–384. [Google Scholar] [CrossRef]
- Bootsma, A.N.; Doney, A.C.; Wheeler, S.E. Tuning Stacking Interactions between Asp–Arg Salt Bridges and Heterocyclic Drug Fragments. J. Chem. Inf. Model. 2019, 59, 149–158. [Google Scholar] [CrossRef]
- Brandl, M.; Weiss, M.S.; Jabs, A.; Sühnel, J.; Hilgenfeld, R. C–H … π-Interaction in Proteins. J. Mol. Biol. 2001, 307, 357–377. [Google Scholar] [CrossRef]
- Nishiyo, M.; Umezawa, Y.; Fantini, J.; Weiss, M.S.; Chakrabarti, P. CH–π hydrogen bonds in biological macromolecules. Phys. Chem. Chem. Phys. 2014, 16, 12648–12683. [Google Scholar] [CrossRef]
- Sahakyan, A.B.; Vendruscolo, M. Analysis of the Contributions of Ring Current and Electric Field Effects to the Chemical Shifts of RNA Bases. J. Phys. Chem. B 2013, 117, 1989–1998. [Google Scholar] [CrossRef]
- Widdifield, C.M.; Farrell, J.D.; Cole, J.C.; Howard, J.A.K.; Hodgkinson, P. Resolving alternative organic crystal structures using density functional theory and NMR chemical shifts. Chem. Sci. 2020, 11, 2987–2992. [Google Scholar] [CrossRef] [Green Version]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Boys, S.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
- Frish, M.J.; Trucks, J.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision D.01; Gaussian, Inc.: Wallingford, UK, 2013. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First principles simulation: Ideas, illustrations, and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Kristallogr. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Pickard, C.J.; Mauri, F. All-electron magnetic response with pseudopotentials: NMR chemical shifts. Phys. Rev. B 2001, 63. [Google Scholar] [CrossRef] [Green Version]
- Yates, J.R.; Pickard, C.J.; Mauri, F. Calculations of NMR chemical shifts for extended systems using ultrasoft pseudopotentials. Phys. Rev. B 2007, 76. [Google Scholar] [CrossRef]
- BIOVIA Materials Studio. Dassault Systèmes, Vélizy-Villacoublay: Paris, France. Available online: https://www.3ds.com/products-services/biovia/products/molecular-modeling-simulation/biovia-materials-studio/ (accessed on 22 September 2020).
- Gao, S.-P.; Pickard, C.J.; Perlov, A.; Milman, V. Core-Level Spectroscopy Calculation and the Plane Wave Pseudopotential Method. J. Phys. Condens. Matter 2009, 21. [Google Scholar] [CrossRef] [PubMed]
- Halkier, A.; Helgaker, T.; Jørgensen, P.; Klopper, W.; Koch, H.; Olsen, J.; Wilson, A.K. Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 1998, 286, 243–252. [Google Scholar] [CrossRef]
- Patkowski, K. Recent developments in symmetry-adapted perturbation theory. Wiley Interdiscip. Rev. Comput. Mol. Phys. 2019, 10. [Google Scholar] [CrossRef]
- Hesselmann, A.; Jansen, G.; Schütz, M. Density-functional theory-symmetry-adapted intermolecular perturbation theory with density fitting: A new efficient method to study intermolecular interaction energies. J. Chem. Phys. 2005, 122. [Google Scholar] [CrossRef]
- Hesselmann, A.; Jansen, G.; Schütz, M. Interaction Energy Contributions of H-Bonded and Stacked Structures of the AT and GC DNA Base Pairs from the Combined Density Functional Theoryand Intermolecular Perturbation Theory Approach. J. Am. Chem. Soc. 2006, 128, 11730–11731. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Hesselmann, A.; Kats, D.; Kohn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152. [Google Scholar] [CrossRef] [Green Version]
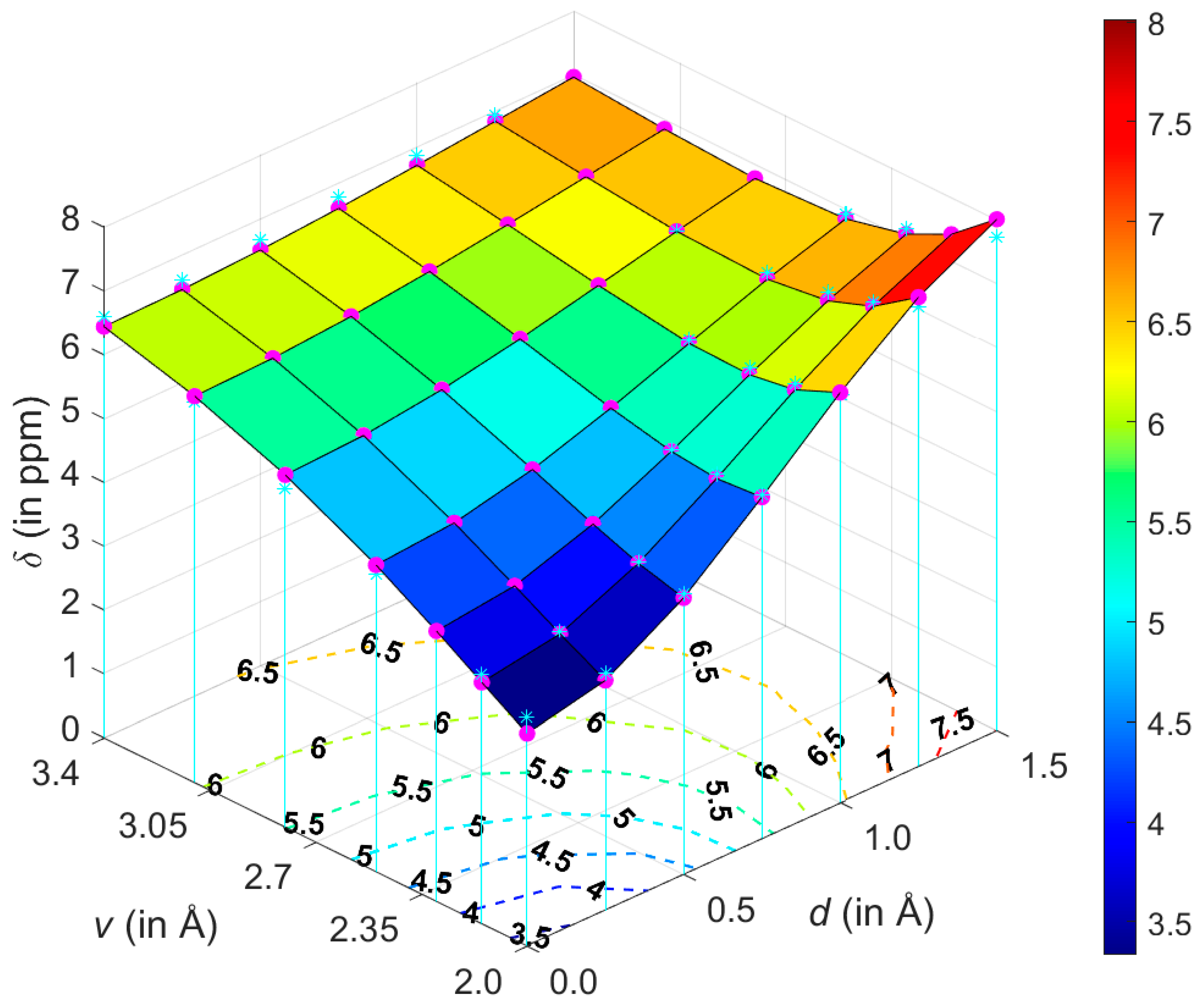
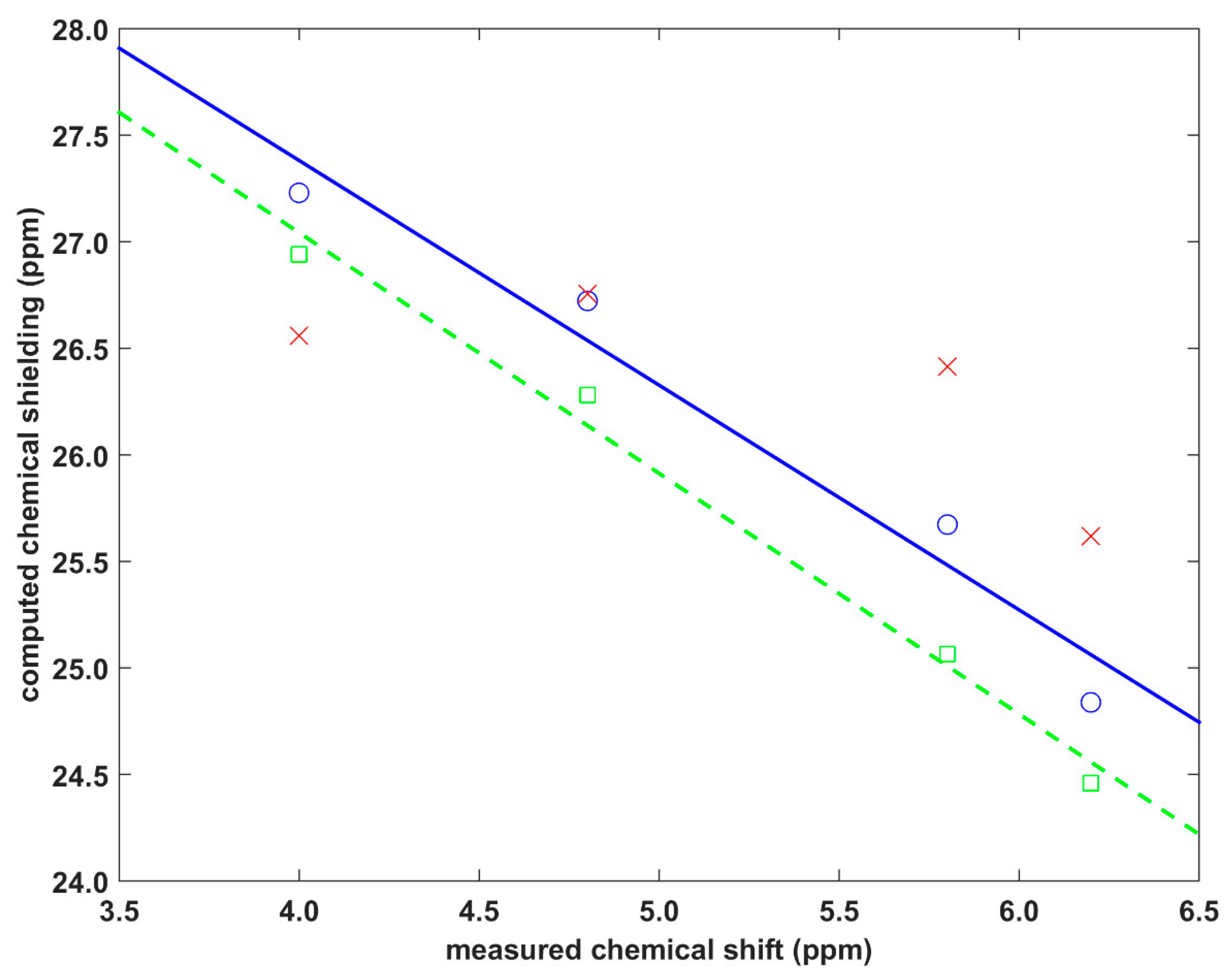
| Crystal | Site | v (in Å) | d (in Å) | δ (in ppm) | σ/δ’ Periodic (in ppm) | σ/δ’ Cluster (in ppm) | σ/δ’ Fit (in ppm) |
|---|---|---|---|---|---|---|---|
| Dithianon–pyrimethanil | H25 | 2.5238 | 0.5056 | 4.0 | 26.9417/3.9 | 27.2285/4.6 | 26.5599/5.3 |
| H2 | 2.6975 | 0.9521 | 6.2 | 24.4601/6.4 | 24.8389/7.0 | 25.6178/6.2 | |
| The isocyanide | H10′ | 2.6009 | 0.1846 | 4.8 | 26.2797/4.6 | 26.7231/5.1 | 26.7550/5.1 |
| H11′ | 2.7557 | 0.2720 | 5.8 | 25.0655/5.8 | 25.6729/6.2 | 26.4137/5.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czernek, J.; Brus, J. Parametrizing the Spatial Dependence of 1H NMR Chemical Shifts in π-Stacked Molecular Fragments. Int. J. Mol. Sci. 2020, 21, 7908. https://doi.org/10.3390/ijms21217908
Czernek J, Brus J. Parametrizing the Spatial Dependence of 1H NMR Chemical Shifts in π-Stacked Molecular Fragments. International Journal of Molecular Sciences. 2020; 21(21):7908. https://doi.org/10.3390/ijms21217908
Chicago/Turabian StyleCzernek, Jiří, and Jiří Brus. 2020. "Parametrizing the Spatial Dependence of 1H NMR Chemical Shifts in π-Stacked Molecular Fragments" International Journal of Molecular Sciences 21, no. 21: 7908. https://doi.org/10.3390/ijms21217908
APA StyleCzernek, J., & Brus, J. (2020). Parametrizing the Spatial Dependence of 1H NMR Chemical Shifts in π-Stacked Molecular Fragments. International Journal of Molecular Sciences, 21(21), 7908. https://doi.org/10.3390/ijms21217908