Double Mutant Cycles as a Tool to Address Folding, Binding, and Allostery
Abstract
1. Introduction
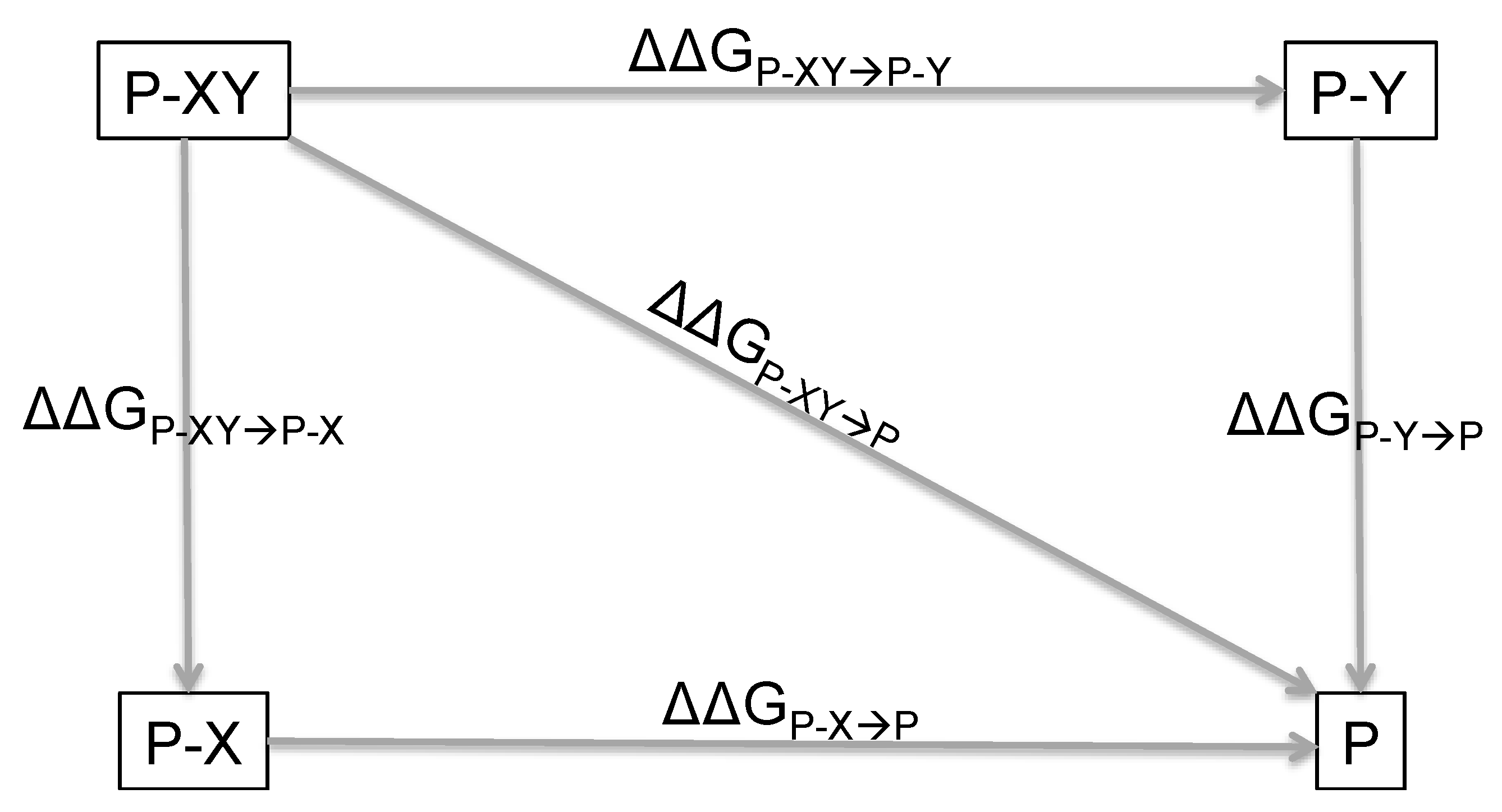
2. Principles of Double Mutant Cycles and Basic Equations
3. The Double Mutant Cycle: Strengths, Caveats, and Pitfalls
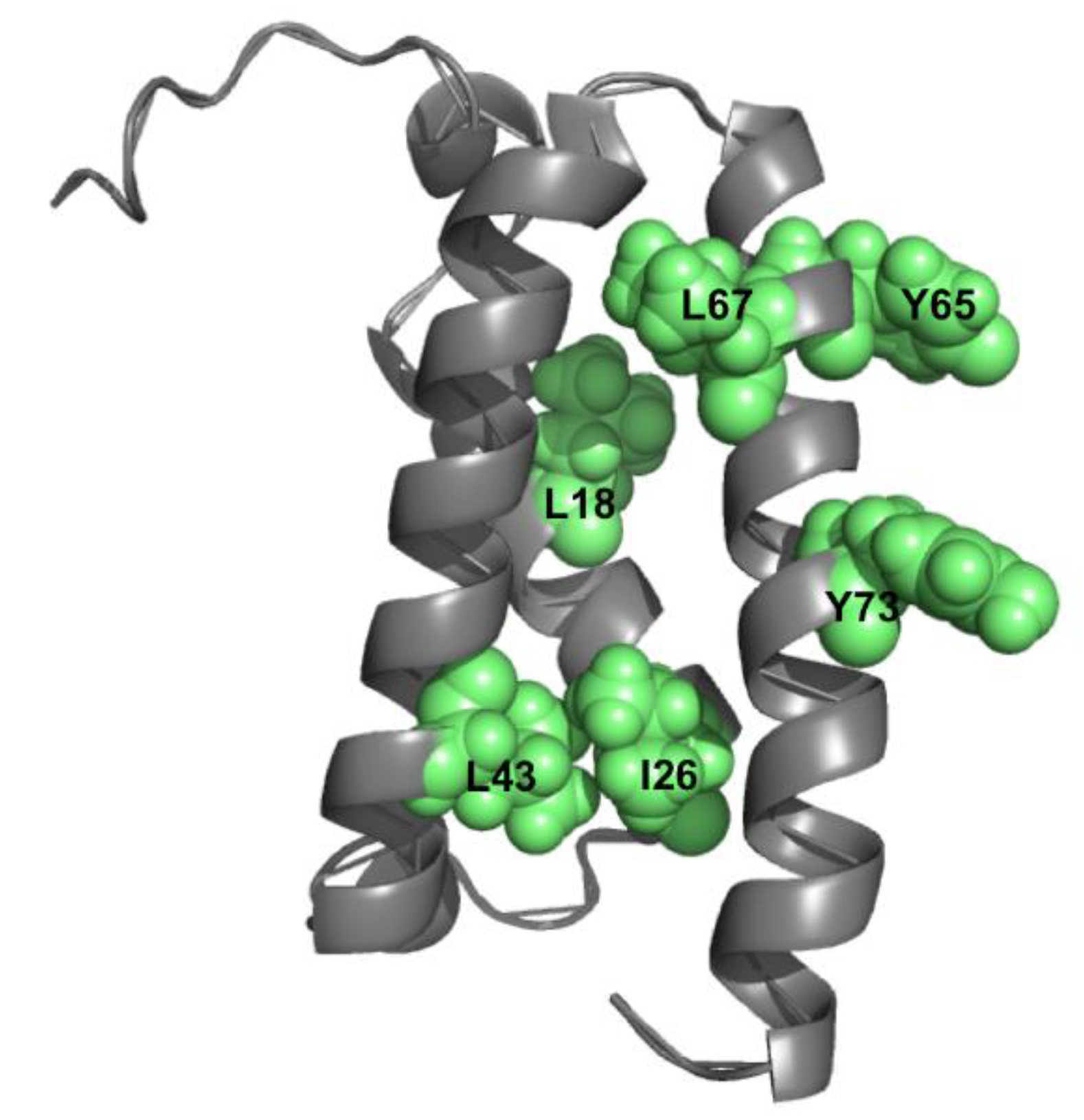
4. Double Mutant Cycles to Understand Intramolecular Interactions
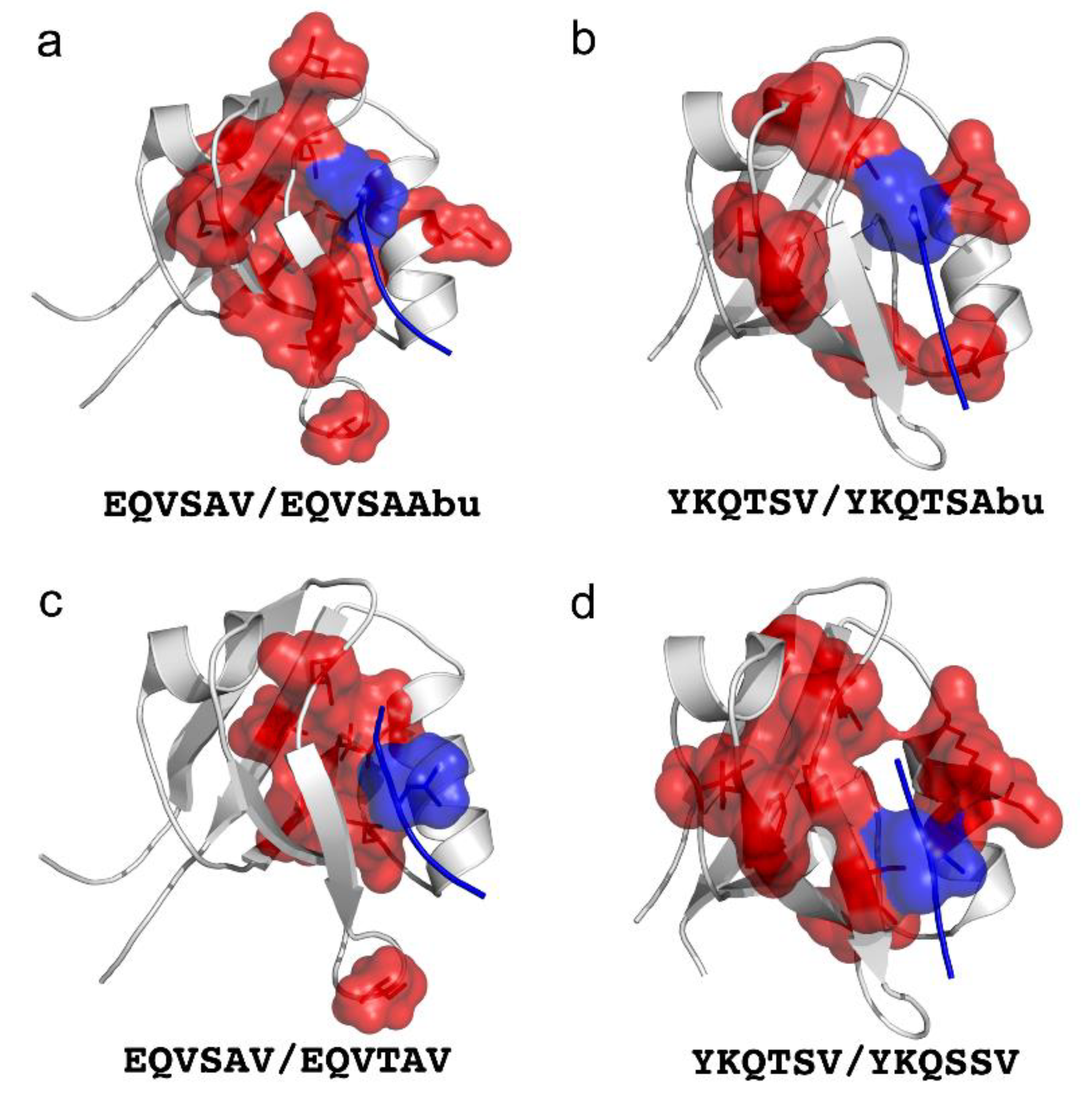
5. Protein Binding and Allostery
6. Double Mutant Cycles In Silico
7. Double Mutant Cycles by Native Mass Spectrometry
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yip, K.M.; Fischer, N.; Paknia, E.; Chari, A.; Stark, H. Atomic-resolution protein structure determination by cryo-EM. Nature 2020, 587, 157–161. [Google Scholar] [CrossRef] [PubMed]
- Wüthrich, K. Protein structure determination in solution by nmr spectroscopy. World Sci. Res. 1995, 5, 11–14. [Google Scholar]
- Dobson, C.M. Biophysical techniques in structural biology. Annu. Rev. Biochem. 2019, 88, 25–33. [Google Scholar] [CrossRef] [PubMed]
- Fersht, A.R. Structure and Mechanism in Protein Science; Freeman: New York, NY, USA, 1999. [Google Scholar]
- Horovitz, A.; Fleisher, R.C.; Mondal, T. Double-mutant cycles: New directions and applications. Curr. Opin. Struct. Biol. 2019, 58, 10–17. [Google Scholar] [CrossRef]
- Horovitz, A. Double-mutant cycles: A powerful tool for analyzing protein structure and function. Fold. Des. 1996, 1, 121–126. [Google Scholar] [CrossRef]
- Cockroft, S.L.; Hunter, C.A. Chemical double-mutant cycles: Dissecting non-covalent interactions. Chem. Soc. Rev. 2007, 36, 172–188. [Google Scholar] [CrossRef]
- Sali, D.; Bycroft, M.; Fersht, A.R. Surface electrostatic interactions contribute little of stability of barnase. J. Mol. Biol. 1991, 220, 779–788. [Google Scholar]
- Otzen, D.E.; Fersht, A.R. Analysis of protein-protein interactions by mutagenesis: Direct versus indirect effects. Protein. Eng. 1999, 12, 41–45. [Google Scholar] [CrossRef]
- Bateson, W. Mendel’s Principles of Heredity: A Defence; Cambridge University Press: Cambridge, UK, 1902. [Google Scholar]
- Moore, J.H. A global view of epistasis. Nat. Genet. 2005, 37, 13–14. [Google Scholar] [CrossRef]
- Starr, T.N.; Thornton, J.W. Epistasis in protein evolution. Protein Sci. 2016, 25, 1204–1218. [Google Scholar] [CrossRef]
- Winter, G.; Fersht, A.R.; Wilkinson, A.J.; Zoller, M.; Smith, M. Redesigning enzyme structure by site-directed mutagenesis: Tyrosyl tRNA synthetase and ATP binding. Nature 1982, 299, 756–758. [Google Scholar] [CrossRef] [PubMed]
- Carter, P.J.; Winter, G.; Wilkinson, A.J.; Fersht, A.R. The use of double mutants to detect structural changes in the active site of the tyrosyl-tRNA synthetase (Bacillus stearothermophilus). Cell 1984, 38, 835–840. [Google Scholar] [CrossRef]
- Fersht, A.R.; Sato, S. Φ-Value analysis and the nature of protein-folding transition states. Proc. Natl. Acad. Sci. USA 2004, 101, 7976–7981. [Google Scholar] [CrossRef] [PubMed]
- Horovitz, A.; Fersht, A.R. Strategy for analysing the co-operativity of intramolecular interactions in peptides and proteins. J. Mol. Biol. 1990, 214, 613–617. [Google Scholar] [CrossRef]
- Fersht, A.R.; Matouschek, A.; Serrano, L. The folding of an enzyme. I. Theory of protein engineering analysis of stability and pathway of protein folding. J. Mol. Biol. 1992, 224, 771–782. [Google Scholar] [CrossRef]
- Serrano, L.; Horovitz, A.; Avron, B.; Bycroft, M.; Fersht, A.R. Estimating the contribution of engineered surface electrostatic interactions to protein stability by using double-mutant cycles. Biochemistry 1990, 29, 9343–9352. [Google Scholar] [CrossRef]
- Sato, S.; Religa, T.L.; Fersht, A.R. Φ-Analysis of the folding of the b domain of protein a using multiple optical probes. J. Mol. Biol. 2006, 360, 850–864. [Google Scholar] [CrossRef] [PubMed]
- Serrano, L.; Bycroft, M.; Fersht, A.R. Aromatic-aromatic interactions and protein stability: Investigation by double-mutant cycles. J. Mol. Biol. 1991, 218, 465–475. [Google Scholar] [CrossRef]
- Horovitz, A.; Serrano, L.; Avron, B.; Bycroft, M.; Fersht, A.R. Strength and co-operativity of contributions of surface salt bridges to protein stability. J. Mol. Biol. 1990, 216, 1031–1044. [Google Scholar] [CrossRef]
- Vaughan, C.K.; Harryson, P.; Buckle, A.M.; Fersht, A.R. A structural double-mutant cycle: Estimating the strength of a buried salt bridge in barnase. Acta Crystallogr. D 2002, 58, 591–600. [Google Scholar] [CrossRef]
- Green, S.M.; Shortle, D. Patterns of nonadditivity between pairs of stability mutations in staphylococcal nuclease. Biochemistry 1993, 32, 10131–10139. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Stites, W.E. Energetics of side chain packing in staphylococcal nuclease assessed by systematic double mutant cycles. Biochemistry 2001, 40, 14004–14011. [Google Scholar] [CrossRef] [PubMed]
- Marqusee, S.; Sauer, R.T. Contributions of a hydrogen bond/salt bridge network to the stability of secondary and tertiary structure in lambda repressor. Protein Sci. 1994, 3, 2217–2225. [Google Scholar] [CrossRef] [PubMed]
- Myers, J.K.; Oas, T.G. Contribution of a buried hydrogen bond to λ repressor folding kinetics. Biochemistry 1999, 38, 6761–6768. [Google Scholar] [CrossRef] [PubMed]
- Thakur, J.K.; Yadav, A.; Yadav, G. Molecular recognition by the KIX domain and its role in gene regulation. Nucleic Acids Res. 2014, 42, 2112–2125. [Google Scholar] [CrossRef] [PubMed]
- Troilo, F.; Bonetti, D.; Toto, A.; Visconti, L.; Brunori, M.; Longhi, S.; Gianni, S. The folding pathway of the KIX domain. J. Am. Chem. Soc. 2017, 12, 1683–1690. [Google Scholar] [CrossRef]
- Myers, J.K.; Pace, C.N.; Scholtz, J.M. Denaturant m values and heat capacity changes: Relation to changes in accessible surface areas of protein unfolding. Protein Sci. 1995, 4, 2138–2148. [Google Scholar] [CrossRef]
- Scaloni, F.; Gianni, S.; Federici, L.; Falini, B.; Brunori, M. Folding mechanism of the C-terminal domain of nucleophosmin: Residual structure in the denatured state and its pathophysiological significance. Fed. Proc. 2009, 23, 2360–2365. [Google Scholar] [CrossRef]
- Perutz, M.F.; Kendrew, J.C.; Watson, H.C. Structure and function of haemoglobin: II. Some relations between polypeptide chain configuration and amino acid sequence. J. Mol. Biol. 1965, 13, 669–678. [Google Scholar] [CrossRef]
- Goodey, N.M.; Benkovic, S.J. Allosteric regulation and catalysis emerge via a common route. Nat. Chem. Biol. 2008, 4, 474–482. [Google Scholar] [CrossRef]
- Schreiber, G.; Fersht, A.R. Rapid, electrostatically assisted association of proteins. Nat. Struct. Biol. 1996, 3, 427–431. [Google Scholar] [CrossRef] [PubMed]
- Ming, D.; Chen, R.; Huang, H. Amino-acid network clique analysis of protein mutation non-additive effects: A case study of lysozme. Int. J. Mol. Sci. 2018, 19, 1427. [Google Scholar] [CrossRef] [PubMed]
- Rajasekaran, N.; Sekhar, A.; Naganathan, A.N. A universal pattern in the percolation and dissipation of protein structural perturbations. J. Phys. Chem. Lett. 2017, 8, 4779–4784. [Google Scholar] [CrossRef] [PubMed]
- Horovitz, A. Non-additivity in protein-protein interactions. J. Mol. Biol. 1987, 196, 733–735. [Google Scholar] [CrossRef]
- Nussinov, R.; Tsai, C.-J. Allostery without a conformational change? Revisiting the paradigm. Curr. Opin. Struct. Biol. 2015, 30, 17–24. [Google Scholar] [CrossRef]
- Schreiber, G.; Fersht, A.R. Energetics of protein-protein interactions: Analysis of the Barnase-barstar interface by single mutations and double mutant cycles. J. Mol. Biol. 1995, 248, 478–486. [Google Scholar] [CrossRef]
- Ibarra-Molero, B.; Zitzewitz, J.A.; Matthews, C.R. Salt-bridges can stabilize but do not accelerate the folding of the homodimeric coiled-coil peptide GCN4-p1. J. Mol. Biol. 2004, 336, 989–996. [Google Scholar] [CrossRef]
- Jemth, P.; Gianni, S. PDZ domains: Folding and binding. Biochemistry 2007, 46, 8701–8708. [Google Scholar] [CrossRef]
- Gianni, S.; Haq, S.R.; Montemiglio, L.C.; Jürgens, M.C.; Engström, Å.; Chi, C.N.; Brunori, M.; Jemth, P. Sequence-specific long range networks in PSD-95/Discs Large/ZO-1 (PDZ) domains tune their binding selectivity. J. Biol. Chem. 2011, 286, 27167–27175. [Google Scholar] [CrossRef]
- Hultqvist, G.; Haq, S.R.; Punekar, A.S.; Chi, C.N.; Engström, Å.; Bach, A.; Strømgaard, K.; Selmer, M.; Gianni, S.; Jemth, P. Energetic pathway sampling in a protein interaction domain. Structure 2013, 21, 1193–1202. [Google Scholar] [CrossRef]
- Eildal, J.N.N.; Hultqvist, G.; Balle, T.; Stuhr-Hansen, N.; Padrah, S.; Gianni, S.; Strømgaard, K.; Jemth, P. Probing the role of backbone hydrogen bonds in protein-peptide interactions by amide-to-ester mutations. J. Am. Chem. Soc. 2013, 135, 12998–13007. [Google Scholar] [CrossRef] [PubMed]
- Malagrinò, F.; Troilo, F.; Bonetti, D.; Toto, A.; Gianni, S. Mapping the allosteric network within a SH3 domain. Sci. Rep. 2019, 9, 8279. [Google Scholar] [CrossRef] [PubMed]
- Laursen, L.; Kliche, J.; Gianni, S.; Jemth, P. Supertertiary protein structure affects an allosteric network. Proc. Natl. Acad. Sci. USA 2020, 117, 24294–24304. [Google Scholar] [CrossRef] [PubMed]
- Horovitz, A.; Bochkareva, E.S.; Yifrach, O.; Girshovich, A.S. Prediction of an inter-residue interaction in the chaperonin groel from multiple sequence alignment is confirmed by double-mutant cycle analysis. J. Mol. Biol. 1994, 238, 133–138. [Google Scholar] [CrossRef]
- Lockless, S.W.; Ranganathan, R. Evolutionarily conserved pathways of energetic connectivity in protein families. Science 1999, 286, 295–299. [Google Scholar] [CrossRef] [PubMed]
- Chi, C.N.; Elfstrom, L.; Shi, Y.; Snall, T.; Engstrom, A.; Jemth, P. Reassessing a sparse energetic network within a single protein domain. Proc. Natl. Acad. Sci. USA 2008, 105, 4679–4684. [Google Scholar] [CrossRef]
- Fodor, A.A.; Aldrich, R.W. On evolutionary conservation of thermodynamic coupling in proteins. J. Biol. Chem. 2004, 279, 19046–19050. [Google Scholar] [CrossRef] [PubMed]
- Gautier, C.; Troilo, F.; Cordier, F.; Malagrinò, F.; Toto, A.; Visconti, L.; Zhu, Y.; Brunori, M.; Wolff, N.; Gianni, S. Hidden kinetic traps in multidomain folding highlight the presence of a misfolded but functionally competent intermediate. Proc. Natl. Acad. Sci. USA 2020, 117, 19963–19969. [Google Scholar] [CrossRef]
- Sokolovski, M.; Cveticanin, J.; Hayoun, D.; Korobko, I.; Sharon, M.; Horovitz, A. Measuring inter-protein pairwise interaction energies from a single native mass spectrum by double-mutant cycle analysis. Nat. Commun. 2017, 8, 212. [Google Scholar] [CrossRef]
- Chandler, S.A.; Benesch, J.L. Mass spectrometry beyond the native state. Curr. Opin. Chem. Biol. 2018, 42, 130–137. [Google Scholar] [CrossRef]
- Mehmood, S.; Allison, T.M.; Robinson, C.V. Mass spectrometry of protein complexes: From origins to applications. Annu. Rev. Phys. Chem. 2015, 66, 453–474. [Google Scholar] [CrossRef] [PubMed]
- Lössl, P.; van de Waterbeemd, M.; Heck, A.J. The diverse and expanding role of mass spectrometry in structural and molecular biology. EMBO Rep. 2016, 35, 2634–2657. [Google Scholar] [CrossRef] [PubMed]
- Sharon, M.; Horovitz, A. Probing allosteric mechanisms using native mass spectrometry. Curr. Opin. Struct. Biol. 2015, 34, 7–16. [Google Scholar] [CrossRef]
- Cveticanin, J.; Netzer, R.; Arkind, G.; Fleishman, S.J.; Horovitz, A.; Sharon, M. Estimating interprotein pairwise interaction energies in cell lysates from a single native mass spectrum. Anal. Chem. 2018, 90, 10090–10094. [Google Scholar] [CrossRef] [PubMed]
- Cveticanin, J.; Mondal, T.; Meiering, E.M.; Sharon, M.; Horovitz, A. Insight into the autosomal-dominant inheritance pattern of SOD1-associated ALS from native mass spectrometry. J. Mol. Biol. 2020, 432, 5995–6002. [Google Scholar] [CrossRef] [PubMed]
- Chiti, F.; Dobson, C.M. Protein misfolding, amyloid formation, and human disease: A summary of progress over the last decade. Annu. Rev. Biochem. 2017, 86, 27–68. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pagano, L.; Toto, A.; Malagrinò, F.; Visconti, L.; Jemth, P.; Gianni, S. Double Mutant Cycles as a Tool to Address Folding, Binding, and Allostery. Int. J. Mol. Sci. 2021, 22, 828. https://doi.org/10.3390/ijms22020828
Pagano L, Toto A, Malagrinò F, Visconti L, Jemth P, Gianni S. Double Mutant Cycles as a Tool to Address Folding, Binding, and Allostery. International Journal of Molecular Sciences. 2021; 22(2):828. https://doi.org/10.3390/ijms22020828
Chicago/Turabian StylePagano, Livia, Angelo Toto, Francesca Malagrinò, Lorenzo Visconti, Per Jemth, and Stefano Gianni. 2021. "Double Mutant Cycles as a Tool to Address Folding, Binding, and Allostery" International Journal of Molecular Sciences 22, no. 2: 828. https://doi.org/10.3390/ijms22020828
APA StylePagano, L., Toto, A., Malagrinò, F., Visconti, L., Jemth, P., & Gianni, S. (2021). Double Mutant Cycles as a Tool to Address Folding, Binding, and Allostery. International Journal of Molecular Sciences, 22(2), 828. https://doi.org/10.3390/ijms22020828






