Time-Dependent Unitary Transformation Method in the Strong-Field-Ionization Regime with the Kramers-Henneberger Picture
Abstract
:1. Introduction
2. Numerical Method
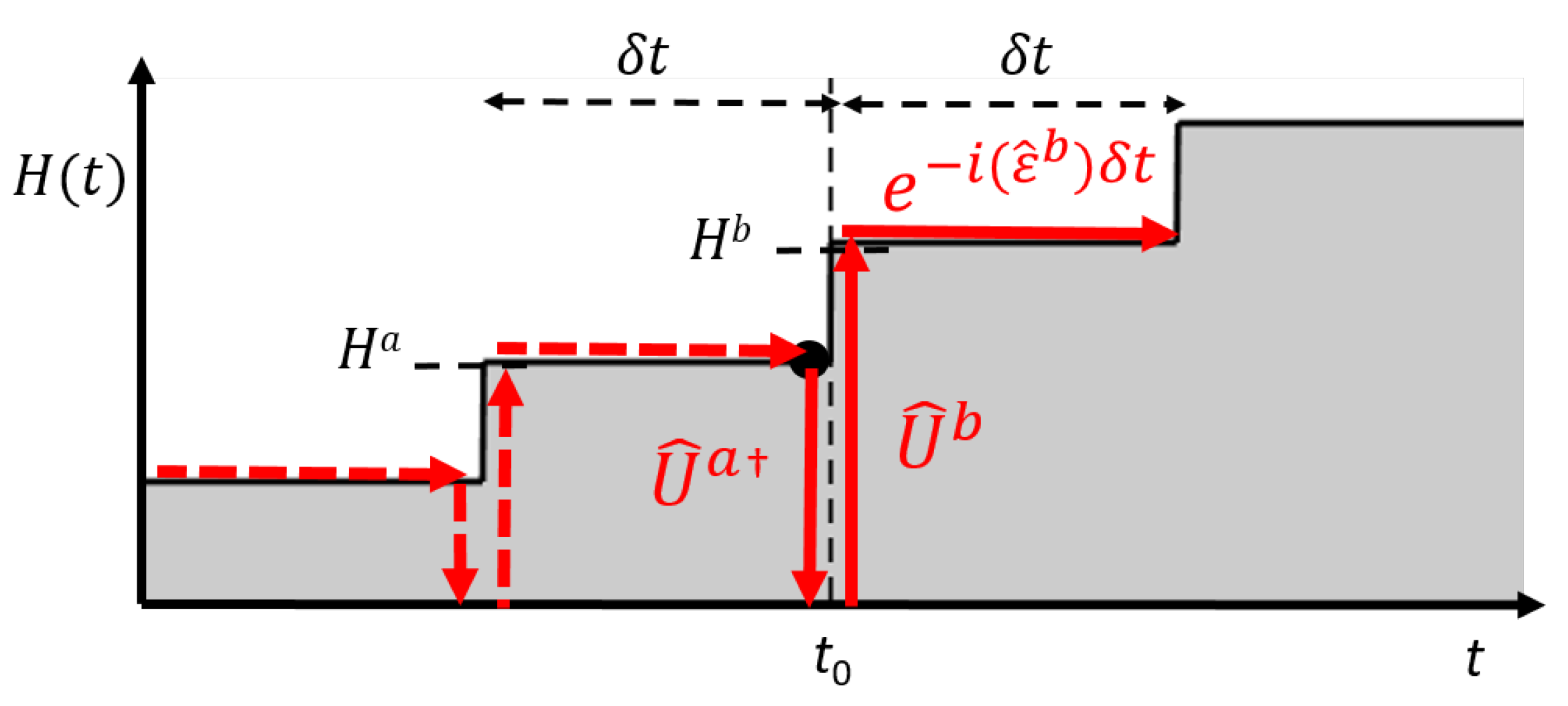
2.1. Time-Dependent Unitary Transformation Method (TDUT) in Discretized Systems
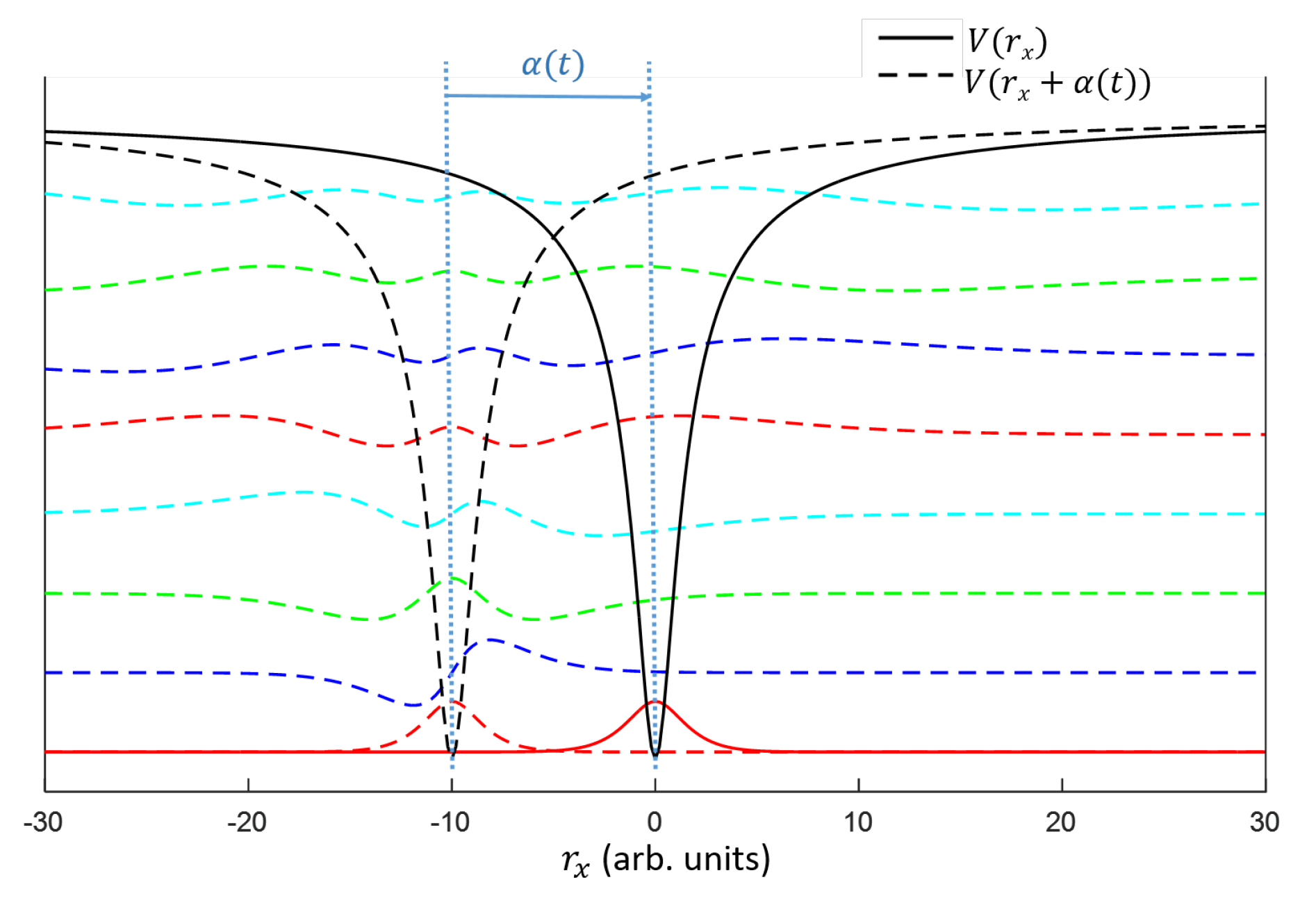
2.2. TDUT in the Strong-Field Ionization Regime
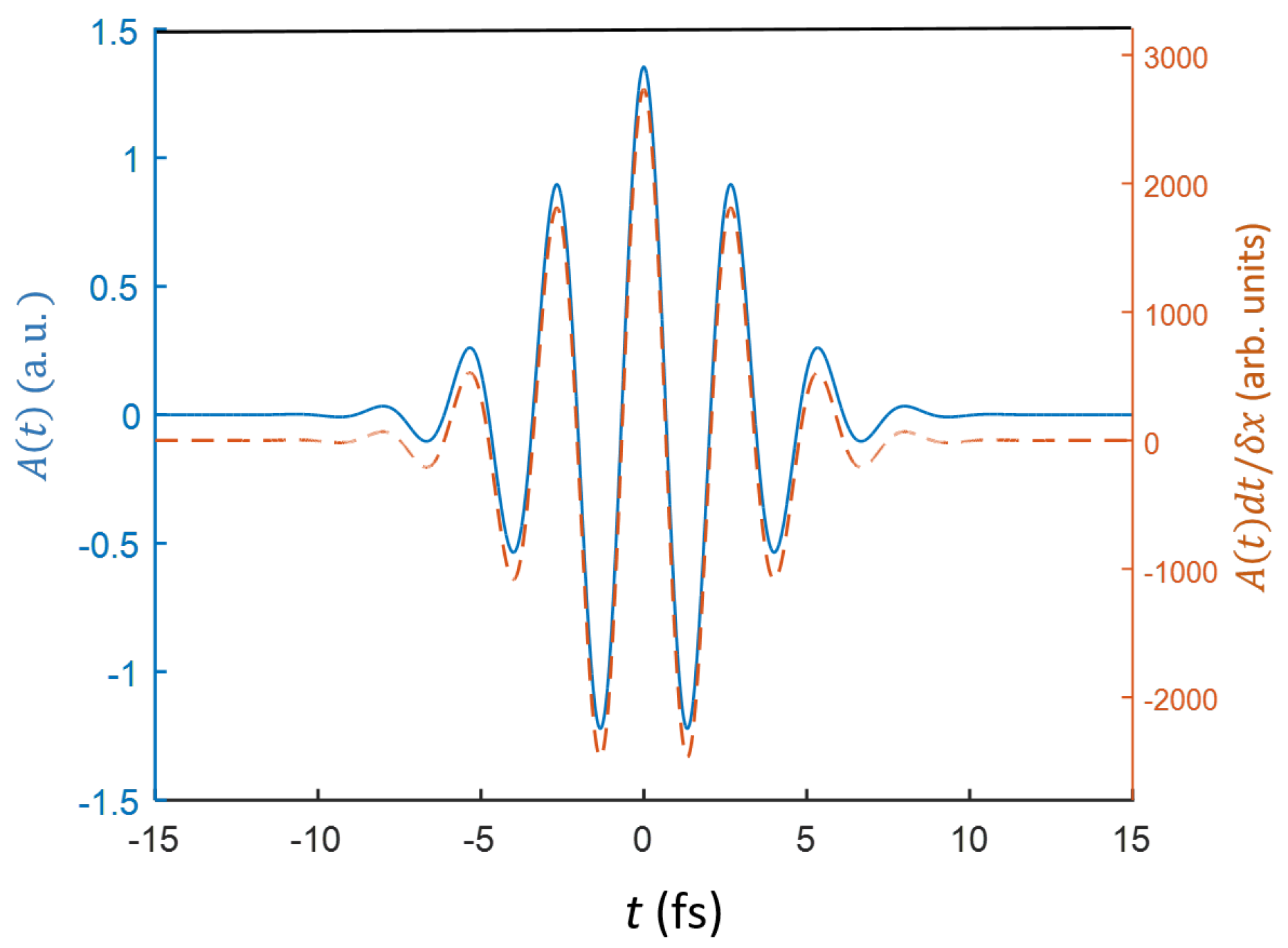
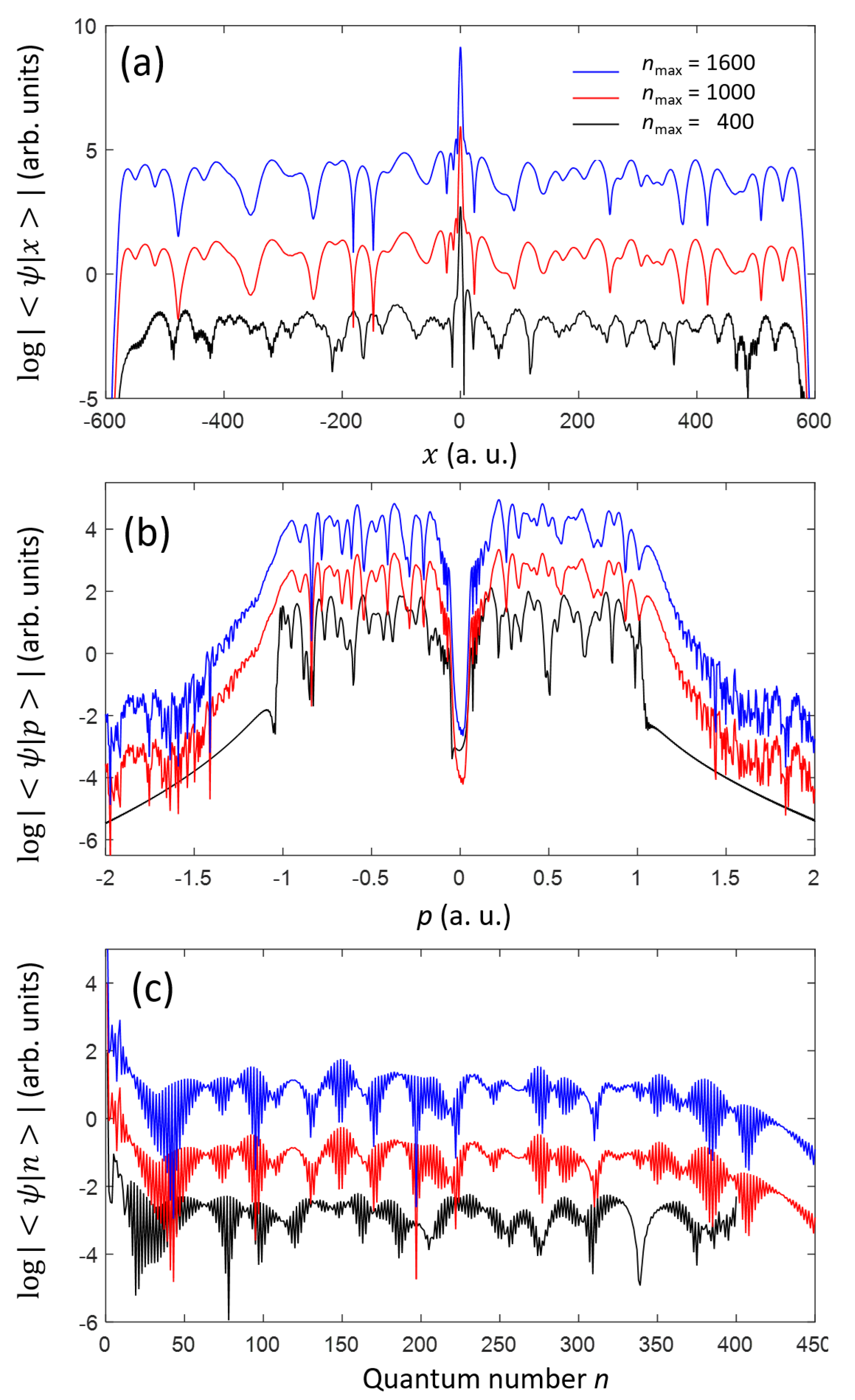
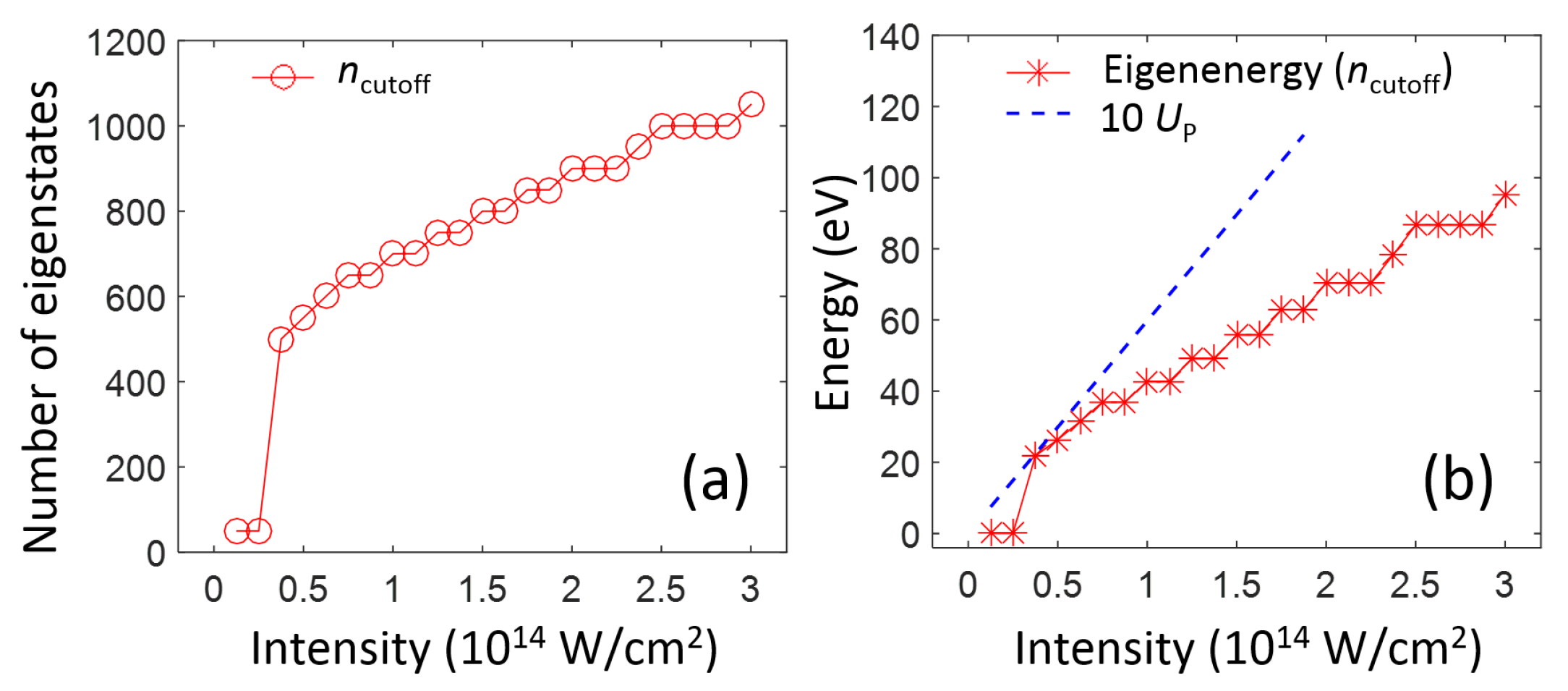
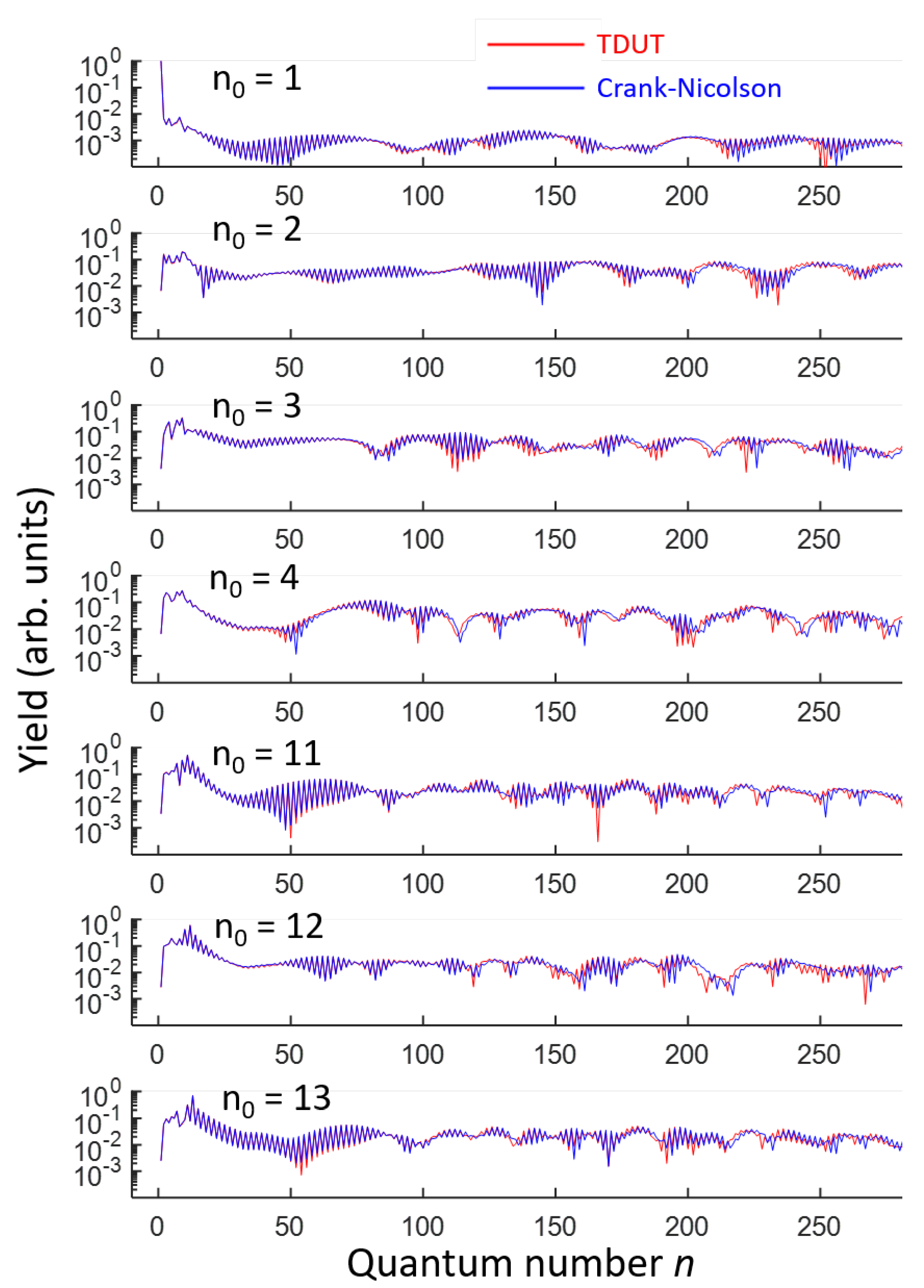
3. Results of the Simulation
4. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TISE | Time-independent Schrödinger equation |
| TDSE | Time-dependent Schrödinger equation |
| KH | Kramers-Henneberger |
| SFA | Strong-field approximation |
| FTI | Frustrated tunneling ionization |
| ATI | Above-threshold ionization |
| HHG | High-harmonic generation |
| TDUT | Time-dependent unitary transformation |
| FWHM | Full width at half maximum |
References
- Popruzhenko, S.V. Keldysh Theory of Strong Field Ionization: History, Applications, Difficulties and Perspectives. J. Phys. B At. Mol. Opt. Phys. 2014, 47, 204001. [Google Scholar] [CrossRef]
- Amini, K.; Biegert, J.; Calegari, F.; Chacón, A.; Ciappina, M.F.; Dauphin, A.; Efimov, D.K.; Faria, C.F.d.M.; Giergiel, K.; Gniewek, P.; et al. Symphony on Strong Field Approximation. Rep. Prog. Phys. 2019, 82, 116001. [Google Scholar] [CrossRef] [Green Version]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of High-Harmonic Generation by Low-Frequency Laser Fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef]
- Corkum, P.B. Plasma Perspective on Strong Field Multiphoton Ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [Green Version]
- Krause, J.L.; Schafer, K.J.; Kulander, K.C. High-Order Harmonic Generation from Atoms and Ions in the High Intensity Regime. Phys. Rev. Lett. 1992, 68, 3535–3538. [Google Scholar] [CrossRef] [Green Version]
- Macklin, J.J.; Kmetec, J.D.; Gordon, C.L. High-Order Harmonic Generation Using Intense Femtosecond Pulses. Phys. Rev. Lett. 1993, 70, 766–769. [Google Scholar] [CrossRef]
- Suárez, N.; Chacón, A.; Ciappina, M.F.; Biegert, J.; Lewenstein, M. Above-Threshold Ionization and Photoelectron Spectra in Atomic Systems Driven by Strong Laser Fields. Phys. Rev. A 2015, 92, 063421. [Google Scholar] [CrossRef] [Green Version]
- Mohideen, U.; Sher, M.H.; Tom, H.W.K.; Aumiller, G.D.; Wood, O.R.; Freeman, R.R.; Boker, J.; Bucksbaum, P.H. High Intensity Above-Threshold Ionization of He. Phys. Rev. Lett. 1993, 71, 509–512. [Google Scholar] [CrossRef]
- Nubbemeyer, T.; Gorling, K.; Saenz, A.; Eichmann, U.; Sandner, W. Strong-Field Tunneling without Ionization. Phys. Rev. Lett. 2008, 101, 233001. [Google Scholar] [CrossRef]
- Eichmann, U.; Nubbemeyer, T.; Rottke, H.; Sandner, W. Acceleration of Neutral Atoms in Strong Short-Pulse Laser Fields. Nature 2009, 461, 1261–1264. [Google Scholar] [CrossRef]
- Xiong, W.H.; Xiao, X.R.; Peng, L.Y.; Gong, Q. Correspondence of Below-Threshold High-Order-Harmonic Generation and Frustrated Tunneling Ionization. Phys. Rev. A 2016, 94, 013417. [Google Scholar] [CrossRef]
- Popruzhenko, S.V. Quantum Theory of Strong-Field Frustrated Tunneling. J. Phys. B At. Mol. Opt. Phys. 2017, 51, 014002. [Google Scholar] [CrossRef]
- Popruzhenko, S.V.; Lomonosova, T.A. Frustrated Ionization of Atoms in the Multiphoton Regime. Laser Phys. Lett. 2020, 18, 015301. [Google Scholar] [CrossRef]
- Cao, C.; Li, M.; Liang, J.; Guo, K.; Zhou, Y.; Lu, P. Frustrated Tunneling Ionization in Strong Circularly Polarized Two-Color Laser Fields. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 035601. [Google Scholar] [CrossRef]
- Mun, J.H.; Ivanov, I.A.; Yun, H.; Kim, K.T. Strong-Field-Approximation Model for Coherent Extreme-Ultraviolet Emission Generated through Frustrated Tunneling Ionization. Phys. Rev. A 2018, 98, 063429. [Google Scholar] [CrossRef]
- Yun, H.; Mun, J.H.; Hwang, S.I.; Park, S.B.; Ivanov, I.A.; Nam, C.H.; Kim, K.T. Coherent Extreme-Ultraviolet Emission Generated through Frustrated Tunnelling Ionization. Nat. Photonics 2018, 12, 620–624. [Google Scholar] [CrossRef]
- Strelkov, V. Role of Autoionizing State in Resonant High-Order Harmonic Generation and Attosecond Pulse Production. Phys. Rev. Lett. 2010, 104, 123901. [Google Scholar] [CrossRef]
- Chini, M.; Wang, X.; Cheng, Y.; Wang, H.; Wu, Y.; Cunningham, E.; Li, P.C.; Heslar, J.; Telnov, D.A.; Chu, S.I.; et al. Coherent Phase-Matched VUV Generation by Field-Controlled Bound States. Nat. Photonics 2014, 8, 437–441. [Google Scholar] [CrossRef]
- Li, P.C.; Sheu, Y.L.; Laughlin, C.; Chu, S.I. Role of Laser-Driven Electron-Multirescattering in Resonance-Enhanced below-Threshold Harmonic Generation in He Atoms. Phys. Rev. A 2014, 90, 041401. [Google Scholar] [CrossRef] [Green Version]
- Camp, S.; Schafer, K.J.; Gaarde, M.B. Interplay between Resonant Enhancement and Quantum Path Dynamics in Harmonic Generation in Helium. Phys. Rev. A 2015, 92, 013404. [Google Scholar] [CrossRef] [Green Version]
- Beaulieu, S.; Camp, S.; Descamps, D.; Comby, A.; Wanie, V.; Petit, S.; Légaré, F.; Schafer, K.J.; Gaarde, M.B.; Catoire, F.; et al. Role of Excited States In High-Order Harmonic Generation. Phys. Rev. Lett. 2016, 117, 203001. [Google Scholar] [CrossRef] [Green Version]
- Karamatskou, A.; Pabst, S.; Santra, R. Adiabaticity and Diabaticity in Strong-Field Ionization. Phys. Rev. A 2013, 87, 043422. [Google Scholar] [CrossRef] [Green Version]
- Saalmann, U.; Giri, S.K.; Rost, J.M. Adiabatic Passage to the Continuum: Controlling Ionization with Chirped Laser Pulses. Phys. Rev. Lett. 2018, 121, 153203. [Google Scholar] [CrossRef] [Green Version]
- Rubbmark, J.R.; Kash, M.M.; Littman, M.G.; Kleppner, D. Dynamical Effects at Avoided Level Crossings: A Study of the Landau-Zener Effect Using Rydberg Atoms. Phys. Rev. A 1981, 23, 3107–3117. [Google Scholar] [CrossRef]
- Clark, W.; Greene, C.H. Adventures of a Rydberg Electron in an Anisotropic World. Rev. Mod. Phys. 1999, 71, 821–833. [Google Scholar] [CrossRef]
- von Stecher, J.; Greene, C.H. Spectrum and Dynamics of the BCS-BEC Crossover from a Few-Body Perspective. Phys. Rev. Lett. 2007, 99, 090402. [Google Scholar] [CrossRef] [Green Version]
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-Body Physics with Ultracold Gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef] [Green Version]
- Dürr, S.; Volz, T.; Marte, A.; Rempe, G. Observation of Molecules Produced from a Bose-Einstein Condensate. Phys. Rev. Lett. 2004, 92, 020406. [Google Scholar] [CrossRef] [Green Version]
- Mun, J.H.; Sakai, H. Improving Molecular Orientation by Optimizing Relative Delay and Intensities of Two-Color Laser Pulses. Phys. Rev. A 2018, 98, 013404. [Google Scholar] [CrossRef]
- Mun, J.H.; Sakai, H.; González-Férez, R. Orientation of Linear Molecules in Two-Color Laser Fields with Perpendicularly Crossed Polarizations. Phys. Rev. A 2019, 99, 053424. [Google Scholar] [CrossRef]
- Mun, J.H.; Kim, D.E. Field-Free Molecular Orientation by Delay- and Polarization-Optimized Two Fs Pulses. Sci. Rep. 2020, 10, 18875. [Google Scholar] [CrossRef] [PubMed]
- Henneberger, W.C. Perturbation Method for Atoms in Intense Light Beams. Phys. Rev. Lett. 1968, 21, 838–841. [Google Scholar] [CrossRef]
- Chen, R.; Guo, H. The Chebyshev Propagator for Quantum Systems. Comput. Phys. Commun. 1999, 119, 19–31. [Google Scholar] [CrossRef]
- Guiang, C.S.; Wyatt, R.E. Quantum dynamics with Lanczos subspace propagation: Application to a laser-driven molecular system. Int. J. Quantum Chem. 1998, 67, 273–285. [Google Scholar] [CrossRef]
- Bandrauk, A.D.; Shen, H. Exponential Split Operator Methods for Solving Coupled Time-dependent Schrödinger Equations. J. Chem. Phys. 1993, 99, 1185–1193. [Google Scholar] [CrossRef]
- Parzyński, R.; Wieczorek, S. Interference Stabilization of Rydberg Atoms Enhanced by Multiple V-Type Resonances. Phys. Rev. A 1998, 58, 3051–3057. [Google Scholar] [CrossRef] [Green Version]
- Scrinzi, A.; Elander, N.; Piraux, B. Stabilization of Rydberg Atoms in Superintense Laser Fields. Phys. Rev. A 1993, 48, R2527–R2530. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mun, J.-H.; Sakai, H.; Kim, D.-E. Time-Dependent Unitary Transformation Method in the Strong-Field-Ionization Regime with the Kramers-Henneberger Picture. Int. J. Mol. Sci. 2021, 22, 8514. https://doi.org/10.3390/ijms22168514
Mun J-H, Sakai H, Kim D-E. Time-Dependent Unitary Transformation Method in the Strong-Field-Ionization Regime with the Kramers-Henneberger Picture. International Journal of Molecular Sciences. 2021; 22(16):8514. https://doi.org/10.3390/ijms22168514
Chicago/Turabian StyleMun, Je-Hoi, Hirofumi Sakai, and Dong-Eon Kim. 2021. "Time-Dependent Unitary Transformation Method in the Strong-Field-Ionization Regime with the Kramers-Henneberger Picture" International Journal of Molecular Sciences 22, no. 16: 8514. https://doi.org/10.3390/ijms22168514
APA StyleMun, J.-H., Sakai, H., & Kim, D.-E. (2021). Time-Dependent Unitary Transformation Method in the Strong-Field-Ionization Regime with the Kramers-Henneberger Picture. International Journal of Molecular Sciences, 22(16), 8514. https://doi.org/10.3390/ijms22168514





