Next Article in Journal
QSAR Implementation for HIC Retention Time Prediction of mAbs Using Fab Structure: A Comparison between Structural Representations
Previous Article in Journal
Cannabinoids Inhibited Pancreatic Cancer via P-21 Activated Kinase 1 Mediated Pathway
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 21
Issue 21
10.3390/ijms21218036
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Interaction between Trinuclear Regium Complexes of Pyrazolate and Anions, a Computational Study

by
Ibon Alkorta
1,*,
José Elguero
1,
Cristina Trujillo
2 and
Goar Sánchez-Sanz
3,4,*
1
Instituto de Química Médica, CSIC, Juan de la Cierva, 3, E-28006 Madrid, Spain
2
Trinity Biomedical Sciences Institute, School of Chemistry, Trinity Dublin College, D02 R590 Dublin 2, Ireland
3
Irish Centre of High-End Computing, Grand Canal Quay, Dublin 2, Ireland
4
School of Chemistry, University College Dublin, Belfield, D02 HP83 Dublin 4, Ireland
*
Authors to whom correspondence should be addressed.
Int. J. Mol. Sci. 2020, 21(21), 8036; https://doi.org/10.3390/ijms21218036
Submission received: 8 October 2020 / Revised: 22 October 2020 / Accepted: 23 October 2020 / Published: 28 October 2020
(This article belongs to the Section Physical Chemistry and Chemical Physics)
Browse Figures
Versions Notes

Abstract

:
The geometry, energy and electron density properties of the 1:1, 1:2 and 1:3 complexes between cyclic (Py-M)3 (M = Au, Ag and Cu) and halide ions (F−, Cl− and Br−) were studied using Møller Plesset (MP2) computational methods. Three different configurations were explored. In two of them, the anions interact with the metal atoms in planar and apical dispositions, while in the last configuration, the anions interact with the CH(4) group of the pyrazole. The energetic results for the 1:2 and 1:3 complexes are a combination of the specific strength of the interaction plus a repulsive component due to the charge:charge coulombic term. However, stable minima structures with dissociation barriers for the anions indicate that those complexes are stable and (Py-M)3 can hold up to three anions simultaneously. A search in the CSD confirmed the presence of (Pyrazole-Cu)3 systems with two anions interacting in apical disposition.

1. Introduction

In biochemistry, supramolecular chemistry, molecular recognition and materials science, non-covalent interactions are of utmost importance; examples of their importance are their role in protein shapes [1], protein–protein interactions [2], anion recognition [3,4], drug recognition [5,6] and absorption on surfaces [7]. The oldest and most important non-covalent interaction is the hydrogen bond [8,9,10,11,12] but other interactions associated with atoms of columns 17–14 of the periodic table were described in the literature [13] such as halogen [14], chalcogen [15,16], pnictogen [17,18] and tetrel bonds [19,20], respectively. They were rationalized based on positive regions of the electrostatic potential surrounding the atoms acting as Lewis acids, with these regions being known as σ-holes [21].
More recently, the possibility to find σ-hole regions within atoms of column 11 of the periodic table (the coinage metals Cu, Ag and Au) in organometallic molecules or small nanoclusters was described [22,23,24,25]. However, only a limited number of complexes between derivatives of coinage atoms acting as Lewis acids and electron donors were explored in the literature [26]. This interaction was named the regium bond or metal-coinage bond [27]. However, it is worth noting that gold is an inert metal in bulk but in small nanostructures or in organometallic clusters it becomes a powerful catalyst [28,29].
Focusing on complexes with gold derivatives, the structures of the OC⋯AuX (with X = F, Cl and Br) [30], H2S⋯AuI [31] and H2⋯AuCl [32] complexes were determined by microwave spectroscopy. Additionally, the interaction of iodoperfluorobenzene derivatives with gold nanoparticles was investigated by Obenchain et al. using different spectroscopic techniques [33]. Besides, the NMR properties of tri(3,5-bis-trifluoromethyl-1H-pyrazole-silver) were determined in solution and in the solid state and compared with GIAO and ZORA calculated chemical shifts [34].
From the theoretical perspective, several computational studies were carried out in order to characterize this new type of interaction, mainly focusing on Au derivatives. Some examples can be: B⋯AuX complexes, with B = OC, H2O, H2S, C2H2 and C2H4 and X = F, Cl and Br, which were studied using the density functional theory at the BP86 level [35]. Additionally, the complexes between acetylene and AuX (X = OH, F, Cl, Br, CH3, CCH, CN and NC) presenting a π regium bond were also characterized at the MP2 computational level [36]. In addition, the strength and characteristics of regium bonded complexes were compared with other non-covalent interactions, for instance with halogen bond complexes by means of MP2 and coupled cluster (CCSD(T)) computational methods [37]. Furthermore, using atoms in molecules (AIM) and natural bond orbital (NBO) methods, the nature of the complexes between H2O and H2S acting as the Lewis basis and AuCl as a Lewis acid was characterized [38], and the intermolecular interaction between phosphines (XH2P with X = H, CH3, F, CN and NO2) and MY molecules (M = Cu, Ag, Au and Y = F, Cl, Br and I) [39]. Cooperativity in ternary complexes involving the regium bond was also explored [40,41,42,43]. The properties of complexes of Au(I) and Au(III) were compared using the CCSD(T)/CBS computational level [44]. Additionally, the spectroscopy of Au(CN)3 anions was described [45].
Focusing on diatomic Au2 and Aun clusters; the spectroscopic properties of the Au2 complexes were calculated at the density functional theory (DFT) and coupled cluster levels [46,47]. Puru et al. studied the role of superatom model in gold clusters and nanoparticles [48]. Besides, the complexes of neutral and charged Au2 and Au with CO were examined at DFT (BP86, PW91 and B3LYP) and ab initio (MP2 and CCSD(T)) levels [49]. Non-conventional hydrogen bonds were established between small gold clusters (Au3–7) and formamide, formic acid, hydrogen fluoride and DNA bases [50,51,52]. In addition, the complexes between Aun clusters (n = 2–6) with NH3 and NCH were characterized at the MP2 level [25] and the competition between halogen and regium bonds in binary complexes between CF3X (X = Cl, Br) and Aun (n  =  2, 3 and 4) clusters was also explored [53]. In fact, the electrostatic properties of Aun clusters with n = 2, 13, 55 and 147 were compared with the interaction energy of the mentioned complexes with CO and H2O [22]. It is also worth noting that different clusters of Au and AuCl can form regium-π bonds with aromatic systems [23,24]. In a recent paper, we studied the problem of regium vs. hydrogen bonds in M2⋯HX complexes, with M = Au, Ag and Cu, in which we found that regium bonds are not only competitive but in most of the cases stronger that hydrogen bonds [54,55].
Triangular structures corresponding to nine-membered rings (three metal atoms and six atoms of the ligands) are well-known and they were reported in the literature (Figure 1, left hand side), for instance, imidazolates with coinage metals [56], phenylenes (most examples correspond to o-tetrafluorophenylene) with mercury [57,58] and 1,2-dicarba-closo-dodecaboranes with gold(I) [59,60]. Pyrazolate ligands (Py) with coinage metals, forming regium bonds, are also common, in any oxidation state: Cu(I)/Cu(II), Ag(I) and Au(I)/Au(III) [56,61,62,63,64,65,66]. Particularly, cyclic [Py-M(I)]3 systems with M = Cu, Ag and Au were studied [67] and the experimental evidences of the (Py-Cu)3 systems with simultaneous interactions of the three copper atoms with one hydroxyl group were recently reviewed [68]. So, these aforementioned systems present very interesting features, which make them good candidates for exhibiting regium bonds.
On a different topic, interaction between charged systems, i.e., anion–anion and cation–cation are very interesting, and were found both within the gas phase [69,70,71,72,73,74,75,76,77,78,79] and crystal structures [80,81]. This rare type of interaction, which, in principle should be repulsive, should lead to unstable complexes, i.e., they will revert into the separated ions. However, in the last decade, it was demonstrated that complexes exhibiting positive interaction energies are indeed minima and therefore stable structures [82,83]. Some examples can be found in the literature in which two charged conducting spheres can attract each other when they are in a close range distance [84]. The F⋯F interaction in negatively charged dimers was studied at MP2 level and using symmetry-adapted perturbation theory [85,86].
In the present work we will focus our efforts in the study of trinuclear regium pyrazolate systems interacting with one, two and three anions simultaneously to infer whether regium bonds or hydrogen bonds can be established and stabilize structures, which in principle should not be stable. We will investigate the interaction of (Pz-M)3, M = Cu, Ag and Au, with three anions (F−, Cl− and Br−) limiting to the lowest oxidation states (I) of the three coinage metals (Figure 2).

2. Results and Discussion

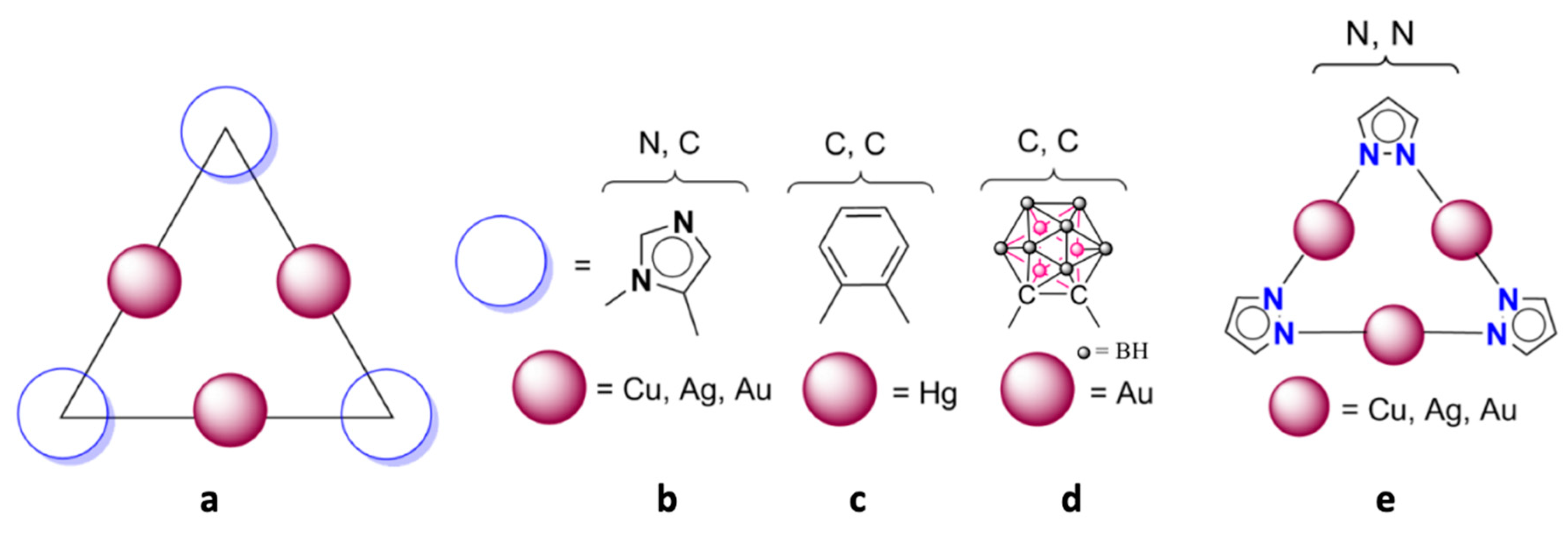
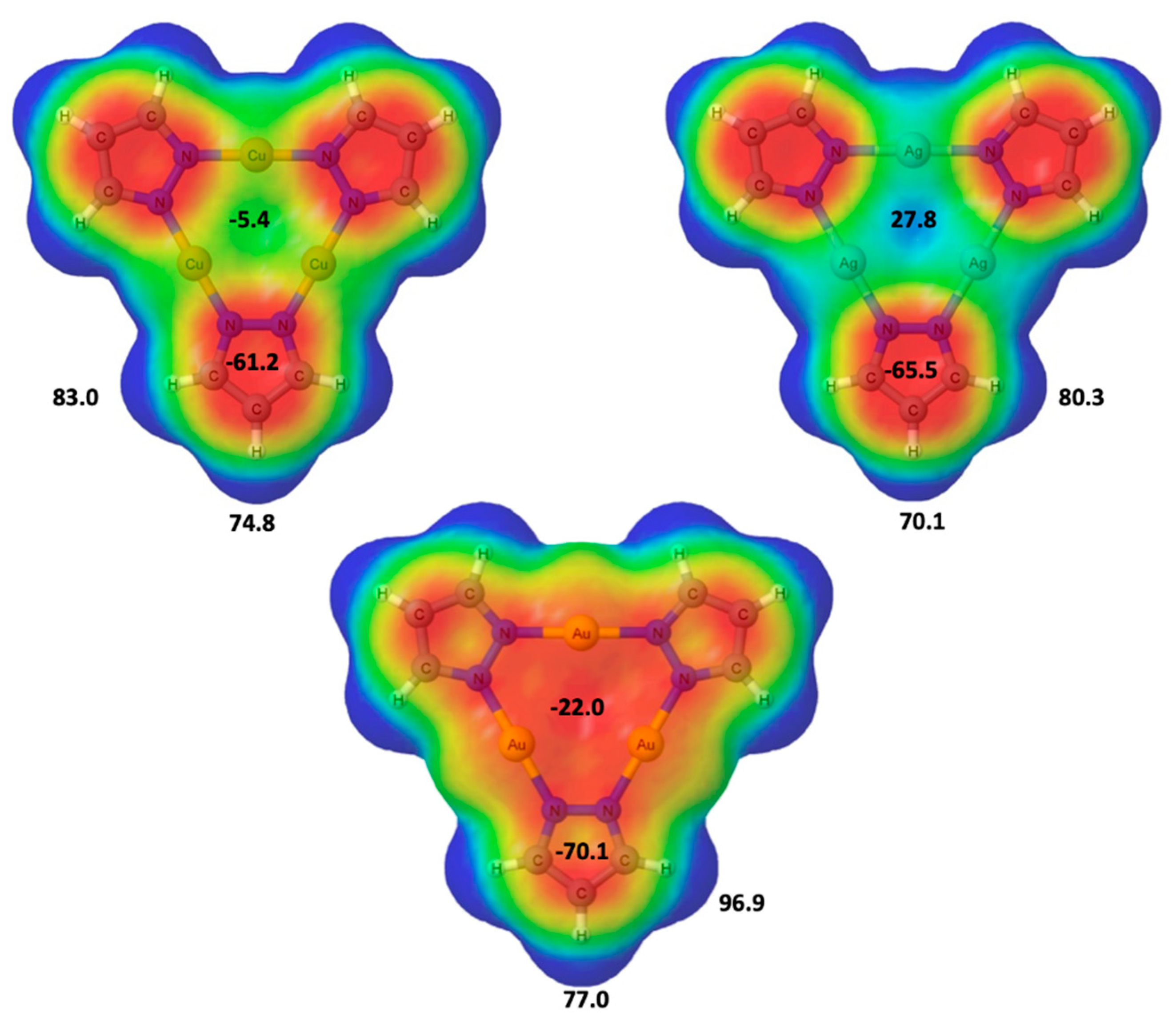
2.1. Isolated (Pz-M)3 Monomers

The isolated (Pz-M)3 compounds (M = Cu, Ag and Au) were optimized at the MP2/aug’-cc-pVDZ computational level. All three of them showed a D3h symmetry with each metal atom (M) located equidistantly between the two nitrogen atoms of the adjacent pyrazole rings. In fact, the calculated M-N distances are 1.817, 2.039 and 1.970, Å for the copper, silver and gold derivatives, respectively.
To evaluate the areas of possible electrophilic attack, the molecular electrostatic potential (MESP) was calculated and plotted on the 0.001 au electron density isosurface in Figure 3. MESP showed negative (red) regions above and below of the pyrazole rings while the positive (blue) regions were associated to the hydrogen atoms in the periphery. The values were associated with four stationary points one minimum (over the pyrazole ring) and three maxima: two corresponding to the C-H bonds and one over the center of the system (C3 axis), for each of the three systems were also indicated in Figure 3 by their corresponding value. It is interesting to notice the dependence of the MESP sign along the C3 axis with the metal considered. While for the Au derivative the maximum shows a negative value (−22 kJ/mol), it becomes positive for silver (+28 kJ/mol) and very small and negative for copper (−5 kJ/mol) derivatives. Regarding the maxima associated to the CH groups of the pyrazole, in all cases the CH(4) exhibits is less positive MESP values than the CH(3) one, being the values of the former between 70 and 77 kJ/mol and those for the latter between 97 and 80 kJ/mol.

2.2. 1:1 Complexes

We began by studying the complexes established between a (Pz-M)3 unit and a single halide anion. All the molecular graphs have been included in Tables S1–S3. Three different energetic minima were found for each coinage metal derivative (Figure 4): (a) 1:1 apical, where the anion is located along the C3 symmetry axes and interacting simultaneously with the three metal atoms, (b) 1:1 planar, where the anion is within the molecular plane and simultaneously interacting with a metal atom and two CH(3) groups and (c) 1:1 CH(4), in which the anion interacts directly with a single hydrogen atom from the CH(4) group.
The binding energies, Eb, obtained as the difference of the energy of the complex minus the energy of the isolated monomers, for the 1:1 complexes were gathered in Table 1 and plotted in Figure 5. All the binding energies are shown to be large and negative as expected for the interaction between an anion with a neutral molecule, ranging between −204 and −35 kJ mol−1. The most stable complex of each configuration highly depends on the metal atom and on the anion considered. For instance, 1:1 apical complexes were found to be the most stable for silver and copper derivatives, while for gold derivatives 1:1 planar complexes are the most stable. The only exception is the copper complex with F– where the planar complex is even more stable than the apical one. In all cases, the complexes showing only the interaction with the CH(4) group are the least stables ones.
Considering the same configuration, 1:1 apical and planar complexes, the most stable complex for a given anion corresponds to the silver derivative, followed by the copper and the gold derivative. The only exception corresponds to the 1:1 planar complexes with F− where the copper complex is more stable than the silver one and the trend is Au < Ag < Cu. Similar trends, involving the metal atom, were already described in the literature for M⋯O interactions [87] and ethylene coinage metal complexes [88]. For all of the different 1:1 CH(4) complexes, in order of the most to least stable derivative we found gold, followed by copper and lastly silver.
Concerning the geometrical parameters, the M⋯X− distances within the 1:1 apical and planar configurations were influenced by the size of the metal (Au >Ag > Cu) and the anion (F < Cl < Br) considered (Table 2). Focusing on configurations for the same metal and anion, in all the cases the M-X distance in the planar configuration was about 0.12 Å shorter than the apical one. This can be due to the fact that in the apical configuration, the anion was simultaneously interacting with three metals and thus the interaction was weakening (as observed for the binding energies) and therefore the M⋯X− distance became longer. In the case of planar configuration, the anion was interacting with only one metal, plus there was a geometrical constraint due to the interactions with the CH(3) groups. Regarding the CH(4) configurations, the H⋯X− distances found were shorter than those found for the CH(3)⋯X− ones. The dependence on H(3)⋯X distances for a given anion change with the metal atom shows the following trend: Ag > Au > Cu, while for the H(4)⋯X− it is Ag > Cu > Au.
No clear relationships between the binding energies and intermolecular distances were found for any of the complexes, except for the CH(4) complexes. This can highlight the complexity of the M⋯X− interaction. The lack of correlation between those quantities can be associated with the electronic repulsion between the anion and the rest of the atoms in the (Pz-M)3 system. Additionally, the number of simultaneous interactions acting in 1:1 apical and planar configurations can play a role deviating the correlation between Eb and M⋯X− distances.
Finally, the QTAIM analysis of the electron density (Figure 4 and Tables S1–S3) indicates the presence of three symmetrical bond paths in the apical configuration connecting the X− anion and the three metal atoms. In the planar configuration, another three bond paths were found too, but in this case only one of them connects the anion with the metal atom while the other two corresponded to CH(3)⋯X− interactions.
Regarding, CH(4) configuration only one bond path was found between the anion and the CH(4) group. The electron density values of the intermolecular bond critical points (BCP; Table S4) present positive values of the Laplacian and negative values of the total energy density for the anion–metal bonds in the apical and planar configurations as an indication of the partial covalent nature of the interaction [89,90].

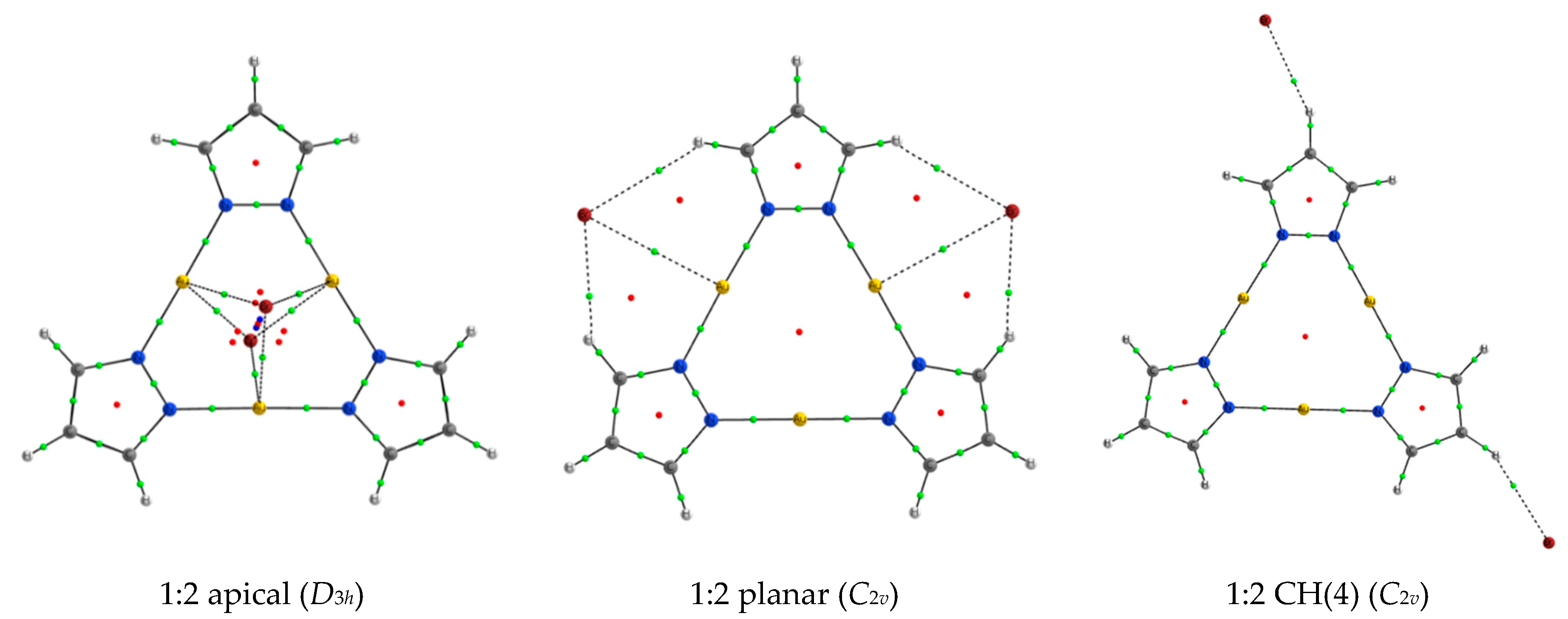
2.3. 1:2 Complexes

After analyzing the 1:1 complexes and their binding energies, the arising question was: can those negatively charged 1:1 complexes interact with another anion and produce stable structures? To address this question, three different 1:2 configurations were considered using the 1:1 complexes configurations as parental structures, i.e., 1:2 apical, 1:2 planar and 1:2 CH(4). There were a large number of possible combinations for the second anion to interact with the 1:1 complex, but for the sake of simplicity only two similar interactions will be explored simultaneously. In Figure 6 the structures corresponding to the 1:2 (Pz-M)3: Br2 complex were depicted as an illustrative example. In all the cases, the 1:2 apical complexes show D3h symmetry while the planar and CH(4) ones present C2v symmetry.
The binding energies for the 1:2 complexes (Table 3) varied from configuration to configuration ranging from +140 to −82 kJ mol−1. In the case of complexes with the largest halogen anions, Br− and Cl−, the binding energies are found to be positive indicating a repulsive force within the complex. Only one exception was found for those anions, the 1:2 planar complex with silver were the binding energies were negative (−24 and −26 kJ mol−1, respectively). In contrast, the complexes with F− present negative binding energies save for the 1:2 apical complexes with gold, which was positive (+113 kJ mol−1). As occurred for the 1:1 complexes, for each anion and configuration, the most stable complex corresponded to the silver one, except for the 1:2 planar and CH(4) configuration with F− where the 1:2 planar with copper and gold were a more stable complex.
However, the existence of a stable minimum with positive values of the binding energy resembles to those minima in complexes between molecules with the same charge (anion–anion or cation–cation). When an energy scan corresponding to the separation of one of the anions from the rest of the system (X−⋯Pz-M-X−) in the apical complexes is done, it is observed a maximum in the potential energy surface that prevents the spontaneous dissociation of the anion (Figure S1 and Table S5). This fact has been previously described for anion–anion and cation–cation complexes in the literature [69,82,83]. The largest barriers were found for the F− anion, reaching up to 96 kJ mol−1 for the 1:2 (Pz-Cu)3:F2. In contrast, the dissociation barriers for the 1:2 (Pz-Au)3:Cl2. and 1:2 (Pz-Au)3:Br2 were found to be small, 9 and 7 kJ mol−1, respectively.
The energetic differences within the 1:2 complexes were clearly influenced by the electronic repulsion between the two X− anions, which was essentially related to their X⋯X interatomic distance (Table S6). The shortest interatomic distances in the anions were found in the 1:2 apical complexes (between 2.7 and 5.5 Å), followed by the 1:2 planar complexes (between 7.4 and 12.2 Å) being the longest distances in the 1:2 CH(4) ones (between 13.2 and 16.0 Å), this means that the repulsive interaction between anions within the 1:2 apical configuration will be larger than those in the planar and CH(4) configuration. This is clearly observed in the binding energies for apical and planar configurations. However, when CH(4) complexes were taken into account, they did not follow the trend. This can be explained in terms of the type of interaction involved, since the binding energy depended both on the type/strength of the interaction involved plus the electronic repulsion between the anions. It is clear that while in the CH(4) the repulsion between the anions would be very small, the interaction C-H⋯X was also very weak.
One way to analyze the repulsion, or in other words, to narrow down the binding energy contribution of the anion–anion repulsion is to correct the binding energy by subtracting the charge–charge repulsion using the location of the anions with a charge of -1e [82]. As observed for the value in Table S7, corrected binding energies were in all the cases negative, which was aligned with the existence of those minima. However, in planar and CH(4) configurations, these values were smaller, in the absolute value, than twice of those for the 1:1 complexes, as expected for two identical charge transfer interactions over a neutral molecule. In contrast, in most of the 1:2 apical complexes the corrected energy was larger (in absolute value) than twice the 1:1 complexes binding energies, highlighting the importance of the charge transfer and polarization in these complexes.
Regarding the interatomic M⋯X and H⋯X distances (Table 4) in the 1:2 complexes, those were found to be slightly longer than the ones found for 1:1 complexes. This was consistent with the fact that the anions tend to separate from each other (due to Coulombic repulsion) while maintaining the same interaction patterns shown in the 1:1 complexes. The only exception corresponded to the planar 1:2(Pz-Au)3:F2 where each anion exclusively interacted with one of the H(3) atoms as shown in its molecular graph (Table S1).
Regarding the QTAIM analysis, the electron density properties (Table S8) show similar bond paths between the anions and the (Pz-M)3 systems in 1:2 complexes than those found for 1:1 complexes, with the aforementioned exception of the planar 1:2(Pz-Au)3:F2 complex. Another interesting feature of the QTAIM analysis in 1:2(Pz-Au)3:F2 complex was the presence of a bond path linking the two F− anions.
As it is clear from the discussed result, the (Pz-Au)3 was capable of forming stable complexes with two anions simultaneously, but what is the limit of those complexes? Can 1:2(Pz-M)3:X2 form stable complexes with a third anion?

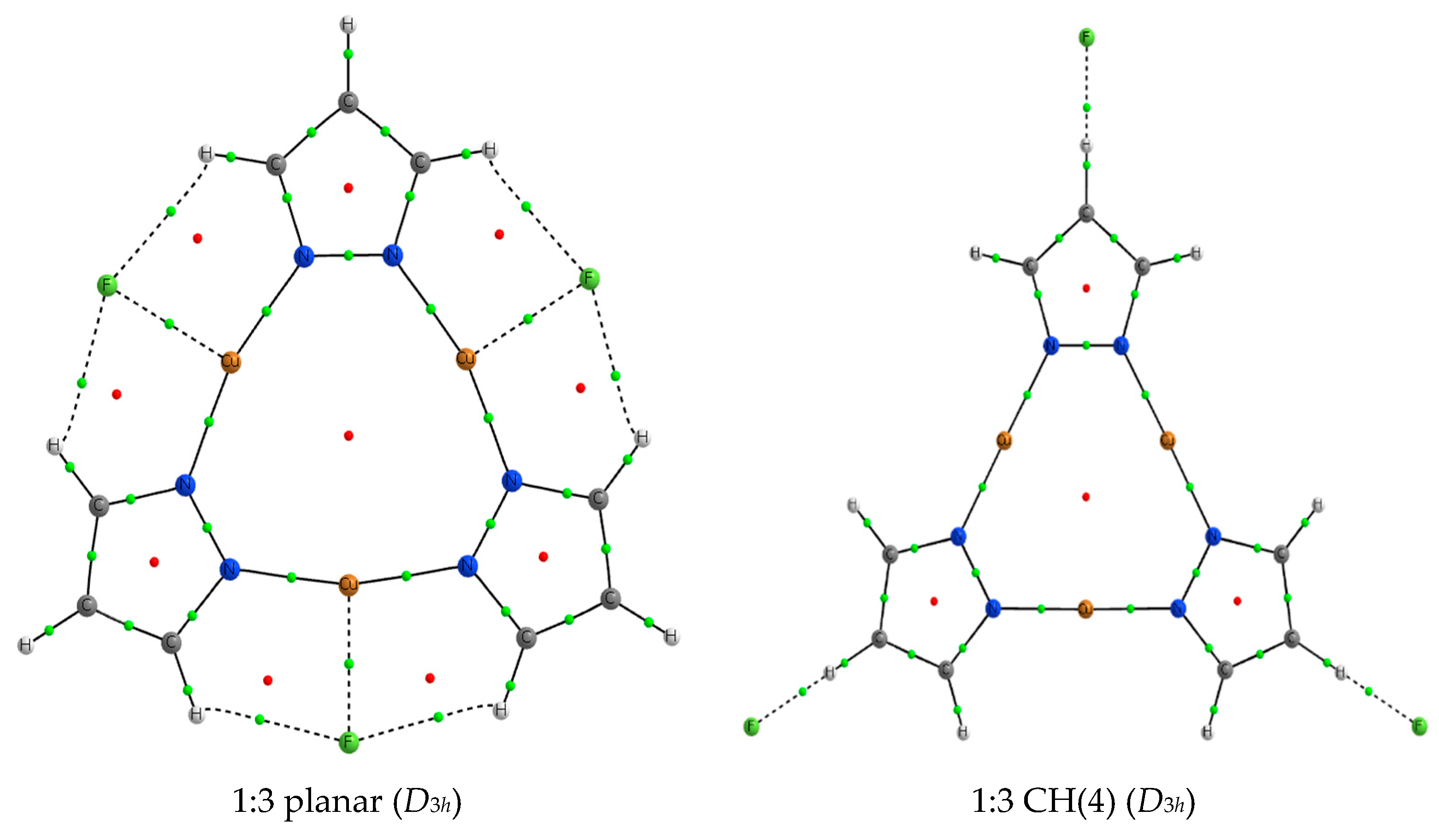
2.4. 1:3 Complexes

Following the same premises as that of 1:2 complexes, 1:3 complexes for the planar and CH(4) configuration were explored. Energetic minima structures were found for all the 1:3 CH(4) complexes and also for four of the nine 1:3 planar complexes. However, for the rest of the possible complexes, the anions dissociated spontaneously from the (Pz-M)3 molecule. In those stable cases, all the systems present D3h symmetry. Two illustrative examples are shown in Figure 7.
The binding energies for the 1:3 complexes are gathered in Table 5. As occurred for 1:2 complexes, 1:3 complexes exhibit positive binding energies ranging between 160 and 260 kJ mol−1, much larger than those for the 1:2 complexes, although the structures found are still minima in the potential energy surface. Binding energies suggest that CH(4) configurations were more stable than the corresponding planar ones, while the other way around happened for the 1:2 complexes. In fact, in the latter, the shorter X−⋯X− distances (Table S9) in the planar configuration (between 7.5 and 9.4 Å) penalize the binding energy versus those in CH(4) configuration where the anions were further away (between 13.2 and 15.6 Å). As for the 1:2 cases, removing the X−⋯X− electrostatic repulsion term (Table S10) provided with a better picture of the binding energies. Corrected Eb values were negative but smaller than three times the binding energies found for the 1:1 complexes indicating a certain degree of anti-cooperativity in the 1:3 complexes.
Regarding the intermolecular M⋯X and H⋯X distances, selected geometrical parameters of the 1:3 minima are listed in Table 6. The comparison of these parameters with the corresponding in the 1:1 and 1:2 complexes ( Table 1; Table 3), indicates that within the (Pz-Ag)3X− planar configuration there was a lengthening in the M⋯X− distance from 1:3 vs. the 1:2 (∆RM⋯X = 0.084, 0.291 and 0.389 Å for F−, Cl− and Br− respectively), which was larger than the difference between 1:2 and 1:1(Pz-Ag)3X− complexes (0.071, 0.111 and 0.127 Å). This is an indication of a larger anti-cooperativity effect in the former than in the later complexes. Additionally, these effects were more acute for heavier halogens than for lighter ones. In case of CH(4) configuration, a similar pattern was found but the increment was milder across the halogen series. Curiously, the metal M also has influence on the H⋯X− along the 1:1, 1:2 and 1:3 series for the CH(4) configuration, with a much larger increase for the (Pz-Cu)3X− > (Pz-Ag)3X− > (Pz-Au)3X−.
The molecular graph of the 1:3 planar complexes show three BCP between each anion and the (Pz-M)3 system, two of them with the CH(3) and one with the metal. In the case of the CH complexes a single bond path per anion was found. The BCPs (Table S11) exhibited similar electron density characteristics to those found for the 1:1 and 1:2 complexes.
A general analysis of all the BCPs extracted from this article shows excellent correlations between the electron density and the interatomic distance for each pair of atoms involved in the interactions (Figure S2). These results were in agreement with previous reports that have shown similar relationships [91,92,93].

2.5. CSD Search

A search in the CSD looking for (Pz-M)3 interacting with halides was carried out to investigate the number of crystals structures available. The search shows a total of thirteen crystal structures with the presence of halogen atoms in apical disposition interacting with copper (II) atoms linking the pyrazole rings. Of those structures, only one exhibited fluoride anions (CCDC refcode HUXWUU [94]), chloride is present in 10 crystal structures (JALKIT [95], OBOQAY [96], OBOQEC [96], OBOQIG [96], RETQIR [97], RUYGUN [98], RUYHAU [98], UWOMAW [99], VADYAB [100] and VAZCUX [101]) and bromide in two (ELODIS [102] and ELODOY [102]). It was observed that, in all these cases, two of the anions were simultaneously interacting with a single (Pz-M)3 molecule in the apical position as shown in Figure 8.
Ten of these structures (OBOQAY, OBOQEC, OBOQIG, RETQIR, RUYGUN, RUYHAU, UWOMAW, VAZCUX, ELODIS and ELODOY) present an additional halogen atom interacting with each copper atoms in planar configuration (see Figure 8 for two examples). The charge of the systems was compensated by the presence of bulky cations in the crystal (1-butyl-3-methyl-1H-imidazol-3-ium in VAZCUX and tetra-n-butylammonium in the rest).
The discrepancies between the interaction energies found for the 1:2 complexes in which planar complexes exhibited more negative interaction energies than apical ones could be due to the presence of counterions in the crystal structures that compensate the charge of the systems and the the repulsion of the anions that are absent in the gas phase calculations and due to crystal packing constraints.
The metal–halogen intermolecular distances were gathered in Table S12. As observed, those distances ranged between 2.38 and 2.61 (Cu-F), 2.34 and 3.06 (Cu-Cl) and 2.50 and 3.06 Å (Cu-Br), being the average distances 2.51, 2.61 and 2.72 Å for the Cu-F, Cu-Cl and Cu-Br interactions, respectively. In the case of Cu-F, the computational distance (2.11 Å) was shorter than the crystal one, while for the Cu-Cl and Cu-Br the computational distances were in fair agreement with the experimental ones.

3. Materials and Methods

The geometries of systems were fully optimized at the MP2 computational level [103] with a combination of the aug’-cc-pVDZ and the aug-cc-pVDZ-PP basis sets [104,105]. The aug’-cc-pVDZ basis set is built using aug-cc-pVDZ for C, N, F and Cl atoms and cc-pVDZ for the H atoms. For the heavy (coinage) atoms (Cu, Ag and Au) the effective core potential basis set, aug-cc-pVDZ-PP was used. Frequency calculations at the same computational level were carried out to confirm that the structures obtained correspond to energetic minima. These calculations were carried out with the Gaussian-16 program [106]. The electronic energy and geometry of all systems were gathered in Tables S1–S3.
The binding energy was calculated as the difference of the electronic energy of the complexes minus the sum of the energies of the isolated monomers in their minimum energy. Positive and negative values of the binding energies correspond to unfavorable (repulsive) and favorable (attractive) interactions.
The topological characteristics of the electron density were studied within the quantum theory of atoms in molecules (QTAIM) [107,108] framework with the AIMAll program [109]. The molecular electrostatic potential (MESP) of the isolated monomers was represented with the Jmol program [110] and analyzed on the 0.001 au electron density isosurface with the Multiwfn program [111].
A search in the Cambridge Structural Database (CSD) [112] (Version 5.41 with updates of March, May and August 2020) was carried in order to find crystal structures of (Py-M)3 structures with halides. It should be noted that complementary studies focused on the analysis of the crystal structures that show the interaction between (Py-M)3 molecules and the hydroxyl anion are available in the literature [68].

4. Conclusions

The interactions between trinuclear regium complexes of pyrazolate with anions (F, Cl and Br) were studied by means of MP2 theory.
It was found that pyrazolate complexes could establish three type of modes of interactions, apical, planar and CH(4) involving different type of interactions and the strength of each interactions was highly dependent on the type of metal and anion considered.
Considering the 1:1 complexes, (Pz-Ag)3F− stood out as the strongest ones particularly within the planar configuration.
The most interesting question, which lay beneath the study, was: can those negatively charged (PzM)3X− complexes interact and form stable complexes with another anion? Energetically speaking, stable 1:2 complexes were found but the binding energy was shown to be positive, which indicates a repulsive interaction. However, once the repulsion between anions was subtracted, the resulting corrected binding energies were negative. Potential energy surfaces corresponding to the removal of one of the anions indicated the existence of a barrier that prevented the anion dissociation.
Going one step forward, and trying to see what is the maximum number of anions that a pyrazolate complex can hold, the 1:3 complexes were also explored, finding that (Pz-Ag)3X (F, Cl and Br) were stable with large positive binding energies for both planar and CH(4) configurations.
A search in the CSD shows the presence of thirteen crystal structures of (Py-Cu)3 systems with two anions interacting in apical disposition.
This study involving anion⋯anion interactions will be very useful to analyze future interaction with transition metals and can bring more insight on these types of interactions, particularly in the crystal structure domain.

Supplementary Materials

Supplementary Materials can be found at https://www.mdpi.com/1422-0067/21/21/8036/s1. Table S1. Molecular graph, electronic energy and geometry of the (Pz-Au)3:X− n complexes; Table S2. Molecular graph, electronic energy and geometry of the (Pz-Ag)3:X− n complexes; Table S3. Molecular graph, electronic energy and geometry of the (Pz-Cu)3:X− n complexes; Table S4. Electron density properties at the intermolecular BCPs in the 1:1 complexes; Table S5. Barriers (kJ mol−1) and interhalogen distance (Å) in the maximum of the dissociation curve (Figure S1) of the 1:2 apical complexes; Table S6. Interatomic distances (Å) of the anions in the 1:2 complexes; Table S7. Anion-Anion repulsion corrected binding energies (kJ mol−1) in the 1:2 complexes; Table S8. Electron density properties at the intermolecular BCPs in the 1:2 complexes; Table S9. Interatomic distances (Å) of the anions in the 1:3 complexes; Table S10. Anion-Anion repulsion corrected binding energies (kJ/mol) in the 1:3 complexes; Table S11. Electron density properties at the intermolecular BCPs in the 1:3 complexes; Table S12. Anion-Metal distances in the CSD search; Figure S1. Energy profiles (kJ mol−1) as a function of the X-X distance (Å) in the 1:2 apical complexes. Only one of the X anions in move further away from the (Pz-M)3 system; Figure S2. Electron density at the BCP (au) vs. the interatomic distance (Å).

Author Contributions

Investigation, I.A., C.T., J.E., G.S.-S.; data curation, I.A., C.T., G.S.-S.; writing—original draft preparation, I.A., C.T., J.E., G.S.-S.; writing—review and editing, I.A., C.T., J.E., G.S.-S.; funding acquisition, I.A., C.T. All authors have read and agreed to the published version of the manuscript.

Funding

The research was financially supported by the Spanish Ministerio de Ciencia, Innovación y Universidades (Projects PGC2018-094644-B-C2), Dirección General de Investigación e Innovación de la Comunidad de Madrid (PS2018/EMT-4329 AIRTEC-CM) and Science Foundation of Ireland (SFI), grant number 18/SIRG/5517.

Acknowledgments

Thanks are given to the CTI (CSIC) and the Irish Centre for High-End Computing (ICHEC) for their continued computational support, and to Lee O’Riordan for his careful reading and suggestions.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Frieden, E. Non-covalent interactions: Key to biological flexibility and specificity. J. Chem. Educ. 1975, 52, 754. [Google Scholar] [CrossRef] [PubMed]
  2. Zhu, H.; Sommer, I.; Lengauer, T.; Domingues, F.S. Alignment of Non-Covalent Interactions at Protein-Protein Interfaces. PLoS ONE 2008, 3, e1926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Busschaert, N.; Caltagirone, C.; Van Rossom, W.; Gale, P.A. Applications of Supramolecular Anion Recognition. Chem. Rev. 2015, 115, 8038–8155. [Google Scholar] [CrossRef] [PubMed]
  4. Molina, P.; Zapata, F.; Caballero, A. Anion Recognition Strategies Based on Combined Noncovalent Interactions. Chem. Rev. 2017, 117, 9907–9972. [Google Scholar] [CrossRef]
  5. Cockroft, S.L.; Hunter, C.A. Chemical double-mutant cycles: Dissecting non-covalent interactions. Chem. Soc. Rev. 2007, 36, 172–188. [Google Scholar] [CrossRef] [PubMed]
  6. Maharramov, A.M.; Mahmudov, K.T.; Kopylovich, M.N.; Pombeiro, A.J.L. Non-Covalent Interactions in the Synthesis and Design of New Compounds; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
  7. Mahadevi, A.S.; Sastry, G.N. Cation−π Interaction: Its Role and Relevance in Chemistry, Biology, and Material Science. Chem. Rev. 2013, 113, 2100–2138. [Google Scholar] [CrossRef] [PubMed]
  8. Pimentel, G.; McClellan, A. The Hydrogen Bond; W.H. Freeman and Company: San Francisco, CA, USA, 1960. [Google Scholar]
  9. Hadzi, D. Hydrogen Bonding. In Proceedings of the Symposium on Hydrogen Bonding, Ljubljana, Slovenia, 29 July–3 August 1957; Pergamon Press: London, UK, 1957. [Google Scholar]
  10. Speakman, J.C. The Hydrogen Bond and other Inter-Molecular Forces; The Chemical Society: London, UK, 1975. [Google Scholar]
  11. Jeffrey, G.A.; Saenger, W. Hydrogen Bonding in Biological Structures; Springer: Berlin, Germany, 1994. [Google Scholar]
  12. Desiraju, G.R.; Steiner, T. The Weak Hydrogen Bond; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
  13. Alkorta, I.; Elguero, J.; Frontera, A. Not Only Hydrogen Bonds: Other Noncovalent Interactions. Crystals 2020, 10, 180. [Google Scholar] [CrossRef] [Green Version]
  14. Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [Green Version]
  15. Wang, W.; Ji, B.; Zhang, Y. Chalcogen Bond: A Sister Noncovalent Bond to Halogen Bond. J. Phys. Chem. A 2009, 113, 8132–8135. [Google Scholar] [CrossRef]
  16. Minyaev, R.M.; Minkin, V.I. Theoretical study of O - > X (S, Se, Te) coordination in organic compounds. Can. J. Chem. 1998, 76, 776–788. [Google Scholar] [CrossRef]
  17. Zahn, S.; Frank, R.; Hey-Hawkins, E.; Kirchner, B. Pnicogen Bonds: A New Molecular Linker? Chem. Eur. J. 2011, 17, 6034–6038. [Google Scholar] [CrossRef]
  18. Del Bene, J.E.; Alkorta, I.; Elguero, J. The Pnicogen Bond in Review. In Structures, Binding Energies, Bonding Properties, and Spin-Spin Coupling Constants of Complexes Stabilized by Pnicogen Bonds; Scheiner, S., Ed.; Noncovalent Forces; Springer International Publishing: Cham, Germany, 2015; pp. 191–263. [Google Scholar]
  19. Alkorta, I.; Rozas, I.; Elguero, J. Molecular Complexes between Silicon Derivatives and Electron-Rich Groups. J. Phys. Chem. A 2001, 105, 743–749. [Google Scholar] [CrossRef]
  20. Bauzá, A.; Mooibroek, T.J.; Frontera, A. Tetrel-Bonding Interaction: Rediscovered Supramolecular Force? Angew. Chem. Int. Ed. 2013, 52, 12317–12321. [Google Scholar] [CrossRef]
  21. Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other [sigma]-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
  22. Stenlid, J.H.; Brinck, T. Extending the σ-Hole Concept to Metals: An Electrostatic Interpretation of the Effects of Nanostructure in Gold and Platinum Catalysis. J. Am. Chem. Soc. 2017, 139, 11012–11015. [Google Scholar] [CrossRef] [PubMed]
  23. Bauzá, A.; Frontera, A. Regium-π vs Cation-π Interactions in M2 and MCl (M = Cu, Ag and Au) Complexes with Small Aromatic Systems: An ab Initio Study. Inorganics 2018, 6, 64. [Google Scholar] [CrossRef] [Green Version]
  24. Frontera, A.; Bauzá, A. Regium–π bonds: An Unexplored Link between Noble Metal Nanoparticles and Aromatic Surfaces. Chem. Eur. J. 2018, 24, 7228–7234. [Google Scholar] [CrossRef]
  25. Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Regium bonds between Mn clusters (M = Cu, Ag, Au and n = 2–6) and nucleophiles NH3 and HCN. Phys. Chem. Chem. Phys. 2018, 20, 22498–22509. [Google Scholar] [CrossRef] [Green Version]
  26. Legon, A.C.; Walker, N.R. What’s in a name? ‘Coinage-metal’ non-covalent bonds and their definition. Phys. Chem. Chem. Phys. 2018, 20, 19332–19338. [Google Scholar] [CrossRef] [Green Version]
  27. Halldin Stenlid, J.; Johansson, A.J.; Brinck, T. σ-Holes and σ-lumps direct the Lewis basic and acidic interactions of noble metal nanoparticles: Introducing regium bonds. Phys. Chem. Chem. Phys. 2018, 20, 2676–2692. [Google Scholar] [CrossRef] [Green Version]
  28. Assadollahzadeh, B.; Schwerdtfeger, P. A systematic search for minimum structures of small gold clusters Aun (n = 2–20) and their electronic properties. J. Chem. Phys. 2009, 131, 064306. [Google Scholar] [CrossRef] [PubMed]
  29. Slaughter, L.M. Homogeneous Gold Catalysis; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
  30. Evans, C.J.; Reynard, L.M.; Gerry, M.C.L. Pure Rotational Spectra, Structures, and Hyperfine Constants of OC−AuX (X = F, Cl, Br). Inorg. Chem. 2001, 40, 6123–6131. [Google Scholar] [CrossRef] [PubMed]
  31. Medcraft, C.; Bittner, D.M.; Tew, D.P.; Walker, N.R.; Legon, A.C. Geometries of H2S⋯MI (M = Cu, Ag, Au) complexes studied by rotational spectroscopy: The effect of the metal atom. J. Chem. Phys. 2016, 145, 194306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Obenchain, D.A.; Frank, D.S.; Grubbs, G.S.; Pickett, H.M.; Novick, S.E. The covalent interaction between dihydrogen and gold: A rotational spectroscopic study of H2–AuCl. J. Chem. Phys. 2017, 146, 204302. [Google Scholar] [CrossRef] [Green Version]
  33. Blakey, I.; Merican, Z.; Rintoul, L.; Chuang, Y.-M.; Jack, K.S.; Micallef, A.S. Interactions of iodoperfluorobenzene compounds with gold nanoparticles. Phys. Chem. Chem. Phys. 2012, 14, 3604–3611. [Google Scholar] [CrossRef]
  34. Alkorta, I.; Elguero, J.; Dias, H.V.R.; Parasar, D.; Martín-Pastor, M. An experimental and computational NMR study of organometallic nine-membered rings: Trinuclear silver(I) complexes of pyrazolate ligands. Mag. Res. Chem. 2020, 58, 319–328. [Google Scholar] [CrossRef]
  35. Zhang, G.; Yue, H.; Weinhold, F.; Wang, H.; Li, H.; Chen, D. Resonance Character of Copper/Silver/Gold Bonding in Small Molecule⋅⋅⋅M-X (X=F, Cl, Br, CH3, CF3) Complexes. ChemPhysChem 2015, 16, 2424–2431. [Google Scholar] [CrossRef]
  36. Li, H.; Li, Q.; Li, R.; Li, W.; Cheng, J. Prediction and characterization of HCCH⋅⋅⋅AuX (X = OH, F, Cl, Br, CH3, CCH, CN, and NC) complexes: A π Au-bond. J. Chem. Phys. 2011, 135, 074304. [Google Scholar] [CrossRef]
  37. Gao, M.; Li, Q.; Li, H.-B.; Li, W.; Cheng, J. How do organic gold compounds and organic halogen molecules interact? Comparison with hydrogen bonds. RSC Adv. 2015, 5, 12488–12497. [Google Scholar] [CrossRef]
  38. Zhang, G.; Zhao, X.; Chen, D. Dual Bonding between H2O/H2S and AgCl/CuCl: Cu/Ag Bond, Sister Bond to Au Bond. J. Phys. Chem. A 2013, 117, 10944–10950. [Google Scholar] [CrossRef]
  39. Wang, Z.; Liu, Y.; Zheng, B.; Zhou, F.; Jiao, Y.; Liu, Y.; Ding, X.; Lu, T. A theoretical investigation on Cu/Ag/Au bonding in XH2P⋯MY(X = H, CH3, F, CN, NO2; M = Cu, Ag, Au; Y = F, Cl, Br, I) complexes. J. Chem. Phys. 2018, 148, 194106. [Google Scholar] [CrossRef] [PubMed]
  40. Gao, M.; Yang, X.; Cheng, J.; Li, Q.; Li, W.; Loffredo, R.E. Interplay between Metal⋯π Interactions and Hydrogen Bonds: Some Unusual Synergetic Effects of Coinage Metals and Substituents. ChemPhysChem 2013, 14, 3341–3347. [Google Scholar] [CrossRef] [PubMed]
  41. Gao, M.; Li, Q.; Li, W.; Cheng, J. Interplay between Cation–π and Coinage-Metal–Oxygen Interactions: An Ab Initio Study and Cambridge Structural Database Survey. ChemPhysChem 2015, 16, 1008–1016. [Google Scholar] [CrossRef] [PubMed]
  42. Wei, Y.; Cheng, J.; Li, W.; Li, Q. Regulation of coin metal substituents and cooperativity on the strength and nature of tetrel bonds. RSC Adv. 2017, 7, 46321–46328. [Google Scholar] [CrossRef] [Green Version]
  43. Zheng, B.; Liu, Y.; Huang, L.; Wang, Z.; Liu, H.; Liu, Y. Cooperative effects between F … Ag bonded and X … Br (Cl) halogen-bonded interaction in BrF(ClF) … AgX … BrF(ClF) (X = F, Cl, Br) complexes: A theoretical study. Mol. Phys. 2018, 116, 1834–1843. [Google Scholar] [CrossRef]
  44. Trujillo, C.; Sánchez-Sanz, G.; Elguero, J.; Alkorta, I. The Lewis acidities of gold(I) and gold(III) derivatives: A theoretical study of complexes of AuCl and AuCl3. Struct. Chem. 2020, 31, 1909–1918. [Google Scholar] [CrossRef]
  45. Samanta, D.; Wu, M.M.; Jena, P. Unique Spectroscopic Signature of Nearly Degenerate Isomers of Au(CN)3 Anion. J. Phys. Chem. Lett. 2011, 2, 3027–3031. [Google Scholar] [CrossRef]
  46. Wang, X.; Wan, X.; Zhou, H.; Takami, S.; Kubo, M.; Miyamoto, A. Electronic structures and spectroscopic properties of dimers Cu2, Ag2, and Au2 calculated by density functional theory. J. Mol. Struct. THEOCHEM 2002, 579, 221–227. [Google Scholar] [CrossRef]
  47. Wesendrup, R.; Laerdahl, J.K.; Schwerdtfeger, P. Relativistic effects in gold chemistry. VI. Coupled cluster calculations for the isoelectronic series AuPt−, Au2, and AuHg+. J. Chem. Phys. 1999, 110, 9457–9462. [Google Scholar] [CrossRef]
  48. Jena, P. Beyond the Periodic Table of Elements: The Role of Superatoms. J. Phys. Chem. Lett. 2013, 4, 1432–1442. [Google Scholar] [CrossRef]
  49. Schwerdtfeger, P.; Lein, M.; Krawczyk, R.P.; Jacob, C.R. The adsorption of CO on charged and neutral Au and Au2: A comparison between wave-function based and density functional theory. J. Chem. Phys. 2008, 128, 124302. [Google Scholar] [CrossRef]
  50. Kryachko, E.S.; Remacle, F. Complexes of DNA Bases and Gold Clusters Au3 and Au4 Involving Nonconventional N−H⋯Au Hydrogen Bonding. Nano Lett. 2005, 5, 735–739. [Google Scholar] [CrossRef] [PubMed]
  51. Kryachko, E.S.; Remacle, F. Three-gold clusters form nonconventional hydrogen bonds O–H⋯Au and N–H⋯Au with formamide and formic acid. Chem. Phys. Lett. 2005, 404, 142–149. [Google Scholar] [CrossRef]
  52. Kryachko, E.S.; Karpfen, A.; Remacle, F. Nonconventional Hydrogen Bonding between Clusters of Gold and Hydrogen Fluoride. J. Phys. Chem. A 2005, 109, 7309–7318. [Google Scholar] [CrossRef] [PubMed]
  53. Zhao, Q. The X⋯Au interactions in the CF3X (X = Cl, Br) ⋯Aun (n = 2, 3, and 4) complexes. J. Mol. Model. 2014, 20, 2133. [Google Scholar] [CrossRef] [PubMed]
  54. Sánchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Understanding Regium Bonds and their Competition with Hydrogen Bonds in Au2:HX Complexes. ChemPhysChem 2019, 20, 1572–1580. [Google Scholar] [CrossRef]
  55. Sanchez-Sanz, G.; Trujillo, C.; Alkorta, I.; Elguero, J. Rivalry between regium and hydrogen bonds established within diatomic coinage molecules and Lewis acids/bases. ChemPhysChem 2020, in press. [Google Scholar] [CrossRef]
  56. Tekarli, S.M.; Cundari, T.R.; Omary, M.A. Rational Design of Macrometallocyclic Trinuclear Complexes with Superior π-Acidity and π-Basicity. JACS 2008, 130, 1669–1675. [Google Scholar] [CrossRef] [Green Version]
  57. Awad, S.B.; Brown, D.S.; Cohen, S.C.; Humphries, R.E.; Massey, A.G. A reinvestigation of phenylene- and polyphenylene-mercurials. J. Organomet. Chem. 1977, 127, 127–138. [Google Scholar] [CrossRef]
  58. Tsunoda, M.; Gabbaï, F.P. μ6-η2:η2:η2:η2:η2:η2 As a New Bonding Mode for Benzene. J. Am. Chem. Soc. 2000, 122, 8335–8336. [Google Scholar] [CrossRef]
  59. Aullón, G.; Laguna, A.; Oliva, J.M. Electronic structure and geometries of o-carborane derived cyclic structures [{μ-1,2-(C2B10H10)nMn}Agm]z−, M = {Au, Hg}, n = {3, 4}, m = {0, 1, 2}, z = {n − m, −m}. Dalton Trans. 2012, 41, 14146–14150. [Google Scholar] [CrossRef] [PubMed]
  60. Aullón, G.; Laguna, A.; Filippov, O.A.; Oliva-Enrich, J.M. Trinuclear Gold–Carborane Cluster as a Host Structure. Eur. J. Inorg. Chem. 2019, 2019, 18–22. [Google Scholar] [CrossRef] [Green Version]
  61. Yang, G.; Raptis, R.G. Supramolecular Assembly of Trimeric Gold(I) Pyrazolates through Aurophilic Attractions. Inorg. Chem. 2003, 42, 261–263. [Google Scholar] [CrossRef] [PubMed]
  62. Yang, G.; Martínez, J.R.; Raptis, R.G. Dinuclear gold(III) pyrazolato complexes—Synthesis, structural characterization and transformation to their trinuclear gold(I) and gold(I/III) analogues. Inorg. Chim. Acta 2009, 362, 1546–1552. [Google Scholar] [CrossRef]
  63. Osuga, T.; Murase, T.; Hoshino, M.; Fujita, M. A Tray-Shaped, PdII-Clipped Au3 Complex as a Scaffold for the Modular Assembly of [3×n] Au Ion Clusters. Angew. Chem. Int. Ed. 2014, 53, 11186–11189. [Google Scholar] [CrossRef]
  64. Rasika Dias, H.V.; Palehepitiya Gamage, C.S. Arene-Sandwiched Silver(I) Pyrazolates. Angew. Chem. Int. Ed. 2007, 46, 2192–2194. [Google Scholar] [CrossRef]
  65. Saotome, M.; Shimizu, D.; Itagaki, A.; Young, D.J.; Fujisawa, K. Structures and Photoluminescence of Silver(I) and Gold(I) Cyclic Trinuclear Complexes with Aryl Substituted Pyrazolates. Chem. Lett. 2019, 48, 533–536. [Google Scholar] [CrossRef] [Green Version]
  66. Zheng, J.; Lu, Z.; Wu, K.; Ning, G.-H.; Li, D. Coinage-Metal-Based Cyclic Trinuclear Complexes with Metal–Metal Interactions: Theories to Experiments and Structures to Functions. Chem. Rev. 2020, 120, 9675–9742. [Google Scholar] [CrossRef]
  67. Caramori, G.F.; Piccoli, R.M.; Segala, M.; Muñoz-Castro, A.; Guajardo-Maturana, R.; Andrada, D.M.; Frenking, G. Cyclic trinuclear copper(i), silver(i), and gold(i) complexes: A theoretical insight. Dalton Trans. 2015, 44, 377–385. [Google Scholar] [CrossRef] [Green Version]
  68. Pandolfo, L.; Pettinari, C. Trinuclear copper(ii) pyrazolate compounds: A long story of serendipitous discoveries and rational design. CrystEngComm 2017, 19, 1701–1720. [Google Scholar] [CrossRef]
  69. Mata, I.; Alkorta, I.; Molins, E.; Espinosa, E. Electrostatics at the Origin of the Stability of Phosphate-Phosphate Complexes Locked by Hydrogen Bonds. ChemPhysChem 2012, 13, 1421–1424. [Google Scholar] [CrossRef] [PubMed]
  70. Mata, I.; Alkorta, I.; Molins, E.; Espinosa, E. Tracing environment effects that influence the stability of anion–anion complexes: The case of phosphate–phosphate interactions. Chem. Phys. Lett. 2013, 555, 106–109. [Google Scholar] [CrossRef]
  71. Weinhold, F.; Klein, R.A. Anti-Electrostatic Hydrogen Bonds. Angew. Chem. Int. Ed. 2014, 126, 11396–11399. [Google Scholar] [CrossRef]
  72. Frenking, G.; Caramori, G.F. No Need for a Re-examination of the Electrostatic Notation of the Hydrogen Bonding: A Comment. Angew. Chem. Int. Ed. 2015, 54, 2596–2599. [Google Scholar] [CrossRef]
  73. Mata, I.; Molins, E.; Alkorta, I.; Espinosa, E. The paradox of hydrogen-bonded anion-anion aggregates in oxoanions: A fundamental electrostatic problem explained in terms of electrophilic...nucleophilic interactions. J. Phys. Chem. A 2015, 119, 183–194. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  74. Wang, G.; Chen, Z.; Xu, Z.; Wang, J.; Yang, Y.; Cai, T.; Shi, J.; Zhu, W. Stability and Characteristics of the Halogen Bonding Interaction in an Anion-Anion Complex: A Computational Chemistry Study. J. Phys. Chem. B 2016, 120, 610–620. [Google Scholar] [CrossRef]
  75. Chalanchi, S.M.; Alkorta, I.; Elguero, J.; Quinonero, D. Hydrogen Bond versus Halogen Bond in Cation-Cation Complexes: Effect of the Solvent. ChemPhysChem 2017, 18, 3462–3468. [Google Scholar] [CrossRef]
  76. Prohens, R.; Portell, A.; Font-Bardia, M.; Bauzá, A.; Frontera, A. H-Bonded anion–anion complex trapped in a squaramido-based receptor. Chem. Comm. 2018, 54, 1841–1844. [Google Scholar] [CrossRef]
  77. Iribarren, Í.; Montero-Campillo, M.M.; Alkorta, I.; Elguero, J.; Quiñonero, D. Cations brought together by hydrogen bonds: The protonated pyridine–boronic acid dimer explained. Phys. Chem. Chem. Phys. 2019, 21, 5796–5802. [Google Scholar] [CrossRef] [Green Version]
  78. Azofra, L.M.; Elguero, J.; Alkorta, I. A Conceptual DFT Study of Phosphonate Dimers: Dianions Supported by H-Bonds. J. Phys. Chem. A 2020, 124, 2207–2214. [Google Scholar] [CrossRef]
  79. Azofra, L.M.; Elguero, J.; Alkorta, I. Stabilisation of dianion dimers trapped inside cyanostar macrocycles. Phys. Chem. Chem. Phys 2020, 22, 11348–11353. [Google Scholar] [CrossRef] [PubMed]
  80. Chesman, A.S.R.; Hodgson, J.L.; Izgorodina, E.I.; Urbatsch, A.; Turner, D.R.; Deacon, G.B.; Batten, S.R. Anion-Anion Interactions in the Crystal Packing of Functionalized Methanide Anions: An Experimental and Computational Study. Crys.Growth Des. 2014, 14, 1922–1932. [Google Scholar] [CrossRef]
  81. Martínez-Camarena, Á.; Savastano, M.; Bazzicalupi, C.; Bianchi, A.; García-España, E. Stabilisation of Exotic Tribromide (Br3−) Anions via Supramolecular Interaction with a Tosylated Macrocyclic Pyridinophane. A Serendipitous Case. Molecules 2020, 25, 3155. [Google Scholar] [CrossRef] [PubMed]
  82. Alkorta, I.; Mata, I.; Molins, E.; Espinosa, E. Charged versus Neutral Hydrogen-Bonded Complexes: Is There a Difference in the Nature of the Hydrogen Bonds? Chem. Eur. J. 2016, 22, 9226–9234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  83. Quinonero, D.; Alkorta, I.; Elguero, J. Cation-cation and anion-anion complexes stabilized by halogen bonds. Phys. Chem. Chem. Phys 2016, 18, 27939–27950. [Google Scholar] [CrossRef] [Green Version]
  84. Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Do surfaces of positive electrostatic potential on different halogen derivatives in molecules attract? like attracting like! J. Comput. Chem. 2018, 39, 343–350. [Google Scholar] [CrossRef] [PubMed]
  85. Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Can Combined Electrostatic and Polarization Effects Alone Explain the F⋯F Negative-Negative Bonding in Simple Fluoro-Substituted Benzene Derivatives? A First-Principles Perspective. Computation 2018, 6, 51. [Google Scholar] [CrossRef] [Green Version]
  86. Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Is the Fluorine in Molecules Dispersive? Is Molecular Electrostatic Potential a Valid Property to Explore Fluorine-Centered Non-Covalent Interactions? Molecules 2019, 24, 379. [Google Scholar] [CrossRef] [Green Version]
  87. Dau, T.M.; Asamoah, B.D.; Belyaev, A.; Chakkaradhari, G.; Hirva, P.; Jänis, J.; Grachova, E.V.; Tunik, S.P.; Koshevoy, I.O. Adjustable coordination of a hybrid phosphine–phosphine oxide ligand in luminescent Cu, Ag and Au complexes. Dalton Trans. 2016, 45, 14160–14173. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  88. Lu, W.; Kinjo, R. Coordination of Asymmetric Diborenes towards Cationic Coinage Metals (Au, Ag, Cu). Chem. Eur. J. 2018, 24, 15656–15662. [Google Scholar] [CrossRef]
  89. Rozas, I.; Alkorta, I.; Elguero, J. Behavior of Ylides Containing N, O, and C Atoms as Hydrogen Bond Acceptors. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
  90. Cremer, D.; Kraka, E. A description of the chemical bond in terms of local properties of electron density and energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
  91. Mata, I.; Alkorta, I.; Molins, E.; Espinosa, E. Universal Features of the Electron Density Distribution in Hydrogen-Bonding Regions: A Comprehensive Study Involving H⋅⋅⋅X (X=H, C, N, O, F, S, Cl, π) Interactions. Chem. Eur. J. 2010, 16, 2442–2452. [Google Scholar] [CrossRef] [PubMed]
  92. Sanchez-Sanz, G.; Alkorta, I.; Elguero, J. Theoretical study of the HXYH dimers (X, Y = O, S, Se). Hydrogen bonding and chalcogen-chalcogen interactions. Mol. Phys. 2011, 109, 2543–2552. [Google Scholar] [CrossRef]
  93. Alkorta, I.; Solimannejad, M.; Provasi, P.; Elguero, J. Theoretical Study of Complexes and Fluoride Cation Transfer between N2F+ and Electron Donors. J. Phys. Chem. A 2007, 111, 7154–7161. [Google Scholar] [CrossRef] [PubMed]
  94. Mathivathanan, L.; Al-Ameed, K.; Lazarou, K.; Trávníček, Z.; Sanakis, Y.; Herchel, R.; McGrady, J.E.; Raptis, R.G. A trigonal prismatic Cu6-pyrazolato complex containing a μ6-F ligand. Dalton Trans. 2015, 44, 20685–20691. [Google Scholar] [CrossRef] [Green Version]
  95. Shi, K.; Mathivathanan, L.; Raptis, R.G. Crystal structure of [mu]6-chlorido-nonakis([mu]-4-chloropyrazolato)bis-[mu]3-methoxo-hexacopper(II). Acta Crystallogr. E 2017, 73, 266–269. [Google Scholar] [CrossRef] [PubMed]
  96. Mezei, G.; Raptis, R.G. Effect of pyrazole-substitution on the structure and nuclearity of Cu(II)-pyrazolato complexes. Inorg. Chim. Acta 2004, 357, 3279–3288. [Google Scholar] [CrossRef]
  97. Mezei, G.; Raptis, R.G.; Telser, J. Trinuclear, Antiferromagnetically Coupled CuII Complex with an EPR Spectrum of Mononuclear CuII:  Effect of Alcoholic Solvents. Inorg. Chem. 2006, 45, 8841–8843. [Google Scholar] [CrossRef]
  98. Angaridis, P.A.; Baran, P.; Boča, R.; Cervantes-Lee, F.; Haase, W.; Mezei, G.; Raptis, R.G.; Werner, R. Synthesis and Structural Characterization of Trinuclear CuII−Pyrazolato Complexes Containing μ3-OH, μ3-O, and μ3-Cl Ligands. Magnetic Susceptibility Study of [PPN]2[(μ3-O)Cu3(μ-pz)3Cl3]. Inorg. Chem. 2002, 41, 2219–2228. [Google Scholar] [CrossRef]
  99. Surmann, S.A.; Mezei, G. Halogen-bonded network of trinuclear copper(II) 4-iodopyrazolate complexes formed by mutual breakdown of chloroform and nanojars. Acta Crystallogr. E 2016, 72, 1517–1520. [Google Scholar] [CrossRef]
  100. Kamiyama, A.; Kajiwara, T.; Ito, T. Cage-Type Hexacopper(II) Complex Formed by Chloride Template. Chem. Lett. 2002, 31, 980–981. [Google Scholar]
  101. Boudalis, A.K.; Rogez, G.; Heinrich, B.; Raptis, R.G.; Turek, P. Towards ionic liquids with tailored magnetic properties: Bmim+ salts of ferro- and antiferromagnetic CuII3 triangles. Dalton Trans. 2017, 46, 12263–12273. [Google Scholar] [CrossRef] [Green Version]
  102. Boča, R.; Dlháň, L.; Mezei, G.; Ortiz-Pérez, T.; Raptis, R.G.; Telser, J. Triangular, Ferromagnetically-Coupled CuII3−Pyrazolato Complexes as Possible Models of Particulate Methane Monooxygenase (pMMO). Inorg. Chem. 2003, 42, 5801–5803. [Google Scholar] [CrossRef]
  103. Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
  104. Dunning, T.H. Gaussian-Basis Sets for Use in Correlated Molecular Calculations .1. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  105. Peterson, K.A.; Puzzarini, C. Systematically convergent basis sets for transition metals. II. Pseudopotential-based correlation consistent basis sets for the group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) elements. Theor. Chem. Acc. 2005, 114, 283–296. [Google Scholar] [CrossRef]
  106. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 c01; Gaussian. Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  107. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
  108. Popelier, P.L.A. Atoms In Molecules; An introduction; Prentice Hall: Harlow, UK, 2000. [Google Scholar]
  109. Keith, T.A. In TK Gristmill Software, Overland Park, KS, USA. Version 17.11.14 B. Available online: aim.tkgristmill.com (accessed on 1 June 2020).
  110. Jmol: An open-Source Java Viewer for Chemical Structures in 3D. Available online: http://www.jmol.org/ (accessed on 1 June 2020).
  111. Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  112. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B 2016, 72, 171–179. [Google Scholar] [CrossRef]
Ijms 21 08036 g001 550
Figure 1. Structure of the studied compounds. (a) General structure, full red circles the metal; empty blue circles the ligand. (b) Imidazolate ligands linked by N and C atoms. (c) Phenylene ligands linked by C atoms. (d) 1,2-Dicarba-closo-dodecaborane ligands linked by C atoms; the structure of 1,2-dicarba-closo-dodecaborane was simplified. (e) Pyrazolate ligands linked by N atoms.
Figure 1. Structure of the studied compounds. (a) General structure, full red circles the metal; empty blue circles the ligand. (b) Imidazolate ligands linked by N and C atoms. (c) Phenylene ligands linked by C atoms. (d) 1,2-Dicarba-closo-dodecaborane ligands linked by C atoms; the structure of 1,2-dicarba-closo-dodecaborane was simplified. (e) Pyrazolate ligands linked by N atoms.
Ijms 21 08036 g001
Ijms 21 08036 g002 550
Figure 2. Schematic view of the possible complexes with X− (X = F, Cl and Br). The scheme shows the possible interaction sites.
Figure 2. Schematic view of the possible complexes with X− (X = F, Cl and Br). The scheme shows the possible interaction sites.
Ijms 21 08036 g002
Ijms 21 08036 g003 550
Figure 3. Molecular electrostatic potential of the (Pz-M)3 compound on the 0.001 au electron density isosurface. The color range associated to the MESP is between red ≤ −0.020 au and blue ≥ 0.015. Stationary values are given in kJ/mol.
Figure 3. Molecular electrostatic potential of the (Pz-M)3 compound on the 0.001 au electron density isosurface. The color range associated to the MESP is between red ≤ −0.020 au and blue ≥ 0.015. Stationary values are given in kJ/mol.
Ijms 21 08036 g003
Ijms 21 08036 g004 550
Figure 4. Molecular graph of the three minima located for the 1:1 (Pz-Au)3: Cl−. The symmetry of each complex is indicated. Small green and red dots indicate the position of the bond and ring critical points, respectively.
Figure 4. Molecular graph of the three minima located for the 1:1 (Pz-Au)3: Cl−. The symmetry of each complex is indicated. Small green and red dots indicate the position of the bond and ring critical points, respectively.
Ijms 21 08036 g004
Ijms 21 08036 g005 550
Figure 5. Binding energies in kJ/mol for each type of complex and anions with respect to the metal involved at the MP2/aug’-cc-pVDZ computational level.
Figure 5. Binding energies in kJ/mol for each type of complex and anions with respect to the metal involved at the MP2/aug’-cc-pVDZ computational level.
Ijms 21 08036 g005
Ijms 21 08036 g006 550
Figure 6. Molecular graph of the three minima located for the 1:2 (Pz-Au)3 and Br−. The symmetry of each complex is indicated. Small green, red and blue dots indicate the position of the bond, ring and cage critical points, respectively.
Figure 6. Molecular graph of the three minima located for the 1:2 (Pz-Au)3 and Br−. The symmetry of each complex is indicated. Small green, red and blue dots indicate the position of the bond, ring and cage critical points, respectively.
Ijms 21 08036 g006
Ijms 21 08036 g007 550
Figure 7. Molecular graph of the two minima located for the 1:3 (Pz-Au)3:F−. The symmetry of each complex is indicated. Small green and red dots indicate the position of the bond and ring critical points, respectively.
Figure 7. Molecular graph of the two minima located for the 1:3 (Pz-Au)3:F−. The symmetry of each complex is indicated. Small green and red dots indicate the position of the bond and ring critical points, respectively.
Ijms 21 08036 g007
Ijms 21 08036 g008 550
Figure 8. Structure of refcodes ELODOY (up) and OBOQAY (down). Only the (Pz-M)3: anions are shown for clarity.
Figure 8. Structure of refcodes ELODOY (up) and OBOQAY (down). Only the (Pz-M)3: anions are shown for clarity.
Ijms 21 08036 g008
Table
Table 1. Binding energy, Eb, (kJ mol−1) for the 1:1 complexes.
Table 1. Binding energy, Eb, (kJ mol−1) for the 1:1 complexes.
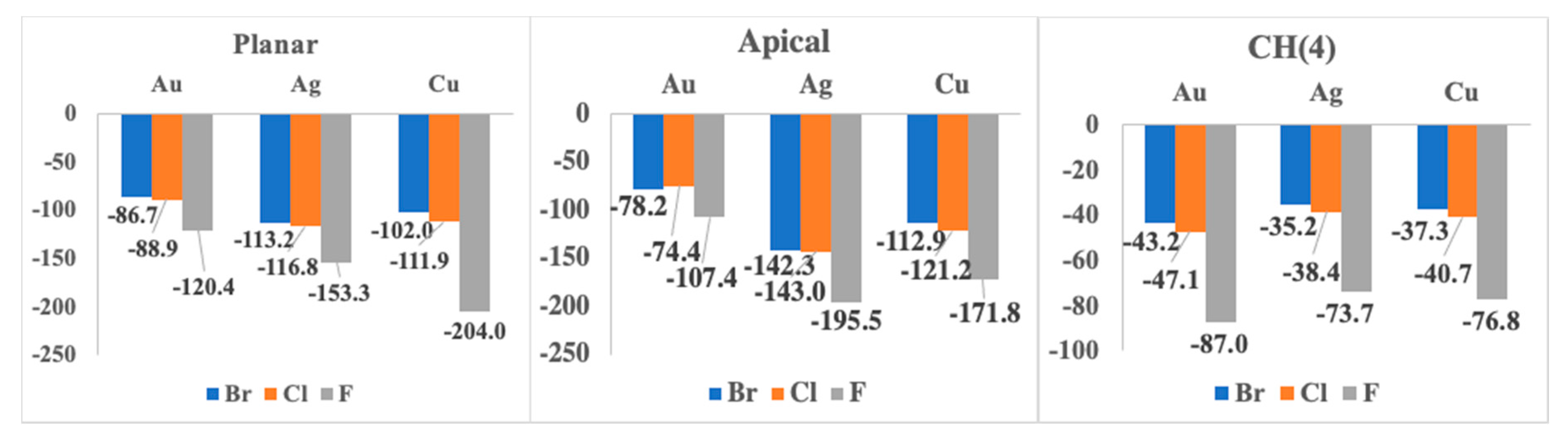
F−1:1 Apical1:1 Planar1:1 CH (4)
Au−107.4−120.4−87.0
Ag−195.5−153.3−73.7
Cu−171.8−204.0−76.8
Cl−
Au−74.4−88.9−47.1
Ag−143.0−116.8−38.4
Cu−121.2−111.9−40.7
Br−
Au−78.2−86.7−43.2
Ag−142.3−113.2−35.2
Cu−112.9−102.0−37.3
Table
Table 2. Geometrical intermolecular M⋯X− and H⋯X− distances (Å) in the 1:1 complexes.
Table 2. Geometrical intermolecular M⋯X− and H⋯X− distances (Å) in the 1:1 complexes.
F−Cl−Br−
ComplexDist.AuAgCuAuAgCuAuAgCu
ApicalM⋯X2.5582.3792.1353.0172.7582.5563.1272.8562.692
PlanarM⋯X2.4342.2562.0162.9562.6232.4303.0882.7222.575
H(3)⋯X2.3362.4832.2792.6142.7902.5752.7062.8892.665
CH(4)H(4)⋯X1.5081.5541.5512.3172.3662.3572.5072.5562.547
Table
Table 3. Binding energies (kJ mol−1) of the 1:2 complexes, (Pz-M)3: X2− at the MP2/aug’-cc-pVDZ computational level.
Table 3. Binding energies (kJ mol−1) of the 1:2 complexes, (Pz-M)3: X2− at the MP2/aug’-cc-pVDZ computational level.
1:2 Apical1:2 Planar1:2 CH(4)
F(-)
Au113.1−35.7−39.6
Ag−46.4−79.0−18.6
Cu−34.7−82.3−20.3
Cl(-)
Au139.523.915.8
Ag23.3−25.829.2
Cu93.52.128.1
Br(-)
Au120.420.218.8
Ag15.3−24.031.2
Cu94.110.630.3
Table
Table 4. Intermolecular M⋯X− and H⋯X− distances (Å) in the 1:2 complexes.
Table 4. Intermolecular M⋯X− and H⋯X− distances (Å) in the 1:2 complexes.
F−Cl−Br−
ComplexDist.AuAgCuAuAgCuAuAgCu
ApicalM⋯X2.6132.4372.2113.2262.8452.7073.3392.9492.892
PlanarM⋯X4.424 a2.3272.0903.3252.7342.6393.4552.8492.962
H(3)⋯·X b1.5922.1792.2602.5912.7202.5502.7272.8272.640
CH(4)H(4)⋯·X1.6191.6601.6592.4782.5382.5322.6962.7752.756
a In this complex, the F− ions interact only with one H(3) atoms. b The shorter of the two X⋯H(3) distances is listed.
Table
Table 5. Binding energies (kJ mol−1) for the 1:3 planar and CH(4) complexes.
Table 5. Binding energies (kJ mol−1) for the 1:3 planar and CH(4) complexes.
F−Cl−Br−
1:3 Planar1:3 CH(4)1:3 Planar1:3 CH(4)1:3 Planar1:3 CH(4)
AuDissociation136.2Dissociation188.1Dissociation188.2
Ag224.6160.3260.2203.1252.3201.9
Cu252.1163.9Dissociation206.3Dissociation205.0
Table
Table 6. Geometrical intermolecular distances (Å) in the 1:3 complexes.
Table 6. Geometrical intermolecular distances (Å) in the 1:3 complexes.
F−Cl−Br−
ComplexDist.AuAgCuAuAgCuAuAgCu
PlanarM⋯X 2.4112.211 3.025 3.238
H(3)⋯·X 2.4612.387 2.863 2.942
CH(4)H(4)⋯·X1.7351.7771.7812.6512.7402.7432.8642.9692.970
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Alkorta, I.; Elguero, J.; Trujillo, C.; Sánchez-Sanz, G. Interaction between Trinuclear Regium Complexes of Pyrazolate and Anions, a Computational Study. Int. J. Mol. Sci. 2020, 21, 8036. https://doi.org/10.3390/ijms21218036

AMA Style

Alkorta I, Elguero J, Trujillo C, Sánchez-Sanz G. Interaction between Trinuclear Regium Complexes of Pyrazolate and Anions, a Computational Study. International Journal of Molecular Sciences. 2020; 21(21):8036. https://doi.org/10.3390/ijms21218036

Chicago/Turabian Style

Alkorta, Ibon, José Elguero, Cristina Trujillo, and Goar Sánchez-Sanz. 2020. "Interaction between Trinuclear Regium Complexes of Pyrazolate and Anions, a Computational Study" International Journal of Molecular Sciences 21, no. 21: 8036. https://doi.org/10.3390/ijms21218036

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop