The Influence of a Terminal Chlorine Substituent on the Kinetics and the Mechanism of the Solvolyses of n-Alkyl Chloroformates in Hydroxylic Solvents
Abstract
1. Introduction
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- D’Souza, M.J.; Wirick, J.; Deol, J.; Kevill, D.N. Classical tosylate/chloride leaving group approach supports a tetrahedral transition state for additions to trigonal carbon. Trends in Org. Chem. 2018, 19, 1–11. [Google Scholar]
- Kevill, D.N.; D’Souza, M.J. Concerning the two reaction channels for the solvolyses of ethyl chloroformate and ethyl chlorothioformate. J. Org. Chem. 1998, 63, 2120–2124. [Google Scholar] [CrossRef]
- Kyong, J.B.; Won, H.; Kevill, D.N. Application of the extended Grunwald-Winstein equation to solvolyses of n-propyl chloroformate. Int. J. Mol. Sci. 2005, 6, 87–96. [Google Scholar] [CrossRef]
- Chapman, N.R.; Shorter, J. Correlation Analysis in Organic Chemistry; Plenum: New York, NY, USA, 1978. [Google Scholar]
- D’Souza, M.J.; Kevill, D.N. Application of the Grunwald–Winstein equations to studies of solvolytic reactions of chloroformate and fluoroformate esters. Recent Res. Dev. Org. Chem. 2013, 13, 1–38. [Google Scholar] [PubMed]
- Queen, A. Kinetics of the hydrolysis of acyl chlorides in pure water. Can. J. Chem. 1967, 45, 1619–1629. [Google Scholar] [CrossRef]
- Yew, K.H.; Koh, H.J.; Lee, H.W.; Lee, I. Nucleophilic substitution reactions of phenyl chloroformate. J. Chem. Soc. Perkin Trans 2 1995, 2263–2268. [Google Scholar] [CrossRef]
- Koo, I.S.; Yang, K.; Kang, K.; Lee, I.; Bentley, T.W. Stoichiometric solvation effects. Part 3. Product–rate correlations for solvolyses of p-nitrophenyl chloroformate in alcohol–water mixtures. J. Chem. Soc. Perkin Trans 2 1998, 1179–1183. [Google Scholar] [CrossRef]
- Bentley, T.W.; Jones, R.O. Stoichiometric solvation effects. Part 1. New equations relating product selectivities to alcohol–water solvent compositions for hydrolyses of p-nitrobenzoyl chloride. J. Chem. Soc. Perkin Trans. 2 1993, 2351–2357. [Google Scholar] [CrossRef]
- Koo, I.S.; Yang, K.; Kang, K.; Lee, I. Transition-state variation in the solvolyses of para-substituted phenyl chloroformates in alcohol-water mixtures. Bull. Korean Chem. Soc. 1998, 19, 968–973. [Google Scholar]
- Kevill, D.N.; Koyoshi, F.; D’Souza, M.J. Correlation of the specific rates of solvolysis of aromatic carbamoyl chlorides, chloroformates, chlorothionoformates, and chlorodithioformates revisited. Int. J. Mol. Sci. 2007, 8, 346–352. [Google Scholar] [CrossRef]
- La, S.; Koh, K.S.; Lee, I. Nucleophilic Substitution at a Carbonyl Carbon Atom (XI). Solvolysis of Methyl Chloroformate and Its Thioanalogues in Methanol, Ethanol and Ethanol-Water Mixtures. J. Korean Chem. Soc. 1980, 24, 1–7. [Google Scholar]
- La, S.; Koh, K.S.; Lee, I. Nucleophilic Substitution at a Carbonyl Carbon Atom (XII). Solvolysis of Methyl Chloroformate and Its Thioanalogues in CH3CN-H2O and CH3COCH3-H2O Mixtures. J. Korean Chem. Soc. 1980, 24, 8–14. [Google Scholar]
- Kevill, D.N.; Kim, J.C.; Kyong, J.B. Correlation of the Rates of Methyl Chloroformate with Solvent Properties. J. Chem. Res. Synop. 1999, 150–151. [Google Scholar] [CrossRef]
- Grunwald, E.; Winstein, S. The correlation of solvolysis rates. J. Am. Chem. Soc. 1948, 70, 846–854. [Google Scholar] [CrossRef]
- Bentley, T.W.; Carter, G.E. The SN2-SN1 spectrum. 4. The SN2 (intermediate) mechanism for solvolyses of tert-butyl chloride: A revised Y scale of solvent ionizing power based on solvolyses of 1-adamantyl chloride. J. Am. Chem. Soc. 1982, 104, 5741–5747. [Google Scholar] [CrossRef]
- Winstein, S.; Grunwald, E.; Jones, H.W. The correlation of solvolyses rates and the classification of solvolysis reactions into mechanistic categories. J. Am. Chem. Soc. 1951, 73, 2700–2707. [Google Scholar] [CrossRef]
- Bentley, T.W.; Schleyer, P.v.R. Medium effects on the rates and mechanisms of solvolytic reactions. Adv. Phys. Org. Chem. 1977, 14, 1–67. [Google Scholar]
- Bentley, T.W.; Llewellyn, G. Yx scales of solvent ionizing power. Prog. Phys. Org. Chem. 1990, 17, 121–158. [Google Scholar]
- Kevill, D.N.; Anderson, S.W. Essentially solvent-independent rates of solvolysis of the 1-adamantyldimethylsulfonium ion. Implications regarding nucleophilic assistance in solvolyses of tert-butyl derivatives and the NKL solvent nucleophilicity scale. J. Am. Chem. Soc. 1986, 108, 1579–1585. [Google Scholar] [CrossRef]
- Kevill, D.N.; Anderson, S.W. An improved scale of solvent nucleophilicity based on the solvolysis of the S-methyldibenzothiophenium ion. J. Org. Chem. 1991, 56, 1845–1850. [Google Scholar] [CrossRef]
- Kevill, D.N. Development and uses of scales of solvent nucleophilicity. In Advances in Quantitative Structure-Property Relationships; Charton, M., Ed.; JAI Press: Greenwich, CT, USA, 1996; Volume 1, pp. 81–115. [Google Scholar]
- D’Souza, M.J.; McAneny, M.J.; Kevill, D.N.; Kyong, J.B.; Choi, S.H. Kinetic evaluation of the solvolysis of isobutyl chloro- and chlorothioformate esters. Beilstein J. Org. Chem. 2011, 7, 543–552. [Google Scholar] [CrossRef] [PubMed]
- Kevill, D.N.; D’Souza, M.J. Sixty years of the Grunwald–Winstein equation: Development and recent applications. J. Chem. Res. 2008, 61–66. [Google Scholar] [CrossRef]
- D’Souza, M.J.; Sandosky, B.; Fernandez-Bueno, G.A.; McAneny, M.J.; Kevill, D.N. LFER studies evaluating solvent effects on an α-chloro-and two β,β,β-trichloro-ethyl chloroformate esters. Can. Chem. Trans. 2014, 2, 160–174. [Google Scholar] [PubMed]
- D’Souza, M.J.; Reed, D.N.; Erdman, K.J.; Kyong, J.B.; Kevill, D.N. Grunwald-Winstein analysis—Isopropyl chloroformate solvolysis revisited. Int. J. Mol. Sci. 2009, 10, 862–879. [Google Scholar] [CrossRef]
- Crunden, E.W.; Hudson, R.F. The mechanism of hydrolysis of acid chlorides. Part VII. Alkyl Chloroformates. J. Chem. Soc. 1961, 3748–3755. [Google Scholar] [CrossRef]
- Kevill, D.N.; D’Souza, M.J. Correlation of the rates of solvolysis of phenyl chloroformate. J. Chem. Soc. Perkin Trans. 2 1997, 1721–1724. [Google Scholar] [CrossRef]
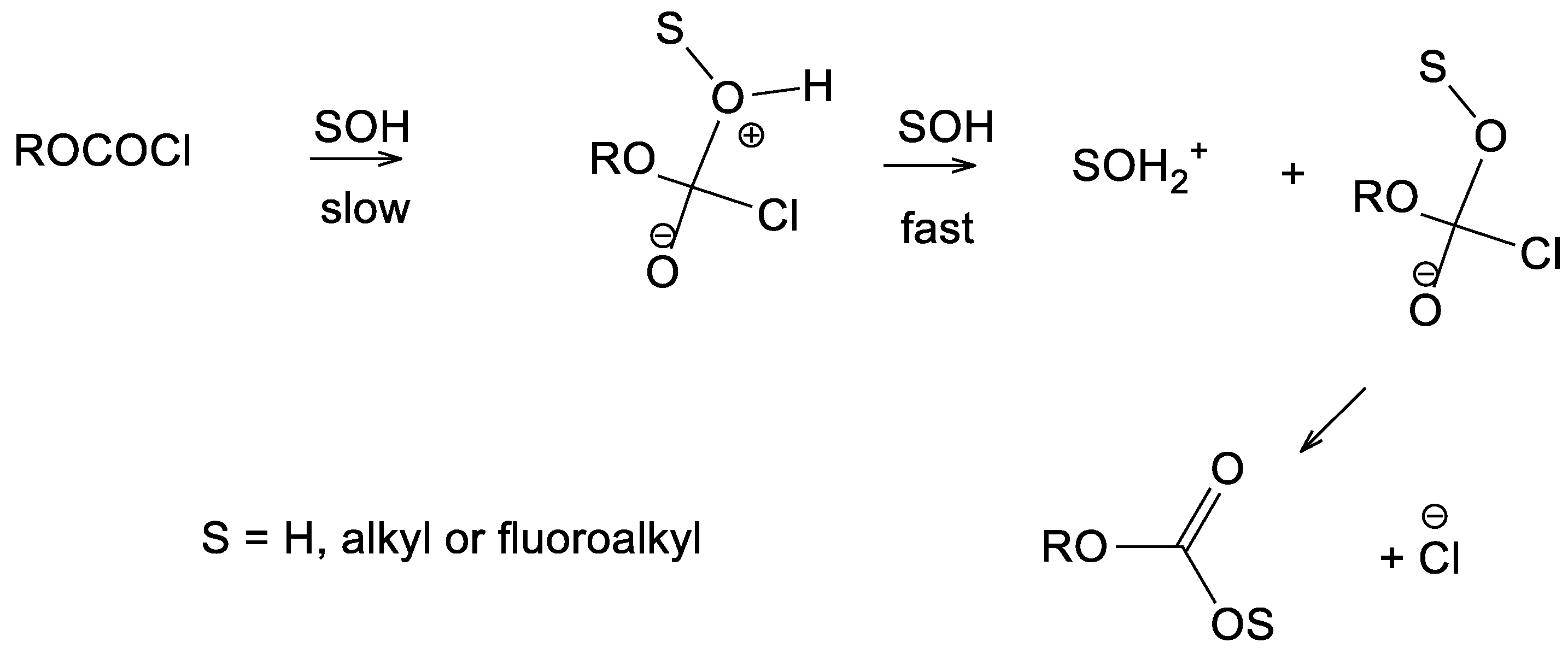
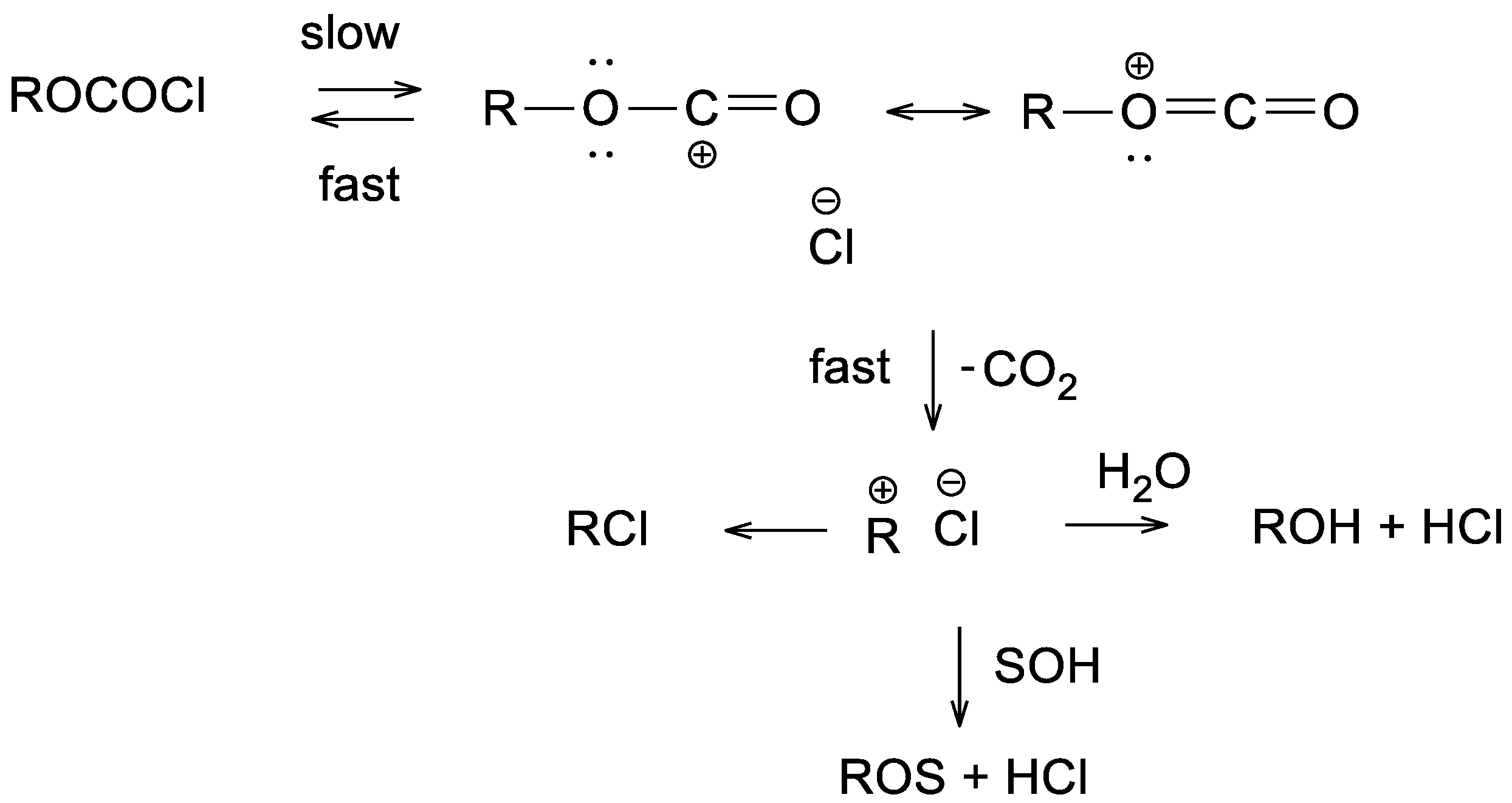
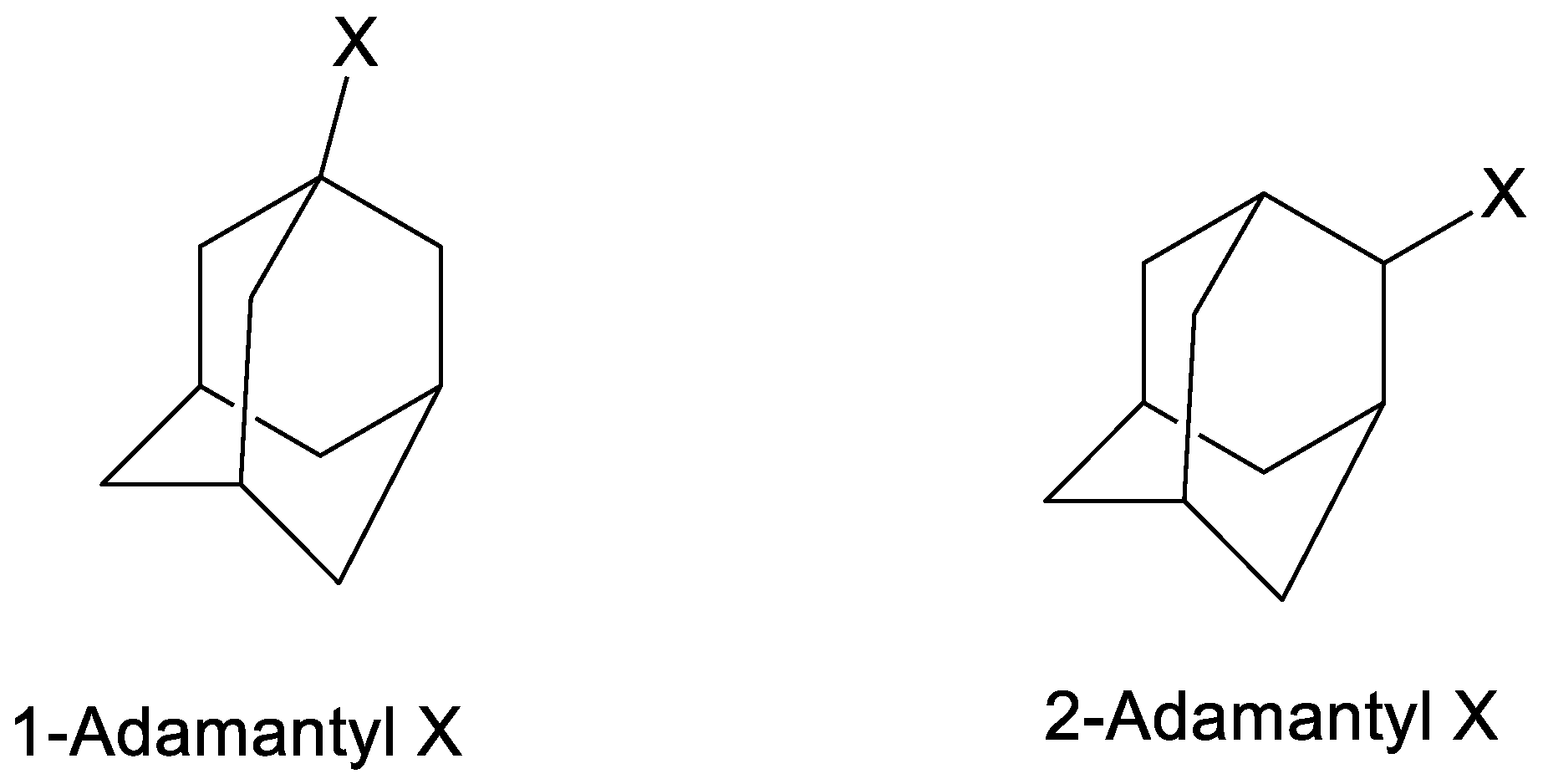
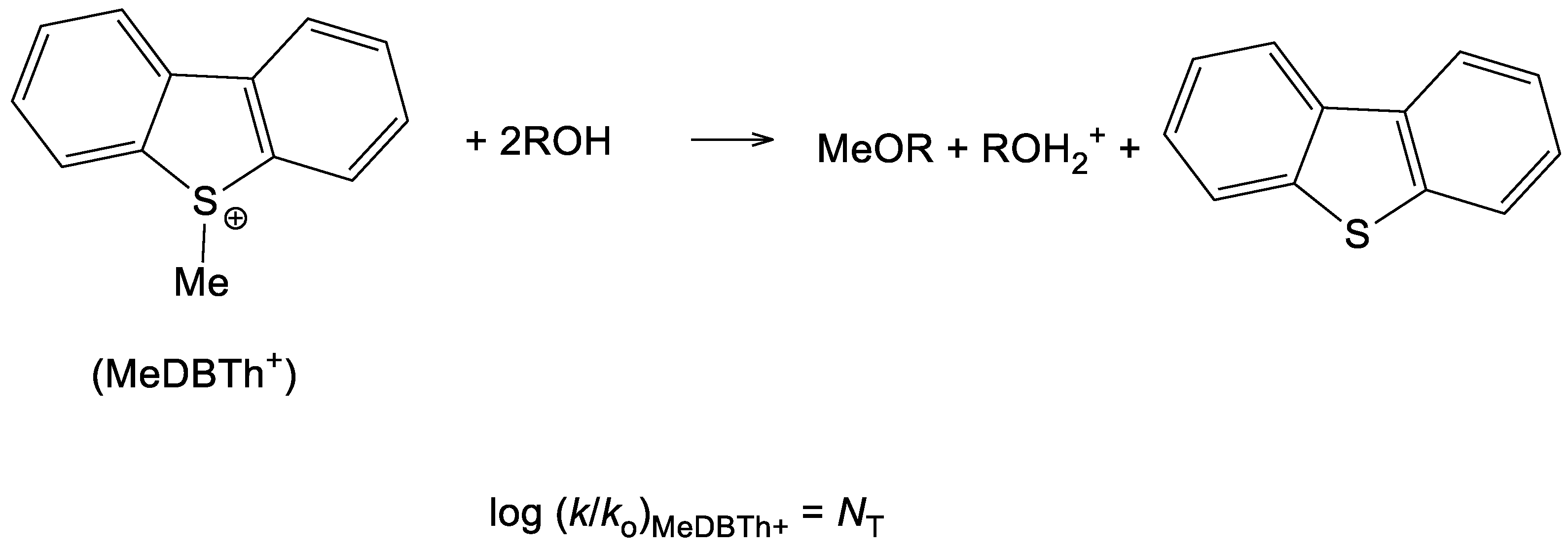
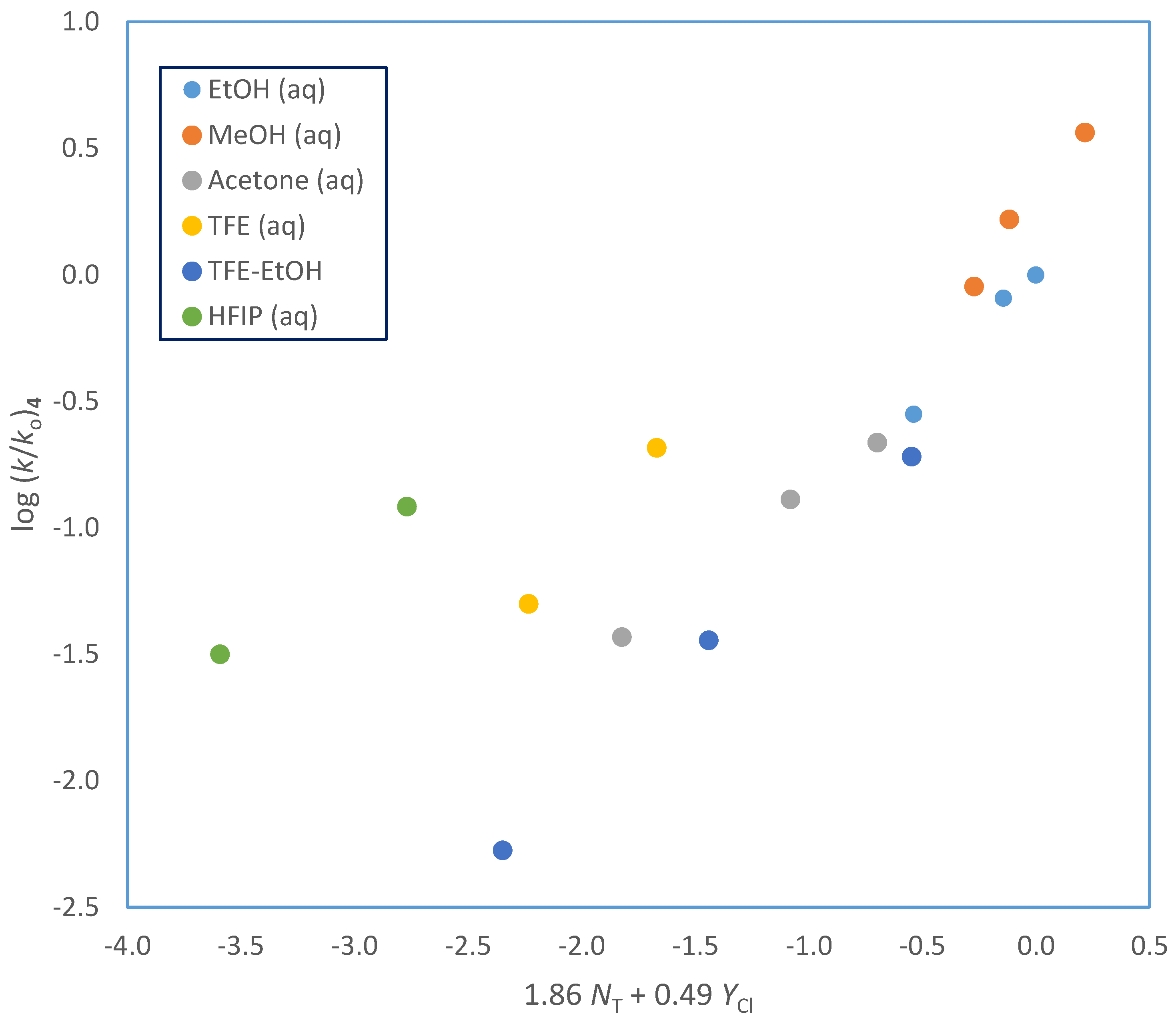
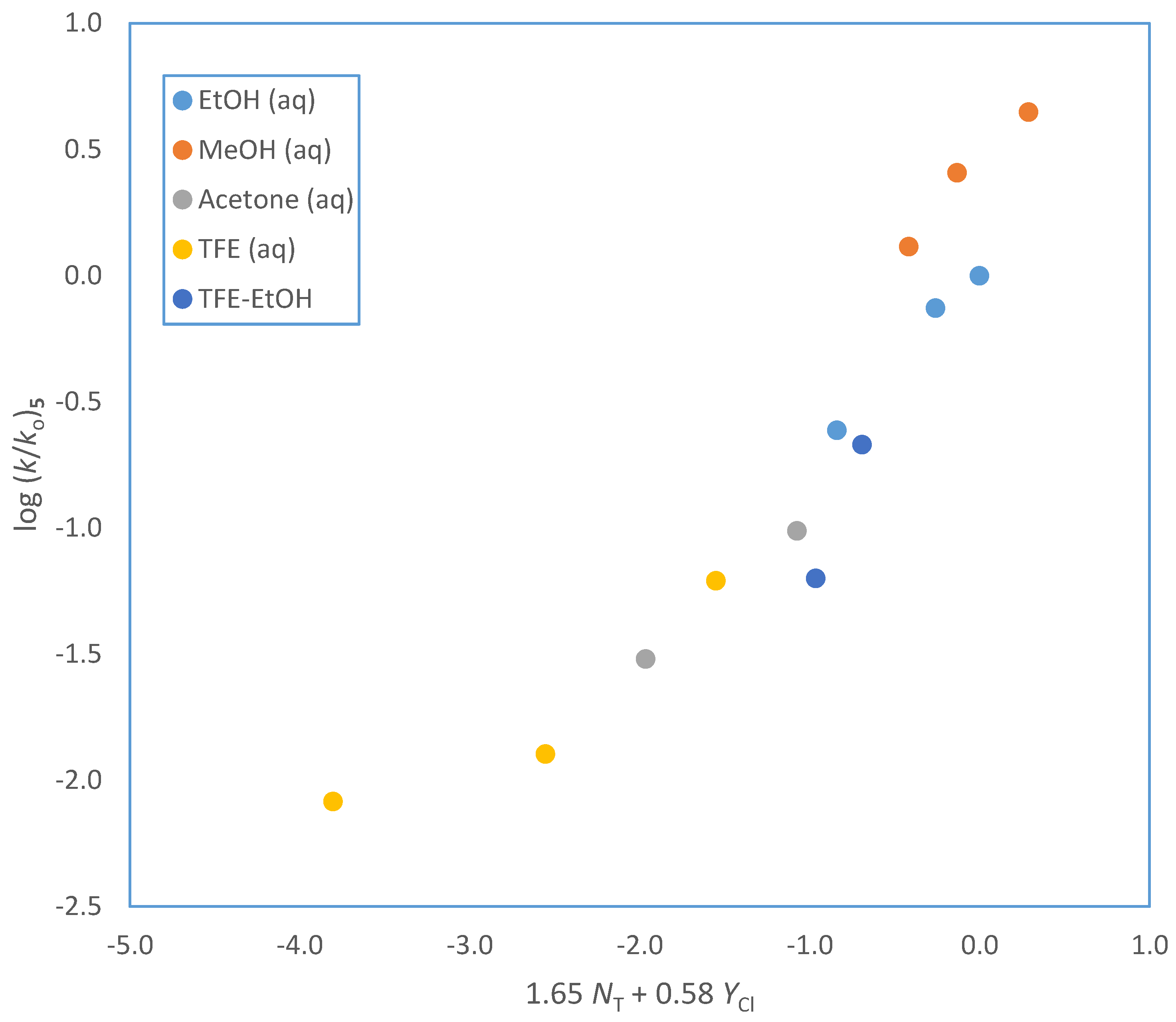
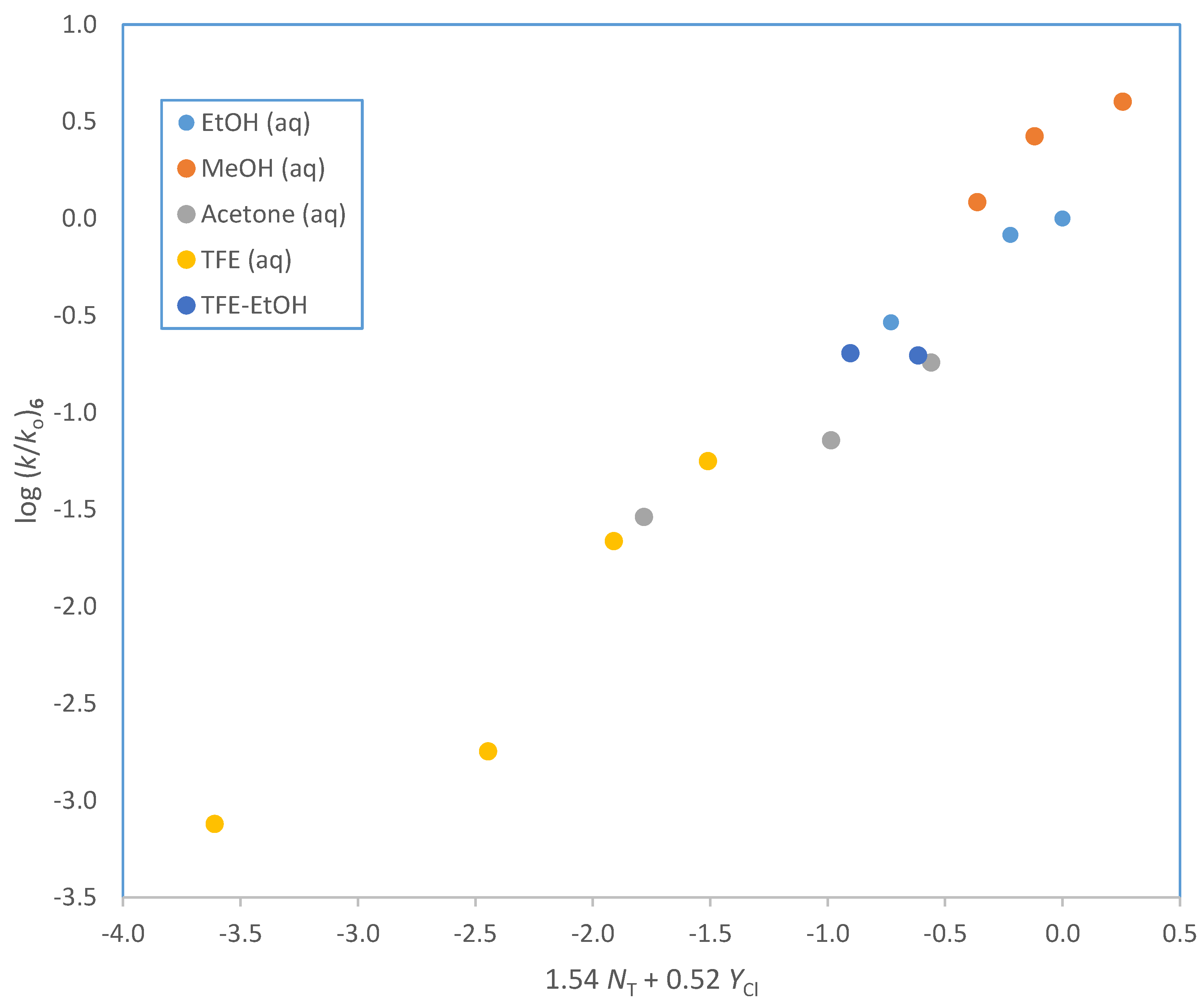
| Solventa | 105 k·s−1 (3)b,c | 105 k·s−1 (4)b | 105 k·s−1 (5)b | 105 k·s−1 (6)b | NT d | YCl e |
|---|---|---|---|---|---|---|
| 100% EtOH | 2.20 ± 0.03 | 6.36 ± 0.07 | 1.73 ± 0.09 | 3.56 ± 0.02 | 0.37 | −2.50 |
| 90% EtOH | 5.64 ± 0.04 | 18.3 ± 1.1 | 5.26 ± 0.14 | 10.1 ± 0.4 | 0.16 | −0.94 |
| 80% EtOH | 7.92 ± 0.05 | 22.6 ± 1.3 | 7.08 ± 0.17 | 12.2 ± 0.3 | 0.00 | 0.00 |
| 100% MeOH | 8.88 ± 0.05 | 20.3 ± 1.5 | 9.21 ± 0.18 | 14.9 ± 1.3 | 0.17 | −1.17 |
| 90% MeOH | 18.8 ± 0.2 | 37.4 ± 1.3 | 18.1 ± 0.7 | 32.5 ± 1.4 | −0.01 | −0.18 |
| 80% MeOH | 27.7 ± 0.3 | 82.5 ± 1.6 | 31.5 ± 1.4 | 48.9 ± 3.1 | −0.06 | 0.67 |
| 90% Acetone | 0.307 ± 0.003 | 0.837 ± 0.021 | 0.214 ± 0.010 | 0.354 ± 0.017 | −0.35 | −2.22 |
| 80% Acetone | 0.942 ± 0.007 | 2.92 ± 0.14 | 0.689 ± 0.029 | 0.881 ± 0.012 | −0.37 | −0.83 |
| 70 % Acetone | 1.91 ± 0.01 | 4.91 ± 0.14 | 2.21 ± 0.19 | −0.42 | 0.17 | |
| 97% TFE | 0.0650 ± 0.004 | 0.0583 ± 0.009 | 0.0092 ± 0.0005 | −3.30 | 2.83 | |
| 90% TFE | 0.0935 ± 0.0002 | 0.0899 ± 0.0015 | 0.0220 ± 0.0022 | −2.55 | 2.85 | |
| 70% TFE | 0.591 ± 0.005 | 1.13 ± 0.04 | 0.438 ± 0.016 | 0.265 ± 0.011 | −1.98 | 2.96 |
| 50% TFE | 1.92 ± 0.02 | 4.68 ± 0.14 | 0.685 ± 0.009 | −1.73 | 3.16 | |
| 80T-20E | 0.0666 ± 0.0003 | 0.120 ± 0.010 | −1.76 | 1.89 | ||
| 60T-40E | 0.342 ± 0.002 | 0.811 ± 0.052 | −0.94 | 0.63 | ||
| 50T-50E | 0.446 ± 0.010 | 0.721 ± 0.007 | -0.64 | 0.16 | ||
| 20T-80E | 1.60 ± 0.02 | 4.32 ± 0.15 | 1.51 ± 0.06 | 2.40 ± 0.09 | 0.08 | −1.42 |
| 70% HFIP | 0.499 ± 0.014 | 0.714 ± 0.011 | -2.94 | 3.83 | ||
| 50% HFIP | 1.15 ± 0.02 | 2.74 ± 0.13 | -2.49 | 3.80 |
| Substrate | n | l | m | c | R | F | Dominant Mechanism |
|---|---|---|---|---|---|---|---|
| PhOCOCl | 49a | 1.66 ± 0.05 | 0.56 ± 0.03 | 0.15 ± 0.07 | 0.980 | 568 | A-E |
| MeOCOCl | 19b | 1.59 ± 0.09 | 0.58 ±0.05 | 0.16 ± 0.07 | 0.977 | 171 | A-E |
| EtOCOCl (1) | 28c | 1.56 ± 0.09 | 0.56 ± 0.03 | 0.19 ± 0.24 | 0.967 | 178 | A-E |
| EtOCOCl (1) | 7c | 0.69 ± 0.13 | 0.82 ± 0.16 | −2.40 ± 0.07 | 0.946 | 17 | I |
| Cl(CH2)2OCOCl (2) | 19d | 1.57 ± 0.21 | 0.61 ± 0.13 | 0.14 ± 0.17 | 0.903 | 35 | A-E |
| Cl(CH2)2OCOCl (2) | 16e | 1.72 ± 0.18 | 0.54 ± 0.09 | 0.13 ± 0.12 | 0.943 | 53 | A-E |
| CH3CHClCOCl | 18f | 1.43 ± 0.15 | 0.38 ± 0.10 | 0.17 ± 0.13 | 0.963 | 96 | A-E |
| n-C3H7OCOCl (3) | 22g | 1.57 ± 0.12 | 0.56 ± 0.06 | 0.15 ± 0.18 | 0.947 | 83 | A-E |
| n-C3H7OCOCl (3) | 6g | 0.40 ± 0.12 | 0.64 ± 0.13 | −2.45 ± 0.47 | 0.942 | 11 | I |
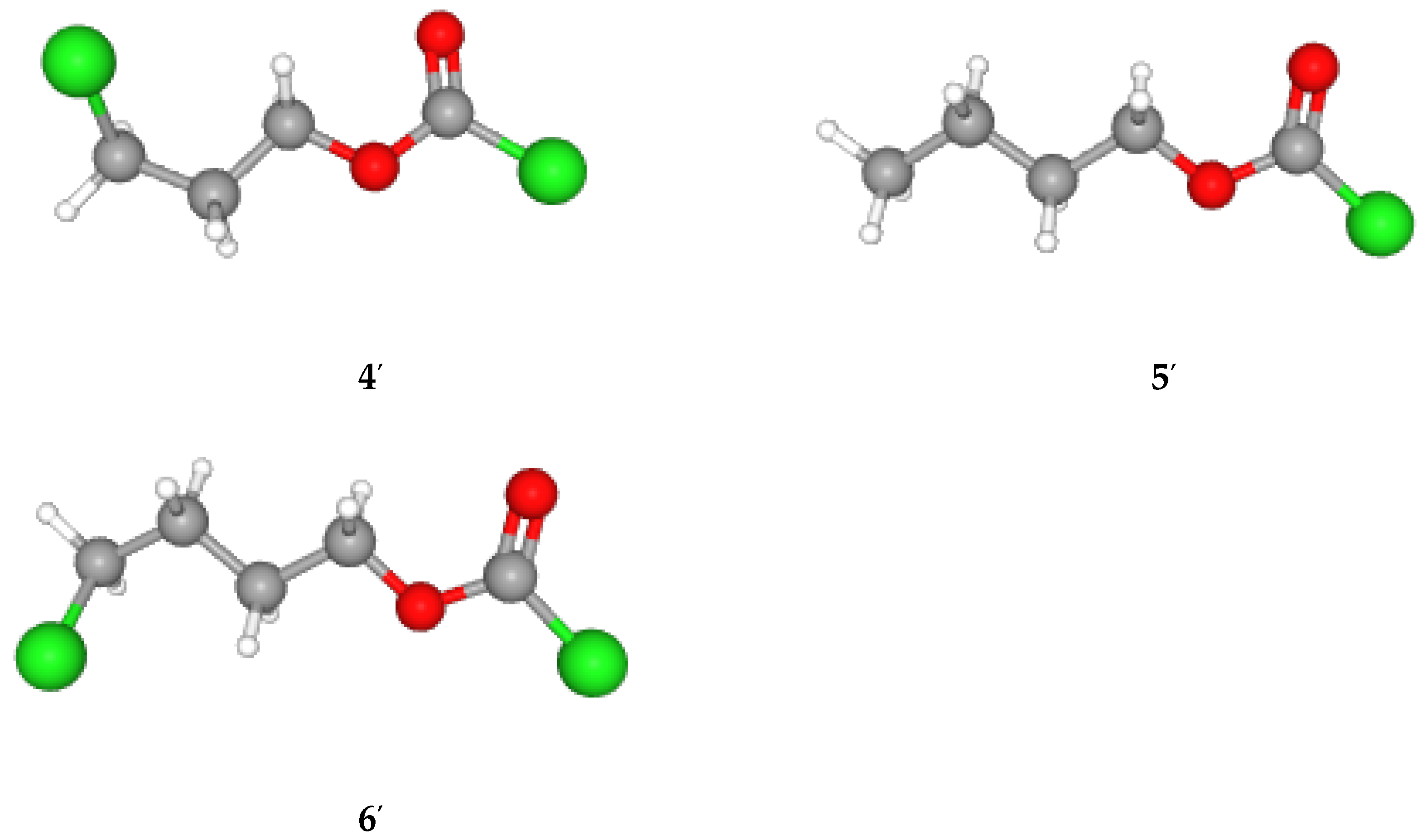
| Cl(CH2)3OCOCl (4) | 15h | 1.39 ± 0.25 | 0.52 ± 0.12 | 0.08 ± 0.16 | 0.874 | 21 | A-E |
| Cl(CH2)3OCOCl (4) | 12i | 1.86 ± 0.14 | 0.49 ± 0.06 | 0.12 ± 0.18 | 0.977 | 93 | A-E |
| n-BuOCOCl (5) | 11j | 1.65 ± 0.21 | 0.58 ± 0.09 | 0.22 ± 0.12 | 0.940 | 30 | A-E |
| Cl(CH2)4OCOCl (6) | 15k | 1.54 ± 0.13 | 0.52 ± 0.08 | 0.16 ± 0.11 | 0.971 | 100 | A-E |
| i-PrOCOCl | 9l,m | 1.35 ± 0.12 | 0.40 ± 0.05 | 0.18 ± 0.07 | 0.960 | 33 | A-E |
| i-PrOCOCl | 16l,n | 0.28 ± 0.04 | 0.59 ± 0.04 | −0.32 ± 0.06 | 0.982 | 176 | I |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Souza, M.J.; Wirick, J.; Mahmoud, O.; Kevill, D.N.; Kyong, J.B. The Influence of a Terminal Chlorine Substituent on the Kinetics and the Mechanism of the Solvolyses of n-Alkyl Chloroformates in Hydroxylic Solvents. Int. J. Mol. Sci. 2020, 21, 4387. https://doi.org/10.3390/ijms21124387
D’Souza MJ, Wirick J, Mahmoud O, Kevill DN, Kyong JB. The Influence of a Terminal Chlorine Substituent on the Kinetics and the Mechanism of the Solvolyses of n-Alkyl Chloroformates in Hydroxylic Solvents. International Journal of Molecular Sciences. 2020; 21(12):4387. https://doi.org/10.3390/ijms21124387
Chicago/Turabian StyleD’Souza, Malcolm J., Jeremy Wirick, Osama Mahmoud, Dennis N. Kevill, and Jin Burm Kyong. 2020. "The Influence of a Terminal Chlorine Substituent on the Kinetics and the Mechanism of the Solvolyses of n-Alkyl Chloroformates in Hydroxylic Solvents" International Journal of Molecular Sciences 21, no. 12: 4387. https://doi.org/10.3390/ijms21124387
APA StyleD’Souza, M. J., Wirick, J., Mahmoud, O., Kevill, D. N., & Kyong, J. B. (2020). The Influence of a Terminal Chlorine Substituent on the Kinetics and the Mechanism of the Solvolyses of n-Alkyl Chloroformates in Hydroxylic Solvents. International Journal of Molecular Sciences, 21(12), 4387. https://doi.org/10.3390/ijms21124387






