A Robust Model for Circadian Redox Oscillations
Abstract
:1. Introduction
2. Results
2.1. Derivation of a Kinetic Model for Circadian Redox Oscillations
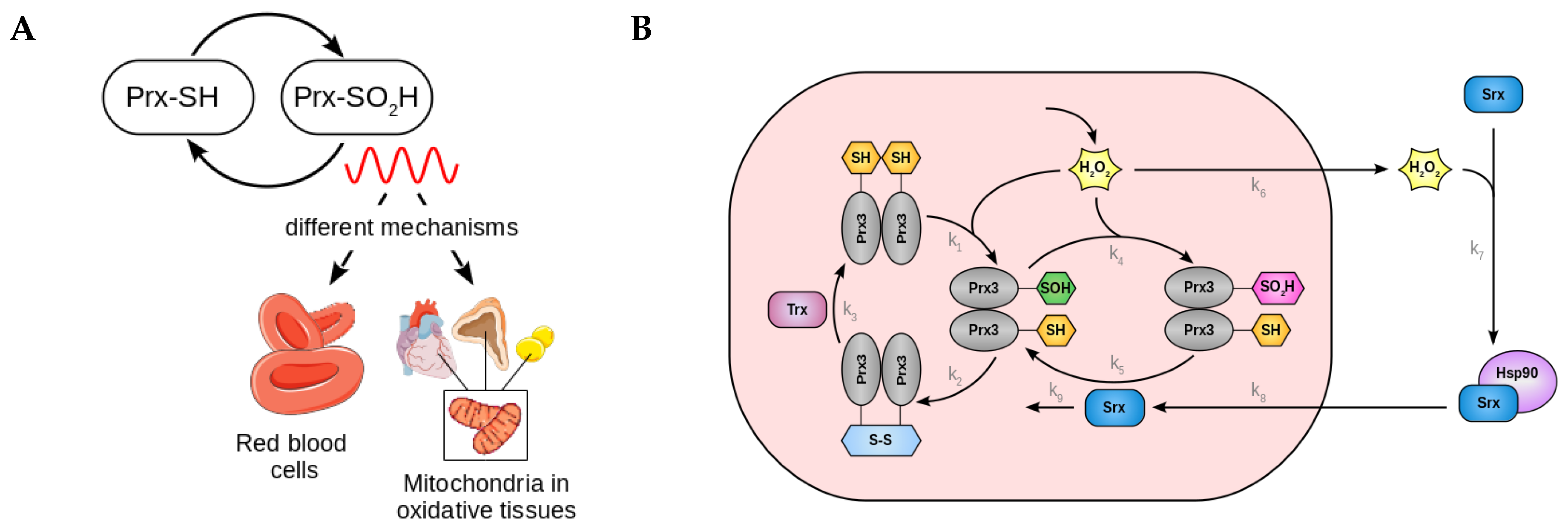
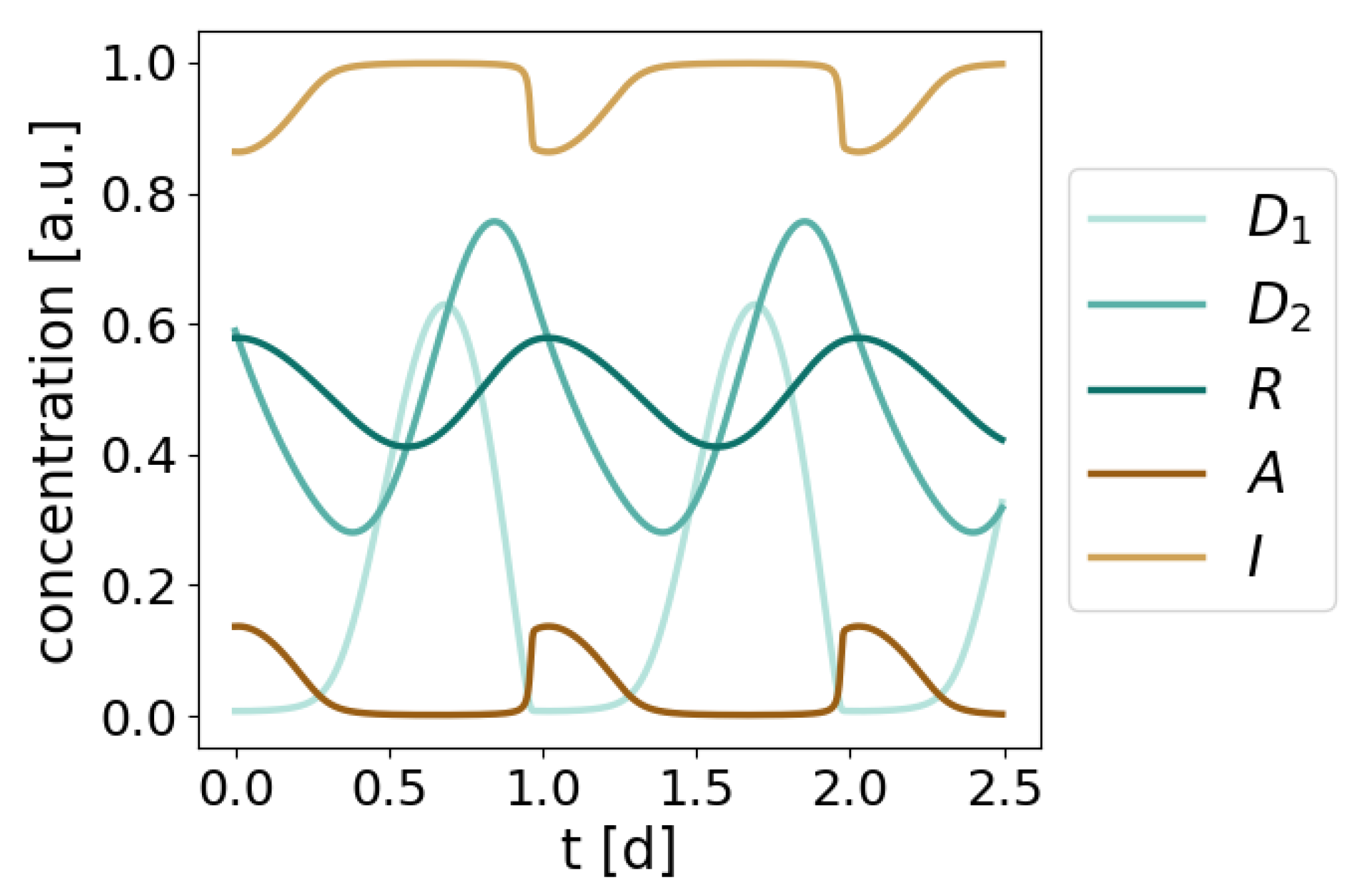
2.2. A Low Dimensional Model Represents the Core Prx3-SO2H/Srx Circadian Oscillator
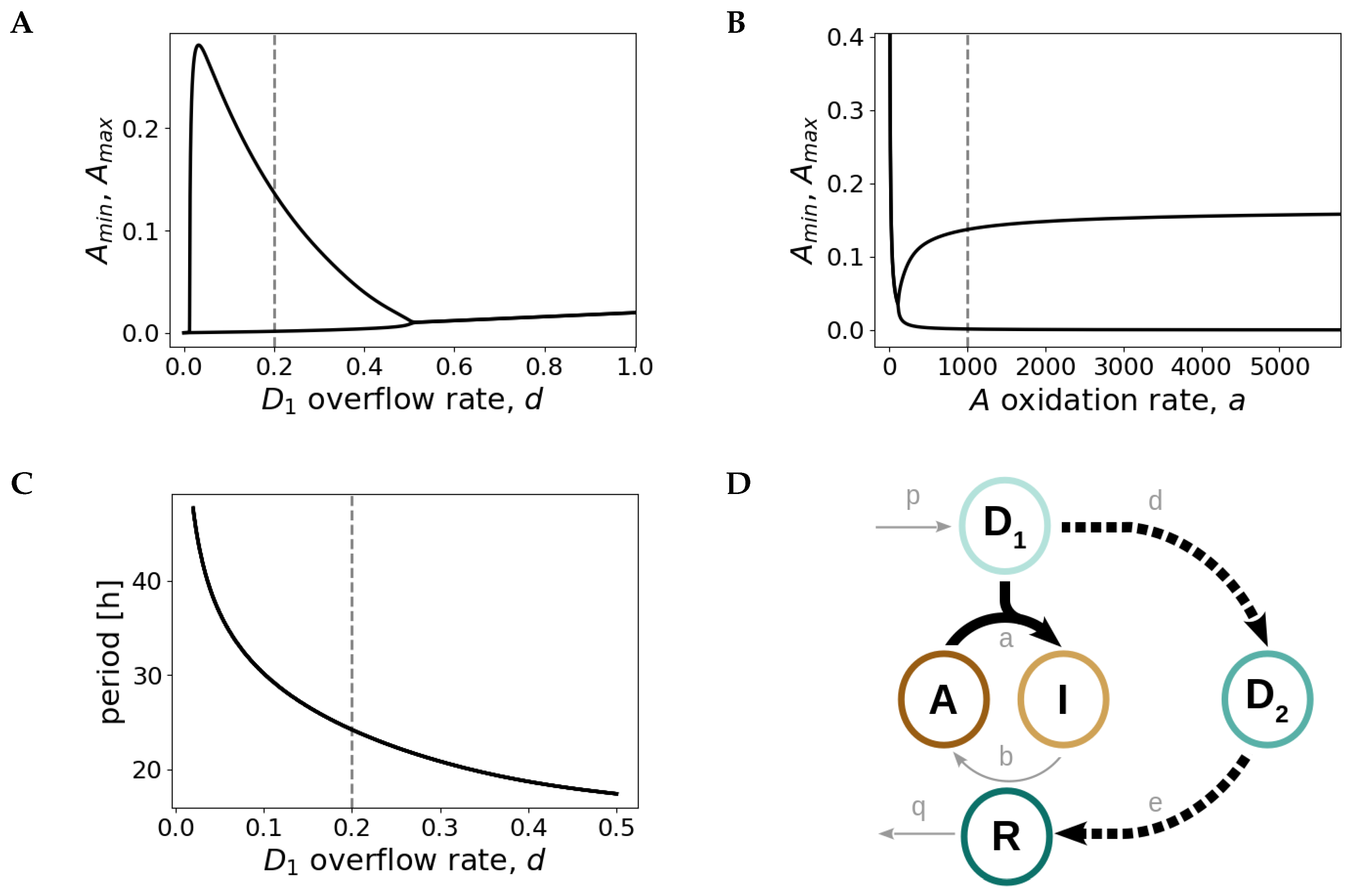
2.3. Design Principles of the Redox Oscillator: Fast A Inactivation Followed by a Slow Negative Feedback Loop
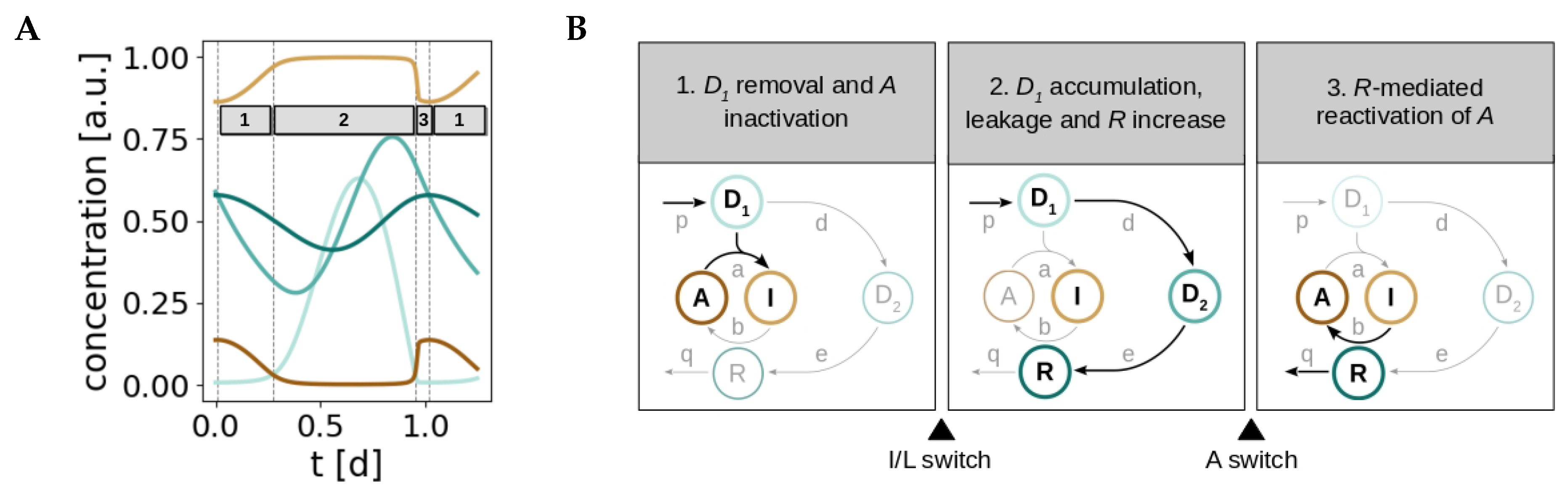
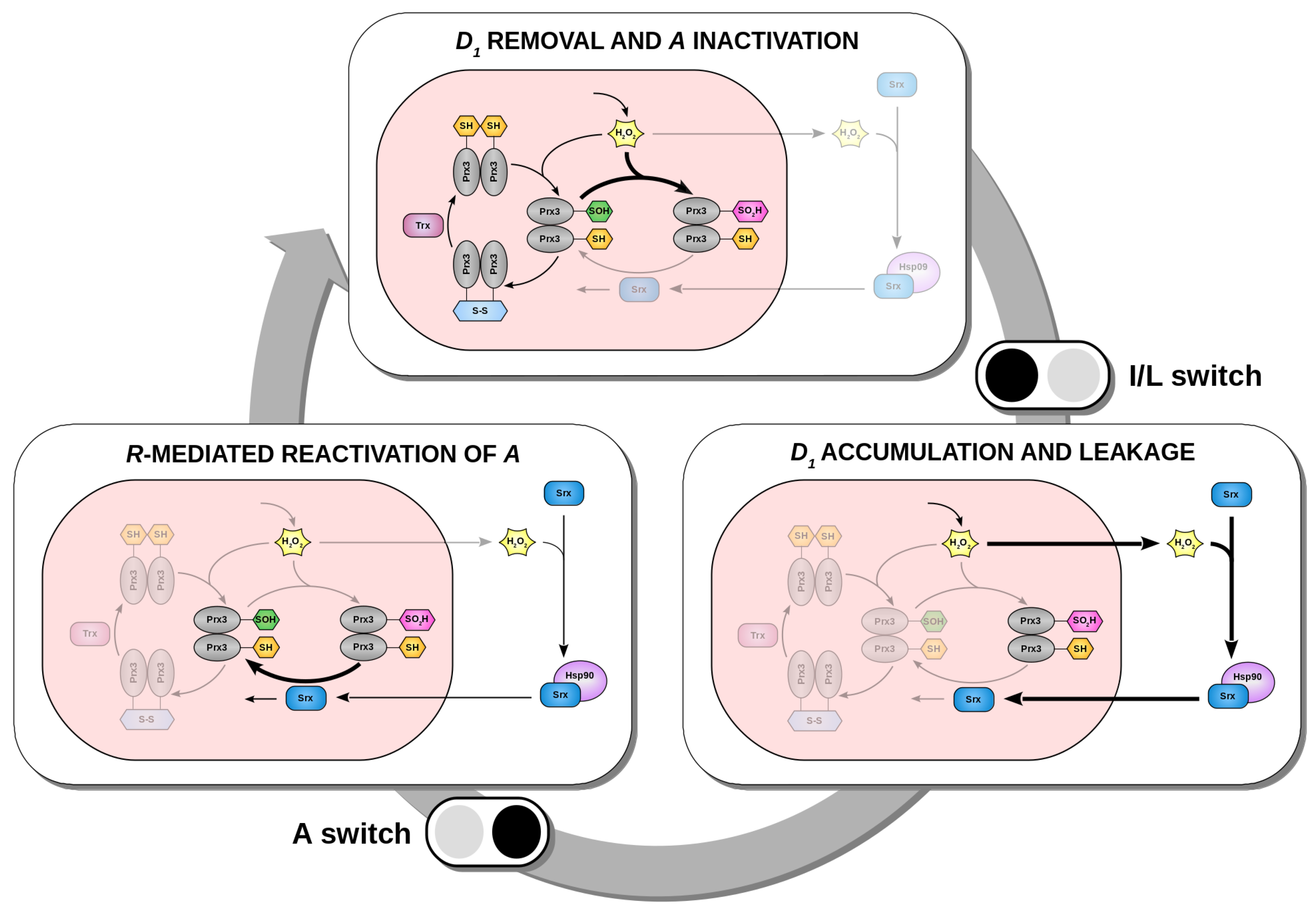
2.4. The Redox Oscillator is Characterized by Three Phases and Two Temporal Switches
3. Discussion
3.1. A Novel Circadian Redox Oscillator Model
3.2. Alternative Views on the Nature of the Negative Feedback in the Redox Oscillator
3.3. Crosstalk between Prx Rhythms and the TTFL in Eukaryotic Organisms
3.4. Model Predictions
3.5. Concluding Remarks
4. Materials and Methods
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A | Active Prx3 (Prx3-SOH) |
| A | Activation |
| Aqp | Aquaporin |
| a.u. | Arbitrary unit |
| Cys | Cysteine |
| d | Day |
| Danger 1 (mitochondrial H2O2) | |
| Danger 2 (cytosolic H2O2) | |
| h | Hour |
| H2O | Water |
| H2O2 | Hydrogen peroxide |
| I | Inactive Prx3 (Prx3-SO2H) |
| I/L | Inactivation-Leakage |
| MAPK | Mitogen-activated protein kinase |
| ODE | Ordinary differential equation |
| Prx | Peroxiredoxin |
| R | Rescuer (Srx) |
| ROS | Reactive oxygen species |
| Srx | Sulfiredoxin |
| Trx | Thioredoxin |
| TTFL | Transcription-translation feedback loop |
Appendix A. Detailed Model of Redox Oscillations
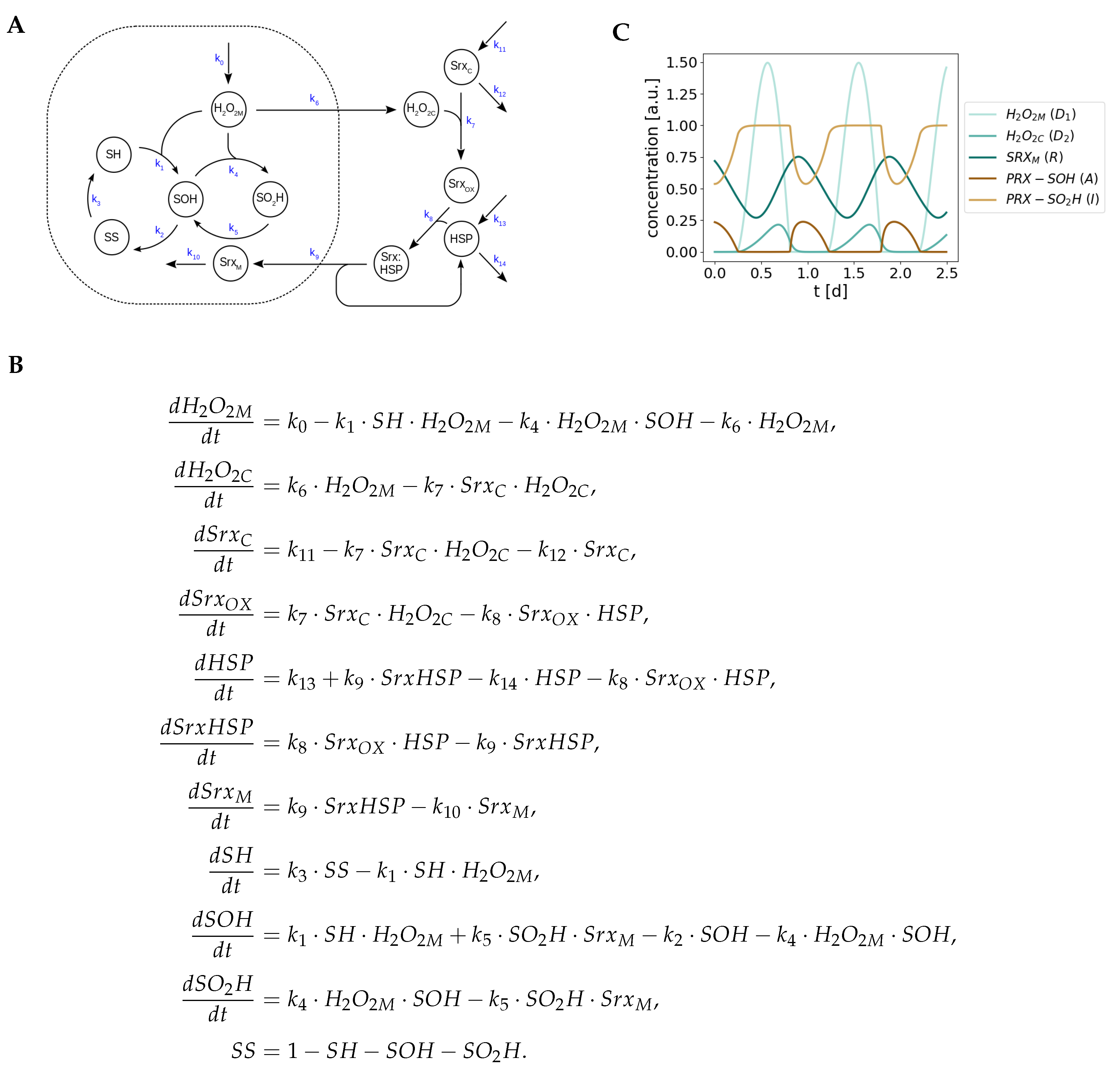
Appendix B. Model Simplification
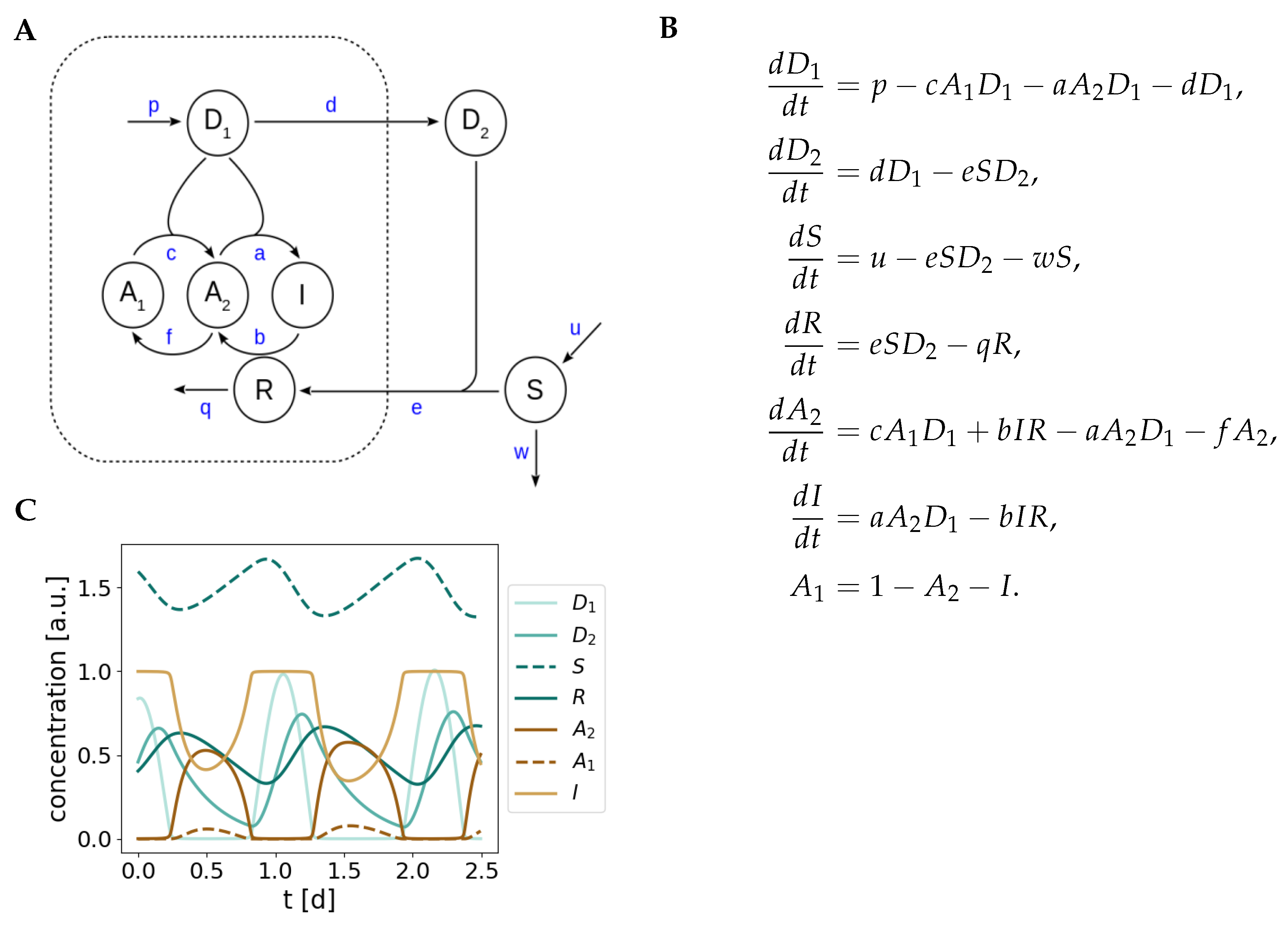
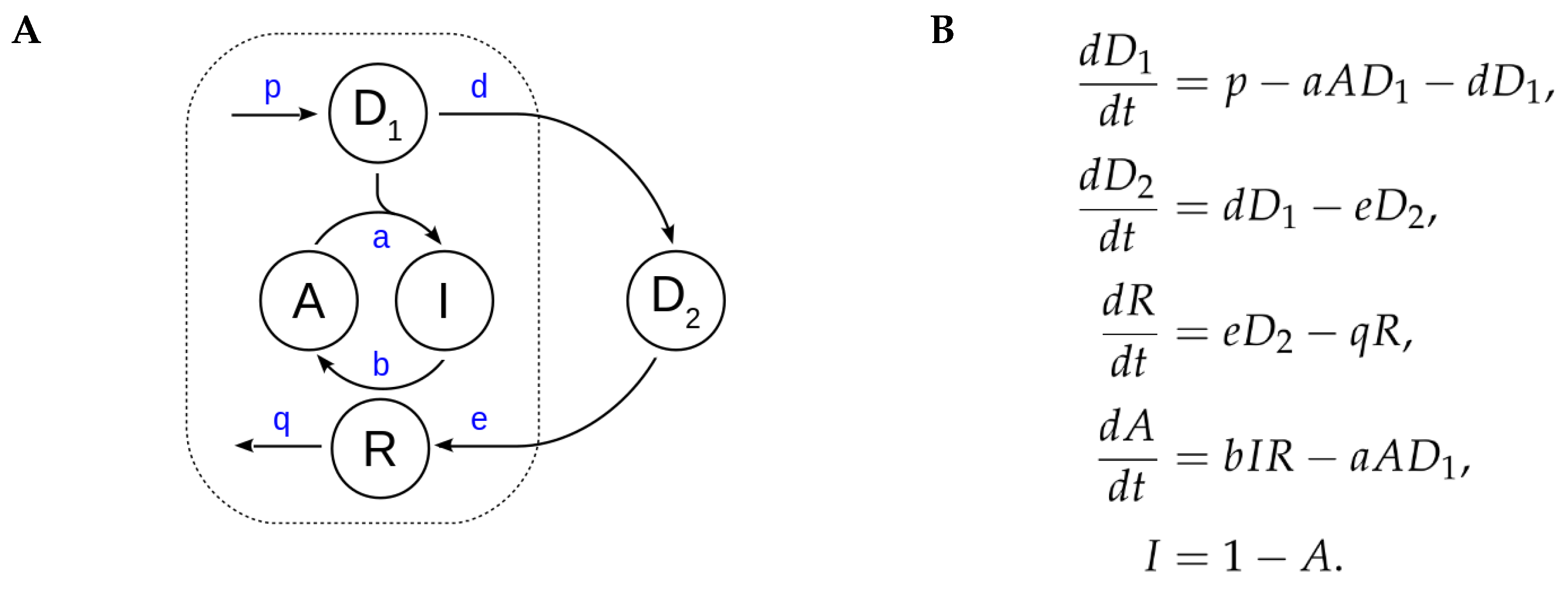
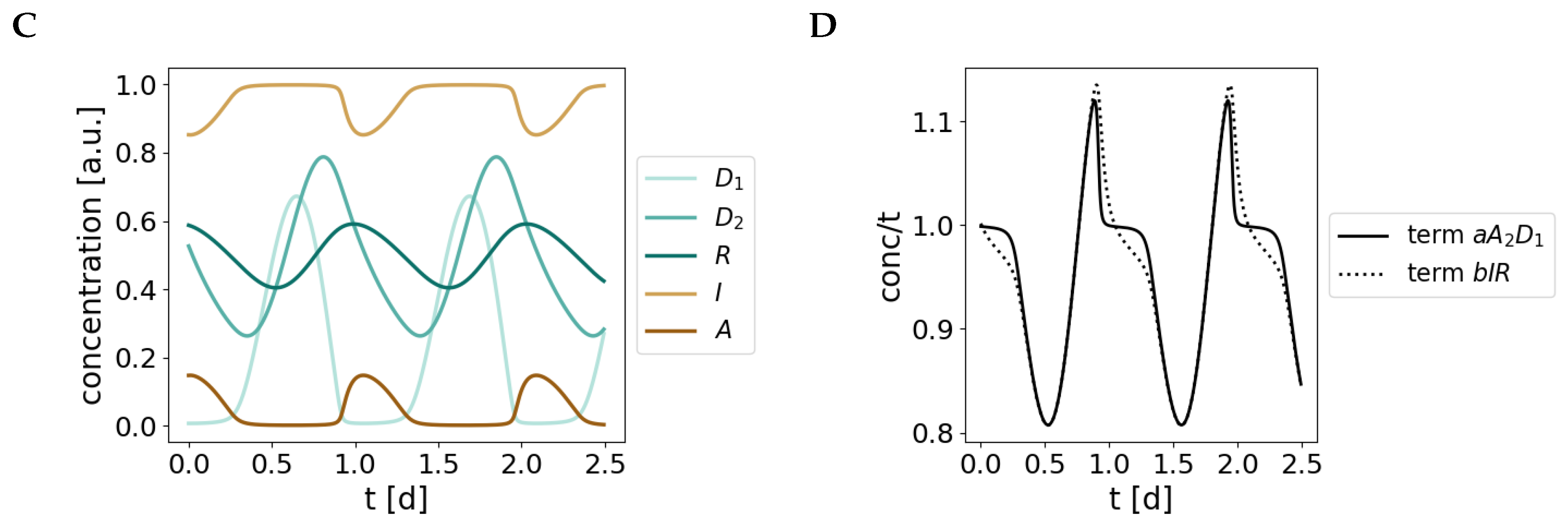
Appendix C. Bifurcation Analyses
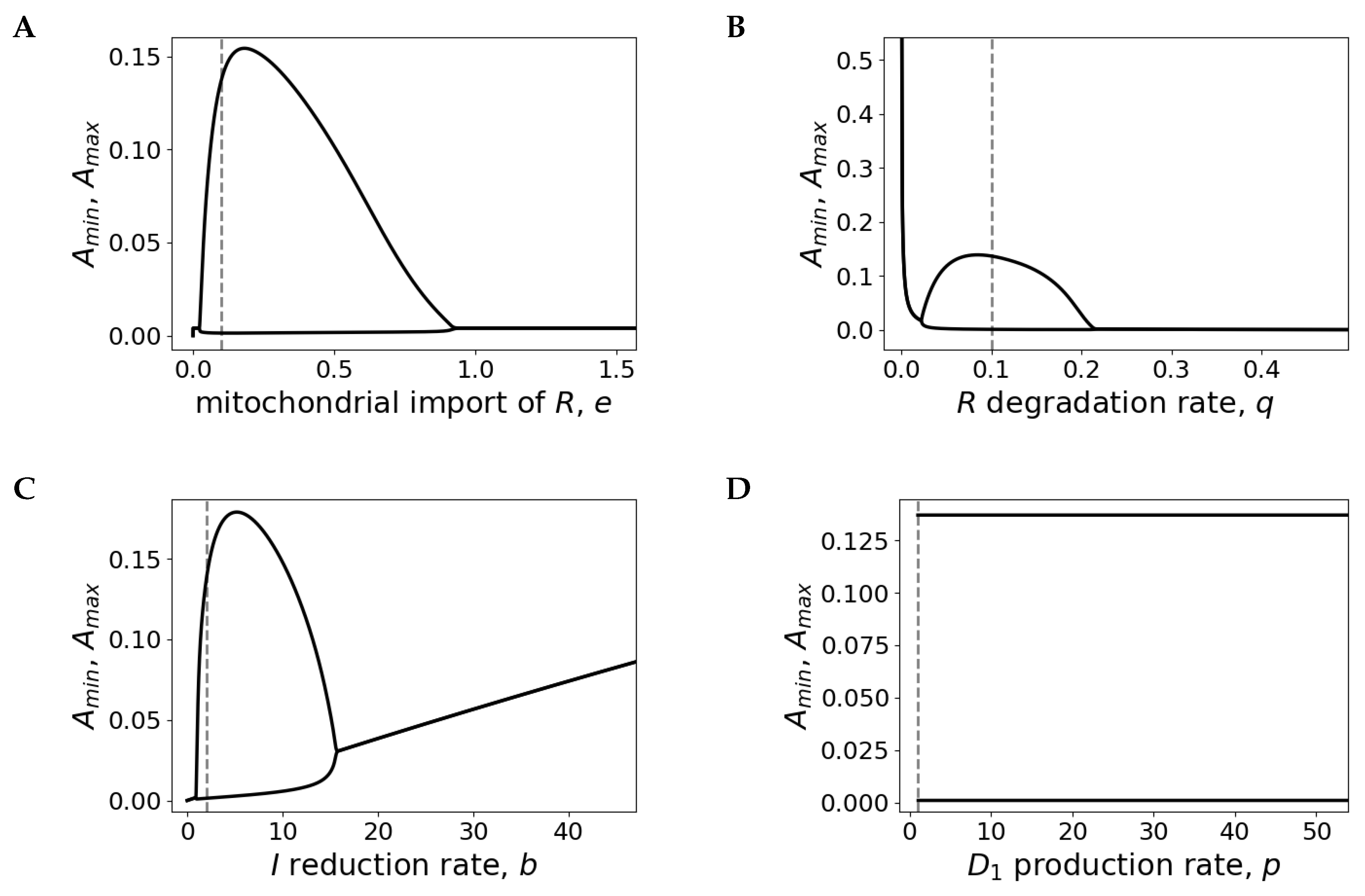
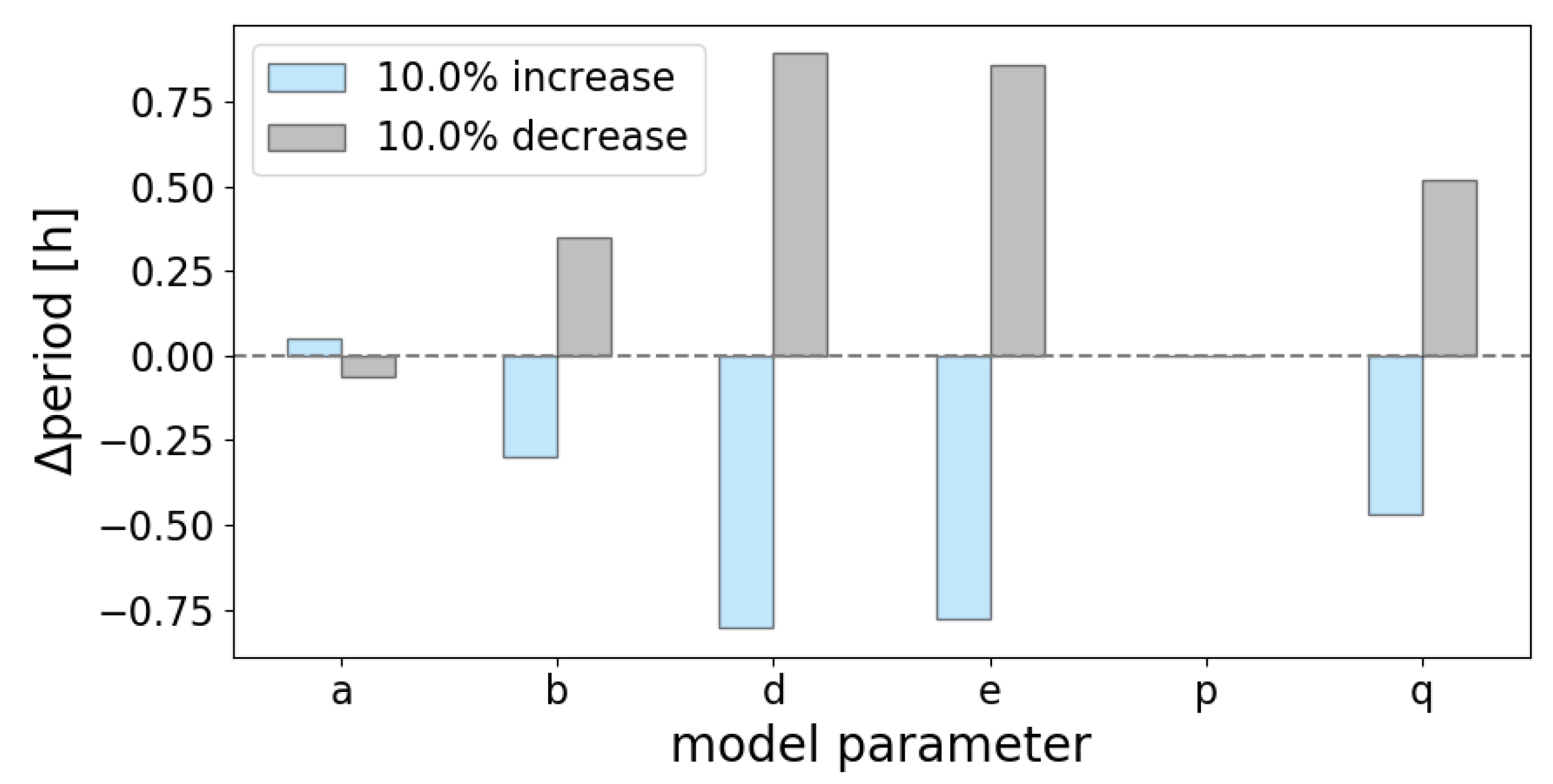
Appendix D. Period Sensitivity Analyses
References
- Lowrey, P.L.; Takahashi, J.S. Mammalian circadian biology: Elucidating genome-wide levels of temporal organization. Annu. Rev. Genom. Hum. Genet. 2004, 5, 407–441. [Google Scholar] [CrossRef] [PubMed]
- Reppert, S.M.; Weaver, D.R. Coordination of circadian timing in mammals. Nature 2002, 418, 935–941. [Google Scholar] [CrossRef]
- Ouyang, Y.; Andersson, C.R.; Kondo, T.; Golden, S.S.; Johnson, C.H. Resonating circadian clocks enhance fitness in cyanobacteria. Proc. Natl. Acad. Sci. USA 1998, 95, 8660–8664. [Google Scholar] [CrossRef]
- Hardin, P.E.; Hall, J.C.; Rosbash, M. Feedback of the Drosophila period gene product on circadian cycling of its messenger RNA levels. Nature 1990, 343, 536–540. [Google Scholar] [CrossRef]
- Brown, S.A.; Azzi, A. Peripheral circadian oscillators in mammals. In Circadian Clocks; Kramer, A., Merrow, M., Eds.; Springr: Berlin/Heidelberg, Germany, 2013; pp. 335–358. [Google Scholar]
- Nakajima, M.; Imai, K.; Ito, H.; Nishiwaki, T.; Murayama, Y.; Iwasaki, H.; Oyama, T.; Kondo, T. Reconstitution of circadian oscillation of cyanobacterial KaiC phosphorylation in vitro. Science 2005, 308, 414–415. [Google Scholar] [CrossRef]
- Sweeney, B.M.; Haxo, F.T. Persistence of a photosynthetic rhythm in enucleated Acetabularia. Science 1961, 134, 4674–4677. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, J.S.; Reddy, A.B. Circadian clocks in human red blood cells. Nature 2011, 469, 498–503. [Google Scholar] [CrossRef] [PubMed]
- Wood, Z.A.; Schröder, E.; Robin Harris, J.; Poole, L.B. Structure, mechanism and regulation of peroxiredoxins. Trends Biochem. Sci. 2003, 28, 32–40. [Google Scholar] [CrossRef]
- Edgar, R.S.; Green, E.W.; Zhao, Y.; Van Ooijen, G.; Olmedo, M.; Qin, X.; Xu, Y.; Pan, M.; Valekunja, U.K.; Feeney, K.A.; et al. Peroxiredoxins are conserved markers of circadian rhythms. Nature 2012, 485, 459–464. [Google Scholar] [CrossRef]
- Kil, I.S.; Ryu, K.W.; Lee, S.K.; Kim, J.Y.; Chu, S.Y.; Kim, J.H.; Park, S.; Rhee, S.G. Circadian oscillation of sulfiredoxin in the mitochondria. Mol. Cell 2015, 59, 651–663. [Google Scholar] [CrossRef] [PubMed]
- Cho, C.S.; Yoon, H.J.; Kim, J.Y.; Woo, H.A.; Rhee, S.G. Circadian rhythm of hyperoxidized peroxiredoxin II is determined by hemoglobin autoxidation and the 20S proteasome in red blood cells. Proc. Natl. Acad. Sci. USA 2014, 111, 12043–12048. [Google Scholar] [CrossRef]
- Rhee, S.G.; Jeong, W.; Chang, T.S.; Woo, H.A. Sulfiredoxin, the cysteine sulfinic acid reductase specific to 2-Cys peroxiredoxin: Its discovery, mechanism of action, and biological significance. Kidney Int. Suppl. 2007, 72, S3–S8. [Google Scholar] [CrossRef]
- Pett, J.P.; Korenčič, A.; Wesener, F.; Kramer, A.; Herzel, H. Feedback loops of the mammalian circadian clock constitute repressilator. PLoS Comput. Biol. 2016, 12, e1005266. [Google Scholar] [CrossRef]
- Flach, E.H.; Schnell, S. Use and abuse of the quasi-steady-state approximation. Syst. Biol. (Stevenage) 2006, 153, 187–191. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.K.; Josić, K.; Bennett, M.R. The relationship between stochastic and deterministic quasi-steady state approximations. BMC Syst. Biol. 2015, 9, 87. [Google Scholar] [CrossRef] [PubMed]
- Kil, I.S.; Lee, S.K.; Ryu, K.W.; Woo, H.A.; Hu, M.C.; Bae, S.H.; Rhee, S.G. Feedback control of adrenal steroidogenesis via H2O2-dependent, reversible inactivation of peroxiredoxin III in mitochondria. Mol. Cell 2012, 46, 584–594. [Google Scholar] [CrossRef] [PubMed]
- Peskin, A.V.; Dickerhof, N.; Poynton, R.A.; Paton, L.N.; Pace, P.E.; Hampton, M.B.; Winterbourn, C.C. Hyperoxidation of peroxiredoxins 2 and 3. J. Biol. Chem. 2013, 288, 14170–14177. [Google Scholar] [CrossRef]
- Roussel, X.; Béchade, G.; Kriznik, A.; Van Dorsselaer, A.; Sanglier-Cianferani, S.; Branlant, G.; Rahuel-Clermont, S. Evidence for the formation of a covalent thiosulfinate intermediate with peroxiredoxin in the catalytic mechanism of sulfiredoxin. J. Biol. Chem. 2008, 283, 22371–22382. [Google Scholar] [CrossRef] [PubMed]
- Bienert, G.P.; Schjoerring, J.K.; Jahn, T.P. Membrane transport of hydrogen peroxide. Biochim. Biophys. Acta 2006, 1758, 994–1003. [Google Scholar] [CrossRef]
- Verkman, A.S. Aquaporins at a glance. J. Cell Sci. 2011, 124, 2107–2112. [Google Scholar] [CrossRef]
- Li, X.; Wang, X.; Yang, Y.; Li, R.; He, Q.; Fang, X.; Luu, D.T.; Maurel, C.; Lin, J. Single-molecule analysis of PIP2;1 dynamics and partitioning reveals multiple modes of Arabidopsis plasma membrane aquaporin regulation. Plant Cell 2011, 23, 3780–3797. [Google Scholar] [CrossRef] [PubMed]
- Packer, L.; Cadenas, E. Methods in Enzymology: Hydrogen Peroxide and Cell Signaling, Part B; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Kim, H.; Jung, Y.; Shin, B.S.; Kin, H.; Song, H.; Bae, S.H.; Rhee, S.G.; Jeong, W. Redox regulation of lipopolysaccharide-mediated sulfiredoxin induction, which depends on both AP-1 and Nrf2. J. Biol. Chem. 2010, 285, 34419–34428. [Google Scholar] [CrossRef] [PubMed]
- Novák, B.; Tyson, J.J. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 2008, 9, 981–991. [Google Scholar] [CrossRef]
- Bordyugov, G.; Westermark, P.O.; Korenčič, A.; Bernard, S.; Herzel, H. Mathematical modeling in chronobiology. In Circadian Clocks; Kramer, A., Merrow, M., Eds.; Springr: Berlin/Heidelberg, Germany, 2013; pp. 45–66. [Google Scholar]
- MacDonald, N. Biological Delay Systems: Linear Stability Theory; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Relogio, A.; Westermark, P.O.; Wallach, T.; Schellenberg, K.; Kramer, A.; Herzel, H. Tuning the mammalian circadian clock: Robust synergy of two loops. PLoS Comput. Biol. 2011, 7, e1002309. [Google Scholar] [CrossRef]
- Vanselow, K.; Vanselow, J.T.; Westermark, P.O.; Reischl, S.; Maier, B.; Korte, T.; Herrmann, A.; Herzel, H.; Schlosser, A.; Kramer, A. Differential effects of PER2 phosphorylation: Molecular basis for the human familial advanced sleep phase syndrome (FASPS). Genes Dev. 2006, 20, 2660–2672. [Google Scholar] [CrossRef] [PubMed]
- Gérard, C.; Gonze, D.; Goldbeter, A. Dependence of the period on the rate of protein degradation in minimal models for circadian oscillations. Philos. Trans. A Math. Phys. Eng. Sci. 2009, 3674, 4665–4683. [Google Scholar] [CrossRef] [PubMed]
- Griffith, J.S. Mathematics of cellular control processes. I. Negative feedback to one gene. J. Theor. Biol. 1968, 20, 202–208. [Google Scholar] [CrossRef]
- Tyson, J.J.; Chen, K.C.; Novak, B. Sniffers, buzzers, toggles and blinkers: Dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003, 15, 221–231. [Google Scholar] [CrossRef]
- Ferrell, J.E.J.; Tsai, T.Y.; Yang, Q. Modeling the cell cycle: Why do certain circuits oscillate? Cell 2011, 144, 874–885. [Google Scholar] [CrossRef]
- Blüthgen, N.; Legewie, S.; Herzel, H.; Kholodenko, B. Mechanisms generating ultrasensitivity, bistability, and oscillations in signal transduction. In Introduction to Systems Biology; Choi, S., Ed.; Humana Press: New York, NY, USA, 2007; Chapter 15; pp. 282–299. [Google Scholar]
- Gonze, D.; Abou-Jaoudé, W. The Goodwin model: Behind the Hill function. PLoS ONE 2013, 8, e69573. [Google Scholar] [CrossRef]
- Kim, J.K. Protein sequestration versus Hill-type repression in circadian clock models. IET Syst. Biol. 2016, 10, 125–135. [Google Scholar] [CrossRef]
- Ferrell, J.E.J.; Ha, S. Ultrasensitivity part I: Michaelian responses and zero-order ultrasensitivity. Trends Biochem. Sci. 2014, 39, 496–503. [Google Scholar] [CrossRef]
- Ferrell, J.E.J.; Ha, S. Ultrasensitivity part II: Multisite phosphorylation, stoichiometric inhibitors, and positive feedback. Trends Biochem. Sci. 2014, 39, 556–569. [Google Scholar] [CrossRef]
- Ferrell, J.E.J.; Ha, S. Ultrasensitivity part III: Cascades, bistable switches, and oscillators. Trends Biochem. Sci. 2014, 39, 612–618. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry and Engineering; Westview Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Ananthasubramaniam, B.; Herzel, H. Positive feedback promotes oscillations in negative feedback loops. PLoS ONE 2014, 9, e104761. [Google Scholar] [CrossRef] [PubMed]
- Santos, S.D.M.; Ferrell, J.E.J. On the cell cycle and its switches. Nature 2008, 454, 288–289. [Google Scholar] [CrossRef]
- Ferrell, J.E.J.; Pomerening, J.R.; Kim, S.Y.; Trunnell, N.B.; Xiong, W.; Huang, C.Y.; Machleder, E.M. Simple, realistic models of complex biological processes: Positive feedback and bistability in a cell fate switch and a cell cycle oscillator. FEBS Lett. 2009, 583, 3999–4005. [Google Scholar] [CrossRef]
- Zhang, E.E.; Liu, A.C.; Hirota, T.; Miraglia, L.J.; Welch, G.; Pongsawakul, P.Y.; Liu, X.; Atwood, A.; Huss, J.W.; Janes, J.; et al. A genome-wide RNAi screen for modifiers of the circadian clock in human cells. Cell 2009, 139, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Buijs, R.M.; Kalsbeek, A. Hypothalamic integration of central and peripheral clocks. Nat. Rev. Neurosci. 2001, 2, 521–526. [Google Scholar] [CrossRef]
- Oster, H.; Damerow, S.; Kiessling, S.; Jakubcakova, V.; Abraham, D.; Tian, J.; Hoffmann, M.W.; Eichele, G. The circadian rhythm of glucocorticoids is regulated by a gating mechanism residing in the adrenal cortical clock. Cell Metab. 2006, 4, 163–173. [Google Scholar] [CrossRef] [PubMed]
- Peek, C.B.; Affinati, A.H.; Ramsey, K.M.; Kuo, H.Y.; Yu, W.; Sena, L.A.; Ilkayeva, O.; Marcheva, B.; Kobayashi, Y.; Omura, C.; et al. Circadian clock NAD+ cycle drives mitochondrial oxidative metabolism in mice. Science 2013, 342, 1243417. [Google Scholar] [CrossRef]
- Schmalen, R.; Reischl, S.; Wallach, T.; Klemz, R.; Grudziecki, A.; Prabu, J.R.; Benda, C.; Kramer, A.; Wolf, E. Interaction of circadian clock proteins CRY1 and PER2 is modulated by zinc binding and disulfide bond formation. Cell 2014, 157, 1203–1215. [Google Scholar] [CrossRef] [PubMed]
- Gupta, N.; Ragsdale, S.W. Thiol-disulfide redox dependence of heme binding and heme ligand switching in nuclear hormone receptor Rev-erbβ. J. Biol. Chem. 2010, 286, 4392–4403. [Google Scholar] [CrossRef]
- Rutter, J.; Reick, M.; Wu, L.C.; McKnight, S.L. Regulation of clock and NPAS2 DNA binding by the redox state of NAD cofactors. Science 2001, 293, 510–514. [Google Scholar] [CrossRef]
- Nivala, M.; Korge, P.; Nivala, M.; Weiss, J.N.; Qu, Z. Linking flickering to waves and whole-cell oscillations in a mitochondrial network model. Biophys. J. 2011, 101, 2102–2111. [Google Scholar] [CrossRef] [PubMed]
- Goldbeter, A. Biochemical Oscillations and Cellular Rhythms. The Molecular Bases of Periodic and Chaotic Behavior; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Elowitz, M.B.; Leibler, S. A synthetic oscillatory network of transcriptional regulators. Nature 2000, 403, 335–338. [Google Scholar] [CrossRef] [PubMed]
- Atkinson, M.R.; Savageau, M.A.; Myers, J.T.; Ninfa, A.J. Development of genetic circuitry exhibiting toggle switch or oscillatory behavior in Escherichia coli. Cell 2003, 113, 597–607. [Google Scholar] [CrossRef]
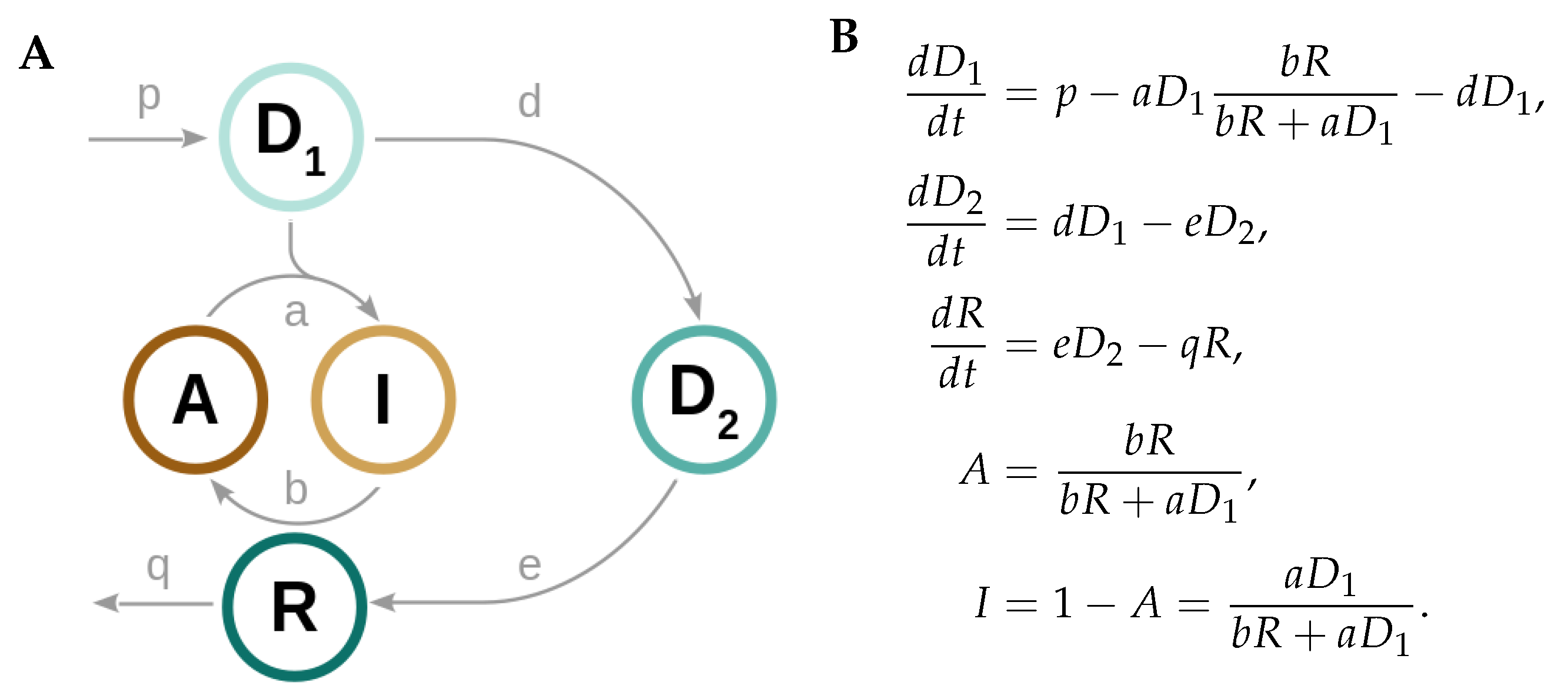
| Model Parameter | Reaction Rate | Physiological Values | References |
|---|---|---|---|
| p | mitochondrial H2O2 production | - | - |
| a | Prx3-SOH hyperoxidation (and Prx3 inactivation) | 104 M−1 s−1 | [18] |
| b | Prx3-SO2H reduction (and Prx3 reactivation) | 2 M−1 s−1 | [19] |
| d | H2O2 translocation to cytosol | 1 s−1 * | [20,21,22,23] |
| e | Srx translocation to mitochondria | - | - |
| q | mitochondrial Srx degradation | h−1 | [11,24] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
del Olmo, M.; Kramer, A.; Herzel, H. A Robust Model for Circadian Redox Oscillations. Int. J. Mol. Sci. 2019, 20, 2368. https://doi.org/10.3390/ijms20092368
del Olmo M, Kramer A, Herzel H. A Robust Model for Circadian Redox Oscillations. International Journal of Molecular Sciences. 2019; 20(9):2368. https://doi.org/10.3390/ijms20092368
Chicago/Turabian Styledel Olmo, Marta, Achim Kramer, and Hanspeter Herzel. 2019. "A Robust Model for Circadian Redox Oscillations" International Journal of Molecular Sciences 20, no. 9: 2368. https://doi.org/10.3390/ijms20092368
APA Styledel Olmo, M., Kramer, A., & Herzel, H. (2019). A Robust Model for Circadian Redox Oscillations. International Journal of Molecular Sciences, 20(9), 2368. https://doi.org/10.3390/ijms20092368





