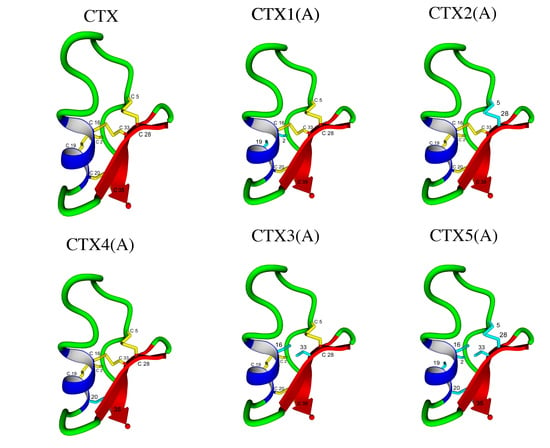
Effects of Selective Substitution of Cysteine Residues on the Conformational Properties of Chlorotoxin Explored by Molecular Dynamics Simulations
Abstract
1. Introduction
2. Results
2.1. General Properties
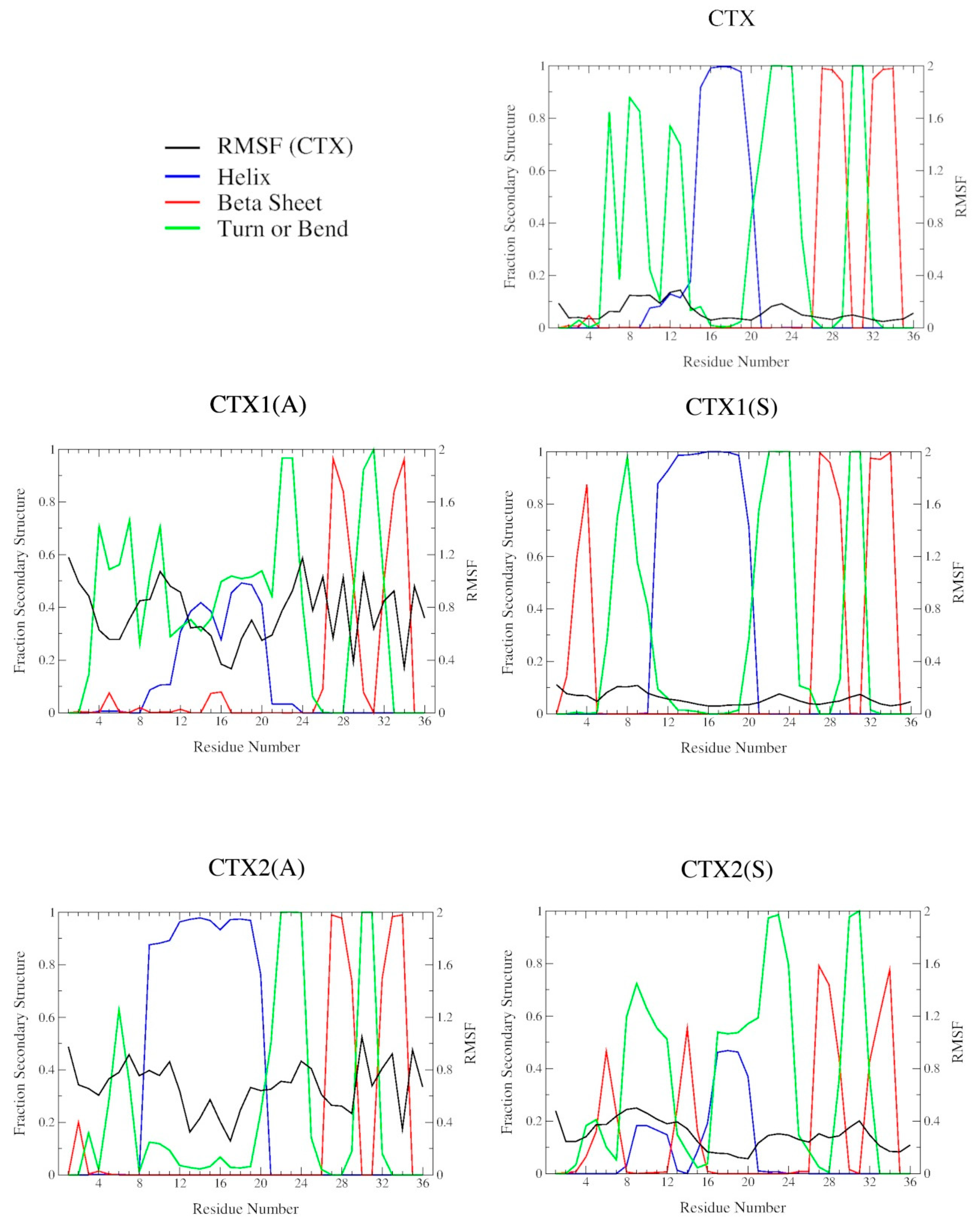
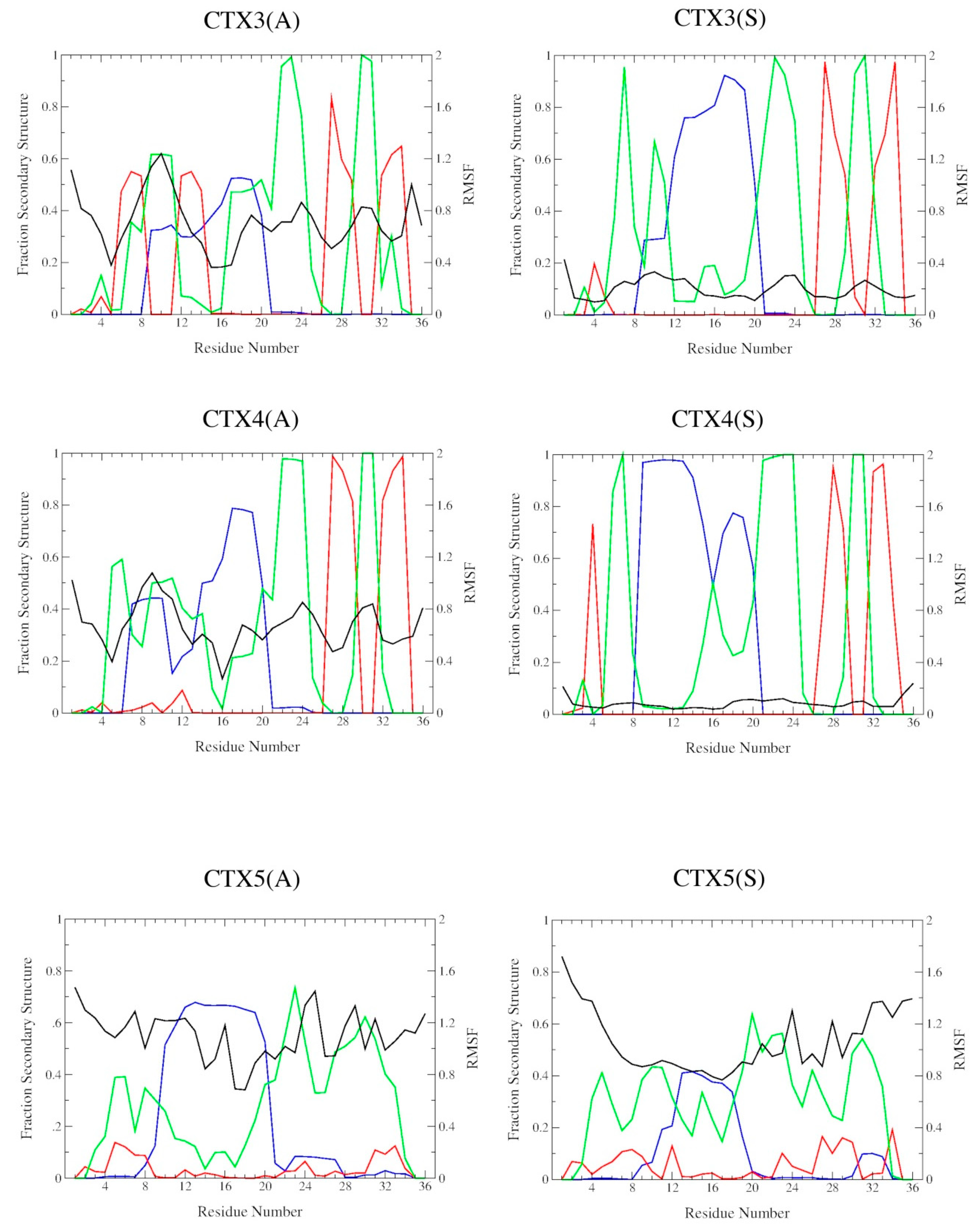
2.2. DSSP Secondary Structure
2.3. Structural Flexibility
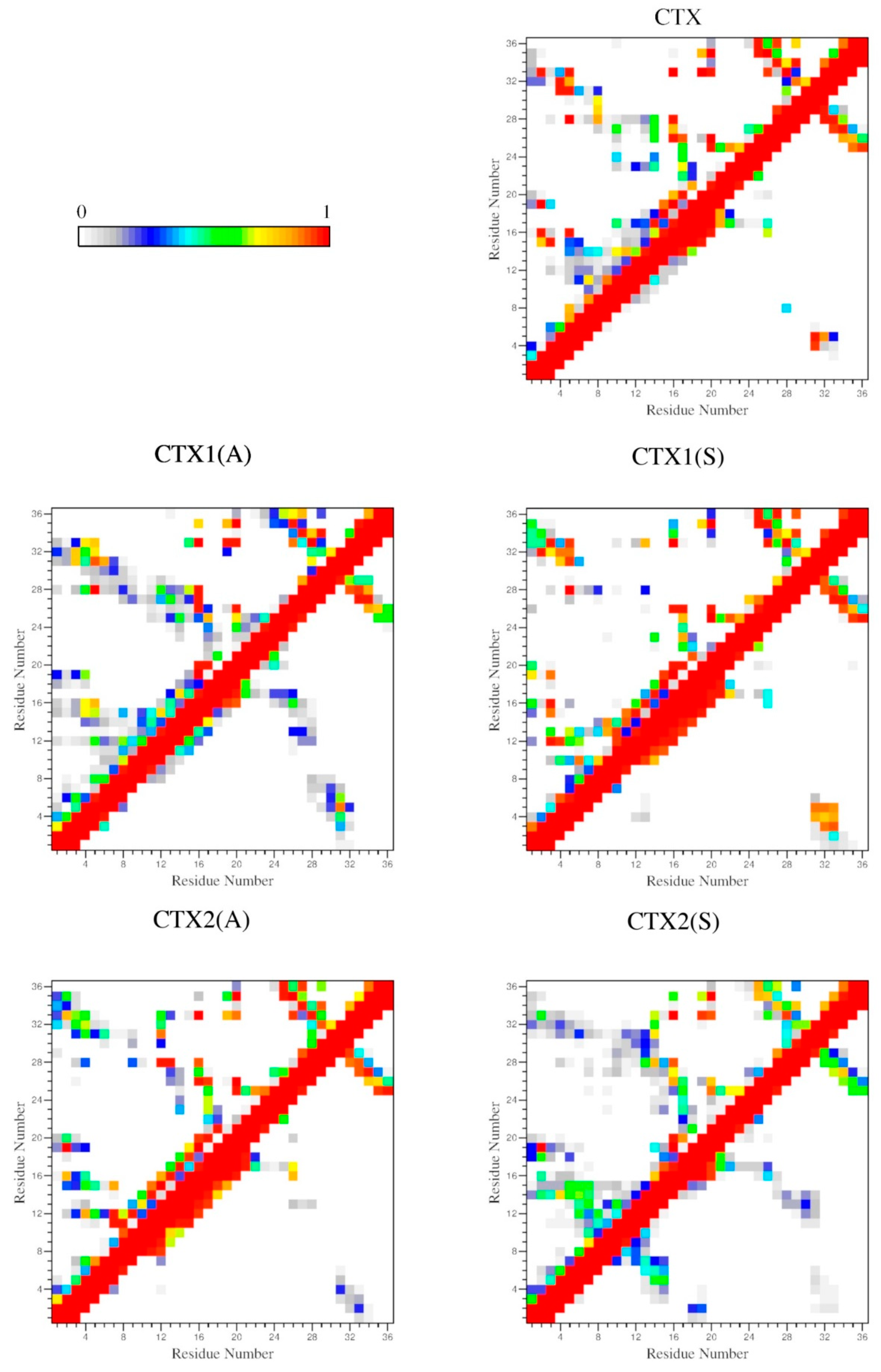
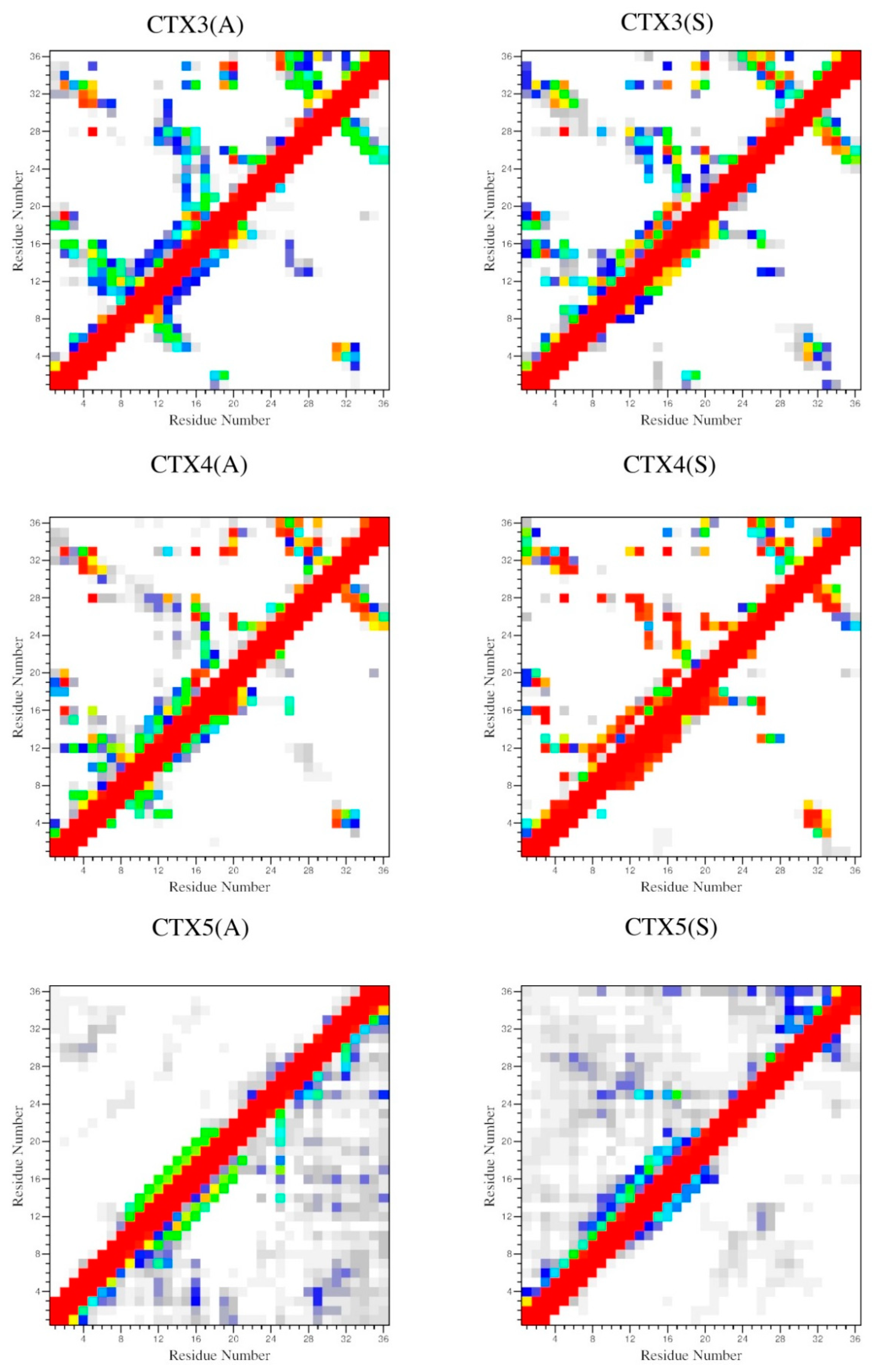
2.4. Interactions
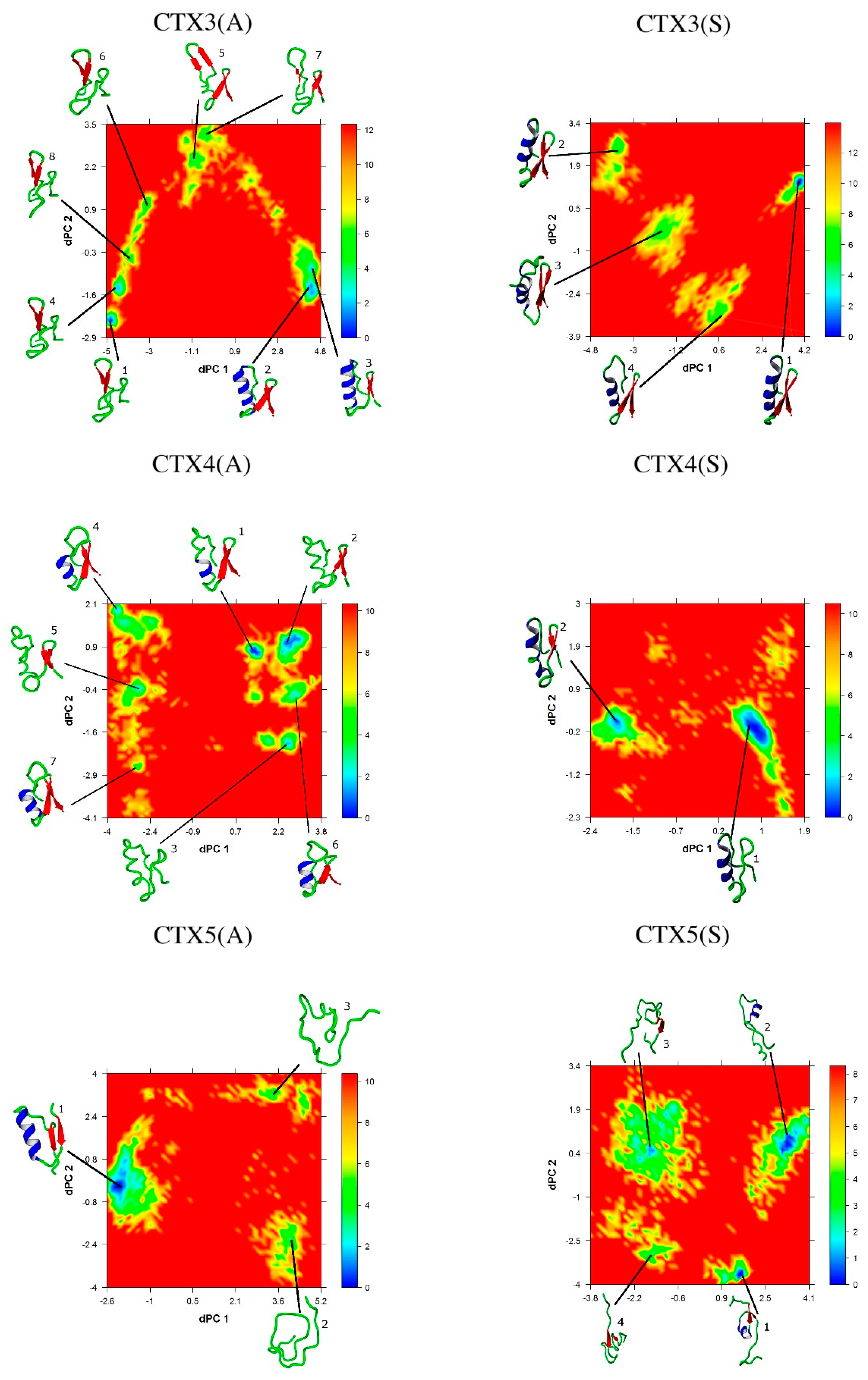
2.5. Conformational Analysis
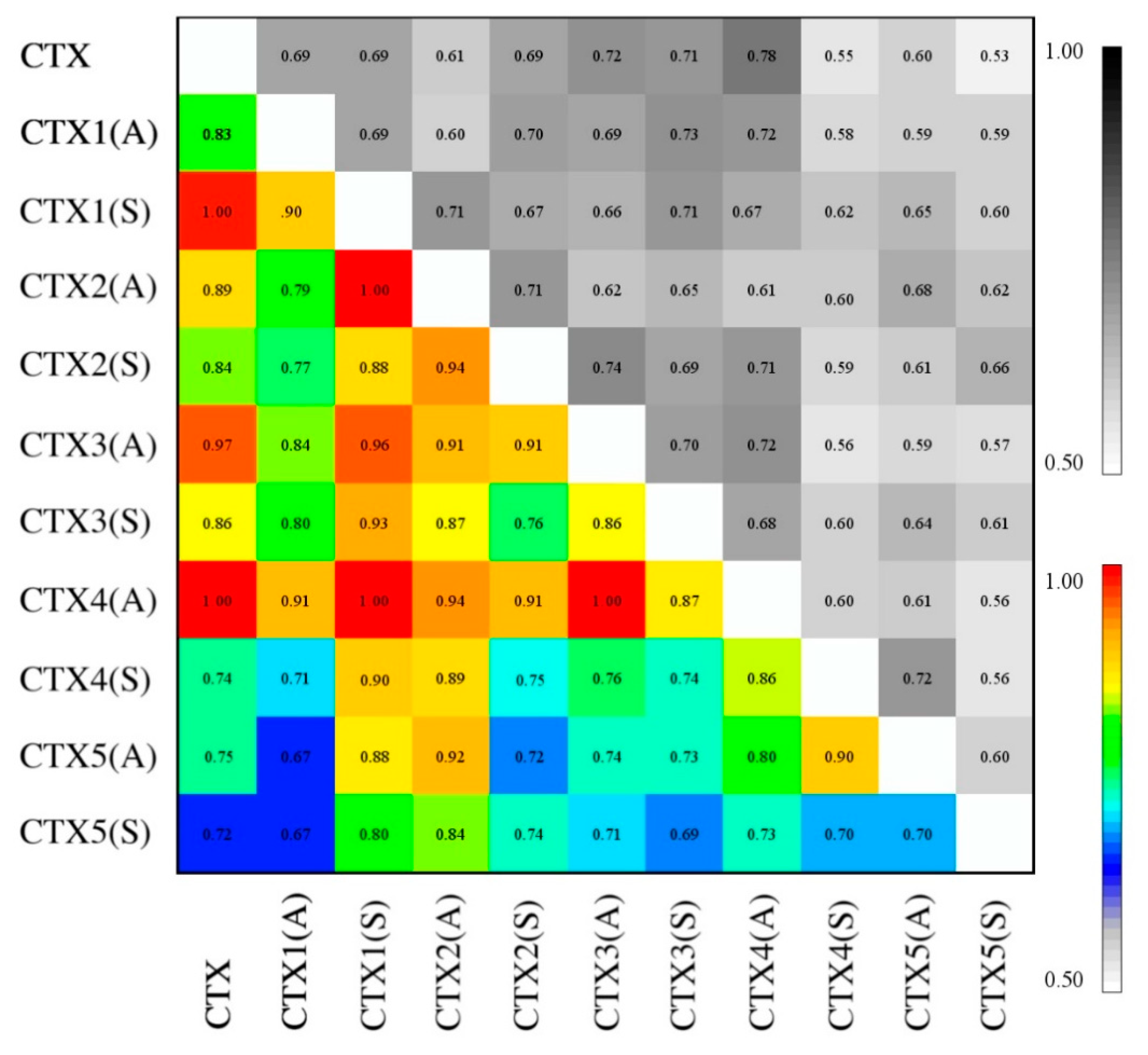
2.6. Essential Subspace Analysis
3. Discussion
4. Materials and Methods
4.1. Initial Peptide Structures
4.2. Molecular Dynamics
4.3. Trajectory Analysis
4.3.1. Biophysical Properties
4.3.2. Interactions
4.3.3. Conformational Analysis
4.3.4. Essential Subspace Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Abu | l-α-aminobutyric acid |
| AVG | average |
| BB–BB | Backbone–backbone |
| CTX | chlorotoxin |
| CD | circular dichroism |
| CI95 | One-sided 95% confidence interval |
| HPLC | high-performance liquid chromatography |
| MD | molecular dynamics |
| nRMSIP | normalized root-mean-square inner product |
| NMR | nuclear magnetic resonance spectroscopy |
| NPT | constant number, pressure, and temperature |
| Rg | radius of gyration |
| rSASA | relative solvent-accessible surface area |
| RMSD | root-mean-square deviation |
| RMSF | root-mean-square fluctuation |
| RMSIP | root-mean-square inner product |
| SASA | solvent-accessible surface area |
| SC–SC | sidechain–sidechain |
| SD | standard deviation |
Appendix A
Appendix A.1. Assignments of Force Field Parameters for L-α-Aminobutyric Acid (Abu)
[ ABU ]
[ atoms ]
N NH1 -0.470 0
HN H 0.310 1
CA CT1 0.070 2
HA HB1 0.090 3
CB CT2 -0.180 4
HB1 HA2 0.090 5
HB2 HA2 0.090 6
CG CT3 -0.270 7
HG1 HA3 0.090 8
HG2 HA3 0.090 9
HG3 HA3 0.090 10
C C 0.510 11
O O -0.510 12
[ bonds ]
CB CA
CG CB
N HN
N CA
C CA
C +N
CA HA
CB HB1
CB HB2
CG HG1
CG HG2
CG HG3
O C
[ impropers ]
N -C CA HN
C CA +N O
[ cmap ]
-C N CA C +N
|
Appendix A.2. MD Simulations of Model Peptides
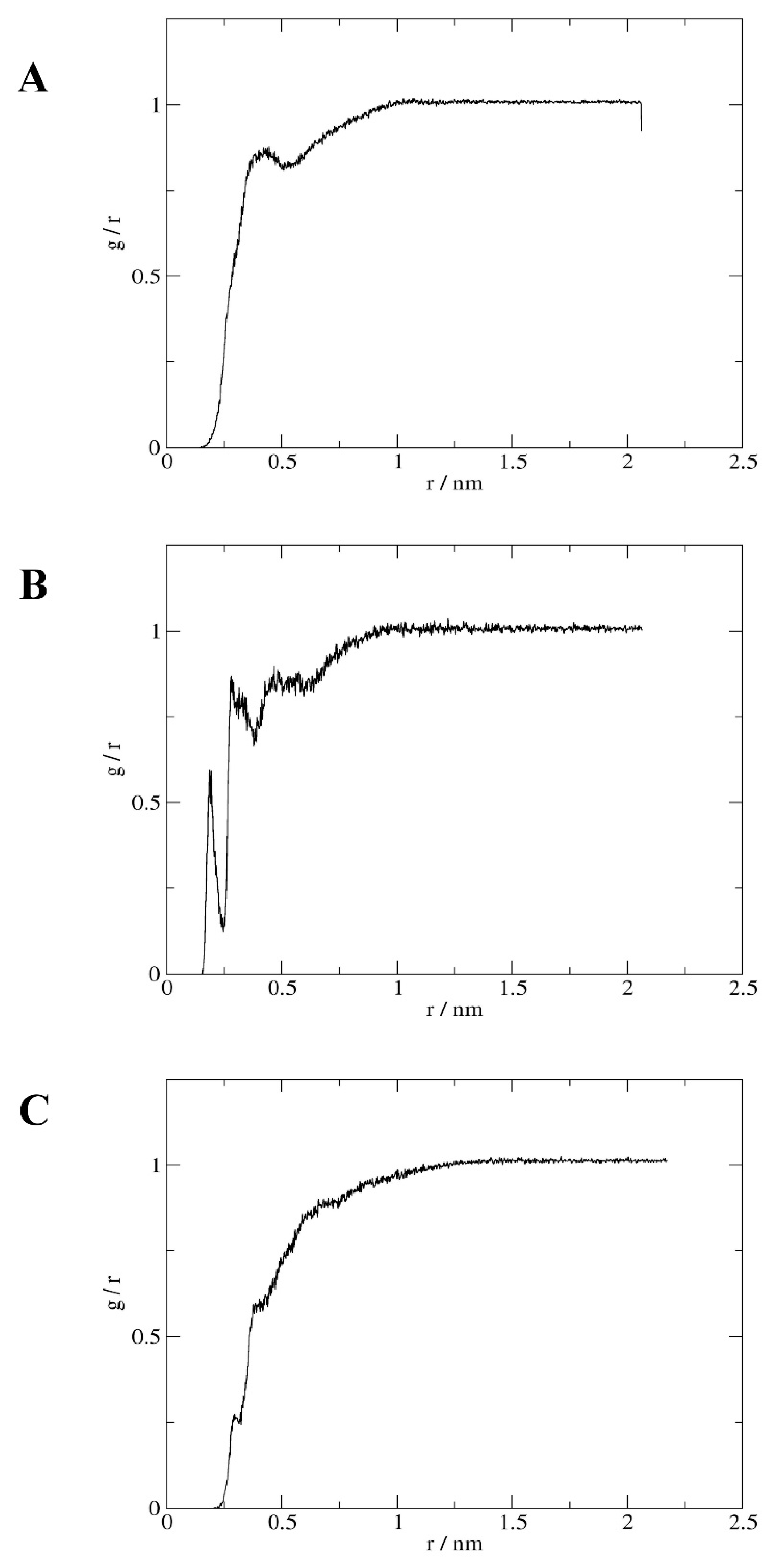
References
- DeBin, J.A.; Strichartz, G.R. Chloride Channel Inhibition by the venom of the scorpion Leiurus Quinquestriatus. Toxicon 1991, 29, 1403–1408. [Google Scholar] [CrossRef]
- DeBin, J.A.; Maggio, J.E.; Strichartz, G.R. Purification and characterization of chlorotoxin, a chloride channel ligand from the venom of the scorpion. Am. J. Physiol. 1993, 264 Pt 1, C361–C369. [Google Scholar] [CrossRef]
- Olsen, M.L.; Schade, S.; Lyons, S.A.; Amaral, M.D.; Sontheimer, H. Expression of voltage-gated chloride channels in human glioma cells. J. Neurosci. 2003, 23, 5572–5582. [Google Scholar] [CrossRef] [PubMed]
- Soroceanu, L.; Gillespie, Y.; Khazaeli, M.B.; Sontheimer, H. Use of chlorotoxin for targeting of primary brain tumors. Cancer Res. 1998, 58, 4871–4879. [Google Scholar] [PubMed]
- Lyons, S.A.; O’Neal, J.; Sontheimer, H. Chlorotoxin, a scorpion-derived peptide, specifically binds to gliomas and tumors of neuroectodermal origin. Glia 2002, 39, 162–173. [Google Scholar] [CrossRef] [PubMed]
- Mamelak, A.N.; Jacoby, D.B. Targeted delivery of antitumoral therapy to glioma and other malignancies with synthetic chlorotoxin (TM-601). Expert. Opin. Drug Deliv. 2007, 4, 175–186. [Google Scholar] [CrossRef]
- Veiseh, O.; Gunn, J.W.; Kievit, F.M.; Sun, C.; Fang, C.; Lee, J.S.H.; Zhang, M. Inhibition of tumor-cell invasion with chlorotoxin-bound superparamagnetic nanoparticles. Small 2009, 5, 256–264. [Google Scholar] [CrossRef]
- Veiseh, M.; Gabikian, P.; Bahrami, S.B.; Veiseh, O.; Zhang, M.; Hackman, R.C.; Ravanpay, A.C.; Stroud, M.R.; Kusuma, Y.; Hansen, S.J.; et al. Tumor paint: A chlorotoxin:Cy5.5 bioconjugate for intraoperative visualization of cancer foci. Cancer Res. 2007, 67, 6882–6888. [Google Scholar] [CrossRef]
- Akcan, M.; Stroud, M.R.; Hansen, S.J.; Clark, R.J.; Daly, N.L.; Craik, D.; Olson, J.M. Chemical re-engineering of chlorotoxin improves bioconjugation properties for tumor imaging and targeted therapy. J. Med. Chem. 2011, 54, 782–787. [Google Scholar] [CrossRef]
- Akcan, M.; Stroud, M.R.; Hansen, S.J.; Clark, R.J.; Daly, N.L.; Craik, D.; Olson, J.M. Correction to Chemical Re-engineering of Chlorotoxin Improves Bioconjugation Properties for Tumor Imaging and Targeted Therapy. J. Med. Chem. 2013, 56, 9807. [Google Scholar] [CrossRef]
- Rosso, J.P.; Rochat, H. Characterization of ten proteins from the venom of the Moroccan scorpion Androctonus mauretanicus mauretanicus, six of which are toxic to the mouse. Toxicon 1985, 23, 113–125. [Google Scholar] [CrossRef]
- Ali, S.A.; Stoeva, S.; Schütz, J.; Kayed, R.; Abbasi, A.; Zaidi, Z.H.; Voelter, W. Purification and primary structure of low molecular mass peptides from scorpion (Buthus sindicus) venom. Comput. Biochem. Physiol. A Mol. Integr. Physiol. 1998, 121, 323–332. [Google Scholar] [CrossRef]
- Possani, L.D.; Becerril, B.; Delepierre, M.; Tytgat, J. Scorpion toxins specific for Na+-channels. Eur. J. Biochem. 1999, 264, 287–300. [Google Scholar] [CrossRef] [PubMed]
- Possani, L.D.; Merino, E.; Corona, M.; Bolivar, F.; Becerril, B. Peptides and genes coding for scorpion toxins that affect ion-channels. Biochimie 2000, 82, 861–868. [Google Scholar] [CrossRef]
- Fry, B.G.; Roelants, K.; Champagne, D.E.; Scheib, H.; Tyndall, J.D.; King, G.F.; Nevalainen, T.J.; Norman, J.A.; Lewis, R.J.; Norton, R.S.; et al. The toxicogenomic multiverse: Convergent recruitment of proteins into animal venoms. Annu. Rev. Genomics Hum. Genet. 2009, 10, 483–511. [Google Scholar] [CrossRef] [PubMed]
- Bontems, F.; Roumestand, C.; Gilquin, B.; Menez, A.; Toma, F. Refined structure of charybdotoxin: Common motifs in scorpion toxins and insect defensins. Science 1991, 254, 1521–1523. [Google Scholar] [CrossRef] [PubMed]
- Bonmatin, J.M.; Bonnat, J.L.; Gallet, X.; Vovelle, F.; Ptak, M.; Reichart, J.M.; Hoffman, J.A.; Keppi, E.; Legrain, M.; Achstetter, T. Two-dimensional 1H NMR study of recombinant insect defensin A in water: Resonance assignments, secondary structure and global folding. J. Biomol. NMR 1992, 2, 235–256. [Google Scholar] [CrossRef]
- Cornet, B.; Bonmatin, J.M.; Hetru, C.; Hoffmann, J.A.; Ptak, M.; Vovelle, F. Refined three-dimensional solution structure of insect defensin A. Structure 1995, 3, 435–448. [Google Scholar] [CrossRef]
- Bruix, M.; Jimenez, M.A.; Santoro, J.; Gonzalez, C.; Colilla, F.J.; Mendez, E.; Rico, M. Solution structure of gamma 1-H and gamma 1-P thionins from barley and wheat endosperm determined by 1H-NMR: A structural motif common to toxic arthropod proteins. Biochemistry 1993, 32, 715–724. [Google Scholar] [CrossRef] [PubMed]
- Craik, D.J.; Daly, N.L.; Waine, C. The cystine knot motif in toxins and implications for drug design. Toxicon 2001, 39, 43–60. [Google Scholar] [CrossRef]
- Ali, S.A.; Alam, M.; Abbasi, A.; Undheim, E.A.B.; Fry, B.G.; Kalbacher, H.; Voelter, W. Structure-Activity Relationship of Chlorotoxin-Like Peptides. Toxins 2016, 8, 36. [Google Scholar] [CrossRef] [PubMed]
- Mouhat, S.; Jouirou, B.; Mosbah, A.; De Waard, M.; Sabatier, J.M. Diversity of folds in animal toxins acting on ion channels. Biochem. J. 2004, 378 Pt 3, 717–726. [Google Scholar] [CrossRef]
- Bulaj, G. Formation of disulfide bonds in proteins and peptides. Biotechnol. Adv. 2005, 23, 87–92. [Google Scholar] [CrossRef] [PubMed]
- Sabatier, J.M.; Lecomte, C.; Mabrouk, K.; Darbon, H.; Oughideni, R.; Canarelli, S.; Rochat, H.; Martin-Eauclaire, M.F.; van Rietschoten, J. Synthesis and characterization of leiurotoxin I analogs lacking one disulfide bridge: Evidence that disulfide pairing 3–21 is not required for full toxin activity. Biochemistry 1996, 35, 10641–10647. [Google Scholar] [CrossRef] [PubMed]
- Drakopoulou, E.; Vizzavona, J.; Neyton, J.; Aniort, V.; Bouet, F.; Virelizier, H.; Ménez, A.; Vita, C. Consequence of the removal of evolutionary conserved disulfide bridges on the structure and function of charybdotoxin and evidence that particular cysteine spacings govern specific disulfide bond formation. Biochemistry 1998, 37, 1292–1301. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Q.; Liang, S.; Martin, L.; Gasparini, S.; Menez, A.; Vita, C. Role of disulfide bonds in folding and activity of leiurotoxin I: Just two disulfides suffice. Biochemistry 2002, 41, 11488–11494. [Google Scholar] [CrossRef] [PubMed]
- Song, J.; Gilquin, B.; Jamin, N.; Drakopoulou, E.; Guenneugues, M.; Dauplais, M.; Vita, C.; Ménez, A. NMR solution structure of a two-disulfide derivative of charybdotoxin: Structural evidence for conservation of scorpion toxin alpha/beta motif and its hydrophobic side chain packing. Biochemistry 1997, 36, 3760–3766. [Google Scholar] [CrossRef] [PubMed]
- Ojeda, P.G.; Wang, C.K.; Craik, D.J. Chlorotoxin: Structure, activity, and potential uses in cancer therapy. Biopolymers 2016, 106, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Ojeda, P.G.; Chan, L.Y.; Poth, A.G.; Wang, C.K.; Craik, D.J. The role of disulfide bonds in structure and activity of chlorotoxin. Future Med. Chem. 2014, 6, 1617–1628. [Google Scholar] [CrossRef] [PubMed]
- Lippens, G.; Najib, J.; Wodak, S.J.; Tartar, A. NMR sequential assignments and solution structure of chlorotoxin, a small scorpion toxin that blocks chloride channels. Biochemistry 1995, 34, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Frishman, D.; Argos, P. Knowledge-based protein secondary structure assignment. Proteins 1995, 23, 566–579. [Google Scholar] [CrossRef]
- Vita, C.; Aniort, V.; Menez, A.; Toma, F. Charybdotoxin Analogs Missing One Disulfide Bridge. In Innovation and Perspectives in Solid Phase Synthesis: Peptides, Proteins and Nucleic Acids: Biological and Biomedical Applications, Proceedings of the Third International Symposium, Oxford, England, UK, 31 August–4 September 1993; Epton, R., Ed.; Mayflower Worldwide: Birmingham, UK, 1994; pp. 201–206. ISBN 0951573519-978-0951573519. [Google Scholar]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmüller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.; Mittal, J.; Feig, M.; Mackerell, A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone phi, psi and side-chain chi(1) and chi(2) dihedral angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- Mackerell, A.D., Jr.; Feig, M.; Brooks, C.L., 3rd. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2009, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Páll, S.; Abraham, M.J.; Kutzner, C.; Hess, B.; Lindahl, E. Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS. In Solving Software Challenges for Exascale: International Conference on Exascale Applications and Software Proceedings of the EASC2014, Stockholm, Sweden, 2–3 April 2014; Markidis, S., Laure, E., Eds.; Springer International Publishing: Heidelberg, Germany, 2015; pp. 3–27. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef]
- Van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Lindahl, E.; Hess, B.; van der Spoel, D. GROMACS 3.0: A package for molecular simulation and trajectory analysis. J. Mol. Mod. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Abraham, M.J.; van der Spoel, D.; Lindahl, E.; Hess, B.; the GROMACS Development Team. GROMACS User Manual Version 5.1.2. Available online: http://www.gromacs.org (accessed on 1 June 2017).
- Bjelkmar, P.; Larsson, P.; Cuendet, M.A.; Hess, B.; Lindahl, E. Implementation of the CHARMM Force Field in GROMACS: Analysis of Protein Stability Effects from Correction Maps, Virtual Interaction Sites, and Water Models. J. Chem. Theory Comput. 2010, 6, 459–466. [Google Scholar] [CrossRef] [PubMed]
- Krieger, E.; Vriend, G. YASARA View-molecular graphics for all devices—from smartphones to workstations. Bioinformatics 2014, 30, 2981–2982. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Klaus, W.; Broger, C.; Gerber, P.; Senn, H. Determination of the disulfide bonding pattern in proteins by local and global analysis of nuclear magnetic resonance data. Application to flavoridin. J. Mol. Biol. 1993, 232, 897–906. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Richards, F.M. The interpretation of protein structures: Estimation of static accessibility. J. Mol. Biol. 1971, 55, 379–400. [Google Scholar] [CrossRef]
- Zielenkiewicz, P.; Saenger, W. Residue solvent accessibilities in the unfolded polypeptide chain. Biophys. J. 1992, 63, 1483–1486. [Google Scholar] [CrossRef]
- Tien, M.Z.; Meyer, A.G.; Sydykova, D.K.; Spielman, S.J.; Wilke, C.O. Maximum allowed solvent accessibilities of residues in proteins. PLoS ONE 2013, 8, e80635. [Google Scholar] [CrossRef] [PubMed]
- White, A.D.; Keefe, A.J.; Ella-Menye, J.R.; Nowinski, A.K.; Shao, Q.; Pfaendtner, J.; Jiang, S. Free energy of solvated salt bridges: A simulation and experimental study. J. Phys. Chem. B 2013, 117, 7254–7259. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, B.L.; Pettitt, B.M. Effects of Acids, Bases, and Heteroatoms on Proximal Radial Distribution Functions for Proteins. J. Chem. Theory Comput. 2015, 11, 1399–1409. [Google Scholar] [CrossRef] [PubMed]
- Mu, Y.; Nguyen, P.H.; Stock, G. Energy landscape of a small peptide revealed by dihedral angle principal component analysis. Proteins 2005, 58, 45–52. [Google Scholar] [CrossRef] [PubMed]
- Altis, A.; Nguyen, P.H.; Hegger, R.; Stock, G. Dihedral angle principal component analysis of molecular dynamics simulations. J. Chem. Phys. 2007, 126, 244111. [Google Scholar] [CrossRef] [PubMed]
- Ligges, U.; Maechler, M. scatterplot3d—An R Package for Visualizing Multivariate Data. J. Stat. Softw. 2003, 8, 1–20. [Google Scholar] [CrossRef]
- Akima, H.; Gebhardt, A.; Petzold, T.; Maechler, M. Akima: Interpolation of Irregularly and Regularly Spaced Data. Available online: https://cran.r-project.org/web/packages/akima/ (accessed on 6 August 6 2018).
- Sarkar, D.; Andrews, F. latticeExtra: Extra Graphical Utilities Based on Lattice. Available online: https://cran.r-project.org/web/packages/latticeExtra/ (accessed on 6 August 2018).
- R Core Team. R: A language and environment for statistical computing. Available online: http://www.R-project.org/ (accessed on 6 August 2018).
- Maechler, M.; Rousseeuw, P.; Struyf, A.; Hubert, M.; Hornik, K.; Studer, M.; Roudier, P.; Gonzalez, J.; Kozlowski, K. Cluster: Methods for Cluster Analysis. Available online: https://cran.r-project.org/web/packages/cluster/ (accessed on 6 August 2018).
- Tan, P.-N.; Steinbach, M.; Kumar, V. Cluster Analysis: Basic Concepts and Algorithms. In Introduction to Data Mining, 2nd ed.; Pearson Addison Wesley: Boston, MA, USA, 2005; pp. 487–568. ISBN 0133128903-978-0133128901. [Google Scholar]
- Tan, P.-N.; Steinbach, M.; Kumar, V. Cluster Analysis: Additional Issues and Algorithms. In Introduction to Data Mining, 2nd ed.; Pearson Addison Wesley: Boston, MA, USA, 2005; pp. 569–650. ISBN 0133128903-978-0133128901. [Google Scholar]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Thinsungnoen, T.; Kaoungku, N.; Durongdumronchai, P.; Kerdprasop, K.; Kerdprasop, N. The Clustering Validity with Silhouette and Sum of Squared Errors. In Proceedings of the 3rd International Conference on Industrial Application Engineering, Kitakyushu, Japan, 28–31 March 2015; Ehara, F., Nakashima, S., Eds.; Institute of Industrial Applications Engineers (IIAE): Kitakyushu, Japan, 2015; Volume 3, pp. 44–51. [Google Scholar] [CrossRef]
- Andricioaei, I.; Karplus, M. On the calculation of entropy from covariance matrices of the atomic fluctuations. J. Chem. Phys. 2001, 115, 6289–6292. [Google Scholar] [CrossRef]
- Hess, B. Convergence of sampling in protein simulations. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002, 65 Pt 1, 031910. [Google Scholar] [CrossRef]
- D’Alessandro, M.; Paci, M.; Amadei, A. Characterization of the conformational behavior of peptide Contryphan Vn: A theoretical study. Biopolymers 2004, 74, 448–456. [Google Scholar] [CrossRef] [PubMed]
- Martin-Garcia, F.; Papaleo, E.; Gomez-Puertas, P.; Boomsma, W.; Lindorff-Larsen, K. Comparing molecular dynamics force fields in the essential subspace. PLoS ONE 2015, 10, e0121114. [Google Scholar] [CrossRef] [PubMed]
- Turpin, E.R.; Mulholland, S.; Teale, A.M.; Boyan, B.; Boneva, B.B.; Hirst, J.D. New CHARMM force field parameters for dehydrated amino acid residues, the key to lantibiotic molecular dynamics simulations. RSC Adv. 2014, 4, 48621–48631. [Google Scholar] [CrossRef]
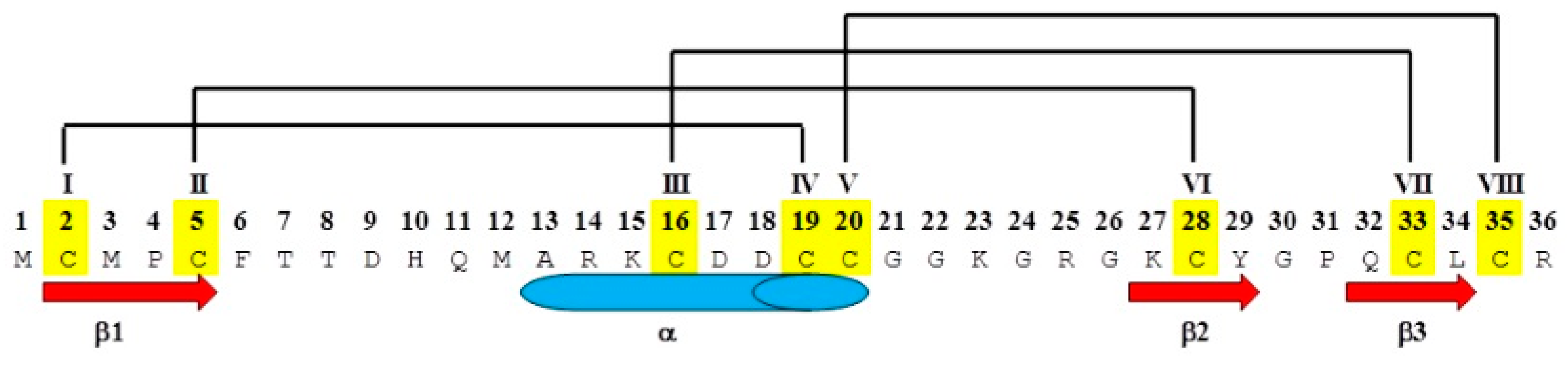

| Peptide | Abu Substitution | Ser-Substitution | Homology Disulfide Bond(s) Removed |
|---|---|---|---|
| CTX | None | ||
| CTX1(A) | 2, 19 | I–IV | |
| CTX1(S) | 2, 19 | I–IV | |
| CTX2(A) | 5, 28 | II–VI | |
| CTX2(S) | 5, 28 | II–VI | |
| CTX3(A) | 16, 33 | III–VII | |
| CTX3(S) | 16, 33 | III–VII | |
| CTX4(A) | 20, 35 | V–VIII | |
| CTX4(S) | 20, 35 | V–VII | |
| CTX5(A) | 2, 5, 16, 19, 20, 28, 33, 35 | All | |
| CTX5(S) | 2, 5, 16, 19, 20, 28, 33, 35 | All |
| Peptide | RMSD/nm | ρ | |||
|---|---|---|---|---|---|
| CTX a | AVG b | α-Helix | β-Sheet | β-Turn/Bend | |
| CTX | 0.73 ± 0.02 | 0.73 ± 0.02 | 0.31 ± 0.05 | 0.16 ± 0.02 | 0.17 ± 0.05 |
| CTX1(A) | 0.71 ± 0.02 | 0.74 ± 0.02 | 0.39 ± 0.09 | 0.14 ± 0.05 | 0.11 ± 0.09 |
| CTX1(S) | 0.73 ± 0.02 | 0.73 ± 0.02 | 0.27 ± 0.04 | 0.20 ± 0.03 | 0.26 ± 0.02 |
| CTX2(A) | 0.73 ± 0.02 | 0.73 ± 0.02 | 0.23 ± 0.07 | 0.16 ± 0.03 | 0.31 ± 0.04 |
| CTX2(S) | 0.73 ± 0.02 | 0.74 ± 0.02 | 0.34 ± 0.08 | 0.16 ± 0.08 | 0.08 ± 0.07 |
| CTX3(A) | 0.73 ± 0.02 | 0.76 ± 0.02 | 0.31 ± 0.07 | 0.19 ± 0.06 | 0.13 ± 0.14 |
| CTX3(S) | 0.73 ± 0.02 | 0.72 ± 0.02 | 0.29 ± 0.06 | 0.13 ± 0.06 | 0.22 ± 0.08 |
| CTX4(A) | 0.73 ± 0.02 | 0.72 ± 0.02 | 0.32 ± 0.08 | 0.16 ± 0.04 | 0.19 ± 0.07 |
| CTX4(S) | 0.72 ± 0.02 | 0.72 ± 0.02 | 0.30 ± 0.06 | 0.14 ± 0.04 | 0.27 ± 0.06 |
| CTX5(A) | 0.72 ± 0.02 | 0.61 ± 0.02 | 0.28 ± 0.09 | 0.03 ± 0.05 | 0.21 ± 0.14 |
| CTX5(S) | 0.73 ± 0.02 | 0.65 ± 0.02 | 0.30 ± 0.09 | 0.05 ± 0.06 | 0.09 ± 0.10 |
| D (ρ) | ||||
|---|---|---|---|---|
| Peptide | 2–19 | 5–28 | 16–33 | 20–35 |
| CTX | 0.24 ± 0.01 (0.98) | 0.21 ± 0.01 (0.99) | 0.26 ± 0.01 (0.71) | 0.21 ± 0.01 (1.00) |
| CTX1(A) | 0.45 ± 0.08 (0.02) | 0.22 ± 0.02 (1.00) | 0.21 ± 0.01 (1.00) | 0.21 ± 0.01 (1.00) |
| CTX1(S) | 0.43 ± 0.04 (0.00) | 0.22 ± 0.02 (1.00) | 0.21 ± 0.01 (1.00) | 0.21 ± 0.01 (1.00) |
| CTX2(A) | 0.22 ± 0.02 (0.97) | 0.49 ± 0.08 (0.00) | 0.24 ± 0.02 (0.84) | 0.21 ± 0.01 (1.00) |
| CTX2(S) | 0.23 ± 0.02 (0.89) | 0.46 ± 0.11 (0.01) | 0.21 ± 0.02 (0.98) | 0.21 ± 0.01 (1.00) |
| CTX3(A) | 0.24 ± 0.02 (0.67) | 0.22 ± 0.01 (1.00) | 0.33 ± 0.07 (0.13) | 0.21 ± 0.01 (1.00) |
| CTX3(S) | 0.24 ± 0.02 (0.77) | 0.22 ± 0.01 (0.99) | 0.26 ± 0.05 (0.70) | 0.21 ± 0.01 (1.00) |
| CTX4(A) | 0.22 ± 0.02 (0.99) | 0.22 ± 0.01 (1.00) | 0.24 ± 0.02 (0.80) | 0.22 ± 0.03 (0.90) |
| CTX4(S) | 0.23 ± 0.01 (0.99) | 0.21 ± 0.01 (1.00) | 0.23 ± 0.01 (1.00) | 0.30 ± 0.08 (0.39) |
| CTX5(A) | 0.62 ± 0.28 (0.04) | 0.65 ± 0.22 (0.01) | 0.55 ± 0.18 (0.01) | 0.62 ± 0.19 (0.02) |
| CTX5(S) | 0.78 ± 0.30 (0.01) | 0.69 ± 0.28 (0.05) | 0.70 ± 0.21 (0.00) | 0.75 ± 0.25 (0.00) |
| Peptide | Residue | |||||||
|---|---|---|---|---|---|---|---|---|
| 2 | 5 | 16 | 19 | 20 | 28 | 33 | 35 | |
| CTX | 0.066 | 0.044 | 0.013 | 0.076 | 0.020 | 0.049 | 0.019 | 0.094 |
| (0.27) | (0.09) | (0.02) | (0.38) | (0.14) | (0.10) | (0.11) | (0.45) | |
| CTX1(A) | 0.173 | 0.016 | 0.012 | 0.113 | 0.022 | 0.037 | 0.017 | 0.086 |
| (0.79) | (0.08) | (0.01) | (0.50) | (0.15) | (0.11) | (0.15) | (0.44) | |
| CTX1(S) | 0.147 | 0.070 | 0.028 | 0.121 | 0.018 | 0.087 | 0.041 | 0.081 |
| (0.56) | (0.16) | (0.01) | (0.55) | (0.15) | (0.41) | (0.04) | (0.38) | |
| CTX2(A) | 0.077 | 0.144 | 0.013 | 0.084 | 0.015 | 0.060 | 0.012 | 0.081 |
| (0.24) | (0.56) | (0.01) | (0.42) | (0.16) | (0.30) | (0.07) | (0.41) | |
| CTX2(S) | 0.086 | 0.186 | 0.033 | 0.066 | 0.027 | 0.104 | 0.032 | 0.079 |
| (0.27) | (0.50) | (0.04) | (0.27) | (0.17) | (0.30) | (0.17) | (0.40) | |
| CTX3(A) | 0.090 | 0.035 | 0.078 | 0.059 | 0.025 | 0.044 | 0.053 | 0.070 |
| (0.33) | (0.10) | (0.15) | (0.23) | (0.15) | (0.18) | (0.24) | (0.32) | |
| CTX3(S) | 0.079 | 0.032 | 0.050 | 0.061 | 0.029 | 0.048 | 0.060 | 0.086 |
| (0.37) | (0.09) | (0.02) | (0.30) | (0.17) | (0.22) | (0.14) | (0.41) | |
| CTX4(A) | 0.075 | 0.032 | 0.031 | 0.093 | 0.038 | 0.052 | 0.024 | 0.111 |
| (0.22) | (0.06) | (0.02) | (0.46) | (0.15) | (0.25) | (0.07) | (0.49) | |
| CTX4(S) | 0.082 | 0.006 | 0.024 | 0.076 | 0.046 | 0.026 | 0.025 | 0.165 |
| (0.33) | (0.05) | (0.00) | (0.48) | (0.13) | (0.20) | (0.03) | (0.56) | |
| CTX5(A) | 0.101 | 0.138 | 0.101 | 0.138 | 0.126 | 0.124 | 0.123 | 0.138 |
| (0.69) | (0.61) | (0.35) | (0.64) | (0.58) | (0.54) | (0.53) | (0.59) | |
| CTX5(S) | 0.203 | 0.194 | 0.156 | 0.166 | 0.202 | 0.172 | 0.182 | 0.204 |
| (0.76) | (0.72) | (0.44) | (0.65) | (0.75) | (0.53) | (0.62) | (0.71) | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gregory, A.J.; Voit-Ostricki, L.; Lovas, S.; Watts, C.R. Effects of Selective Substitution of Cysteine Residues on the Conformational Properties of Chlorotoxin Explored by Molecular Dynamics Simulations. Int. J. Mol. Sci. 2019, 20, 1261. https://doi.org/10.3390/ijms20061261
Gregory AJ, Voit-Ostricki L, Lovas S, Watts CR. Effects of Selective Substitution of Cysteine Residues on the Conformational Properties of Chlorotoxin Explored by Molecular Dynamics Simulations. International Journal of Molecular Sciences. 2019; 20(6):1261. https://doi.org/10.3390/ijms20061261
Chicago/Turabian StyleGregory, Andrew J., Leah Voit-Ostricki, Sándor Lovas, and Charles R. Watts. 2019. "Effects of Selective Substitution of Cysteine Residues on the Conformational Properties of Chlorotoxin Explored by Molecular Dynamics Simulations" International Journal of Molecular Sciences 20, no. 6: 1261. https://doi.org/10.3390/ijms20061261
APA StyleGregory, A. J., Voit-Ostricki, L., Lovas, S., & Watts, C. R. (2019). Effects of Selective Substitution of Cysteine Residues on the Conformational Properties of Chlorotoxin Explored by Molecular Dynamics Simulations. International Journal of Molecular Sciences, 20(6), 1261. https://doi.org/10.3390/ijms20061261