Modeling the Effect of Hypoxia and DNA Repair Inhibition on Cell Survival after Photon Irradiation
Abstract
1. Introduction
2. Results
2.1. Modeling Hypoxia-Induced Radioresistence
2.2. Modeling Cell Survival of DNA-PK-Impaired Cell Lines
2.3. Modeling Cell Survival of Cell Lines with Pharmacologically-Inhibited ATM
3. Discussion
4. Materials and Methods
4.1. Experimental Data from Literature
4.2. Cell Culture, Clonogenic Survival Assay, and Irradiation
4.3. Dose Planning and Simulations
4.4. Modeling Approach
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| LET | Linear energy transfer |
| UNIVERSE | Unique and versatile engine |
| DSB | (DNA) Double strand break |
| iDSB | Isolated DSB |
| cDSB | Complex DSB |
| OER | Oxygen enhancement ratio |
| HRF | Hypoxia reduction factor |
| ATM | Ataxia-telangiectasia mutated |
| NHEJ | Non-homologous end joining |
| DDR | DNA damage repair |
| CHO | Chinese hamster ovary |
| GLOBLE | Giant loop binary lesion |
| CT | Computed tomography |
| LQ | Linear quadratic (model) |
References
- Delaney, G.; Jacob, S.; Featherstone, C.; Barton, M. The role of radiotherapy in cancer treatment: Estimating optimal utilization from a review of evidence-based clinical guidelines. Cancer 2005, 104, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
- Dale, R.G.; Jones, B. Radiobiological Modelling in Radiation Oncology; British Institute of Radiology: London, UK, 2007; ISBN 978-0-905749-60-0. [Google Scholar]
- Joiner, M.; van der Kogel, A. Basic Clinical Radiobiology, 5th ed.; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2018; ISBN 978-1-4441-7963-7. [Google Scholar]
- Tawk, B.; Schwager, C.; Deffaa, O.; Dyckhoff, G.; Warta, R.; Linge, A.; Krause, M.; Weichert, W.; Baumann, M.; Herold-Mende, C.; et al. Comparative analysis of transcriptomics based hypoxia signatures in head-and neck squamous cell carcinoma. Radiother. Oncol. 2016, 118, 350–358. [Google Scholar] [CrossRef] [PubMed]
- Rofstad, E.K.; Sundfør, K.; Lyng, H.; Tropé, C.G. Hypoxia-induced treatment failure in advanced squamous cell carcinoma of the uterine cervix is primarily due to hypoxia-induced radiation resistance rather than hypoxia-induced metastasis. Br. J. Cancer 2000, 83, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Carlson, D.J.; Stewart, R.D.; Semenenko, V.A. Effects of oxygen on intrinsic radiation sensitivity: A test of the relationship between aerobic and hypoxic linear-quadratic (LQ) model parameters. Med. Phys. 2006, 33, 3105–3115. [Google Scholar] [CrossRef]
- Batey, M.A.; Zhao, Y.; Kyle, S.; Richardson, C.; Slade, A.; Martin, N.M.B.; Lau, A.; Newell, D.R.; Curtin, N.J. Preclinical evaluation of a novel ATM inhibitor, KU59403, in vitro and in vivo in p53 functional and dysfunctional models of human cancer. Mol. Cancer Ther. 2013, 12, 959–967. [Google Scholar] [CrossRef]
- Dohmen, A.J.C.; Qiao, X.; Duursma, A.; Wijdeven, R.H.; Lieftink, C.; Hageman, F.; Morris, B.; Halonen, P.; Vens, C.; van den Brekel, M.W.M.; et al. Identification of a novel ATM inhibitor with cancer cell specific radiosensitization activity. Oncotarget 2017, 8, 73925–73937. [Google Scholar] [CrossRef]
- Durant, S.T.; Zheng, L.; Wang, Y.; Chen, K.; Zhang, L.; Zhang, T.; Yang, Z.; Riches, L.; Trinidad, A.G.; Fok, J.H.L.; et al. The brain-penetrant clinical ATM inhibitor AZD1390 radiosensitizes and improves survival of preclinical brain tumor models. Sci. Adv. 2018, 4, eaat1719. [Google Scholar] [CrossRef] [PubMed]
- Klein, C.; Dokic, I.; Mairani, A.; Mein, S.; Brons, S.; Häring, P.; Haberer, T.; Jäkel, O.; Zimmermann, A.; Zenke, F.; et al. Overcoming hypoxia-induced tumor radioresistance in non-small cell lung cancer by targeting DNA-dependent protein kinase in combination with carbon ion irradiation. Radiat. Oncol. 2017, 12, 208. [Google Scholar] [CrossRef]
- Mairani, A.; Böhlen, T.T.; Dokic, I.; Cabal, G.; Brons, S.; Haberer, T. Modelling of cell killing due to sparsely ionizing radiation in normoxic and hypoxic conditions and an extension to high LET radiation. Int. J. Radiat. Biol. 2013, 89, 782–793. [Google Scholar] [CrossRef]
- Elsässer, T.; Weyrather, W.K.; Friedrich, T.; Durante, M.; Iancu, G.; Krämer, M.; Kragl, G.; Brons, S.; Winter, M.; Weber, K.-J.; et al. Quantification of the Relative Biological Effectiveness for Ion Beam Radiotherapy: Direct Experimental Comparison of Proton and Carbon Ion Beams and a Novel Approach for Treatment Planning. Int. J. Radiat. Oncol. Biol. Phys. 2010, 78, 1177–1183. [Google Scholar] [CrossRef]
- Friedrich, T.; Durante, M.; Scholz, M. Modeling cell survival after photon irradiation based on double-strand break clustering in megabase pair chromatin loops. Radiat. Res. 2012, 178, 385–394. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, T.; Scholz, U.; Elsässer, T.; Durante, M.; Scholz, M. Calculation of the biological effects of ion beams based on the microscopic spatial damage distribution pattern. Int. J. Radiat. Oncol. Biol. Phys. 2012, 88, 103–107. [Google Scholar] [CrossRef] [PubMed]
- Yokota, H.; van den Engh, G.; Hearst, J.E.; Sachs, R.K.; Trask, B.J. Evidence for the organization of chromatin in megabase pair-sized loops arranged along a random walk path in the human G0/G1 interphase nucleus. J. Cell Biol. 1995, 130, 1239–1249. [Google Scholar] [CrossRef] [PubMed]
- Sachs, R.K.; van den Engh, G.; Trask, B.; Yokota, H.; Hearst, J.E. A random-walk/giant-loop model for interphase chromosomes. Proc. Natl. Acad. Sci. USA 1995, 92, 2710–2714. [Google Scholar] [CrossRef] [PubMed]
- Solovjeva, L.; Svetlova, M.; Stein, G.; Chagin, V.; Rozanov, Y.; Zannis-Hadjopoulos, M.; Price, G.; Tomilin, N. Conformation of Replicated Segments of Chromosome Fibres in Human S-phase Nucleus. Chromosome Res. 1998, 6, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Johnston, P.J.; Bryant, P.E. A component of DNA double-strand break repair is dependent on the spatial orientation of the lesions within the higher-order structures of chromatin. Int. J. Radiat. Biol. 1994, 66, 531–536. [Google Scholar] [CrossRef]
- Johnston, P.J.; Olive, P.L.; Bryant, P.E. Higher-order chromatin structure-dependent repair of DNA double-strand breaks: Modeling the elution of DNA from nucleoids. Radiat. Res. 1997, 148, 561–567. [Google Scholar] [CrossRef]
- Johnston, P.J.; MacPhail, S.H.; Banáth, J.P.; Olive, P.L. Higher-order chromatin structure-dependent repair of DNA double-strand breaks: Factors affecting elution of DNA from nucleoids. Radiat. Res. 1998, 149, 533–542. [Google Scholar] [CrossRef]
- Gauter, B.; Zlobinskaya, O.; Weber, K.-J. Rejoining of radiation-induced DNA double-strand breaks: Pulsed-field electrophoresis analysis of fragment size distributions after incubation for repair. Radiat. Res. 2002, 157, 721–733. [Google Scholar] [CrossRef]
- Tommasino, F.; Friedrich, T.; Scholz, U.; Taucher-Scholz, G.; Durante, M.; Scholz, M. A DNA double-strand break kinetic rejoining model based on the local effect model. Radiat. Res. 2013, 180, 524–538. [Google Scholar] [CrossRef]
- Tommasino, F.; Friedrich, T.; Jakob, B.; Meyer, B.; Durante, M.; Scholz, M. Induction and Processing of the Radiation-Induced Gamma-H2AX Signal and Its Link to the Underlying Pattern of DSB: A Combined Experimental and Modelling Study. PLoS ONE 2015, 10, e0129416. [Google Scholar] [CrossRef][Green Version]
- Banáth, J.P.; Klokov, D.; MacPhail, S.H.; Banuelos, C.A.; Olive, P.L. Residual gammaH2AX foci as an indication of lethal DNA lesions. BMC Cancer 2010, 10, 4. [Google Scholar] [CrossRef] [PubMed]
- Koch, U.; Höhne, K.; von Neubeck, C.; Thames, H.D.; Yaromina, A.; Dahm-Daphi, J.; Baumann, M.; Krause, M. Residual γH2AX foci predict local tumour control after radiotherapy. Radiother. Oncol. 2013, 108, 434–439. [Google Scholar] [CrossRef] [PubMed]
- Hufnagl, A.; Herr, L.; Friedrich, T.; Durante, M.; Taucher-Scholz, G.; Scholz, M. The link between cell-cycle dependent radiosensitivity and repair pathways: A model based on the local, sister-chromatid conformation dependent switch between NHEJ and HR. DNA Repair (Amst.) 2015, 27, 28–39. [Google Scholar] [CrossRef] [PubMed]
- Carlson, D.J.; Keall, P.J.; Loo, B.W.; Chen, Z.J.; Brown, J.M. Hypofractionation results in reduced tumor cell kill compared to conventional fractionation for tumors with regions of hypoxia. Int. J. Radiat. Oncol. Biol. Phys. 2011, 79, 1188–1195. [Google Scholar] [CrossRef] [PubMed]
- Alper, T.; Howard-Flanders, P. Role of Oxygen in Modifying the Radiosensitivity of E. Coli B. Nature 1956, 178, 978–979. [Google Scholar] [CrossRef] [PubMed]
- Blackford, A.N.; Jackson, S.P. ATM, ATR, and DNA-PK: The Trinity at the Heart of the DNA Damage Response. Mol. Cell 2017, 66, 801–817. [Google Scholar] [CrossRef]
- Cartwright, I.M.; Su, C.; Haskins, J.S.; Salinas, V.A.; Sunada, S.; Yu, H.; Uesaka, M.; Hirakawa, H.; Chen, D.J.; Fujimori, A.; et al. DNA Repair Deficient Chinese Hamster Ovary Cells Exhibiting Differential Sensitivity to Charged Particle Radiation under Aerobic and Hypoxic Conditions. Int. J. Mol. Sci. 2018, 19, 2228. [Google Scholar] [CrossRef]
- Jeggo, P.A.; Kemp, L.M. X-ray-sensitive mutants of Chinese hamster ovary cell line isolation and cross-sensitivity to other DNA-damaging agents. Mutat. Res. DNA Repair Rep. 1983, 112, 313–327. [Google Scholar] [CrossRef]
- Whitmore, G.F.; Varghese, A.J.; Gulyas, S. Cell Cycle Responses of Two X-ray Sensitive Mutants Defective in DNA Repair. Int. J. Radiat. Biol. 1989, 56, 657–665. [Google Scholar] [CrossRef]
- Kastan, M.B.; Lim, D.S. The many substrates and functions of ATM. Nat. Rev. Mol. Cell Biol. 2000, 1, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Shiloh, Y. ATM and ATR: Networking cellular responses to DNA damage. Curr. Opin. Genet. Dev. 2001, 11, 71–77. [Google Scholar] [CrossRef]
- Shiloh, Y.; Kastan, M.B. ATM: Genome stability, neuronal development, and cancer cross paths. Adv. Cancer Res. 2001, 83, 209–254. [Google Scholar] [PubMed]
- Frankenberg-Schwager, M. Review of repair kinetics for DNA damage induced in eukaryotic cells in vitro by ionizing radiation. Radiother. Oncol. 1989, 14, 307–320. [Google Scholar] [CrossRef]
- Prise, K.M.; Ahnström, G.; Belli, M.; Carlsson, J.; Frankenberg, D.; Kiefer, J.; Löbrich, M.; Michael, B.D.; Nygren, J.; Simone, G.; et al. A review of dsb induction data for varying quality radiations. Int. J. Radiat. Biol. 1998, 74, 173–184. [Google Scholar] [CrossRef]
- Prise, K.M.; Pinto, M.; Newman, H.C.; Michael, B.D. A review of studies of ionizing radiation-induced double-strand break clustering. Radiat. Res. 2001, 156, 572–576. [Google Scholar] [CrossRef]
- Asaithamby, A.; Chen, D.J. Cellular responses to DNA double-strand breaks after low-dose γ-irradiation. Nucleic Acids Res. 2009, 37, 3912–3923. [Google Scholar] [CrossRef]
- Freyer, J.P.; Jarrett, K.; Carpenter, S.; Raju, M.R. Oxygen enhancement ratio as a function of dose and cell cycle phase for radiation-resistant and sensitive CHO cells. Radiat. Res. 1991, 127, 297–307. [Google Scholar] [CrossRef]
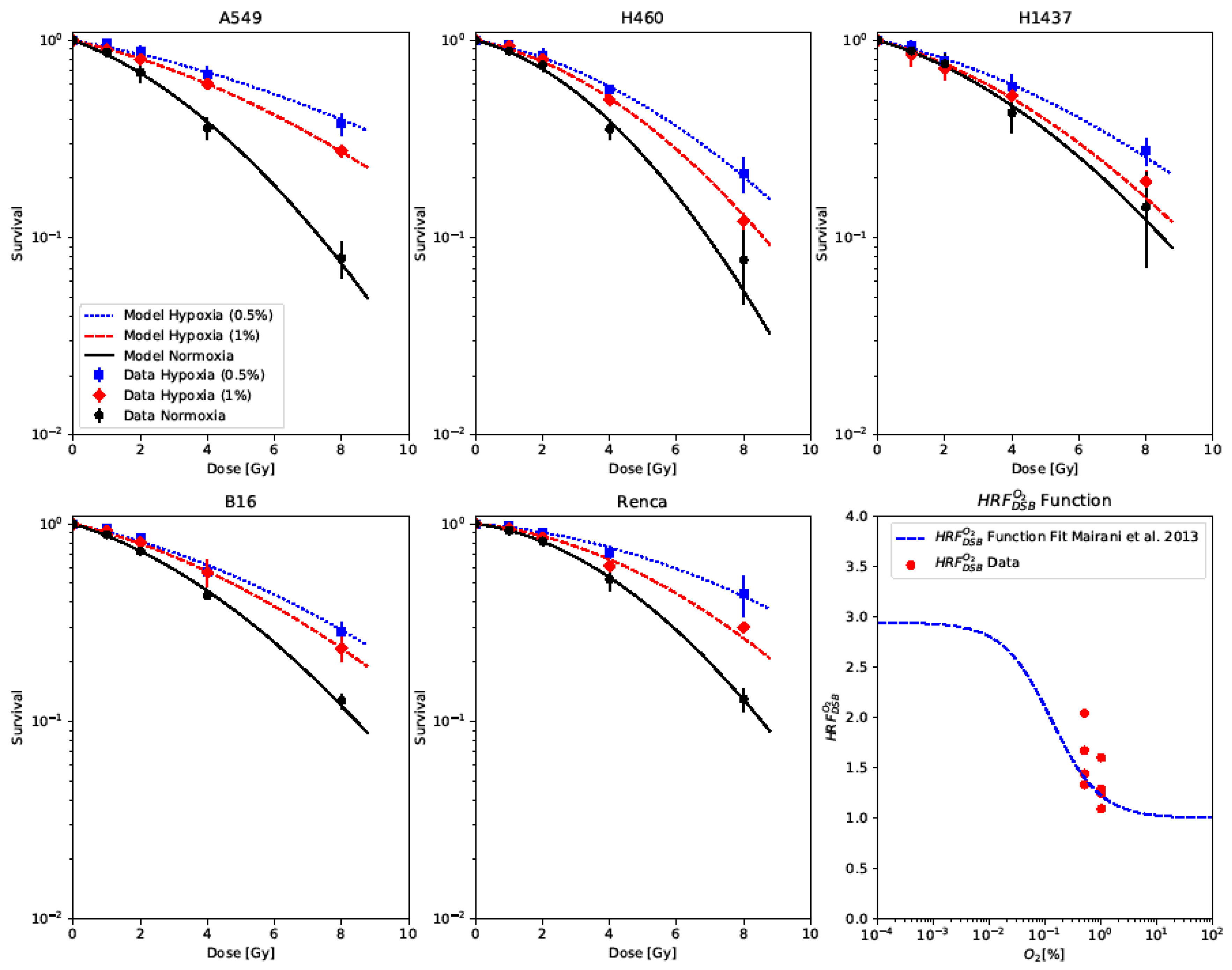
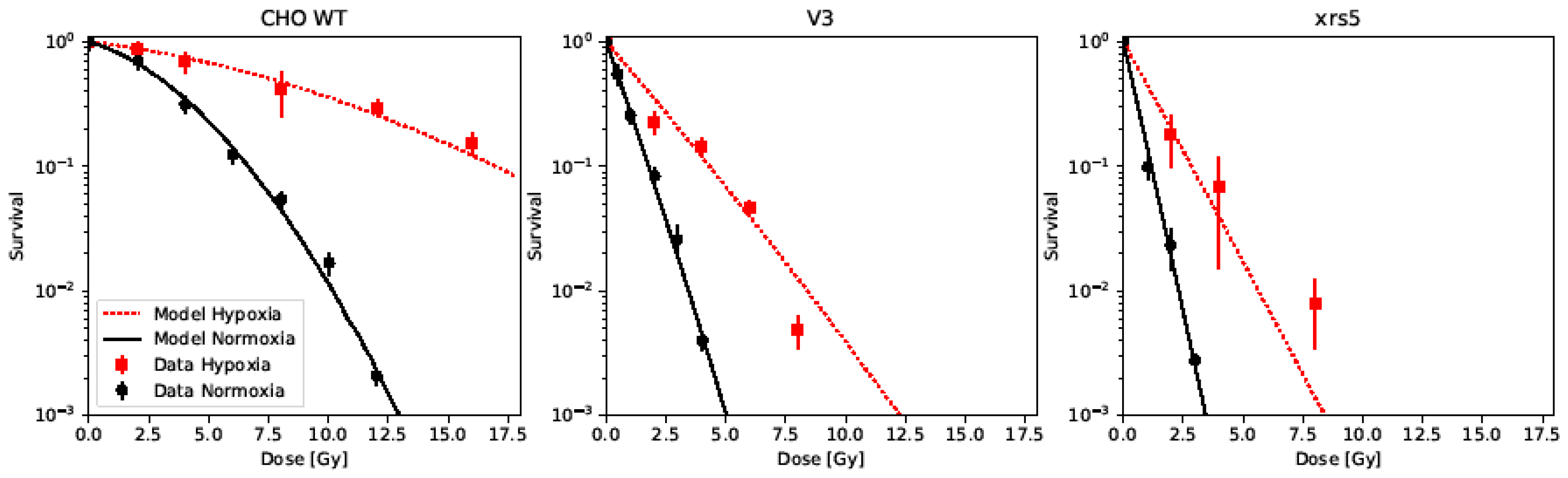
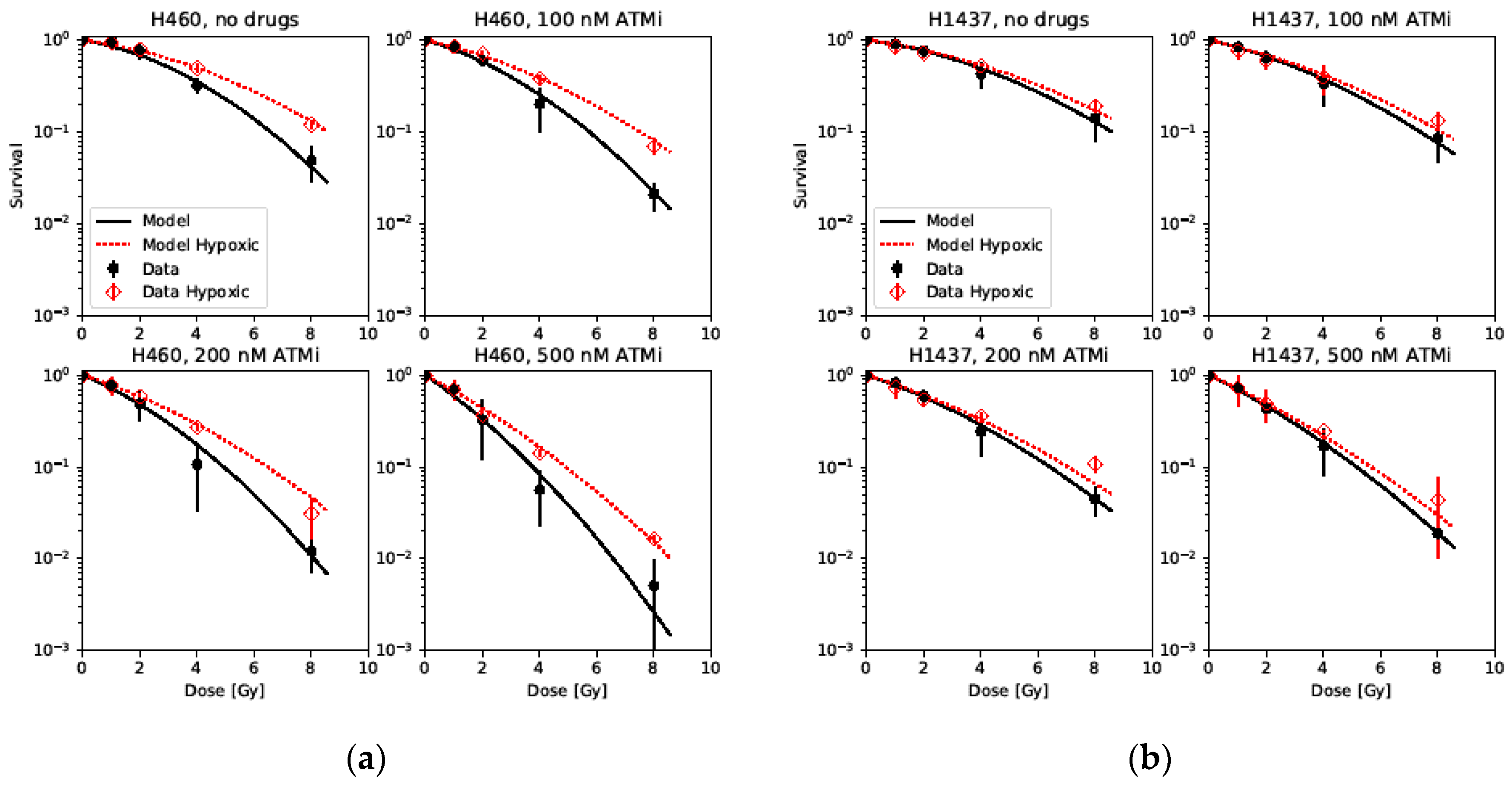
| Cell Line | ||||
|---|---|---|---|---|
| A549 | 4.83 × 10−3 ± 0.88 × 10−3 | 1.69 × 10−1 ± 0.31 × 10−1 | 1.60 | 2.04 |
| H460 | 3.28 × 10−3 ± 1.20 × 10−3 | 2.41 × 10−1 ± 0.86 × 10−1 | 1.24 | 1.44 |
| H1437 | 3.83 × 10−3 ± 0.83 × 10−3 | 1.37 × 10−1 ± 0.38 × 10−1 | 1.09 | 1.33 |
| B16F10 | 4.05 × 10−3 ± 0.44 × 10−3 | 1.34 × 10−1 ± 0.18 × 10−1 | 1.29 | 1.44 |
| Renca | 1.67 × 10−3 ± 0.18 × 10−3 | 2.04 × 10−1 ± 0.06 × 10−1 | 1.28 | 1.67 |
| Cell Line | RSF V3 | RSF Xrs5 | |||
|---|---|---|---|---|---|
| CHO WT | 4.38 × 10−3 ± 1.37 × 10−3 | 2.33 × 10−1 ± 0.27 × 10−1 | 2.44 | 9.60 ± 0.19 | 14.85 ± 0.50 |
| Cell Line | RSF 100 nM | RSF 200 nM | RSF 500 nM | |||
|---|---|---|---|---|---|---|
| H460 | 3.88 × 10−3 ± 2.19 × 10−3 | 2.55 × 10−1 ± 0.85 × 10−1 | 1.31 | 1.73 ± 0.15 | 2.56 ± 0.27 | 4.21 ± 0.59 |
| H1437 | 3.11 × 10−3 ± 0.86 × 10−3 | 1.50 × 10−1 ± 0.35 × 10−1 | 1.10 | 1.77 ± 0.12 | 2.52 ± 0.13 | 3.77 ± 0.15 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liew, H.; Klein, C.; Zenke, F.T.; Abdollahi, A.; Debus, J.; Dokic, I.; Mairani, A. Modeling the Effect of Hypoxia and DNA Repair Inhibition on Cell Survival after Photon Irradiation. Int. J. Mol. Sci. 2019, 20, 6054. https://doi.org/10.3390/ijms20236054
Liew H, Klein C, Zenke FT, Abdollahi A, Debus J, Dokic I, Mairani A. Modeling the Effect of Hypoxia and DNA Repair Inhibition on Cell Survival after Photon Irradiation. International Journal of Molecular Sciences. 2019; 20(23):6054. https://doi.org/10.3390/ijms20236054
Chicago/Turabian StyleLiew, Hans, Carmen Klein, Frank T. Zenke, Amir Abdollahi, Jürgen Debus, Ivana Dokic, and Andrea Mairani. 2019. "Modeling the Effect of Hypoxia and DNA Repair Inhibition on Cell Survival after Photon Irradiation" International Journal of Molecular Sciences 20, no. 23: 6054. https://doi.org/10.3390/ijms20236054
APA StyleLiew, H., Klein, C., Zenke, F. T., Abdollahi, A., Debus, J., Dokic, I., & Mairani, A. (2019). Modeling the Effect of Hypoxia and DNA Repair Inhibition on Cell Survival after Photon Irradiation. International Journal of Molecular Sciences, 20(23), 6054. https://doi.org/10.3390/ijms20236054





