Hot Spots and Their Contribution to the Self-Assembly of the Viral Capsid: In Silico Prediction and Analysis
Abstract
1. Introduction
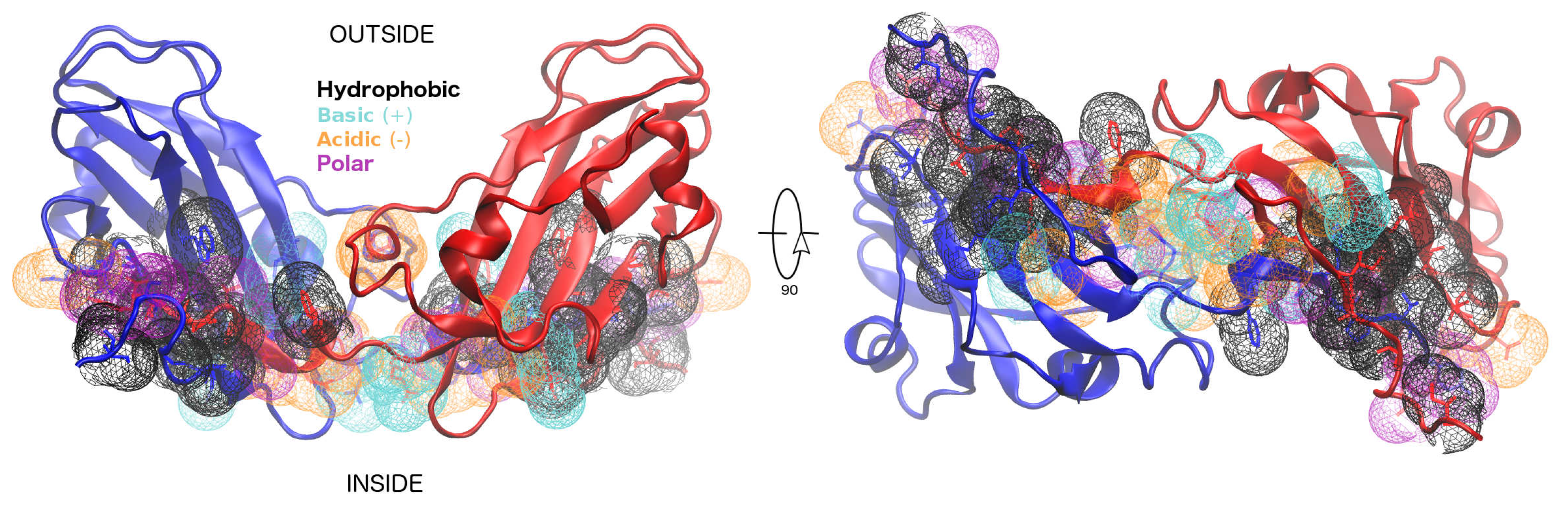
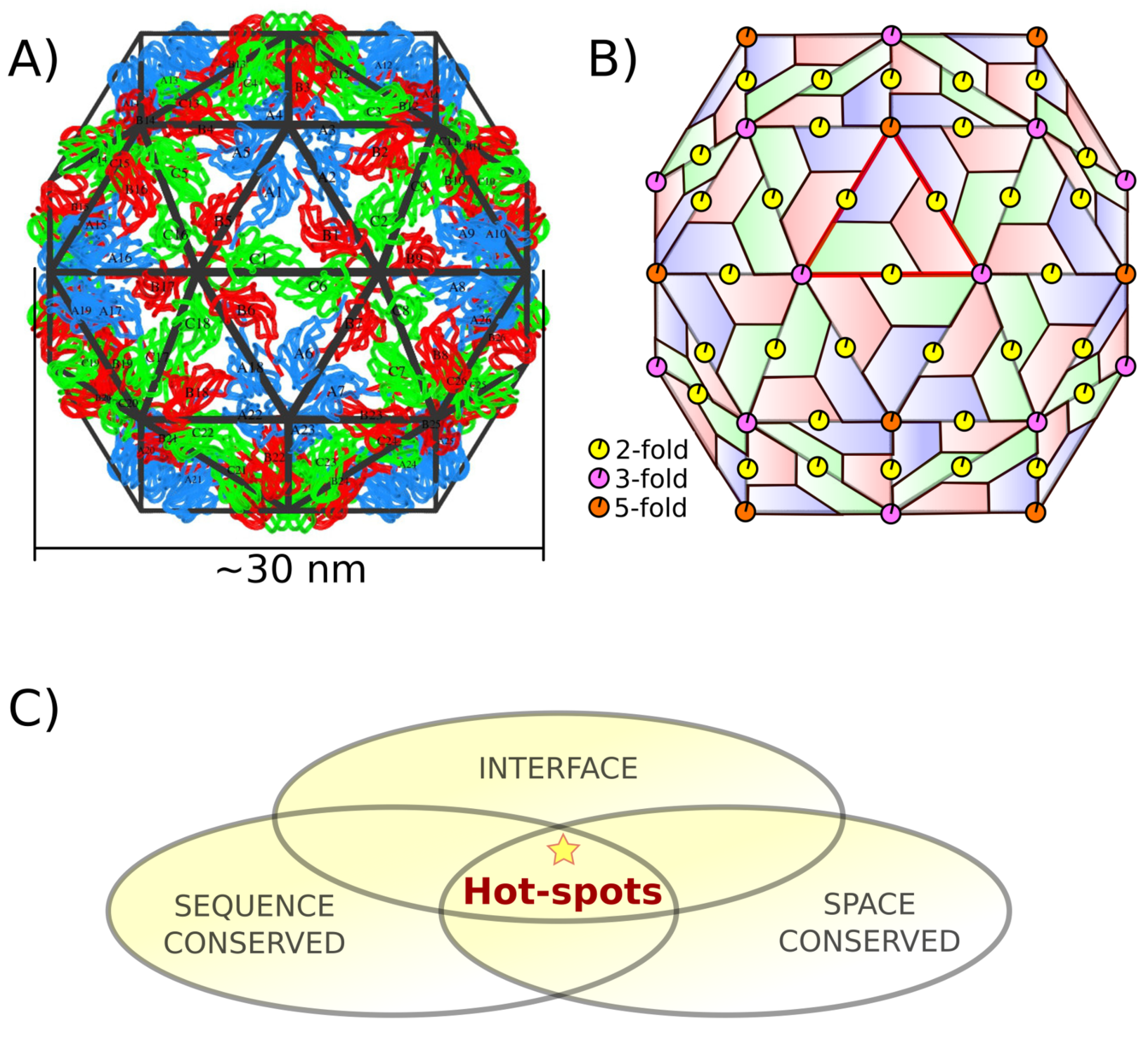
1.1. Capsid Quaternary Structure
1.2. Protein–Protein Interface Hot Spot Prediction
2. Results
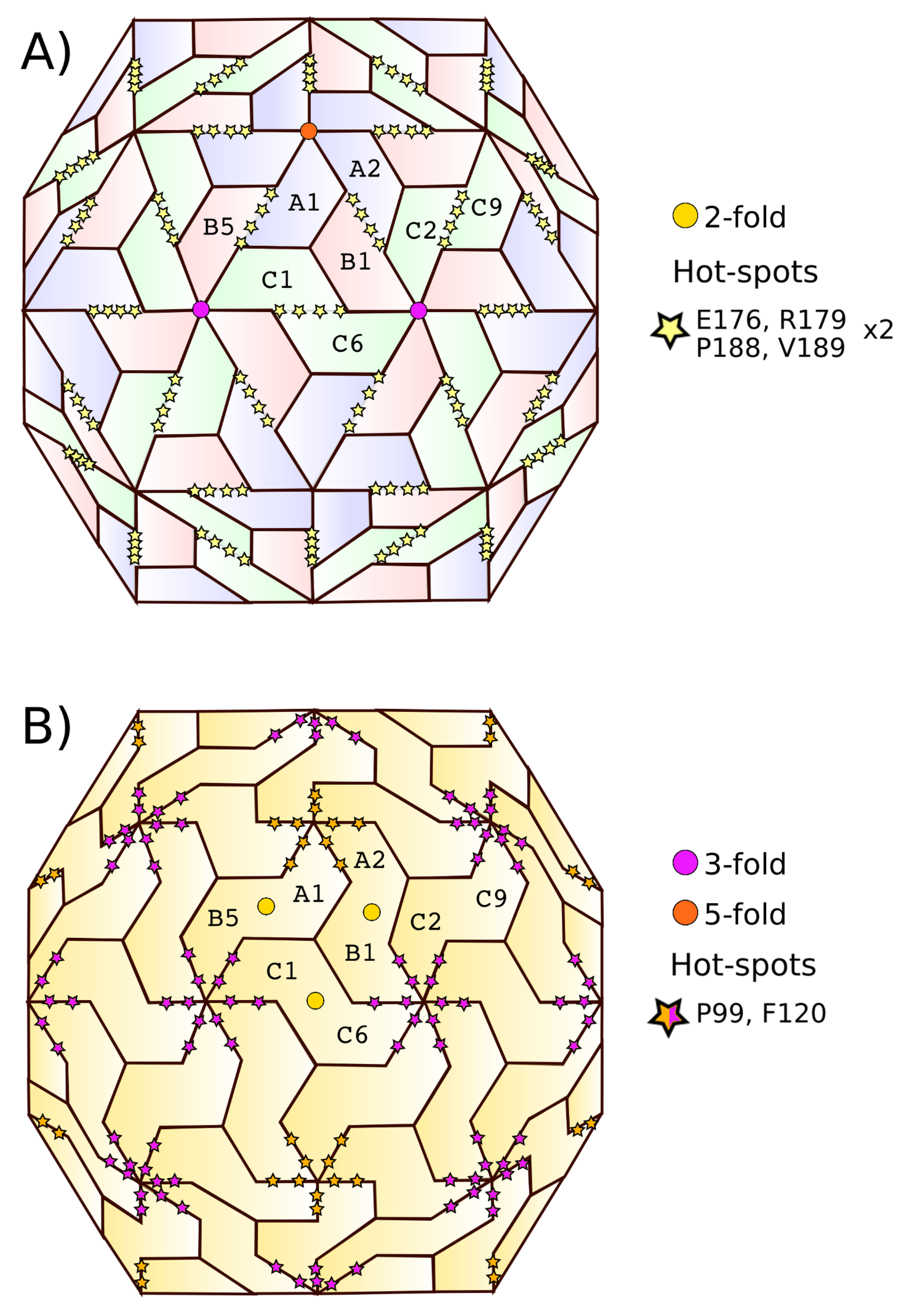
2.1. Hot Spot Prediction
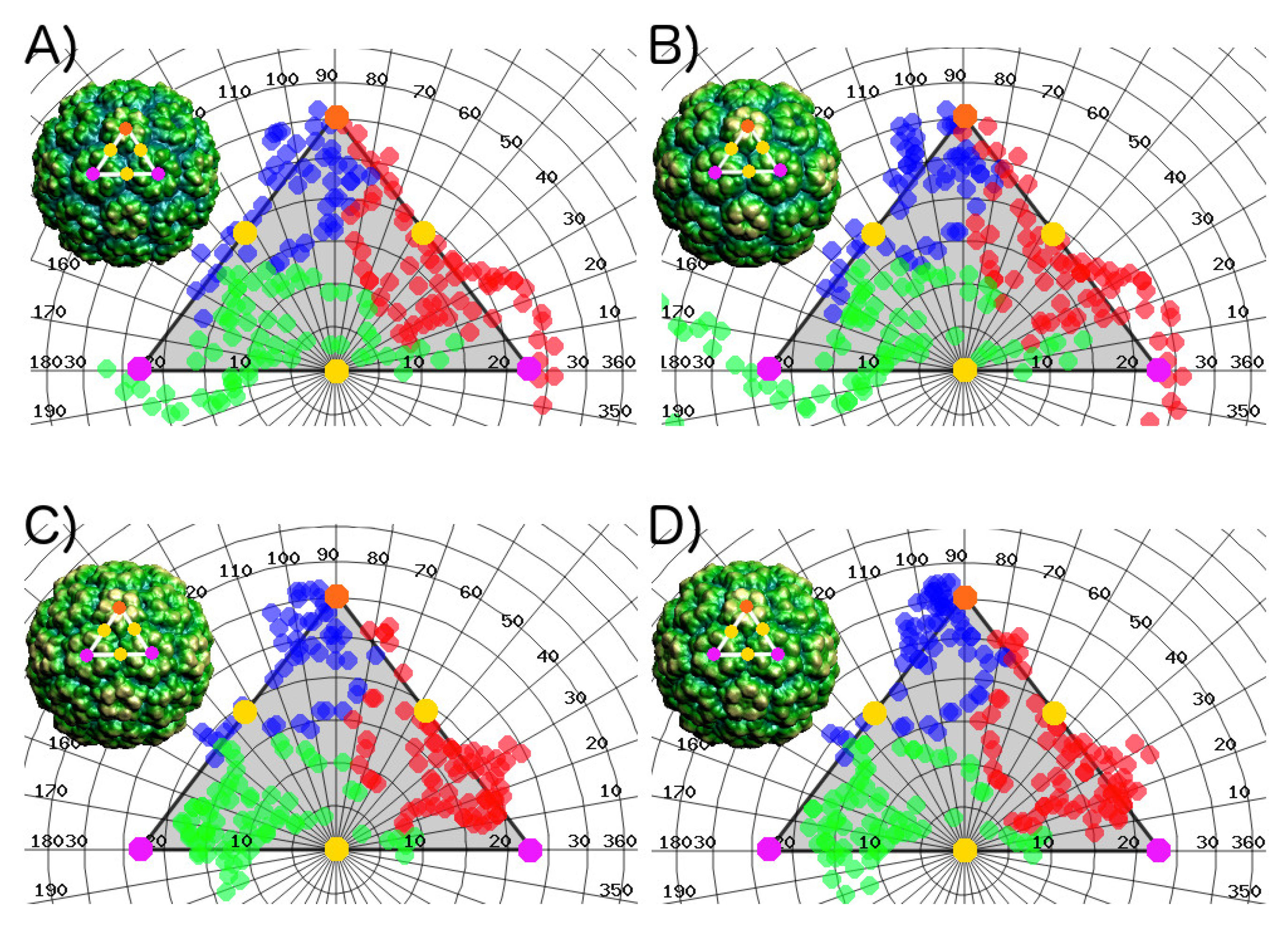
2.1.1. Sequence Conservation of Interface Residues
2.1.2. Space Conservation of Interface Residues
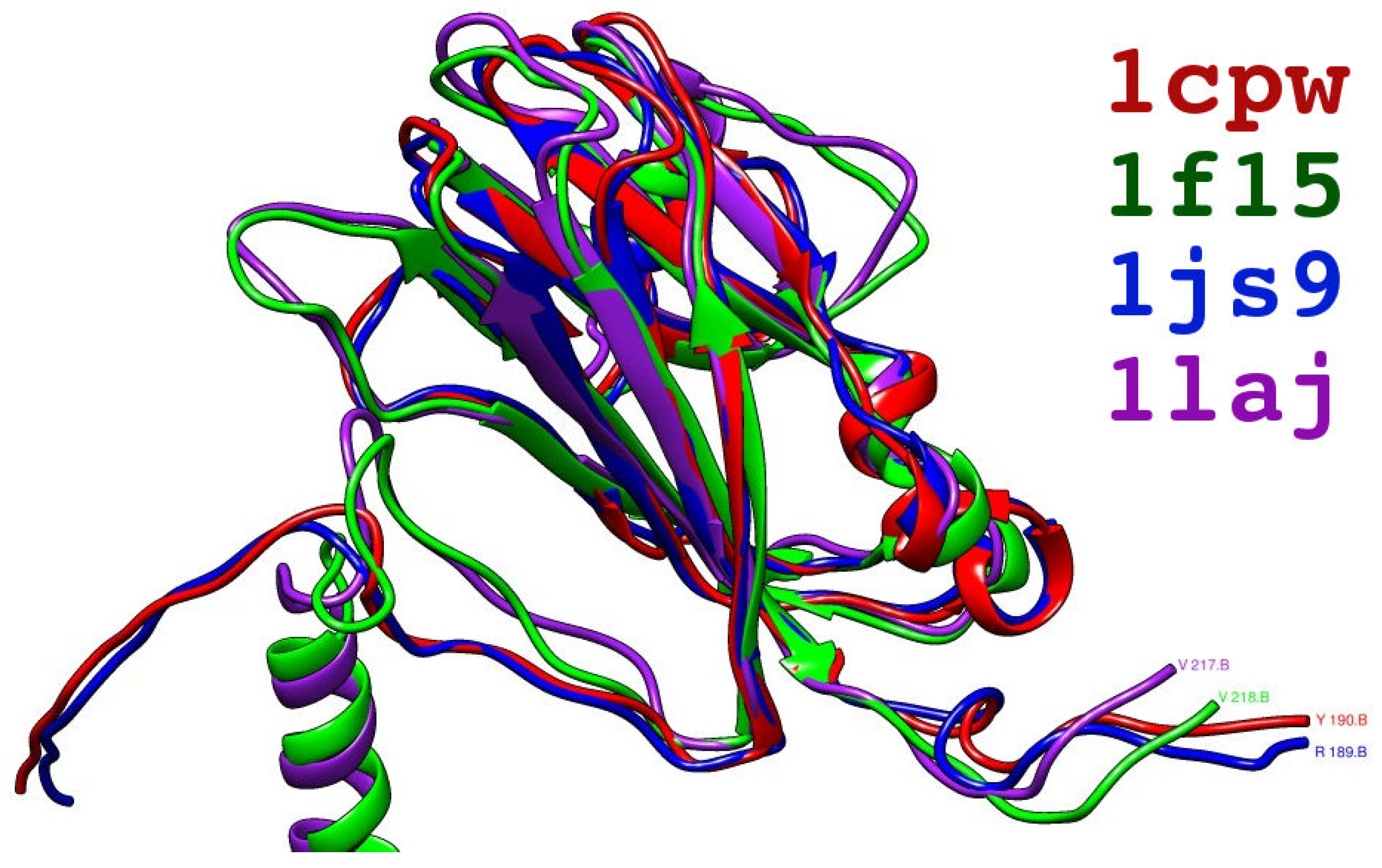
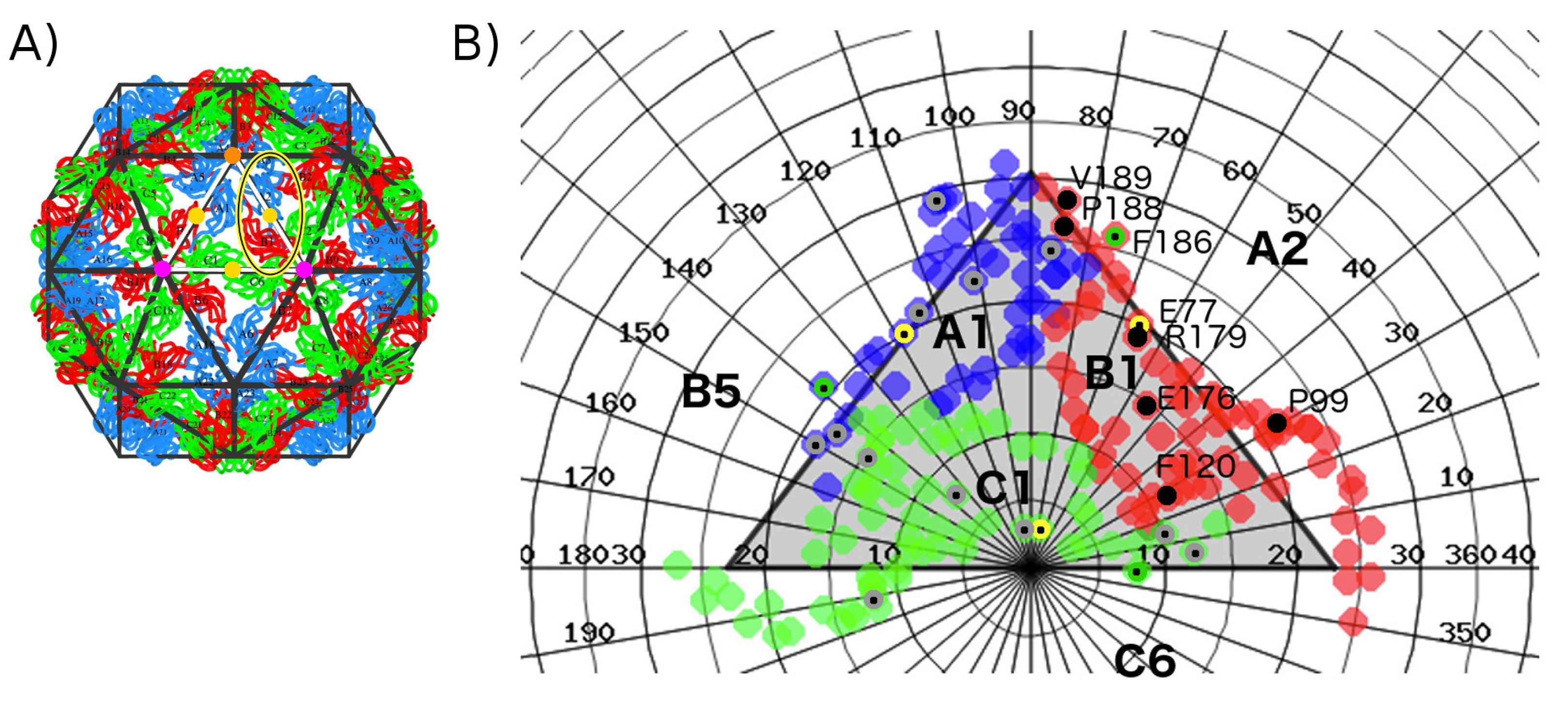
2.1.3. Hot Spot Predictions by the Structural Conservation Method
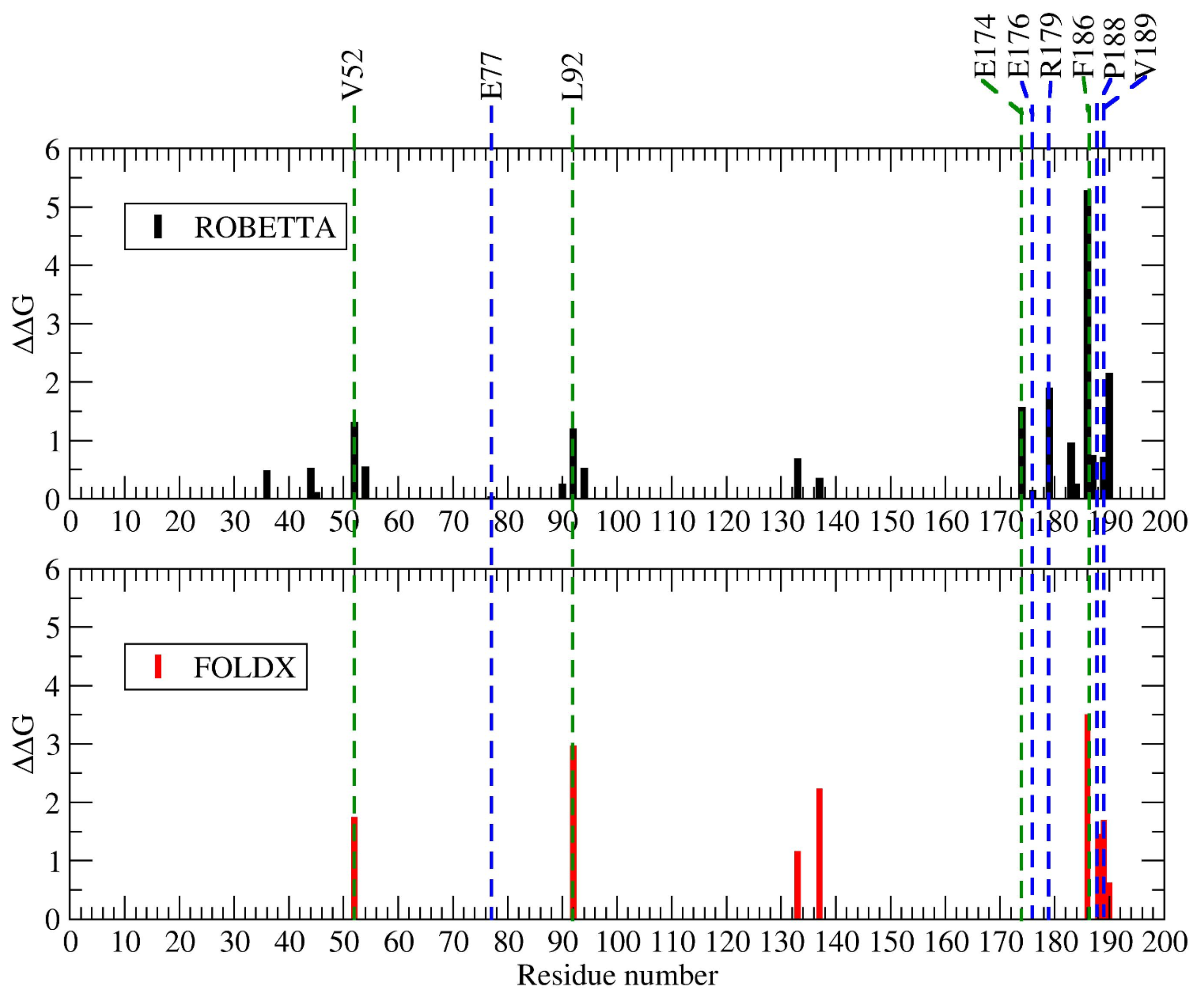
2.1.4. Hot Spot Predictions by Averaged Energy-Based Alanine Scanning Mutagenesis Approximation Methods
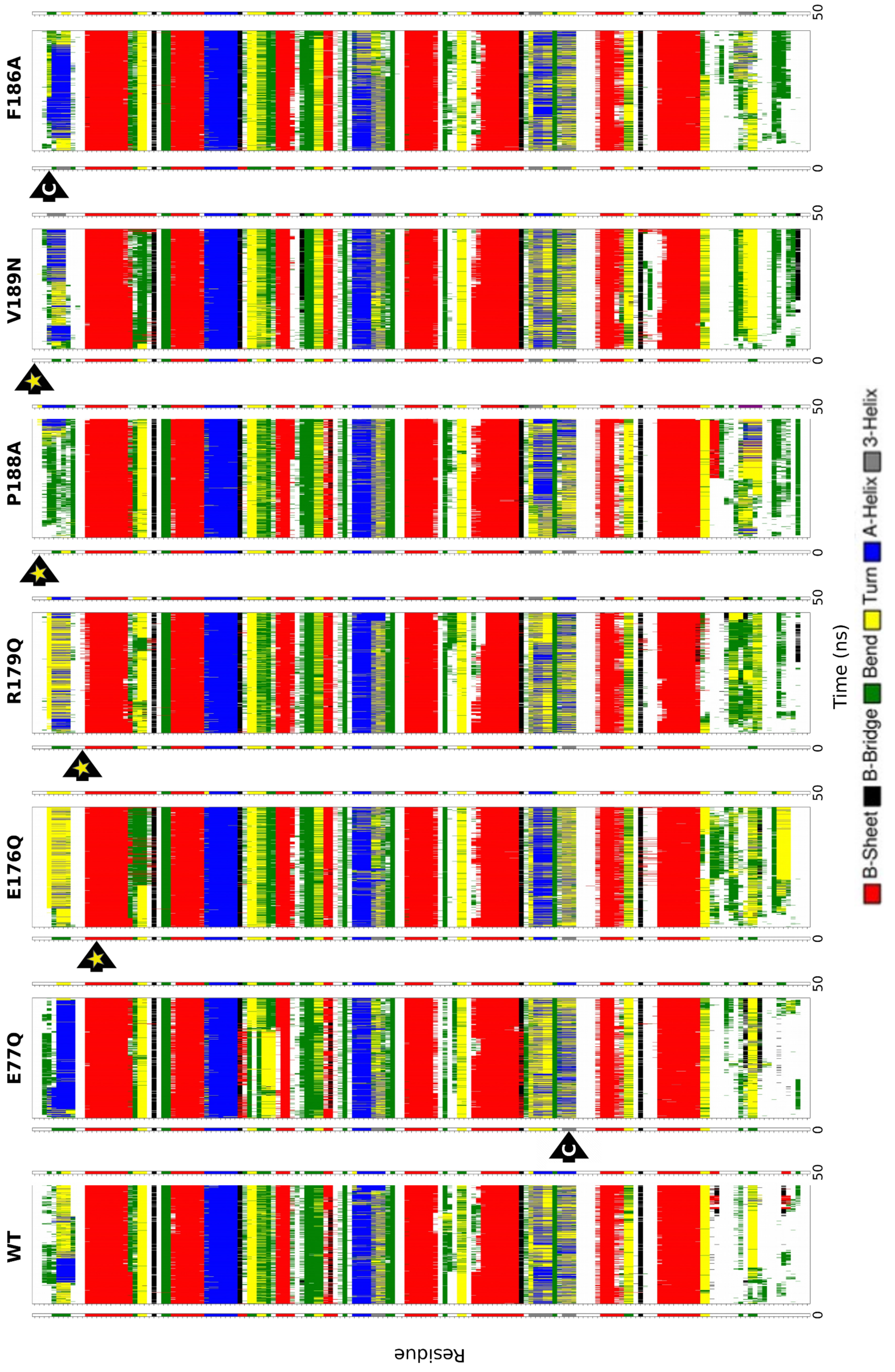
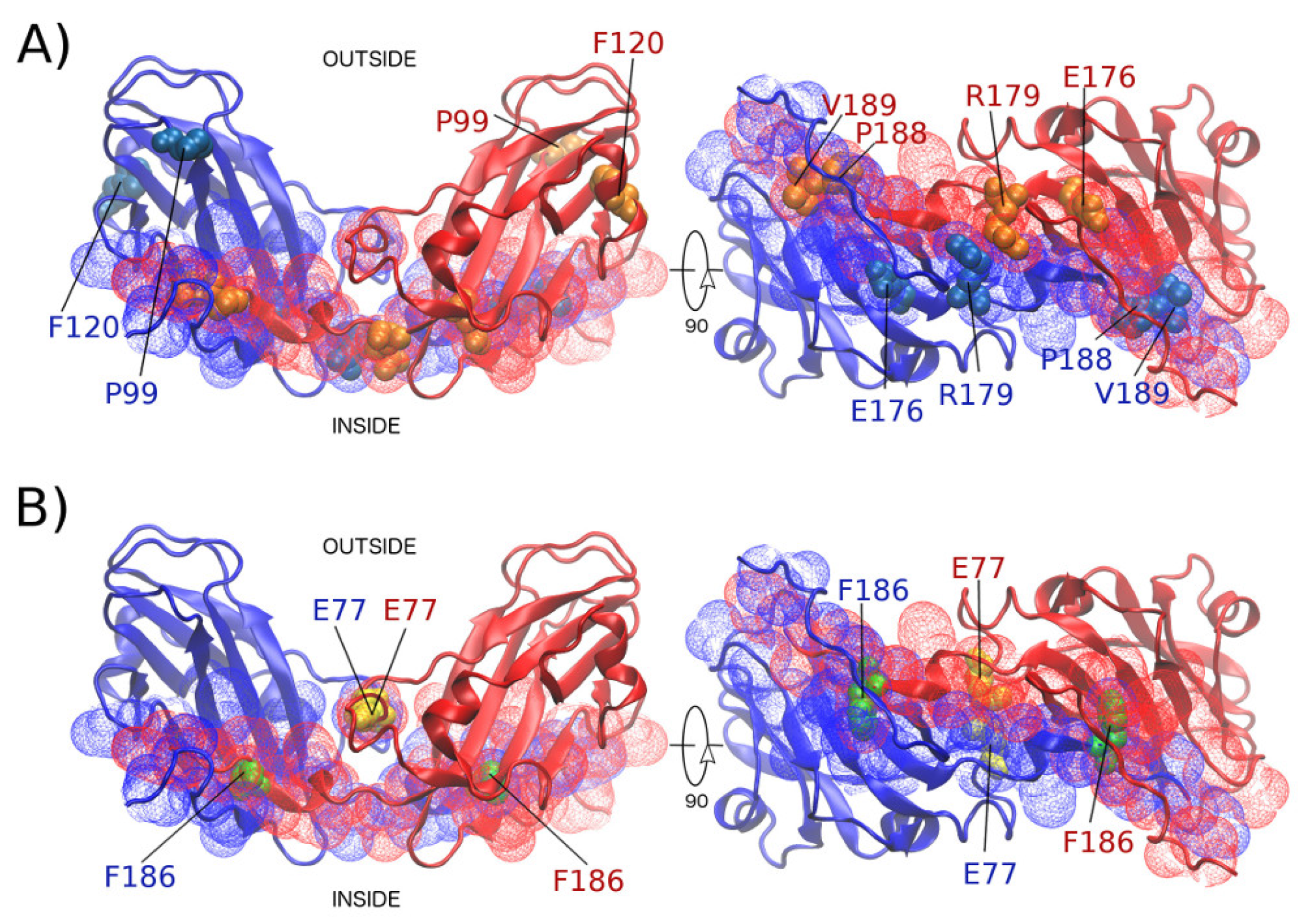
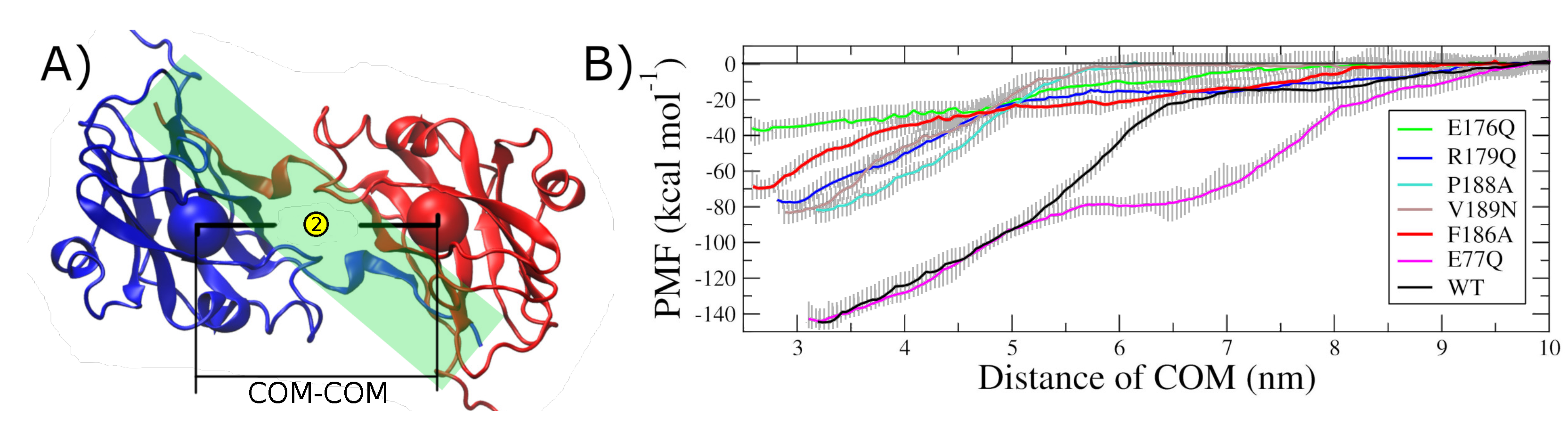
2.2. Hot Spot Validation Through a Rigorous Physical Framework
3. Discussion
4. Materials and Methods
4.1. Multiple Sequence Alignment
4.2. Interface Residues and Quaternary Structure Alignment
4.3. Hot Spot In Silico Mutations
4.4. Alanine Scanning Mutagenesis
4.5. Steered Molecular Dynamics
4.6. Umbrella Sampling
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CCMV | Cowpea Chlorotic Mottle Virus |
| CP | capsid protein |
| WT | wild type |
| COM | center-of-mass |
| MD | Molecular Dynamics |
| SMD | Steered Molecular Dynamics |
Appendix A. Supplementary Data
Appendix A.1. Composition of the 2-Fold-Related Interface

| Group | Nonpolar | Polar | Negative | Positive | Total | CYS | TRP |
|---|---|---|---|---|---|---|---|
| Interface | 33 (20) | 14 (9) | 12 (8) | 10 (6) | 69 (42) | W94 | |
| Dimer a | 14 (9) | 5 (3) | 5 (3) | 3 (1) | 27 (16) | W94 | |
| Core | 22 (13) | 8 (5) | 2 (1) | 1 (1) | 33 (20) | C59, C108 | |
| Surf-Out | 31 (19) | 20 (12) | 2 (1) | 2 (1) | 55 (34) | W55 | |
| Surf-In | 4 (2) | 2 (1) | 0 (0) | 1 (1) | 7 (4) | W47 | |
| Total | 90 (54) | 44 (27) | 16 (10) | 14 (9) | 164 (100) |
| Group | H | SASA | AEne | SolvEne | BSA |
|---|---|---|---|---|---|
| Interface | 18.5 | 2382.3 | −147.1 | −51.4 | 6351.9 |
| Dimer a | 8.6 | 864.2 | −87.1 | −34.4 | 3707.0 |
| Core | 19.2 | 78.4 | −0.2 | −0.1 | 8.9 |
| Surf-Out | 14.6 | 2853.5 | −3.4 | −0.8 | 171.1 |
| Surf-In | 2.2 | 604.3 | −2.5 | −1.2 | 118.4 |


References
- Twarock, R.; Luque, A. Structural puzzles in virology solved with an overarching icosahedral design principle. Nat. Commun. 2019, 10, 4414. [Google Scholar] [CrossRef] [PubMed]
- Castón, J.R.; Carrascosa, J.L. The Basic Architecture of Viruses. In Structure and Physics of Viruses: An Integrated Textbook; Mateu, M.G., Ed.; Springer: Dordrecht, The Netherlands, 2013; pp. 53–75. [Google Scholar]
- Crick, F.H.C.; Watson, J.D. Structure of Small Viruses. Nature 1956, 177, 473–475. [Google Scholar] [CrossRef] [PubMed]
- Caspar, D.L.D.; Klug, A. Physical Principles in the Construction of Regular Viruses. Cold Spring Harb. Symp. Quant. Biol. 1962, 27, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Kortemme, T.; Kim, D.E.; Baker, D. Computational Alanine Scanning of Protein–Protein Interfaces. Sci. STKE 2004, 2004, pl2. [Google Scholar] [CrossRef] [PubMed]
- Schymkowitz, J.; Borg, J.; Stricher, F.; Nys, R.; Rousseau, F.; Serrano, L. The FoldX web server: An online force field. Nucleic Acids Res. 2005, 33, W382–W388. [Google Scholar] [CrossRef]
- Moreira, I.S.; Koukos, P.I.; Melo, R.; Almeida, J.G.; Preto, A.J.; Schaarschmidt, J.; Trellet, M.; Gümüş, Z.H.; Costa, J.; Bonvin, A.M.J.J. SpotOn: High Accuracy Identification of Protein–Protein Interface Hot Spots. Sci. Rep. 2017, 7, 8007. [Google Scholar] [CrossRef] [PubMed]
- Qiao, Y.; Xiong, Y.; Gao, H.; Zhu, X.; Chen, P. Protein-protein interface hot spots prediction based on a hybrid feature selection strategy. BMC Bioinform. 2018, 19, 14. [Google Scholar] [CrossRef]
- Assi, S.A.; Tanaka, T.; Rabbitts, T.H.; Fernandez-Fuentes, N. PCRPi: Presaging Critical Residues in Protein interfaces, a new computational tool to chart hot spots in protein interfaces. Nucleic Acids Res. 2009, 38, e86. [Google Scholar] [CrossRef]
- Cho, K.i.; Kim, D.; Lee, D. A feature-based approach to modeling protein–protein interaction hot spots. Nucleic Acids Res. 2009, 37, 2672–2687. [Google Scholar] [CrossRef]
- Darnell, S.J.; Page, D.; Mitchell, J.C. An automated decision-tree approach to predicting protein interaction hot spots. Proteins Struct. Funct. Bioinform. 2007, 68, 813–823. [Google Scholar] [CrossRef]
- Lise, S.; Archambeau, C.; Pontil, M.; Jones, D.T. Prediction of hot spot residues at protein–protein interfaces by combining machine learning and energy-based methods. BMC Bioinform. 2009, 10, 365. [Google Scholar] [CrossRef] [PubMed]
- Huo, S.; Massova, I.; Kollman, P.A. Computational alanine scanning of the 1:1 human growth hormone–receptor complex. J. Comput. Chem. 2002, 23, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Rajamani, D.; Thiel, S.; Vajda, S.; Camacho, C.J. Anchor residues in protein–protein interactions. Proc. Natl. Acad. Sci. USA 2004, 101, 11287–11292. [Google Scholar] [CrossRef] [PubMed]
- Tuncbag, N.; Gursoy, A.; Keskin, O. Identification of computational hot spots in protein interfaces: Combining solvent accessibility and inter-residue potentials improves the accuracy. Bioinformatics 2009, 25, 1513–1520. [Google Scholar] [CrossRef]
- Carrillo-Tripp, M.; Brooks, C.L.; Reddy, V.S. A novel method to map and compare protein–protein interactions in spherical viral capsids. Proteins 2008, 73, 644–655. [Google Scholar] [CrossRef]
- Carrillo-Tripp, M.; Montiel-García, D.J.; Brooks, C.L.; Reddy, V.S. CapsidMaps: Protein-protein interaction pattern discovery platform for the structural analysis of virus capsids using Google Maps. J. Struct. Biol. 2015, 190, 47–55. [Google Scholar] [CrossRef]
- Carrillo-Tripp, M.; Shepherd, C.M.; Borelli, I.A.; Venkataraman, S.; Lander, G.; Natarajan, P.; Johnson, J.E.; Brooks, C.L.; Reddy, V.S. VIPERdb2: An enhanced and web API enabled relational database for structural virology. Nucleic Acids Res. 2009, 37, D436–D442. [Google Scholar] [CrossRef]
- Notredame, C.; Higgins, D.G.; Heringa, J. T-coffee: A novel method for fast and accurate multiple sequence alignment11Edited by J. Thornton. J. Mol. Biol. 2000, 302, 205–217. [Google Scholar] [CrossRef]
- Montiel-García, D.J.; Mannige, R.V.; Reddy, V.S.; Carrillo-Tripp, M. Structure based sequence analysis of viral and cellular protein assemblies. J. Struct. Biol. 2016, 196, 299–308. [Google Scholar] [CrossRef]
- Katen, S.; Zlotnick, A. The Thermodynamics of Virus Capsid Assembly. In Biothermodynamics, Part A; Methods in Enzymology; Academic Press: Cambridge, MA, USA, 2009; Volume 455, Chapter 14; pp. 395–417. [Google Scholar]
- Reddy, V.S.; Giesing, H.A.; Morton, R.T.; Kumar, A.; Post, C.B.; Brooks, C.L.; Johnson, J.E. Energetics of Quasiequivalence: Computational Analysis of Protein–Protein Interactions in Icosahedral Viruses. Biophys. J. 1998, 74, 546–558. [Google Scholar] [CrossRef]
- Horton, N.; Lewis, N. Calculation of the free energy of association for protein complexes. Protein Sci. 1992, 1, 169–181. [Google Scholar] [CrossRef] [PubMed]
- Eisenberg, D.; McLachlan, A.D. Solvation energy in protein folding and binding. Nature 1986, 319, 199–203. [Google Scholar] [CrossRef] [PubMed]
- Zlotnick, A.; Aldrich, R.; Johnson, J.M.; Ceres, P.; Young, M.J. Mechanism of Capsid Assembly for an Icosahedral Plant Virus. Virology 2000, 277, 450–456. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Ashkenazy, H.; Abadi, S.; Martz, E.; Chay, O.; Mayrose, I.; Pupko, T.; Ben-Tal, N. ConSurf 2016: An improved methodology to estimate and visualize evolutionary conservation in macromolecules. Nucleic Acids Res. 2016, 44, W344–W350. [Google Scholar] [CrossRef]
- Lemkul, J.A.; Bevan, D.R. Assessing the Stability of Alzheimer’s Amyloid Protofibrils Using Molecular Dynamics. J. Phys. Chem. B 2010, 114, 1652–1660. [Google Scholar] [CrossRef]
- Buck, M.; Bouguet-Bonnet, S.; Pastor, R.W.; MacKerell, A.D. Importance of the CMAP Correction to the CHARMM22 Protein Force Field: Dynamics of Hen Lysozyme. Biophys. J. 2006, 90, L36–L38. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Torrie, G.; Valleau, J. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Mehler, E.L. Quantitative expression of protein heterogeneity: Response of amino acid side chains to their local environment. Proteins Struct. Funct. Bioinform. 2008, 72, 646–659. [Google Scholar] [CrossRef]
- Marsh, J.A. Buried and Accessible Surface Area Control Intrinsic Protein Flexibility. J. Mol. Biol. 2013, 425, 3250–3263. [Google Scholar] [CrossRef] [PubMed]
| Residue | SASA | AEne | SolvEne | BSA | NumInt |
|---|---|---|---|---|---|
| Proline P99 a | 9.70 | −3.29 | −2.03 | 141.20 | 5 |
| Phenylalanine F120 a | 11.10 | −0.73 | −0.35 | 34.73 | 1 |
| Glutamic Acid E176 b | 0.00 | −0.16 | −0.10 | 6.74 | 1 |
| Arginine R179 b | 64.50 | −2.80 | 0.32 | 138.64 | 3 |
| Proline P188 b | 39.20 | −5.03 | −3.47 | 203.97 | 1 |
| Valine V189 b | 28.70 | −4.48 | −2.92 | 187.98 | 4 |
| Glutamic Acid E77 c | 65.50 | −2.72 | −0.54 | 112.78 | 1 |
| Phenylalanine F186 c | 1.70 | −9.58 | −6.70 | 385.04 | 7 |
| Variant | Property | Mutant | Property | G | G |
|---|---|---|---|---|---|
| WT | −144.9 ± 4.9 | 0.0 | |||
| Glutamic Acid E176 a | Negative Charge | Glutamine Q | Neutral | −37.4 ± 5.3 | 107.6 |
| Arginine R179 a | Positive Charge | Glutamine Q | Neutral | −77.5 ± 6.1 | 67.5 |
| Proline P188 a | Special case | Alanine A | Small | −82.0 ± 5.8 | 63.0 |
| Valine V189 a | Nonpolar | Asparagine N | Polar | −83.2 ± 5.6 | 61.8 |
| Glutamic Acid E77 b | Negative Charge | Glutamine Q | Neutral | −144.1 ± 5.8 | 0.9 |
| Phenylalanine F186 b | Big | Alanine A | Small | −69.6 ± 5.9 | 75.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Valle, A.; Falcón-González, J.M.; Carrillo-Tripp, M. Hot Spots and Their Contribution to the Self-Assembly of the Viral Capsid: In Silico Prediction and Analysis. Int. J. Mol. Sci. 2019, 20, 5966. https://doi.org/10.3390/ijms20235966
Díaz-Valle A, Falcón-González JM, Carrillo-Tripp M. Hot Spots and Their Contribution to the Self-Assembly of the Viral Capsid: In Silico Prediction and Analysis. International Journal of Molecular Sciences. 2019; 20(23):5966. https://doi.org/10.3390/ijms20235966
Chicago/Turabian StyleDíaz-Valle, Armando, José Marcos Falcón-González, and Mauricio Carrillo-Tripp. 2019. "Hot Spots and Their Contribution to the Self-Assembly of the Viral Capsid: In Silico Prediction and Analysis" International Journal of Molecular Sciences 20, no. 23: 5966. https://doi.org/10.3390/ijms20235966
APA StyleDíaz-Valle, A., Falcón-González, J. M., & Carrillo-Tripp, M. (2019). Hot Spots and Their Contribution to the Self-Assembly of the Viral Capsid: In Silico Prediction and Analysis. International Journal of Molecular Sciences, 20(23), 5966. https://doi.org/10.3390/ijms20235966






