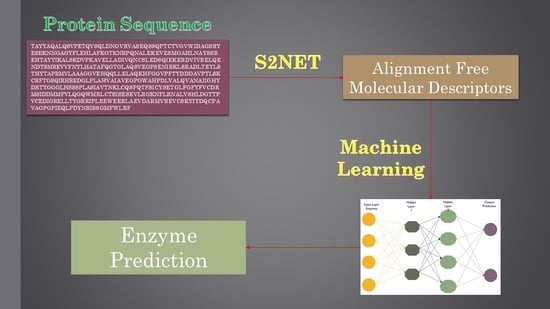
Alignment-Free Method to Predict Enzyme Classes and Subclasses

The Enzyme Classification (EC) number is a numerical classification scheme for enzymes, established using the chemical reactions they catalyze. This classification is based on the recommendation of the Nomenclature Committee of the International Union of Biochemistry and Molecular Biology. Six enzyme classes were recognised in the first Enzyme Classification and Nomenclature List, reported by the International Union of Biochemistry in 1961. However, a new enzyme group was recently added as the six existing EC classes could not describe enzymes involved in the movement of ions or molecules across membranes. Such enzymes are now classified in the new EC class of translocases (EC 7). Several computational methods have been developed in order to predict the EC number. However, due to this new change, all such methods are now outdated and need updating. In this work, we developed a new multi-task quantitative structure–activity relationship (QSAR) method aimed at predicting all 7 EC classes and subclasses. In so doing, we developed an alignment-free model based on artificial neural networks that proved to be very successful. View Full-Text