Discrimination of DNA Methylation Signal from Background Variation for Clinical Diagnostics
Abstract
1. Introduction
2. Results
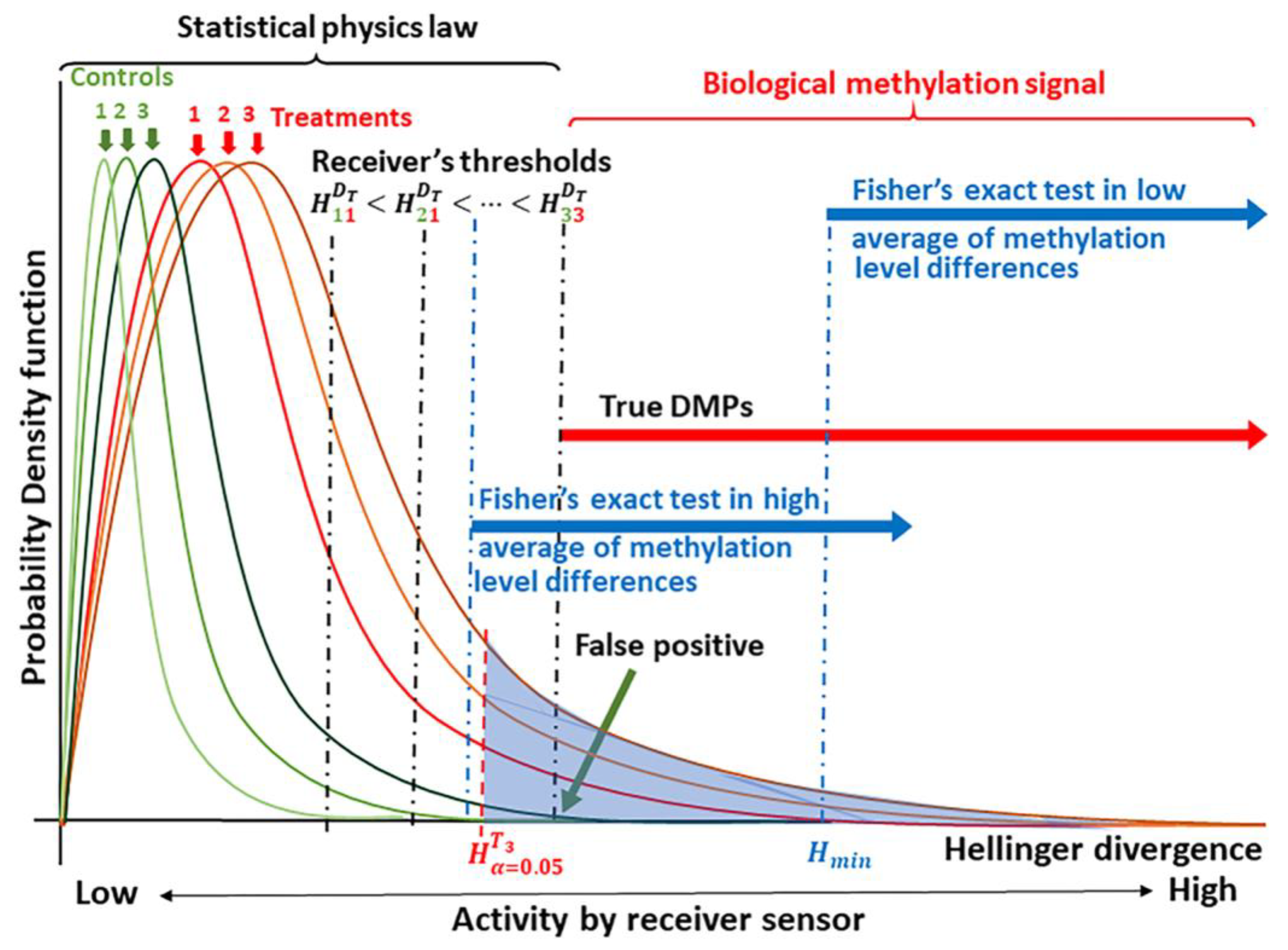
2.1. Detection of the Methylation Signal
2.2. Simulation Study
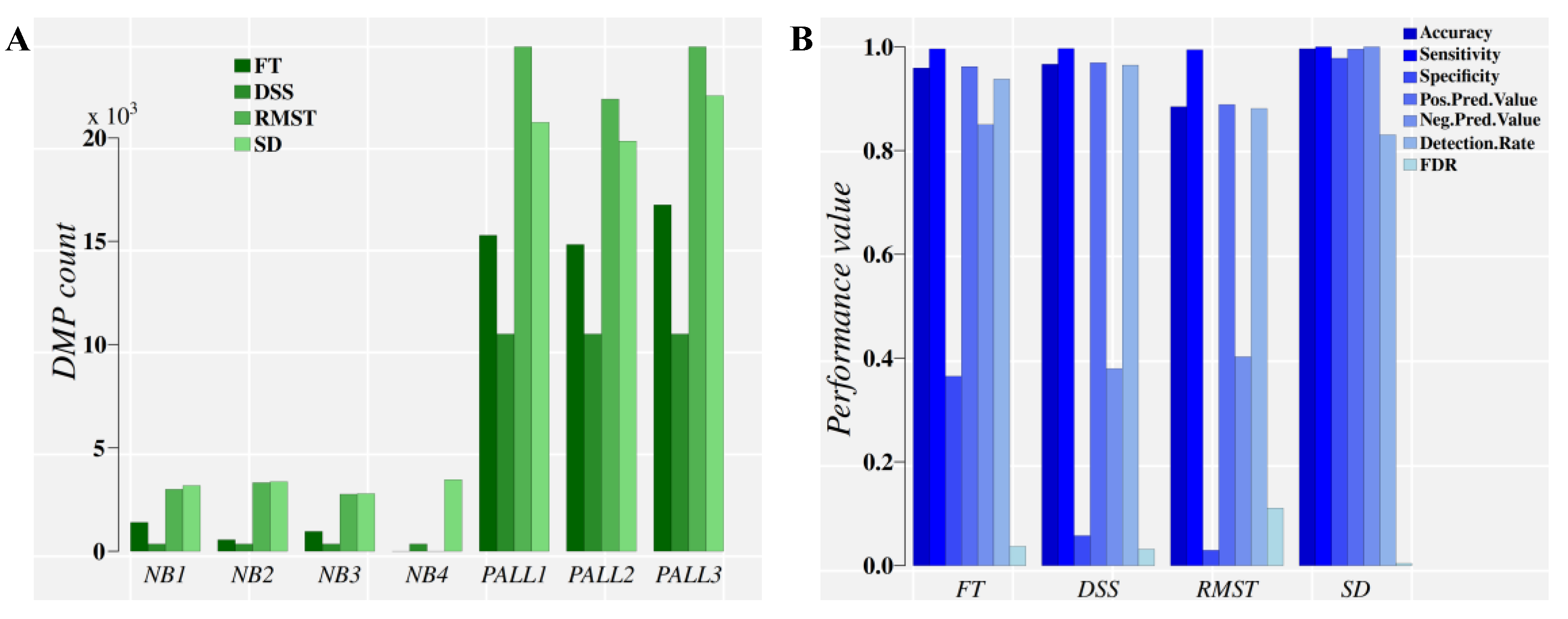
2.3. Analyses of Experimental Datasets
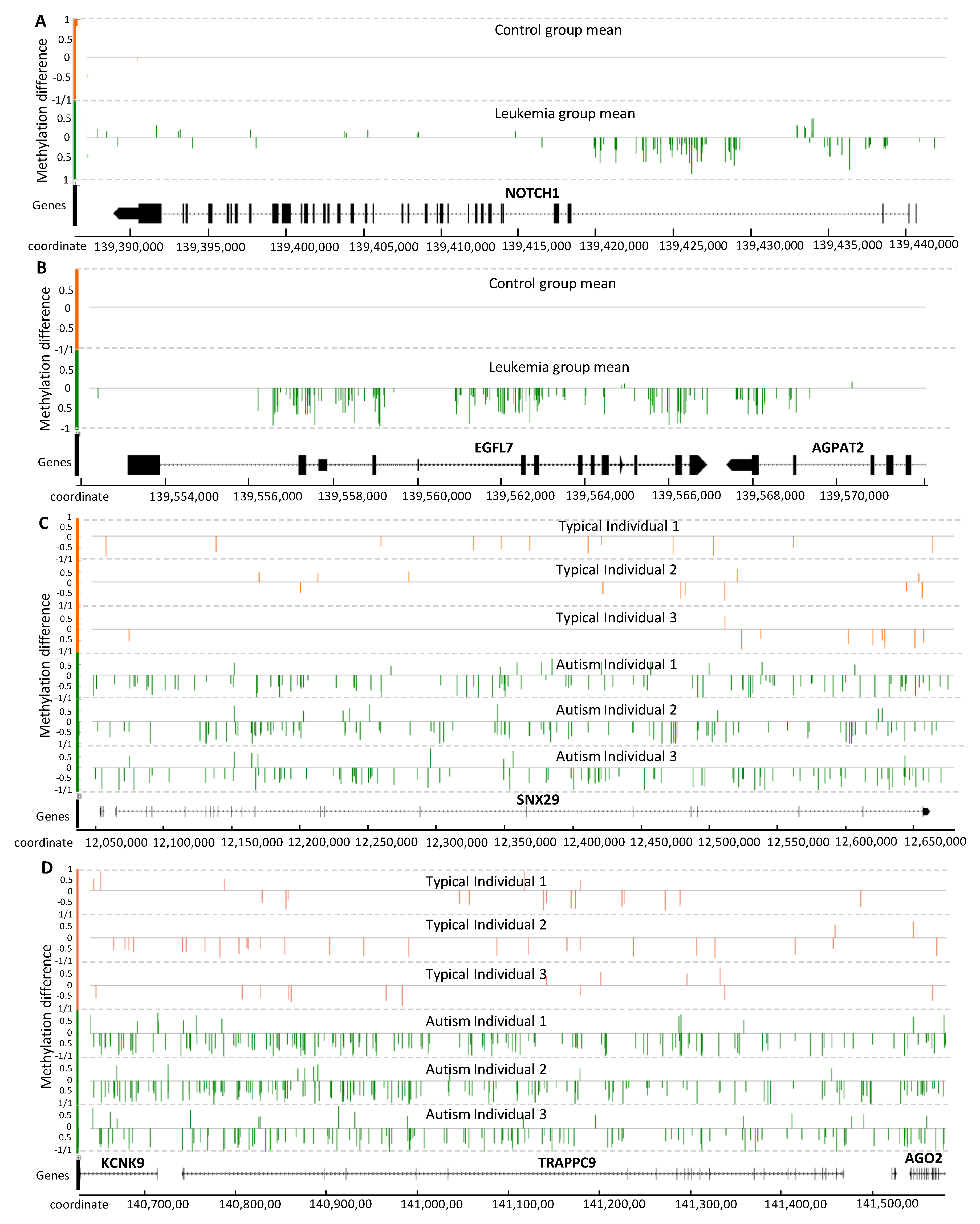
2.3.1. Analysis of PALL Dataset
2.3.2. Analysis of Placenta from Typically Developing and Autistic Children
2.3.3. Methylation Signal Association with Genes Involved in Disease Development
3. Discussion
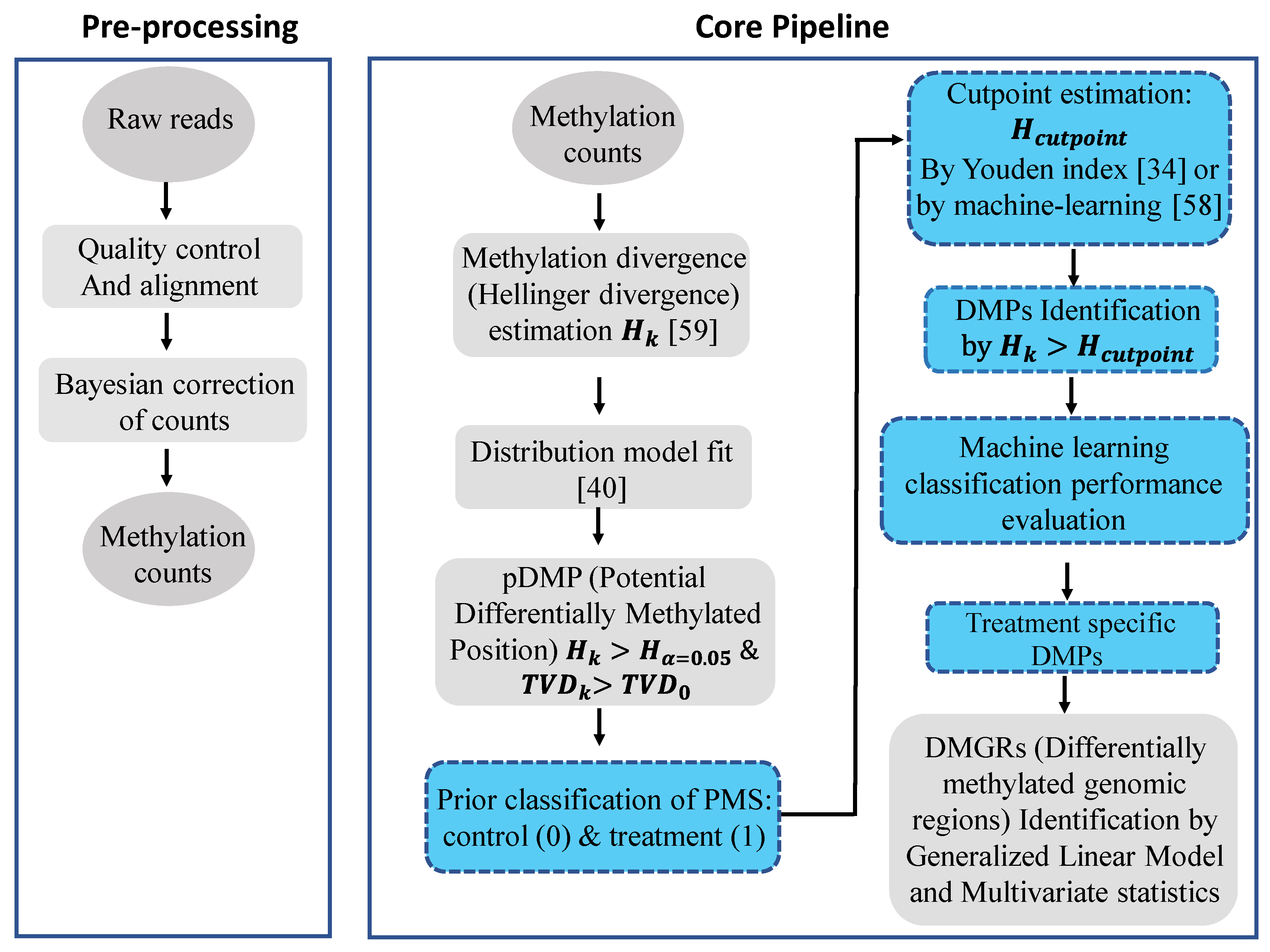
4. Materials and Methods
4.1. Divergences of Methylation Levels
4.2. Non-Linear Fit of Distribution Functions
4.3. Detection of the Methylation Signal
4.4. DMP Prediction Based on Machine Learning Model Classifiers
4.5. Simulations
4.6. Experimental Methylation Datasets
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| ADP | Autistic developing placenta |
| CDM | Cytosine DNA methylation |
| DMPs | Differentially methylated position |
| FDR | False discovery rate |
| FT | Fisher’s exact test |
| HD | Hellinger divergence |
| ML | Machine learning |
| PALL | Pediatric acute lymphoblastic leukemia |
| RMST | Root mean squared test |
| SD | Signal detection (used to denote the signal detection approach) |
| TDP | Typically developing placenta |
| TV | Total variation distance (absolute value of methylation level difference) |
References
- Severin, P.M.D.; Zou, X.; Gaub, H.E.; Schulten, K. Cytosine Methylation Alters DNA Mechanical Properties. Nucleic Acids Res. 2011, 39, 8740–8751. [Google Scholar] [CrossRef] [PubMed]
- Cortini, R.; Barbi, M.; Caré, B.R.; Lavelle, C.; Lesne, A.; Mozziconacci, J.; Victor, J.M. The Physics of Epigenetics. Rev. Mod. Phys. 2016, 88, 025002. [Google Scholar] [CrossRef]
- Li, E.; Zhang, Y. DNA Methylation in Mammals. Cold Spring Harb. Perspect. Biol. 2014. [Google Scholar] [CrossRef] [PubMed]
- Kaminsky, Z.A.; Tang, T.; Wang, S.C.; Ptak, C.; Oh, G.H.T.; Wong, A.H.C.; Feldcamp, L.A.; Virtanen, C.; Halfvarson, J.; Tysk, C.; et al. DNA Methylation Profiles in Monozygotic and Dizygotic Twins. Nat. Genet. 2009. [Google Scholar] [CrossRef]
- Heyn, H.; Moran, S.; Hernando-Herraez, I.; Sayols, S.; Gomez, A.; Sandoval, J.; Monk, D.; Hata, K.; Marques-Bonet, T.; Wang, L.; et al. DNA Methylation Contributes to Natural Human Variation. Genome Res. 2013, 23, 1363–1372. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Van Emburgh, B.O.; Robertson, K.D. DNA Methylation in Development and Human Disease. Mutat. Res. 2008, 647, 30–38. [Google Scholar] [CrossRef]
- Smith, Z.D.; Meissner, A. DNA Methylation: Roles in Mammalian Development. Nat. Rev. Genet. 2013, 14, 204–220. [Google Scholar] [CrossRef]
- Martin, E.M.; Fry, R.C. Environmental Influences on the Epigenome: Exposure- Associated DNA Methylation in Human Populations. Annu. Rev. Public Health 2018, 39, 309–333. [Google Scholar] [CrossRef]
- Heyn, H.; Esteller, M. DNA Methylation Profiling in the Clinic: Applications and Challenges. Nat. Rev. Genet. 2012, 13, 679–692. [Google Scholar] [CrossRef]
- Tang, J.; Xiong, Y.; Zhou, H.H.; Chen, X.P. DNA Methylation and Personalized Medicine. J. Clin. Pharm. Ther. 2014, 39, 621–627. [Google Scholar] [CrossRef]
- Berdasco, M.; Esteller, M. Clinical Epigenetics: Seizing Opportunities for Translation. Nat. Rev. Genet. 2019, 20, 109–127. [Google Scholar] [CrossRef] [PubMed]
- Wojdacz, T.K. Methylation Biomarker Development in the Context of the Eu Regulations for Clinical Use of In-Vitro Diagnostic Devices. Expert Rev. Mol. Diagn. 2019, 19, 439–441. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Conneely, K.N.; Wu, H. A Bayesian Hierarchical Model to Detect Differentially Methylated Loci from Single Nucleotide Resolution Sequencing Data. Nucleic Acids Res. 2014, 42, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Hebestreit, K.; Dugas, M.; Klein, H.U. Detection of Significantly Differentially Methylated Regions in Targeted Bisulfite Sequencing Data. Bioinformatics 2013, 29, 1647–1653. [Google Scholar] [CrossRef] [PubMed]
- Akalin, A.; Kormaksson, M.; Li, S.; Garrett-Bakelman, F.; Figueroa, M.; Melnick, A.; Mason, C. MethylKit: A Comprehensive R Package for the Analysis of Genome-Wide DNA Methylation Profiles. Genome Biol. 2012, 13, R87. [Google Scholar] [CrossRef] [PubMed]
- Schultz, M.D.; He, Y.; Whitaker, J.W.; Hariharan, M.; Mukamel, E.A.; Leung, D.; Rajagopal, N.; Nery, J.R.; Urich, M.A.; Chen, H.; et al. Human Body Epigenome Maps Reveal Noncanonical DNA Methylation Variation. Nature 2015, 530, 242. [Google Scholar] [CrossRef] [PubMed]
- Perkins, W.; Tygert, M.; Ward, R. Computing the Confidence Levels for a Root-Mean-Square Test of Goodness-of-Fit. Appl. Math. Comput. 2011, 217, 9072–9084. [Google Scholar] [CrossRef]
- Ngo, T.T.M.; Yoo, J.; Dai, Q.; Zhang, Q.; He, C.; Aksimentiev, A.; Ha, T. Effects of Cytosine Modifications on DNA Flexibility and Nucleosome Mechanical Stability. Nat. Commun. 2016, 7, 10813. [Google Scholar] [CrossRef]
- McAdams, H.H.; Arkin, A. Stochastic Mechanisms in Gene Expression. Proc. Natl. Acad. Sci. USA 1997, 94, 814–819. [Google Scholar] [CrossRef]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic Gene Expression in a Single Cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef]
- Hippenstiel, R.D. Detection Theory: Applications and Digital Signal Processing; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Pierre, K.; Moreno, W.; Jeong, C.S. System Testability Threshold Design Effectiveness via Signal Detection Theory. Conf. Proc. IEEE Southeastcon 2015, 2015-June, 1–9. [Google Scholar] [CrossRef]
- Rota, M.; Antolini, L.; Valsecchi, M.G. Optimal Cut-Point Definition in Biomarkers: The Case of Censored Failure Time Outcome. BMC Med. Res. Methodol. 2015, 15, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Linden, A.; Yarnold, P.R.; Ph, D. Identifying Maximum-Accuracy Cut- Points for Diagnostic Indexes via ODA. Optimal Data Anal. 2018, 7, 59–65. [Google Scholar]
- Min, W.; Jiang, L.; Yu, J.; Kou, S.C.; Qian, H.; Xie, X.S. Nonequilibrium Steady State of a Nanometric Biochemical System: Determining the Thermodynamic Driving Force from Single Enzyme Turnover Time Traces. Nano Lett. 2005, 5, 2373–2378. [Google Scholar] [CrossRef] [PubMed]
- Koslover, E.F.; Spakowitz, A.J. Force Fluctuations Impact Kinetics of Biomolecular Systems. Phys. Rev. E. Stat. Nonlin. Soft Matter Phys. 2012, 86, 011906. [Google Scholar] [CrossRef]
- Samoilov, M.S.; Price, G.; Arkin, A.P. From Fluctuations to Phenotypes: The Physiology of Noise. Sci. STKE 2006, 2006. [Google Scholar] [CrossRef]
- Jin, X.; Ge, H. Nonequilibrium Steady State of Biochemical Cycle Kinetics under Non-Isothermal Conditions. N. J. Phys. 2018, 20, 043030. [Google Scholar] [CrossRef]
- Lucia, U.; Grisolia, G. Second Law Efficiency for Living Cells. Front. Biosci. (Schol. Ed) 2017, 9, 270–275. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy Production Fluctuation Theorem and the Nonequilibrium Work Relation for Free Energy Differences. Phys. Rev. E 1999, 60, 2721–2726. [Google Scholar] [CrossRef]
- Demirel, Y. Information in Biological Systems and the Fluctuation Theorem. Entropy 2014, 16, 1931–1948. [Google Scholar] [CrossRef]
- Park, S.J.; Song, S.; Yang, G.S.; Kim, P.M.; Yoon, S.; Kim, J.H.; Sung, J. The Chemical Fluctuation Theorem Governing Gene Expression. Nat. Commun. 2018, 9, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Joshi, R.S.; Watson, C.; Sharp, A.J.; Sciences, G. A Survey of DNA Methylation Polymorphism Identifies Environmentally Responsive Co-Regulated Networks of Epigenetic Variation in the Human Genome. PLoS Genet. 2018, 14, 1–24. [Google Scholar]
- Youden, W.J. Index for Rating Diagnostic Tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Carter, J.V.; Pan, J.; Rai, S.N.; Galandiuk, S. ROC-Ing along: Evaluation and Interpretation of Receiver Operating Characteristic Curves. Surgery 2016, 159, 1638–1645. [Google Scholar] [CrossRef]
- López-Ratón, M.; Rodríguez-Álvarez, M.X.; Cadarso-Suárez, C.; Gude-Sampedro, F. OptimalCutpoints: An R Package for Selecting Optimal Cut point s in Diagnostic Tests. J. Stat. Softw. 2014, 61, 1–36. [Google Scholar] [CrossRef]
- Provost, F.; Fawcett, T. Analysis and Visualization of Classifier Performance: Comparison Under Imprecise Class and Cost Distributions. In Proceedings of the Third International Conference on Knowledge Discovery and Data Mining; KDD’97. AAAI Press: Menlo Park, CA, USA, 1997; pp. 43–48. [Google Scholar]
- Wahlberg, P.; Lundmark, A.; Nordlund, J.; Busche, S.; Raine, A.; Tandre, K.; Rönnblom, L.; Sinnett, D.; Forestier, E.; Pastinen, T.; et al. DNA Methylome Analysis of Acute Lymphoblastic Leukemia Cells Reveals Stochastic de Novo DNA Methylation in CpG Islands. Epigenomics 2016, 8, 1367–1387. [Google Scholar] [CrossRef]
- Schroeder, D.I.; Schmidt, R.J.; Crary-Dooley, F.K.; Walker, C.K.; Ozonoff, S.; Tancredi, D.J.; Hertz-Picciotto, I.; LaSalle, J.M. Placental Methylome Analysis from a Prospective Autism Study. Mol. Autism 2016, 7, 1–12. [Google Scholar] [CrossRef]
- Sanchez, R.; Mackenzie, S.A. Information Thermodynamics of Cytosine DNA Methylation. PLoS ONE 2016, 11, e0150427. [Google Scholar] [CrossRef]
- Linden, A.; Yarnold, P.R.; Nallamothu, B.K. Using Machine Learning to Model Dose–Response Relationships. J. Eval. Clin. Pract. 2016, 22, 856–863. [Google Scholar] [CrossRef]
- Krueger, F.; Andrews, S.R. Bismark: A Flexible Aligner and Methylation Caller for Bisulfite-Seq Applications. Bioinformatics 2011, 27, 1571–1572. [Google Scholar] [CrossRef]
- Lancashire, L.; Ball, G. Computational and Statistical Methodologies for Data Mining in Bioinformatics. In Key Topics in Surgical Research and Methodology; Athanasiou, T., Debas, H., Darzi, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Brownlee, J. Master Machine Learning Algorithms. Discover How They Work and Implement Them from Scratch; Machine Learning Mastery: Vermont, VIC, Australia, 2016. [Google Scholar]
- Park, Y.; Wu, H. Differential Methylation Analysis for BS-Seq Data under General Experimental Design. Bioinformatics 2016, 32, 1446–1453. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.-C.C.; Lin, S.-J.J.; Shih, H.-Y.Y.; Chou, C.-H.H.; Chu, H.-H.H.; Chiu, C.-C.C.; Yuh, C.-H.H.; Yeh, T.-H.H.; Cheng, Y.-C.C. Epigenetic Regulation of NOTCH1 and NOTCH3 by KMT2A Inhibits Glioma Proliferation. Oncotarget 2017, 5, 63110–63120. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Waibel, M.; Vervoort, S.J.; Kong, I.Y.; Heinzel, S.; Ramsbottom, K.M.; Martin, B.P.; Hawkins, E.D.; Johnstone, R.W. Epigenetic Targeting of Notch1-Driven Transcription Using the HDACi Panobinostat Is a Potential Therapy against T-Cell Acute Lymphoblastic Leukemia. Leukemia 2018, 32, 237–241. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Wang, Y.-L.; Sun, D.; Zhu, X.-L.; Li, Z.; Ni, C.-F. Increased Expression of Epidermal Growth Factor-like Domain-Containing Protein 7 Is Predictive of Poor Prognosis in Patients with Hepatocellular Carcinoma. J. Cancer Res. Ther. 2018, 14, 867–872. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, J.; Gao, H.; Yuan, T.; Kang, J.; Jin, L.; Gui, S.; Zhang, Y. Role of EGFL7/EGFR-Signaling Pathway in Migration and Invasion of Growth Hormone-Producing Pituitary Adenomas. Sci. China Life Sci. 2018, 61, 893–901. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Q.; Gao, H.; Wan, D.; Li, C.; Li, Z.; Zhang, Y. EGFL7 Participates in Regulating Biological Behavior of Growth Hormone–Secreting Pituitary Adenomas via Notch2/DLL3 Signaling Pathway. Tumor Biol. 2017, 39, 1010428317706203. [Google Scholar] [CrossRef]
- Triantafyllou, E.A.; Georgatsou, E.; Mylonis, I.; Simos, G.; Paraskeva, E. Expression of AGPAT2, an Enzyme Involved in the Glycerophospholipid/Triacylglycerol Biosynthesis Pathway, Is Directly Regulated by HIF-1 and Promotes Survival and Etoposide Resistance of Cancer Cells under Hypoxia. Biochim. Biophys. Acta Mol. Cell Biol. Lipids 2018, 1863, 1142–1152. [Google Scholar] [CrossRef]
- Børglum, A.D.; Demontis, D.; Grove, J.; Pallesen, J.; Hollegaard, M.V.; Pedersen, C.B.; Hedemand, A.; Mattheisen, M.; Uitterlinden, A.; Nyegaard, M.; et al. Genome-Wide Study of Association and Interaction with Maternal Cytomegalovirus Infection Suggests New Schizophrenia Loci. Mol. Psychiatry 2014, 19, 325–333. [Google Scholar] [CrossRef]
- Abbasi, A.A.; Blaesius, K.; Hu, H.; Latif, Z.; Picker-Minh, S.; Khan, M.N.; Farooq, S.; Khan, M.A.; Kaindl, A.M. Identification of a Novel Homozygous TRAPPC9 Gene Mutation Causing Non-Syndromic Intellectual Disability, Speech Disorder, and Secondary Microcephaly. Am. J. Med. Genet. Part B Neuropsychiatr. Genet. 2017, 174, 839–845. [Google Scholar] [CrossRef]
- Graham, J.M.; Zadeh, N.; Kelley, M.; Tan, E.S.; Liew, W.; Tan, V.; Deardorff, M.A.; Wilson, G.N.; Sagi-Dain, L.; Shalev, S.A. KCNK9 Imprinting Syndrome—Further Delineation of a Possible Treatable Disorder. Am. J. Med. Genet. Part A 2016, 170, 2632–2637. [Google Scholar] [CrossRef]
- Sananbenesi, F.; Fischer, A. New Friends for Ago2 in Neuronal Plasticity. EMBO J. 2015, 34, 2213–2214. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gershoni-Emek, N.; Altman, T.; Ionescu, A.; Costa, C.J.; Gradus-Pery, T.; Willis, D.E.; Perlson, E. Localization of RNAi Machinery to Axonal Branch Points and Growth Cones Is Facilitated by Mitochondria and Is Disrupted in ALS. Front. Mol. Neurosci. 2018, 11, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Fallah, H.; Ganji, M.; Arsang-Jang, S.; Sayad, A.; Taheri, M. Consideration of the Role of MALAT1 Long Noncoding RNA and Catalytic Component of RNA-Induced Silencing Complex (Argonaute 2, AGO2) in Autism Spectrum Disorders: Yes, or No? Meta Gene 2019, 19, 193–198. [Google Scholar] [CrossRef]
- El Naqa, I.; Ruan, D.; Valdes, G.; Dekker, A.; McNutt, T.; Ge, Y.; Wu, Q.J.; Oh, J.H.; Thor, M.; Smith, W.; et al. Machine Learning and Modeling: Data, Validation, Communication Challenges. Med. Phys. 2018, 45, e834–e840. [Google Scholar] [CrossRef]
- Basu, A.; Mandal, A.; Pardo, L. Hypothesis Testing for Two Discrete Populations Based on the Hellinger Distance. Stat. Probab. Lett. 2010, 80, 206–214. [Google Scholar] [CrossRef][Green Version]
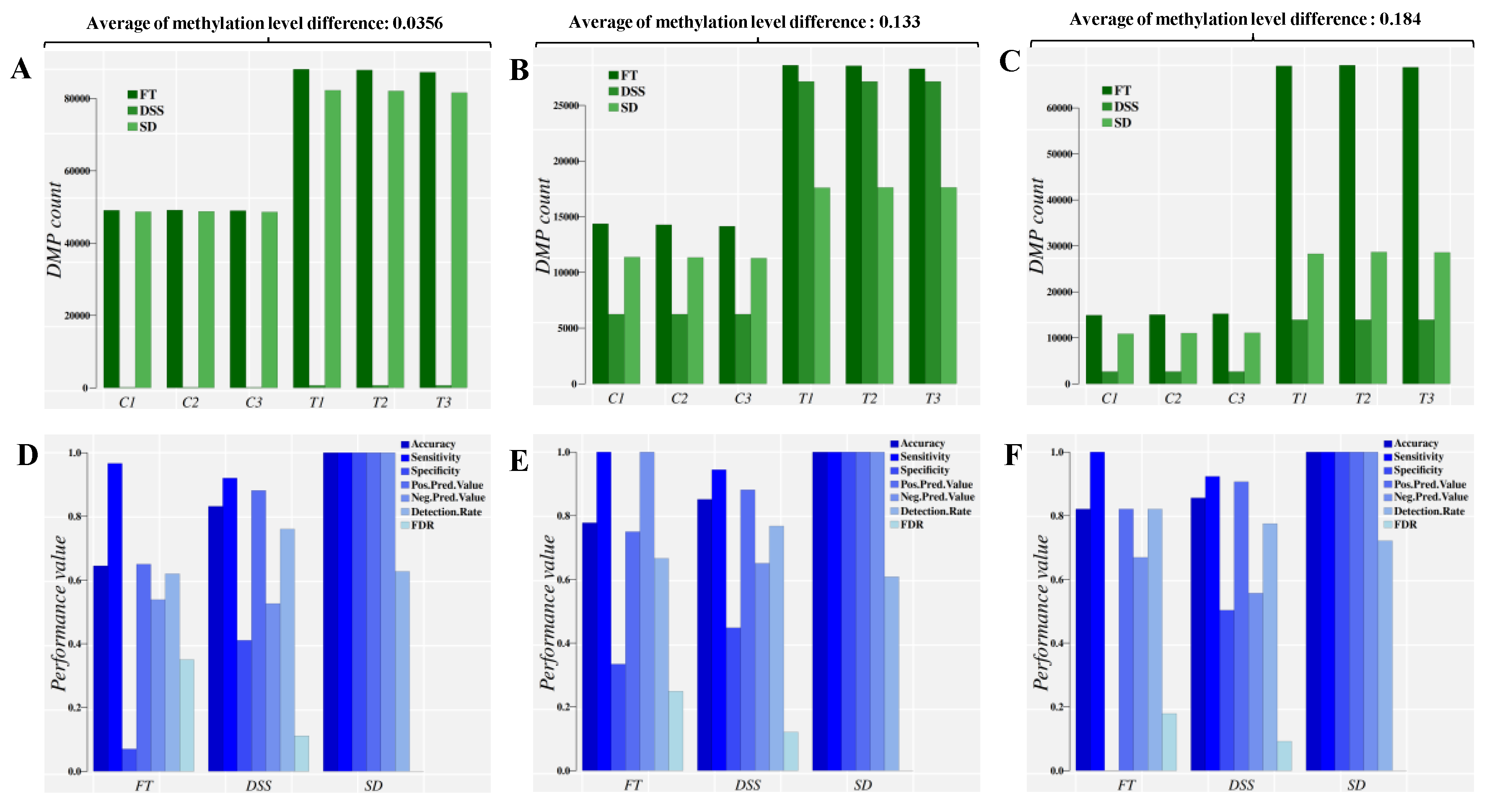
| Dataset | TV Average | Cytosine Sites/Sample | Samples/Group * | Cut-Point | Accuracy | Sen. | Spe. | FDR |
|---|---|---|---|---|---|---|---|---|
| 1. Model building & cross-validation | 0.0356 | 1,000,000 | 3 | 0.3500 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 2. Model building & cross-validation | 0.1332 | 1,000,000 | 3 | 0.9404 | 0.9998 | 0.9997 | 1.0000 | 0.0000 |
| 3. Model building & cross-validation | 0.1845 | 1,000,000 | 3 | 0.9251 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 4. External data for validation | 0.0356 | 1,000,000 | 50 | 0.3500 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 5. External data for validation | 0.1332 | 1,000,000 | 50 | 0.9404 | 0.9998 | 1.0000 | 1.0000 | 0.0000 |
| 6. External data for validation | 0.1845 | 1,000,000 | 50 | 0.9251 | 1.0000 | 0.9999 | 1.0000 | 0.0000 |
| 7. Model building & cross-validation | 0.0356 | 1,000,000 | 50 | 0.3500 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 8. Model building & cross-validation | 0.1332 | 1,000,000 | 50 | 0.8667 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 9. Model building & cross-validation | 0.1845 | 1,000,000 | 50 | 0.8306 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 10. External data for validation | 0.0356 | 1,000,000 | 50 | 0.3500 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 11. External data for validation | 0.1332 | 1,000,000 | 50 | 0.8667 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| 12. External data for validation | 0.1845 | 1,000,000 | 50 | 0.8306 | 1.0000 | 1.0000 | 1.0000 | 0.0000 |
| Group | Accuracy | Sensitivity | Specificity | Detection Rate | FDR | Classifier |
|---|---|---|---|---|---|---|
| G1 | 0.995 | 0.998 | 0.966 | 0.906 | 0.004 | PCA-QDA |
| G2 | 1.000 | 1.000 | 1.000 | 0.994 | 0.000 | PCA-QDA |
| G2 pred. G1 | 0.935 | 0.996 | 0.332 | 0.904 | 0.064 | LDA |
| G1 pred. G2 | 1.000 | 1.000 | 1.000 | 0.994 | 0.000 | LDA |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sanchez, R.; Yang, X.; Maher, T.; Mackenzie, S.A. Discrimination of DNA Methylation Signal from Background Variation for Clinical Diagnostics. Int. J. Mol. Sci. 2019, 20, 5343. https://doi.org/10.3390/ijms20215343
Sanchez R, Yang X, Maher T, Mackenzie SA. Discrimination of DNA Methylation Signal from Background Variation for Clinical Diagnostics. International Journal of Molecular Sciences. 2019; 20(21):5343. https://doi.org/10.3390/ijms20215343
Chicago/Turabian StyleSanchez, Robersy, Xiaodong Yang, Thomas Maher, and Sally A. Mackenzie. 2019. "Discrimination of DNA Methylation Signal from Background Variation for Clinical Diagnostics" International Journal of Molecular Sciences 20, no. 21: 5343. https://doi.org/10.3390/ijms20215343
APA StyleSanchez, R., Yang, X., Maher, T., & Mackenzie, S. A. (2019). Discrimination of DNA Methylation Signal from Background Variation for Clinical Diagnostics. International Journal of Molecular Sciences, 20(21), 5343. https://doi.org/10.3390/ijms20215343





