Neglog: Homology-Based Negative Data Sampling Method for Genome-Scale Reconstruction of Human Protein–Protein Interaction Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data and Materials
2.1.1. Positive Training Data
2.1.2. Negative Training Data
2.1.3. Independent Test Data
2.1.4. PPIs in STRING to Be Validated
2.2. Feature Construction
2.3. L2-regularized Logistic Regression as Base Classifier
2.4. Experimental Setting and Model Evaluation
3. Results
3.1. Validating the Assumption of Neglog
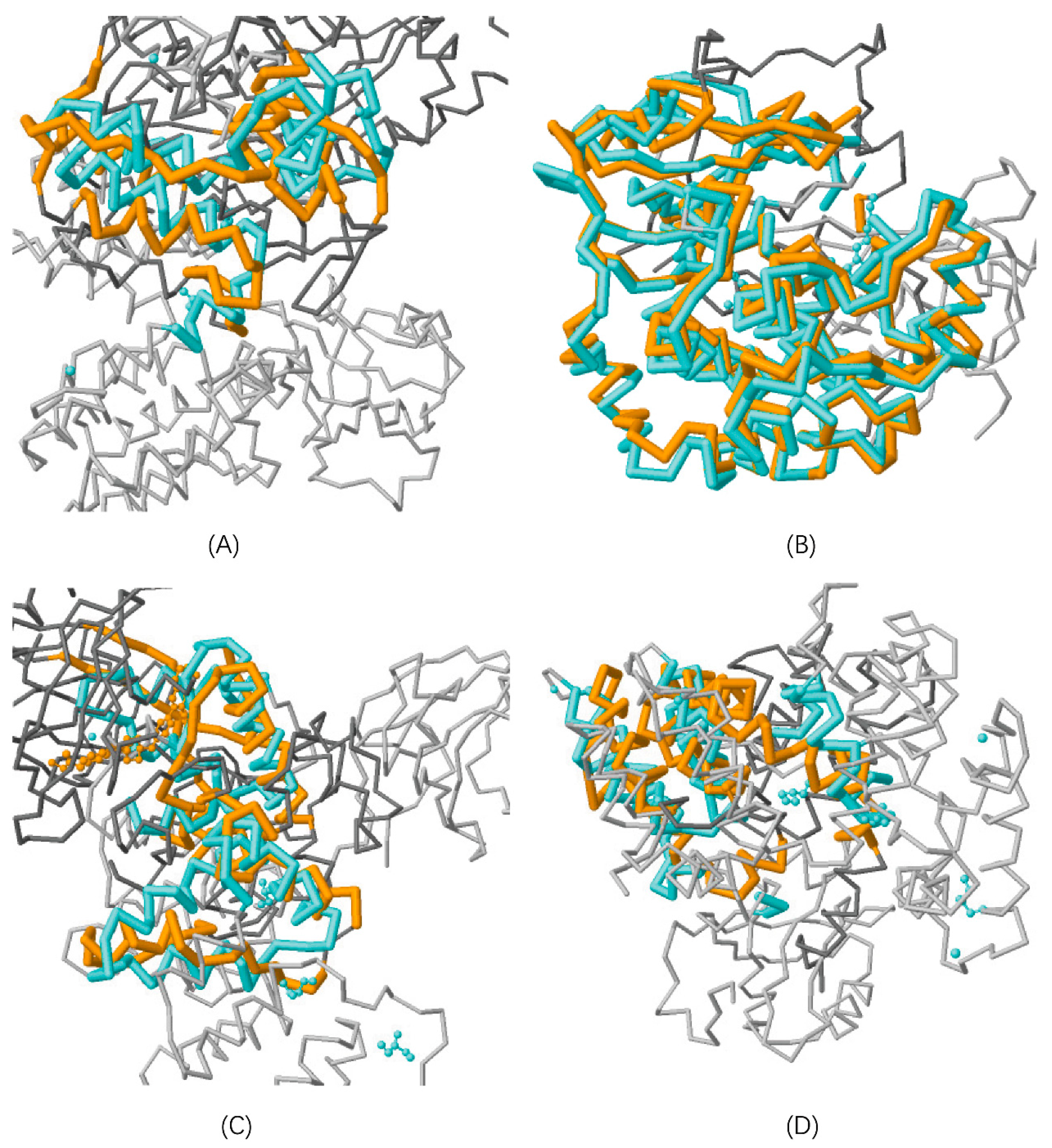
3.1.1. Protein Structure Alignment
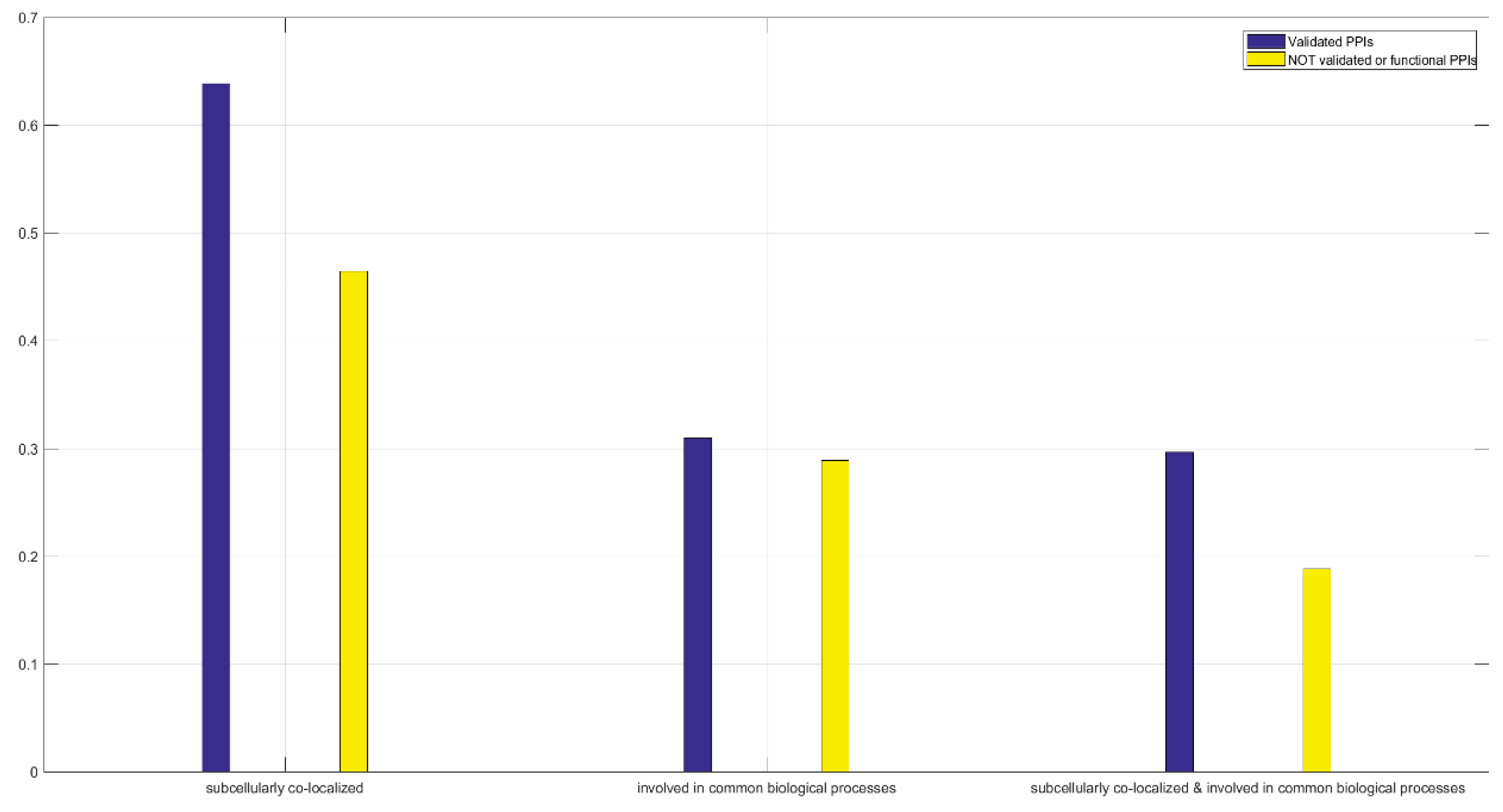
3.1.2. Functional Validation
3.2. Performance of Cross Validation and Independent Test
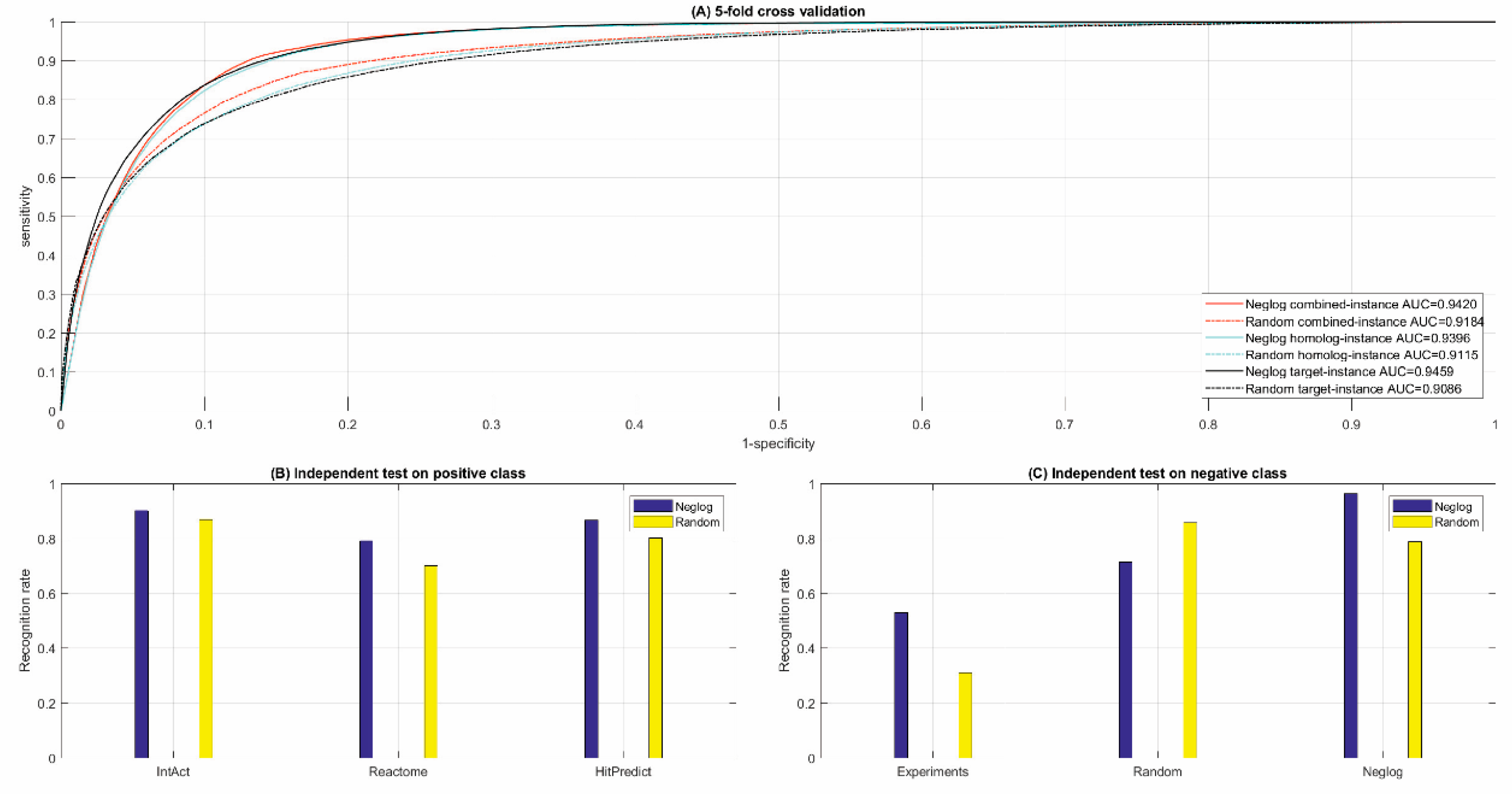
3.2.1. Cross Validation
3.2.2. Independent Test
3.3. Comparison with Random Sampling
3.3.1. Cross Validation
3.3.2. Independent Test
3.4. Comparison with Existing Methods
3.4.1. Subcellularly Restricted Sampling Methods
3.4.2. Sequence Feature Based Methods
3.4.3. GO Feature Based Methods
3.5. Validation of Human Protein-Protein Interactions in STRING [7]
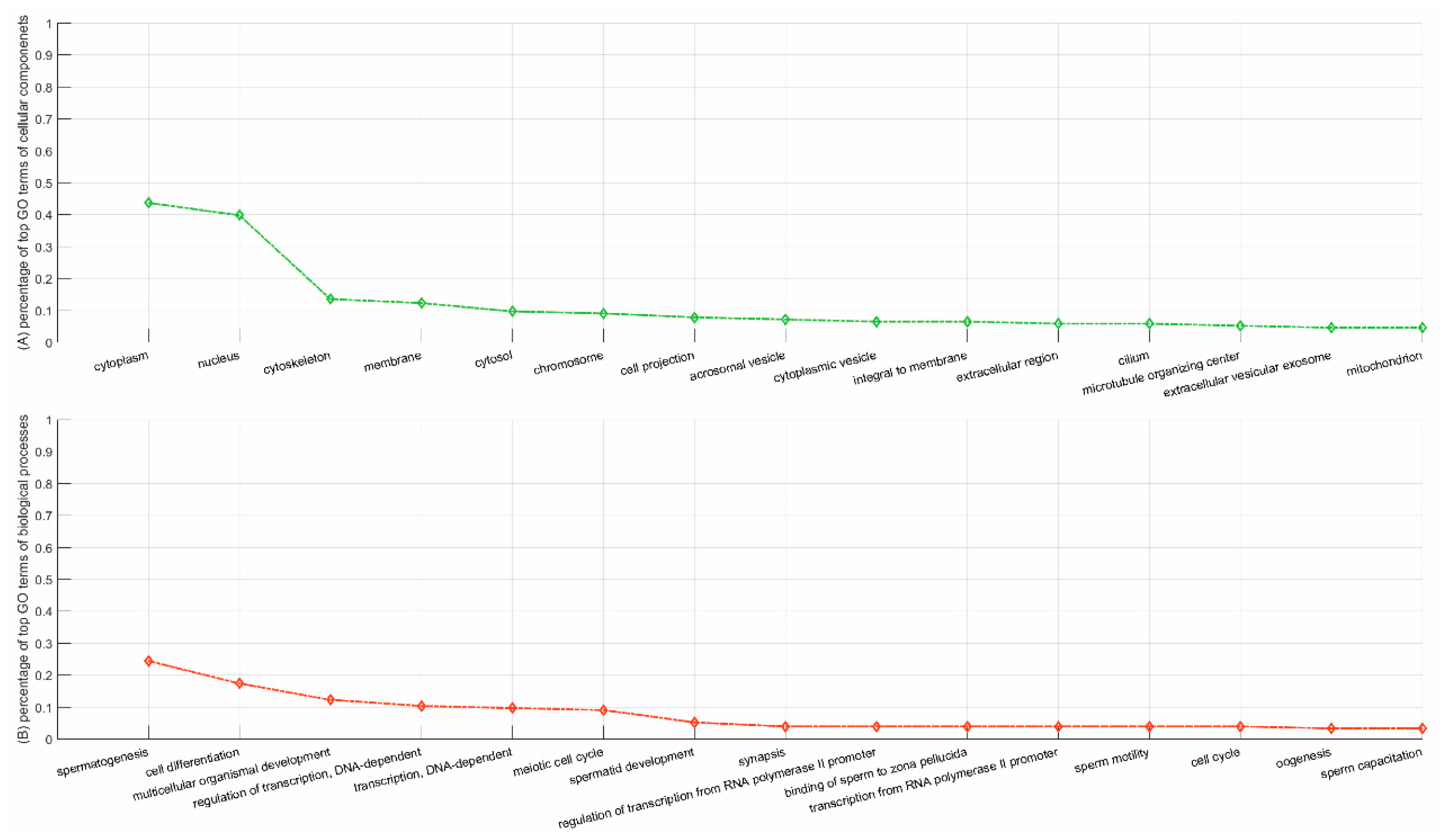
3.5.1. Statistics of PPI Validation
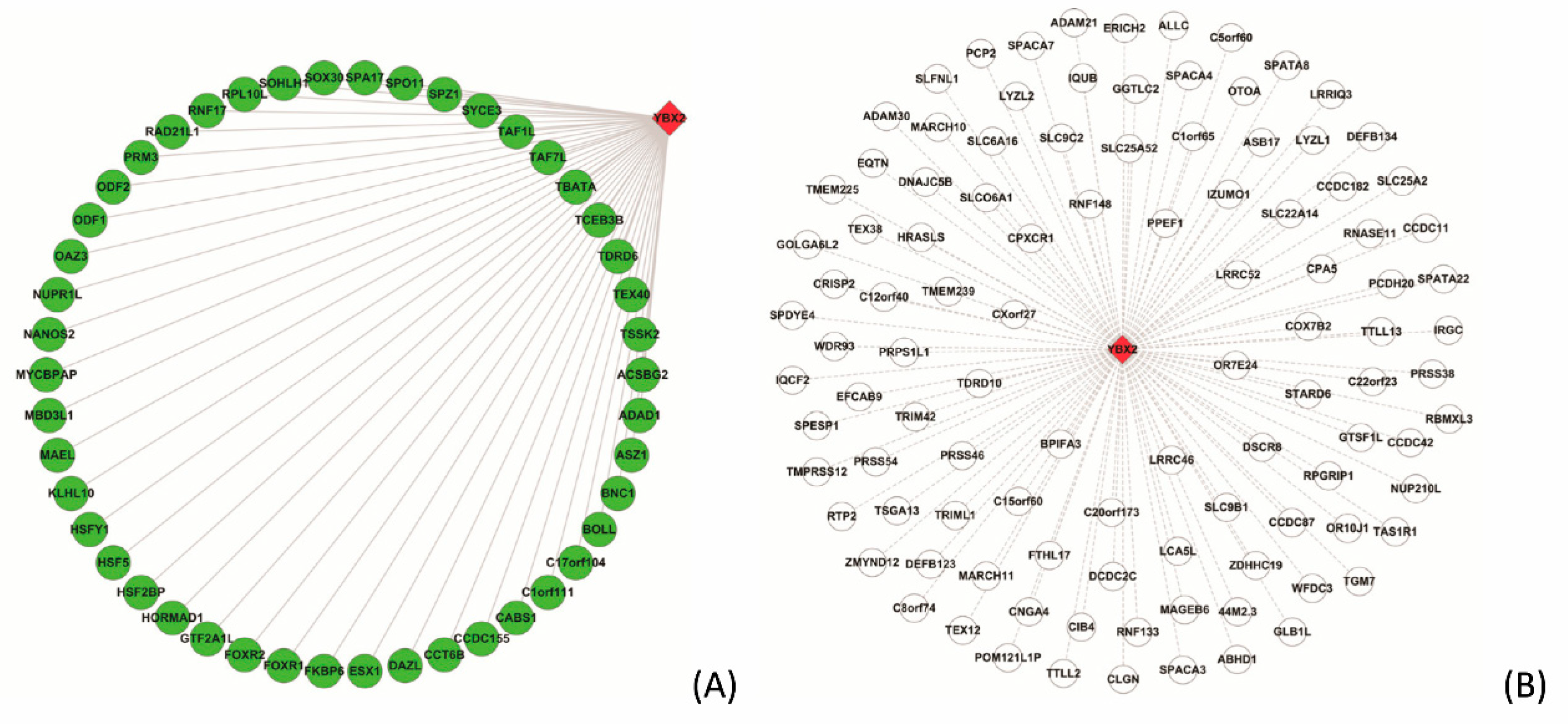
3.5.2. Case Study on YBX2
4. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Keshava Prasad, T.S.; Goel, R.; Kandasamy, K.; Keerthikumar, S.; Kumar, S.; Mathivanan, S.; Telikicherla, D.; Raju, R.; Shafreen, B.; Venugopal, A.; et al. Human Protein Reference Database—2009 update. Nucleic Acids Res. 2009, 37, D767–D772. [Google Scholar] [CrossRef] [PubMed]
- Chatr-Aryamontri, A.; Breitkreutz, B.J.; Oughtred, R.; Boucher, L.; Heinicke, S.; Stark, C.; Breitkreutz, A.; Kolas, N.; O’Donnell, L.; Reguly, T.; et al. The BioGRID interaction database: 2015 update. Nucleic Acids Res. 2015, 43, D470–D478. [Google Scholar] [CrossRef]
- Fabregat, A.; Jupe, S.; Matthews, L.; Sidiropoulos, K.; Gillespie, M.; Garapati, P.; Haw, R.; Jassal, B.; Korninger, F.; May, B.; et al. The Reactome Pathway Knowledgebase. Nucleic Acids Res. 2018, 46, D649–D655. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, S. KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Orchard, S.; Ammari, M.; Aranda, B.; Breuza, L.; Briganti, L. The MIntAct project–IntAct as a common curation platform for 11 molecular interaction databases. Nucleic Acids Res. (Database issue) 2014, 42, D358–D363. [Google Scholar] [CrossRef] [PubMed]
- López, Y.; Nakai, K.; Patil, A. HitPredict version 4: Comprehensive reliability scoring of physical protein-protein interactions from more than 100 species. Database (Oxford) 2015. [Google Scholar] [CrossRef]
- Szklarczyk, D.; Franceschini, A.; Wyder, S.; Forslund, K.; Heller, D.; Huerta-Cepas, J.; Simonovic, M.; Roth, A.; Santos, A.; Tsafou, K.P.; et al. STRING v10: Protein-protein interaction networks, integrated over the tree of life. Nucleic Acids Res. 2015, 43, D447–D452. [Google Scholar] [CrossRef] [PubMed]
- Salwinski, L.; Miller, C.S.; Smith, A.J.; Pettit, F.K.; Bowie, J.U.; Eisenberg, D. The Database of Interacting Proteins: 2004 update. Nucleic Acids Res. 2004, 32, D449–D451. [Google Scholar] [CrossRef] [PubMed]
- Gilbert, D. Biomolecular interaction network database. Brief. Bioinform. 2005, 6, 194–198. [Google Scholar] [CrossRef]
- Krogan, N.J. Global landscape of protein complexes in the yeast Saccharomyces cerevisiae. Nature 2006, 440, 637–643. [Google Scholar] [CrossRef] [PubMed]
- Celaj, A.; Schlecht, U.; Smith, J.; Xu, W.; Suresh, S.; Miranda, M.; Aparicio, A.M.; Proctor, M.; Davis, R.W.; Roth, F.P.; et al. Quantitative analysis of protein interaction network dynamics in yeast. Mol. Syst. Biol. 2017, 13, 934. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, M.W.; Kann, M.G. Chapter 4: Protein interactions and disease. PLoS Comput. Biol. 2012, 8, e1002819. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, J.; Luo, X.; Zhu, W.; Yu, K.; Chen, K.; Li, Y.; Jiang, H. Predicting protein-protein interactions based only on sequences information. Proc. Natl. Acad. Sci. USA 2007, 104, 4337–4341. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Guo, M.; Needham, C.J.; Huang, Y.; Cai, L.; Westhead, D.R. Simple sequence-based kernels do not predict protein-protein interactions. Bioinformatics 2010, 26, 2610–2614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Park, Y.; Marcotte, E.M. Revisiting the negative example sampling problem for predicting protein-protein interactions. Bioinformatics 2011, 27, 3024–3028. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pancaldi, V.; Saraç, O.S.; Rallis, C.; McLean, J.R.; Převorovský, M.; Gould, K.; Beyer, A.; Bähler, J. Predicting the fission yeast protein interaction network. G3 (Bethesda) 2012, 2, 453–467. [Google Scholar] [CrossRef] [PubMed]
- Mei, S. In Silico Enhancing, M. tuberculosis Protein Interaction Networks in STRING To Predict Drug-Res.istance Pathways and Pharmacological Risks. J. Proteome Res. 2018, 17, 1749–1760. [Google Scholar] [CrossRef]
- Zubek, J.; Tatjewski, M.; Boniecki, A.; Mnich, M.; Basu, S.; Plewczynski, D. Multi-level machine learning prediction of protein-protein interactions in Saccharomyces cerevisiae. Peer J. 2015, 3, e1041. [Google Scholar] [CrossRef]
- Kshirsagar, M.; Schleker, S.; Carbonell, J.; Klein-Seetharaman, J. Techniques for transferring host-pathogen protein interactions knowledge to new tasks. Front. Microbiol. 2015, 6, 36. [Google Scholar] [CrossRef]
- Qi, Y.; Tastan, O.; Carbonell, J.G.; Klein-Seetharaman, J.; Weston, J. Semi-supervised multi-task learning for predicting interactions between HIV-1 and human proteins. Bioinformatics 2010, 26, i645–i652. [Google Scholar] [CrossRef]
- Mei, S. Probability weighted ensemble transfer learning for predicting interactions between HIV-1 and human proteins. PLoS ONE 2013, 8, e79. [Google Scholar] [CrossRef] [PubMed]
- Mei, S.; Zhu, H. Computational reconstruction of proteome-wide protein interaction networks between HTLV retroviruses and Homo sapiens. BMC Bioinform. 2014, 15, 245. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Rezaei, J.; Hugo, W.; Gao, S.; Jin, J.; Fan, M.; Yong, C.H.; Wozniak, M.; Wong, L. Stringent DDI-based prediction of H. sapiens-M. tuberculosis H37Rv protein-protein interactions. BMC Syst. Biol. 2013, 7 (Suppl. 6), S6. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Gao, S.; Nguyen, N.N.; Fan, M.; Jin, J.; Liu, B.; Zhao, L.; Xiong, G.; Tan, M.; Li, S.; et al. Stringent homology-based prediction of H. sapiens-M. tuberculosis H37Rv protein-protein interactions. Biol. Direct. 2014, 9, 5. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.P.; Wang, J.; Qiu, Y.Q.; Leung, R.K.; Zhang, X.S.; Zhang, X.S.; Tsui, S.K.; Chen, L. Inferring a protein interaction map of Mycobacterium tuberculosis based on sequences and interologs. BMC Bioinformatics 2012, 13 (Suppl. 7), S6. [Google Scholar] [CrossRef] [PubMed]
- Lin, N.; Wu, B.; Jansen, R.; Gerstein, M.; Zhao, H. Information assessment on predicting protein-protein interactions. BMC Bioinform. 2004, 5, 154. [Google Scholar] [CrossRef] [PubMed]
- Maetschke, S.; Simonsen, M.; Davis, M.; Ragan, M.A. Gene Ontology-driven inference of protein–protein interactions using inducers. Bioinformatics 2012, 28, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Eid, F.E.; ElHefnawi, M.; Heath, L.S. DeNovo: Virus-host sequence-based protein-protein interaction prediction. Bioinformatics 2016, 32, 1144–1150. [Google Scholar] [CrossRef]
- Han, J.D.; Bertin, N.; Hao, T.; Goldberg, D.S.; Berriz, G.F.; Zhang, L.V.; Dupuy, D.; Walhout, A.J.; Cusick, M.E.; Roth, F.P.; et al. Evidence for dynamically organized modularity in the yeast protein–protein interaction network. Nature 2004, 430, 88–93. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Noble, W. Choosing negative examples for the prediction of protein-protein interactions. BMC Bioinform. 2006, 7, S2. [Google Scholar] [CrossRef]
- Blohm, P.; Frishman, G.; Smialowski, P.; Goebels, F.; Wachinger, B.; Ruepp, A.; Frishman, D. Negatome 2.0: A database of non-interacting proteins derived by literature mining, manual annotation and protein structure analysis. Nucleic Acids Res. 2014, 42, D396–D400. [Google Scholar] [CrossRef] [PubMed]
- Trabuco, L.G.; Betts, M.J.; Russell, R.B. Negative protein-protein interaction datasets derived from large-scale two-hybrid experiments. Methods 2012, 58, 343–348. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Luscombe, N.M.; Lu, H.X.; Zhu, X. Annotation transfer between genomes: Protein-protein interologs and protein-DNA regulogs. Genome Res. 2004, 14, 1107–1118. [Google Scholar] [CrossRef] [PubMed]
- Kelley, L.A.; Mezulis, S.; Yates, C.M.; Wass, M.N.; Sternberg, M.J. The Phyre2 web portal for protein modeling, prediction and analysis. Nat. Protoc. 2015, 10, 845–858. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hosur, R.; Peng, J.; Vinayagam, A.; Stelzl, U.; Xu, J.; Perrimon, N.; Bienkowska, J.; Berger, B. A computational framework for boosting confidence in high-throughput protein-protein interaction datasets. Genome Biol. 2012, 13, R76. [Google Scholar] [CrossRef] [PubMed]
- Boeckmann, B.; Bairoch, A.; Apweiler, R.; Blatter, M.C.; Estreicher, A. The SWISS-PROT protein knowledgebase and its supplement TrEMBL in 2003. Nucleic Acids Res. 2003, 31, 365–370. [Google Scholar] [CrossRef]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef]
- Barrell, D.; Dimmer, E.; Huntley, R.P.; Binns, D.; O’Donovan, C. The GOA database in 2009—An integrated Gene Ontology Annotation resource. Nucleic Acids Res. 2009, 37, D396–D403. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar]
- Yu, F.; Huang, F.; Lin, C. Dual coordinate descent methods for logistic regression and maximum entropy models. Mach. Learn 2011, 85, 41–75. [Google Scholar] [CrossRef]
- Fan, R.; Chang, K.; Hsieh, C.; Wang, X.; Lin, C. LIBLINEAR: A Library for Large Linear Classification. Mach. Learn Res. 2008, 9, 1871–1874. [Google Scholar]
- Häuser, R.; Ceol, A.; Rajagopala, S.V.; Mosca, R.; Siszler, G.; Wermke, N.; Sikorski, P.; Schwarz, F.; Schick, M.; Wuchty, S.; et al. A second-generation protein-protein interaction network of Helicobacter pylori. Mol. Cell Proteomics 2014, 13, 1318–1329. [Google Scholar] [CrossRef] [PubMed]
- Aloy, P.; Russell, R.B. Structural systems biology: Modelling protein interactions. Nat. Rev. Mol. Cell Biol. 2006, 7, 188–197. [Google Scholar] [CrossRef] [PubMed]
- Prlic, A.; Bliven, S.; Rose, P.W.; Bluhm, W.F.; Bizon, C.; Godzik, A.; Bourne, P.E. Pre-calculated protein structure alignments at the RCSB PDB website. Bioinformatics 2010, 26, 2983–2985. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Feng, X.; Stein, L. A human functional protein interaction network and its application to cancer data analysis. Genome Biol. 2010, 11, R53. [Google Scholar] [CrossRef] [PubMed]
- Sun, T.; Zhou, B.; Lai, L.; Pei, J. Sequence-based prediction of protein protein interaction using a deep-learning algorithm. BMC Bioinform. 2017, 18, 277. [Google Scholar] [CrossRef] [PubMed]
| Cross Validation. | Size | Combined-Instance | Homolog-Instance | Target-Instance | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PR | SE | MCC | PR | SE | MCC | PR | SE | MCC | |||||
| Positive class | 55,862 | 0.8653 | 0.9154 | 0.7957 | 0.8641 | 0.8944 | 0.7786 | 0.8617 | 0.9112 | 0.7864 | |||
| Negative class | 55,862 | 0.9098 | 0.8568 | 0.7934 | 0.8896 | 0.8582 | 0.7767 | 0.9018 | 0.8480 | 0.7823 | |||
| [Acc; MCC; ROC-AUC] | [88.62%; 0.7935; 0.9420] | [87.64%; 0.7773; 0.9396] | [87.64%; 0.7773; 0.9459] | ||||||||||
| F1 Score | 0.8897 | 0.8790 | 0.8858 | ||||||||||
| Independent test | Positive class * | Negative class * | |||||||||||
| IntAct | Reactome | HitPredict | Experimental | Random | Neglog | ||||||||
| 90.20% | 79.14% | 86.76% | 53.00% | 71.38% | 96.40% | ||||||||
| Cross Validation | Size | Combined-Instance | Homolog-Instance | Target-Instance | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PR | SE | MCC | PR | SE | MCC | PR | SE | MCC | |||||
| Positive class | 55,862 | 0.8366 | 0.8726 | 0.7368 | 0.8269 | 0.8544 | 0.7137 | 0.8168 | 0.8714 | 0.7086 | |||
| Negative class | 55,862 | 0.8647 | 0.8269 | 0.7332 | 0.8443 | 0.8154 | 0.7090 | 0.8454 | 0.7825 | 0.6951 | |||
| [Acc; MCC; ROC-AUC] | [85.00%; 0.7345;0.9184] | [83.52%; 0.7113;0.9115] | [83.52%; 0.7113;0.9086] | ||||||||||
| F1 Score | 0.8542 | 0.8404 | 0.8432 | ||||||||||
| Independent test | Positive class * | Negative class * | |||||||||||
| IntAct | Reactome | HitPredict | Experimental | Random | Neglog | ||||||||
| 86.99% | 70.02% | 80.20% | 31.00% | 85.85% | 78.74% | ||||||||
| Experiments | co-Expression | Database | Fusion | co-Occurrence | Text Mining | |
|---|---|---|---|---|---|---|
| Size | 38,323 | 148,227 | 93,225 | 987 | 11,435 | 289,826 |
| Positive Rate | 81.69 % | 54.23 % | 77.41 % | 50.05 % | 46.01 % | 71.09% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, S.; Zhang, K. Neglog: Homology-Based Negative Data Sampling Method for Genome-Scale Reconstruction of Human Protein–Protein Interaction Networks. Int. J. Mol. Sci. 2019, 20, 5075. https://doi.org/10.3390/ijms20205075
Mei S, Zhang K. Neglog: Homology-Based Negative Data Sampling Method for Genome-Scale Reconstruction of Human Protein–Protein Interaction Networks. International Journal of Molecular Sciences. 2019; 20(20):5075. https://doi.org/10.3390/ijms20205075
Chicago/Turabian StyleMei, Suyu, and Kun Zhang. 2019. "Neglog: Homology-Based Negative Data Sampling Method for Genome-Scale Reconstruction of Human Protein–Protein Interaction Networks" International Journal of Molecular Sciences 20, no. 20: 5075. https://doi.org/10.3390/ijms20205075






