Independent Component Analysis for Unraveling the Complexity of Cancer Omics Datasets
Abstract
1. Introduction
2. Methodology of ICA Application to Cancer Omics Data
2.1. Brief Introduction into Matrix Factorization Applied to Omics Data
2.2. ICA Algorithms
2.3. Various Ways to Apply ICA to Omics Data
2.4. Assessment and Comparison with Other Matrix Factorization Methods
2.5. Estimating the Number of Independent Components
2.6. Methods for Interpretation of Independent Components
3. Applications of ICA in Cancer Research
3.1. Applications to Data Preprocessing, Classification, Dimensionality Reduction, and Clustering
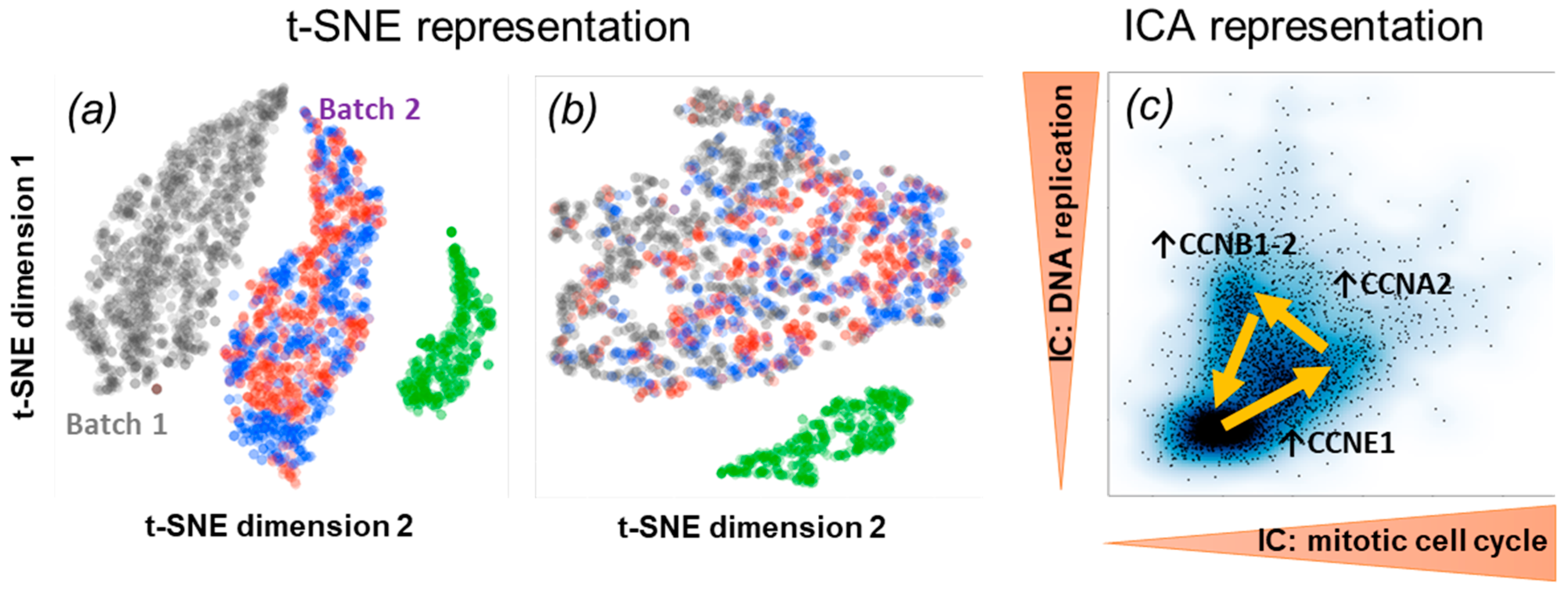
3.2. ICA for Unraveling Functional Subsystems of a Living Cell or a Cell Ecosystem
3.3. Applications to Unsupervised Cell Type Deconvolution
3.4. ICA Applications to Single-Cell Omics Data Analysis
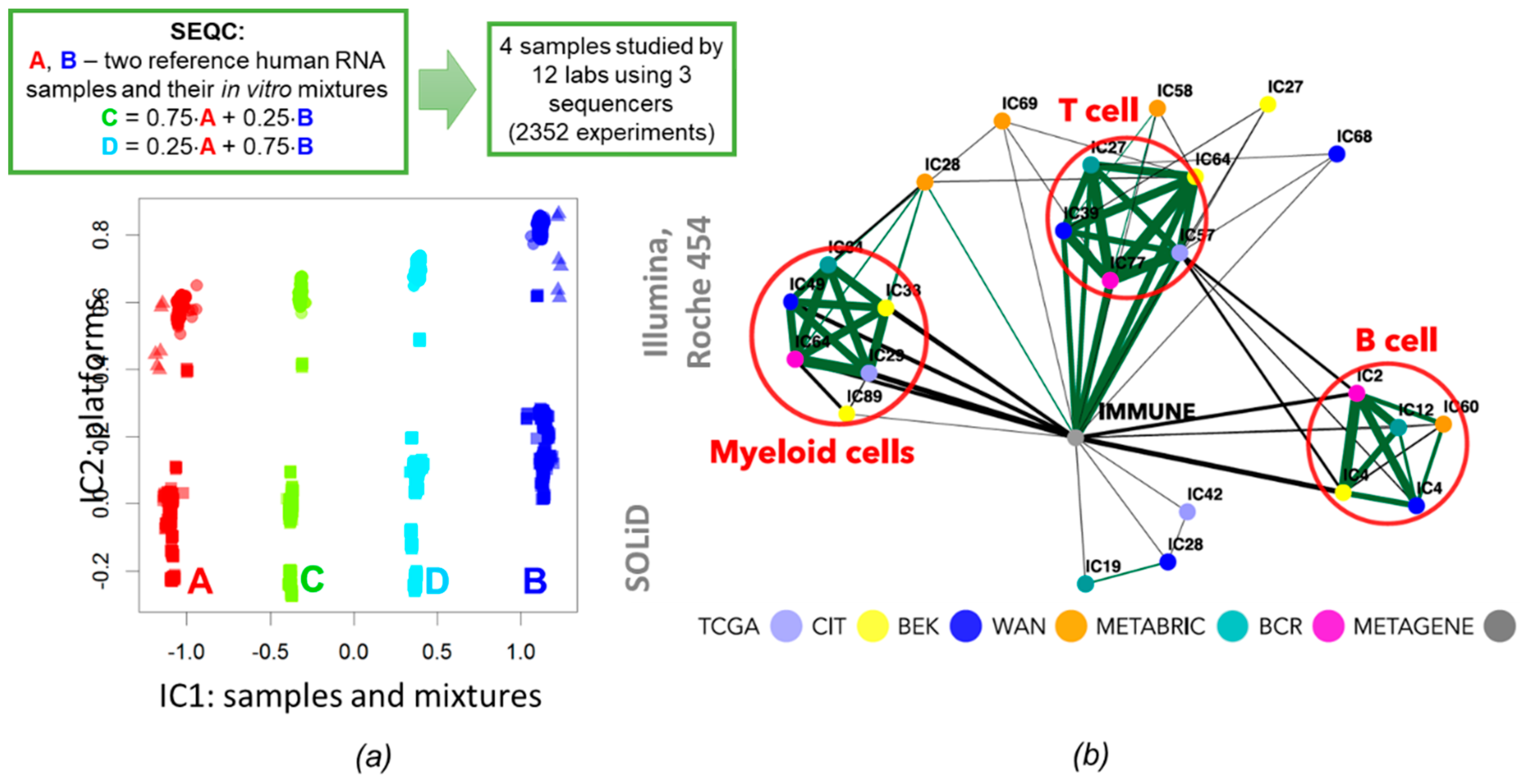
3.5. Multi-Omics ICA Applications in Cancer Research
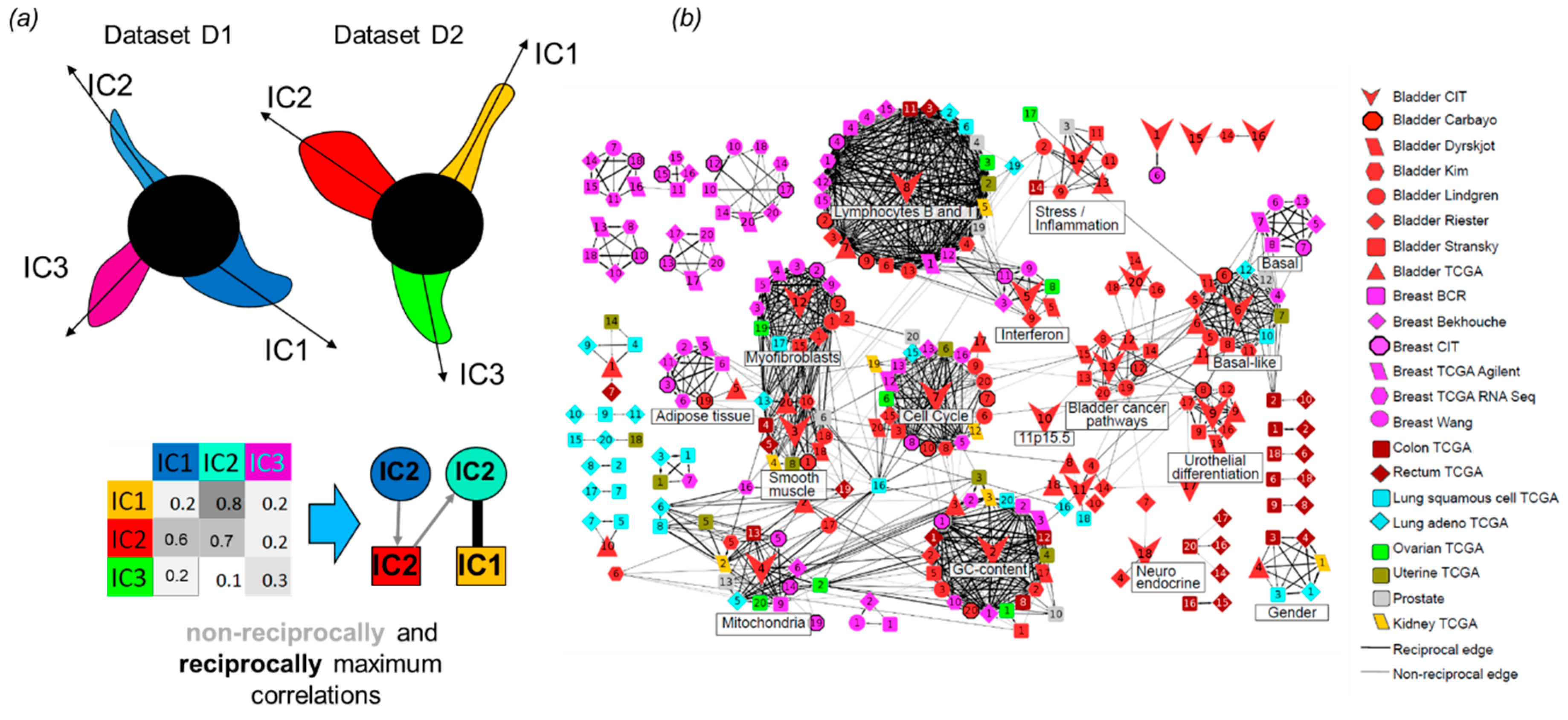
3.6. Correlations and Interactions among Functional Subsystems Defined by ICA
4. Discussion
Funding
Conflicts of Interest
Abbreviations
| ICA | Independent Component Analysis |
| PCA | Principal Component Analysis |
| NMF | Non-Negative Matrix Factorization |
| MSTD | Maximally Stable Transcriptomic Dimension |
| fMRI | functional Magnetic Resonance Imaging |
| TCGA | The Cancer Genome Atlas |
| BIC | Bayesian Information Criterion |
| FOBI | Fourth-Order Blind Identification |
| SEQC | Sequencing Quality Control consortium |
| t-SNE | t-Distributed Stochastic Neighbor Embedding |
References
- Liebermeister, W. Linear modes of gene expression determined by independent component analysis. Bioinformatics 2002, 18, 51–60. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.-I.; Batzoglou, S. Application of independent component analysis to microarrays. Genome Biol. 2003, 4, R76. [Google Scholar] [CrossRef] [PubMed]
- Saidi, S.A.; Holland, C.M.; Kreil, D.P.; MacKay, D.J.C.; Charnock-Jones, D.S.; Print, C.G.; Smith, S.K. Independent component analysis of microarray data in the study of endometrial cancer. Oncogene 2004, 23, 6677–6683. [Google Scholar] [CrossRef] [PubMed]
- Frigyesi, A.; Veerla, S.; Lindgren, D.; Höglund, M. Independent component analysis reveals new and biologically significant structures in micro array data. BMC Bioinform. 2006, 7, 290. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wang, Q.; Li, Q.; Mi, R.; Ye, H.; Zhang, H.; Chen, B.; Li, Y.; Huang, G.; Xia, J. Radiomics nomogram building from multiparametric MRI to predict grade in patients with glioma: A cohort study. J. Magn. Reson. Imaging 2019, 49, 825–833. [Google Scholar] [CrossRef]
- Levine, A.B.; Schlosser, C.; Grewal, J.; Coope, R.; Jones, S.J.M.; Yip, S. Rise of the machines: Advances in deep learning for cancer diagnosis. Trends Cancer 2019, 5, 157–169. [Google Scholar] [CrossRef]
- Tandel, G.S.; Biswas, M.G.; Kakde, O.; Tiwari, A.S.; Suri, H.; Turk, M.; Laird, J.R.; Asare, C.K.; Ankrah, A.N.; Khanna, N.; et al. A Review on a deep learning perspective in brain cancer classification. Cancers (Basel) 2019, 11, 111. [Google Scholar] [CrossRef]
- Hosny, A.; Parmar, C.; Quackenbush, J.; Schwartz, L.H.; Aerts, H.J.W.L. Artificial intelligence in radiology. Nat. Rev. Cancer 2018, 18, 500–510. [Google Scholar] [CrossRef]
- Gao, Z.; Wu, S.; Liu, Z.; Luo, J.; Zhang, H.; Gong, M.; Li, S. Learning the implicit strain reconstruction in ultrasound elastography using privileged information. Med. Image Anal. 2019, 58, 101534. [Google Scholar] [CrossRef]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef]
- Ehteshami Bejnordi, B.; Veta, M.; Johannes van Diest, P.; Van Ginneken, B.; Karssemeijer, N.; Litjens, G.; Van der Laak, J.A.W.M.; Hermsen, M.; Manson, Q.F.; Balkenhol, M.; et al. Diagnostic assessment of deep learning algorithms for detection of lymph node metastases in women with breast cancer. JAMA 2017, 318, 2199–2210. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, K.; Poirion, O.B.; Lu, L.; Garmire, L.X. Deep learning–based multi-omics integration robustly predicts survival in liver cancer. Clin. Cancer Res. 2018, 24, 1248–1259. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, C.M.D. Anderson breaks with IBM Watson, raising questions about artificial intelligence in oncology. J. Natl. Cancer Inst. 2017, 109, 5. [Google Scholar] [CrossRef] [PubMed]
- Gorban, A.N.; Mirkes, E.M.; Tyukin, I.Y. How Deep should be the depth of convolutional neural networks: A backyard dog case study. Cognit. Comput. 2019, 1–10. [Google Scholar] [CrossRef]
- Karhunen, J.; Oja, E.; Wang, L.; Vigario, R.; Joutsensalo, J. A class of neural networks for independent component analysis. IEEE Trans. Neural Netw. 1997, 8, 486–504. [Google Scholar] [CrossRef] [PubMed]
- Brunet, J.P.; Tamayo, P.; Golub, T.R.; Mesirov, J.P. Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl. Acad. Sci. USA 2004, 101, 4164–4169. [Google Scholar] [CrossRef] [PubMed]
- Gorban, A.N.; Zinovyev, A.Y. Principal graphs and manifolds. In Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods and Techniques; IGI Global: Hershey, PA, USA, 2008; ISBN 9781605667669. [Google Scholar]
- Zinovyev, A.; Kairov, U.; Karpenyuk, T.; Ramanculov, E. Blind source separation methods for deconvolution of complex signals in cancer biology. Biochem. Biophys. Res. Commun. 2013, 430, 1182–1187. [Google Scholar] [CrossRef]
- Bell, A.J.; Sejnowski, T.J. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995, 7, 1129–1159. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Cardoso, J.-F. High-order contrasts for independent component analysis. Neural Comput. 1999, 11, 157–192. [Google Scholar] [CrossRef]
- Zhou, W.; Altman, R.B. Data-driven human transcriptomic modules determined by independent component analysis. BMC Bioinform. 2018, 19, 327. [Google Scholar] [CrossRef] [PubMed]
- Risk, B.B.; Matteson, D.S.; Ruppert, D.; Eloyan, A.; Caffo, B.S. An evaluation of independent component analyses with an application to resting-state fMRI. Biometrics 2014, 70, 224–236. [Google Scholar] [CrossRef] [PubMed]
- Krumsiek, J.; Suhre, K.; Illig, T.; Adamski, J.; Theis, F.J. Bayesian Independent Component Analysis Recovers Pathway Signatures from Blood Metabolomics Data. J. Proteome Res. 2012, 11, 4120–4131. [Google Scholar] [CrossRef] [PubMed]
- Bach, F.R. Kernel independent component analysis. J. Mach. Learn. Res. 2002, 3, 1–48. [Google Scholar]
- Zibulevsky, M.; Pearlmutter, B.A. Blind source separation by sparse decomposition in a signal dictionary. Neural Comput. 2001, 13, 863–882. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E.; Journée, M.; Absil, P.A.; Sepulchre, R.; Caldas, C. Elucidating the altered transcriptional programs in breast cancer using independent component analysis. PLoS Comput. Biol. 2007, 3, e161. [Google Scholar] [CrossRef] [PubMed]
- Virta, J.; Taskinen, S.; Nordhausen, K. Applying fully tensorial ICA to fMRI data. In Proceedings of the 2016 IEEE Signal Processing in Medicine and Biology Symposium (SPMB), Philadelphia, PA, USA, 6 December 2016; pp. 1–6. [Google Scholar]
- Virta, J.; Li, B.; Nordhausen, K.; Oja, H. Independent component analysis for tensor-valued data. J. Multivar. Anal. 2017, 162, 172–192. [Google Scholar] [CrossRef]
- Bach, F.R.; Jordan, M.I. Beyond independent components: Trees and clusters. J. Mach. Learn. Res. 2003, 4, 1205–1233. [Google Scholar]
- Meyer-Bäse, A.; Theis, F.J.; Lange, O.; Puntonet, C.G. Tree-Dependent and topographic independent component analysis for fMRI analysis. In International Conference on Independent Component Analysis and Signal Separation; Springer: Berlin/Heidelberg, Germany, 2004; pp. 782–789. [Google Scholar]
- Avila Cobos, F.; Vandesompele, J.; Mestdagh, P.; De Preter, K. Computational deconvolution of transcriptomics data from mixed cell populations. Bioinformatics 2018, 34, 1969–1979. [Google Scholar] [CrossRef]
- Biton, A.; Bernard-Pierrot, I.; Lou, Y.; Krucker, C.; Chapeaublanc, E.; Rubio-Pérez, C.; López-Bigas, N.; Kamoun, A.; Neuzillet, Y.; Gestraud, P.; et al. Independent component analysis uncovers the landscape of the bladder tumor transcriptome and reveals insights into luminal and basal subtypes. Cell Rep. 2014, 9, 1235–1245. [Google Scholar] [CrossRef]
- Kairov, U.; Cantini, L.; Greco, A.; Molkenov, A.; Czerwinska, U.; Barillot, E.; Zinovyev, A. Determining the optimal number of independent components for reproducible transcriptomic data analysis. BMC Genom. 2017, 18, 712. [Google Scholar] [CrossRef]
- Kong, W.; Vanderburg, C.R.; Gunshin, H.; Rogers, J.T.; Huang, X. A review of independent component analysis application to microarray gene expression data. Biotechniques 2008, 45, 501–520. [Google Scholar] [CrossRef] [PubMed]
- Meng, C.; Zeleznik, O.A.; Thallinger, G.G.; Kuster, B.; Gholami, A.M.; Culhane, A.C. Dimension reduction techniques for the integrative analysis of multi-omics data. Brief. Bioinform. 2016, 17, 628–641. [Google Scholar] [CrossRef] [PubMed]
- Barillot, E.; Calzone, L.; Hupe, P.; Vert, J.-P.; Zinovyev, A. Computational Systems Biology of Cancer; Taylor & Francis: Abington, UK, 2012; ISBN 9781439831441. [Google Scholar]
- Cantini, L.; Kairov, U.; de Reyniès, A.; Barillot, E.; Radvanyi, F.; Zinovyev, A. Assessing reproducibility of matrix factorization methods in independent transcriptomes. Bioinformatics 2019. [Google Scholar] [CrossRef] [PubMed]
- Nazarov, P.V.; Wienecke-Baldacchino, A.K.; Zinovyev, A.; Czerwińska, U.; Muller, A.; Nashan, D.; Dittmar, G.; Azuaje, F.; Kreis, S. Independent component analysis provides clinically relevant insights into the biology of melanoma patients. BMC Med. Genom. 2019, 395145. [Google Scholar] [CrossRef]
- Chiappetta, P.; Roubaud, M.C.; Torrésani, B. Blind source separation and the analysis of microarray data. J. Comput. Biol. 2005, 11, 1090–1109. [Google Scholar] [CrossRef] [PubMed]
- Himberg, J.; Hyvarinen, A. Icasso: Software for investigating the reliability of ICA estimates by clustering and visualization. In Proceedings of the 2003 IEEE XIII Workshop on Neural Networks for Signal Processing (IEEE Cat. No.03TH8718), Toulouse, France, 17–19 September 2003; pp. 259–268. [Google Scholar]
- Czerwinska, U.; Cantini, L.; Kairov, U.; Barillot, E.; Zinovyev, A. Application of independent component analysis to tumor transcriptomes reveals specific and reproducible immune-related signals. In Proceedings of the Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2018; Volume 10891LNCS, pp. 501–513. [Google Scholar]
- Engreitz, J.M.; Daigle, B.J.; Marshall, J.J.; Altman, R.B. Independent component analysis: Mining microarray data for fundamental human gene expression modules. J. Biomed. Inform. 2010, 43, 932–944. [Google Scholar] [CrossRef]
- Greco, A.; Sanchez Valle, J.; Pancaldi, V.; Baudot, A.; Barillot, E.; Caselle, M.; Valencia, A.; Zinovyev, A.; Cantini, L. Molecular inverse comorbidity between Alzheimer’s disease and lung cancer: New insights from matrix factorization. Int. J. Mol. Sci. 2019, 20, 3114. [Google Scholar] [CrossRef]
- Stein-O’Brien, G.L.; Arora, R.; Culhane, A.C.; Favorov, A.V.; Garmire, L.X.; Greene, C.S.; Goff, L.A.; Li, Y.; Ngom, A.; Ochs, M.F.; et al. Enter the matrix: Factorization uncovers knowledge from omics. Trends Genet. 2018, 34, 790–805. [Google Scholar] [CrossRef]
- Way, G.P.; Zietz, M.; Himmelstein, D.S.; Greene, C.S. Sequential compression across latent space dimensions enhances gene expression signatures. bioRxiv 2019. bioRxiv:573782. [Google Scholar] [CrossRef]
- Cangelosi, R.; Goriely, A. Component retention in principal component analysis with application to cDNA microarray data. Biol. Direct 2007, 2, 2. [Google Scholar] [CrossRef] [PubMed]
- Ceruti, C.; Bassis, S.; Rozza, A.; Lombardi, G.; Casiraghi, E.; Campadelli, P. DANCo: An intrinsic dimensionality estimator exploiting angle and norm concentration. Pattern Recognit. 2014, 47, 2569–2581. [Google Scholar] [CrossRef]
- Albergante, L.; Bac, J.; Zinovyev, A. Estimating the effective dimension of large biological datasets using Fisher separability analysis. In Proceedings of the International Joint Conference on Neural Networks, Hungary, Budapest, 14–17 July 2019. [Google Scholar]
- Kuperstein, I.; Grieco, L.; Cohen, D.P.A.; Thieffry, D.; Zinovyev, A.; Barillot, E. The shortest path is not the one you know: Application of biological network resources in precision oncology research. Mutagenesis 2015, 30, 191–204. [Google Scholar] [CrossRef] [PubMed]
- Bonnet, E.; Viara, E.; Kuperstein, I.; Calzone, L.; Cohen, D.P.A.; Barillot, E.; Zinovyev, A. NaviCell Web Service for network-based data visualization. Nucleic Acids Res. 2015, 43, W560–W565. [Google Scholar] [CrossRef] [PubMed]
- Gawron, P.; Ostaszewski, M.; Satagopam, V.; Gebel, S.; Mazein, A.; Kuzma, M.; Zorzan, S.; McGee, F.; Otjacques, B.; Balling, R.; et al. MINERVA-a platform for visualization and curation of molecular interaction networks. NPJ Syst. Biol. Appl. 2016, 2, 16020. [Google Scholar] [CrossRef] [PubMed]
- Cantini, L.; Calzone, L.; Martignetti, L.; Rydenfelt, M.; Blüthgen, N.; Barillot, E.; Zinovyev, A. Classification of gene signatures for their information value and functional redundancy. NPJ Syst. Biol. Appl. 2018, 4, 2. [Google Scholar] [CrossRef] [PubMed]
- Grossmann, P.; Stringfield, O.; El-Hachem, N.; Bui, M.M.; Rios Velazquez, E.; Parmar, C.; Leijenaar, R.T.; Haibe-Kains, B.; Lambin, P.; Gillies, R.J.; et al. Defining the biological basis of radiomic phenotypes in lung cancer. Elife 2017, 6, e23421. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.W.; Yap, Y.L.; Wei, D.; Chen, F.; Danchin, A. Molecular diagnosis of human cancer type by gene expression profiles and independent component analysis. Eur. J. Hum. Genet. 2005, 13, 1303–1311. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.-S.; Zheng, C.-H. Independent component analysis-based penalized discriminant method for tumor classification using gene expression data. Bioinformatics 2006, 22, 1855–1862. [Google Scholar] [CrossRef] [PubMed]
- Zheng, C.H.; Huang, D.S.; Kong, X.Z.; Zhao, X.M. Gene Expression Data Classification Using Consensus Independent Component Analysis. Genom. Proteomics Bioinform. 2008, 6, 74–82. [Google Scholar] [CrossRef]
- Aziz, R.; Verma, C.K.; Srivastava, N. A novel approach for dimension reduction of microarray. Comput. Biol. Chem. 2017, 71, 161–169. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, M.; Silva, F.F.E.; Sáfadi, T.; Nascimento, A.C.C.; Ferreira, T.E.M.; Barroso, L.M.A.; Ferreira Azevedo, C.; Guimarães, S.E.F.; Serão, N.V.L. Independent Component Analysis (ICA) based-clustering of temporal RNA-seq data. PLoS ONE 2017, 12, e0181195. [Google Scholar] [CrossRef] [PubMed]
- Han, H.; Li, X.L. Multi-resolution independent component analysis for high-performance tumor classification and biomarker discovery. BMC Bioinform. 2011, 12, S7. [Google Scholar] [CrossRef]
- Trapnell, C.; Cacchiarelli, D.; Grimsby, J.; Pokharel, P.; Li, S.; Morse, M.; Lennon, N.J.; Livak, K.J.; Mikkelsen, T.S.; Rinn, J.L. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 2014, 32, 381–386. [Google Scholar] [CrossRef] [PubMed]
- Aynaud, M.-M.; Mirabeau, O.; Gruel, N.; Grossetete-Lalami, S.; Boeva, V.; Durand, S.; Surdez, D.; Saulnier, O.; Zaidi, S.; Gribkova, S.; et al. Transcriptional programs define intratumoral heterogeneity of Ewing sarcoma at single cell resolution. bioRxiv 2019. bioRxiv:623710. [Google Scholar] [CrossRef]
- Gorban, A.N.; Pokidysheva, L.I.; Smirnova, E.V.; Tyukina, T.A. Law of the minimum paradoxes. Bull. Math. Biol. 2011, 73, 2013–2044. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gorban, A.N.; Tyukina, T.A.; Smirnova, E.V.; Pokidysheva, L.I. Evolution of adaptation mechanisms: Adaptation energy, stress, and oscillating death. J. Theor. Biol. 2016, 405, 127–139. [Google Scholar] [CrossRef]
- Segal, E.; Friedman, N.; Koller, D.; Regev, A. A module map showing conditional activity of expression modules in cancer. Nat. Genet. 2004, 36, 1090–1098. [Google Scholar] [CrossRef]
- Galon, J.; Mlecnik, B.; Bindea, G.; Angell, H.K.; Berger, A.; Lagorce, C.; Lugli, A.; Zlobec, I.; Hartmann, A.; Bifulco, C.; et al. Towards the introduction of the ‘Immunoscore’ in the classification of malignant tumours. J. Pathol. 2014, 232, 199–209. [Google Scholar] [CrossRef]
- Becht, E.; Giraldo, N.A.; Lacroix, L.; Buttard, B.; Elarouci, N.; Petitprez, F.; Selves, J.; Laurent-Puig, P.; Sautès-Fridman, C.; Fridman, W.H.; et al. Estimating the population abundance of tissue-infiltrating immune and stromal cell populations using gene expression. Genome Biol. 2016, 17, 218. [Google Scholar] [CrossRef]
- Newman, A.M.; Liu, C.L.; Green, M.R.; Gentles, A.J.; Feng, W.; Xu, Y.; Hoang, C.D.; Diehn, M.; Alizadeh, A.A. Robust enumeration of cell subsets from tissue expression profiles. Nat. Methods 2015, 12, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Aran, D.; Hu, Z.; Butte, A.J. xCell: Digitally portraying the tissue cellular heterogeneity landscape. Genome Biol. 2017, 18, 220. [Google Scholar] [CrossRef] [PubMed]
- Racle, J.; de Jonge, K.; Baumgaertner, P.; Speiser, D.E.; Gfeller, D. Simultaneous enumeration of cancer and immune cell types from bulk tumor gene expression data. Elife 2017, 6, e26476. [Google Scholar] [CrossRef] [PubMed]
- Gaujoux, R.; Seoighe, C. Semi-supervised Nonnegative Matrix Factorization for gene expression deconvolution: A case study. Infect. Genet. Evol. 2012, 12, 913–921. [Google Scholar] [CrossRef] [PubMed]
- Nelms, B.D.; Waldron, L.; Barrera, L.A.; Weflen, A.W.; Goettel, J.A.; Guo, G.; Montgomery, R.K.; Neutra, M.R.; Breault, D.T.; Snapper, S.B.; et al. CellMapper: Rapid and accurate inference of gene expression in difficult-to-isolate cell types. Genome Biol. 2016, 17, 201. [Google Scholar] [CrossRef] [PubMed]
- Kotliar, D.; Veres, A.; Nagy, M.A.; Tabrizi, S.; Hodis, E.; Melton, D.A.; Sabeti, P.C. Identifying gene expression programs of cell-type identity and cellular activity with single-cell RNA-Seq. Elife 2019, 8, e43803. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Hoffman, E.P.; Chen, L.; Chen, L.; Zhang, Z.; Liu, C.; Yu, G.; Herrington, D.M.; Clarke, R.; Wang, Y. Mathematical modelling of transcriptional heterogeneity identifies novel markers and subpopulations in complex tissues. Sci. Rep. 2016, 6, 18909. [Google Scholar] [CrossRef] [PubMed]
- Czerwinska, U. Unsupervised deconvolution of bulk omics profiles: Methodology and application to characterize the immune landscape in tumors. Ph.D. Thesis, University Paris Decartes, Paris, France, 2018. [Google Scholar]
- Su, Z.; Łabaj, P.P.; Li, S.; Thierry-Mieg, J.; Thierry-Mieg, D.; Shi, W.; Wang, C.; Schroth, G.P.; Setterquist, R.A.; Thompson, J.F.; et al. A comprehensive assessment of RNA-seq accuracy, reproducibility and information content by the Sequencing Quality Control Consortium. Nat. Biotechnol. 2014, 32, 903–914. [Google Scholar]
- Teschendorff, A.E.; Zheng, S.C. Cell-type deconvolution in epigenome-wide association studies: A review and recommendations. Epigenomics 2017, 9, 757–768. [Google Scholar] [CrossRef]
- Teschendorff, A.E.; Zhuang, J.; Widschwendter, M. Independent surrogate variable analysis to deconvolve confounding factors in large-scale microarray profiling studies. Bioinformatics 2011, 27, 1496–1505. [Google Scholar] [CrossRef]
- Dirkse, A.; Golebiewska, A.; Buder, T.; Nazarov, P.V.; Muller, A.; Poovathingal, S.; Brons, N.H.C.; Leite, S.; Sauvageot, N.; Sarkisjan, D.; et al. Stem cell-associated heterogeneity in Glioblastoma results from intrinsic tumor plasticity shaped by the microenvironment. Nat. Commun. 2019, 10, 1787. [Google Scholar] [CrossRef] [PubMed]
- Francesconi, M.; Di Stefano, B.; Berenguer, C.; de Andrés-Aguayo, L.; Plana-Carmona, M.; Mendez-Lago, M.; Guillaumet-Adkins, A.; Rodriguez-Esteban, G.; Gut, M.; Gut, I.G.; et al. Single cell RNA-seq identifies the origins of heterogeneity in efficient cell transdifferentiation and reprogramming. Elife 2019, 8, e41627. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Mao, Q.; Tang, Y.; Wang, L.; Chawla, R.; Pliner, H.A.; Trapnell, C. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods 2017, 14, 979–982. [Google Scholar] [CrossRef] [PubMed]
- Zhu, D.; Zhao, Z.; Cui, G.; Chang, S.; Hu, L.; See, Y.X.; Lim, M.G.L.; Guo, D.; Chen, X.; Poudel, B.; et al. Single-Cell Transcriptome Analysis Reveals Estrogen Signaling Coordinately Augments One-Carbon, Polyamine, and Purine Synthesis in Breast Cancer. Cell Rep. 2018, 25, 2285–2298. [Google Scholar] [CrossRef] [PubMed]
- Butler, A.; Hoffman, P.; Smibert, P.; Papalexi, E.; Satija, R. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 2018, 36, 411–420. [Google Scholar] [CrossRef] [PubMed]
- DeTomaso, D.; Yosef, N. FastProject: A tool for low-dimensional analysis of single-cell RNA-Seq data. BMC Bioinform. 2016, 17, 315. [Google Scholar] [CrossRef] [PubMed]
- Kondratova, M.; Czerwińska, U.; Sompairac, N.; Amigorena, S.D.; Soumelis, V.; Barillot, E.; Zinovyev, A.; Kuperstein, I. A multiscale signalling network map of innate immune response in cancer reveals signatures of cell heterogeneity and functional polarization. Nat. Commun. 2019. In Press. [Google Scholar]
- Tirosh, I.; Izar, B.; Prakadan, S.M.; Wadsworth, M.H.; Treacy, D.; Trombetta, J.J.; Rotem, A.; Rodman, C.; Lian, C.; Murphy, G.; et al. Dissecting the multicellular ecosystem of metastatic melanoma by single-cell RNA-seq. Science 2016, 352, 189–196. [Google Scholar] [CrossRef]
- Macaulay, I.C.; Svensson, V.; Labalette, C.; Ferreira, L.; Hamey, F.; Voet, T.; Teichmann, S.A.; Cvejic, A. Single-Cell RNA-sequencing reveals a continuous spectrum of differentiation in hematopoietic cells. Cell Rep. 2016, 14, 966–977. [Google Scholar] [CrossRef]
- Risso, D.; Perraudeau, F.; Gribkova, S.; Dudoit, S.; Vert, J.-P. A general and flexible method for signal extraction from single-cell RNA-seq data. Nat. Commun. 2018, 9, 284. [Google Scholar] [CrossRef]
- Forget, A.; Martignetti, L.; Puget, S.; Calzone, L.; Brabetz, S.; Picard, D.; Montagud, A.; Liva, S.; Sta, A.; Dingli, F.; et al. Aberrant ERBB4-SRC signaling as a hallmark of group 4 medulloblastoma revealed by integrative phosphoproteomic profiling. Cancer Cell 2018, 34, 379–395. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Payne, S.H.; Ma, S.; Fenyö, D. Extracting pathway-level signatures from proteogenomic data in breast cancer using independent component analysis. Mol. Cell. Proteom. 2019, 18, S169–S182. [Google Scholar] [CrossRef] [PubMed]
- Teschendorff, A.E.; Jing, H.; Paul, D.S.; Virta, J.; Nordhausen, K. Tensorial blind source separation for improved analysis of multi-omic data. Genome Biol. 2018, 19, 76. [Google Scholar] [CrossRef] [PubMed]
- Sefta, M. Comprehensive Molecular and Clinical Characterization of Retinoblastoma. Ph.D. Thesis, Université Paris-Saclay, 2015. [Google Scholar]
- Renard, E.; Teschendorff, A.E.; Absil, P.-A. Capturing confounding sources of variation in DNA methylation data by spatiotemporal independent component analysis. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning, Bruges, Belgium, 23–25 April 2014; pp. 195–200. [Google Scholar]
- Ma, Z.; Teschendorff, A.; Yu, H.; Taghia, J.; Guo, J. Comparisons of non-gaussian statistical models in DNA methylation analysis. Int. J. Mol. Sci. 2014, 15, 10835–10854. [Google Scholar] [CrossRef] [PubMed]
- Kong, W.; Mou, X.; Deng, J.; Di, B.; Zhong, R.; Wang, S.; Yang, Y.; Zeng, W. Differences of immune disorders between Alzheimer’s disease and breast cancer based on transcriptional regulation. PLoS ONE 2017, 12, e0180337. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; van de Koppel, J.; van de Leemput, I.A.; Levin, S.A.; van Nes, E.H.; et al. Anticipating Critical Transitions. Science 2012, 338, 344–348. [Google Scholar] [CrossRef]
- Mesleh, A.M. Lung cancer detection using multi-layer neural networks with independent component analysis: A comparative study of training algorithms. Jordan J. Biol. Sci. 2017, 10, 239–249. [Google Scholar]
- Han, G.; Liu, X.; Zhang, H.; Zheng, G.; Soomro, N.Q.; Wang, M.; Liu, W. Hybrid resampling and multi-feature fusion for automatic recognition of cavity imaging sign in lung CT. Futur. Gener. Comput. Syst. 2019, 99, 558–570. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sompairac, N.; Nazarov, P.V.; Czerwinska, U.; Cantini, L.; Biton, A.; Molkenov, A.; Zhumadilov, Z.; Barillot, E.; Radvanyi, F.; Gorban, A.; et al. Independent Component Analysis for Unraveling the Complexity of Cancer Omics Datasets. Int. J. Mol. Sci. 2019, 20, 4414. https://doi.org/10.3390/ijms20184414
Sompairac N, Nazarov PV, Czerwinska U, Cantini L, Biton A, Molkenov A, Zhumadilov Z, Barillot E, Radvanyi F, Gorban A, et al. Independent Component Analysis for Unraveling the Complexity of Cancer Omics Datasets. International Journal of Molecular Sciences. 2019; 20(18):4414. https://doi.org/10.3390/ijms20184414
Chicago/Turabian StyleSompairac, Nicolas, Petr V. Nazarov, Urszula Czerwinska, Laura Cantini, Anne Biton, Askhat Molkenov, Zhaxybay Zhumadilov, Emmanuel Barillot, Francois Radvanyi, Alexander Gorban, and et al. 2019. "Independent Component Analysis for Unraveling the Complexity of Cancer Omics Datasets" International Journal of Molecular Sciences 20, no. 18: 4414. https://doi.org/10.3390/ijms20184414
APA StyleSompairac, N., Nazarov, P. V., Czerwinska, U., Cantini, L., Biton, A., Molkenov, A., Zhumadilov, Z., Barillot, E., Radvanyi, F., Gorban, A., Kairov, U., & Zinovyev, A. (2019). Independent Component Analysis for Unraveling the Complexity of Cancer Omics Datasets. International Journal of Molecular Sciences, 20(18), 4414. https://doi.org/10.3390/ijms20184414






