Critical Output Torque of a GHz CNT-Based Rotation Transmission System Via Axial Interface Friction at Low Temperature
Abstract
1. Introduction
2. Results and Discussion
2.1. Rotation Transmission of the Zigzag Model
2.2. Rotation Transmission of the Armchair Model
3. Model and Methods
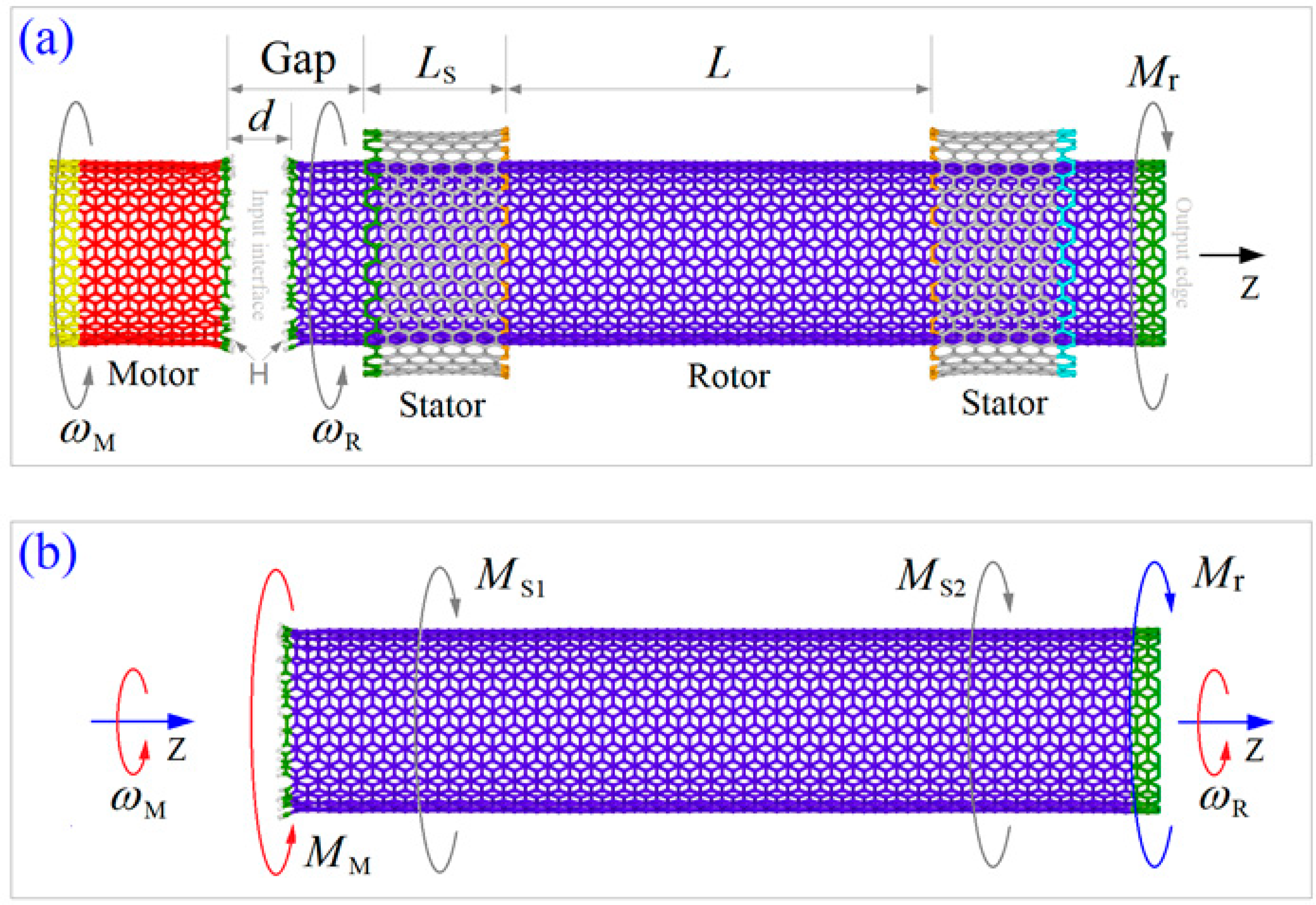
3.1. Model
3.2. Methodology
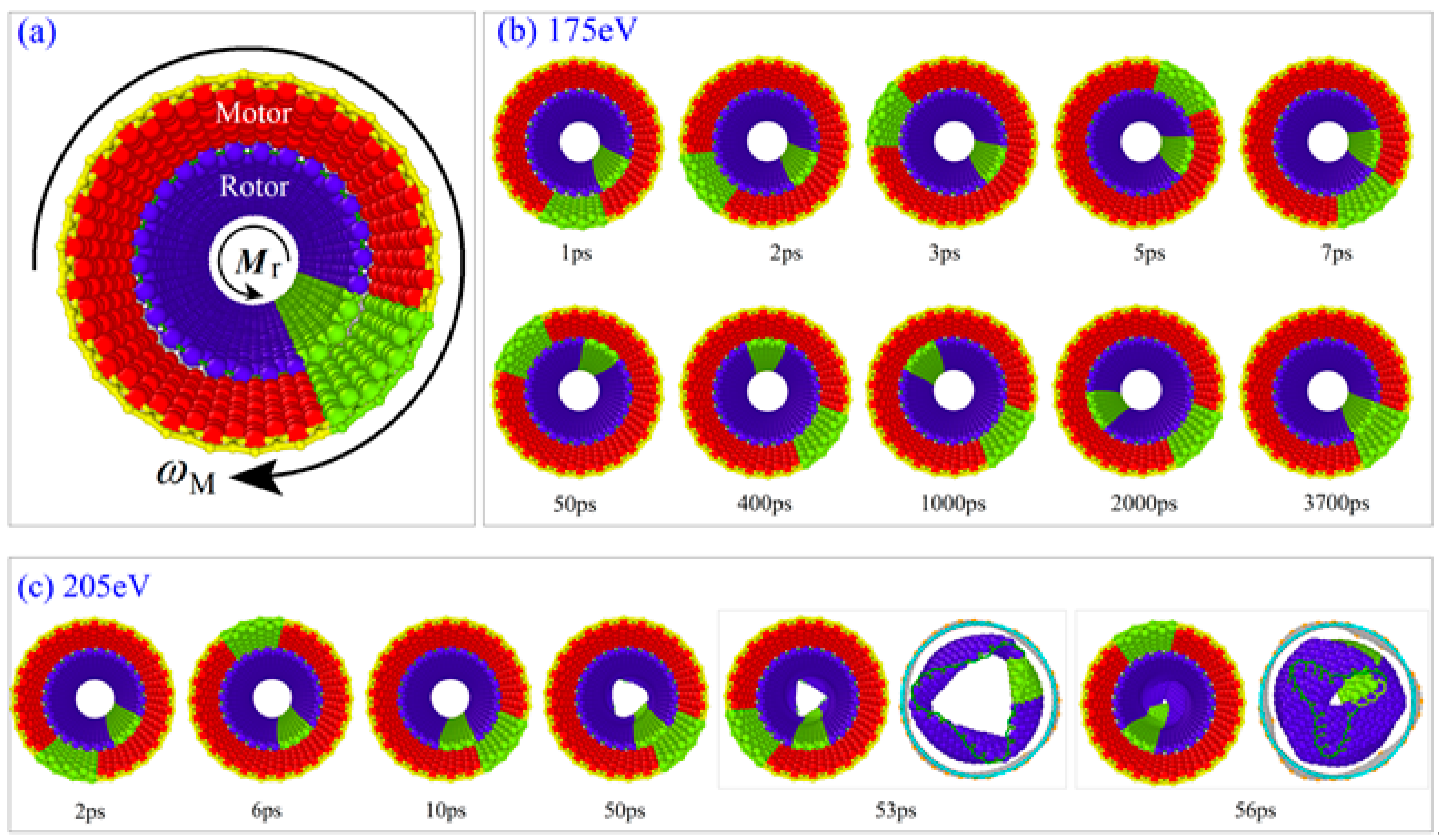
3.2.1. Mechanism of Rotation Transmission
3.2.2. Bi-Section Algorithm for Finding Mrcr
3.2.3. Molecular Dynamics Simulation Approach
3.2.4. Temperature Effect on Torque Transmission
3.2.5. Effect of Input Rotation on Torque Transmission
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Aust, R.B.; Drickamer, H.G. Carbon: A new crystalline phase. Science 1963, 140, 817–819. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Bonard, J.M.; JeanPaul, S.; Tomas, S. Why are carbon nanotubes such excellent field emitters. Ultramicroscopy 1998, 73, 7–10. [Google Scholar] [CrossRef]
- Cumings, J.; Zettl, A. Low-friction nanoscale linear bearing realized from multiwall carbon nanotubes. Science 2000, 289, 602–604. [Google Scholar] [CrossRef]
- Fennimore, A.M.; Yuzvinsky, T.D.; Han, W.Q.; Fuhrer, M.S.; Cumings, J.; Zettl, A. Rotational actuators based on carbon nanotubes. Nature 2003, 424, 408–410. [Google Scholar] [CrossRef]
- Feng, J.; Li, W.B.; Qian, X.F.; Qi, J.S.; Qi, L.; Li, J. Patterning of graphene. Nanoscale 2012, 4, 4883–4899. [Google Scholar] [CrossRef]
- Zhang, R.F.; Ning, Z.Y.; Zhang, Y.Y.; Zheng, Q.S.; Chen, Q.; Xie, H.H.; Zhang, Q.; Qian, W.Z.; Wei, F. Superlubricity in centimetres-long double-walled carbon nanotubes under ambient conditions. Nat. Nanotechnol. 2013, 8, 912–916. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60 buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Jiang, J.W.; Park, H.S. Negative poisson’s ratio in single-layer black phosphorus. Nat. Commun. 2014, 5, 4727. [Google Scholar] [CrossRef]
- Cai, K.; Wan, J.; Wei, N.; Cai, H.F.; Qin, Q.H. Thermal stability of a free nanotube from single-layer black phosphorus. Nanotechnology 2015, 27, 235703. [Google Scholar] [CrossRef]
- Chen, N.; Lusk, M.T.; van Duin, A.C.T.; Goddard, W.A. Mechanical properties of connected carbon nanorings via molecular dynamics simulation. Phys. Rev. B 2005, 72, 085416. [Google Scholar] [CrossRef]
- Guo, W.L.; Zhong, W.Y.; Dai, Y.T.; Li, S.N. Coupled defect-size effects on interlayer friction in multiwalled carbon nanotubes. Phys. Rev. B 2005, 72, 075409. [Google Scholar] [CrossRef]
- Bichoutskaia, E.; Heggie, M.I.; Popov, A.M.; Lozovik, Y.E. Interwall interaction and elastic properties of carbon nanotubes. Phys. Rev. B 2006, 73, 045435. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.D.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Zhang, H.W.; Cai, K.; Wang, L. Deformation of single-walled carbon nanotubes under large axial strains. Mater. Lett. 2008, 62, 3940–3943. [Google Scholar] [CrossRef]
- Ozden, S.; Autreto, P.A.S.; Tiwary, C.S.; Khatiwada, S.; Machado, L.; Galvao, D.S.; Vajtai, R.; Barrera, E.V.; Ajayan, P.M. Unzipping carbon nanotubes at high impact. Nano Lett. 2014, 14, 4131–4137. [Google Scholar] [CrossRef]
- Chernozatonskii, L.A.; Sorokin, P.B.; Kuzubov, A.A.; Sorokin, B.P.; Kvashnin, A.G.; Kvashnin, D.G.; Avramov, P.V.; Yakobson, B.I. The influence of size effect on the electronic and elastic properties of diamond films with nanometer thickness. J. Phys. Chem. C 2011, 115, 132–136. [Google Scholar] [CrossRef]
- Kvashnin, A.G.; Chernozatonskii, L.A.; Yakobson, B.I.; Sorokin, P.B. Phase diagram of quasi-two-dimensional carbon, from graphene to diamond. Nano Lett. 2014, 14, 676–681. [Google Scholar] [CrossRef]
- Zou, J.; Ji, B.; Feng, X.Q.; Gao, H. Self-assembly of single-walled carbon nanotubes into multiwalled carbon nanotubes in water: Molecular dynamics simulations. Nano Lett. 2006, 6, 430–434. [Google Scholar] [CrossRef]
- Cook, E.H.; Buehler, M.J.; Spakovszky, Z.S. Mechanism of friction in rotating carbon nanotube bearings. J. Mech. Phys. Solids 2013, 61, 652–673. [Google Scholar] [CrossRef]
- Zheng, Q.S.; Jiang, Q. Multiwalled carbon nanotubes as gigahertz oscillators. Phys. Rev. Lett. 2002, 88, 045503. [Google Scholar] [CrossRef]
- Legoas, S.B.; Coluci, V.R.; Braga, S.F.; Coura, P.Z.; Dantas, S.O.; Galvao, D.S. Molecular-dynamics simulations of carbon nanotubes as gigahertz oscillators. Phys. Rev. Lett. 2003, 90, 055504. [Google Scholar] [CrossRef]
- Rivera, J.L.; Mccabe, C.; Cummings, P.T. Oscillatory behavior of double-walled nanotubes under extension: A simple nanoscale damped spring. Nano Lett. 2003, 3, 1001–1005. [Google Scholar] [CrossRef]
- Legoas, S.B.; Coluci, V.R.; Braga, S.F.; Coura, P.Z.; Dantas, S.O.; Galvão, D.S. Gigahertz nanomechanical oscillators based on carbon nanotubes. Nanotechnology 2004, 15, S184–S189. [Google Scholar] [CrossRef]
- Rivera, J.L.; McCabe, C.; Cummings, P.T. The oscillatory damped behaviour of incommensurate double-walled carbon nanotubes. Nanotechnology 2005, 16, 186–198. [Google Scholar] [CrossRef]
- Motevalli, B.; Liu, J.Z. Tuning the oscillation of nested carbon nanotubes by insertion of an additional inner tube. J. Appl. Phys. 2013, 114, 56–58. [Google Scholar] [CrossRef]
- Cai, K.; Yin, H.; Qin, Q.H.; Li, Y. Self-excited oscillation of rotating double-walled carbon nanotubes. Nano Lett. 2014, 14, 2558–2562. [Google Scholar] [CrossRef]
- Barreiro, A.; Rurali, R.; Hernández, E.R.; Moser, J.; Pichler, T.; Forró, L.; Bachtold, A. Subnanometer motion of cargoes driven by thermal gradients along carbon nanotubes. Science 2008, 320, 775–778. [Google Scholar] [CrossRef]
- Zambrano, H.A.; Walther, J.H.; Jaffe, R.L. Thermally driven molecular linear motors: A molecular dynamics study. J. Chem. Phys. 2009, 131, 241104. [Google Scholar] [CrossRef]
- Santamaría-Holek, I.; Reguera, D.; Rubi, J.M. Carbon-nanotube-based motor driven by a thermal gradient. J. Phys. Chem. C 2013, 117, 3109–3113. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, W.K.; Ruoff, R.S. Atomistic simulations of double-walled carbon nanotubes (DWCNTs) as rotational bearings. Nano Lett. 2010, 4, 293–297. [Google Scholar] [CrossRef]
- Rueckes, T.; Kim, K.; Joselevich, E.; Tseng, G.Y.; Cheung, C.L.; Lieber, C.M. Carbon nanotube-based nonvolatile random access memory for molecular computing. Science 2000, 289, 94–97. [Google Scholar] [CrossRef]
- Peng, H.B.; Chang, C.W.; Aloni, S.; Yuzvinsky, T.D.; Zettl, A. Ultrahigh frequency nanotube resonators. Phys. Rev. Lett. 2006, 97, 087203. [Google Scholar] [CrossRef]
- Garcia-Sanchez, D.; Paulo, A.S.; Esplandiu, M.J.; Perez-Murano, F.; Forró, L.; Aguasca, A.; Bachtold, A. Mechanical detection of carbon nanotube resonator vibrations. Phys. Rev. Lett. 2007, 99, 085501. [Google Scholar] [CrossRef]
- Lassagne, B.; Tarakanov, Y.; Kinaret, J.; Garcia-Sanchez, D.; Bachtold, A. Coupling mechanics to charge transport in carbon nanotube mechanical resonators. Science 2009, 325, 1107–1110. [Google Scholar] [CrossRef]
- Cai, K.; Yin, H.; Wei, N.; Chen, Z.; Shi, J. A stable high-speed rotational transmission system based on nanotubes. Appl. Phys. Lett. 2015, 106, 021909. [Google Scholar] [CrossRef]
- Shi, J.; Cai, K.; Qin, Q.H. A nanoengine governor based on the end interfacial effect. Nanotechnology 2016, 27, 495704. [Google Scholar] [CrossRef]
- Jiang, H.; Liu, B.; Huang, Y.; Hwang, K.C. Thermal expansion of single wall carbon nanotubes. J. Eng. Mater. Technol. 2004, 126, 265–270. [Google Scholar] [CrossRef]
- Guo, Z.; Chang, T.; Guo, X.; Gao, H. Thermal-induced edge barriers and forces in interlayer interaction of concentric carbon nanotubes. Phys. Rev. Lett. 2011, 107, 105502. [Google Scholar] [CrossRef]
- Cai, K.; Cai, H.F.; Shi, J.; Qin, Q.H. A nano universal joint made from curved double-walled carbon nanotubes. Appl. Phys. Lett. 2015, 106, 241907. [Google Scholar] [CrossRef]
- Yin, H.; Cai, K.; Wei, N.; Qin, Q.H.; Shi, J. Study on the dynamics responses of a transmission system made from carbon nanotubes. J. Appl. Phys. 2015, 117, 234305. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Compu. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Large-Scale Atomic/Molecular Massively Parallel Simulator, LAMMPS. Available online: https://lammps.sandia.gov/ (accessed on 27 March 2019).
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A Gen. Phys. 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
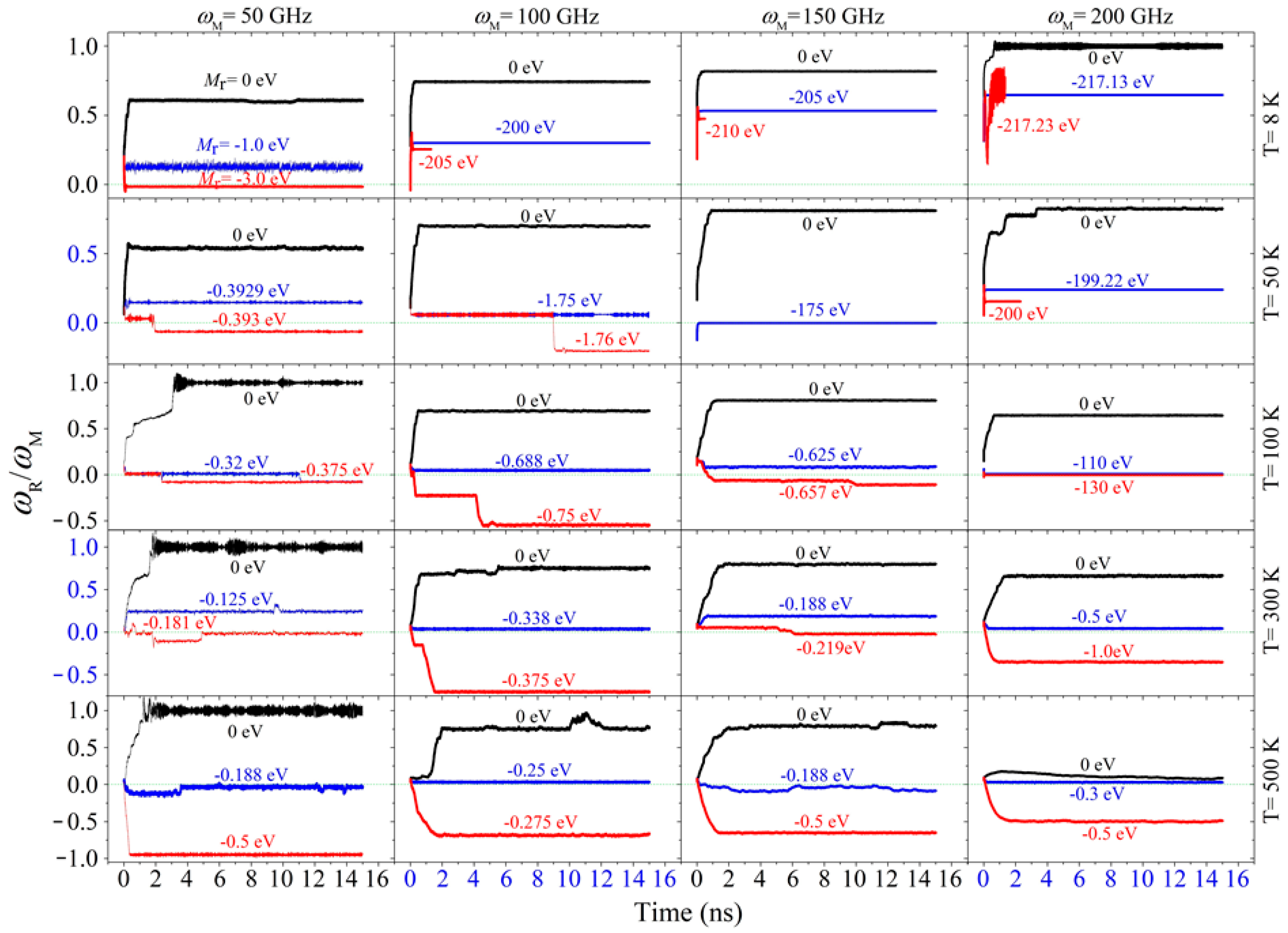
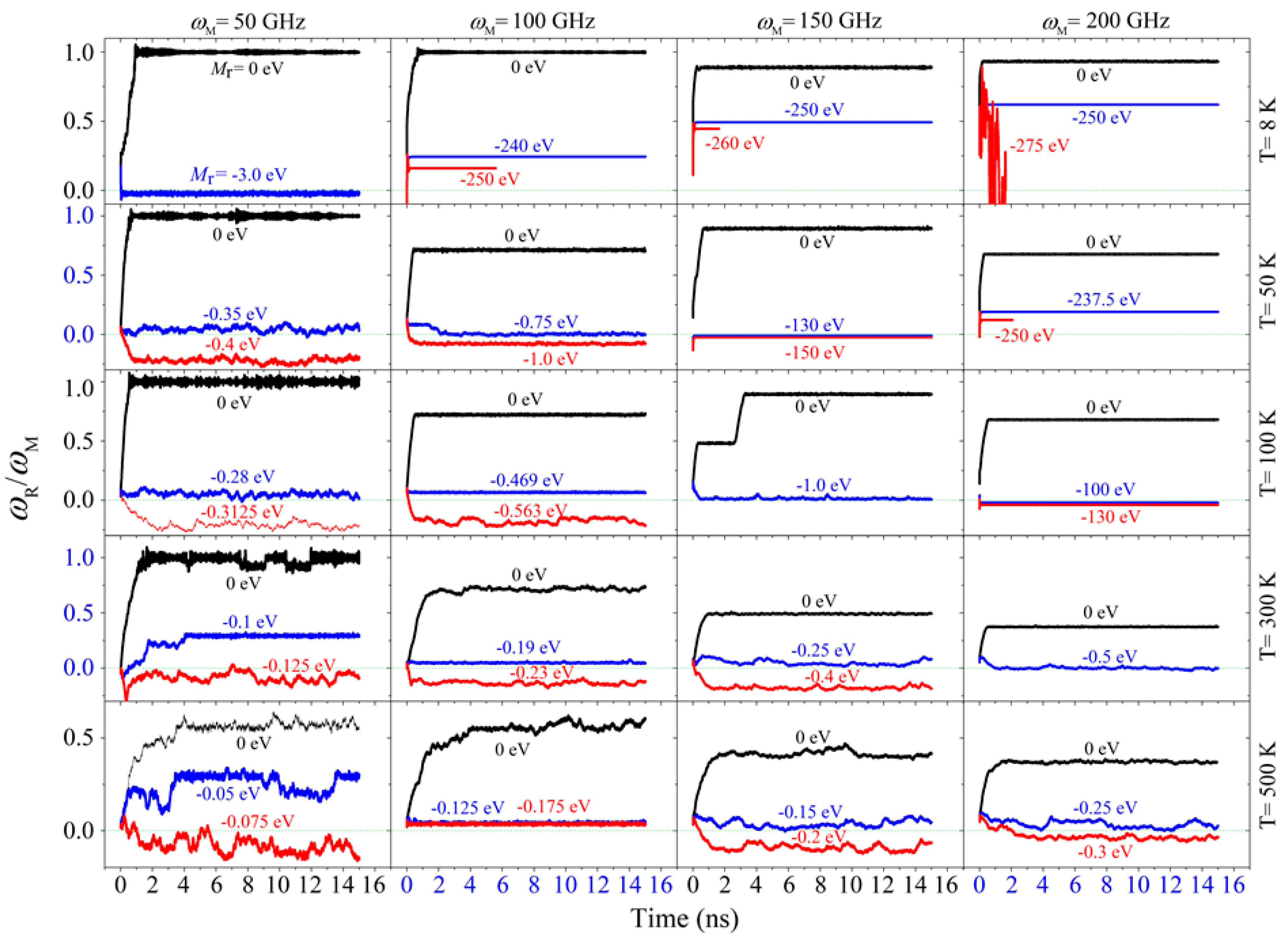
| Temperature | ωM = 50 GHz | ωM = 100 GHz | ωM = 150 GHz | ωM = 200 GHz |
|---|---|---|---|---|
| T = 8 K | 0.60 ± 0.028 | 0.74 ± 0.013 | 0.82 ± 0.009 | 1.0 ± 0.025 |
| T = 50 K | 0.54 ± 0.026 | 0.69 ± 0.048 | 0.80 ± 0.061 | 0.80 ± 0.061 |
| T = 100 K | 0.91 ± 0.180 | 0.68 ± 0.057 | 0.79 ± 0.084 | 0.64 ± 0.045 |
| T = 300 K | 0.95 ± 0.157 | 0.72 ± 0.082 | 0.77 ± 0.113 | 0.64 ± 0.081 |
| T = 500 K | 0.96 ± 0.150 | 0.70 ± 0.202 | 0.76 ± 0.122 | 0.11 ± 0.030 |
| Temperature | ωM = 50 GHz | ωM = 100 GHz | ωM = 150 GHz | ωM = 200 GHz |
|---|---|---|---|---|
| T = 8 K | −3.0 | −205(buckled) | −210(buckled) | −217.23(buckled) |
| T = 50 K | −0.393 | −1.75 | −175 | −200(buckled) |
| T = 100 K | −0.32 | −0.688 | −0.625 | −130 |
| T = 300 K | −0.181 | −0.338 | −0.219 | −0.5 |
| T = 500K | −0.188 | −0.25 | −0.188 | −0.3 |
| Temperature | ωM = 50 GHz | ωM = 100 GHz | ωM = 150 GHz | ωM = 200 GHz |
|---|---|---|---|---|
| T = 8 K | 0.97 ± 0.124 | 0.99 ± 0.049 | 0.89 ± 0.016 | 0.93 ± 0.009 |
| T = 50 K | 0.99 ± 0.089 | 0.71 ± 0.051 | 0.88 ± 0.071 | 0.67 ± 0.022 |
| T = 100 K | 0.99 ± 0.091 | 0.71 ± 0.056 | 0.81 ± 0.167 | 0.67 ± 0.043 |
| T = 300 K | 0.95 ± 0.138 | 0.68 ± 0.109 | 0.48 ± 0.051 | 0.37 ± 0.023 |
| T = 500 K | 0.53 ± 0.097 | 0.52 ± 0.095 | 0.40 ± 0.050 | 0.36 ± 0.033 |
| Temperature | ωM = 50 GHz | ωM = 100 GHz | ωM = 150 GHz | ωM = 200 GHz |
|---|---|---|---|---|
| T = 8 K | −3.0 | −250(buckled) | −260(buckled) | −275(buckled) |
| T = 50 K | −0.35 | −0.75 | −130 | −250(buckled) |
| T = 100 K | −0.28 | −0.469 | −1.0 | −100 |
| T = 300 K | −0.125 | −0.19 | −0.25 | −0.5 |
| T = 500 K | −0.075 | −0.175 | −0.15 | −0.25 |
| Model | L | Motor/Rotor | Stator/Stator | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Chirality | Length | Diameter | Number of Atoms | Chirality | LS | Diameter | Number of Atoms | ||
| Zigzag | 4.75 | (26,0) | 2.20/9.87 | 2.04 | 572C+26H/2444C+26H | (35,0) | 1.56 | 2.74 | 560C/560C |
| Armchair | 4.64 | (15,15) | 1.97/9.84 | 2.03 | 510C+30H/2430C+30H | (20,20) | 1.60 | 2.71 | 560C/560C |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Shi, J.; Wang, J.; Shen, J.; Cai, K. Critical Output Torque of a GHz CNT-Based Rotation Transmission System Via Axial Interface Friction at Low Temperature. Int. J. Mol. Sci. 2019, 20, 3851. https://doi.org/10.3390/ijms20163851
Wu P, Shi J, Wang J, Shen J, Cai K. Critical Output Torque of a GHz CNT-Based Rotation Transmission System Via Axial Interface Friction at Low Temperature. International Journal of Molecular Sciences. 2019; 20(16):3851. https://doi.org/10.3390/ijms20163851
Chicago/Turabian StyleWu, Puwei, Jiao Shi, Jinbao Wang, Jianhu Shen, and Kun Cai. 2019. "Critical Output Torque of a GHz CNT-Based Rotation Transmission System Via Axial Interface Friction at Low Temperature" International Journal of Molecular Sciences 20, no. 16: 3851. https://doi.org/10.3390/ijms20163851
APA StyleWu, P., Shi, J., Wang, J., Shen, J., & Cai, K. (2019). Critical Output Torque of a GHz CNT-Based Rotation Transmission System Via Axial Interface Friction at Low Temperature. International Journal of Molecular Sciences, 20(16), 3851. https://doi.org/10.3390/ijms20163851





