1. Introduction
Symmetry has been mainly regarded as a mathematical attribute [
1,
2,
3]. The Curie-Rosen symmetry principle [
2] is a higher symmetry−higher stability relation that has been seldom, if ever, accepted for consideration of structural stability and process spontaneity (or process irreversibility). Most people accept the higher symmetry−lower entropy relation because entropy is a degree of disorder and symmetry has been erroneously regarded as order [
4]. To prove the symmetry principle, it is necessary to revise information theory where the second law of thermodynamics is a special case of the second law of information theory.
Many authors realized that, to investigate the processes involving molecular self-organization and molecular recognition in chemistry and molecular biology and to make a breakthrough in solving the outstanding problems in physics involving critical phenomena and spontaneity of symmetry breaking process [
5], it is necessary to consider information and its conversion, in addition to material, energy and their conversions [
6]. It is also of direct significance to substantially modify information theory, where three laws of information theory will be given and the similarity principle (entropy increases monotonically with the similarity of the concerned property among the components (
Figure 1) [
7]) will be proved.
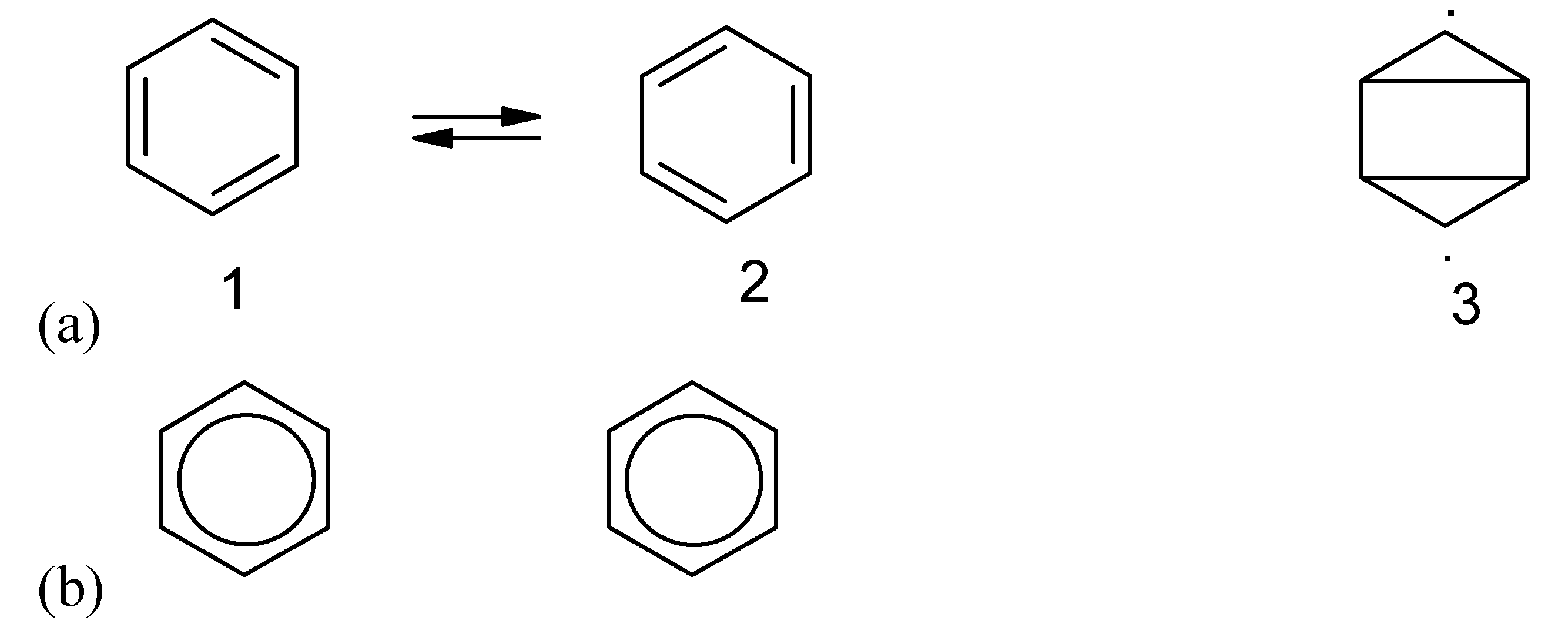
Figure 1.
(a) Correlation of entropy (ordinate) of mixing with similarity (abscissa) according to conventional statistical physics, where entropy of mixing suddenly becomes zero if the components are indistinguishable according to the Gibbs paradox [
21]. Entropy
decreases discontinuously.
Figure 1a expresses Gibbs paradox statement of "same or not the same" relation. (b) von Neumann revised the Gibbs paradox statement and argued that the entropy of mixing
decreases continuously with the increase in the property similarity of the individual components [
21a,
21b,
21d,
21j]. (c) Entropy
increases continuously according to the present author [
7] (not necessarily a straight line because similarity can be defined in different ways).
Figure 1.
(a) Correlation of entropy (ordinate) of mixing with similarity (abscissa) according to conventional statistical physics, where entropy of mixing suddenly becomes zero if the components are indistinguishable according to the Gibbs paradox [
21]. Entropy
decreases discontinuously.
Figure 1a expresses Gibbs paradox statement of "same or not the same" relation. (b) von Neumann revised the Gibbs paradox statement and argued that the entropy of mixing
decreases continuously with the increase in the property similarity of the individual components [
21a,
21b,
21d,
21j]. (c) Entropy
increases continuously according to the present author [
7] (not necessarily a straight line because similarity can be defined in different ways).
Thus, several concepts and their quantitative relation are set up: higher symmetry implies higher similarity, higher entropy, less information and less diversity, while they are all related to higher stability. Finally, we conclude that the definition of symmetry as order [
4] or as “beauty” (see: p1 of ref. 8, also ref. 3) is misleading in science. Symmetry is in principle ugly. It may be related to the perception of beauty only because it contributes to stability.
3. The Three Laws and the Stability Criteria
Parallel to the first and the second laws of thermodynamics, we have:
The first law of information theory: the logarithmic function L (, or the sum of entropy and information, ) of an isolated system remains unchanged.
The second law of information theory: Information I of an isolated system decreases to a minimum at equilibrium.
We prefer to use information
minimization as the second law of information theory because there is a stability criterion of potential energy
minimization in physics (see
section 6). Another form of the second law is the same in form as that of the second law of thermodynamics:
for an isolated system, entropy S increases to a maximum at equilibrium. For other systems (closed system or open system), we define (see: p. 623 of ref. [
14])
and treat the universe formally as an isolated system (Actually we have always done this in thermodynamics following Clausius [
9]). Then, these two laws are expressed as the following:
The function L of the universe is a constant. The entropy S of the universe tends toward a maximum. Therefore, the second law of information theory can be used as the criteria of structural stability and process spontaneity (or process irreversibility) in all cases, whether they are isolated systems or not. If the entropy of system + surroundings increases from structure A to structure B, B is more stable than A. The higher the value
for the final structure, the more spontaneous (or more irreversible) the process will be. For an isolated system the surroundings remain unchanged.
At this point we may recall the definition of equilibrium. Equilibrium means the state of indistinguishability (a symmetry, the highest similarity) [
7], e.g., as shown in
figure 5, the thermal equilibrium between parts A and B means that their temperatures are the same (See also the so-called zeroth law of thermodynamics [
14]).
We have two reasons to revise information theory. Firstly, the entropy concept has been confusing in information theory [
15] which can be illustrated by von Neumann’s private communication with Shannon regarding the terms entropy and information (Shannon told the following story behind the choice of the term “entropy” in his information theory: “My greatest concern was what to call it. I thought of calling it ‘uncertainty’. When I discussed it with John von Neumann, he had a better idea: ‘You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, no one knows what entropy really is, so in a debate you will always have the advantage’ ” [
15a]). Many authors use the two concepts entropy and information interchangeably (see also ref. 7d and citations therein). Therefore a meaningful discussion on the conversion between the logarithmic functions
S and
I is impossible according to the old information theory. Secondly, to the present author's knowledge, none of several versions of information theory has been applied to physics to characterize structural stability. For example, Jaynes' information theory [
16] should have been readily applicable to chemical physics but only a parameter similar to temperature is discussed to deduce that at the highest possible value of that temperature-like parameter, entropy is the maximum. Jaynes' information theory or the so-called maximal entropy principle has been useful for statistics and data reduction (See the papers presented at the annual conference MaxEnt). Brillouin's negentropy concept [
17] has also never been used to characterize structural stability.
To be complete, let us add the third law here also:
The third law of information theory: For a perfect crystal (at zero absolute thermodynamic temperature), the information is zero and the static entropy is at the maximum.
The third law of information theory is completely different from the third law of thermodynamics although the third law of thermodynamics is still valid regarding the dynamic entropy calculation (However, the third law of thermodynamics is useless for assessing the stabilities of different static structures). A more general form of the third law of information theory is “for a perfect symmetric
static structure, the information is zero and the
static entropy is the maximum”. The third law of information theory defines the static entropy and summarizes the conclusion we made on the relation of static symmetry, static entropy and the stability of the static structure [
7d] (The static entropy is independent of thermodynamic temperature. Because it increases with the decrease in the total energy, a negative temperature can be defined corresponding to the static entropy [
7a]. The revised information theory suggests that a negative temperature also can be defined for a dynamic system, e.g., electronic motion in atoms and molecules [
7a]).
The second law of thermodynamics might be regarded as a special case of the second law of information theory because thermodynamics treats only the energy levels as the considered property
X and only the dynamic aspects. In thermodynamics, the symmetry is the energy degeneracy [
18,
19]. We can consider spin orientations and molecular orientations or chirality as relevant properties which can be used to define a static entropy. What kinds of property besides the energy level and their similarities are relevant to structural stability? Are they the so-called observables [
18] in physics? Should these properties be related to energy (i.e., the entropy is related to energy by temperature-like intensive parameters as differential equations where Jaynes' maximal entropy principle might be useful) so that a temperature (either positive or negative [
7a]) can be defined? These problems should be addressed very carefully in future studies.
Similar to the laws of thermodynamics, the validity of the three laws of information theory may only be supported by experimental findings. It is worth reminding that the thermodynamic laws are actually postulates because they cannot be mathematically proved.
4. Similarity Principle and Its Proof
Traditionally symmetry is regarded as a discrete or a "yes-or -no" property. According to Gibbs, the properties are either the same (indistinguishability) or not the same (
figure 1a). A continuous measure of static symmetry has been elegantly discussed by Avnir and coworkers [
20]. Because the maximum similarity is indistinguishability (the sameness) and the minimum is distinguishability, corresponding to the symmetry and nonsymmetry, respectively, naturally similarity can be used as a continuous measure of symmetry (
section 2.1). The similarity refers to the considered property
X of the components (see the definition of labeling in
section 2.3) which affects the similarity of the probability values of all the
w microstates and eventually the value of entropy (equation 1).
Gibbs paradox statement [
21] is a higher similarity−lower entropy relation (
figure 1a), which has been accepted in almost all the standard textbooks of statistical mechanics and thermodynamics. The resolution of the Gibbs paradox of entropy−similarity relation has been very controversial. Some recent debates are listed in reference [
21]. The von Neumann continuous relation of similarity and entropy (the higher the similarity among the components is, the lower value of entropy will be, according to his resolution of Gibbs paradox) is shown in
figure 1b [
21j]. Because neither Gibbs' discontinuous higher similarity−lower entropy relation (where symmetry is regarded as a discrete or a "yes-or -no" property ) nor von Neumann's continuous relation has been proved, they can be at most regarded as postulates or assumptions. Based on all the observed experimental facts [
7d], we must abandon their postulates and accept the following postulate as the most plausible one (
figure 1c):
Similarity principle: The higher the similarity among the components is, the higher the value of entropy will be and the higher the stability will be.
The components can be individual molecules, molecular moieties or phases. The similarity among the components determines the property similarity of the microstates in equation 1. Intuitively we may understand that, the values of the probability pi are related to each other and therefore depend solely on the similarity of the considered property X among the microstates. If the values of the component property are more similar, the values of pi of the microstates are closer (equation 1 and 2). The similarity among the microstates is reflected in the similarity of the values of pi we may observe. There might be many different methods of similarity definition and calculation. However, entropy should be always a monotonically increasing function of any kind of similarity of the relevant property if that similarity is properly defined.
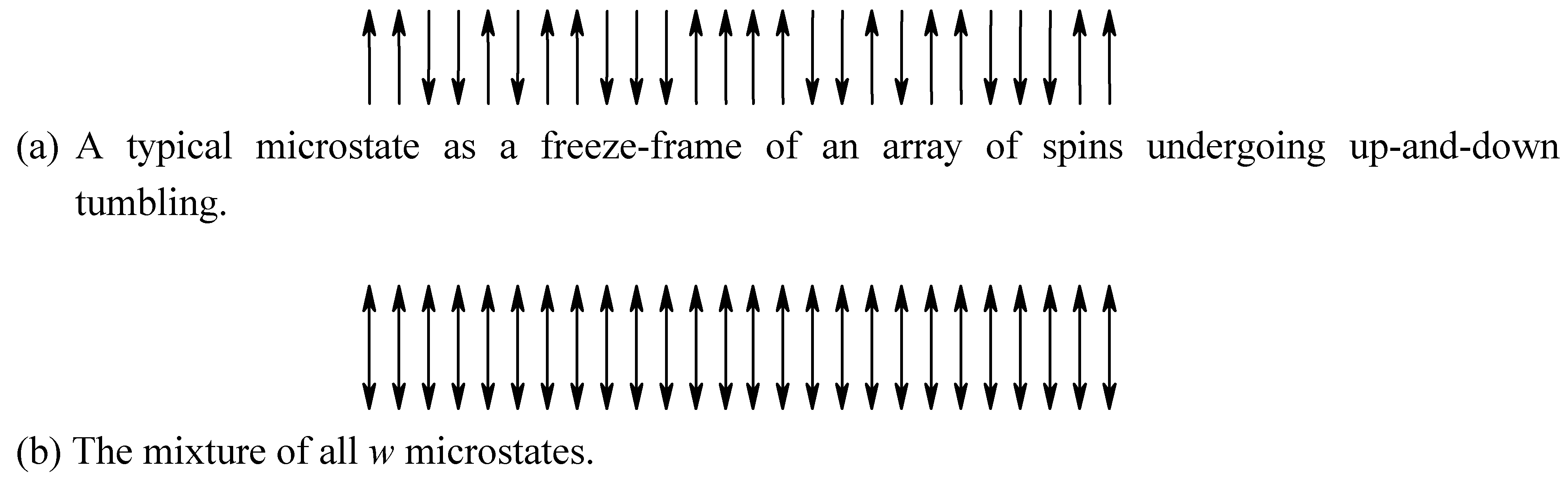
Example 9. Suppose a coin is placed in a container and shaken violently. After opening the container you may find that it is either head-up or head-down (The portrait on the coin is the label). For a bent coin, however, the property of head-up and the probability of head-down will be different. The entropy will be smaller and the symmetry (shape of the coin) will be reduced. In combination with example 2, it is easy to understand that entropy and similarity increase together.
Now, let us perform the following proof: the Gibbs inequality,
has been proved in geometry (see the citations in [
7d]). As
represents the maximum similarity among the considered
w microstates [
18], the general expression of entropy
must increase continuously with the increase in the property similarity among the
w microstates. The maximum value of
in equation 2 corresponds to the highest similarity. Finally, based on the second law of the revised information theory regarding structural stability that says that
the entropy of an isolated system (or system + environment) either remains unchanged or increases, the similarity principle has been proved.
Following the convention of defining similarities [
7d,
7e] as an index in the range of [0,1], we may simply define
as a similarity index (
figure 1c). As mentioned above,
Z can be properly defined in many different expressions and the relation that entropy increases continuously with the increase in the similarity will be still valid (However, the relation will not be necessarily a straight line if the similarity is defined in another way). For example, the
similarities
in a table
can be used to define a similarity value of a system of
N kinds of molecule [
7c,
7e].
5. Curie-Rosen Symmetry Principle and Its Proof
It is straightforward to prove the higher symmetry−higher stability relation (the Curie-Rosen symmetry principle [
2]) as a special case of the similarity principle. Because higher similarity is correlated with a higher degree of symmetry, the similarity principle also implies that entropy can be used to measure the degree of symmetry. We can conclude:
The higher the symmetry (indistinguishability) of the structure is, the higher the value of entropy will be. From the second law of information theory, the higher symmetry−higher entropy relation is proved.
The proof of the higher symmetry−higher entropy relationship can be performed by contradiction also. Higher symmetry number−lower entropy value relation can be found in many textbooks (see citations in [
7] and p. 596 of [
19]) where the existence of a symmetry would result in a decrease in the entropy value:
where σ denotes the symmetry number and
Let the entropy change from
S’ to
S is
Then the change in symmetry number would be a factor
and
where
and
are the two symmetry numbers. This leads to an entropy expression
. However, because any structure would have a symmetry number
, entropy would be a negative value, which contradicts the definition that entropy is always positive. Therefore neither
nor
are valid. The correct form should be equation 4 (
,
). In combination with the second law of information theory, the higher symmetry−higher stability relation (the symmetry principle) is also proved.
Rosen discussed several forms of symmetry principle [
2]. Curie’s causality form of the symmetry principle is that
the effects are more symmetric than the causes. The higher symmetry−higher stability relation has been clearly expressed by Rosen [
2]:
For an isolated system the degree of symmetry cannot decrease as the system evolves, but either remains constant or increases.
This form of symmetry principle is most relevant in form to the second law of thermodynamics. Therefore the second law of information theory might be expressed thus: an isolated system will evolve spontaneously (or irreversibly) towards the most stable structure, which has the highest symmetry. For closed and open systems, the isolated system is replaced by the universe or system + environment.
Because entropy defined in the revised information theory is more broad, symmetry can include both static (the third law of information theory) and dynamic symmetries. Therefore, we can predict the symmetry evolution from a fluid system to a static system when temperature is gradually reduced: the most symmetric static structure will be preferred (vide infra).
6. A Comparison: Information Minimization and Potential Energy Minimization
A complete structural characterization should require the evaluation of both the degree of symmetry (or indistinguishability) and the degree of nonsymmetry (or distinguishability). Based on the above discussion we can define entropy as the logarithmic function of symmetry number wS in equation 4. Similarly, the number wI can be called nonsymmetry number in equation 11.
Other authors briefly discussed the higher symmetry−higher entropy relation previously (see the citation in [
2]). Rosen suggested that a possible scheme for symmetry quantification is to take for the degree of symmetry of a system the order of its symmetry group (or its logarithm) (p.87, reference [
2]). The degree of symmetry of a considered system can be considered in the following increasingly simplified manner: in the language of group theory, the group corresponding to
L is a direct product of the two groups corresponding to the values of entropy
S and information
I:
where
is the group representing the observed symmetry of the system,
the nonsymmetric (distinguishable) part that potentially can become symmetric according to the second law of information, and
is the group representing the maximum symmetry. In the language of the numbers of microstates
where the three numbers are called the maximum symmetry number, the symmetry number and the nonsymmetry numbers, respectively. These numbers of microstate could be the orders of the three groups if they are finite order symmetry groups. However, there are many groups of infinite order such as those of rotational symmetry, which should be considered in detail in our further studies.
The behavior of the logarithmic functions
,
and their relation
can be compared with that of the total energy
E, kinetic energy
and potential energy
which are the eigenvalues of
H and
K and
P in the Hamiltonian expressed conventionally in either classical mechanics or quantum mechanics as two parts:
The energy conservation law and the energy minimization law regarding a spontaneous (or irreversible) process in physics (In thermodynamics they are the first and the second law of thermodynamics) says that
and
(e.g., for a linear harmonic oscillator, the sum of the potential energy and kinetic energy remains unchanged),
for an isolated system (or system +environment). In thermodynamics, Gibbs free energy
G or Helmholtz potential
F (equation 14) are such kinds of potential energy. It is well known that the minimization of the Helmholtz potential or Gibbs free energy is an alternative expression of the second law of thermodynamics. Similarly,
For a spontaneous process of an isolated system,
(the first law of information theory) and
(the second law of information theory or the minimization of the degree of nonsymmetry) or
(the maximization of the degree of symmetry). For an isolated system,
For systems that cannot be isolated, spontaneous processes with both
or
for the systems are possible provided that
for the universe (
for a reversible process.
are impossible process). The maximum symmetry number, the symmetry number and the nonsymmetry number can be calculated as the exponential of the maximum entropy, entropy and information, respectively. These relations will be illustrated by some examples and will be studied in more detail in the future.
The revised information theory provides a new approach to understanding the nature of energy (or energy-matter) conservation and conversion. For example the available potential energy due to distinguishability or nonsymmetry can be calculated. This can be illustrated in a system undergoing spontaneous mass or heat transfer between two parts of a chamber (
figure 5). The distinguishability or nonsymmetry is the cause of the phenomena. Many processes are irreversible because a process does not proceed from a symmetric structure to a nonsymmetric structure.
Figure 5.
Mass (ideal gas) transfer and heat transfer between two parts of a chamber after removal of the barrier. The whole system is an isolated system.
Figure 5.
Mass (ideal gas) transfer and heat transfer between two parts of a chamber after removal of the barrier. The whole system is an isolated system.
7. Interactions
From the second law of information theory, any system with interactions among its components will evolve towards an equilibrium with the minimum information (or maximum symmetry). This general principle leads to the criteria of equilibrium for many kinds of system. For example, in a mechanical system the equilibrium is the balance of forces and the balance of torques.
We may consider symmetry evolution generally in two steps. Step one: bring several components (e.g., parts A and B in
figure 5) to the vicinity as individually isolated parts. We may treat this step as if these parts have no interaction. Step two: let these parts interact by removing electromagnetic insulation, thermal insulation, or mechanical barrier, etc. (e.g., the right side of
figure 5).
For step one, similarity analysis will be satisfactory. For the example shown in
figure 5, we measure if the two parts A and B are of the same temperature (if they are, there will be no heat transfer), the same pressure (if they are, there will be no mass transfer) or the same substances (if they are, there will be no chemical reactions.
We may calculate the total logarithmic function
Ltotal, total entropy (
) and total information of an isolated system of many parts for the first step. In the same way, we may calculate a system of complicated, hierarchical structures. Suppose there are
M hierarchical levels (
, e.g., one level is a galaxy, the other levels are the solar system, a planet, a box of gas, a molecule, an atom, electronic motion and nuclear motion inside the atom, subatomic structures, etc.) and
N parts (
, e.g., different cells in a crystals, individual molecules, atoms or electrons, or spatially different locations). It should be greater than the sum of the individual parts at all the hierachical levels,
because any assembling and any interaction (coupling, etc.) among the parts or any interaction between the different hierachical levels will lead to information loss and entropy increase. Many terms of entropy due to interaction should be included in the entropy expression.
Example 10. The assembling of the same molecules to form a stable crystal structure is a process similar to adding many copies of the same book to the shelves of one library. Suppose there are 1GB information in the book. Even though there are 1,000,000 copies, the information is still the same and the information in this library is . The entropy is 999999 GB.
Example 11. Interaction of the two complementary strands of polymer to form DNA. The combination leads to a more stable structure. The system of these two components (part 1 and part 2) have entropy greater than the sum of the individual parts () because .
However, operator theory or functional analysis might be applied for more vigorous mathematical treatment, which will be presented elsewhere. Application of the revised information theory to specific cases with quantitative calculations also will be topics of further investigations. We will only outline some applications of the theory in the following sections.
Finally, we claim that due to interactions, the universe evolves towards maximum symmetry or minimum information.
10. Similarity Rule and Complementarity Rule
Generally speaking,
all intermolecular processes (molecular recognition and molecular assembling or the formation of any kinds of chemical bond) and intramolecular processes (protein folding [
28], etc.) between molecular moieties are governed either by the similarity rule or by the complementarity rule or both.
Similarity rule (a component in a molecular recognition process loves others of like properties, such as hydrophobic interaction, π-stacking in DNA molecules, similarity in softness of the well-known hard-soft-acid-base rules) predicts the affinity of individuals of
similar properties. On the contrary, complementarity rule predicts the affinity of individuals of certain
different properties. Both types of rule still remain strictly empirical. The similarity rule can be given a theoretical foundation by the similarity principle (
figure 1c) [
7] after rejection of Gibbs' (
figure 1a) and revised (
figure 1b) relations of entropy−similarity.
All kinds of donor−acceptor interaction, such as enzyme and substrate combination, which may involve hydrogen bond, electrostatic interaction and stereochemical key-and-lock docking [
30] (e.g., template and the imprinted molecular cavity [
6]), follow the complementarity rule. For the significance of the complementarity concept in chemistry, see the chapter on Pauling in the book [
1].
Definition: Suppose there are
n kinds of property
X,
Y,
Z, ..., etc. (See the definition of entropy and labeling in
section 2) and
. For a binary system, if the two individuals contrast in
l kinds of property (negative charge-positive charge or convex and concave, etc.) and exactly the same for the rest
m kinds of property, the relation of these two components is complementary. An example is given in
figure 12.
Figure 12.
The print and the imprint [
6b] are complementary.
Figure 12.
The print and the imprint [
6b] are complementary.
Firstly, for stereochemical interaction (key-and-lock docking) following a complementarity rule it can be treated as a special kind of phase separation where the substance and the vacuum (as a different species) separate (cf.
section 8). The final structure is more "complete", more integral, more “solid” and more symmetric. More generally speaking, the components in the structure of the final state become more similar due to the property
offset of the components and the structure is more symmetric. The calculation of symmetry number, entropy and information changes during molecular interaction are numerous topics for further studies.
Complementarity principle: The final structure is more symmetric due to the property offset of the components. It will be more stable.
In the recent book by Hargittai and Hargittai [
1] many observations showed that in our daily life symmetry created by combination of parts means beauty. We may speculate that, in all these cases, the stability of the interaction of the symmetric static images (crystal, etc.) and symmetric dynamic processes (periodicity in time, etc.) may play an important role in our perception. Perception of visual beauty might be our visual organ's interaction with the images or a sequences of images and a tight interaction might result if the similarity rule and the complementarity rule are satisfied.
Normally we consider complementarity of a binary system (two partners). However, it can be an interaction among many components. The component motifs are distinguishable (for a binary system they are contrast) in the considered property or properties.
Chemical bond formation and all kinds of other interaction following the similarity and complementarity rules will lead to more stable
static structures. Actually there are also similarity and complementarity rules for the formation of a stable
dynamic system. The resonance theory is an empirical rule [
29]. Von Neumann tried very hard to use the argument of entropy of mixing but his final conclusion regarding entropy−similarity relation (
figure 1b) was wrong and cannot be employed to explain the stability of quantum systems [
21]). Pauling's resonance theory can be supported by the two principles − similarity principle and complementarity principle for a dynamic system regarding electron motion and electronic configuration [
7]. The final structure as a hybrid or a mixture of a "complete" set (having all the microstates or all the available canonical structures of very similar energy levels, similar configuration, etc. see 1 and 2 in
figure 13a) should be more symmetric. The most complete set of microstates will lead to the highest dynamic entropy and the highest stability. Other structures (e.g., 3 in
figure 13a) cannot contribute significantly to the structure because they are very different from the structure of 1 or 2.
Figure 13.
Information loss due to dynamic electronic motion. The different orientations of the valence bond benzene structures 1 and 2 in (a) can be used for recording information. However, the oscillation makes all the individual benzene molecules the same as shown in (b).
Figure 13.
Information loss due to dynamic electronic motion. The different orientations of the valence bond benzene structures 1 and 2 in (a) can be used for recording information. However, the oscillation makes all the individual benzene molecules the same as shown in (b).
To explain the stability of the systems other than molecular systems, one may replace molecules by individuals or components under consideration and then calculate in a similar way as for molecular systems. At least the relative structural stability may be assessed for different structures where the similarity principle is applicable.
Finally we should emphasize that the similarity rule is always more significant than the complementarity rule, because most properties of the complementary components are the same or very similar (m>l). Examples in chemistry are the HSAB (hard-soft-acid-base) rule where the two components (acid and base) should have similar softness or similar hardness (see any modern texts in inorganic chemistry). Another example is the complementary pair of LUMO (lowest unoccupied molecular orbital) and HOMO (highest occupied MO) where the energy levels of the MO are very close (see a modern textbook of organic chemistry). The formation of a chemical bond can be illustrated by a stable marriage (example 13).
Example 13. Successful marriage might be a consequence of the highest possible similarity and complementarity between the couple. The stability of the relation is directly determined by how identical the partners are: both man and woman have interests in common, have the same goals, common beliefs and principles, and share in wholesome activities. Love and respect between the two are the complementarity at work which is the more interesting aspect of the marriage due to their contrasting attributes: One is submissive, the other not. A beautiful marriage is determined by how adaptable both of them are regarding differences, rather than by how identical they are. God created man and woman to make one as a complement of the other (Genesis 2:18).
11. Periodicity (Repetition) in Space and Time
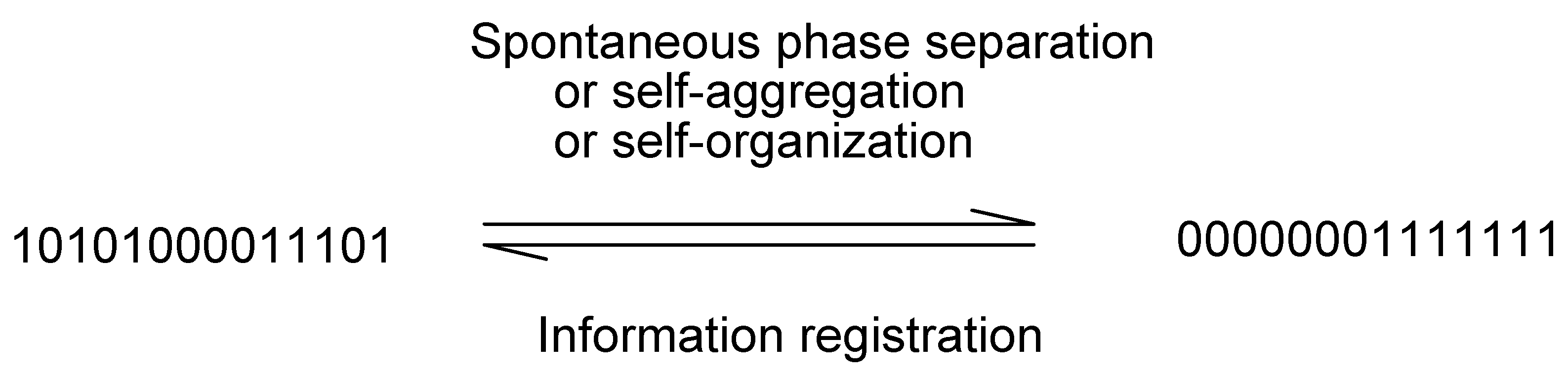
The beauty of periodicity (repetition) or translational symmetry of molecular packing in crystals must be attributed to the corresponding stability. Formatting of a floppy disk or a hard disk will create symmetry and erasure of all the information. Formatting is a necessary preparation for stable storage of information where certain kinds of symmetry are maintained: e.g., books must be "formatted" by pages and lines where periodicity is maintained as background. The DNA molecules are "formatted" by the sugar and phosphate backbone as periodic units.
Steady-state is a special case of a dynamic system. Its stability depends on the symmetry (periodicity in time). The long period of chemical oscillation [
1,
4] happens in a steady-state system. Cars on a highway must run in the same direction at the same velocity. Otherwise, if one car goes much slower, there will be a traffic accident (Curie said “nonsymmetry leads to phenomena” [
2]), and the unfortunate phenomenon is the collision. Many kinds of cycle (heart-beating cycle, sleep-and-wake-up cycles, etc.) are the periodicity in time, which contributes stability, very much the same as the Carnot cycle of an ideal heat engine. However, exact repetition of everyday life must be very boring, even though it makes life simple or easy and stable (vida infra).

 or 0000000 or 1234567. Therefore these properties can be used for labeling.
or 0000000 or 1234567. Therefore these properties can be used for labeling.