I. Introduction
Chemical etching of silicon by fluorine plasma is one of the most important materials tailoring techniques in the manufacture of semiconductor devices [
1,
2]. The etching mechanism with fluorine plasma, which generates a variety of high-energy reactive atoms, ions and even polyatomic radicals, isvery complicated [
3]. There are many theoretical as well as experimental studies but still the mechanism of fluorine etching process is not comprehensively understood [
4,
5,
6]. However, a general consensus has been generated that atomic fluorine is the primary reactive agent in fluorine plasma etching. The points of ambiguity lies in the source (atomic or molecular), mode of attachment (monomer, dimer), desorption phenomenon etc. Molecular halogens are chemisorbed on the Si (100) surface exothermally and form a stable adsorbed structure on the Si (100) surface at low temperatures [
7]. A flux of halogen atoms and molecules exposed to Si surface at elevated temperatures also yields a continuous etching of the Si surfaces. It is generally believed that atomic fluorine is the primary reactive agent in fluorine plasma etching. To understand the etching phenomenon a lot of fluorine-silicon interactions have been modeled using both atomic and molecular fluorine along with XeF
2 with Si (111), Si (100) etc. Although fluorine from all the sources form the adsorption complex with silicon surface but the reactions between atomic F, F
2, XeF
2 and silicon follow different kinetics [
8,
9]. The kinetic differences between the precursors have been attributed primarily to the initial adsorption step, rather than the reaction or desorption steps [
10]. The adsorption and reaction of both molecular and atomic fluorine with the Si (100) surface has been examined by Engstrom et al [
10] under ultra high vacuum conditions with supersonic molecular beam techniques, X-ray photoelectron spectroscopy, quadrupole mass spectrometry and low-energy ion-scattering spectroscopy. They observed that adsorption probability of F (g) exceeds that for F
2 (g) by approximately two orders of magnitude. They also predict that the steady state reaction between F
2 (g) and Si (100) surface involves a reaction between chemisorbed F atoms, which results from the dissociative adsorption of F
2 on Si surface. It is commonly agreed that SiF
4 is the primary etching product [
11]. However, the relative abundance of reaction intermediates and other etch products (e.g. SiF
3, SiF
2, SiF and polysilyl species) are all controversial. Engstrom, Nelson and Engel [
10,
12] found that exposure of Si (100) to an F
2 or mixed F and F
2 beam produces only SiF
2 at low coverage and a mixture of SiF
2 and SiF
4 at higher coverage. It appears from the experimental results that the product distribution (in both gas phase and the adsorbed layer) and the initial reaction mechanism may be quite sensitive to the structure of the silicon surface [i.e. (111) Vs (100)] and the fluorine reagent [i.e. F Vs F
2 Vs XeF
2]. Engstrom et al measured the kinetic of adsorption for F
2 and F atoms on Si (100)-2x1 using modulated molecular beam (MMB) techniques, XPS, TPD. They have observed a rapid rate of adsorption upto 1.5 ML for F
2, followed by much slower rate of fluorine incorporation. The only direct observation of the adsorbed fluorine surface geometry were reported by Bozack et al [
13] and Johnson, Walczak and Madey [
14], who measured the electron-simulated desorption ion angular distributions (ESDIAD) of adsorbed species on a partially fluorinated Si (100)-2x1 surface. The fluorine emission angle with respect to the surface normal was found to be 36±5 by Bozak et al [
13] and 29±3 by the other group. The study of Johnson et al [
14] involved adsorption of HF onto Si (100), presumably forming an H-Si-Si-F monofluoro species. Boland et al for the first time pointed out that dissociative chemisorption of diatomic molecules on Si surface occurs in two ways [
15]. At room temperature dissociation typically occurs at the same side of adjacent dimers of the same row referred as type II site. Although this configuration disrupts the ◦ bonds on two dimmers, but it is still favored over adsorption on a single dimer at low temperature, a type I site. This group has recently validated this proposition by exhaustive scanning tunneling microscopy (STM) results [
16]. Now, water is the most abundant chemical with which a Si-wafer surface comes into contact. The interaction of water with silicon surface was first shown by Ibach et al [
17] followed by other groups [
18,
19]. The interaction withwater follows three major steps as proposed by Graf et al [
20]. The first step is rapid exchange of Si-F with water to form Si-OH, followed by slow nucleophilic attack of OH
- on surface Si-H to produce Si-OH. Finally condensation of Si-OH results in the formation of Si-O-Si bridges and water. The mechanism is well supported by scanning tunneling microscopy and spectroscopy [
21,
22].
Now, it is found that experimental studies have contributed a lot in the understanding of the reactive species and paths involved in chemical etching process. But no direct evidence of the initial steps of fluorination is still available. Here comes the need of using computer simulation to explore the different pathways involved in initial fluorination and to propose a realistic etching mechanism. Seel and Bagus reported [
23] Hartree-Fock (HF) calculations of fluorine adsorption for various sites of an unreconstructed Si (111) surface. Equilibrium properties of at the HF level for fluorine chemisorbed on Si
4H
9 and Si
9H
15 cluster models of unreconstructed Si (111) were also predicted by Illas, Rubio and Ricart [
24] and Mohapatra et al [
25]. Garrison and Goddard [
26] proposed an S
N2 mechanism for the formation of SiF
4 from surface bound SiF
3 groups based on multiconfiguration-self-consistent-field calculations performed on H
3Si-SiF
3+F. Using molecular dynamics, an initial adsorption probability of unity is observed [
27], whereas S=0 for an ordered F monolayer. In another study with ab initio derived molecular dynamics [
28], it was pointed out that many different paths of reaction are competing e.g., fluorination of dangling bonds, breaking of dimer bonds and attack of subsurface Si atoms. This leads to the concurrent formation of adsorbed SiF, SiF
2 and SiF
3. A potential energy function with two body and three body terms to model silicon-silicon, fluorine-fluorine and Silicon-fluorine interaction has been developed by Stillinger and Weber (SW) [
29,
30,
31]. Schoolcraft et al [
32] have used the SW potential to propose that at a beam energy of 2.0 eV, ½ of the fluorine atoms bond to a second-layer atom. The other half makes bond to a surface dimer atom. There are few more experimental papers involving fluorine etching [
33,
34,
35] including the recent one from Ceter et al [
36]. In our recent study we reported the oxidation and stabilization of unreconstructed H- and F-terminated Si (100) surface using periodic density functional study [
37]. We also observed the existence of stable surface Si-F bond in case of unreconstructed surface. The most of the theoretical study, which has been performed using molecular dynamics, deals to show the dependence of the sticking probability of atomic F on Si (100) surface on coverage using thermal fluorine atoms. The electronic structure calculations are few in numbers. There has been so far no systematic theoretical study to monitor the structural change associated with the Si (100) surface before and after interaction with fluorine. There are also no theoretical studies to validate the mechanism of fluorine etching in presence of water or in other way the role of water in etching process is yet to be validated. This also helps to monitor the preliminary etching mechanism on Si (100) surface.
In the present study we carried out density functional calculations related to initial fluorination of Si (100) surface (both reconstructed and unreconstructed) using silicon clusters. Two high-symmetric pathways and subsequent adsorption sites were examined. We calculated activation barriers and equilibrium surface configurations as a function of fluorine coverage up to 2.0 ML. We also report the harmonic vibration frequencies for surface fluorosilyl species. We compared the stability of the fluorinated surface in terms of the sequence of fluorination. Then we have studied the effect of water on fluorosilyl species on the surface. We further compare our results with previous experimental and theoretical data. We finally propose a plausible mechanism of the initial stage of fluorine etching to explicitly monitor the role of water in the etching phenomenon.
III. Results and Discussion
We investigated a number of possible pathways at different fluorine coverage starting from 0.5 ML to 2 ML with a steady increment of 0.5 ML. Two high symmetry pathways and consequent adsorption sites were tested: (i) adsorption of fluorine atom directly on a silicon dangling bond to form a mono coordinated species (ii) adsorption of fluorine atom directly on top of a Si dimer to form a dicoordinated bridging species. Redondo and Goddard [
45] have predicted earlier that the coupling between dangling bonds on Si dimer is very weak, with a singlet-triplet splitting energy (
![Ijms 02 00040 i001]()
E
ST) is 0.03 eV. We performed the full optimization of Si
9H
16 cluster with DFT. The value for singlet-triplet splitting is 0.025 eV. The values are given in
Table 1.This shows that the dangling bonds on the surface are very active. As we find that the direction of the dangling bond is outward from the Si dimer bond, it looks Si-F mono coordinated bond formation is more feasible. We also observed in our calculation that, when F approaches the dangling bond it forms a very stable bond (6.34 eV) both for the unreconstructed surface and for the reconstructed surface (6.22 eV), with no activation barrier. It also forms a stable bridge bond (3.0 eV) with a Si dimer. This shows the greater stability of the dangling bond, which further indicates the feasibility of the fluorine approach towards the dangling bond direction. But in the second case we find that bridging F atom slide toward the dangling bond to form the mono coordinated species without any barrier, which will be discussed in later sections. The results are shown in
Table 2. The bond energies have been calculated by using the following equations.
Table 1.
Singlet-triplet splitting energy calculated using DFT and compared with earlier theoretical results.
Table 1.
Singlet-triplet splitting energy calculated using DFT and compared with earlier theoretical results.
| State | DFT Total energy (au) | RCI* energy (au) |
|---|
| 1A1 | -2619.7832 | -2605.2435 |
| 3B1 | -2619.7822 | -2605.2426 |
| ΔEST | 0.025 eV | 0.03 eV |
Table 2.
Total energy of the clusters and fluorine along with the Si-F bond stabilization energy for both dangling and bridging bond situations.
Table 2.
Total energy of the clusters and fluorine along with the Si-F bond stabilization energy for both dangling and bridging bond situations.
| Species | Total energy (au) | Bond Stabilization energy (eV) |
|---|
| F | -98.4786 | |
| Si9H16 | -2619.7623 | |
| Si9H16F | -2718.4750 | 6.34a |
| Si9H14 | -2614.5734 | |
| Si9H13F | -2713.2797 | 6.22a |
| Si9H12F | -2723.9887 | 3.0b |
| Si9H12F2 | -2811.9431 | 11.22a |
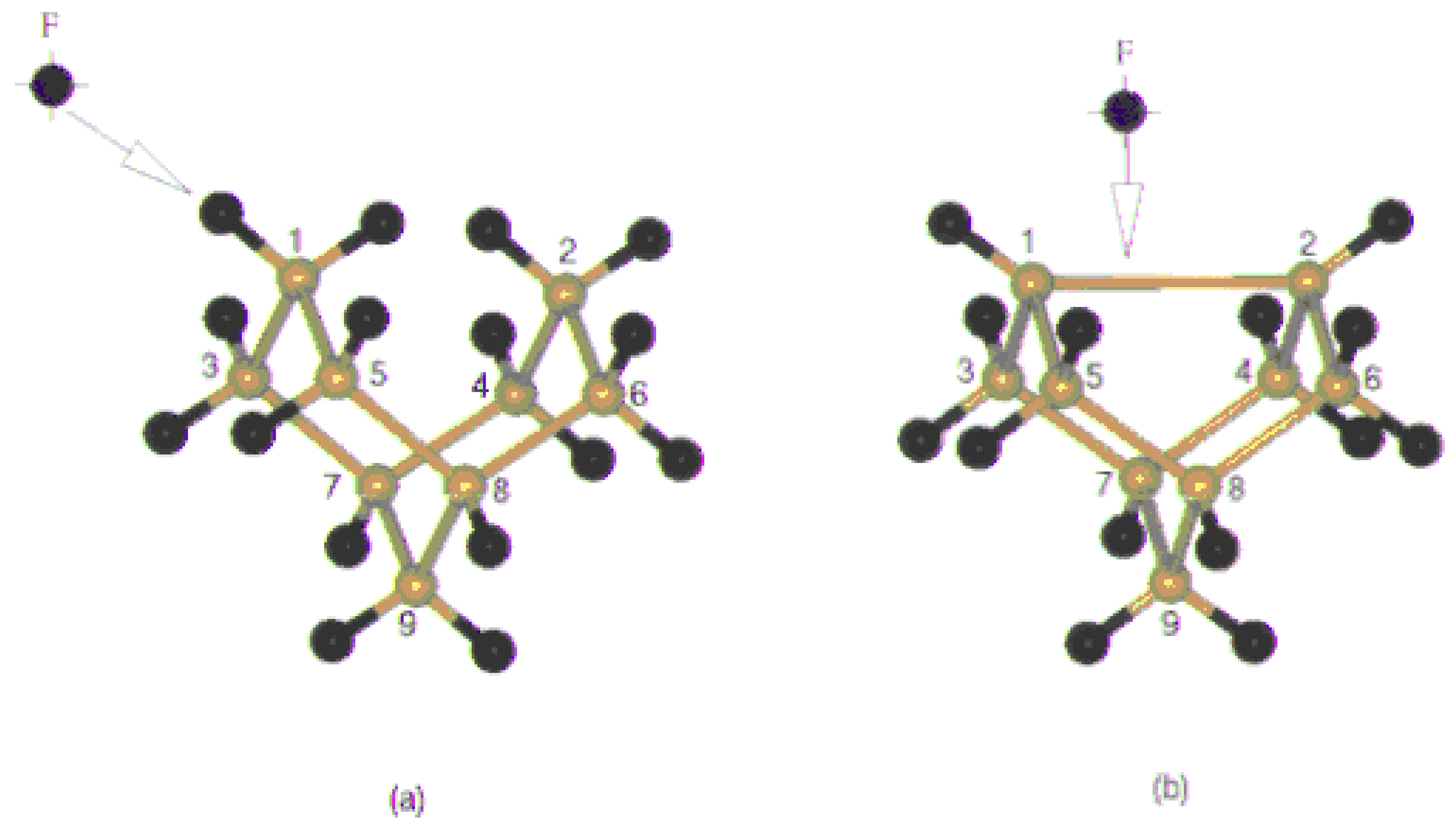
Figure 2 (a),
Figure 2(b) shows the approach of fluorine to the clusters. There are two ways one is through the direction of dangling bond and the other is the on top direction.
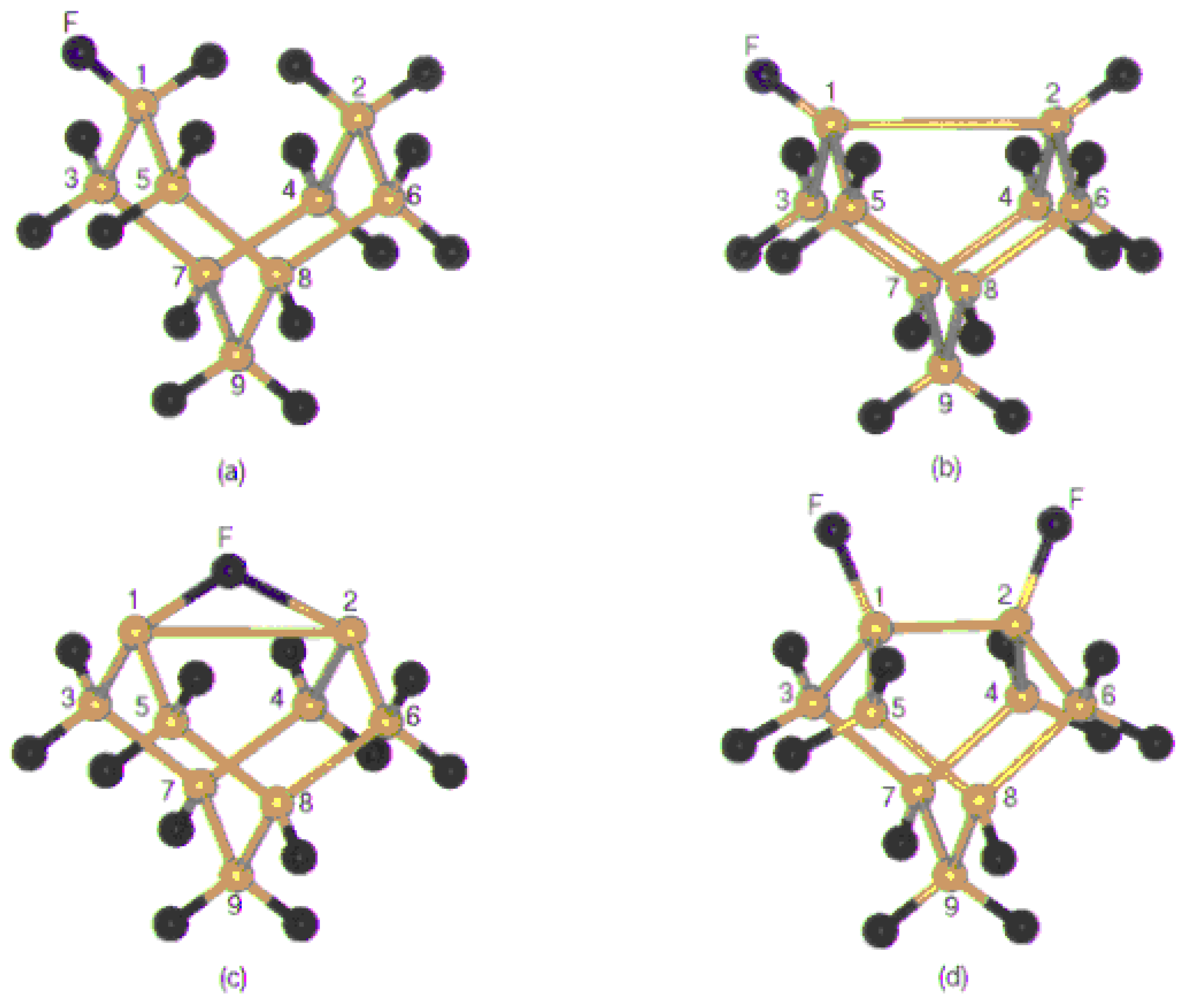
Figure 3 (a), (b), (c) and (d) shows the optimized structure of the Si
9H
15F, Si
9H
13F and Si
9H
12F, Si
9H
12F
2 clusters, respectively.
Figure 2.
The pathways of fluorine adsorption: (a) Directly onto a Si dangling bond (b) on top of a Si dimer.
Figure 2.
The pathways of fluorine adsorption: (a) Directly onto a Si dangling bond (b) on top of a Si dimer.
The first two clusters represent the situation when the fluorine atom is approaching towards the dangling bond and form a mono coordinated linkage with Si surface, where as the third cluster represents the on top attachment resulting in the formation of dicoordinated fluorine bridge with silicon. The fourth structure is a representation of the surface dimer, in which two of the dangling bonds are saturated with fluorine.
Figure 3.
The optimized structure of (a) Si
9H
15F, (b) Si
9H
13F (c) Si
9H
12F and (d) Si
9H
12F
2 following the pathways of
figure 2.
Figure 3.
The optimized structure of (a) Si
9H
15F, (b) Si
9H
13F (c) Si
9H
12F and (d) Si
9H
12F
2 following the pathways of
figure 2.
The geometrical parameters of the optimized cluster for both the unreconstructed and reconstructed surface were compared in a situation where the atomic F approaches the dangling bonds. The results are shown in
Table 3. It is observed that, the calculated equilibrium Si-F bond length is 1.643 Å, Si dimer bond length is 2.426 Å, and the distance between a surface Si-atom and a second layer Si atom is 2.350 Å. The latter value is in exact accord with the known bulk bond length in silicon [
46]. The Si-Si bond length does not change considerably before and after addition of fluorine, as expected with the localized bonding scenario. There are no experimental results so far to compare with the calculated numbers for the surface Si-F distance. We compare this number with our periodic calculations [
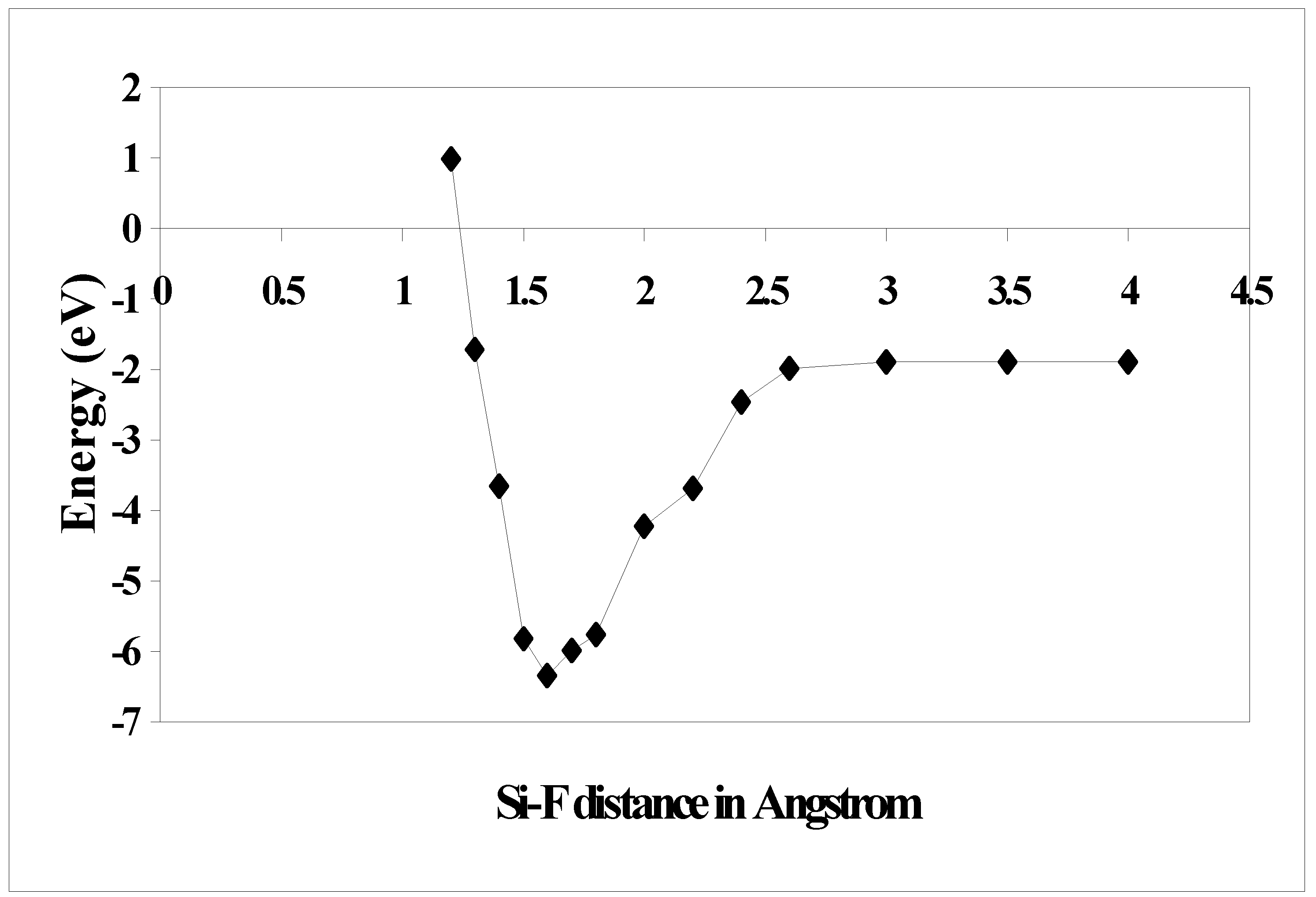
37] and also with the semiempirical calculation prediction and it is found that the results are matching well. We also calculated the trajectory for F attacking Si (100) –2x1 surface along the dangling bond direction for the reconstructed surface. The potential energy curves calculated at the DFT levels are plotted in
Figure 4. It is observed that the minimum energy lies at Si-F distance of 1.6 Å and then it slowly increases and reaches a plateau at a distance of 2.5 Å onwards. It shows that the reaction does not have an activation barrier, suggesting that the initial sticking probability of atomic F may be close to unity. This is consistent with empirical [
27] and
ab initio [
28] derived molecular dynamic simulations, which also recommends a near unity sticking probability.
Table 3.
The important internal co-ordinates of optimized (a) Si9H15F and (b) Si9H14F.
Table 3.
The important internal co-ordinates of optimized (a) Si9H15F and (b) Si9H14F.
| Bond length in Angstrom | Bond angles in Degrees |
|---|
| F-Si1 | (a) 1.643
(b) 1.646 | F-Si1-Si2 | (a) 115.2
(b) 113.4 |
| Si1-Si2 | (a) 2.435
(b) 2.426 | F-Si1-Si3=F-Si1-Si5 | (a) 112.2
(b) 114.0 |
| Si1-Si3 = Si1-Si5 | (a) 2.346
(b) 2.350 | Si3-Si1-Si2=Si5-Si1-Si2 | (a) 105.1
(b) 105.3 |
| Si2-Si4=Si2-Si6 | (a) 2.363
(b) 2.360 | Si4-Si2-Si1=Si6-Si2-Si1 | (a) 104.1
(b) 104.1 |
| Si3-Si7=Si5-Si8 | (a) 2.365
(b) 2.361 | Si3-Si1-Si5 | (a) 103.7
(b) 103.8 |
| Si4-Si7=Si6-Si8 | (a) 2.366
(b) 2.365 | Si4-Si2-Si6 | (a) 101.5
(b) 101.7 |
| Si7-Si9=Si8-Si9 | (a) 2.354
(b) 2.352 | | |
| Si3-Si4=Si5-Si6 | (a) 3.629
(b) 3.624 | | |
| Si3-Si5 | 3.695
3.698 | | |
| Si4-Si6 | 3.662
3.660 | | |
Figure 4.
Potential curve for F atom approaching a Si dimer along the dangling bond direction as a function of Si-F distance.
Figure 4.
Potential curve for F atom approaching a Si dimer along the dangling bond direction as a function of Si-F distance.
In order to rationalize doping effects on etching, it is worth to ascertain the charge on fluorine atom located on the Si (100)-2x1 surface. We calculated the charge distribution on the constituent atoms for the four clusters having fluorine atom at the dangling bond position. The results are shown in
Table 4. We found that nearly 0.36 e is transferred to the adsorbed fluorine primarily from the silicon atom that forms the Si-F bond. The other Si atom on the surface dimer (reconstructed) and all other subsurfacesilicon atoms remain nearly neutral. The embedded H atoms also remain almost neutral. This shows that the adsorption of fluorine atom on the dangling bond of silicon surface both reconstructed and unreconstructed leads to a Si-F bond with localized ionic character.
Table 4.
The net charges (au) for F, Si and H atoms obtained from Mulliken population analysis for optimized bare and fluorinated clusters.
Table 4.
The net charges (au) for F, Si and H atoms obtained from Mulliken population analysis for optimized bare and fluorinated clusters.
| Positions | Centers | Si9H16 | Si9H15F | Si9H14 | Si9H13F |
|---|
| Adsorbate | F | | -0.37 | | -0.39 |
| Surface layer | Si | +0.05 | +0.42 | +0.05 | +0.44 |
| H | +0.06 | +0.08 | +0.05 | +0.06 |
| Second layer | Si | -0.12 | -0.15 | -0.14 | -0.17 |
| H | +0.05 | -0.13 | +0.05 | -0.12 |
| Third layer | Si | -0.01 | -0.05 | -0.03 | -0.07 |
| H | +0.06 | +0.08 | +0.05 | +0.09 |
| Fourth layer | Si | -0.15 | -0.14 | -0.13 | -0.12 |
| H | +0.06 | +0.08 | +0.08 | +0.07 |
As observed in earlier section that the mono coordinated Si-F bond formation is more feasible in comparison to bridging situation, it is likely that F atoms adsorbed initially near a bridge site will move to onefold F. We estimated this diffusion of F atom from the bridge to the dangling bond site by drawing a potential curve for a F atom moving from the equilibrium bridge bond position (R|| = 0 Å) toward a dangling bond of the silicon dimer, keeping the vertical distance fixed between the F atom and the Si (100)-2x1 surface at R⊥, eq = 1.6 Å. Substrate relaxation was not allowed. The resulting curve is shown in
Fig. 5. The minimum energy position in the potential curve (R|| = 1.6 Å, R⊥= 1.6 Å) is exactly at the equilibrium position of the Si-F bond in the fully optimized Si
9H
15F cluster, showing the viability of the rigid cluster approximation used in this calculation.
After one Si-F bond formation it is possible to saturate the other dangling bond for reconstructed surface and the two other bonds in unreconstructed Si (100) surface excepting the two bonded with hydrogen. First we compared the geometric parameters of the situation for two Si-F dangling bond formations for both the surfaces. The results are shown in
Table 5. The geometric parameters show the similar trend as observed in case of mono-coordinated species. Mulliken population analysis results show that 0.39 e is transferred to the F atom directly from the Si atom to which it is bonded, while all subsurface Si atoms retain nearly the same charge distribution as that of bare cluster and monofluoro cluster. When the dangling bonds are saturated the dimer bonds remain intact. This allows us to precede for fluorination greater than 1.0 ML and upto 2.0 ML. The formation of SiF
2 on the surface of dimer leads to a cleavage of the dimer bond at the cost of 3.34 eV. This results in the formation of a difluoro Si species along with a bare surface Si atom with two unpaired dangling bonds. Mulliken population analysis we observed that each F atom in SiF
2 receives 0.19 e to show its less ionicity. However, the charge on Si species in difluoro species is just doubles that of the monofluoro species (0.40 e). These matches with the XPS observation in terms of the core level shift distinguishing SiF and SiF
2 species [
47,
48]. These results also validate the proposition of Wu et al [
47]. They said from their ab initio calculations of embedded silicon clusters containing 0-4 fluorine atoms, that although SiF
2 is an extremely stable species in the gas phase, it is predicted to be much less favorable than Si-F on the surface due to lateral interactions. Thus for a perfect Si (100) surface, monofluorination will occurbefore difluortination. However, difluorination may take place early at defect sites during etching, as the silicon atoms at defect sites are expected to be highly unsaturated. It is expected tat with increase of fluorine coverage the repulsion between neighboring fluorine atoms become significant. To estimate the total strain involved in this process lattice energy minimization will be useful. We are currently investigating the scenario by pseudopotential ab initio lattice minimization technique.
Figure 5.
Potential curve for F atom diffusion from the twofold bridge-bonded position (R|| = 0 Å) to the onefold dangling-bond site of a silicon dimer (R|| = 1.6 Å), as a function of the parallel distance (R||) between the F atom and the original twofold bridge-bonded position. The vertical distance between the F atom and the surface was kept fixed. At R⊥ = 1.6 Å.
Figure 5.
Potential curve for F atom diffusion from the twofold bridge-bonded position (R|| = 0 Å) to the onefold dangling-bond site of a silicon dimer (R|| = 1.6 Å), as a function of the parallel distance (R||) between the F atom and the original twofold bridge-bonded position. The vertical distance between the F atom and the surface was kept fixed. At R⊥ = 1.6 Å.
Table 5.
The important internal co-ordinates of optimized (a) Si9H14F2 and (b) Si9H12F2.
Table 5.
The important internal co-ordinates of optimized (a) Si9H14F2 and (b) Si9H12F2.
| Bond length in Angstrom | Bond angles in Degrees |
|---|
| F-Si1 | (a)1.641
(b)1.643 | F1-Si1-Si2=F2-Si2-Si1 | (a)115.1
(b)113.1 |
| Si1-Si2 | (a)2.429
(b)2.435 | F1-Si1-Si3=F1-Si1-Si5 | (a)112.8
(b)114.5 |
| Si1-Si3 = Si1-Si5 | (a)2.352
(b)2.348 | F2-Si2-Si4=F2-Si2-Si6 | (a)112.3
(b)114.5 |
| Si2-Si4=Si2-Si6 | (a)2.365
(b)2.362 | Si3-Si1-Si5=Si4-Si2-Si6 | (a)103.7
(b)104.4 |
| Si3-Si7=Si5-Si8 | (a)2.365
(b)2.362 | Si3-Si1-Si2=Si5-Si1-Si2 | (a)103.9
(b)104.7 |
| Si4-Si7=Si6-Si8 | (a)2.365
(b)2.362 | Si4-Si2-Si1=Si6-Si2-Si1 | (a)103.9
(b)104.7 |
| Si7-Si9=Si8-Si9 | (a)2.354
(b)2.352 | | |
| Si3-Si4=Si5-Si6 | (a)3.629
(b)3.624 | | |
| Si3-Si5 | (a)3.624
(b)3.618 | | |
| Si4-Si6 | (a)3.624
(b)3.610 | | |
The vibrational frequency results are shown in
Table 6. The harmonic vibrational frequencies of the optimized cluster were obtained from a normal mode analysis, which generates a fairly localized stretching mode at 932 cm
-1 and 924 cm
-1 for reconstructed and unreconstructed surface respectively. Other modes (e.g. bending frequencies) coupled with motions of substrate silicon atoms occur at 165-250 cm
-1. The symmetric stretching for difluoro dangling bond situation in both reconstructed and unreconstructed surface is 670 cm
-1 and 615 cm
-1 respectively. These vibrational frequencies are in resemblance with the experimental results [
6,
39].
Table 6.
Harmonic vibrational frequency results for surface fluoro species.
Table 6.
Harmonic vibrational frequency results for surface fluoro species.
| Cluster | Si-F frequency |
|---|
| Stretching* cm-1 | Bending cm-1 |
|---|
| Si9H15F | 932 (892) | 169 (149) |
| Si9H14F2 | 670 (612) | 185 |
| Si9H13F | 924 | 223 (180) |
| Si9H12F2 | 615 | 243 |
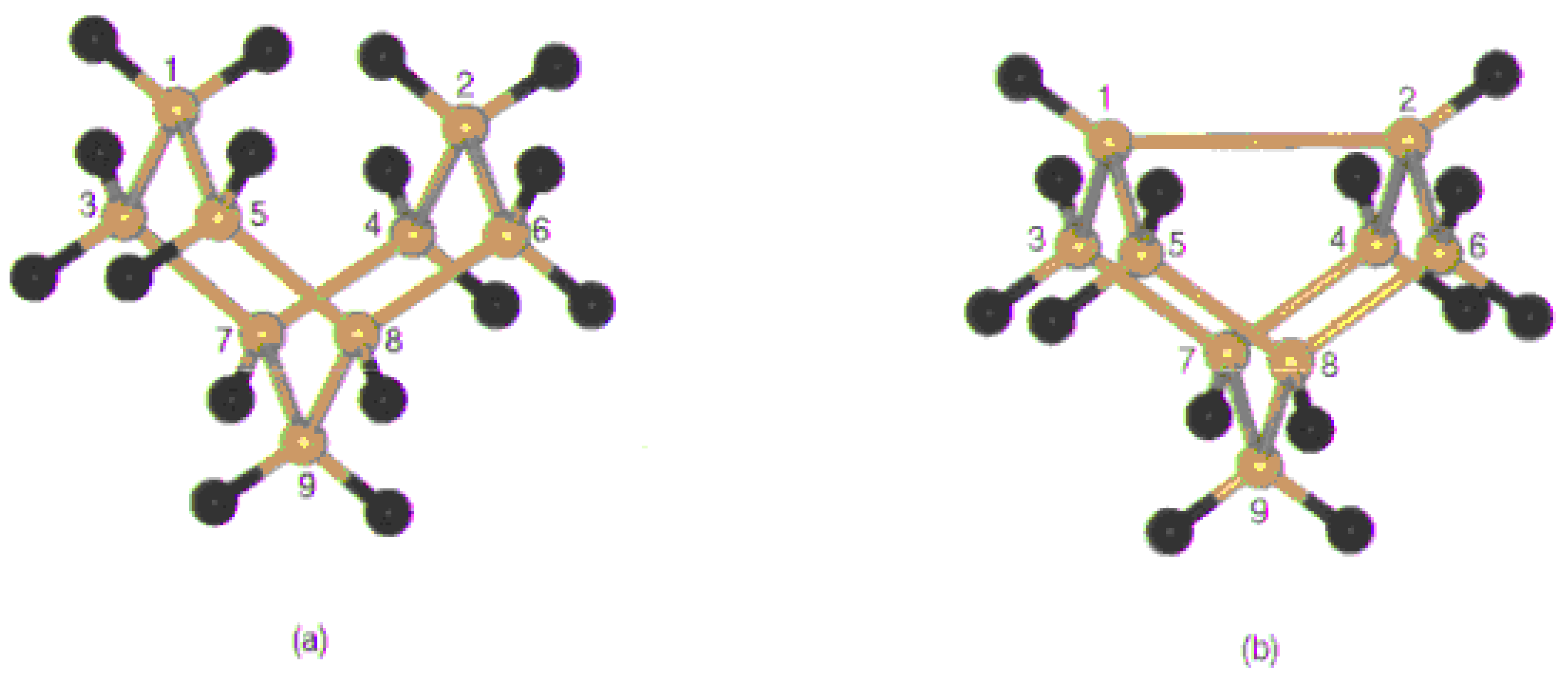
Now, we explored all the bonding possibilities of bond formation of fluorine with both reconstructed and unreconstructed surfaces. We then compared their relative stabilization energy in
Figure 6. We used a typical nomenclature for the surfaces as shown in the following:
| For unreconstructed surface: | | | For reconstructed surface: |
| 1) F-H-H-H | | | 1) Si9H13F |
| 2) F-H-H-F | | | 2) Si9H12F2 |
| 3) H-F-F-H | | | |
| 4) H-F-H-F = F-H-F-H | | | |
Figure 6.
Comparison of relative stabilization energy for different clusters representing both recon-structed and unreconstructed Si (100) surface for different fluorine coverage. The nomenclatures are the following with two groups 1-4 clusters are for unreconstructed surface and 5-6 is for reconstructed surface. The cluster formulas and detail ordering are mentioned in the text.
Figure 6.
Comparison of relative stabilization energy for different clusters representing both recon-structed and unreconstructed Si (100) surface for different fluorine coverage. The nomenclatures are the following with two groups 1-4 clusters are for unreconstructed surface and 5-6 is for reconstructed surface. The cluster formulas and detail ordering are mentioned in the text.
The results show that situation with alternate fluorination both on the unreconstructed and reconstructed surface shows the maximum stability in comparison to others. The experimental observation also supports this finding.
Table 7.
Total energy of the clusters along with water (au.) and their respective interaction energy (kcal/mol).
Table 7.
Total energy of the clusters along with water (au.) and their respective interaction energy (kcal/mol).
| Species | Total energy (au.) | Interaction energy (kcal./mol) BSSE corrected |
|---|
| Water | -76.4489 | |
| Si9H14 | -2614.5734 | |
| Si9H13F | -2713.2797 | |
| Si9H12F2 | -2811.9431 | |
| Water + Si9H14 | -2691.0312 | 5.55 |
| Water + Si9H13F | -2789.7286 | 3.42 |
| Water + Si9H12F2 | -2888.3920 | 7.66 |
To monitor the effect of water interaction on Si-wafer dipped in H-F the cluster representing reconstructed Si (100) surface was used. The results were compared for three different situations with all hydrogen, alternate fluorine and all fluorine structures. The interaction energy of water with all the three structures was shown in
Table 7. For all the three cases the starting configuration of water was kept the same. The results show that in all the cases with fluorine on the surface there exists a bond-breaking phenomenon, which is virtually absent in case of hydrogen-saturated surface. The most stable interaction complex exists in the case where water is interacted with the reconstructed surface with alternate fluorine. To rationalize the scenario molecular electrostatic potential map were drawn. The MESP was plotted for a potential range of –0.05 au +0.05 au. The results were shown for the polarization of the hydrogen of the water molecule to extract the fluorine from the Si (100) surface. The polarization was compared between three situations. The results show three different potential diagrams with the exception being with that of all hydrogen surfaces as shown in
Fig. 7. The interaction of fluorine with water hydrogen looks most feasible in case of alternate fluorine on the Si (100) surface as shown in
Fig. 8. In case of all fluorine surface the strong negative potential around fluorine repels the water molecule to orient in such a way that one of the water hydrogen comes closer to the fluorine present on the Si (100) surface as shown in
Fig. 9. For all hydrogen surface the water molecule feels the repulsion due to the positive hydrogen on the surface. These MESP map clearly shows the existence of bond polarization, which results from the interaction of water molecule and the Si (100) surface in presence of surface fluorine. The interaction is most feasible in case of surface with alternate occurrence of fluorine. So the surface with alternate occurrence of hydrogen and fluorine is the most active surface to interact with water. Now the reaction mechanism is shown in
Figure 10. To follow the experimentally proposed mechanism a static cluster calculation is performed. The aim is to compare the stability of the products generated after each step. This will validate the experimental mechanism along with will support our proposition of activity of the surface resulted from fluorine etching. The mechanism is traced through the most active surface i.e. with the surface with alternate occurrence of hydrogen and fluorine. The first step is the replacement of HF through the formation ofsurface hydroxyl group. The cost of this reaction is 2.1 eV. This is followed by the slow replacement of Si-H by Si-OH. This reaction is due to a nuclephilic attack of OH
- ions on Si-H bonds [
50]. The cost involved is 1.6 eV. The final step is the condensation reaction. This involves evolution of water with the formation of Si-O-Si bond. The energy involved is 1.2 eV. The mechanism validates the proposition of Graf et al [
18].
Figure 7.
MESP for water interaction with all hydrogen on Si (100) surface dimer. The +ve (+0.05 to 0.00 au.) and –ve (-0.05 to 0.00 au.) potential contours are shown as green and red shades respectively. The color code is as follows: Si (yellow), H (black), and O (red).
Figure 7.
MESP for water interaction with all hydrogen on Si (100) surface dimer. The +ve (+0.05 to 0.00 au.) and –ve (-0.05 to 0.00 au.) potential contours are shown as green and red shades respectively. The color code is as follows: Si (yellow), H (black), and O (red).
Figure 8.
MESP for water interaction with alternate hydrogen and fluorine on Si (100) surface dimer. The +ve (+0.05 to 0.00 au.) and –ve (-0.05 to 0.00 au.) potential contours are shown as green and red shades respectively. The color code is as follows: Si (yellow), H (black), F (Blue) and O (red).
Figure 8.
MESP for water interaction with alternate hydrogen and fluorine on Si (100) surface dimer. The +ve (+0.05 to 0.00 au.) and –ve (-0.05 to 0.00 au.) potential contours are shown as green and red shades respectively. The color code is as follows: Si (yellow), H (black), F (Blue) and O (red).
Figure 9.
MESP for water interaction with all fluorine on Si (100) surface dimer. The +ve (+0.05 to 0.00 au.) and –ve (-0.05 to 0.00 au.) potential contours are shown as green and red shades respectively. The color code is as follows: Si (yellow), H (black), F (Blue) and O (red).
Figure 9.
MESP for water interaction with all fluorine on Si (100) surface dimer. The +ve (+0.05 to 0.00 au.) and –ve (-0.05 to 0.00 au.) potential contours are shown as green and red shades respectively. The color code is as follows: Si (yellow), H (black), F (Blue) and O (red).
Figure 10.
The reaction mechanism to show the interaction of water with Si (100) surface. The color code is as follows: Si (yellow), H (black), F (Blue) and O (red).
Figure 10.
The reaction mechanism to show the interaction of water with Si (100) surface. The color code is as follows: Si (yellow), H (black), F (Blue) and O (red).
So this is rationalized from the above results that at the initial stage of fluorine etching the fluorine interaction is most feasible through dangling bond and once the dangling bonds are saturated SiF
2 formation is possible. But SiF
2 formation is energetically unfavorable, as it needs higher activation barrier, which is associated with bond breaking in case of Si-dimer. For unreconstructed surface SiF
2 formation is also hindered for mutual strong repulsion of the adjacent fluorine atoms. To demonstrate the role of water on Si-wafer we followed the mechanism of Graf et al [
20], who for the first time proposed experimentally the model mechanism. We explored the said mechanism to validate our observation in terms of the composition of the fluorine-terminated surface. We located the optimized surface composition for favorable water interaction. The bond breaking and the polarizability of interacting water molecule along with the surface fluorine atom show that surface with alternate occurrence of fluorine is the most stable. The results also justify the use of DFT in explaining the structural behavior of the Si (100) surface successfully. The optimistic results pave the way to study the water interaction exhaustively in the next part of this article using periodic ab initio calculations.
 EST) is 0.03 eV. We performed the full optimization of Si9H16 cluster with DFT. The value for singlet-triplet splitting is 0.025 eV. The values are given in Table 1.This shows that the dangling bonds on the surface are very active. As we find that the direction of the dangling bond is outward from the Si dimer bond, it looks Si-F mono coordinated bond formation is more feasible. We also observed in our calculation that, when F approaches the dangling bond it forms a very stable bond (6.34 eV) both for the unreconstructed surface and for the reconstructed surface (6.22 eV), with no activation barrier. It also forms a stable bridge bond (3.0 eV) with a Si dimer. This shows the greater stability of the dangling bond, which further indicates the feasibility of the fluorine approach towards the dangling bond direction. But in the second case we find that bridging F atom slide toward the dangling bond to form the mono coordinated species without any barrier, which will be discussed in later sections. The results are shown in Table 2. The bond energies have been calculated by using the following equations.
EST) is 0.03 eV. We performed the full optimization of Si9H16 cluster with DFT. The value for singlet-triplet splitting is 0.025 eV. The values are given in Table 1.This shows that the dangling bonds on the surface are very active. As we find that the direction of the dangling bond is outward from the Si dimer bond, it looks Si-F mono coordinated bond formation is more feasible. We also observed in our calculation that, when F approaches the dangling bond it forms a very stable bond (6.34 eV) both for the unreconstructed surface and for the reconstructed surface (6.22 eV), with no activation barrier. It also forms a stable bridge bond (3.0 eV) with a Si dimer. This shows the greater stability of the dangling bond, which further indicates the feasibility of the fluorine approach towards the dangling bond direction. But in the second case we find that bridging F atom slide toward the dangling bond to form the mono coordinated species without any barrier, which will be discussed in later sections. The results are shown in Table 2. The bond energies have been calculated by using the following equations.