Using Persistent Homology as a New Approach for Super-Resolution Localization Microscopy Data Analysis and Classification of γH2AX Foci/Clusters
Abstract
:1. Introduction
2. Results
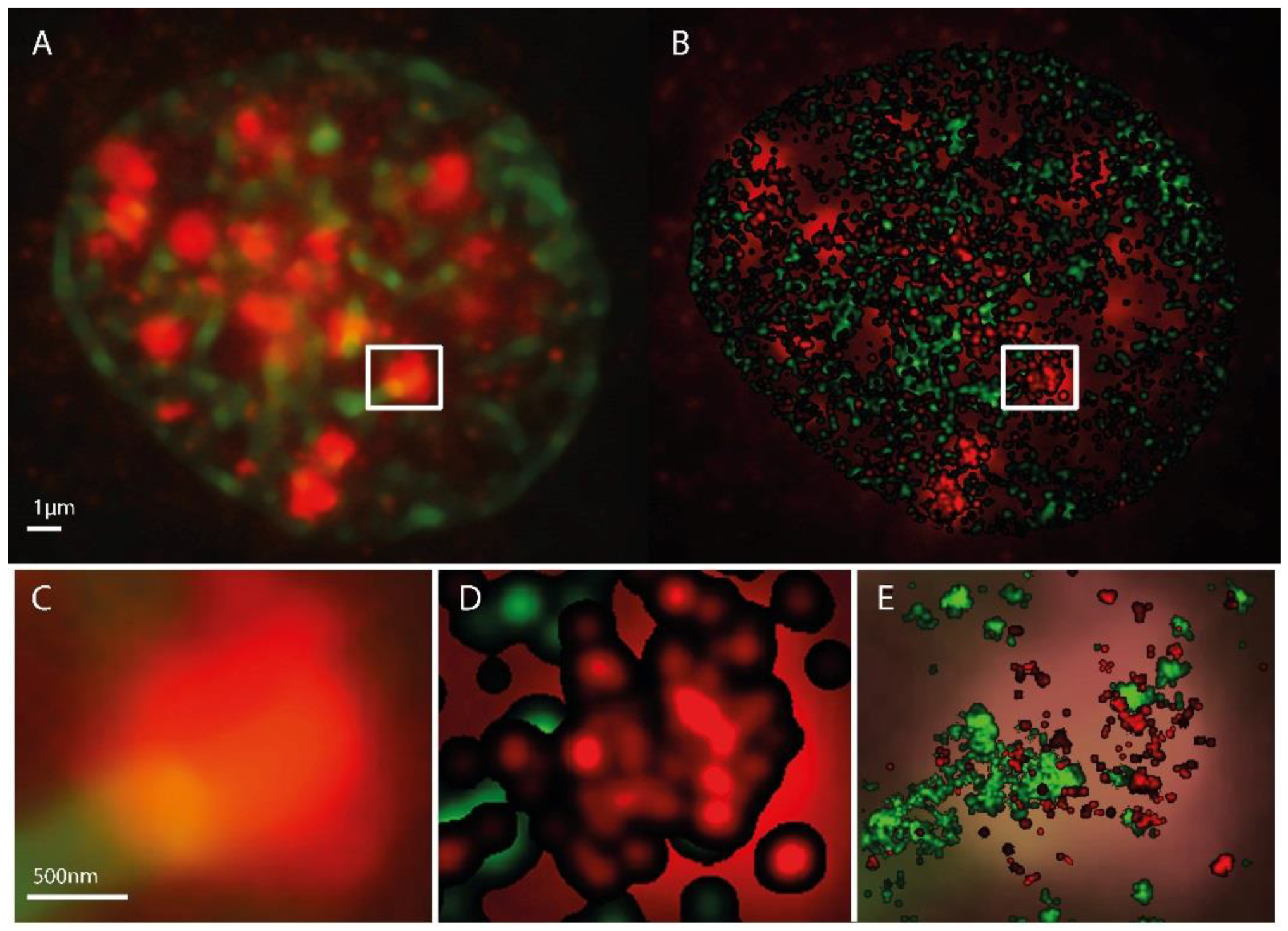
2.1. SMLM Data Processing
2.2. γH2AX Cluster Recognition and Cluster Classification
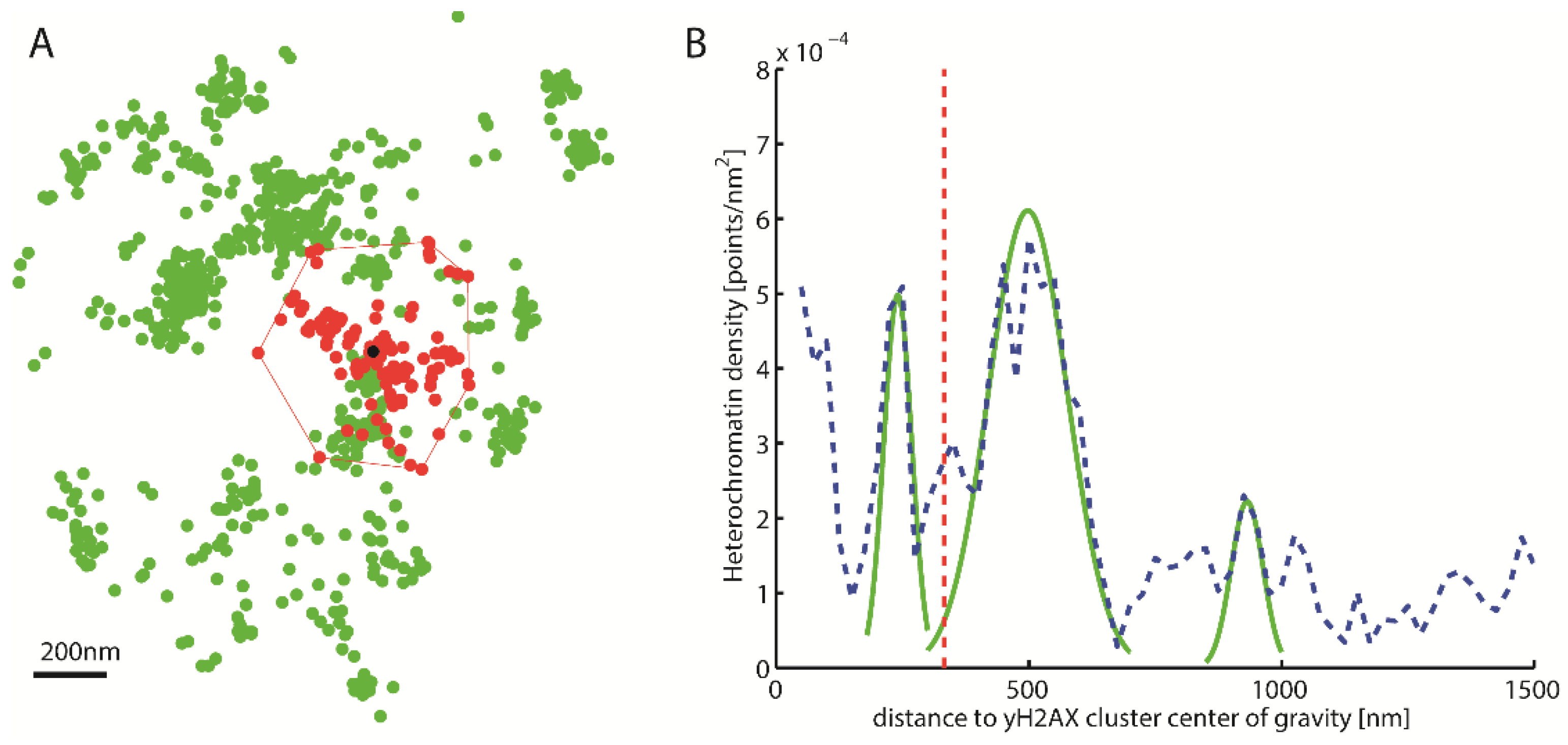
2.3. Topological Analysis of the Clusters
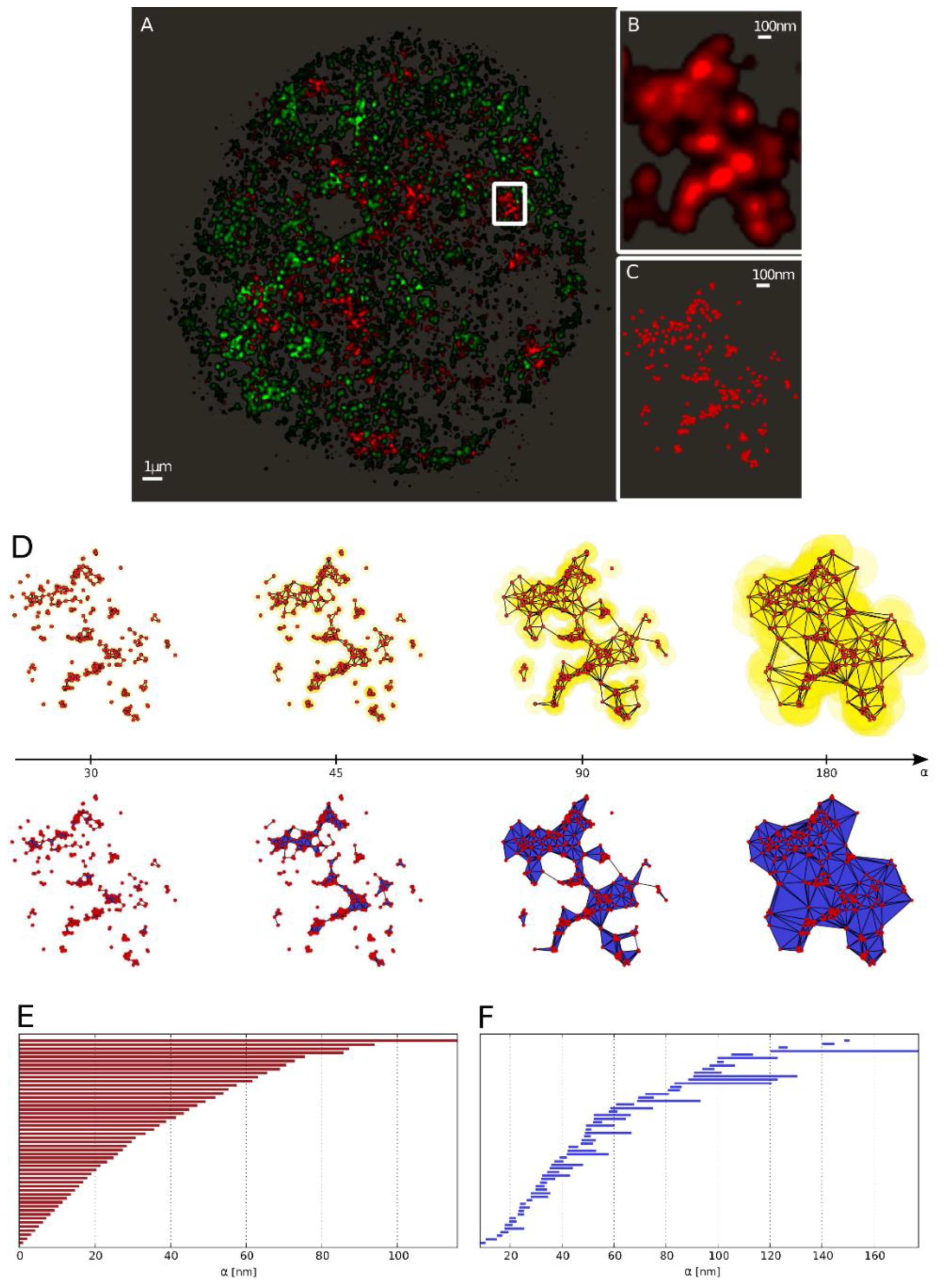
2.3.1. Barcodes as a Representation for a Pointillist Structure
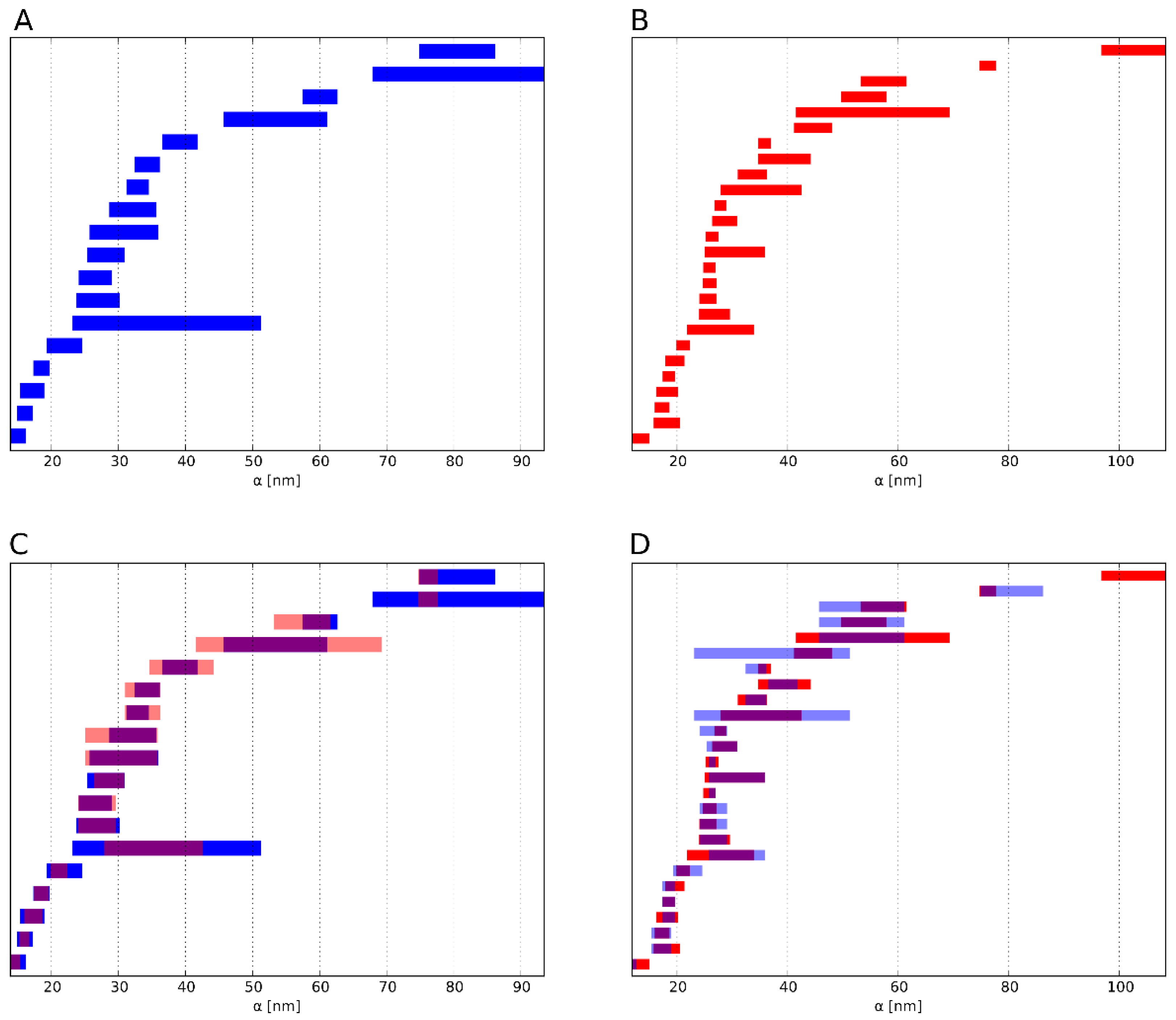
2.3.2. Similarity of Barcodes
2.4. Proof-of-Concept Experiments
3. Discussion
4. Materials and Methods
4.1. Sample Preparation
4.2. Single Molecule Localization Microscopy (SMLM)
4.3. Sample Irradiation
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Máté, G.; Müller, P.; Hillebrandt, S.; Krufczik, M.; Bach, M.; Kaufmann, R.; Hausmann, M.; Heermann, D.W. Radiation induced chromatin conformation changes analysed by fluorescent localization microscopy, statistical physics, and graph theory. PLoS ONE 2015, 10, e0128555. [Google Scholar] [CrossRef] [PubMed]
- Jakob, B.; Splinter, J.; Conrad, S.; Voss, K.O.; Zink, D.; Durante, M.; Löbrich, M.; Taucher-Scholz, G. DNA double-strand breaks in heterochromatin elicit fast repair protein recruitment, histone H2AX phosphorylation and relocation to euchromatin. Nucleic Acids Res. 2011, 39, 6489–6499. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Du, G.; Drexler, G.A.; Friedland, W.; Greubel, C.; Hable, V.; Krücken, R.; Kugler, A.; Tonelli, L.; Friedl, A.A.; Dollinger, G. Spatial dynamics of DNA damage response protein foci along the ion trajectory of high-LET particles. Radiat. Res. 2011, 176, 706–715. [Google Scholar] [CrossRef] [PubMed]
- Lowndes, N.F.; Toh, G.W. DNA repair: The importance of phosphorylating histone H2AX. Curr. Biol. 2005, 15, 99–102. [Google Scholar] [CrossRef] [PubMed]
- Löbrich, M.; Shibata, A.; Beucher, A.; Fisher, A.; Ensminger, M.; Goodarzi, A.A.; Barton, O.; Jeggo, P.A. γ-H2AX foci analysis for monitoring DNA double-strand repair: Strengths, limitations and optimization. Cell Cycle 2010, 9, 662–669. [Google Scholar] [CrossRef] [PubMed]
- Rogakou, E.P.; Pilch, D.R.; Orr, A.H.; Ivanova, V.S.; Bonner, W.M. DNA double-starnd breaks induce histone H2AX phosphorylation on serine 139. J. Biol. Chem. 1998, 273, 5858–5868. [Google Scholar] [CrossRef] [PubMed]
- Rogakou, E.P.; Boon, C.; Redon, C.; Bonner, W.M. Megabase chromatin domains involved in DNA double-strand breaks in vivo. J. Cell Biol. 1999, 146, 905–916. [Google Scholar] [CrossRef] [PubMed]
- Falk, M.; Hausmann, M.; Lukášová, E.; Biswas, A.; Hildenbrand, G.; Davídková, M.; Krasavin, E.; Kleibl, Z.; Falková, I.; Ježková, L.; et al. Giving OMICS spatiotemporal dimensions by challenging microscopy: From functional networks to structural organization of cell nuclei elucidating mechanisms of complex radiation damage response and chromatin repair—PART A (Radiomics). Crit. Rev. Eukaryot. Gene Express. 2014, 24, 205–223. [Google Scholar] [CrossRef]
- Falk, M.; Hausmann, M.; Lukášová, E.; Biswas, A.; Hildenbrand, G.; Davídková, M.; Krasavin, E.; Kleibl, Z.; Falková, I.; Ježková, L.; et al. Giving OMICS spatiotemporal dimensions by challenging microscopy: From functional networks to structural organization of cell nuclei elucidating mechanisms of complex radiation damage response and chromatin repair—PART B (Structuromics). Crit. Rev. Eukaryot. Gene Express. 2014, 24, 225–247. [Google Scholar] [CrossRef]
- Ceccaldi, R.; Rondinelli, B.; Andrea, A.D.D. Repair pathway choices and consequences at the double-strand break. Trends Biol. 2016, 26, 52–64. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, S.; Nandi, S. Choices have consequences: The nexus between DNA repair pathways and genomic instability in cancer. Clin. Trans. Med. 2016, 5, 45. [Google Scholar] [CrossRef] [PubMed]
- Mladenov, E.; Magin, S.; Soni, A.; Iliakis, G. DNA double-strand-break repair in higher eukaryotes and its role in genomic instability and cancer: Cell cycle and proliferation-dependent regulation. Sem. Cancer Biol. 2016, 37–38, 51–64. [Google Scholar] [CrossRef] [PubMed]
- Schipler, A.; Iliakis, G. DNA double-strand–break complexity levels and their possible contributions to the probability for error-prone processing and repair pathway choice. Nucleic Acids Res. 2013, 41, 7589–7605. [Google Scholar] [CrossRef] [PubMed]
- Tsouroula, K.; Fürst, A.; Rogier, M.; Heyer, V.; Maglott-Roth, A.; Ferrand, A.; Reina-San-Martin, B.; Soutoglou, E. Temporal and spatial uncoupling of DNA double strand break repair pathways within mammalian heterochromatin. Mol. Cell 2016, 63, 293–305. [Google Scholar] [CrossRef] [PubMed]
- Dueva, R.; Iliakis, G. Alternative pathways of non-homologous end joining (NHEJ) in genomic instability and cancer. Transl. Cancer Res. 2013, 2, 163–177. [Google Scholar]
- Biehs, R.; Steinlage, M.; Barton, O.; Juhász, S.; Künzel, J.; Spies, J.; Shibata, A.; Jeggo, P.A.; Löbrich, M. DNA double-strand break resection occurs during non-homologous end joining in G1 but is distinct from resection during homologous recombination. Mol. Cell 2017, 65, 671–684. [Google Scholar] [CrossRef] [PubMed]
- Shibata, A.; Conrad, S.; Birraux, J.; Geuting, V.; Barton, O.; Ismail, A.; Kakarougkas, A.; Meek, K.; taucher-Scholz, G.; Löbrich, M.; et al. Factors determining DNA double-strand break repair pathway choice in G2 phase. EMBO J. 2011, 30, 1079–1092. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mladenov, E.; Magin, S.; Soni, A.; Iliakis, G. DNA double-strand break repair as determinant of cellular radiosensitivity to killing and target in radiation therapy. Front. Oncol. 2013, 3, 113. [Google Scholar] [CrossRef] [PubMed]
- Löbrich, M.; Jeggo, P.A. A process of resection-dependent non-homologous end joining involving the goddess artemis. Trends Biol. Sci. 2017, 42, 690–701. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Yuan, D.; Guo, F.; Chen, X.; Zhu, L.; Zhang, H.; Wang, C.; Shao, C. Chromatin remodeling modulates radiosensitivity of the daughter cells derived from cell population exposed to low- and high-LET irradiation. Oncotarget 2017, 8, 52823–52836. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reid, D.A.; Conlin, M.P.; Yin, Y.; Chang, H.H.; Watanabe, G.; Lieber, M.R.; Ramsden, D.A.; Rothenberg, E. Bridging of double-starnded breaks by the non-homologous end-joining ligation complex is modulated by DNA end chemistry. Nucleic Acids Res. 2017, 45, 1872–1878. [Google Scholar] [CrossRef] [PubMed]
- Reid, D.A.; Keegan, S.; Leo-Macias, A.; Watanabe, G.; Strande, N.T.; Chang, H.H.; Oksuz, B.A.; Fenyo, D.; Lieber, M.R.; Ramsden, D.A.; et al. Organization and dynamics of the non-homologous end-joining machinery during DNA double-strand break repair. Proc. Natl. Acad. Sci. USA 2015, 112, E2575–E2584. [Google Scholar] [CrossRef] [PubMed]
- Natale, F.; Rapp, A.; Yu, W.; Maiser, A.; Harz, H.; Schall, A.; Grulich, S.; Anton, T.; Hörl, D.; Chen, W.; et al. Identification of the elementary structural units of the DNA damage response. Nat. Commun. 2017, 8, 15760. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reindl, J.S.; Girst, S.; Walsh, D.W.M.; Geubel, C.; Schwarz, B.; Siebenwirth, C.; Drexler, G.A.; Friedl, A.A.; Dollinger, G. Chromatin organization revealed by nanostructure of irradiation induced γH2AX, 53BP1 and Rad51 foci. Sci. Rep. 2017, 7, 40616. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lorat, Y.; Bunner, C.U.; Schanz, S.; Jacob, B.; Taucher-Scholz, G.; Rübe, C.E. Nanoscale analysis of clustered DNA damage after high-LET irradiation by quantitative electron microscopy—The heavy burden to repair. DNA Repair 2015, 28, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Lorat, Y.; Timm, S.; Jacob, B.; Taucher-Scholz, G.; Rübe, C.E. Clustered double-strand breaks in heterochromatin perturb DNA repair after high linear energy transfer irradiation. Radiother. Oncol. 2016, 121, 427–437. [Google Scholar] [CrossRef] [PubMed]
- Szcurek, A.T.; Prakash, K.; Lee, H.K.; Zurek-Biesiada, D.; Best, G.; Hagmann, M.; Dobrucki, J.W.; Cremer, C.; Birk, U. Single molecule localization microscopy of the distribution of chromatin using Hoechst and DAPI fluorescent probes. Nucleus 2014, 5, 331–340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hausmann, M.; Wagner, E.; Lee, J.-H.; Schrock, G.; Schaufler, W.; Krufczik, M.; Papenfuß, F.; Port, M.; Bestvater, F.; Scherthan, H. Super-resolution microscopy of radiation-induced histone H2AX phosphorylation in relation to H3K9-trimethylation in HeLa cells. Nanoscale 2018, 10, 4320–4331. [Google Scholar] [CrossRef] [PubMed]
- Eryilmaz, M.; Schmitt, E.; Krufczik, M.; Theda, F.; Lee, J.-H.; Cremer, C.; Bestvater, F.; Schaufler, W.; Hausmann, M.; Hildenbrand, G. Localization microscopy analyses of MRE11 clusters in 3D-conserved cell nuclei of different cell lines. Cancers 2018, 10, 25. [Google Scholar] [CrossRef] [PubMed]
- Bach, M.; Savini, C.; Krufczik, M.; Cremer, C.; Rösl, F.; Hausmann, M. Super-resolution localization microscopy of γ-H2AX and heterochromatin after folate deficiency. Int. J. Mol. Sci. 2017, 18, 1726. [Google Scholar] [CrossRef] [PubMed]
- Eberle, J.P.; Rapp, A.; Krufczik, M.; Eryilmaz, M.; Gunkel, M.; Erfle, H.; Hausmann, M. Super-resolution microscopy techniques and their potential for applications in radiation biophysics. Methods Mol. Biol. 2017, 1663, 1–13. [Google Scholar] [PubMed]
- Morales, M.E.; White, T.B.; Streva, V.A.; DeFreece, C.B.; Hedges, D.J.; Deininger, P.L. The contribution of Alu elements to mutagenic DNA double-strand break repair. PLoS Genet. 2015, 11, e1005016. [Google Scholar] [CrossRef] [PubMed]
- Krufczik, M.; Sievers, A.; Hausmann, A.; Lee, J.-H.; Hildenbrand, G.; Schaufler, W.; Hausmann, M. Combining low temperature fluorescence DNA-hybridization, immunostaining, and super-resolution localization microscopy for nano-structure analysis of ALU elements and their influence on chromatin structure. Int. J. Mol. Sci. 2017, 18, 1005. [Google Scholar] [CrossRef] [PubMed]
- Hausmann, M.; Ilić, N.; Pilarczyk, G.; Lee, J.-H.; Logeswaran, A.; Borroni, A.P.; Krufczik, M.; Theda, F.; Waltrich, N.; Bestvater, F.; et al. Challenges for super-resolution localization microscopy and biomolecular fluorescent nano-probing in cancer research. Int. J. Mol. Sci. 2017, 18, 2066. [Google Scholar] [CrossRef] [PubMed]
- Cremer, C.; Masters, B.R. Resolution enhancement techniques in microscopy. Eur. Phys. J. H 2013, 38, 281–344. [Google Scholar] [CrossRef] [Green Version]
- Müller, P.; Lemmermann, N.A.; Kaufmann, R.; Gunkel, M.; Paech, D.; Hildenbrand, G.; Holtappels, R.; Cremer, C.; Hausmann, M. Spatial distribution and structural arrangement of a murine cytomegalovirus glycoprotein detected by SPDM localization microscopy. Histochem. Cell Biol. 2014, 142, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Bohn, M.; Diesinger, P.; Kaufmann, R.; Weiland, Y.; Müller, P.; Gunkel, M.; von Ketteler, A.; Lemmer, P.; Hausmann, M.; Heermann, D.W.; et al. Localization microscopy reveals expression-dependent parameters of chromatin nanostructure. Biophys. J. 2010, 99, 1358–1367. [Google Scholar] [CrossRef] [PubMed]
- Pilarczyk, G.; Nesnidal, I.; Gunkel, M.; Bach, M.; Bestvater, F.; Hausmann, M. Localisation microscopy of breast epithelial ErbB-2 receptors and gap junctions: Trafficking after gamma-irradiation, Neuregulin-1b and Herceptin application. Int. J. Mol. Sci. 2017, 18, 362. [Google Scholar] [CrossRef] [PubMed]
- Cremer, C.; Kaufmann, R.; Gunkel, M.; Pres, S.; Weiland, Y.; Müller, P.; Ruckelshausen, T.; Lemmer, P.; Geiger, F.; Degenhard, M.; et al. Superresolution imaging of biological nanostructures by Spectral Precision Distance Microscopy (SPDM). Biotechnol. J. 2011, 6, 1037–1051. [Google Scholar] [CrossRef] [PubMed]
- Lemmer, P.; Gunkel, M.; Baddeley, D.; Kaufmann, R.; Urich, A.; Weiland, Y.; Reymann, J.; Müller, P.; Hausmann, M.; Cremer, C. SPDM—Light microscopy with single molecule resolution at the nanoscale. Appl. Phys. B 2018, 93, 1–12. [Google Scholar] [CrossRef]
- Lemmer, P.; Gunkel, M.; Weiland, Y.; Müller, P.; Baddeley, D.; Kaufmann, R.; Urich, A.; Eipel, H.; Amberger, R.; Hausmann, M.; et al. Using conventional fluorescent markers for far-field fluorescence localization nanoscopy allows resolution in the 10 nm range. J. Microsc. 2009, 235, 163–171. [Google Scholar] [CrossRef] [PubMed]
- Thompson, R.E.; Larson, D.R.; Webb, W.W. Precise nanometer localization analysis for individual fluorescent probes. Biophys. J. 2002, 82, 2775–2783. [Google Scholar] [CrossRef]
- Deschout, H.; Cella Zanacchi, F.; Mlodzianoski, M.; Diaspro, A.; Bewersdorf, J.; Hess, S.T.; Braeckmans, K. Precisely and accurately localizing single emitters in fluorescent microscopy. Nat. Methods 2014, 11, 253–266. [Google Scholar] [CrossRef] [PubMed]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. Am. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Maté, G.; Hofmann, A.; Wenzel, N.; Heermann, D.W. A topological similarity measure for proteins. Biochim. Biophys. Acta Biomembr. 2014, 1838, 1180–1190. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.-L.; Xiang, J.-F.; Kong, N.; Cai, X.-J.; Xie, A.-J. Buried territories: Heterochromatic response to DNA double-strand breaks. Acta Biochim. Biophys. Sin. 2016, 48, 594–602. [Google Scholar] [CrossRef] [PubMed]
- Kruhlak, M.J.; Celeste, A.; Dellaire, G.; Fernandez-Capetillo, O.; Muller, W.G.; McNally, J.G.; Bazett-Jones, D.P.; Nussenzweig, A. Changes in chromatin structure and mobility in living cells at sites of DNA double-strand breaks. J. Cell Biol. 2006, 172, 823–834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sak, A.; Kübler, D.; Bannik, K.; Groneberg, M.; Stuschke, M. Dependence of radiation-induced H2AX phosphorylation on histone methylation: Evidence from the chromatin immunoprecipitation assay. Int. J. Radiat. Biol. 2015, 91, 346–353. [Google Scholar] [CrossRef] [PubMed]
- Ryu, T.; Spatola, B.; Delabaere, L.; Bowlin, K.; Hopp, H.; Kunitake, R.; Karpen, G.H.; Chiolo, I. Heterochromatic breaks move to the nuclear periphery to continue recombinational repair. Nat. Cell Biol. 2015, 17, 1401–1411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sander, J.; Ester, M.; Kriegel, H.-P.; Xu, X. Density-Based Clustering in Spatial Databases: The Algorithm GDBSCAN and Its Applications. Data Min. Knowl. Discov. 1998, 2, 169–194. [Google Scholar] [CrossRef]
- Braden, B. The surveyor’s area formula. Coll. Math. J. 1986, 17, 326–337. [Google Scholar] [CrossRef]
- Jaccard, P. Etude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull. Soc. Vaud. Sci. Nat. 1901, 37, 547–579. [Google Scholar]
- Engel, L.W.; Young, N.A. human breast carcinoma cells in continous culture: A review. Cancer Res. 1978, 38, 4327–4339. [Google Scholar] [PubMed]
- Lacroix, M.; Leclercq, G. Relevance of breast cancer cell lines as models for breast tumours: An update. Breast Cancer Res. Treat. 2004, 83, 249–289. [Google Scholar] [CrossRef] [PubMed]
- Becker, J.S.; Nicetto, D.; Zaret, K.S. H3K9me3-dependent heterochromatin: Barrier to cell fate changes. Trends Genet. 2016, 32, 29–41. [Google Scholar] [CrossRef] [PubMed]
- Allshire, R.C.; Madhani, H.D. Ten principles of heterochromatin formation and function. Nat. Rev. Mol. Cell Biol. 2018, 19, 229–244. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hofmann, A.; Krufczik, M.; Heermann, D.W.; Hausmann, M. Using Persistent Homology as a New Approach for Super-Resolution Localization Microscopy Data Analysis and Classification of γH2AX Foci/Clusters. Int. J. Mol. Sci. 2018, 19, 2263. https://doi.org/10.3390/ijms19082263
Hofmann A, Krufczik M, Heermann DW, Hausmann M. Using Persistent Homology as a New Approach for Super-Resolution Localization Microscopy Data Analysis and Classification of γH2AX Foci/Clusters. International Journal of Molecular Sciences. 2018; 19(8):2263. https://doi.org/10.3390/ijms19082263
Chicago/Turabian StyleHofmann, Andreas, Matthias Krufczik, Dieter W. Heermann, and Michael Hausmann. 2018. "Using Persistent Homology as a New Approach for Super-Resolution Localization Microscopy Data Analysis and Classification of γH2AX Foci/Clusters" International Journal of Molecular Sciences 19, no. 8: 2263. https://doi.org/10.3390/ijms19082263
APA StyleHofmann, A., Krufczik, M., Heermann, D. W., & Hausmann, M. (2018). Using Persistent Homology as a New Approach for Super-Resolution Localization Microscopy Data Analysis and Classification of γH2AX Foci/Clusters. International Journal of Molecular Sciences, 19(8), 2263. https://doi.org/10.3390/ijms19082263





