Nonnative Energetic Frustrations in Protein Folding at Residual Level: A Simulation Study of Homologous Immunoglobulin-like β-Sandwich Proteins
Abstract
1. Introduction
2. Results and Discussions
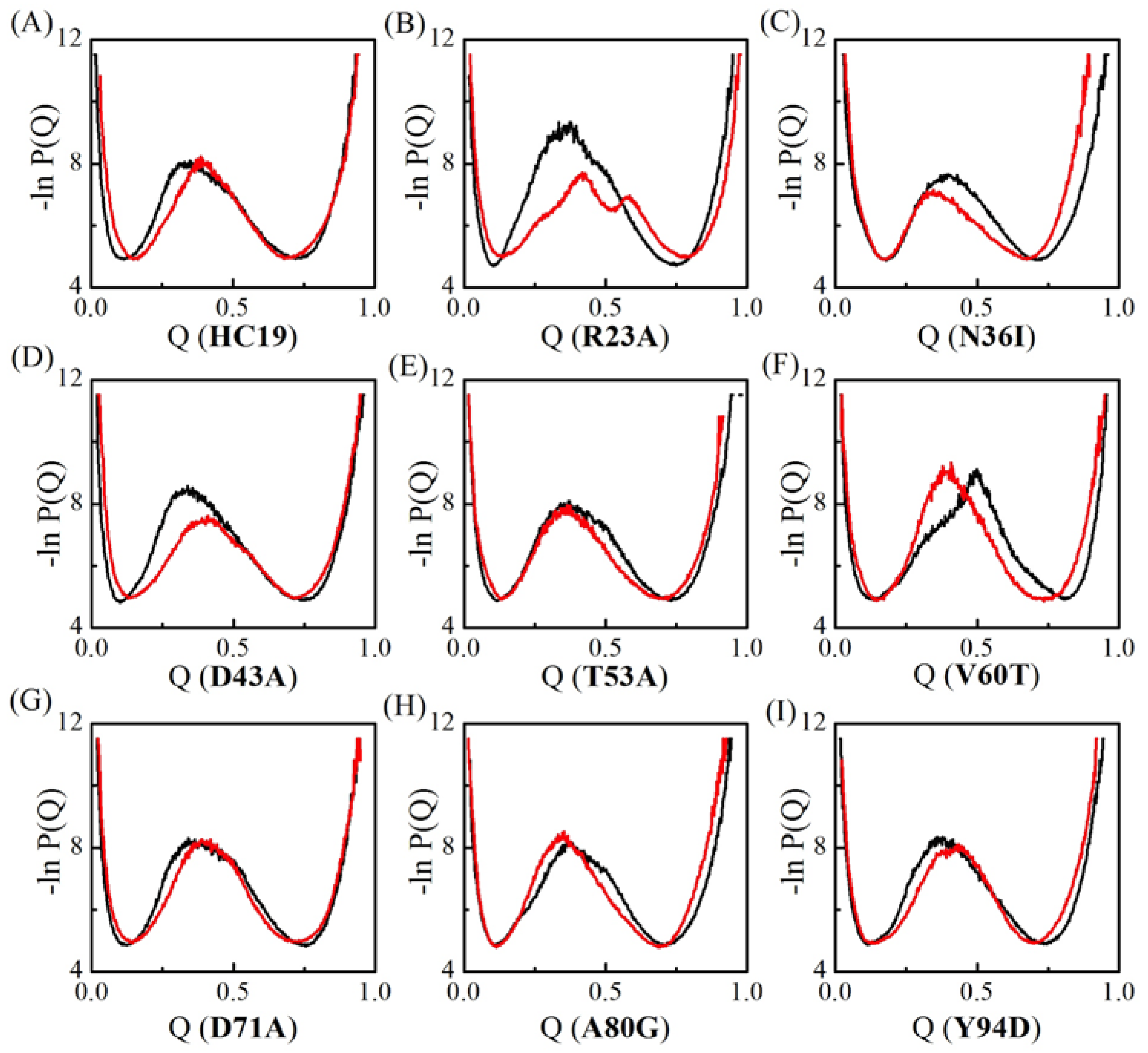
2.1. Transition State Ensembles of Ig-like β-Sandwich Folds are Sensitive To the Energetic Frustration Mutation Centers
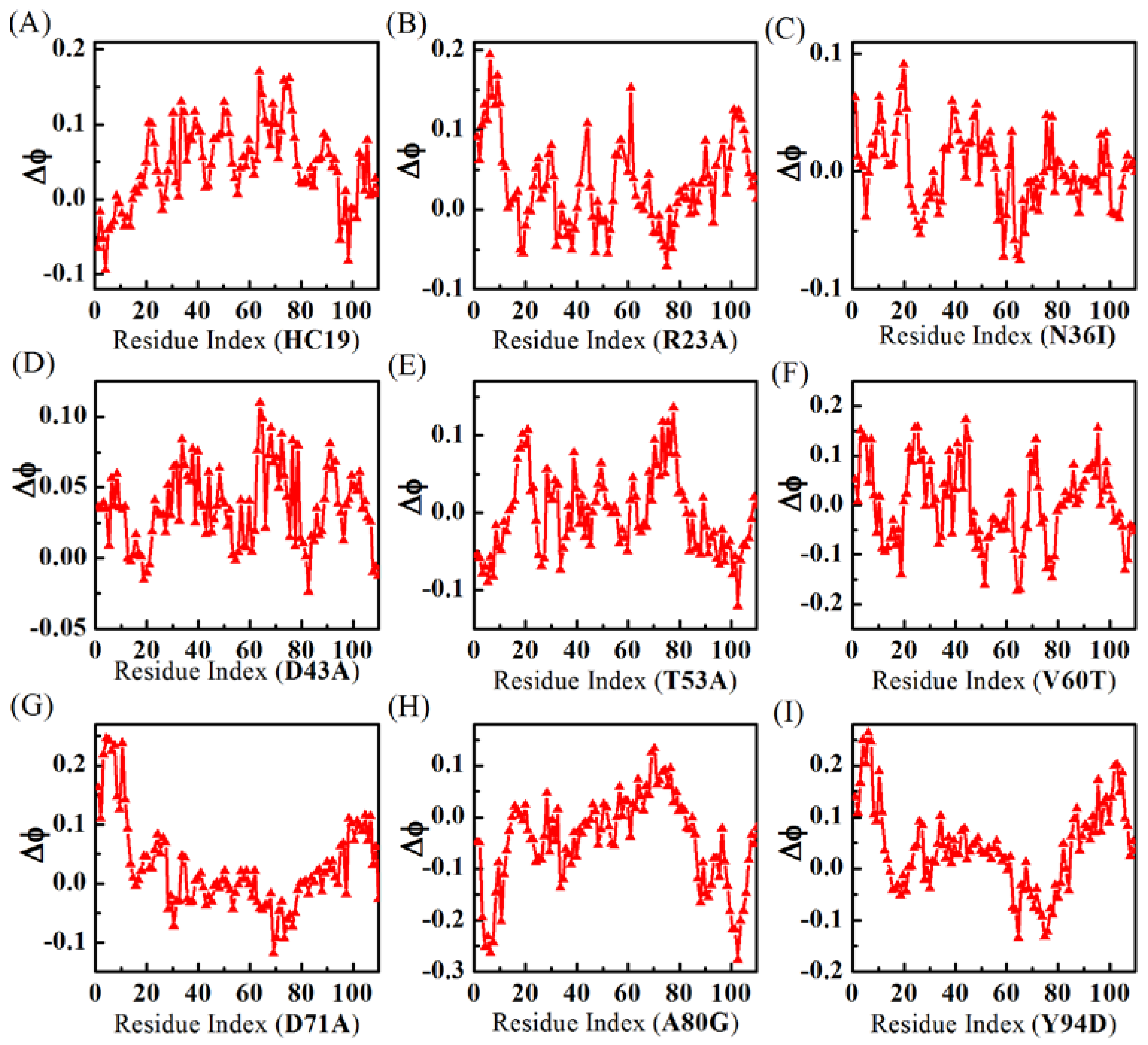
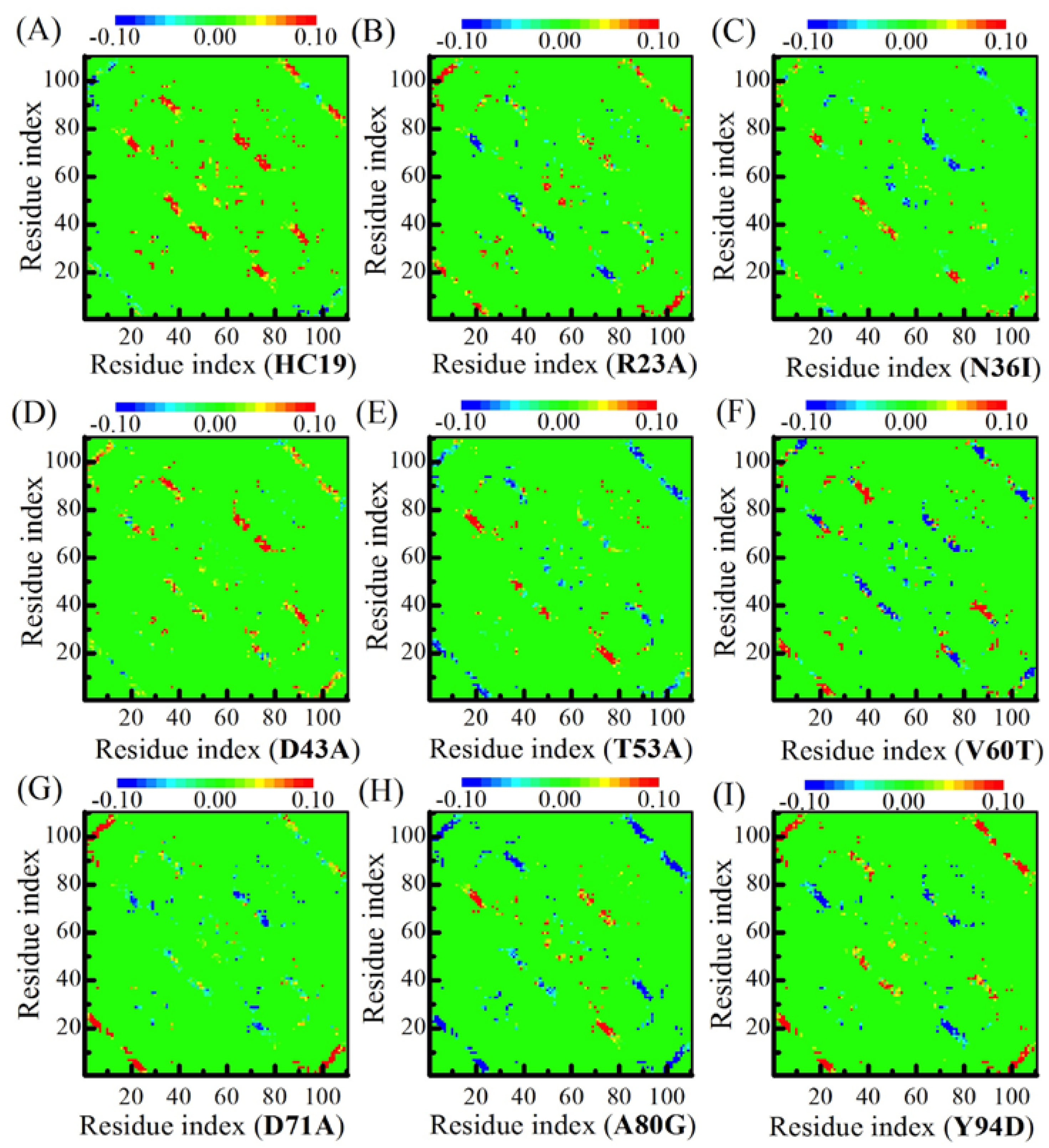
2.2. Energetic Frustrations Have Highly Heterogeneous Effects on the Folding of Ig-like β-Sandwich folds
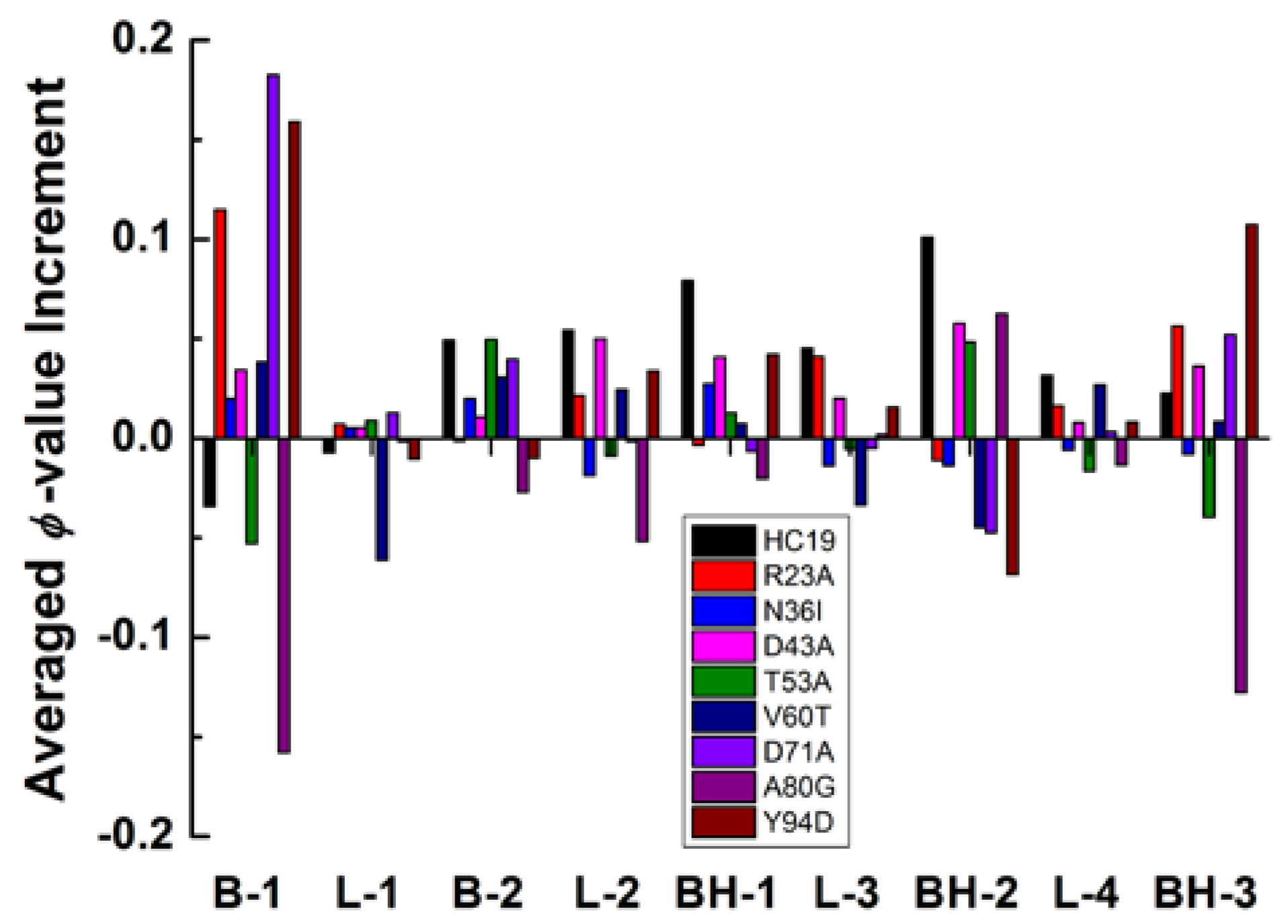
2.3. Energetic Frustration Alter the Folding Consistency Between the Folding Patches in β-Sandwich Structures
3. Methods
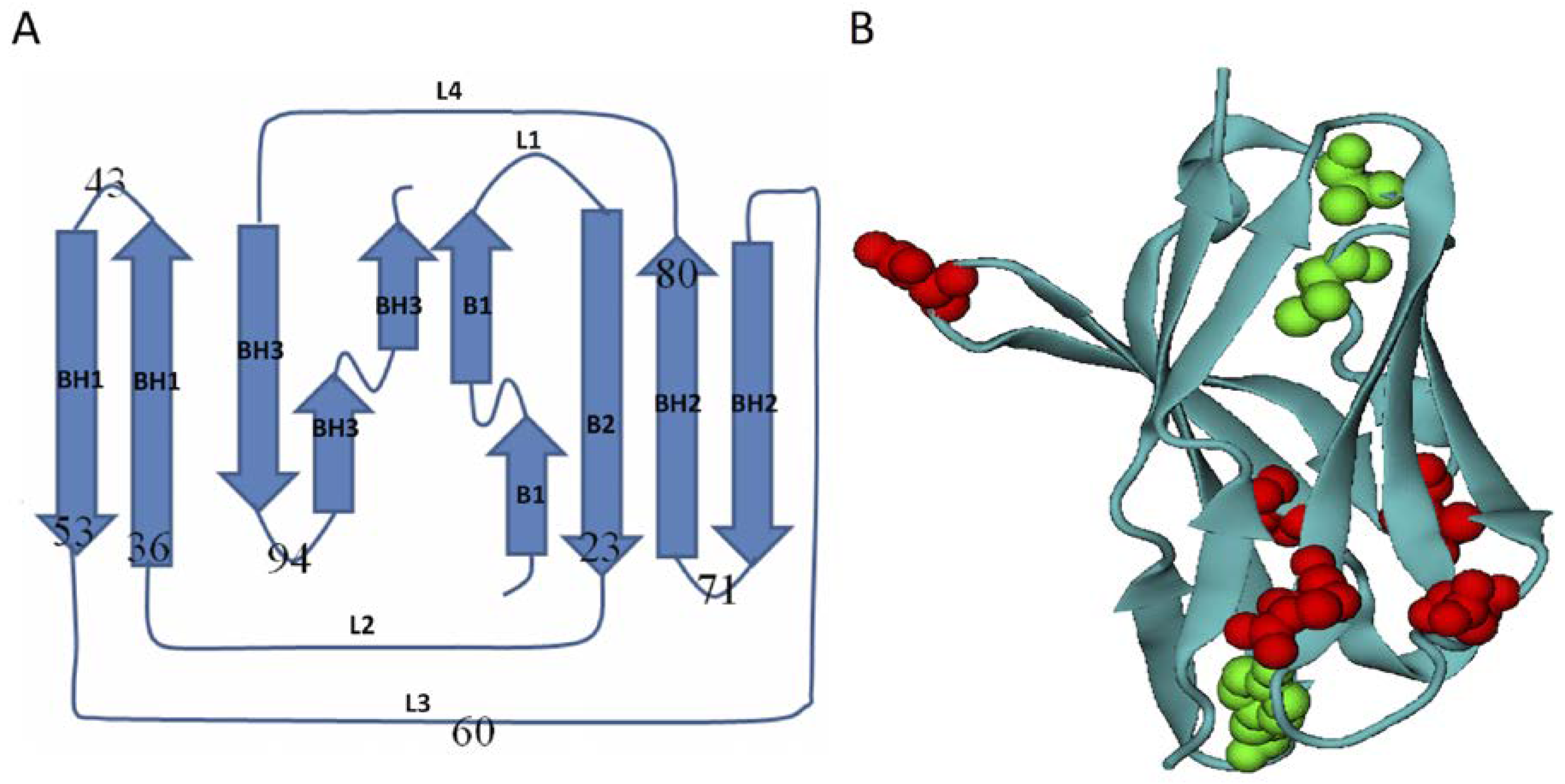
3.1. Homologous Domains of Immunoglobulin-Like β-Sandwich Structures
3.2. Energetic Frustration Model
3.3. The Variable Temperature Protein Folding Simulation
3.4. φ-Value Analysis and Contact Maps
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Dill, K.A.; MacCallum, J.L. The protein-folding problem, 50 years on. Science 2012, 338, 1042–1046. [Google Scholar] [CrossRef] [PubMed]
- Matouschek, A.; Kellis, J.T., Jr.; Serrano, L.; Fersht, A.R. Mapping the transition state and pathway of protein folding by protein engineering. Nature 1989, 340, 122–126. [Google Scholar] [CrossRef] [PubMed]
- Clementi, C.; Jennings, P.A.; Onuchic, J.N. How native-state topology affects the folding of dihydrofolate reductase and interleukin-1beta. Proc. Natl. Acad. Sci. USA 2000, 97, 5871–5876. [Google Scholar] [CrossRef] [PubMed]
- Vendruscolo, M.; Paci, E.; Dobson, C.M.; Karplus, M. Three key residues form a critical contact network in a protein folding transition state. Nature 2001, 409, 641–645. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Hummer, G.; Eaton, W.A. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17874–17879. [Google Scholar] [CrossRef] [PubMed]
- Taketomi, H.; Ueda, Y.; Go, N. Studies on protein folding, unfolding and fluctuations by computer simulation. I. The effect of specific amino acid sequence represented by specific inter-unit interactions. Int. J. Pept. Protein Res 1975, 7, 445–459. [Google Scholar] [CrossRef] [PubMed]
- Bryngelson, J.D.; Onuchic, J.N.; Socci, N.D.; Wolynes, P.G. Funnels, pathways, and the energy landscape of protein folding: A synthesis. Proteins 1995, 21, 167–195. [Google Scholar] [CrossRef] [PubMed]
- Bryngelson, J.D.; Wolynes, P.G. Spin glasses and the statistical mechanics of protein folding. Proc. Natl. Acad. Sci. USA 1987, 84, 7524–7528. [Google Scholar] [CrossRef] [PubMed]
- Go, N. Theoretical studies of protein folding. Annu. Rev. Biophys. Bioeng. 1983, 12, 183–210. [Google Scholar] [CrossRef] [PubMed]
- Leopold, P.E.; Montal, M.; Onuchic, J.N. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc. Natl. Acad. Sci. USA 1992, 89, 8721–8725. [Google Scholar] [CrossRef] [PubMed]
- Onuchic, J.N.; Luthey-Schulten, Z.; Wolynes, P.G. Theory of protein folding: The energy landscape perspective. Annu. Rev. Phys. Chem. 1997, 48, 545–600. [Google Scholar] [CrossRef] [PubMed]
- Onuchic, J.N.; Nymeyer, H.; Garcia, A.E.; Chahine, J.; Socci, N.D. The energy landscape theory of protein folding: Insights into folding mechanisms and scenarios. Adv. Protein Chem. 2000, 53, 87–152. [Google Scholar] [PubMed]
- Karplus, M. The Levinthal paradox: Yesterday and today. Fold Des. 1997, 2, S69–S75. [Google Scholar] [CrossRef]
- Durup, J. On “Levinthal paradox” and the theory of protein folding. Theochem-J. Mol. Struct. 1998, 424, 157–169. [Google Scholar] [CrossRef]
- Garcia-Manyes, S.; Dougan, L.; Badilla, C.L.; Brujic, J.; Fernandez, J.M. Direct observation of an ensemble of stable collapsed states in the mechanical folding of ubiquitin. Proc. Natl. Acad. Sci. USA 2009, 106, 10534–10539. [Google Scholar] [CrossRef] [PubMed]
- Olsson, U.; Wolf-Watz, M. Overlap between folding and functional energy landscapes for adenylate kinase conformational change. Nat. Commun. 2010, 1. [Google Scholar] [CrossRef] [PubMed]
- Whitford, P.C.; Onuchic, J.N. What protein folding teaches us about biological function and molecular machines. Curr. Opin. Struct. Biol. 2015, 30, 57–62. [Google Scholar] [CrossRef] [PubMed]
- Di Nardo, A.A.; Korzhnev, D.M.; Stogios, P.J.; Zarrine-Afsar, A.; Kay, L.E.; Davidson, A.R. Dramatic acceleration of protein folding by stabilization of a nonnative backbone conformation. Proc. Natl. Acad. Sci. USA 2004, 101, 7954–7959. [Google Scholar] [CrossRef] [PubMed]
- Brockwell, D.J.; Radford, S.E. Intermediates: Ubiquitous species on folding energy landscapes? Curr. Opin. Struct. Biol. 2007, 17, 30–37. [Google Scholar] [CrossRef] [PubMed]
- Religa, T.L.; Markson, J.S.; Mayor, U.; Freund, S.M.; Fersht, A.R. Solution structure of a protein denatured state and folding intermediate. Nature 2005, 437, 1053–1056. [Google Scholar] [CrossRef] [PubMed]
- Morton, V.L.; Friel, C.T.; Allen, L.R.; Paci, E.; Radford, S.E. The effect of increasing the stability of non-native interactions on the folding landscape of the bacterial immunity protein Im9. J. Mol. Biol. 2007, 371, 554–568. [Google Scholar] [CrossRef] [PubMed]
- Neudecker, P.; Zarrine-Afsar, A.; Choy, W.Y.; Muhandiram, D.R.; Davidson, A.R.; Kay, L.E. Identification of a collapsed intermediate with non-native long-range interactions on the folding pathway of a pair of Fyn SH3 domain mutants by NMR relaxation dispersion spectroscopy. J. Mol. Biol. 2006, 363, 958–976. [Google Scholar] [CrossRef] [PubMed]
- Viguera, A.R.; Vega, C.; Serrano, L. Unspecific hydrophobic stabilization of folding transition states. Proc. Natl. Acad. Sci. USA 2002, 99, 5349–5354. [Google Scholar] [CrossRef] [PubMed]
- Chung, H.S.; Piana-Agostinetti, S.; Shaw, D.E.; Eaton, W.A. Structural origin of slow diffusion in protein folding. Science 2015, 349, 1504–1510. [Google Scholar] [CrossRef] [PubMed]
- Wensley, B.G.; Batey, S.; Bone, F.A.; Chan, Z.M.; Tumelty, N.R.; Steward, A.; Kwa, L.G.; Borgia, A.; Clarke, J. Experimental evidence for a frustrated energy landscape in a three-helix-bundle protein family. Nature 2010, 463, 685–688. [Google Scholar] [CrossRef] [PubMed]
- Neudecker, P.; Robustelli, P.; Cavalli, A.; Walsh, P.; Lundstrom, P.; Zarrine-Afsar, A.; Sharpe, S.; Vendruscolo, M.; Kay, L.E. Structure of an intermediate state in protein folding and aggregation. Science 2012, 336, 362–366. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Mirny, L.A.; Shakhnovich, E.I. Kinetics, thermodynamics and evolution of non-native interactions in a protein folding nucleus. Nat. Struct. Biol. 2000, 7, 336–342. [Google Scholar] [PubMed]
- Clementi, C.; Plotkin, S.S. The effects of nonnative interactions on protein folding rates: Theory and simulation. Protein Sci. 2004, 13, 1750–1766. [Google Scholar] [CrossRef] [PubMed]
- Sosnick, T.R.; Mayne, L.; Hiller, R.; Englander, S.W. The Barriers in Protein-Folding. Nat. Struct. Biol. 1994, 1, 149–156. [Google Scholar] [CrossRef] [PubMed]
- Shea, J.E.; Onuchic, J.N.; Brooks, C.L., 3rd. Exploring the origins of topological frustration: Design of a minimally frustrated model of fragment B of protein A. Proc. Natl. Acad. Sci. USA 1999, 96, 12512–12517. [Google Scholar] [CrossRef] [PubMed]
- Sutto, L.; Latzer, J.; Hegler, J.A.; Ferreiro, D.U.; Wolynes, P.G. Consequences of localized frustration for the folding mechanism of the IM7 protein. Proc Natl. Acad. Sci. USA 2007, 104, 19825–19830. [Google Scholar] [CrossRef] [PubMed]
- Ferreiro, D.U.; Hegler, J.A.; Komives, E.A.; Wolynes, P.G. Localizing frustration in native proteins and protein assemblies. Proc. Natl. Acad. Sci. USA 2007, 104, 19819–19824. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Chan, H.S. Competition between native topology and nonnative interactions in simple and complex folding kinetics of natural and designed proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 2920–2925. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, R.J.; Whitford, P.C.; Chahine, J.; Wang, J.; Onuchic, J.N.; Leite, V.B. The origin of nonmonotonic complex behavior and the effects of nonnative interactions on the diffusive properties of protein folding. Biophys. J. 2010, 99, 600–608. [Google Scholar] [CrossRef] [PubMed]
- Zarrine-Afsar, A.; Wallin, S.; Neculai, A.M.; Neudecker, P.; Howell, P.L.; Davidson, A.R.; Chan, H.S. Theoretical and experimental demonstration of the importance of specific nonnative interactions in protein folding. Proc. Natl. Acad. Sci. USA 2008, 105, 9999–10004. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Chan, H.S. Native contact density and nonnative hydrophobic effects in the folding of bacterial immunity proteins. PLoS Comput. Biol. 2015, 11, e1004260. [Google Scholar] [CrossRef] [PubMed]
- Truong, H.H.; Kim, B.L.; Schafer, N.P.; Wolynes, P.G. Funneling and frustration in the energy landscapes of some designed and simplified proteins. J. Chem. Phys. 2013, 139, 121908. [Google Scholar] [CrossRef] [PubMed]
- Faisca, P.F.; Nunes, A.; Travasso, R.D.; Shakhnovich, E.I. Non-native interactions play an effective role in protein folding dynamics. Protein Sci. 2010, 19, 2196–2209. [Google Scholar] [CrossRef] [PubMed]
- Enciso, M.; Rey, A. Improvement of structure-based potentials for protein folding by native and nonnative hydrogen bonds. Biophys. J. 2011, 101, 1474–1482. [Google Scholar] [CrossRef] [PubMed]
- Thirumalai, D.; Klimov, D.K. Deciphering the timescales and mechanisms of protein folding using minimal off-lattice models. Curr. Opin. Struct. Biol. 1999, 9, 197–207. [Google Scholar] [CrossRef]
- Nelson, E.D.; Teneyck, F.; Onuchic, J.N. Symmetry and kinetic optimization of proteinlike heteropolymers. Phys. Rev. Lett. 1997, 79, 3534–3537. [Google Scholar] [CrossRef]
- Onuchic, J.N.; Socci, N.D.; Luthey-Schulten, Z.; Wolynes, P.G. Protein folding funnels: The nature of the transition state ensemble. Fold Des. 1996, 1, 441–450. [Google Scholar] [CrossRef]
- Shea, J.E.; Onuchic, J.N.; Brooks, C.L. Energetic frustration and the nature of the transition state in protein folding. J. Chem. Phys. 2000, 113, 7663–7671. [Google Scholar] [CrossRef]
- Sun, Y.; Yin, S.; Feng, Y.; Li, J.; Zhou, J.; Liu, C.; Zhu, G.; Guo, Z. Molecular basis of the general base catalysis of an alpha/beta-hydrolase catalytic triad. J. Biol. Chem. 2014, 289, 15867–15879. [Google Scholar] [CrossRef] [PubMed]
- Murzin, A.G.; Brenner, S.E.; Hubbard, T.; Chothia, C. SCOP: A structural classification of proteins database for the investigation of sequences and structures. J. Mol. Biol. 1995, 247, 536–540. [Google Scholar] [CrossRef]
- Cho, S.S.; Levy, Y.; Wolynes, P.G. Quantitative criteria for native energetic heterogeneity influences in the prediction of protein folding kinetics. Proc. Natl. Acad Sci. USA 2009, 106, 434–439. [Google Scholar] [CrossRef] [PubMed]
- Fersht, A.R.; Itzhaki, L.S.; elMasry, N.F.; Matthews, J.M.; Otzen, D.E. Single versus parallel pathways of protein folding and fractional formation of structure in the transition state. Proc. Natl. Acad. Sci. USA 1994, 91, 10426–10429. [Google Scholar] [CrossRef] [PubMed]
- Zarrine-Afsar, A.; Larson, S.M.; Davidson, A.R. The family feud: Do proteins with similar structures fold via the same pathway? Curr. Opin. Struct. Biol. 2005, 15, 42–49. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Sun, Y.; Ming, D. Energetic frustrations in protein folding at residue resolution: A homologous simulation study of Im9 proteins. PLoS ONE 2014, 9, e87719. [Google Scholar] [CrossRef] [PubMed]
- Fowler, S.B.; Clarke, J. Mapping the folding pathway of an immunoglobulin domain: Structural detail from Phi value analysis and movement of the transition state. Structure 2001, 9, 355–366. [Google Scholar] [CrossRef]
- Nickson, A.A.; Clarke, J. What lessons can be learned from studying the folding of homologous proteins? Methods 2010, 52, 38–50. [Google Scholar] [CrossRef] [PubMed]
- Clarke, J.; Cota, E.; Fowler, S.B.; Hamill, S.J. Folding studies of immunoglobulin-like beta-sandwich proteins suggest that they share a common folding pathway. Structure 1999, 7, 1145–1153. [Google Scholar] [CrossRef]
- Han, J.H.; Batey, S.; Nickson, A.A.; Teichmann, S.A.; Clarke, J. The folding and evolution of multidomain proteins. Nat. Rev. Mol. Cell Biol. 2007, 8, 319–330. [Google Scholar] [CrossRef] [PubMed]
- Lappalainen, I.; Hurley, M.G.; Clarke, J. Plasticity within the obligatory folding nucleus of an immunoglobulin-like domain. J. Mol. Biol. 2008, 375, 547–559. [Google Scholar] [CrossRef] [PubMed]
- Andreeva, A.; Howorth, D.; Chandonia, J.M.; Brenner, S.E.; Hubbard, T.J.; Chothia, C.; Murzin, A.G. Data growth and its impact on the SCOP database: New developments. Nucleic Acids Res. 2008, 36, D419–D425. [Google Scholar] [CrossRef] [PubMed]
- Karanicolas, J.; Brooks, C.L., 3rd. The origins of asymmetry in the folding transition states of protein L and protein G. Protein Sci. 2002, 11, 2351–2361. [Google Scholar] [CrossRef] [PubMed]
- Baumketner, A.; Hiwatari, Y. Diffusive dynamics of protein folding studied by molecular dynamics simulations of an off-lattice model. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2002, 66, 011905. [Google Scholar] [CrossRef] [PubMed]
- Ming, D.; Anghel, M.; Wall, M.E. Hidden structure in protein energy landscapes. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2008, 77, 021902. [Google Scholar] [CrossRef] [PubMed]
- Nakagawa, N.; Peyrard, M. The inherent structure landscape of a protein. Proc. Natl. Acad. Sci. USA 2006, 103, 5279–5284. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; Keyes, T. Influence of Go-like interactions on global shapes of energy landscapes in beta-barrel forming model proteins: Inherent structure analysis and statistical temperature molecular dynamics simulation. J. Phys. Chem. B 2008, 112, 954–966. [Google Scholar] [CrossRef] [PubMed]
- Karanicolas, J.; Brooks, C.L., 3rd. Improved Go-like models demonstrate the robustness of protein folding mechanisms towards non-native interactions. J. Mol. Biol. 2003, 334, 309–325. [Google Scholar] [CrossRef] [PubMed]
- Miyazawa, S.; Jernigan, R.L. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 1985, 18, 534–552. [Google Scholar] [CrossRef]
- Miyazawa, S.; Jernigan, R.L. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J. Mol. Biol. 1996, 256, 623–644. [Google Scholar] [CrossRef] [PubMed]
- Hills, R.D., Jr.; Brooks, C.L., 3rd. Insights from coarse-grained go models for protein folding and dynamics. Int. J. Mol. Sci. 2009, 10, 889–905. [Google Scholar] [CrossRef] [PubMed]
- Estacio, S.G.; Krobath, H.; Vila-Vicosa, D.; Machuqueiro, M.; Shakhnovich, E.I.; Faisca, P.F. A simulated intermediate state for folding and aggregation provides insights into DeltaN6 beta2-microglobulin amyloidogenic behavior. PLoS Comput. Biol. 2014, 10, e1003606. [Google Scholar] [CrossRef] [PubMed]
- Krobath, H.; Estacio, S.G.; Faisca, P.F.; Shakhnovich, E.I. Identification of a conserved aggregation-prone intermediate state in the folding pathways of Spc-SH3 amyloidogenic variants. J. Mol. Biol. 2012, 422, 705–722. [Google Scholar] [CrossRef] [PubMed]
- Krobath, H.; Rey, A.; Faisca, P.F. How determinant is N-terminal to C-terminal coupling for protein folding? Phys. Chem. Chem. Phys. 2015, 17, 3512–3524. [Google Scholar] [CrossRef] [PubMed]
- Krobath, H.; Shakhnovich, E.I.; Faisca, P.F. Structural and energetic determinants of co-translational folding. J. Chem. Phys. 2013, 138, 215101. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Daggett, V. Characterization of the transition state of protein unfolding by use of molecular dynamics: Chymotrypsin inhibitor 2. Proc. Natl. Acad. Sci. USA 1994, 91, 10430–10434. [Google Scholar] [CrossRef] [PubMed]
- Fersht, A.R. Characterizing transition states in protein folding: An essential step in the puzzle. Curr. Opin. Struct. Biol. 1995, 5, 79–84. [Google Scholar] [CrossRef]
- Thirumalai, D.; Klimov, D.K. Intermediates and transition states in protein folding. Methods Mol. Biol. 2007, 350, 277–303. [Google Scholar] [PubMed]
- Nymeyer, H.; Socci, N.D.; Onuchic, J.N. Landscape approaches for determining the ensemble of folding transition states: Success and failure hinge on the degree of frustration. Proc. Natl. Acad. Sci. USA 2000, 97, 634–639. [Google Scholar] [CrossRef] [PubMed]
- Dinner, A.R.; Sali, A.; Smith, L.J.; Dobson, C.M.; Karplus, M. Understanding protein folding via free-energy surfaces from theory and experiment. Trends Biochem. Sci. 2000, 25, 331–339. [Google Scholar] [CrossRef]
- Paci, E.; Friel, C.T.; Lindorff-Larsen, K.; Radford, S.E.; Karplus, M.; Vendruscolo, M. Comparison of the transition state ensembles for folding of Im7 and Im9 determined using all-atom molecular dynamics simulations with phi value restraints. Proteins 2004, 54, 513–525. [Google Scholar] [CrossRef] [PubMed]
- Vendruscolo, M.; Najmanovich, R.; Domany, E. Protein folding in contact map space. Phys. Rev. Lett. 1999, 82, 656–659. [Google Scholar] [CrossRef]
- Park, K.; Vendruscolo, M.; Domany, E. Toward an energy function for the contact map representation of proteins. Proteins-Struct. Funct. Genet. 2000, 40, 237–248. [Google Scholar] [CrossRef]
- Shao, Y.; Bystroff, C. Predicting interresidue contacts using templates and pathways. Proteins-Struct. Funct. Genet. 2003, 53, 497–502. [Google Scholar] [CrossRef] [PubMed]
- Wolek, K.; Gomez-Sicilia, A.; Cieplak, M. Determination of contact maps in proteins: A combination of structural and chemical approaches. J. Chem. Phys. 2015, 143, 243105. [Google Scholar] [CrossRef] [PubMed]

| Protein | HC19 | R23A | N36I | A80G | Y94D |
|---|---|---|---|---|---|
| HC19 | 0 | ||||
| R23A | 0.62/0.51 | 0 | |||
| N36I | 0.53/0.47 | 0.58/0.48 | 0 | ||
| A80G | 0.57/0.52 | 0.61/0.54 | 0.53/0.49 | 0 | |
| Y94D | 0.76/0.79 | 0.77/0.73 | 0.65/0.62 | 0.69/0.64 | 0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Y.; Ding, F.; Ming, D. Nonnative Energetic Frustrations in Protein Folding at Residual Level: A Simulation Study of Homologous Immunoglobulin-like β-Sandwich Proteins. Int. J. Mol. Sci. 2018, 19, 1515. https://doi.org/10.3390/ijms19051515
Sun Y, Ding F, Ming D. Nonnative Energetic Frustrations in Protein Folding at Residual Level: A Simulation Study of Homologous Immunoglobulin-like β-Sandwich Proteins. International Journal of Molecular Sciences. 2018; 19(5):1515. https://doi.org/10.3390/ijms19051515
Chicago/Turabian StyleSun, Yunxiang, Feng Ding, and Dengming Ming. 2018. "Nonnative Energetic Frustrations in Protein Folding at Residual Level: A Simulation Study of Homologous Immunoglobulin-like β-Sandwich Proteins" International Journal of Molecular Sciences 19, no. 5: 1515. https://doi.org/10.3390/ijms19051515
APA StyleSun, Y., Ding, F., & Ming, D. (2018). Nonnative Energetic Frustrations in Protein Folding at Residual Level: A Simulation Study of Homologous Immunoglobulin-like β-Sandwich Proteins. International Journal of Molecular Sciences, 19(5), 1515. https://doi.org/10.3390/ijms19051515





