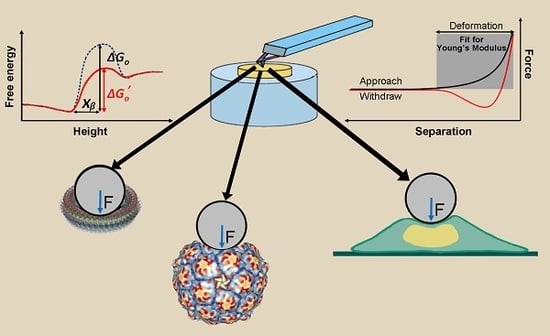
Compressive Force Spectroscopy: From Living Cells to Single Proteins
Abstract
1. Introduction
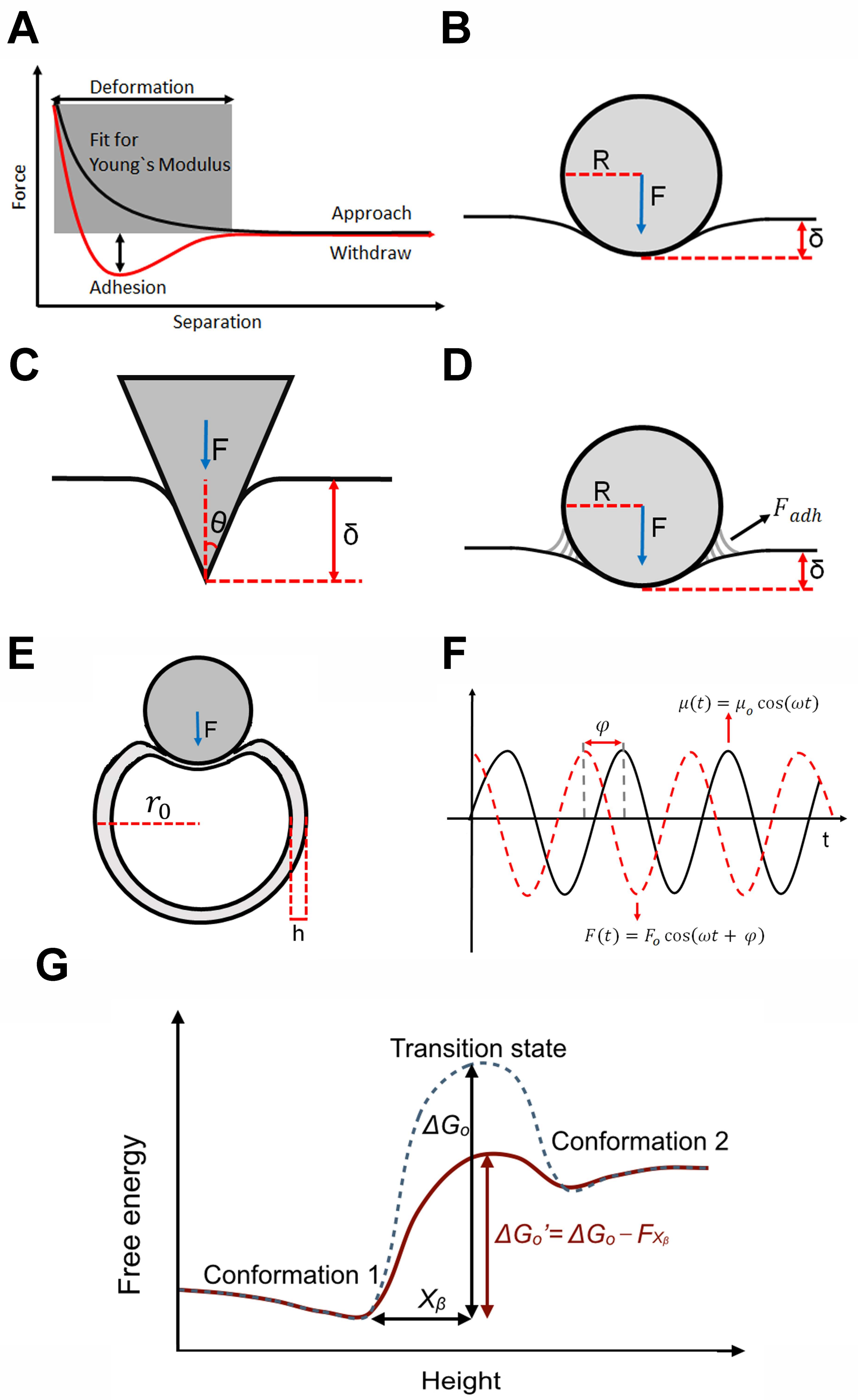
2. Theoretical Considerations
2.1. Elastic Theory for Macroscopic Biological Structures: Cells
2.2. Elastic Theory for Macroscopic Biological Structures: Viruses
2.3. Viscoelastic Theory for Macroscopic Biological Structures
2.4. Theoretical Treatment for Single Molecule Transitions: Rate Theory
3. CFS of Cells: Elucidation of the Mechano-Phenotype
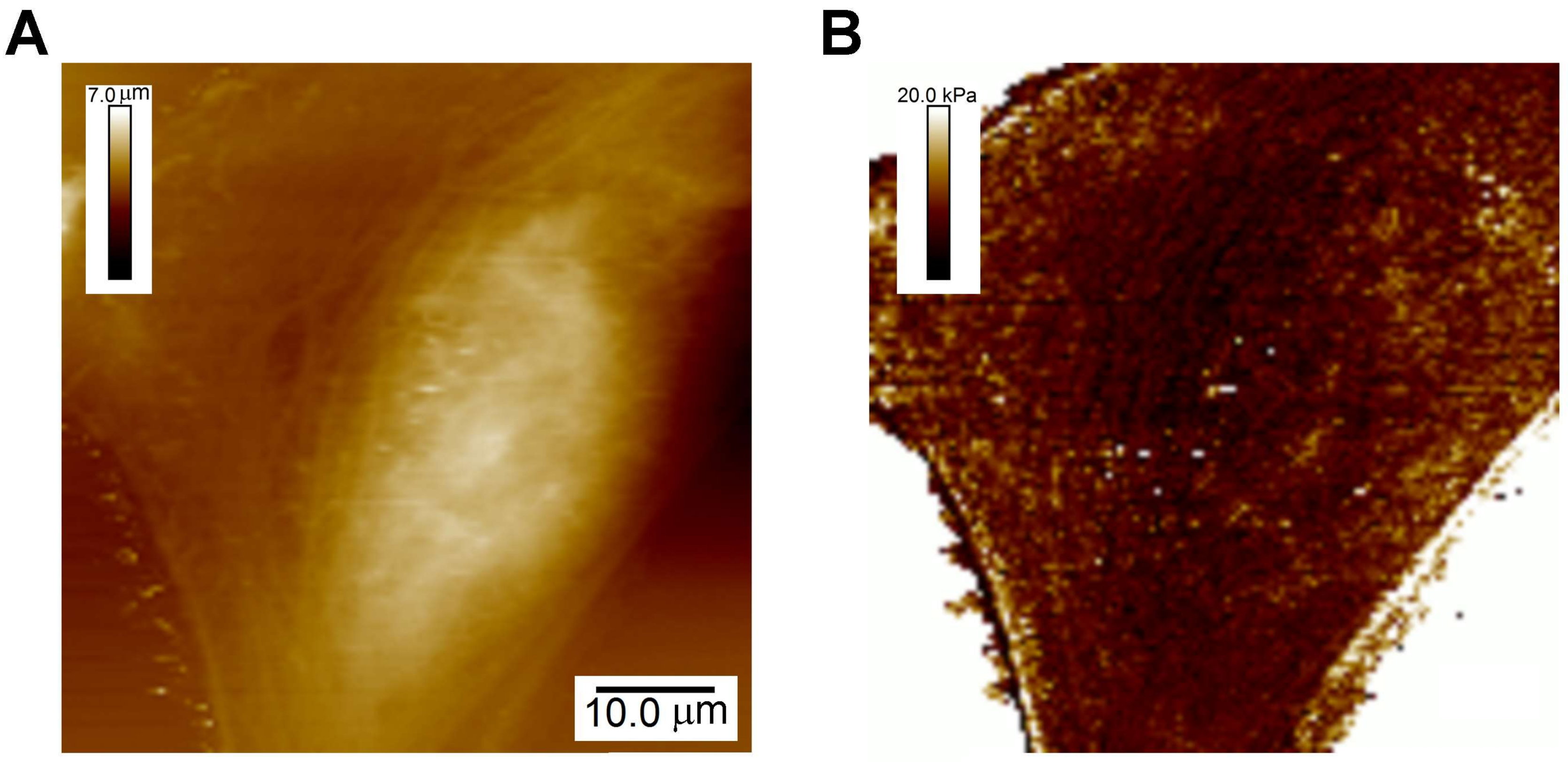
3.1. Elastic Moduli of Cells: A General Characteristic of Cell Function
3.1.1. Elastic Moduli of Different Cell Types
3.1.2. Elastic Moduli of Different Cell States
3.1.3. Use of Cell Elasticity Measurements in Cancer Diagnosis
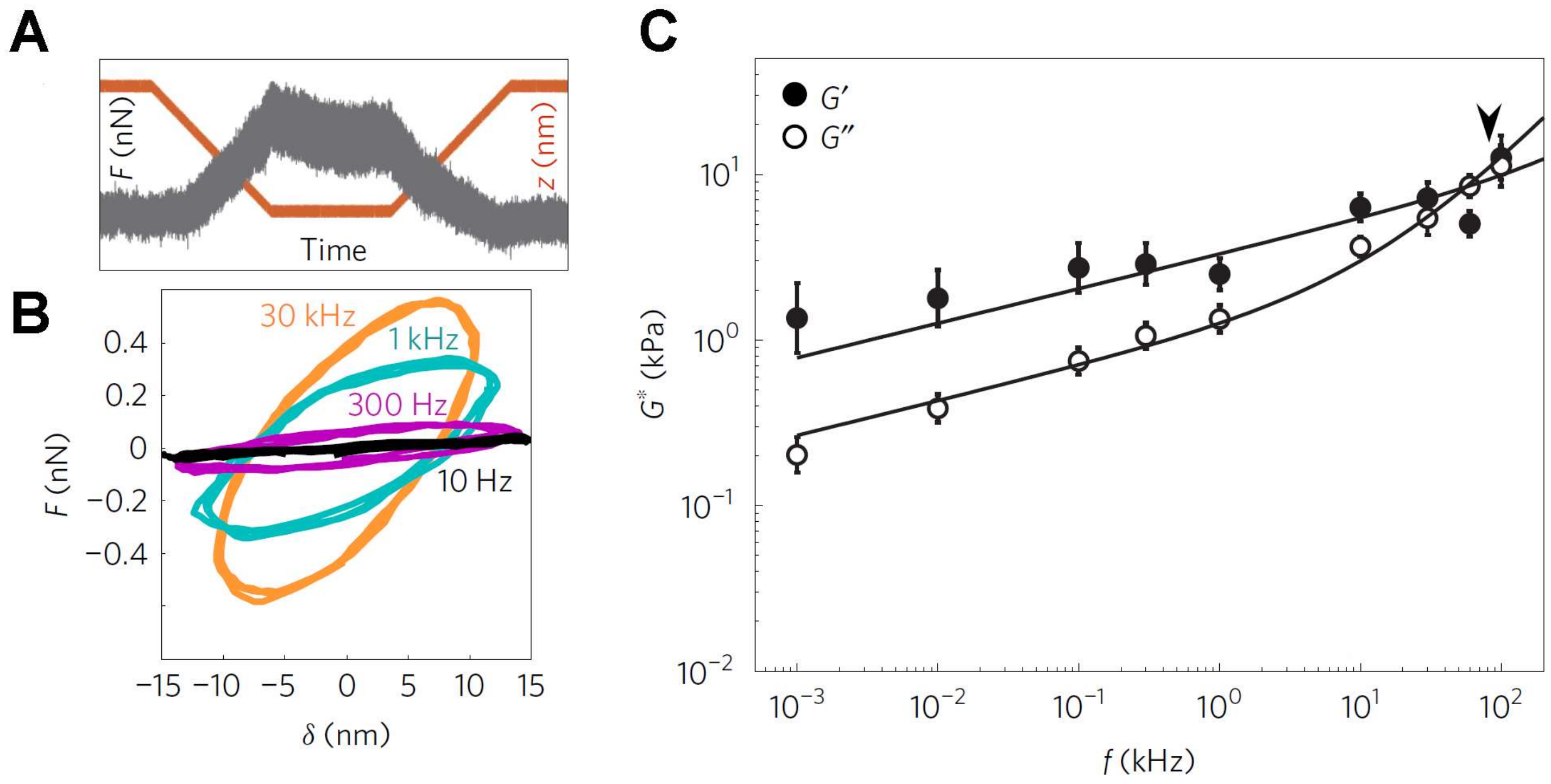
3.2. Measurements of Viscoelastic Properties of Cells
4. CFS Measurements of Sub-Cellular Structures
Measurements of Elastic Properties of Viruses
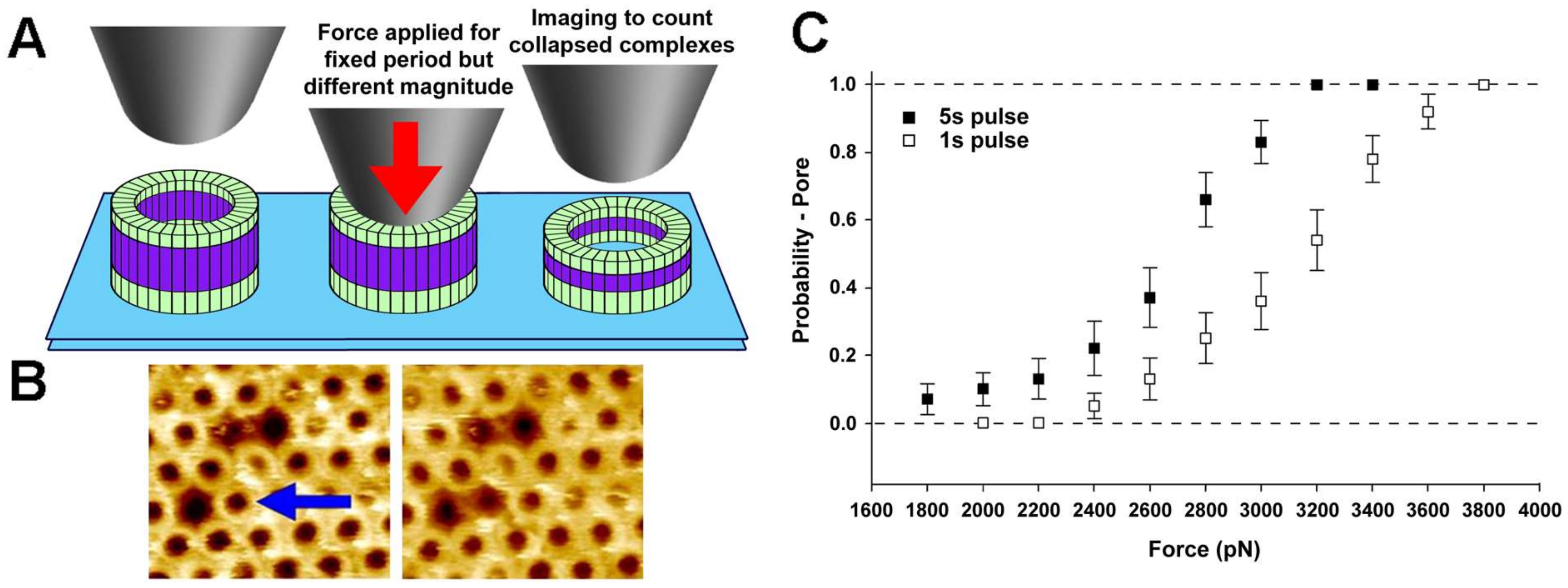
5. CFS of Single Proteins
6. Future Perspectives
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AFM | Atomic force microscopy |
| TFS | Tensile force spectroscopy |
| CFS | Compressive force spectroscopy |
| DMT | Derjaguin–Muller–Toporov |
References
- Shao, Z.; Mou, J.; Czajkowsky, D.M.; Yang, J.; Yuan, J.-Y. Biological atomic force microscopy: What is achieved and what is needed. Adv. Phys. 1996, 45, 1–86. [Google Scholar] [CrossRef]
- Czajkowsky, D.M.; Shao, Z. Submolecular resolution of single macromolecules with atomic force microscopy. FEBS Lett. 1998, 430, 51–54. [Google Scholar] [CrossRef]
- Mou, J.; Yang, J.; Shao, Z. An optical detection low temperature atomic force microscope at ambient pressure for biological research. Rev. Sci. Instrum. 1993, 64, 1483–1488. [Google Scholar] [CrossRef]
- Scheuring, S.; Sturgis, J.N. Chromatic adaptation of photosynthetic membranes. Science 2005, 309, 484–487. [Google Scholar] [CrossRef] [PubMed]
- Bippes, C.A.; Muller, D.J. High-resolution atomic force microscopy and spectroscopy of native membrane proteins. Rep. Prog. Phys. 2011, 74, 86601–86643. [Google Scholar] [CrossRef]
- Czajkowsky, D.M.; Sheng, S.; Shao, Z. Staphylococcal α-hemolysin can form hexamers in phospholipid bilayers. J. Mol. Biol. 1998, 276, 325–330. [Google Scholar] [CrossRef] [PubMed]
- Czajkowsky, D.M.; Hotze, E.M.; Shao, Z.; Tweten, R.K. Vertical collapse of a cytolysin prepore moves its transmembrane beta-hairpins to the membrane. EMBO J. 2004, 23, 3206–3215. [Google Scholar] [CrossRef] [PubMed]
- Leung, C.; Dudkina, N.V.; Lukoyanova, N.; Hodel, A.W.; Farabella, I.; Pandurangan, A.P.; Jahan, N.; Pires Damaso, M.; Osmanovic, D.; Reboul, C.F.; et al. Stepwise visualization of membrane pore formation by suilysin, a bacterial cholesterol-dependent cytolysin. eLife 2014, 3, e04247. [Google Scholar] [CrossRef] [PubMed]
- Czajkowsky, D.M.; Iwamoto, H.; Cover, T.L.; Shao, Z. The vacuolating toxin from helicobacter pylori forms hexameric pores in lipid bilayers at low ph. Proc. Natl. Acad. Sci. USA 1999, 96, 2001. [Google Scholar] [CrossRef] [PubMed]
- Chiaruttini, N.; Redondo-Morata, L.; Colom, A.; Humbert, F.; Lenz, M.; Scheuring, S.; Roux, A. Relaxation of loaded escrt-iii spiral springs drives membrane deformation. Cell 2015, 163, 866–879. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Y.; Cherny, D.I.; Heim, G.; Jovin, T.M.; Schäffer, T.E. Dynamic interactions of p53 with DNA in solution by time-lapse atomic force microscopy. J. Mol. Biol. 2001, 314, 233–243. [Google Scholar] [CrossRef] [PubMed]
- Kasas, S.; Dietler, G. DNA-protein interactions explored by atomic force microscopy. Semin. Cell Dev. Biol. 2018, 73, 231–239. [Google Scholar] [CrossRef] [PubMed]
- Billingsley, D.J.; Bonass, W.A.; Crampton, N.; Kirkham, J.; Thomson, N.H. Single-molecule studies of DNA transcription using atomic force microscopy. Phys. Biol. 2012, 9, 021001. [Google Scholar] [CrossRef] [PubMed]
- Czajkowsky, D.M.; Shao, Z. The human igm pentamer is a mushroom-shaped molecule with a flexural bias. Proc. Natl. Acad. Sci. USA 2009, 106, 14960–14965. [Google Scholar] [CrossRef] [PubMed]
- Dufrêne, Y.F.; Ando, T.; Garcia, R.; Alsteens, D.; Martinez-Martin, D.; Engel, A.; Gerber, C.; Müller, D.J. Imaging modes of atomic force microscopy for application in molecular and cell biology. Nat. Nanotechnol. 2017, 12, 295. [Google Scholar] [CrossRef] [PubMed]
- Ando, T.; Kodera, N.; Takai, E.; Maruyama, D.; Saito, K.; Toda, A. A high-speed atomic force microscope for studying biological macromolecules. Proc. Natl. Acad. Sci. USA 2001, 98, 12468–12472. [Google Scholar] [CrossRef] [PubMed]
- Fantner, G.E.; Schitter, G.; Kindt, J.H.; Ivanov, T.; Ivanova, K.; Patel, R.; Holten-Andersen, N.; Adams, J.; Thurner, P.J.; Rangelow, I.W.; et al. Components for high speed atomic force microscopy. Ultramicroscopy 2006, 106, 881–887. [Google Scholar] [CrossRef] [PubMed]
- Kodera, N.; Yamamoto, D.; Ishikawa, R.; Ando, T. Video imaging of walking myosin v by high-speed atomic force microscopy. Nature 2010, 468, 72. [Google Scholar] [CrossRef] [PubMed]
- Casuso, I.; Khao, J.; Chami, M.; Paul-Gilloteaux, P.; Husain, M.; Duneau, J.-P.; Stahlberg, H.; Sturgis, J.N.; Scheuring, S. Characterization of the motion of membrane proteins using high-speed atomic force microscopy. Nat. Nanotechnol. 2012, 7, 525. [Google Scholar] [CrossRef] [PubMed]
- Igarashi, K.; Uchihashi, T.; Koivula, A.; Wada, M.; Kimura, S.; Okamoto, T.; Penttilä, M.; Ando, T.; Samejima, M. Traffic jams reduce hydrolytic efficiency of cellulase on cellulose surface. Science 2011, 333, 1279–1282. [Google Scholar] [CrossRef] [PubMed]
- Ruan, G.X.; Zhang, D.Q.; Zhou, T.; Yamazaki, S.; Mcmahon, D.G. Circadian organization of the mammalian retina. Proc. Natl. Acad. Sci. USA 2006, 103, 9703–9708. [Google Scholar] [CrossRef] [PubMed]
- Uchihashi, T.; Iino, R.; Ando, T.; Noji, H. High-speed atomic force microscopy reveals rotary catalysis of rotorless f1-atpase. Science 2011, 333, 755–758. [Google Scholar] [CrossRef] [PubMed]
- Roca-cusachs, P.; Conte, V.; Trepat, X. Quantifying forces in cell biology. Nat. Cell Biol. 2017, 19, 742. [Google Scholar] [CrossRef] [PubMed]
- Hinterdorfer, P.; Baumgartner, W.; Gruber, H.J.; Schilcher, K.; Schindler, H. Detection and localization of individual antibody-antigen recognition events by atomic force microscopy. Proc. Natl. Acad. Sci. USA 1996, 93, 3477. [Google Scholar] [CrossRef] [PubMed]
- Pfreundschuh, M.; Alsteens, D.; Wieneke, R.; Zhang, C.; Coughlin, S.R.; Tampé, R.; Kobilka, B.K.; Müller, D.J. Identifying and quantifying two ligand-binding sites while imaging native human membrane receptors by afm. Nat. Commun. 2015, 6, 8857. [Google Scholar] [CrossRef] [PubMed]
- Kedrov, A.; Janovjak, H.; Sapra, K.T.; Muller, D.J. Deciphering molecular interactions of native membrane proteins by single-molecule force spectroscopy. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 233. [Google Scholar] [CrossRef] [PubMed]
- Dudko, O.K.; Hummer, G.; Szabo, A. Theory, analysis, and interpretation of single-molecule force spectroscopy experiments. Proc. Natl. Acad. Sci. USA 2008, 105, 15755. [Google Scholar] [CrossRef] [PubMed]
- Hummer, G.; Szabo, A. Free energy reconstruction from nonequilibrium single-molecule pulling experiments. Proc. Natl. Acad. Sci. USA 2001, 98, 3658–3661. [Google Scholar] [CrossRef] [PubMed]
- Marszalek, P.E.; Lu, H.; Li, H.; Carrion-Vazquez, M.; Oberhauser, A.F.; Schulten, K.; Fernandez, J.M. Mechanical unfolding intermediates in titin modules. Nature 1999, 402, 100. [Google Scholar] [CrossRef] [PubMed]
- Rief, M.; Gautel, M.; Oesterhelt, F.; Fernandez, J.M.; Gaub, H.E. Reversible unfolding of individual titin immunoglobulin domains by afm. Science 1997, 276, 1109–1112. [Google Scholar] [CrossRef] [PubMed]
- Kellermayer, M.S.Z.; Bustamante, C. Folding-unfolding transitions in single titin molecules characterized with laser tweezers. Science 1997, 276, 1112. [Google Scholar] [CrossRef] [PubMed]
- Tskhovrebova, L.; Trinick, J.; Sleep, J.A.; Simmons, R.M. Elasticity and unfolding of single molecules of the giant muscle protein titin. Nature 1997, 387, 308–312. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.; Finzi, L.; Bustamante, C. Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads. Science 1992, 258, 1122–1126. [Google Scholar] [CrossRef] [PubMed]
- Strick, T.R.; Allemand, J.-F.; Bensimon, D.; Bensimon, A.; Croquette, V. The elasticity of a single supercoiled DNA molecule. Science 1996, 271, 1835–1837. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Smith, S.B.; Liphardt, J.; Smith, D. Single-molecule studies of DNA mechanics. Curr. Opin. Struct. Biol. 2000, 10, 279–285. [Google Scholar] [CrossRef]
- Yu, H.; Siewny, M.; Edwards, D.; Perkins, T. Hidden dynamics in the unfolding of individual bacteriorhodopsins. Science 2017, 355, 945. [Google Scholar] [CrossRef] [PubMed]
- Radmacher, M.; Tillamnn, R.W.; Fritz, M.; Gaub, H.E. From molecules to cells: Imaging soft samples with the atomic force microscope. Science 1992, 257, 1900–1905. [Google Scholar] [CrossRef] [PubMed]
- Drake, B.; Prater, C.; Weisenhorn, A.; Gould, S.; Albrecht, T.; Quate, C.; Cannell, D.; Hansma, H.; Hansma, P. Imaging crystals, polymers, and processes in water with the atomic force microscope. Science 1989, 243, 1586–1589. [Google Scholar] [CrossRef] [PubMed]
- Weisenhorn, A.L.; Khorsandi, M.; Kasas, S.; Gotzos, V.; Butt, H.J. Deformation and height anomaly of soft surfaces studied with an afm. Nanotechnology 1993, 4, 106. [Google Scholar] [CrossRef]
- Touhami, A.; Nysten, B.; Dufrêne, Y.F. Nanoscale mapping of the elasticity of microbial cells by atomic force microscopy. Langmuir 2003, 19, 4539–4543. [Google Scholar] [CrossRef]
- Kuznetsova, T.G.; Starodubtseva, M.N.; Yegorenkov, N.I.; Chizhik, S.A.; Zhdanov, R.I. Atomic force microscopy probing of cell elasticity. Micron 2007, 38, 824–833. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, Y.G.; Malkin, A.J.; Lucas, R.W.; Plomp, M.; McPherson, A. Imaging of viruses by atomic force microscopy. J. Gen. Virol. 2001, 82, 2025–2034. [Google Scholar] [CrossRef] [PubMed]
- Malkin, A.J.; Plomp, M.; McPherson, A. Unraveling the architecture of viruses by high-resolution atomic force microscopy. In DNA Viruses: Methods and Protocols; Lieberman, P.M., Ed.; Humana Press: Totowa, NJ, USA, 2005; pp. 85–108. [Google Scholar]
- Mateu, M.G. Mechanical properties of viruses analyzed by atomic force microscopy: A virological perspective. Virus Res. 2012, 168, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Ivanovska, I.L.; de Pablo, P.J.; Ibarra, B.; Sgalari, G.; MacKintosh, F.C.; Carrascosa, J.L.; Schmidt, C.F.; Wuite, G.J. Bacteriophage capsids: Tough nanoshells with complex elastic properties. Proc. Natl. Acad. Sci. USA 2004, 101, 7600–7605. [Google Scholar] [CrossRef] [PubMed]
- Roos, W.H. How to perform a nanoindentation experiment on a virus. In Single Molecule Analysis: Methods and Protocols; Peterman, E.J.G., Wuite, G.J.L., Eds.; Humana Press: Totowa, NJ, USA, 2011; pp. 251–264. [Google Scholar]
- Kodama, T.; Ohtani, H.; Arakawa, H.; Ikai, A. Mechanical perturbation-induced fluorescence change of green fluorescent protein. Appl. Phys. Lett. 2005, 86, 043901. [Google Scholar] [CrossRef]
- Czajkowsky, D.M.; Sun, J.; Shen, Y.; Shao, Z. Single molecule compression reveals intra-protein forces drive cytotoxin pore formation. eLife 2015, 4, e08421. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, S.R.; Cao, J.; He, Y.; Lu, H.P. Revealing abrupt and spontaneous ruptures of protein native structure under pico-newton compressive stress force manipulation. ACS Nano 2018. [Google Scholar] [CrossRef] [PubMed]
- Rico, F.; Su, C.; Scheuring, S. Mechanical mapping of single membrane proteins at submolecular resolution. Nano Lett. 2011, 11, 3983–3986. [Google Scholar] [CrossRef] [PubMed]
- Medalsy, I.; Hensen, U.; Muller, D.J. Imaging and quantifying chemical and physical properties of native proteins at molecular resolution by force–volume afm. Angew. Chem. Int. Ed. 2011, 50, 12103–12108. [Google Scholar] [CrossRef] [PubMed]
- Radmacher, M.; Cleveland, J.P.; Fritz, M.; Hansma, H.G.; Hansma, P.K. Mapping interaction forces with the atomic force microscope. Biophys. J. 1994, 66, 2159–2165. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Theory of elasticity. Phys. Today 2009, 13, 107–130. [Google Scholar]
- Prasad, B.V.V.; Schmid, M.F. Principles of virus structural organization. In Viral Molecular Machines; Rossmann, M.G., Rao, V.B., Eds.; Springer: Boston, MA, USA, 2012; pp. 17–47. [Google Scholar]
- Rossmann, M.G. Structure of viruses: A short history. Q. Rev. Biophys. 2013, 46, 133–180. [Google Scholar] [CrossRef] [PubMed]
- Michel, J.P.; Ivanovska, I.L.; Gibbons, M.M.; Klug, W.S.; Knobler, C.M.; Wuite, G.J.; Schmidt, C.F. Nanoindentation studies of full and empty viral capsids and the effects of capsid protein mutations on elasticity and strength. Proc. Natl. Acad. Sci. USA 2006, 103, 6184–6189. [Google Scholar] [CrossRef] [PubMed]
- Gibbons, M.M.; Klug, W.S. Nonlinear finite-element analysis of nanoindentation of viral capsids. Phys. Rev. E 2007, 75, 031901. [Google Scholar] [CrossRef] [PubMed]
- Kononova, O.; Snijder, J.; Kholodov, Y.; Marx, K.A.; Wuite, G.J.L.; Roos, W.H.; Barsegov, V. Fluctuating nonlinear spring model of mechanical deformation of biological particles. PLoS Comput. Biol. 2016, 12, e1004729. [Google Scholar] [CrossRef] [PubMed]
- Radmacher, M.; Tillmann, R.W.; Gaub, H.E. Imaging viscoelasticity by force modulation with the atomic force microscope. Biophys. J. 1993, 64, 735–742. [Google Scholar] [CrossRef]
- Bausch, A.R.; Ziemann, F.; Boulbitch, A.A.; Jacobson, K.; Sackmann, E. Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys. J. 1998, 75, 2038–2049. [Google Scholar] [CrossRef]
- Mackintosh, F.C.; Schmidt, C.F. Microrheology. Curr. Opin. Colloid Interface Sci. 1999, 4, 300–307. [Google Scholar] [CrossRef]
- Yamada, S.; Wirtz, D.; Kuo, S.C. Mechanics of living cells measured by laser tracking microrheology. Biophys. J. 2000, 78, 1736–1747. [Google Scholar] [CrossRef]
- Alcaraz, J.; Buscemi, L.; Grabulosa, M.; Trepat, X.; Fabry, B.; Farré, R.; Navajas, D. Microrheology of human lung epithelial cells measured by atomic force microscopy. Biophys. J. 2003, 84, 2071. [Google Scholar] [CrossRef]
- Lau, A.W.; Hoffman, B.D.; Davies, A.; Crocker, J.C.; Lubensky, T.C. Microrheology, stress fluctuations, and active behavior of living cells. Phys. Rev. Lett. 2003, 91, 198101. [Google Scholar] [CrossRef] [PubMed]
- Pegoraro, A.F.; Janmey, P.; Weitz, D.A. Mechanical properties of the cytoskeleton and cells. Cold Spring Harbor Perspect. Biol. 2017, 9, a022038. [Google Scholar] [CrossRef] [PubMed]
- Calzado-Martin, A.; Encinar, M.; Tamayo, J.; Calleja, M.; San Paulo, A. Effect of actin organization on the stiffness of living breast cancer cells revealed by peak-force modulation atomic force microscopy. ACS Nano 2016, 10, 3365–3374. [Google Scholar] [CrossRef] [PubMed]
- Fabry, B.; Maksym, G.N.; Butler, J.P.; Glogauer, M.; Navajas, D.; Fredberg, J.J. Scaling the microrheology of living cells. Phys. Rev. Lett. 2001, 87, 148102. [Google Scholar] [CrossRef] [PubMed]
- Macosko, C.W. Rheology, Principles Measurements and Applications; VCH: New York, NY, USA, 1994. [Google Scholar]
- Mathur, A.B.; Collinsworth, A.M.; Reichert, W.M.; Kraus, W.E.; Truskey, G.A. Endothelial, cardiac muscle and skeletal muscle exhibit different viscous and elastic properties as determined by atomic force microscopy. J. Biomech. 2001, 34, 1545–1553. [Google Scholar] [CrossRef]
- Mahaffy, R.E.; Park, S.; Gerde, E.; Käs, J.; Shih, C.K. Quantitative analysis of the viscoelastic properties of thin regions of fibroblasts using atomic force microscopy. Biophys. J. 2004, 86, 1777–1793. [Google Scholar] [CrossRef]
- Yan, B.; Ren, J.; Zheng, X.; Liu, Y.; Zou, Q. High-speed broadband monitoring of cell viscoelasticity in real time shows myosin-dependent oscillations. Biomech. Model. Mechanobiol. 2017, 16, 1857–1868. [Google Scholar] [CrossRef] [PubMed]
- Rebelo, L.M.; de Sousa, J.S.; Mendes Filho, J.; Radmacher, M. Comparison of the viscoelastic properties of cells from different kidney cancer phenotypes measured with atomic force microscopy. Nanotechnology 2013, 24, 055102. [Google Scholar] [CrossRef] [PubMed]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Jarzynski, C. Equilibrium free energy differences from nonequilibrium measurements: A master equation approach. Phys. Rev. E Stat. Phys. Plasmas Fluids Related Interdiscip. Top. 1997, 56, 5018–5035. [Google Scholar] [CrossRef]
- Liphardt, J.; Dumont, S.; Smith, S.B.; Tinoco, I., Jr.; Bustamante, C. Equilibrium information from nonequilibrium measurements in an experimental test of jarzynski’s equality. Science 2002, 296, 1832–1835. [Google Scholar] [CrossRef] [PubMed]
- Fernandez, J.M.; Garcia-Manyes, S.; Dougan, L. Force-clamp spectroscopy of single proteins. In Single Molecule Spectroscopy in Chemistry, Physics and Biology: Nobel Symposium; Gräslund, A., Rigler, R., Widengren, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 317–335. [Google Scholar]
- Wang, N.; Ingber, D.E. Control of cytoskeletal mechanics by extracellular matrix, cell shape, and mechanical tension. Biophys. J. 1994, 66, 2181–2189. [Google Scholar] [CrossRef]
- Kumar, S.; Maxwell, I.Z.; Heisterkamp, A.; Polte, T.R.; Lele, T.P.; Salanga, M.; Mazur, E.; Ingber, D.E. Viscoelastic retraction of single living stress fibers and its impact on cell shape, cytoskeletal organization, and extracellular matrix mechanics. Biophys. J. 2006, 90, 3762–3773. [Google Scholar] [CrossRef] [PubMed]
- Stewart, M.P.; Helenius, J.; Toyoda, Y.; Ramanathan, S.P.; Muller, D.J.; Hyman, A.A. Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature 2011, 469, 226–230. [Google Scholar] [CrossRef] [PubMed]
- Charras, G.T.; Horton, M.A. Single cell mechanotransduction and its modulation analyzed by atomic force microscope indentation. Biophys. J. 2002, 82, 2970–2981. [Google Scholar] [CrossRef]
- Rotsch, C.; Radmacher, M. Drug-induced changes of cytoskeletal structure and mechanics in fibroblasts: An atomic force microscopy study. Biophys. J. 2000, 78, 520–535. [Google Scholar] [CrossRef]
- Liu, C.Y.; Lin, H.H.; Tang, M.J.; Wang, Y.K. Vimentin contributes to epithelial-mesenchymal transition cancer cell mechanics by mediating cytoskeletal organization and focal adhesion maturation. Oncotarget 2015, 6, 15966–15983. [Google Scholar] [CrossRef] [PubMed]
- Rathje, L.S.; Nordgren, N.; Pettersson, T.; Rönnlund, D.; Widengren, J.; Aspenström, P.; Gad, A.K. Oncogenes induce a vimentin filament collapse mediated by hdac6 that is linked to cell stiffness. Proc. Natl. Acad. Sci. USA 2014, 111, 1515–1520. [Google Scholar] [CrossRef] [PubMed]
- Hui, O.; Nauman, E.; Shi, R. Contribution of cytoskeletal elements to the axonal mechanical properties. J. Biol. Eng. 2013, 7, 21. [Google Scholar]
- Heidemann, S.R.; Wirtz, D. Towards a regional approach to cell mechanics. Trends Cell Biol. 2004, 14, 160. [Google Scholar] [CrossRef] [PubMed]
- Parekh, S.H.; Chaudhuri, O.; Theriot, J.A.; Fletcher, D.A. Loading history determines the velocity of actin-network growth. Nat. Cell Biol. 2005, 7, 1219–1223. [Google Scholar] [CrossRef] [PubMed]
- Purohit, P.K.; Litvinov, R.I.; Brown, A.E.X.; Discher, D.E.; Weisel, J.W. Protein unfolding accounts for the unusual mechanical behavior of fibrin networks. Acta Biomater. 2011, 7, 2374–2383. [Google Scholar] [CrossRef] [PubMed]
- Abhilash, A.S.; Purohit, P.K.; Joshi, S.P. Stochastic rate-dependent elasticity and failure of soft fibrous networks. Soft Matter 2012, 8, 7004–7016. [Google Scholar] [CrossRef]
- Swift, J.; Ivanovska, I.L.; Buxboim, A.; Harada, T.; Dingal, P.C.D.P.; Pinter, J.; Pajerowski, J.D.; Spinler, K.R.; Shin, J.-W.; Tewari, M.; et al. Nuclear lamin-a scales with tissue stiffness and enhances matrix-directed differentiation. Science 2013, 341, 1240104. [Google Scholar] [CrossRef] [PubMed]
- Braet, F.; Rotsch, C.; Wisse, E.; Radmacher, M. Comparison of fixed and living liver endothelial cells by atomic force microscopy. Appl. Phys. A 1998, 66, S575–S578. [Google Scholar] [CrossRef]
- Rotsch, C.; Jacobson, K.; Radmacher, M. Dimensional and mechanical dynamics of active and stalbe edges in motile fibroblasts investigated by using atomic force microscopy. Proc. Natl. Acad. Sci. USA 1999, 96, 921–926. [Google Scholar] [CrossRef] [PubMed]
- Xiong, Y.; Lee, A.C.; Suter, D.M.; Lee, G.U. Topography and nanomechanics of live neuronal growth cones analyzed by atomic force microscopy. Biophys. J. 2009, 96, 5060–5072. [Google Scholar] [CrossRef] [PubMed]
- Domke, J.; Dannöhl, S.; Parak, W.J.; Müller, O.; Aicher, W.K.; Radmacher, M. Substrate dependent differences in morphology and elasticity of living osteoblasts investigated by atomic force microscopy. Colloids Surf. B Biointerfaces 2000, 19, 367–379. [Google Scholar] [CrossRef]
- Hayashi, K.; Iwata, M. Stiffness of cancer cells measured with an afm indentation method. J. Mech. Behav. Biomed. Mater. 2015, 49, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Dulinska, I.; Targosz, M.; Strojny, W.; Lekka, M.; Czuba, P.; Balwierz, W.; Szymonski, M. Stiffness of normal and pathological erythrocytes studied by means of atomic force microscopy. J. Biochem. Biophys. Methods 2006, 66, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Canetta, E.; Riches, A.; Borger, E.; Herrington, S.; Dholakia, K.; Adya, A.K. Discrimination of bladder cancer cells from normal urothelial cells with high specificity and sensitivity: Combined application of atomic force microscopy and modulated raman spectroscopy. Acta Biomater. 2014, 10, 2043–2055. [Google Scholar] [CrossRef] [PubMed]
- Yourek, G.; Hussain, M.A.; Mao, J.J. Cytoskeletal changes of mesenchymal stem cells during differentiation. ASAIO J. 2007, 53, 219–228. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Mezencev, R.; Kim, B.; Wang, L.; McDonald, J.; Sulchek, T. Cell stiffness is a biomarker of the metastatic potential of ovarian cancer cells. PLoS ONE 2012, 7, e46609. [Google Scholar] [CrossRef] [PubMed]
- Weder, G.; Hendriks-Balk, M.C.; Smajda, R.; Rimoldi, D.; Liley, M.; Heinzelmann, H.; Meister, A.; Mariotti, A. Increased plasticity of the stiffness of melanoma cells correlates with their acquisition of metastatic properties. Nanomed. Nanotechnol. Biol. Med. 2014, 10, 141–148. [Google Scholar] [CrossRef] [PubMed]
- Fuhrmann, A.; Staunton, J.R.; Nandakumar, V.; Banyai, N.; Davies, P.C.W.; Ros, R. Afm stiffness nanotomography of normal, metaplastic and dysplastic human esophageal cells. Phys. Biol. 2011, 8, 015007. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Kuhlenschmidt, T.B.; Li, Q.; Ali, S.; Lezmi, S.; Chen, H.; Pires-Alves, M.; Laegreid, W.W.; Saif, T.A.; Kuhlenschmidt, M.S. A mechanically-induced colon cancer cell population shows increased metastatic potential. Mol. Cancer 2014, 13, 131. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, J.; Liu, Y.; Zong, H.; Che, X.; Zheng, W.; Chen, F.; Zhu, Z.; Yang, D.; Song, X. Alterations in mechanical properties are associated with prostate cancer progression. Med. Oncol. 2014, 31, 876. [Google Scholar] [CrossRef] [PubMed]
- Matzke, R.; Jacobson, K.; Radmacher, M. Direct, high-resolution measurement of furrow stiffening during division of adherent cells. Nat. Cell Biol. 2001, 3, 607–610. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.G.; Wang, Y.L. Signals from the spindle midzone are required for the stimulation of cytokinesis in cultured epithelial cells. Mol. Biol. Cell 1996, 7, 225. [Google Scholar] [CrossRef] [PubMed]
- Fishkind, D.J.; Wang, Y.L. New horizons for cytokinesis. Curr. Opin. Cell Biol. 1995, 7, 23–31. [Google Scholar] [CrossRef]
- Lieber, S.C.; Aubry, N.; Pain, J.; Diaz, G.; Kim, S.J.; Vatner, S.F. Aging increases stiffness of cardiac myocytes measured by atomic force microscopy nanoindentation. Am. J. Physiol. Heart Circ. Physiol. 2004, 287, H645. [Google Scholar] [CrossRef] [PubMed]
- Benech, J.C.; Benech, N.; Zambrana, A.I.; Rauschert, I.; Bervejillo, V.; Oddone, N.; Damián, J.P. Diabetes increases stiffness of live cardiomyocytes measured by atomic force microscopy nanoindentation. Am. J. Physiol. Cell Physiol. 2014, 307, C910–C919. [Google Scholar] [CrossRef] [PubMed]
- Saenz Cogollo, J.F.; Tedesco, M.; Martinoia, S.; Raiteri, R. A new integrated system combining atomic force microscopy and micro-electrode array for measuring the mechanical properties of living cardiac myocytes. Biomed. Microdevices 2011, 13, 613–621. [Google Scholar] [CrossRef] [PubMed]
- Yim, E.K.; Darling, E.M.; Kulangara, K.; Guilak, F.; Leong, K.W. Nanotopography-induced changes in focal adhesions, cytoskeletal organization, and mechanical properties of human mesenchymal stem cells. Biomaterials 2010, 31, 1299–1306. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Inoue, H.; Wu, J.C.; Yamanaka, S. Induced pluripotent stem cell technology: A decade of progress. Nat. Rev. Drug Discov. 2017, 16, 115–130. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J.D.; Li, L.; Wang, Y.; Thoburn, C.; Afsari, B.; Danilova, L.; Douville, C.; Javed, A.A.; Wong, F.; Mattox, A.; et al. Detection and localization of surgically resectable cancers with a multi-analyte blood test. Science 2018, 359, 926–930. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, M.J.; Jain, R.K.; Langer, R. Engineering and physical sciences in oncology: Challenges and opportunities. Nat. Rev. Cancer 2017, 17, 659. [Google Scholar] [CrossRef] [PubMed]
- Lekka, M.; Laidler, P.; Gil, D.; Lekki, J.; Stachura, Z.; Hrynkiewicz, A.Z. Elasticity of normal and cancerous human bladder cells studied by scanning force microscopy. Eur. Biophys. J. 1999, 28, 312–316. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.H.; Lin, H.K.; Lin, I.H.; Yu-Wei, C.; Chen, H.W.; Liu, C.Y.; I-Chen, H.H.; Wen-Tai, C.; Wang, Y.K.; Shen, M.R. Mechanical phenotype of cancer cells: Cell softening and loss of stiffness sensing. Oncotarget 2015, 6, 20946–20958. [Google Scholar] [CrossRef] [PubMed]
- Abramczyk, H.; Imiela, A. The biochemical, nanomechanical and chemometric signatures of brain cancer. Spectrochim. Acta Mol. Biomol. Spectrosc. 2018, 188, 8–19. [Google Scholar] [CrossRef] [PubMed]
- Omidvar, R.; Tafazzoli-Shadpour, M.; Shokrgozar, M.A.; Rostami, M. Atomic force microscope-based single cell force spectroscopy of breast cancer cell lines: An approach for evaluating cellular invasion. J. Biomech. 2014, 47, 3373–3379. [Google Scholar] [CrossRef] [PubMed]
- Swaminathan, V.; Mythreye, K.; O’Brien, E.T.; Berchuck, A.; Blobe, G.C.; Superfine, R. Mechanical stiffness grades metastatic potential in patient tumor cells and in cancer cell lines. Cancer Res. 2011, 71, 5075–5080. [Google Scholar] [CrossRef] [PubMed]
- Plodinec, M.; Loparic, M.; Monnier, C.A.; Obermann, E.C.; Zanetti-Dallenbach, R.; Oertle, P.; Hyotyla, J.T.; Aebi, U.; Bentires-Alj, M.; Lim, R.Y.; et al. The nanomechanical signature of breast cancer. Nat. Nanotechnol. 2012, 7, 757–765. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Zheng, C.; Li, S.; Zhou, X.; Liu, Z.; He, Q.; Zhang, N.; Ngan, A.; Tang, B.; Wang, A. Afm nanoindentation detection of the elastic modulus of tongue squamous carcinoma cells with different metastatic potentials. Nanomed. Nanotechnol. Biol. Med. 2013, 9, 864. [Google Scholar] [CrossRef] [PubMed]
- Bastatas, L.; Martinez-Marin, D.; Matthews, J.; Hashem, J.; Yong, J.L.; Sennoune, S.; Filleur, S.; Martinez-Zaguilan, R.; Park, S. Afm nano-mechanics and calcium dynamics of prostate cancer cells with distinct metastatic potential. Biochim. Biophys. Acta (BBA) Gen. Subj. 2012, 1820, 1111–1120. [Google Scholar] [CrossRef] [PubMed]
- Lekka, M.; Laidler, P.; Ignacak, J.; Łabędź, M.; Lekki, J.; Struszczyk, H.; Stachura, Z.; Hrynkiewicz, A.Z. The effect of chitosan on stiffness and glycolytic activity of human bladder cells. Biochim. Biophys. Acta (BBA) Mol. Cell Res. 2001, 1540, 127–136. [Google Scholar] [CrossRef]
- Watanabe, T.; Kuramochi, H.; Takahashi, A.; Imai, K.; Katsuta, N.; Nakayama, T.; Fujiki, H.; Suganuma, M. Higher cell stiffness indicating lower metastatic potential in b16 melanoma cell variants and in (−)-epigallocatechin gallate-treated cells. J. Cancer Res. Clin. Oncol. 2012, 138, 859–866. [Google Scholar] [CrossRef] [PubMed]
- Cross, S.E.; Jin, Y.S.; Lu, Q.Y.; Rao, J.; Gimzewski, J.K. Green tea extract selectively targets nanomechanics of live metastatic cancer cells. Nanotechnology 2011, 22, 215101. [Google Scholar] [CrossRef] [PubMed]
- Yamazaki, D.; Kurisu, S.; Takenawa, T. Regulation of cancer cell motility through actin reorganization. Cancer Sci. 2005, 96, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Olson, M.F.; Sahai, E. The actin cytoskeleton in cancer cell motility. Clin. Exp. Metast. 2009, 26, 273. [Google Scholar] [CrossRef] [PubMed]
- Grothey, A.; Hashizume, R.; Sahin, A.A.; Mccrea, P.D. Fascin, an actin-bundling protein associated with cell motility, is upregulated in hormone receptor negative breast cancer. Br. J. Cancer 2000, 19, 870–873. [Google Scholar] [CrossRef] [PubMed]
- Honda, K.; Yamada, T.; Endo, R.; Ino, Y.; Gotoh, M.; Tsuda, H.; Yamada, Y.; Chiba, H.; Hirohashi, S. Actinin-4, a novel actin-bundling protein associated with cell motility and cancer invasion. J. Cell Biol. 1998, 140, 1383–1393. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Enomoto, A.; Jijiwa, M.; Kato, T.; Hasegawa, T.; Ishida, M.; Sato, T.; Asai, N.; Murakumo, Y.; Takahashi, M. An actin-binding protein girdin regulates the motility of breast cancer cells. Cancer Res. 2008, 68, 1310–1318. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.H.; Bresnick, A.R. The s100a4 metastasis factor regulates cellular motility via a direct interaction with myosin-iia. Cancer Res. 2006, 66, 5173–5180. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pinner, S.; Sahai, E. Pdk1 regulates cancer cell motility by antagonising inhibition of rock1 by rhoe. Nat. Cell Biol. 2008, 10, 127–137. [Google Scholar] [CrossRef] [PubMed]
- Sahai, E.; Garcia-Medina, R.; Pouysségur, J.; Vial, E. Smurf1 regulates tumor cell plasticity and motility through degradation of rhoa leading to localized inhibition of contractility. J. Cell Biol. 2007, 176, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Nürnberg, A.; Kollmannsperger, A.; Grosse, R. Pharmacological inhibition of actin assembly to target tumor cell motility. Rev. Physiol. Biochem. Pharmacol. 2012, 166, 23–42. [Google Scholar]
- Tomasetti, C.; Marchionni, L.; Nowak, M.A.; Parmigiani, G.; Vogelstein, B. Only three driver gene mutations are required for the development of lung and colorectal cancers. Proc. Natl. Acad. Sci. USA 2015, 112, 118. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.B.; Franze, K.; Seifert, G.; Steinhauser, C.; Kirchhoff, F.; Wolburg, H.; Guck, J.; Janmey, P.; Wei, E.Q.; Kas, J.; et al. Viscoelastic properties of individual glial cells and neurons in the cns. Proc. Natl. Acad. Sci. USA 2006, 103, 17759–17764. [Google Scholar] [CrossRef] [PubMed]
- Rother, J.; Noding, H.; Mey, I.; Janshoff, A. Atomic force microscopy-based microrheology reveals significant differences in the viscoelastic response between malign and benign cell lines. Open Biol. 2014, 4, 140046. [Google Scholar] [CrossRef] [PubMed]
- Rico, F.; Gonzalez, L.; Casuso, I.; Puig-Vidal, M.; Scheuring, S. High-speed force spectroscopy unfolds titin at the velocity of molecular dynamics simulations. Science 2013, 342, 741–743. [Google Scholar] [CrossRef] [PubMed]
- Rigato, A.; Miyagi, A.; Scheuring, S.; Rico, F. High-frequency microrheology reveals cytoskeleton dynamics in living cells. Nat. Phys. 2017, 13, 771–775. [Google Scholar] [CrossRef] [PubMed]
- Costa, K.D.; Sim, A.J.; Yin, F.C. Non-hertzian approach to analyzing mechanical properties of endothelial cells probed by atomic force microscopy. J. Biomech. Eng. 2006, 128, 176–184. [Google Scholar] [CrossRef] [PubMed]
- Gelbart, W.M.; Knobler, C.M. Pressurized viruses. Science 2009, 323, 1682–1683. [Google Scholar] [CrossRef] [PubMed]
- Bauer, D.W.; Li, D.; Huffman, J.; Homa, F.L.; Wilson, K.; Leavitt, J.C.; Casjens, S.R.; Baines, J.; Evilevitch, A. Exploring the balance between DNA pressure and capsid stability in herpesviruses and phages. J. Virol. 2015, 89, 9288–9298. [Google Scholar] [CrossRef] [PubMed]
- Purohit, P.K.; Kondev, J.; Phillips, R. Mechanics of DNA packaging in viruses. Proc. Natl. Acad. Sci. USA 2003, 100, 3173–3178. [Google Scholar] [CrossRef] [PubMed]
- Evilevitch, A.; Lavelle, L.; Knobler, C.M.; Raspaud, E.; Gelbart, W.M. Osmotic pressure inhibition of DNA ejection from phage. Proc. Natl. Acad. Sci. USA 2003, 100, 9292–9295. [Google Scholar] [CrossRef] [PubMed]
- Ivanovska, I.; Wuite, G.; Jonsson, B.; Evilevitch, A. Internal DNA pressure modifies stability of wt phage. Proc. Natl. Acad. Sci. USA 2007, 104, 9603–9608. [Google Scholar] [CrossRef] [PubMed]
- Roos, W.H.; Radtke, K.; Kniesmeijer, E.; Geertsema, H.; Sodeik, B.; Wuite, G.J.L. Scaffold expulsion and genome packaging trigger stabilization of herpes simplex virus capsids. Proc. Natl. Acad. Sci. USA 2009, 106, 9673–9678. [Google Scholar] [CrossRef] [PubMed]
- Falvo, M.R.; Washburn, S.; Superfine, R.; Finch, M.; Brooks, F.P.; Chi, V.; Taylor, R.M. Manipulation of individual viruses: Friction and mechanical properties. Biophys. J. 1997, 72, 1396–1403. [Google Scholar] [CrossRef]
- Zhao, Y.; Ge, Z.; Fang, J. Elastic modulus of viral nanotubes. Phys. Rev. E 2008, 78, 031914. [Google Scholar] [CrossRef] [PubMed]
- Carrasco, C.; Carreira, A.; Schaap, I.A.T.; Serena, P.A.; Gómez-Herrero, J.; Mateu, M.G.; de Pablo, P.J. DNA-mediated anisotropic mechanical reinforcement of a virus. Proc. Natl. Acad. Sci. USA 2006, 103, 13706–13711. [Google Scholar] [CrossRef] [PubMed]
- Castellanos, M.; Pérez, R.; Carrasco, C.; Hernando-Pérez, M.; Gómez-Herrero, J.; de Pablo, P.J.; Mateu, M.G. Mechanical elasticity as a physical signature of conformational dynamics in a virus particle. Proc. Natl. Acad. Sci. USA 2012, 109, 12028–12033. [Google Scholar] [CrossRef] [PubMed]
- Liashkovich, I.; Hafezi, W.; Kühn, J.E.; Oberleithner, H.; Kramer, A.; Shahin, V. Exceptional mechanical and structural stability of hsv-1 unveiled with fluid atomic force microscopy. J. Cell Sci. 2008, 121, 2287–2292. [Google Scholar] [CrossRef] [PubMed]
- Kol, N.; Gladnikoff, M.; Barlam, D.; Shneck, R.Z.; Rein, A.; Rousso, I. Mechanical properties of murine leukemia virus particles: Effect of maturation. Biophys. J. 2006, 91, 767–774. [Google Scholar] [CrossRef] [PubMed]
- Roos, W.H.; Gertsman, I.; May, E.R.; Brooks, C.L.; Johnson, J.E.; Wuite, G.J.L. Mechanics of bacteriophage maturation. Proc. Natl. Acad. Sci. USA 2012, 109, 2342–2347. [Google Scholar] [CrossRef] [PubMed]
- Fuller, D.N.; Raymer, D.M.; Rickgauer, J.P.; Robertson, R.M.; Catalano, C.E.; Anderson, D.L.; Grimes, S.; Smith, D.E. Measurements of single DNA molecule packaging dynamics in bacteriophage λ reveal high forces, high motor processivity, and capsid transformations. J. Mol. Biol. 2007, 373, 1113–1122. [Google Scholar] [CrossRef] [PubMed]
- Kol, N.; Shi, Y.; Tsvitov, M.; Barlam, D.; Shneck, R.Z.; Kay, M.S.; Rousso, I. A stiffness switch in human immunodeficiency virus. Biophys. J. 2007, 92, 1777–1783. [Google Scholar] [CrossRef] [PubMed]
- Castellanos, M.; Perez, R.; Carrillo, P.J.P.; de Pablo, P.J.; Mateu, M.G. Mechanical disassembly of single virus particles reveals kinetic intermediates predicted by theory. Biophys. J. 2012, 102, 2615–2624. [Google Scholar] [CrossRef] [PubMed]
- Kodama, T.; Ohtani, H.; Arakawa, H.; Ikai, A. Observation of the destruction of biomolecules under compression force. Ultramicroscopy 2005, 105, 189–195. [Google Scholar] [CrossRef]
- Müller, D.J.; Büldt, G.; Engel, A. Force-induced conformational change of bacteriorhodopsin. J. Mol. Biol. 1995, 249, 239–243. [Google Scholar] [CrossRef] [PubMed]
- Müller, D.J.; Kessler, M.; Oesterhelt, F.; Möller, C.; Oesterhelt, D.; Gaub, H. Stability of bacteriorhodopsin α-helices and loops analyzed by single-molecule force spectroscopy. Biophys. J. 2002, 83, 3578–3588. [Google Scholar] [CrossRef]
- Rief, M.; Oesterhelt, F.; Heymann, B.; Gaub, H.E. Single molecule force spectroscopy on polysaccharides by atomic force microscopy. Science 1997, 275, 1295–1297. [Google Scholar] [CrossRef] [PubMed]
- Merkel, R.; Nassoy, P.; Leung, A.; Ritchie, K.; Evans, E. Energy landscapes of receptor–ligand bonds explored with dynamic force spectroscopy. Nature 1999, 397, 50. [Google Scholar] [CrossRef] [PubMed]
- Evans, E. Probing the relation between force—Lifetime—And chemistry in single molecular bonds. Annu. Rev. Biophys. Biomol. Struct. 2001, 30, 105–128. [Google Scholar] [CrossRef] [PubMed]
| Cell Source | E (kPa) | Indentation (nm) | Loading Rate | Model | Reference |
|---|---|---|---|---|---|
| Rat Liver endothelial cells | 2 | n.r. | n.r. | Hertz | [90] |
| 3T3 cells | 3–12 | <100 | 0.05 Hz | Sneddon | [91] |
| Neuronal growth cones–C domain | 3–7 | 185 | 0.1 Hz | Hertz | [92] |
| Neuronal growth cones–T domain | 7–23 | 101 | |||
| Neuronal growth cones–P domain | 10–40 | 76 | |||
| Human SaOS2 osteoblast cell line | 5.4–7.6 | n.r. | 0.2 Hz | Sneddon | [93] |
| Human cervix cell line End1/E6E7 | 5.5 | <150 | n.r. | Sneddon | [94] |
| Erythrocytes | 19–33 | 200 | n.r. | Hertz | [95] |
| Normal human urothelial cells | 27.57 | 270~970 | 0.5 Hz | Sneddon | [96] |
| Human mesenchymal stem cells(hMSCs) | 33 | n.r. | 10 Hz | Hertz | [97] |
| hMSCs–chondrocytes | 39 | ||||
| hMSCs–osteoblasts | 52 | ||||
| Human skin cell line | 40 | 300~750 | 0.75 µm/s | Hertz | [83] |
| Skeletal muscle cells | 21–28 | 80 | 0.25 µm/s | Sneddon | [69] |
| Cardiac cells | 90–110 | ||||
| Ovarian cancer cell line (high invasive) | 0.494 | 1000 | n.r. | Hertz | [98] |
| Ovarian cancer cell line (low invasive) | 0.884 | ||||
| Cancerous bladder epithelium cells | 2.46 | 270~970 | 0.5 Hz | Sneddon | [96] |
| Hela cells | 2.48 | <150 | n.r. | Sneddon | [94] |
| Human melanoma cell lines | 0.421 | 500~1000 | 1 µm/s | Hertz | [99] |
| Esophageal cell lines | 2.6 | 1216 | 2 µm/s | Hertz | [100] |
| Human colon cancer cell lines | 0.479 | 1400 | n.r. | Sneddon | [101] |
| Benign prostate tumors | 3.03 | 500 | 8 µm/s | Sneddon | [102] |
| Aggressive prostate tumors | 1.72 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Liu, M.; Shen, Y.; Sun, J.; Shao, Z.; Czajkowsky, D.M. Compressive Force Spectroscopy: From Living Cells to Single Proteins. Int. J. Mol. Sci. 2018, 19, 960. https://doi.org/10.3390/ijms19040960
Wang J, Liu M, Shen Y, Sun J, Shao Z, Czajkowsky DM. Compressive Force Spectroscopy: From Living Cells to Single Proteins. International Journal of Molecular Sciences. 2018; 19(4):960. https://doi.org/10.3390/ijms19040960
Chicago/Turabian StyleWang, Jiabin, Meijun Liu, Yi Shen, Jielin Sun, Zhifeng Shao, and Daniel Mark Czajkowsky. 2018. "Compressive Force Spectroscopy: From Living Cells to Single Proteins" International Journal of Molecular Sciences 19, no. 4: 960. https://doi.org/10.3390/ijms19040960
APA StyleWang, J., Liu, M., Shen, Y., Sun, J., Shao, Z., & Czajkowsky, D. M. (2018). Compressive Force Spectroscopy: From Living Cells to Single Proteins. International Journal of Molecular Sciences, 19(4), 960. https://doi.org/10.3390/ijms19040960