Atomistic Analysis of ToxN and ToxI Complex Unbinding Mechanism
Abstract
1. Introduction
2. Results and Discussion
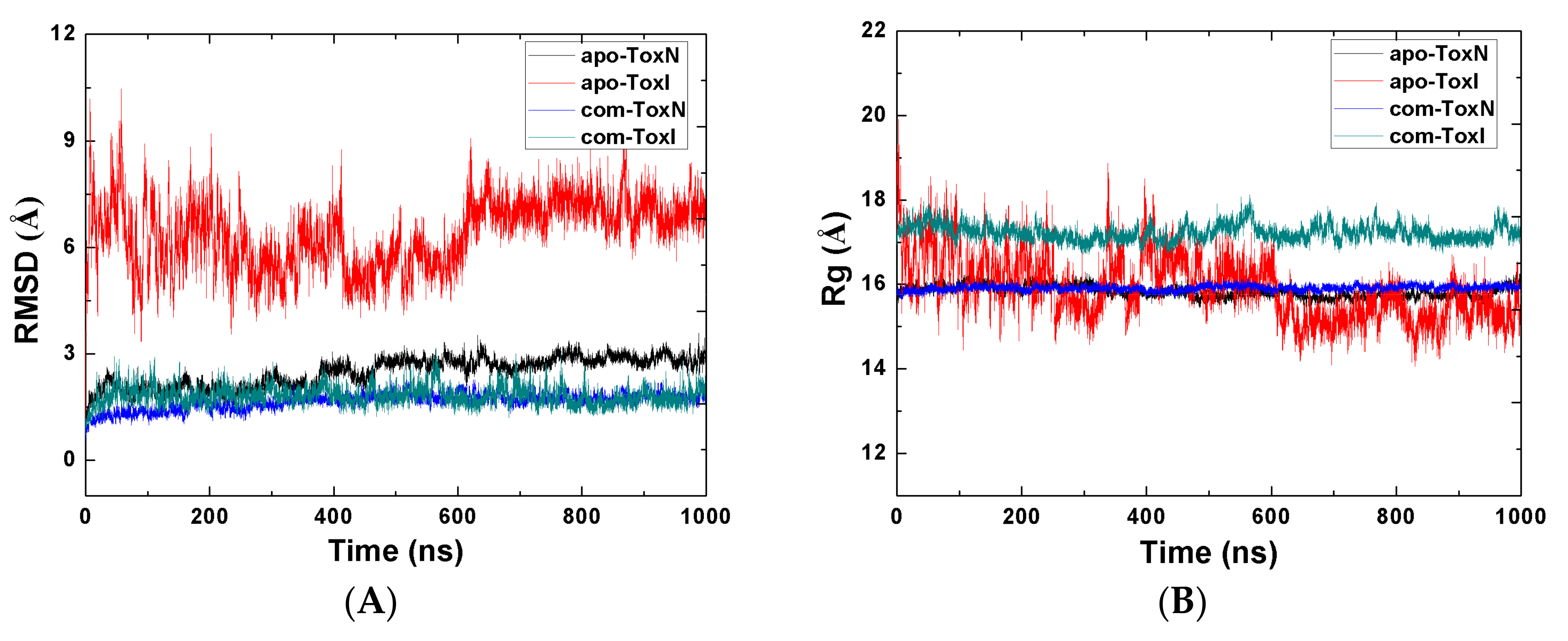
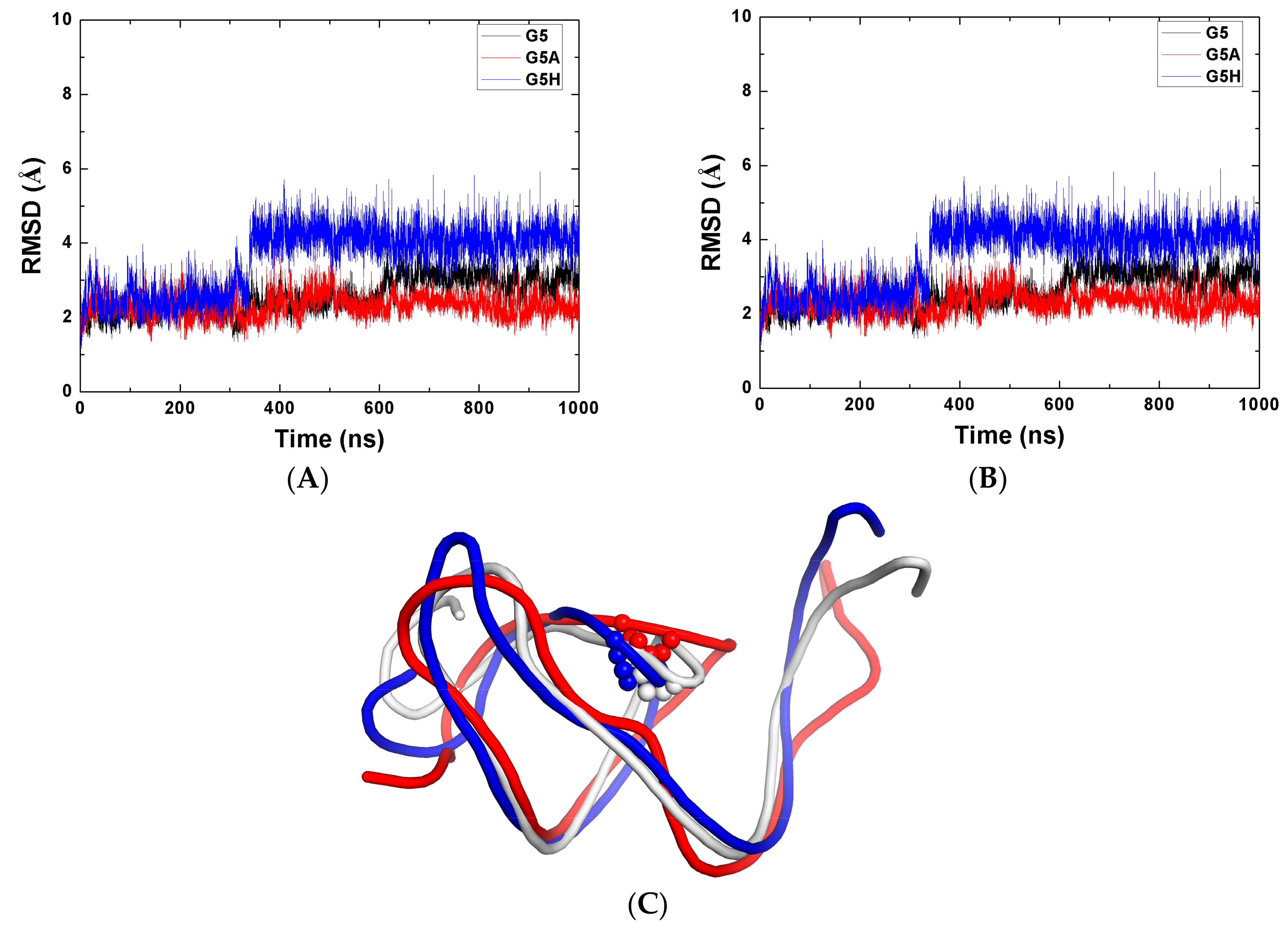
2.1. Stability of the Systems
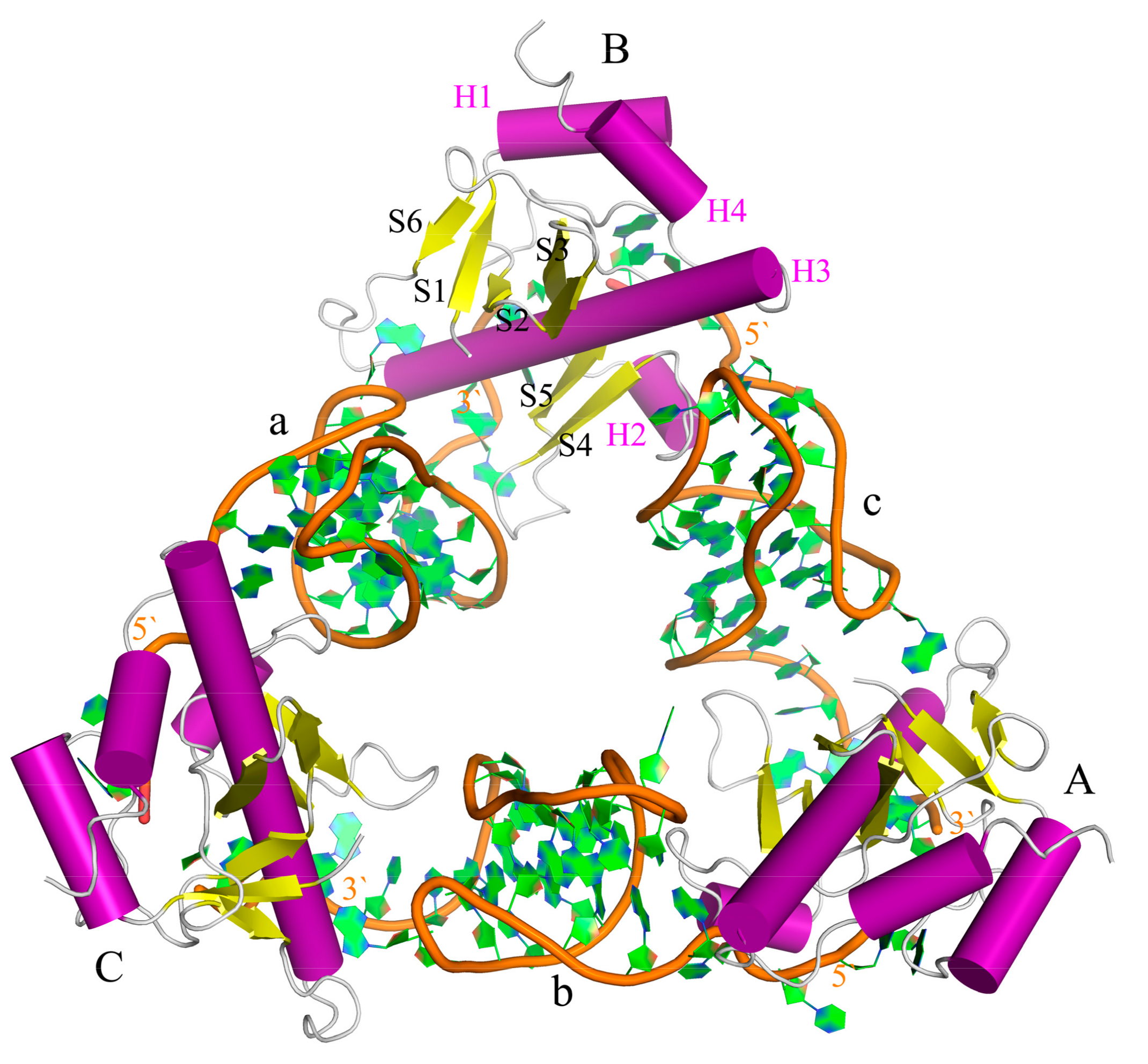
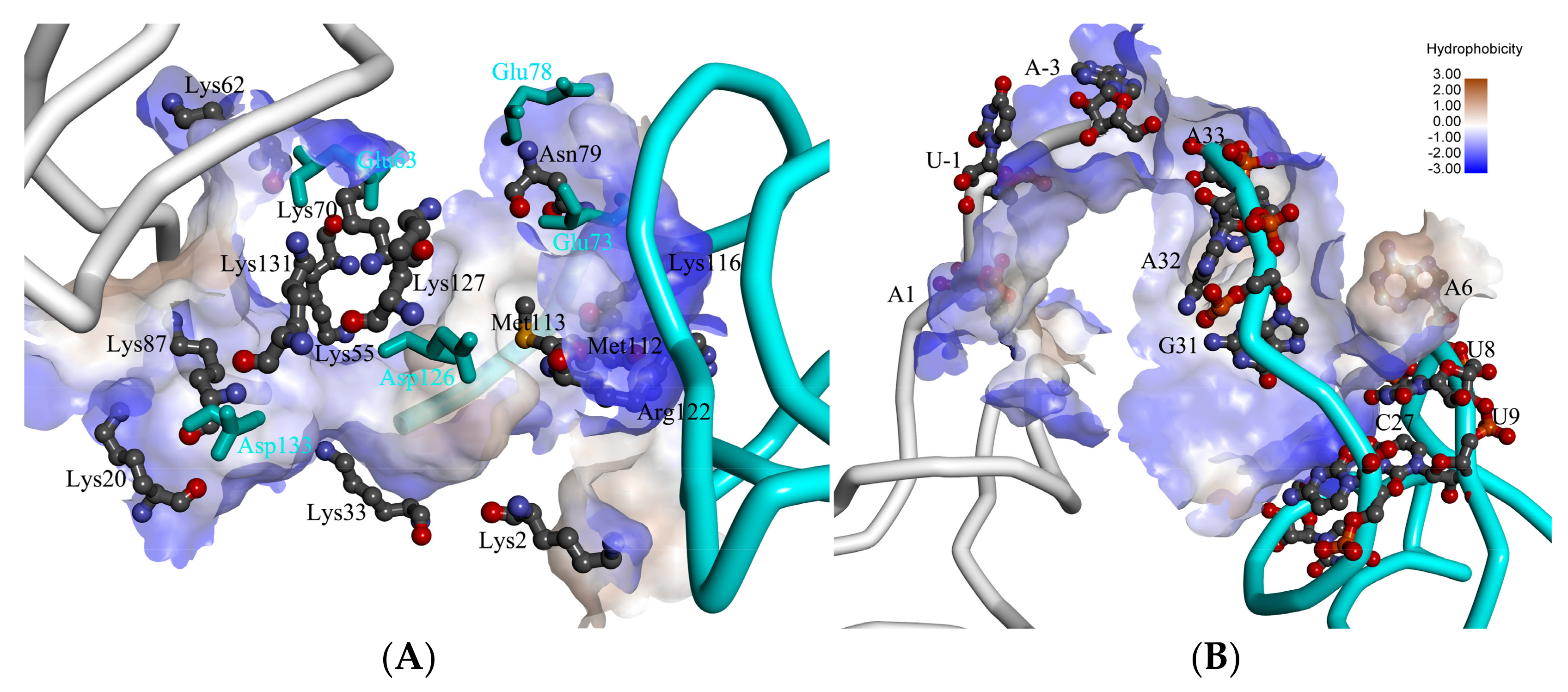
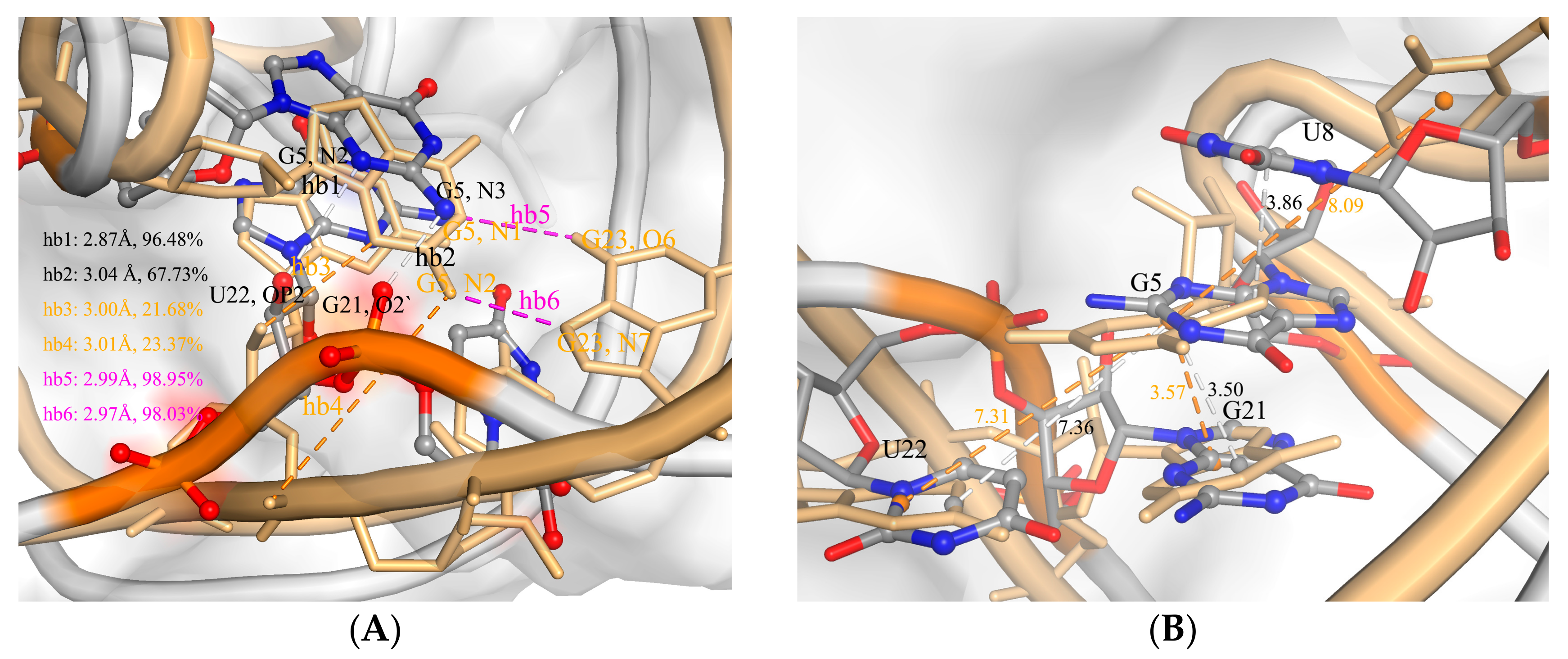
2.2. The Interaction between ToxI and ToxN
2.3. The Function of G5
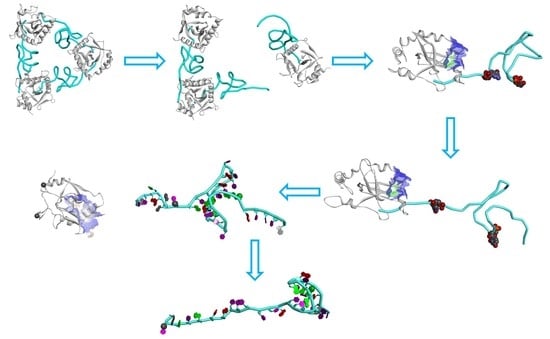
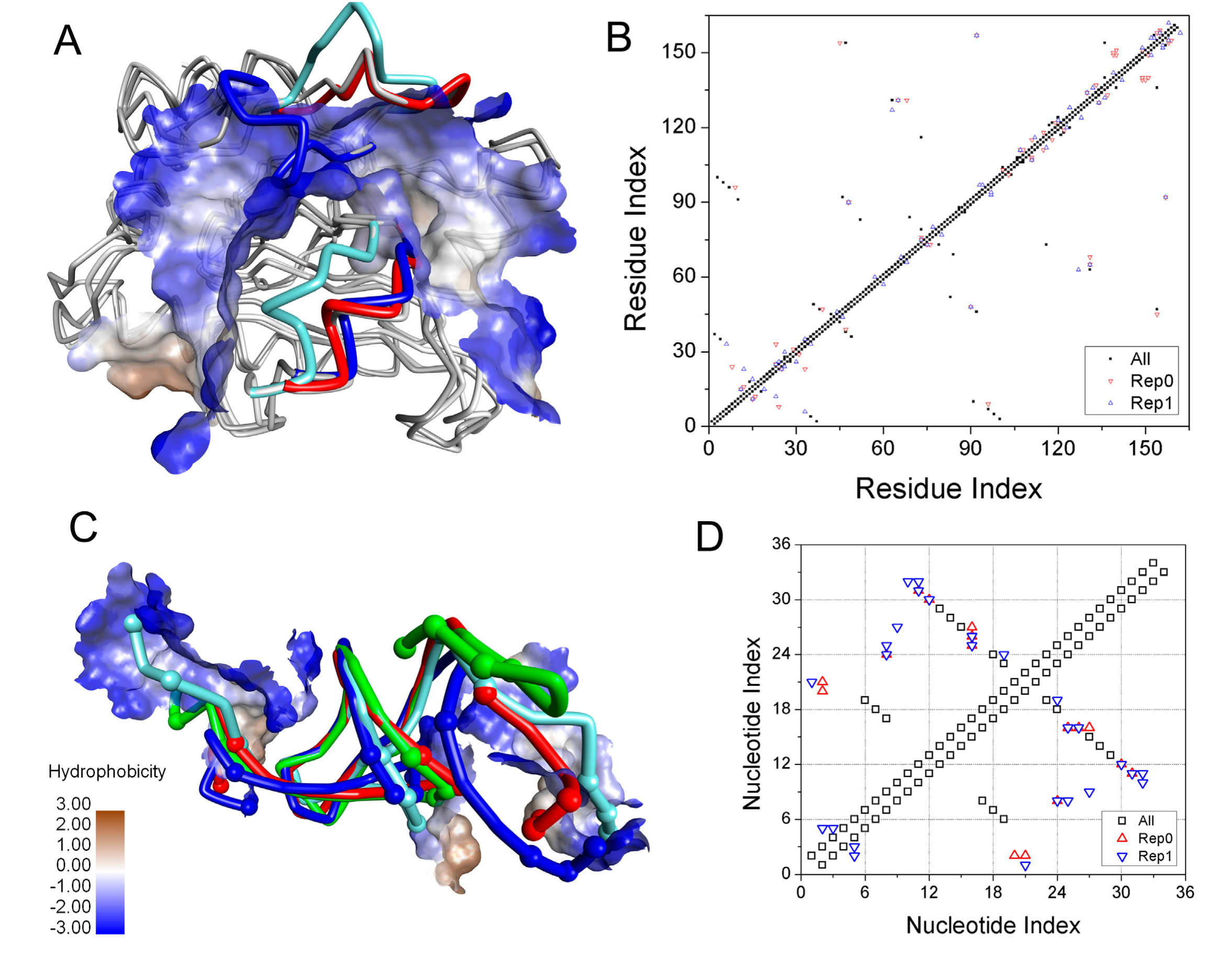
2.4. Induced-Fit Mechanism
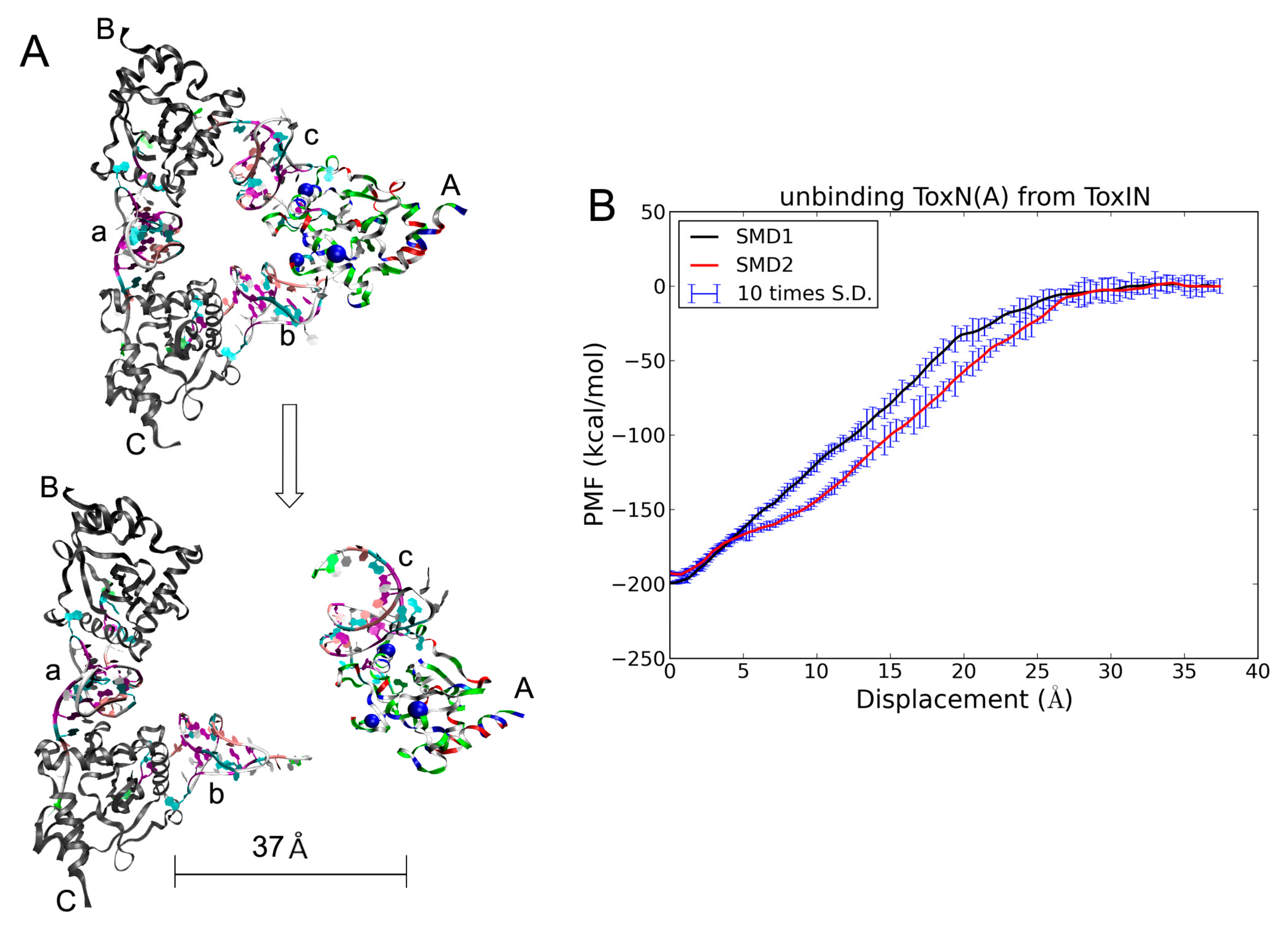
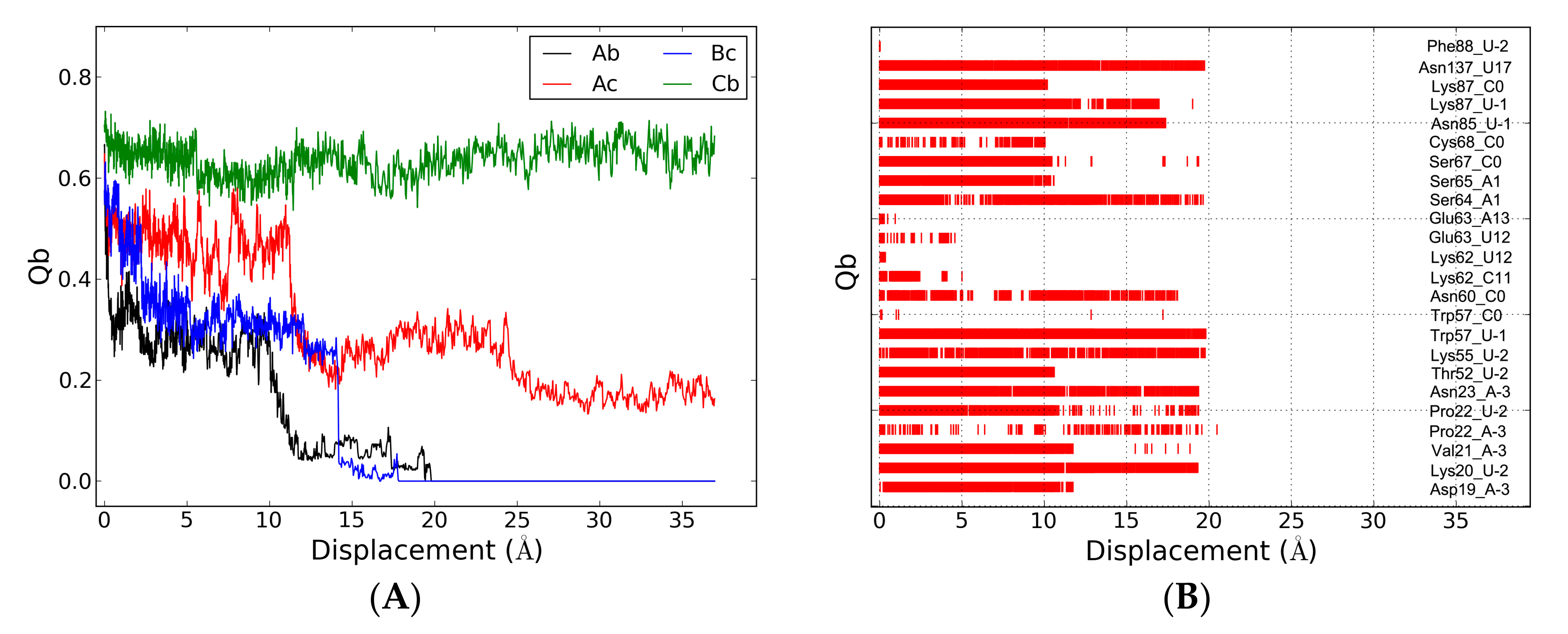
2.5. The Dissociation of ToxN(A) from the ToxIN Complex
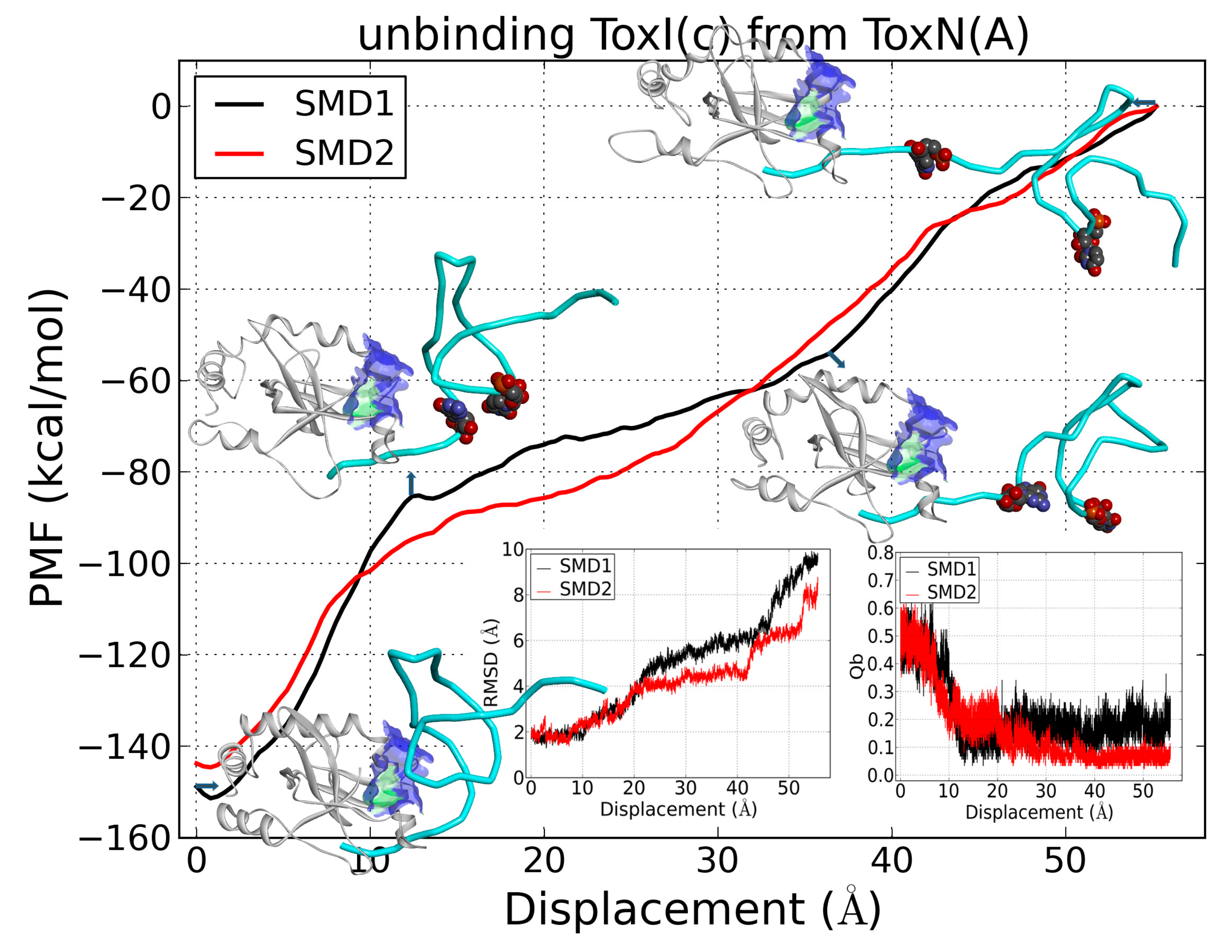
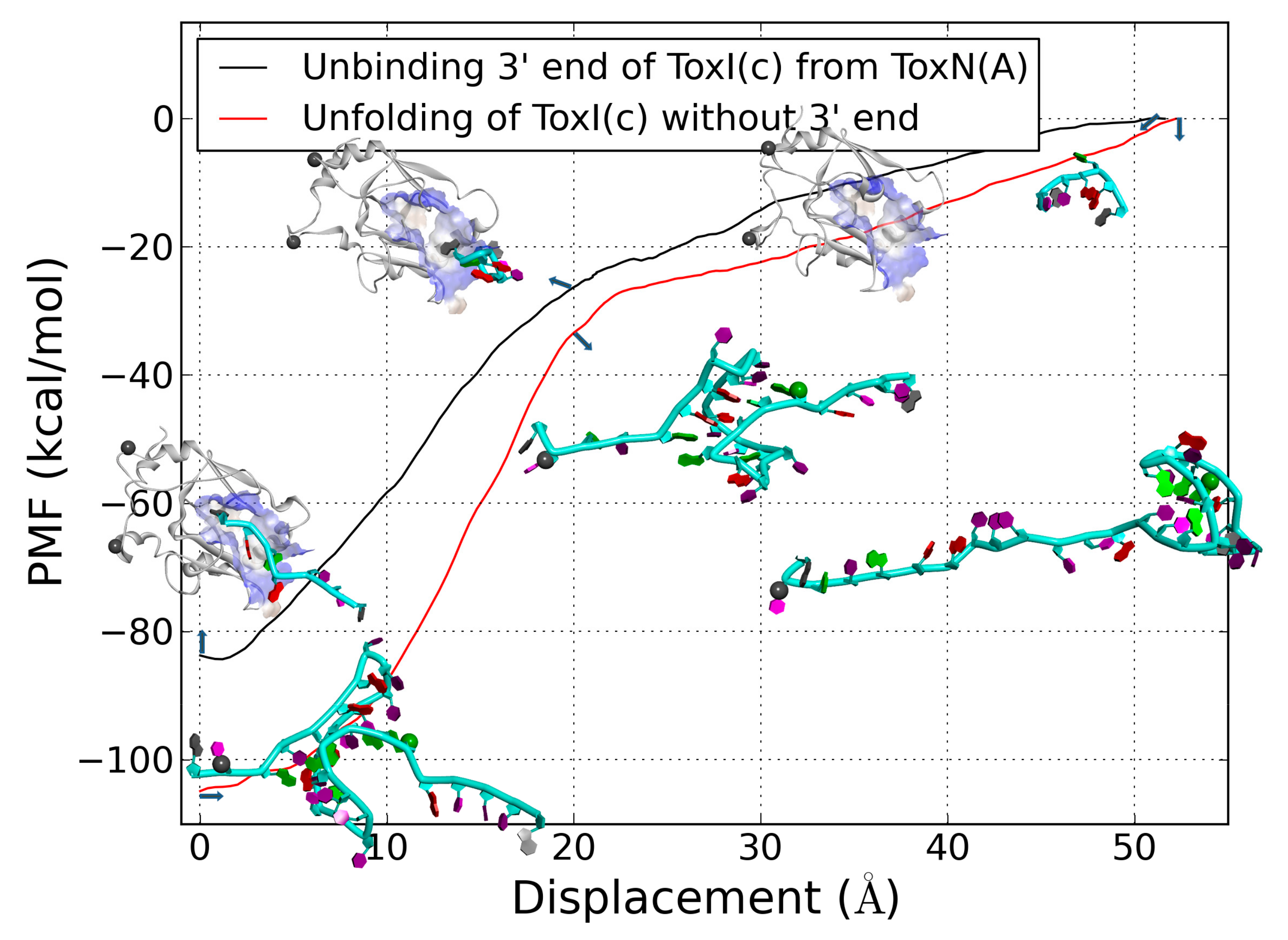
2.6. The Dissociation of ToxI(c) from ToxN(A)
3. Modelling and Simulation
3.1. Molecular Dynamics Simulations
3.2. Residue-Inhibitor Interaction Decomposition
3.3. SMD and PMF in 3nD
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Labrie, S.J.; Samson, J.E.; Moineau, S. Bacteriophage resistance mechanisms. Nat. Rev. Microbiol. 2010, 8, 317–327. [Google Scholar] [CrossRef] [PubMed]
- Sorek, R.; Kunin, V.; Hugenholtz, P. CRISPR—A widespread system that provides acquired resistance against phages in bacteria and archaea. Nat. Rev. Microbiol. 2008, 6, 181–186. [Google Scholar] [CrossRef] [PubMed]
- Fineran, P.C.; Blower, T.R.; Foulds, I.J.; Humphreys, D.P.; Lilley, K.S.; Salmond, G.P. The phage abortive infection system, ToxIN, functions as a protein-RNA toxin-antitoxin pair. Proc. Natl. Acad. Sci. USA 2009, 106, 894–899. [Google Scholar] [CrossRef] [PubMed]
- Blower, T.R.; Fineran, P.C.; Johnson, M.J.; Toth, I.K.; Humphreys, D.P.; Salmond, G.P. Mutagenesis and functional characterization of the RNA and protein components of the toxIN abortive infection and toxin-antitoxin locus of Erwinia. J. Bacterial. 2009, 191, 6029–6039. [Google Scholar] [CrossRef] [PubMed]
- Pandey, D.P.; Gerdes, K. Toxin-antitoxin loci are highly abundant in free-living but lost from host-associated prokaryotes. Nucleic Acids Res. 2005, 33, 966–976. [Google Scholar] [CrossRef] [PubMed]
- Schuster, C.F.; Bertram, R. Toxin-antitoxin systems are ubiquitous and versatile modulators of prokaryotic cell fate. FEMS Microbial. Lett. 2013, 340, 73–85. [Google Scholar] [CrossRef] [PubMed]
- Mruk, I.; Kobayashi, I. To be or not to be: regulation of restriction-modification systems and other toxin-antitoxin systems. Nucleic Acids Res. 2014, 42, 70–86. [Google Scholar] [CrossRef] [PubMed]
- Kedzierska, B.; Hayes, F. Emerging roles of toxin-antitoxin modules in bacterial pathogenesis. Molecules 2016, 21, 790. [Google Scholar] [CrossRef] [PubMed]
- Rao, F.; Short, F.L.; Voss, J.E.; Blower, T.R.; Orme, A.L.; Whittaker, T.E.; Luisi, B.F.; Salmond, G.P. Co-evolution of quaternary organization and novel RNA tertiary interactions revealed in the crystal structure of a bacterial protein-RNA toxin-antitoxin system. Nucleic Acids Res. 2015, 43, 9529–9540. [Google Scholar] [CrossRef] [PubMed]
- Short, F.L.; Pei, X.Y.; Blower, T.R.; Ong, S.L.; Fineran, P.C.; Luisi, B.F.; Salmond, G.P. Selectivity and self-assembly in the control of a bacterial toxin by an antitoxic noncoding RNA pseudoknot. Proc. Natl. Acad. Sci. USA 2013, 110, E241–E249. [Google Scholar] [CrossRef] [PubMed]
- Blower, T.R.; Pei, X.Y.; Short, F.L.; Fineran, P.C.; Humphreys, D.P.; Luisi, B.F.; Salmond, G.P. A processed noncoding RNA regulates an altruistic bacterial antiviral system. Nat. Struct. Mol. Biol. 2011, 18, 185–190. [Google Scholar] [CrossRef] [PubMed]
- Staple, D.W.; Butcher, S.E. Pseudoknots: RNA structures with diverse functions. PLoS Biol. 2005, 3, e213. [Google Scholar] [CrossRef] [PubMed]
- Bian, Y.; Zhang, J.; Wang, J.; Wang, J.; Wang, W. Free energy landscape and multiple folding pathways of an H-type RNA pseudoknot. PLoS ONE 2015, 10, e0129089. [Google Scholar] [CrossRef] [PubMed]
- Adams, P.L.; Stahley, M.R.; Kosek, A.B.; Wang, J.; Strobel, S.A. Crystal structure of a self-splicing group I intron with both exons. Nature 2004, 430, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Egli, M.; Minasov, G.; Su, L.; Rich, A. Metal ions and flexibility in a viral RNA pseudoknot at atomic resolution. Proc. Natl. Acad. Sci. USA 2002, 99, 4302–4307. [Google Scholar] [CrossRef] [PubMed]
- Sussman, D.; Nix, J.C.; Wilson, C. The structural basis for molecular recognition by the vitamin B 12 RNA aptamer. Nat. Struct. Biol. 2000, 7, 53–57. [Google Scholar] [CrossRef] [PubMed]
- Tuerk, C.; MacDougal, S.; Gold, L. RNA pseudoknots that inhibit human immunodeficiency virus type 1 reverse transcriptase. Proc. Natl. Acad. Sci. USA 1992, 89, 6988–6992. [Google Scholar] [CrossRef] [PubMed]
- McDowell, S.E.; Spackova, N.; Sponer, J.; Walter, N.G. Molecular dynamics simulations of RNA: An in silico single molecule approach. Biopolymers 2007, 85, 169–184. [Google Scholar] [CrossRef] [PubMed]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.A.; Jumper, J.M.; Salmon, J.K.; Shan, Y.; et al. Atomic-level characterization of the structural dynamics of proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B. Atomistic molecular simulations of protein folding. Curr. Opin. Struct. Biol. 2012, 22, 52–61. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, J.; Zhu, W. Zinc ion-induced conformational changes in new Delphi metallo-beta-lactamase 1 probed by molecular dynamics simulations and umbrella sampling. Phys. Chem. Chem. Phys. 2017, 19, 3067–3075. [Google Scholar] [CrossRef] [PubMed]
- Estarellas, C.; Otyepka, M.; Koca, J.; Banas, P.; Krepl, M.; Sponer, J. Molecular dynamic simulations of protein/RNA complexes: CRISPR/Csy4 endoribonuclease. Biochim. Biophys. Acta 2015, 1850, 1072–1090. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Li, W.; Wang, W. Localized frustration and binding-induced conformational change in recognition of 5S RNA by TFIIIA zinc finger. J. Phys. Chem. B 2013, 117, 15917–15925. [Google Scholar] [CrossRef] [PubMed]
- Terakawa, T.; Takada, S. Multiscale ensemble modeling of intrinsically disordered proteins: p53 N-terminal domain. Biophys. J. 2011, 101, 1450–1458. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Ma, A.; Wang, J. Ligand selectivity mechanism and conformational changes in guanine riboswitch by molecular dynamics simulations and free energy calculations. J. Chem. Inf. Model. 2017, 57, 918–928. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, X.; Zhu, T.; Zhang, Q.; Zhang, J.Z. A comparative insight into amprenavir resistance of mutations V32I, G48V, I50V, I54V, and I84V in HIV-1 protease based on thermodynamic integration and MM-PBSA methods. J. Chem. Inf. Model. 2015, 55, 1903–1913. [Google Scholar] [CrossRef] [PubMed]
- Hermann, T.; Westhof, E. Simulations of the dynamics at an RNA-protein interface. Nat. Struct. Biol. 1999, 6, 540. [Google Scholar] [CrossRef] [PubMed]
- Mackerell, A.D., Jr.; Nilsson, L. Molecular dynamics simulations of nucleic acid-protein complexes. Curr. Opin. Struct. Biol. 2008, 18, 194–199. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.X.; Gmeiner, W.H. Molecular dynamics simulation of the human U2B′′ protein complex with U2 snRNA hairpin IV in aqueous solution. Biophys. J. 2001, 81, 630–642. [Google Scholar] [CrossRef]
- Grubmuller, H.; Heymann, B.; Tavan, P. Ligand binding: Molecular mechanics calculation of the streptavidin-biotin rupture force. Science 1996, 271, 997–999. [Google Scholar] [CrossRef] [PubMed]
- Patel, J.S.; Berteotti, A.; Ronsisvalle, S.; Rocchia, W.; Cavalli, A. Steered molecular dynamics simulations for studying protein-ligand interaction in cyclin-dependent kinase 5. J. Chem. Inf. Model. 2014, 54, 470–480. [Google Scholar] [CrossRef] [PubMed]
- Li, M.S.; Mai, B.K. Steered molecular dynamics—A promising tool for drug design. Curr. Bioinform. 2012, 7, 342. [Google Scholar]
- Giorgino, T.; De Fabritiis, G. A high-throughput steered molecular dynamics study on the free energy profile of ion permeation through gramicidin A. J. Chem. Theory Comput. 2011, 7, 1943. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.Y. Glycerol modulates water permeation through Escherichia coli aquaglyceroporin GlpF. Biochim. Biophys. Acta 2013, 1828, 1786–1793. [Google Scholar] [CrossRef] [PubMed]
- Henin, J.; Tajkhorshid, E.; Schulten, K.; Chipot, C. Diffusion of glycerol through Escherichia coli aquaglyceroporin GlpF. Biophys. J. 2008, 94, 832–839. [Google Scholar] [CrossRef] [PubMed]
- Mai, B.K.; Viet, M.H.; Li, M.S. Top leads for swine influenza A/H1N1 virus revealed by steered molecular dynamics approach. J. Chem. Inf. Model. 2010, 50, 2236–2247. [Google Scholar] [CrossRef] [PubMed]
- Mai, B.K.; Li, M.S. Neuraminidase inhibitor R-125489—A promising drug for treating influenza virus: Steered molecular dynamics approach. Biochem. Biophys. Res. Commun. 2011, 410, 688–691. [Google Scholar] [CrossRef] [PubMed]
- Colizzi, F.; Perozzo, R.; Scapozza, L.; Recanatini, M.; Cavalli, A. Single-molecule pulling simulations can discern active from inactive enzyme inhibitors. J. Am. Chem. Soc. 2010, 132, 7361–7371. [Google Scholar] [CrossRef] [PubMed]
- Nicolini, P.; Frezzato, D.; Gellini, C.; Bizzarri, M.; Chelli, R. Toward quantitative estimates of binding affinities for protein-ligand systems involving large inhibitor compounds: A steered molecular dynamics simulation route. J. Comput. Chem. 2013, 34, 1561–1576. [Google Scholar] [CrossRef] [PubMed]
- Qin, F.; Jiang, Y.; Chen, Y.; Wu, M.; Yan, G.; Ye, W.; Li, Y.; Zhang, J.; Chen, H.F. Conformational selection or induced fit for Brinker and DNA recognition. Phys. Chem. Chem. Phys. 2011, 13, 1407–1412. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Xu, S.; Wang, J. Characterizing the free-energy landscape of MDM2 protein-ligand interactions by steered molecular dynamics simulations. Chem. Biol. Drug Des. 2015, 86, 1351–1359. [Google Scholar] [CrossRef] [PubMed]
- Roe, D.R.; Cheatham, T.E., 3rd. PTRAJ and CPPTRAJ: Software for processing and analysis of molecular dynamics trajectory data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef] [PubMed]
- Boehr, D.D.; Wright, P.E. Biochemistry. How do proteins interact? Science 2008, 320, 1429–1430. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Ma, B.; Tsai, C.J.; Sinha, N.; Nussinov, R. Folding and binding cascades: Dynamic landscapes and population shifts. Protein Sci. 2000, 9, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Tsai, C.J.; Ma, B.; Nussinov, R. Mechanisms of transcription factor selectivity. Trends Genet. TIG 2010, 26, 75–83. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, R.A.; Yu, L.; Chen, L.Y. Computing protein-protein association affinity with hybrid steered molecular dynamics. J. Chem. Theory Comput. 2015, 11, 4427–4438. [Google Scholar] [CrossRef] [PubMed]
- Sotomayor, M.; Schulten, K. Single-molecule experiments in vitro and in silico. Science 2007, 316, 1144–1148. [Google Scholar] [CrossRef] [PubMed]
- Giorgino, T. PLUMED-GUI: An environment for the interactive development of molecular dynamics analysis and biasing scripts. Comput. Phys. Commun. 2014, 185, 1109–1114. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J.; Wang, W. Atomistic analysis of pseudoknotted RNA unfolding. J. Am. Chem. Soc. 2011, 133, 6882–6885. [Google Scholar] [CrossRef] [PubMed]
- Short, F.L.; Akusobi, C.; Broadhurst, W.R.; Salmond, G.P.C. The bacterial Type III toxin-antitoxin system, ToxIN, is a dynamic protein-RNA complex with stability-dependent antiviral abortive infection activity. Sci. Rep. 2018, 8, 1013. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Buckner, J.K.; Madura, J.D. Computer simulations of organic reactions in solution. Ann. N. Y. Acad. Sci. 1986, 482, 198–209. [Google Scholar] [CrossRef] [PubMed]
- Zgarbova, M.; Otyepka, M.; Sponer, J.; Mladek, A.; Banas, P.; Cheatham, T.E., 3rd; Jurecka, P. Refinement of the cornell et al. nucleic acids force field based on reference quantum chemical calculations of glycosidic torsion profiles. J. Chem. Theory Comput. 2011, 7, 2886–2902. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef] [PubMed]
- Bayly, C.I.; Cieplak, P.; Cornell, W.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Case, D.A.; Darden, T.A.; Cheatham, T.E., III; Simmerling, C.L.; Wang, J.; Duke, R.E.; Luo, R.; Walker, R.C.; Zhang, W.; Merz, K.M.; et al. Amber 12; University of California: San Francisco, CA, USA, 2012. [Google Scholar]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N Log(N) method for Ewald sums in large systems. J. Comput. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical-integration of cartesian equations of motion of a system with constraints-molecular-dynamics of N-Alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Gohlke, H.; Kiel, C.; Case, D.A. Insights into protein-protein binding by binding free energy calculation and free energy decomposition for the Ras-Raf and Ras-RalGDS complexes. J. Mol. Biol. 2003, 330, 891–913. [Google Scholar] [CrossRef]
- Hu, G.; Wang, J. Ligand selectivity of estrogen receptors by a molecular dynamics study. Eur. J. Med. Chem. 2014, 74, 726–735. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Li, H.; Liu, J.Y.; Wang, J. Insight into conformational change for 14-3-3sigma protein by molecular dynamics simulation. Int. J. Mol. Sci. 2014, 15, 2794–2810. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Wang, J.; Zhu, W.; Li, G. A computational analysis of binding modes and conformation changes of MDM2 induced by p53 and inhibitor bindings. J. Comput. Aided Mol. Des. 2013, 27, 965–974. [Google Scholar] [CrossRef] [PubMed]
- Weiser, J.; Shenkin, P.S.; Still, W.C. Approximate atomic surfaces from linear combinations of pairwise overlaps (LCPO). J. Comput. Chem. 1999, 20, 217–230. [Google Scholar] [CrossRef]
- Onufriev, A.; Bashford, D.; Case, D.A. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins 2004, 55, 383–394. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.Y. Thermodynamic integration in 3n dimensions without biases or alchemy for protein interactions. bioRxiv 2017. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.Y. Hybrid steered molecular dynamics approach to computing absolute binding free energy of ligand-protein complexes: A brute force approach that is fast and accurate. J. Chem. Theory Comput. 2015, 11, 1928–1938. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.Y. Nonequilibrium fluctuation-dissipation theorem of Brownian dynamics. J. Chem. Phys. 2008, 129, 144113. [Google Scholar] [CrossRef] [PubMed]
| System | Methods | Total Number of Atoms | MD Length (ns) |
|---|---|---|---|
| ToxIN | Equilibrated MD | 93,408 | 1000 × 3 = 3000 |
| ToxI | Equilibrated MD | 26,478 | 1000 × 3 = 3000 |
| ToxN | Equilibrated MD | 19,351 | 1000 × 3 = 3000 |
| G5A | Equilibrated MD | 17,016 | 1000 |
| G5H | Equilibrated MD | 16,349 | 1000 |
| ToxIN | SMD | 115,152 | 338.8 × 2 = 677.6 |
| ToxN(A)-ToxI(c) | SMD | 50,534 | 338.8 × 2 = 677.6 |
| ToxN(A)-3′ terminus of ToxI(c) | SMD | 43,306 | 338.8 |
| ToxI(c) | SMD | 38,519 | 338.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Yu, X.; Bian, Y.; Cao, Z.; Xu, S.; Zhao, L.; Ji, B.; Wang, W.; Wang, J. Atomistic Analysis of ToxN and ToxI Complex Unbinding Mechanism. Int. J. Mol. Sci. 2018, 19, 3524. https://doi.org/10.3390/ijms19113524
Hu G, Yu X, Bian Y, Cao Z, Xu S, Zhao L, Ji B, Wang W, Wang J. Atomistic Analysis of ToxN and ToxI Complex Unbinding Mechanism. International Journal of Molecular Sciences. 2018; 19(11):3524. https://doi.org/10.3390/ijms19113524
Chicago/Turabian StyleHu, Guodong, Xiu Yu, Yunqiang Bian, Zanxia Cao, Shicai Xu, Liling Zhao, Baohua Ji, Wei Wang, and Jihua Wang. 2018. "Atomistic Analysis of ToxN and ToxI Complex Unbinding Mechanism" International Journal of Molecular Sciences 19, no. 11: 3524. https://doi.org/10.3390/ijms19113524
APA StyleHu, G., Yu, X., Bian, Y., Cao, Z., Xu, S., Zhao, L., Ji, B., Wang, W., & Wang, J. (2018). Atomistic Analysis of ToxN and ToxI Complex Unbinding Mechanism. International Journal of Molecular Sciences, 19(11), 3524. https://doi.org/10.3390/ijms19113524