Thermal Vibration-Induced Rotation of Nano-Wheel: A Molecular Dynamics Study
Abstract
1. Introduction
2. Numerical Tests and Discussion
2.1. Rotation of Rotor in the Stators without Relaxation
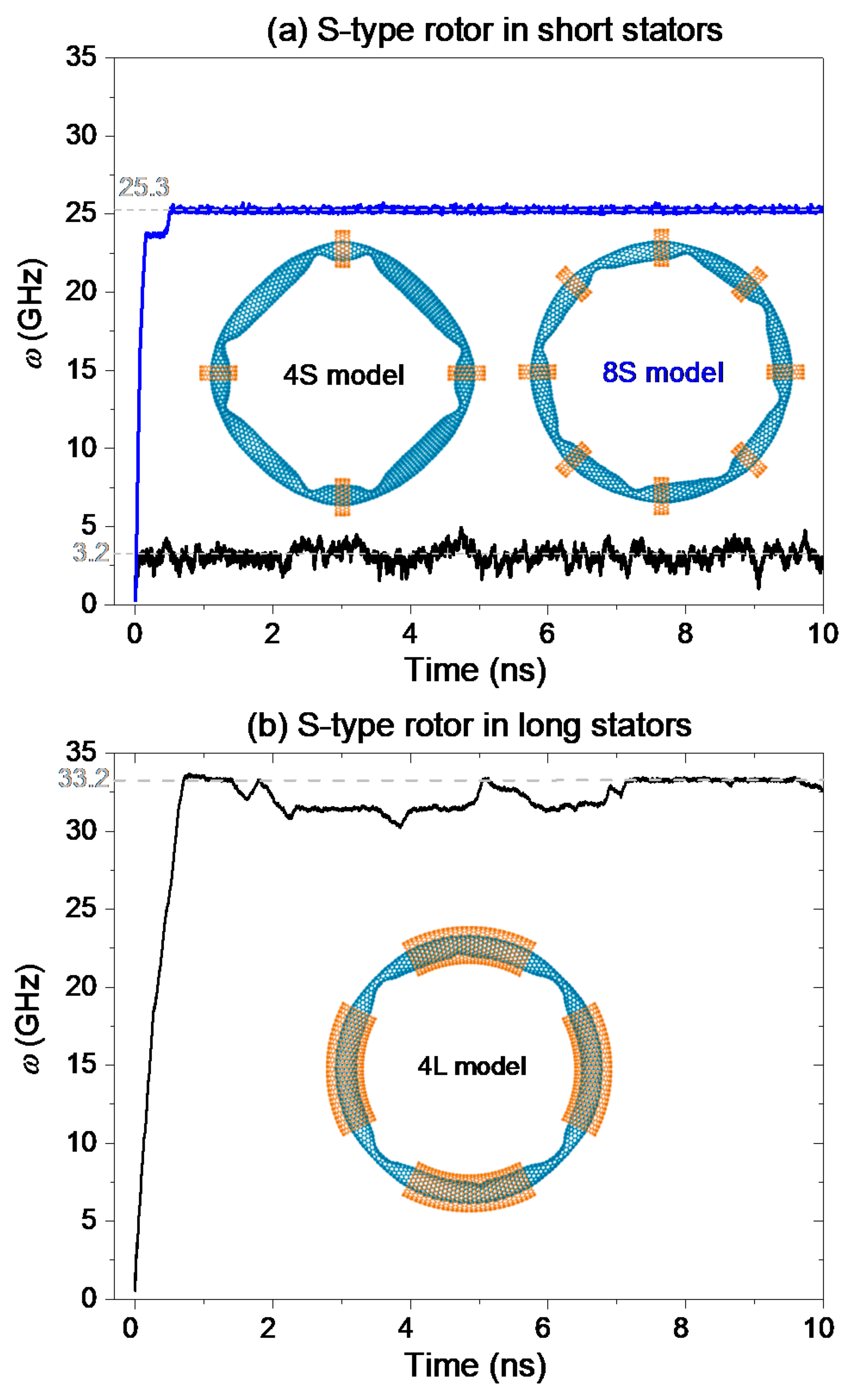
2.1.1. S-Type Rotor
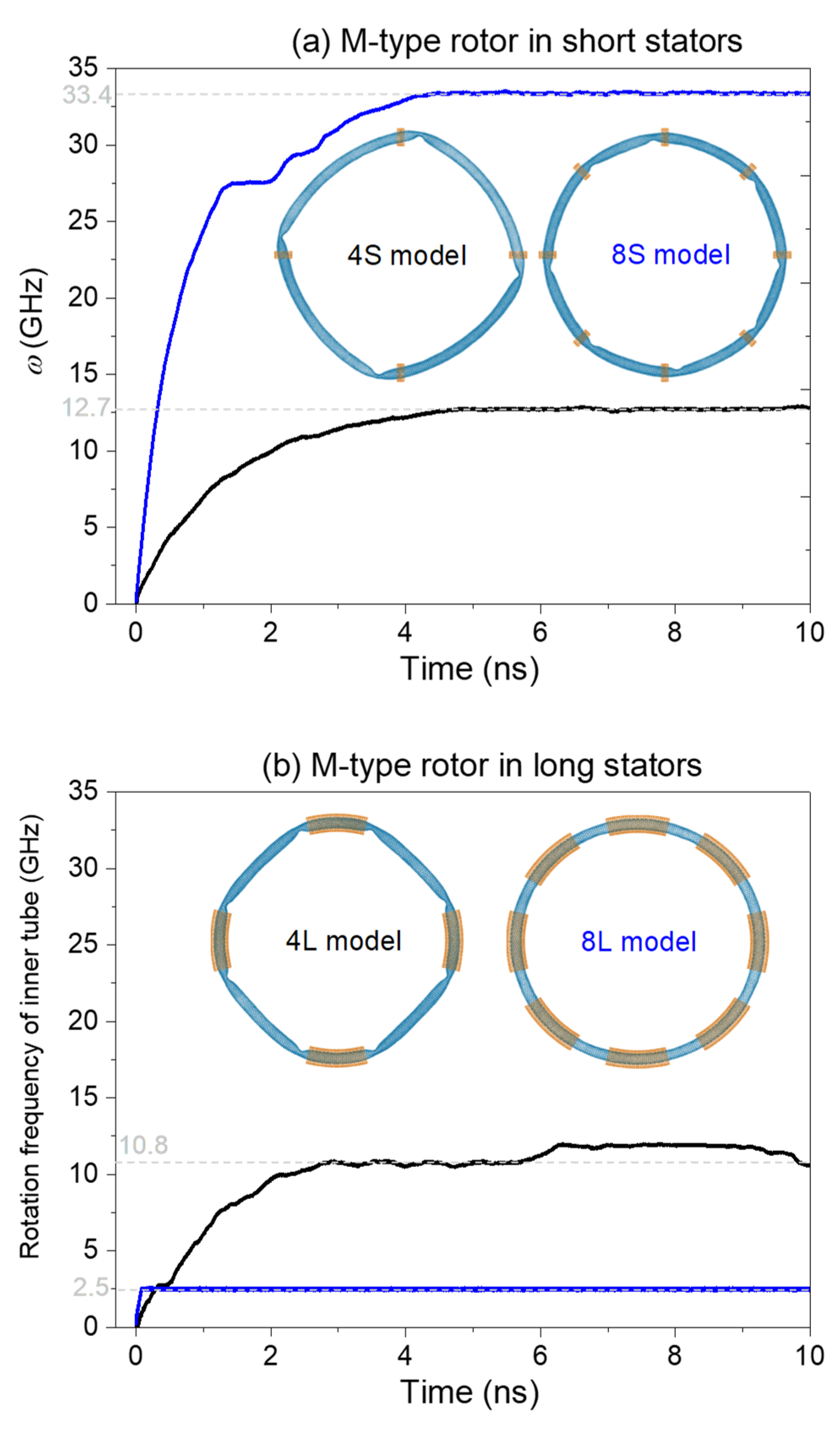
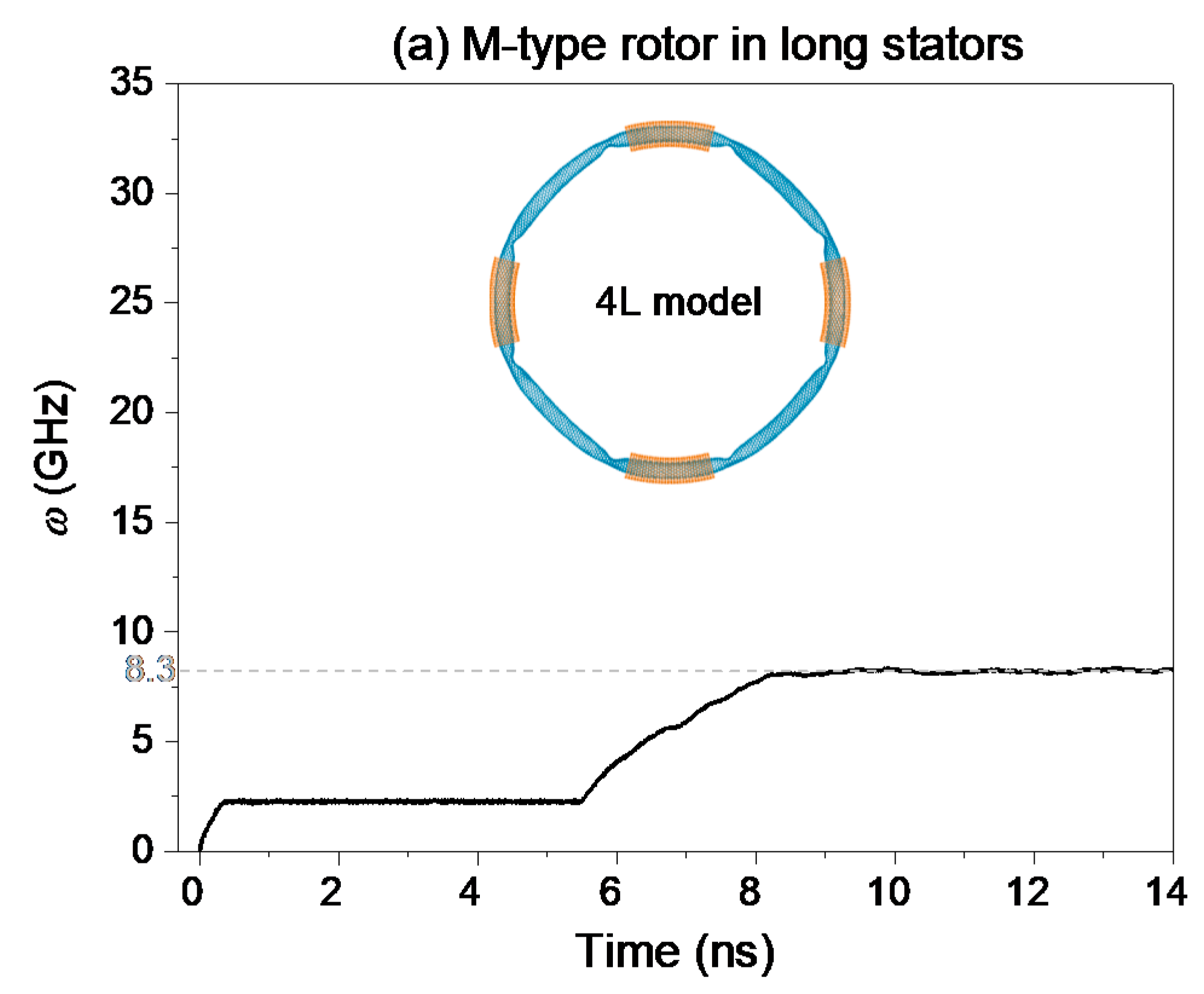
2.1.2. M-Type Rotor
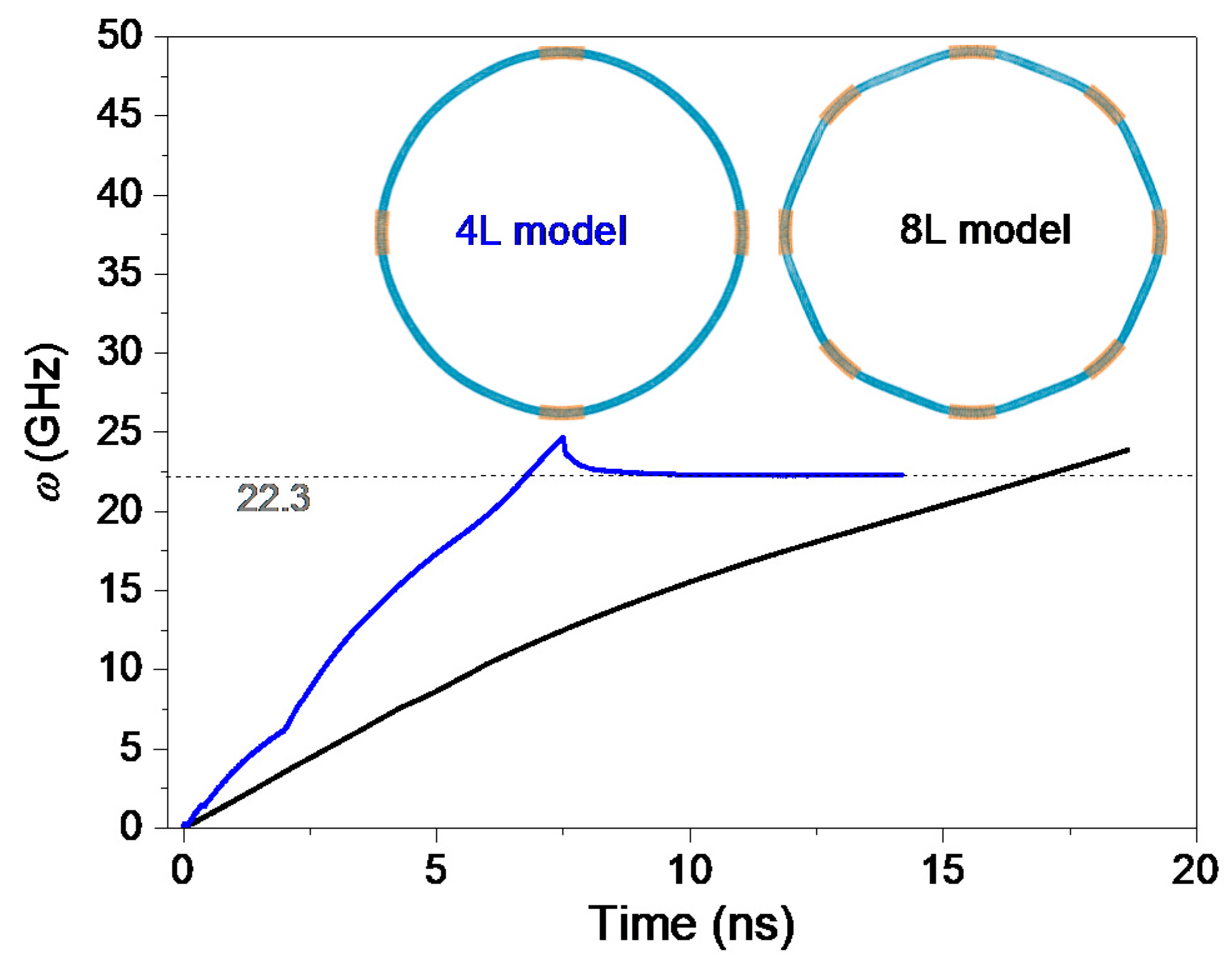
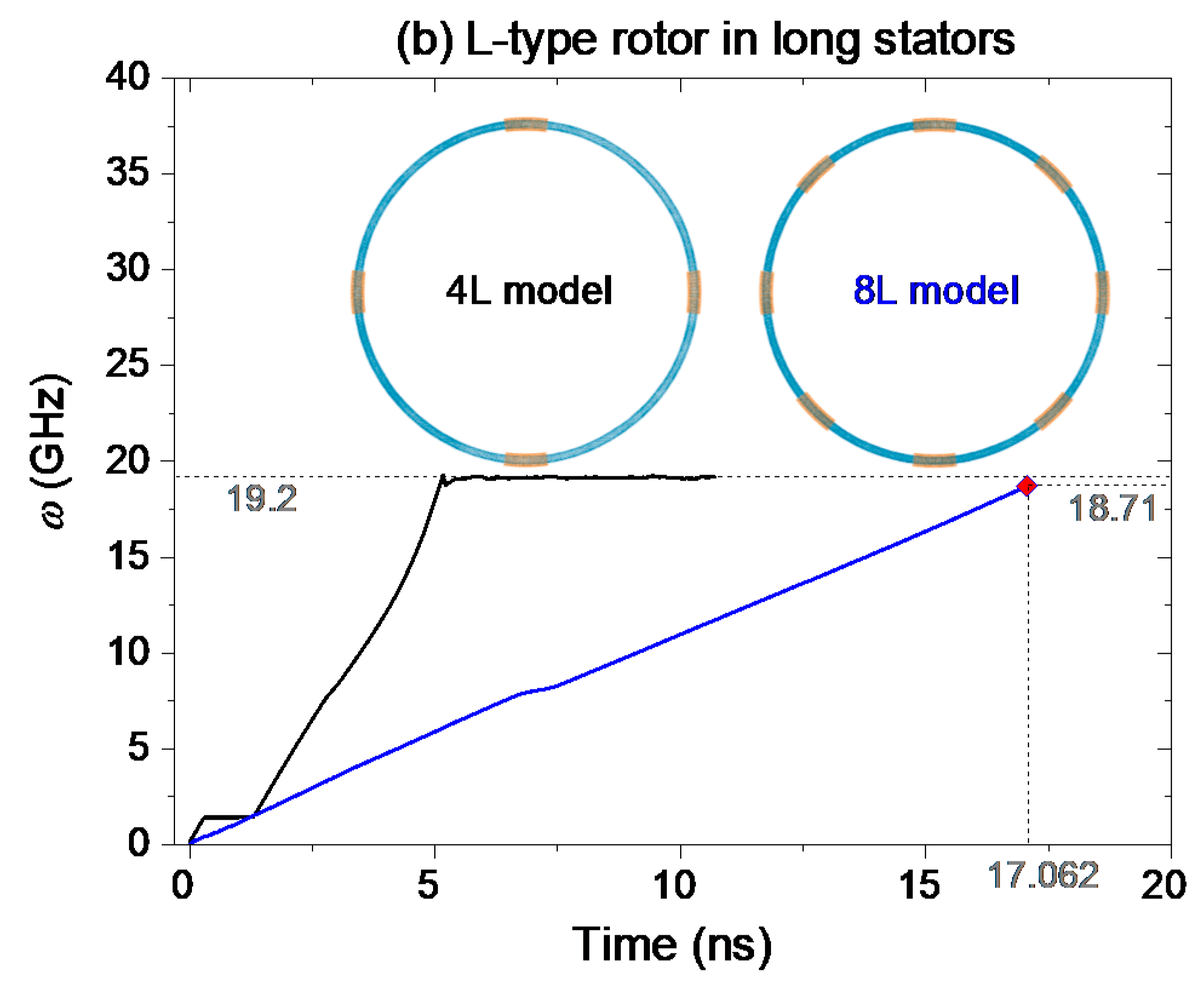
2.1.3. L-Type Rotor
2.2. Rotation of Rotor in the Stators After Relaxation
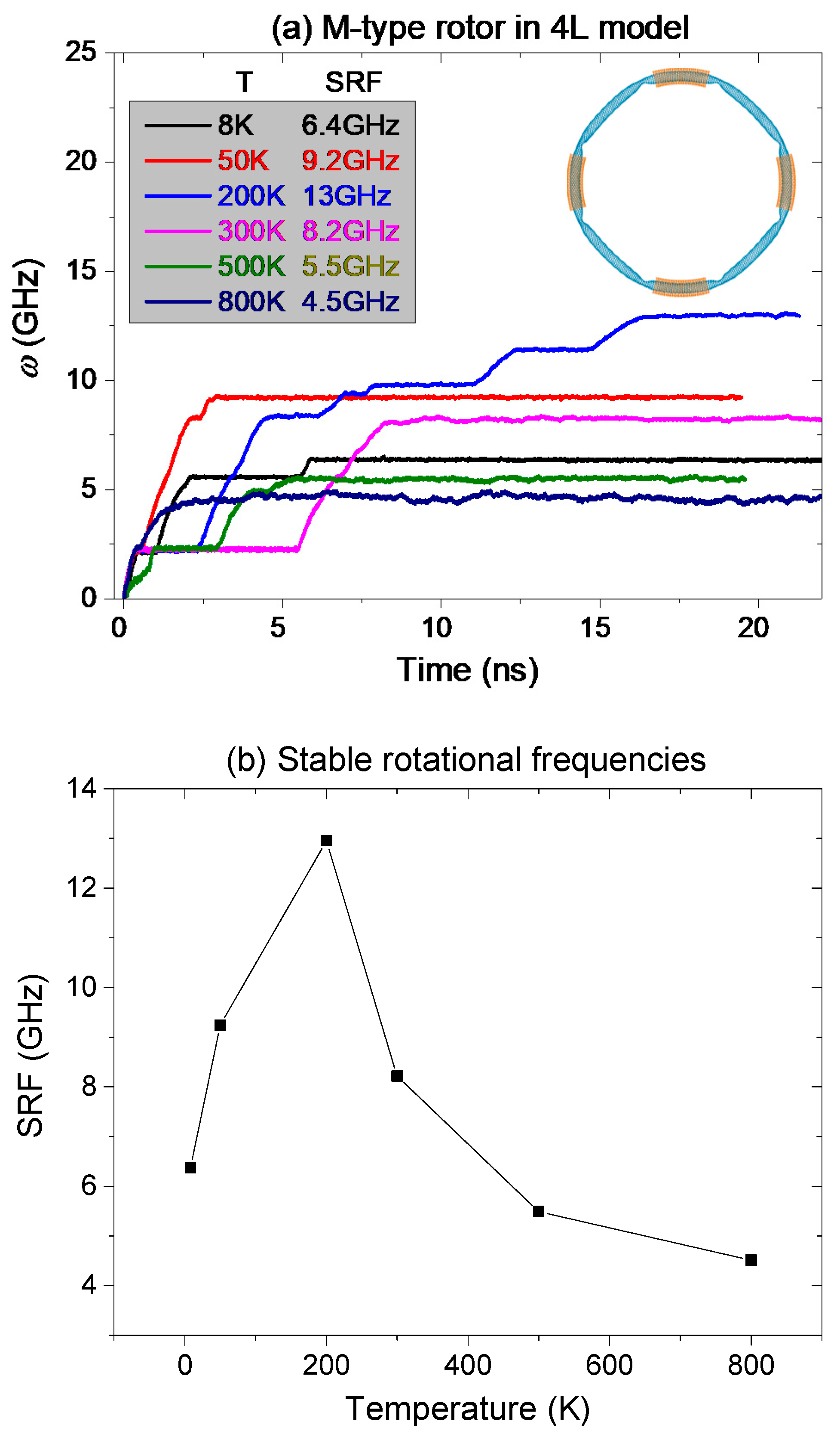
2.3. Temperature Effect on Rotation of Rotor
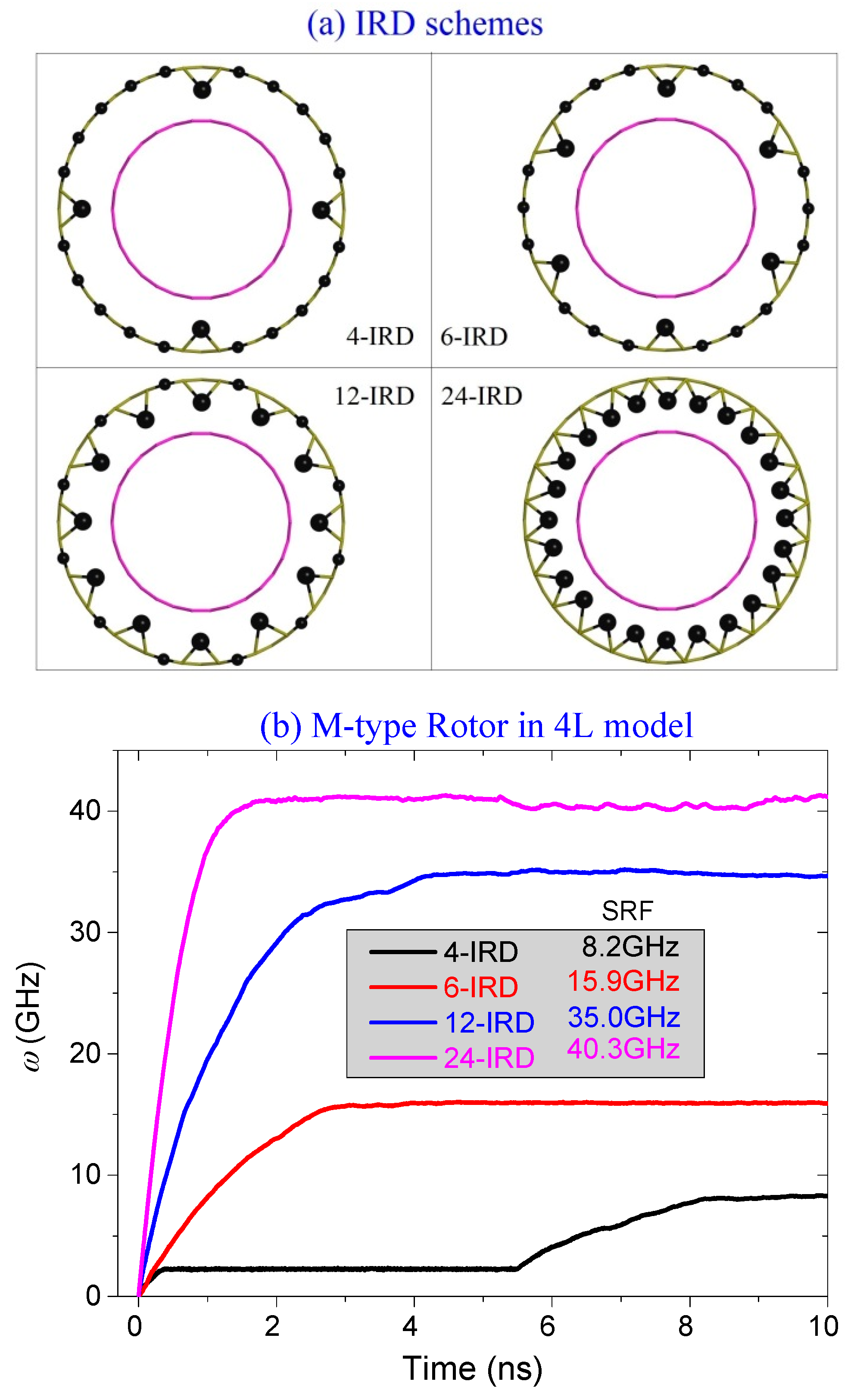
2.4. Effect of IRD Schemes on Rotation of Rotor
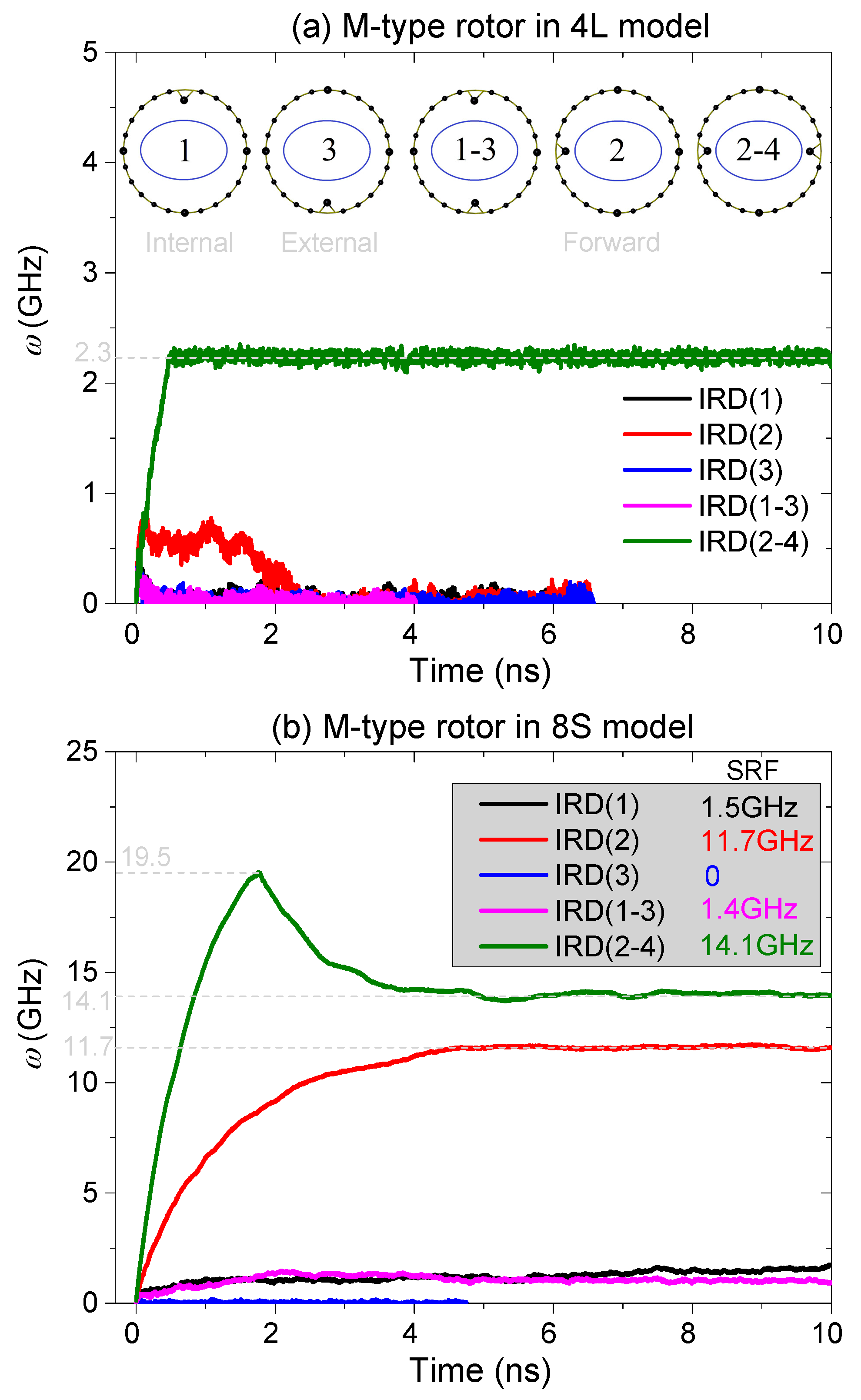
2.4.1. Different Layout of IRD Atom(s)
2.4.2. Different Number of IRD Atoms
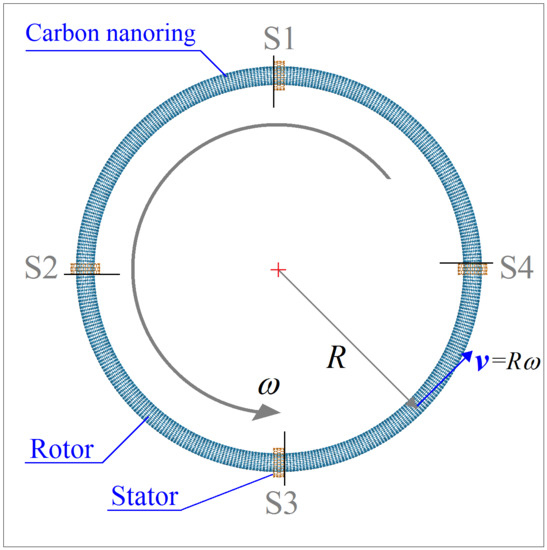
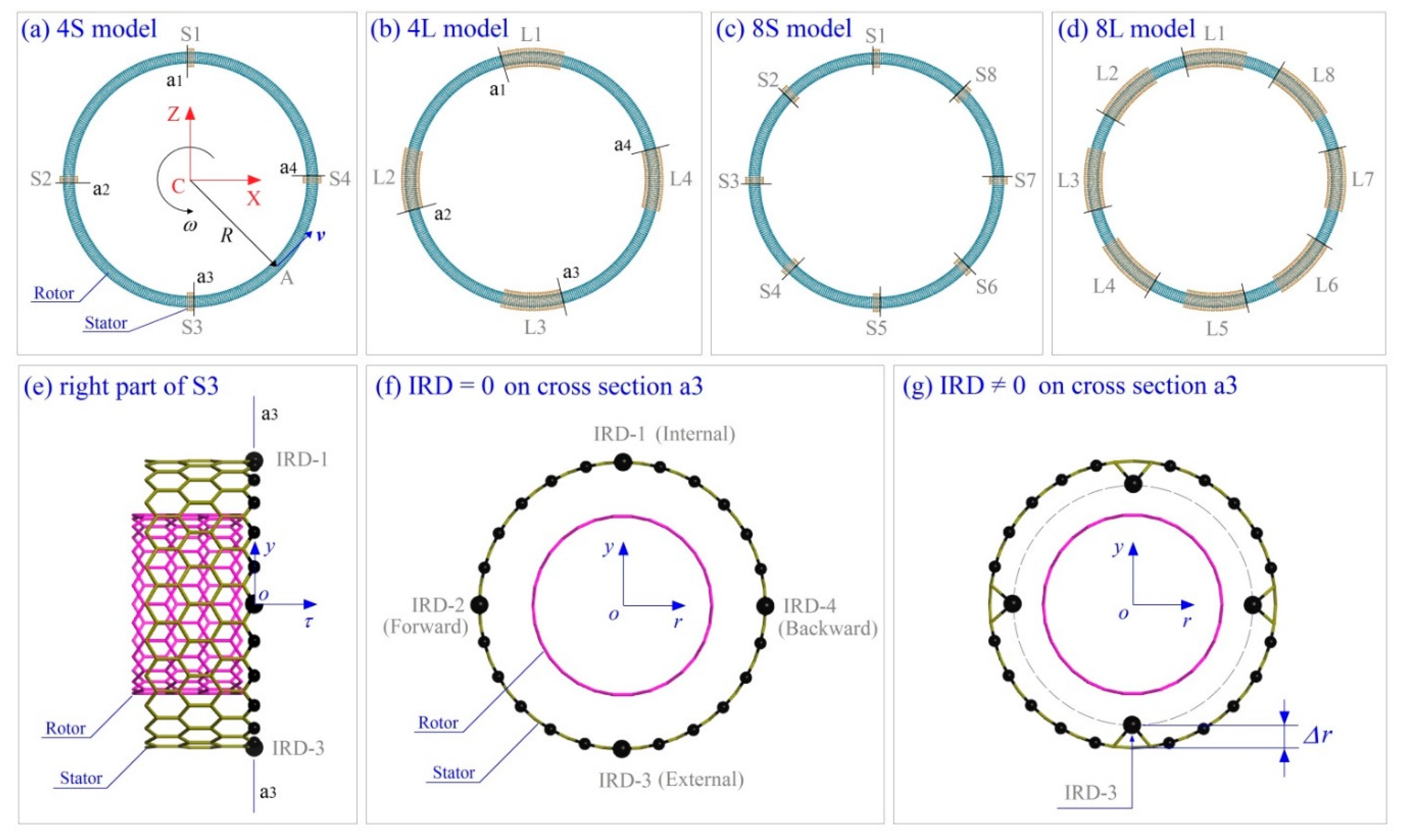
3. Models and Methodology
3.1. Models of Nanowheels
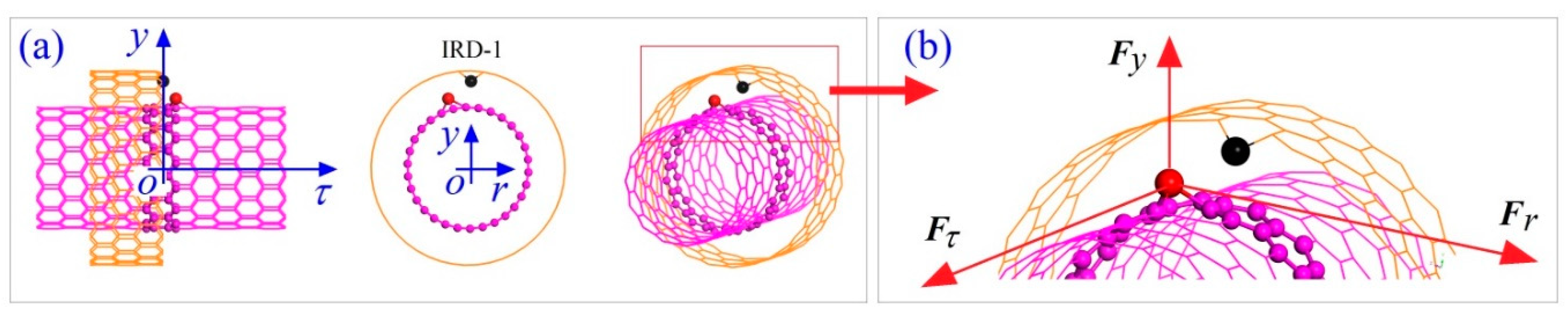
3.2. Reference Frames
3.3. Flowchart of Molecular Dynamics Simulation
3.4. Possible Configuration of Rotors after Relaxation
3.5. Propulsion of a Nanowheel within the NVT Ensemble
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Vogel, P.D. Nature’s design of nanomotors. Eur. J. Pharm. Biopharm. 2005, 60, 267–277. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Pumera, M. Fabrication of micro/nanoscale motors. Chem. Rev. 2015, 115, 8704–8735. [Google Scholar] [CrossRef] [PubMed]
- The Nobel Prize in Physics 2010. Available online: https://www.nobelprize.org/nobel_prizes/physics/laureates/2010/ (accessed on 21 December 2017).
- Somada, H.; Hirahara, K.; Akita, S.; Nakayama, Y. A molecular linear motor consisting of carbon nanotubes. Nano Lett. 2008, 9, 62–65. [Google Scholar] [CrossRef] [PubMed]
- Barreiro, A.; Rurali, R.; Hernandez, E.R.; Moser, J.; Pichler, T.; Forro, L.; Bachtold, A. Subnanometer motion of cargoes driven by thermal gradients along carbon nanotubes. Science 2008, 320, 775–778. [Google Scholar] [CrossRef] [PubMed]
- Kang, J.W.; Hwang, H.J. Nanoscale carbon nanotube motor schematics and simulations for micro-electro-mechanical machines. Nanotechnology 2004, 15, 1633–1638. [Google Scholar] [CrossRef]
- Wang, B.; Vuković, L.; Král, P. Nanoscale rotary motors driven by electron tunneling. Phys. Rev. Lett. 2008, 101, 186808. [Google Scholar] [CrossRef] [PubMed]
- Prokop, A.; Vacek, J.; Michl, J. Friction in carborane-based molecular rotors driven by gas flow or electric field: Classical molecular dynamics. ACS Nano 2012, 6, 1901–1914. [Google Scholar] [CrossRef] [PubMed]
- Cai, K.; Li, Y.; Qin, Q.H.; Yin, H. Gradientless temperature-driven rotating motor from a double-walled carbon nanotube. Nanotechnology 2014, 25, 505701. [Google Scholar] [CrossRef] [PubMed]
- Fennimore, A.; Yuzvinsky, T.; Han, W.-Q.; Fuhrer, M.; Cumings, J.; Zettl, A. Rotational actuators based on carbon nanotubes. Nature 2003, 424, 408–410. [Google Scholar] [CrossRef] [PubMed]
- Cai, K.; Cai, H.; Yin, H.; Qin, Q.H. Dynamic behavior of curved double-wall carbon nanotubes with rotating inner tube. RSC Adv. 2015, 5, 29908–29913. [Google Scholar] [CrossRef]
- Bourlon, B.; Glattli, D.C.; Miko, C.; Forró, L.; Bachtold, A. Carbon nanotube based bearing for rotational motions. Nano Lett. 2004, 4, 709–712. [Google Scholar] [CrossRef]
- Eelkema, R.; Pollard, M.M.; Vicario, J.; Katsonis, N.; Ramon, B.S.; Bastiaansen, C.W.; Broer, D.J.; Feringa, B.L. Molecular machines: Nanomotor rotates microscale objects. Nature 2006, 440, 163. [Google Scholar] [CrossRef] [PubMed]
- Alder, B.J.; Wainwright, T.E. Studies in molecular dynamics. I. General method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar] [CrossRef]
- Qin, Z.; Qin, Q.H.; Feng, X.Q. Mechanical property of carbon nanotubes with intramolecular junctions: Molecular dynamics simulations. Phys. Lett. A 2008, 372, 6661–6666. [Google Scholar] [CrossRef]
- Cai, K.; Liu, L.; Shi, J.; Qin, Q.H. Winding a nanotube from black phosphorus nanoribbon onto a CNT at low temperature: A molecular dynamics study. Mater. Design 2017, 121, 406–413. [Google Scholar] [CrossRef]
- Cai, K.; Wan, J.; Qin, Q.H.; Shi, J. Quantitative control of a rotary carbon nanotube motor under temperature stimulus. Nanotechnology 2016, 27, 055706. [Google Scholar] [CrossRef] [PubMed]
- Tu, Z.; Hu, X. Molecular motor constructed from a double-walled carbon nanotube driven by axially varying voltage. Phys. Rev. B 2005, 72, 033404. [Google Scholar] [CrossRef]
- Yang, L.; Cai, K.; Shi, J.; Qin, Q.H. Significance tests on the output power of a thermally driven rotary nanomotor. Nanotechnology 2017, 28, 215705. [Google Scholar] [CrossRef] [PubMed]
- Cai, K.; Yu, J.; Wan, J.; Yin, H.; Qin, Q.H. Configuration jumps of rotor in a nanomotor from carbon nanostructures. Carbon 2016, 101, 168–176. [Google Scholar] [CrossRef]
- Cai, K.; Yu, J.; Liu, L.; Shi, J.; Qin, Q.H. Rotation measurements of a thermally driven rotary nanomotor with a spring wing. Phys. Chem. Chem. Phys. 2016, 18, 22478–22486. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Liu, L.-N.; Cai, K.; Qin, Q.-H. Conditions for escape of a rotor in a rotary nanobearing from short triple-wall nanotubes. Sci. Rep. 2017, 7, 6772. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.; Kang, Y.L.; Lei, Z.K.; Qin, Q.H.; Li, Q. A new theoretical model of a carbon nanotube strain sensor. Chin. Phys. Lett. 2009, 26, 080701. [Google Scholar]
- Qiu, W.; Kang, Y.L.; Lei, Z.K.; Qin, Q.H.; Li, Q. Experimental study of the Raman strain rosette based on the carbon nanotube strain sensor. J. Raman Spectrosc. 2010, 41, 1216–1220. [Google Scholar] [CrossRef]
- Qiu, W.; Li, Q.; Lei, Z.K.; Qin, Q.H.; Deng, W.L. The use of a carbon nanotube sensor for measuring strain by micro-Raman spectroscopy. Carbon 2013, 53, 161–168. [Google Scholar] [CrossRef]
- Martel, R.; Shea, H.R.; Avouris, P. Rings of single-walled carbon nanotubes. Nature 1999, 398, 299. [Google Scholar] [CrossRef] [PubMed]
- Sano, M.; Kamino, A.; Okamura, J.; Shinkai, S. Ring closure of carbon nanotubes. Science 2001, 293, 1299–1301. [Google Scholar] [CrossRef] [PubMed]
- Geng, J.; Ko, Y.K.; Youn, S.C.; Kim, Y.-H.; Kim, S.A.; Jung, D.-H.; Jung, H.-T. Synthesis of SWNT rings by noncovalent hybridization of porphyrins and single-walled carbon nanotubes. J. Phys. Chem. C 2008, 112, 12264–12271. [Google Scholar] [CrossRef]
- Komatsu, N. Ultrasonic isolation of toroidal aggregates of single-walled carbon nano tubes. Carbon 2006, 44, 2091–2093. [Google Scholar] [CrossRef]
- Guo, A.; Fu, Y.; Guan, L.; Zhang, Z.; Wu, W.; Chen, J.; Shi, Z.; Gu, Z.; Huang, R.; Zhang, X. Spontaneously formed closed rings of single-wall carbon nanotube bundles and their physical mechanism. J. Phys. Chem. C 2007, 111, 3555–3559. [Google Scholar] [CrossRef]
- Chaves Neto, A.M.d.J.; Nero, J.D. Toroidal carbon nanotube as molecular motor. J. Comput. Theor. Nanosci. 2007, 4, 107–110. [Google Scholar]
- Belikov, A.; Lozovik, Y.E.; Nikolaev, A.; Popov, A. Double-wall nanotubes: Classification and barriers to walls relative rotation, sliding and screwlike motion. Chem. Phys. Lett. 2004, 385, 72–78. [Google Scholar] [CrossRef]
- Guo, Z.; Chang, T.; Guo, X.; Gao, H. Thermal-induced edge barriers and forces in interlayer interaction of concentric carbon nanotubes. Phys. Rev. Lett. 2011, 107, 105502. [Google Scholar] [CrossRef] [PubMed]
- Cumings, J.; Zettl, A. Low-friction nanoscale linear bearing realized from multiwall carbon nanotubes. Science 2000, 289, 602–604. [Google Scholar] [CrossRef] [PubMed]
- Cook, E.H.; Buehler, M.J.; Spakovszky, Z.S. Mechanism of friction in rotating carbon nanotube bearings. J. Mech. Phys. Solids 2013, 61, 652–673. [Google Scholar] [CrossRef]
- Zhang, R.; Ning, Z.; Zhang, Y.; Zheng, Q.; Chen, Q.; Xie, H.; Zhang, Q.; Qian, W.; Wei, F. Superlubricity in centimetres-long double-walled carbon nanotubes under ambient conditions. Nat. Nanotechnol. 2013, 8, 912–916. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Jones, J.E. On the determination of molecular fields. II. From the equation of state of a gas. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695. [Google Scholar] [CrossRef]
- Yu, B.; Liu, C.; Hou, P.-X.; Tian, Y.; Li, S.; Liu, B.; Li, F.; Kauppinen, E.I.; Cheng, H.-M. Bulk synthesis of large diameter semiconducting single-walled carbon nanotubes by oxygen-assisted floating catalyst chemical vapor deposition. J. Am. Chem. Soc. 2011, 133, 5232–5235. [Google Scholar] [CrossRef] [PubMed]
- Ye, H.F.; Zheng, Y.G.; Zhang, Z.Q.; Zhang, H.W.; Chen, Z. Controllable deformation of salt water-filled carbon nanotubes using an electric field with application to molecular sieving. Nanotechnology 2016, 27, 315702. [Google Scholar] [CrossRef] [PubMed]
- Cai, K.; Wan, J.; Wei, N.; Shi, J.; Qin, Q.H. Buckling behaviour of composites with double wall nanotubes from carbon and phosphorous. Phys. Chem. Chem. Phys. 2017, 19, 10922–10930. [Google Scholar] [CrossRef] [PubMed]

| Ring (i.e., Rotor) | Stator | ||||||
|---|---|---|---|---|---|---|---|
| Type | Chiral Index | R/nm | Num. Atoms | Type | Chiral Index | Length/nm | Num. Atoms |
| S | (15, 0) | 6.373 | 5640 | Short | (24, 0) | 0.710 | 192 |
| M | (15, 0) | 12.746 | 11,280 | Long | (24, 0) | 6.248 | 1440 |
| L | (15, 0) | 25.493 | 22,560 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, H.; Shi, J.; Cai, K.; Qin, Q.-H. Thermal Vibration-Induced Rotation of Nano-Wheel: A Molecular Dynamics Study. Int. J. Mol. Sci. 2018, 19, 3513. https://doi.org/10.3390/ijms19113513
Duan H, Shi J, Cai K, Qin Q-H. Thermal Vibration-Induced Rotation of Nano-Wheel: A Molecular Dynamics Study. International Journal of Molecular Sciences. 2018; 19(11):3513. https://doi.org/10.3390/ijms19113513
Chicago/Turabian StyleDuan, Haiyan, Jiao Shi, Kun Cai, and Qing-Hua Qin. 2018. "Thermal Vibration-Induced Rotation of Nano-Wheel: A Molecular Dynamics Study" International Journal of Molecular Sciences 19, no. 11: 3513. https://doi.org/10.3390/ijms19113513
APA StyleDuan, H., Shi, J., Cai, K., & Qin, Q.-H. (2018). Thermal Vibration-Induced Rotation of Nano-Wheel: A Molecular Dynamics Study. International Journal of Molecular Sciences, 19(11), 3513. https://doi.org/10.3390/ijms19113513