Design for Additive Bio-Manufacturing: From Patient-Specific Medical Devices to Rationally Designed Meta-Biomaterials
Abstract
1. Introduction
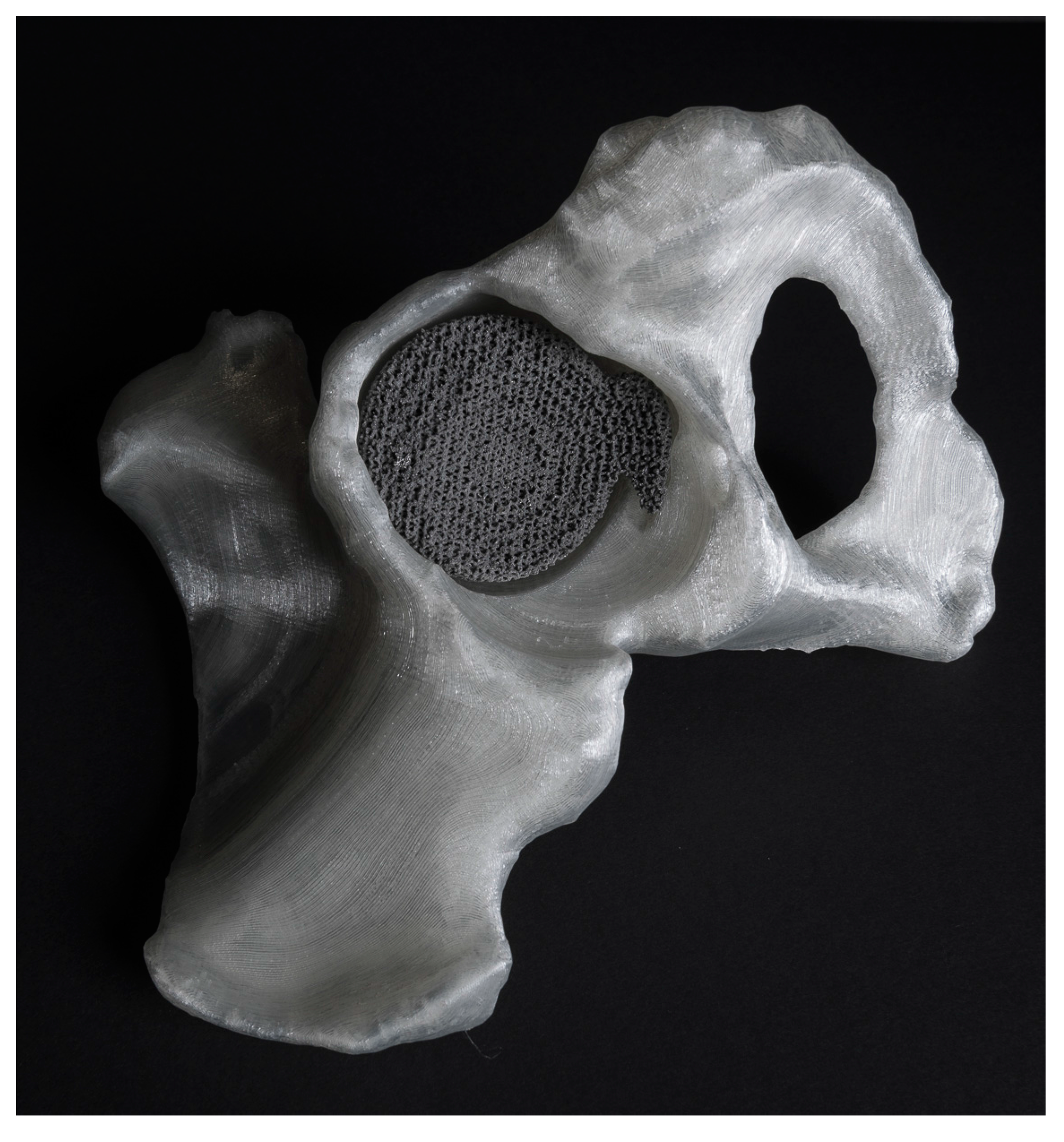
2. Patient-Specific Designs
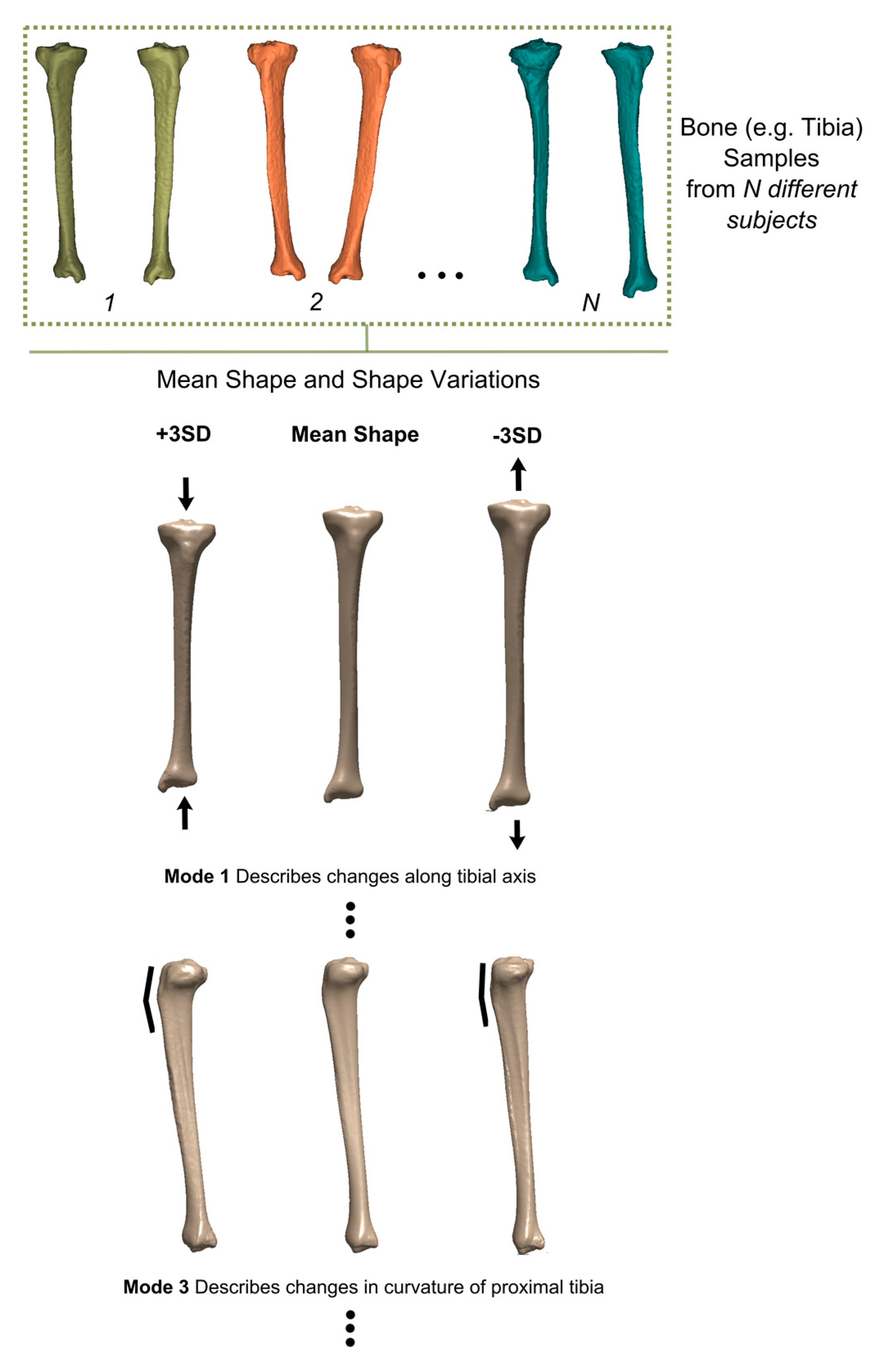
2.1. Image-Based Design Personalization
2.2. Parametric and Non-Parametric Designs
3. Topologically Complex Designs and Metamaterials
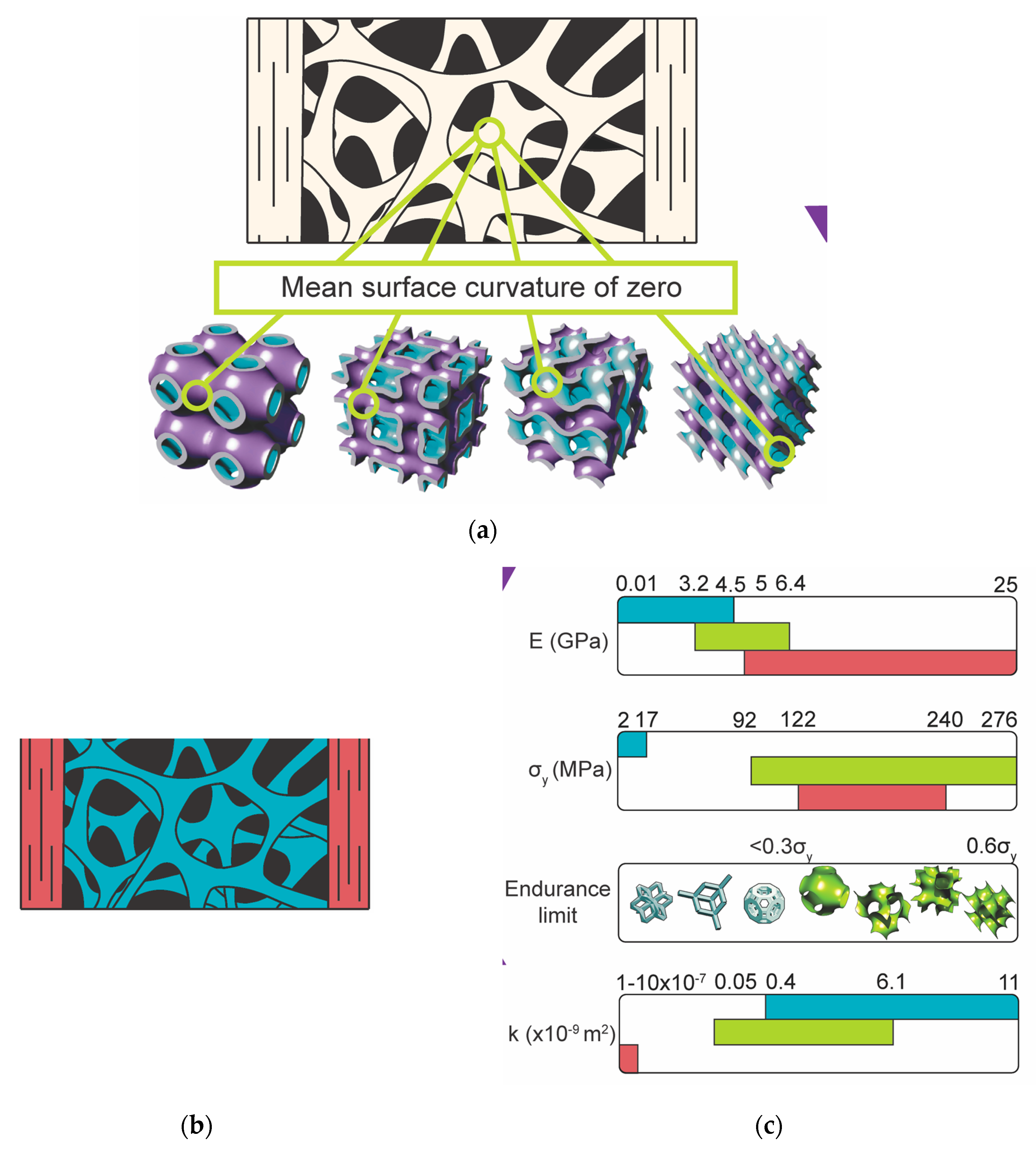
3.1. Metamaterials
3.2. Rational and Computationally Enabled Design
4. Optimal and Bio-Inspired Designs
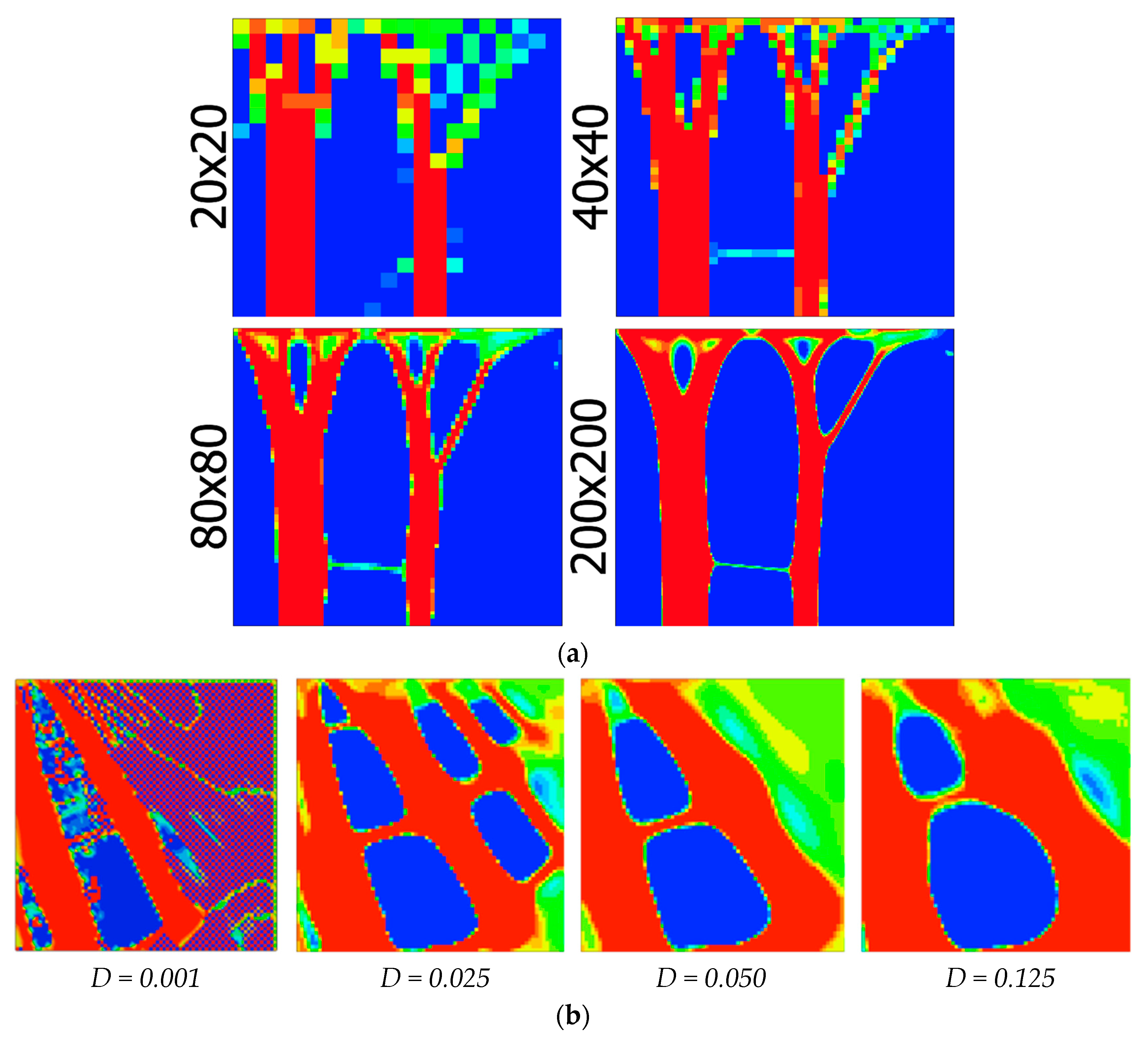
4.1. Topology Optimization
4.2. Bio-Inspired Design
5. Discussion
6. Conclusions
Conflicts of Interest
References
- Zadpoor, A.A.; Malda, J. Additive manufacturing of biomaterials, tissues, and organs. Ann. Biomed. Eng. 2017, 45, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Lyons, B. Additive manufacturing in aerospace: Examples and research outlook. Bridge 2014, 44, 13–19. [Google Scholar]
- ISO (International Organization for Standardization). ASTM/ISO 52900: 2015. In Additive Manufacturing—General Principles—Terminology; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Rengier, F.; Mehndiratta, A.; von Tengg-Kobligk, H.; Zechmann, C.M.; Unterhinninghofen, R.; Kauczor, H.-U.; Giesel, F.L. 3D printing based on imaging data: Review of medical applications. Int. J. Comput. Assist. Radiol. Surg. 2010, 5, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, S.; Dawood, A.; Richards, R.; Henckel, J.; Hart, A. A review of rapid prototyped surgical guides for patient-specific total knee replacement. J. Bone Jt. Surg. Br. 2012, 94, 1457–1461. [Google Scholar] [CrossRef] [PubMed]
- Rankin, T.M.; Giovinco, N.A.; Cucher, D.J.; Watts, G.; Hurwitz, B.; Armstrong, D.G. Three-dimensional printing surgical instruments: Are we there yet? J. Surg. Res. 2014, 189, 193–197. [Google Scholar] [CrossRef] [PubMed]
- Bourell, D.; Stucker, B.; Espalin, D.; Arcaute, K.; Rodriguez, D.; Medina, F.; Posner, M.; Wicker, R. Fused deposition modeling of patient-specific polymethylmethacrylate implants. Rapid Prototyp. J. 2010, 16, 164–173. [Google Scholar]
- Dérand, P.; Rännar, L.-E.; Hirsch, J.-M. Imaging, virtual planning, design, and production of patient-specific implants and clinical validation in craniomaxillofacial surgery. Craniomaxillofac. Trauma Reconstr. 2012, 5, 137–144. [Google Scholar] [CrossRef] [PubMed]
- Jardini, A.L.; Larosa, M.A.; Maciel Filho, R.; de Carvalho Zavaglia, C.A.; Bernardes, L.F.; Lambert, C.S.; Calderoni, D.R.; Kharmandayan, P. Cranial reconstruction: 3D biomodel and custom-built implant created using additive manufacturing. J. Cranio Maxillofac. Surg. 2014, 42, 1877–1884. [Google Scholar] [CrossRef] [PubMed]
- Wauthle, R.; van Der Stok, J.; Yavari, S.A.; van Humbeeck, J.; Kruth, J.-P.; Zadpoor, A.A.; Weinans, H.; Mulier, M.; Schrooten, J. Additively manufactured porous tantalum implants. Acta Biomater. 2015, 14, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Burn, M.B.; Ta, A.; Gogola, G.R. Three-dimensional printing of prosthetic hands for children. J. Hand Surg. 2016, 41, e103–e109. [Google Scholar] [CrossRef] [PubMed]
- Colombo, G.; Filippi, S.; Rizzi, C.; Rotini, F. A new design paradigm for the development of custom-fit soft sockets for lower limb prostheses. Comput. Ind. 2010, 61, 513–523. [Google Scholar] [CrossRef]
- Gretsch, K.F.; Lather, H.D.; Peddada, K.V.; Deeken, C.R.; Wall, L.B.; Goldfarb, C.A. Development of novel 3D-printed robotic prosthetic for transradial amputees. Prosthet. Orthot. Int. 2016, 40, 400–403. [Google Scholar] [CrossRef] [PubMed]
- Creylman, V.; Muraru, L.; Pallari, J.; Vertommen, H.; Peeraer, L. Gait assessment during the initial fitting of customized selective laser sintering ankle foot orthoses in subjects with drop foot. Prosthet. Orthot. Int. 2013, 37, 132–138. [Google Scholar] [CrossRef] [PubMed]
- Mavroidis, C.; Ranky, R.G.; Sivak, M.L.; Patritti, B.L.; DiPisa, J.; Caddle, A.; Gilhooly, K.; Govoni, L.; Sivak, S.; Lancia, M. Patient specific ankle-foot orthoses using rapid prototyping. J. Neuroeng Rehabil 2011, 8, 1. [Google Scholar] [CrossRef] [PubMed]
- Palousek, D.; Rosicky, J.; Koutny, D.; Stoklásek, P.; Navrat, T. Pilot study of the wrist orthosis design process. Rapid Prototyp. J. 2014, 20, 27–32. [Google Scholar] [CrossRef]
- Telfer, S.; Pallari, J.; Munguia, J.; Dalgarno, K.; McGeough, M.; Woodburn, J. Embracing additive manufacture: Implications for foot and ankle orthosis design. BMC Musculoskelet. Disord. 2012, 13, 84. [Google Scholar] [CrossRef] [PubMed]
- Goyanes, A.; Buanz, A.B.; Basit, A.W.; Gaisford, S. Fused-filament 3D printing (3Dp) for fabrication of tablets. Int. J. Pharm. 2014, 476, 88–92. [Google Scholar] [CrossRef] [PubMed]
- Goyanes, A.; Martinez, P.R.; Buanz, A.; Basit, A.W.; Gaisford, S. Effect of geometry on drug release from 3D printed tablets. Int. J. Pharm. 2015, 494, 657–663. [Google Scholar] [CrossRef] [PubMed]
- Goyanes, A.; Wang, J.; Buanz, A.; Martínez-Pacheco, R.; Telford, R.; Gaisford, S.; Basit, A.W. 3D printing of medicines: Engineering novel oral devices with unique design and drug release characteristics. Mol. Pharm. 2015, 12, 4077–4084. [Google Scholar] [CrossRef] [PubMed]
- Khaled, S.A.; Burley, J.C.; Alexander, M.R.; Roberts, C.J. Desktop 3D printing of controlled release pharmaceutical bilayer tablets. Int. J. Pharm. 2014, 461, 105–111. [Google Scholar] [CrossRef] [PubMed]
- Castilho, M.; Dias, M.; Vorndran, E.; Gbureck, U.; Fernandes, P.; Pires, I.; Gouveia, B.; Armés, H.; Pires, E.; Rodrigues, J. Application of a 3D printed customized implant for canine cruciate ligament treatment by tibial tuberosity advancement. Biofabrication 2014, 6, 025005. [Google Scholar] [CrossRef] [PubMed]
- Hespel, A.M.; Wilhite, R.; Hudson, J. Applications for 3D printers in veterinary medicine. Vet. Radiol. Ultrasound 2014, 55, 347–358. [Google Scholar] [CrossRef] [PubMed]
- Doubrovski, Z.; Verlinden, J.C.; Geraedts, J.M. Optimal design for additive manufacturing: Opportunities and challenges. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28–31 August 2011; American Society of Mechanical Engineers: New York, NY, USA, 2011; pp. 635–646. [Google Scholar]
- Reimer, S.M.; Lueth, T.C.; D’Angelo, L.T. Individualized arm shells towards an ergonomic design of exoskeleton robots. In Proceedings of the 2014 IEEE International Conference on Systems, Man and Cybernetics (SMC), San Diego, CA, USA, 5–8 Octomber 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 3958–3965. [Google Scholar]
- Salles, A.S.; Gyi, D.E. An evaluation of personalised insoles developed using additive manufacturing. J. Sports Sci. 2013, 31, 442–450. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, R.; Minuzzi, R. The 3D printing’s panorama in fashion design. Moda Doc. 2015, 11, 1–12. [Google Scholar]
- Melnikova, R.; Ehrmann, A.; Finsterbusch, K. 3D printing of textile-based structures by fused deposition modelling (fdm) with different polymer materials. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Ningbo, China, 27–29 May 2014; IOP Publishing: Bristol, UK, 2014; p. 012018. [Google Scholar]
- Spahiu, T.; Grimmelsmann, N.; Ehrmann, A.; Shehi, E.; Piperi, E. On the possible use of 3D printing for clothing and shoe manufacture. In Proceedings of the 7th International Conference of Textile, Tirana, Albania, 10–11 November 2016. [Google Scholar]
- Lipton, J.I.; Cutler, M.; Nigl, F.; Cohen, D.; Lipson, H. Additive manufacturing for the food industry. Trends Food Sci. Tech. 2015, 43, 114–123. [Google Scholar] [CrossRef]
- Sun, J.; Zhou, W.; Huang, D.; Fuh, J.Y.; Hong, G.S. An overview of 3D printing technologies for food fabrication. Food Bioprocess Technol. 2015, 8, 1605–1615. [Google Scholar] [CrossRef]
- Carroll, Á.M.; Fyfe, N. A comparison of the effect of the aesthetics of digital cosmetic prostheses on body image and well-being. J. Prosthet. Orthot. 2004, 16, 66–68. [Google Scholar] [CrossRef]
- James, M.; Robson, S. Straightforward reconstruction of 3D surfaces and topography with a camera: Accuracy and geoscience application. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Won, J.H.; Lee, M.H.; Park, I.K. Active 3D shape acquisition using smartphones. In Proceedings of the 2012 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Providence, RI, USA, 16–21 June 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 29–34. [Google Scholar]
- Abràmoff, M.D.; Magalhães, P.J.; Ram, S.J. Image processing with imageJ. Biophotonics Int. 2004, 11, 36–42. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671. [Google Scholar] [CrossRef] [PubMed]
- Botha, C.P. Technical report: Devide—The delft visualisation and image processing development environment. May 2006, 31, 1–49. [Google Scholar]
- Buie, H.R.; Campbell, G.M.; Klinck, R.J.; MacNeil, J.A.; Boyd, S.K. Automatic segmentation of cortical and trabecular compartments based on a dual threshold technique for in vivo micro-CT bone analysis. Bone 2007, 41, 505–515. [Google Scholar] [CrossRef] [PubMed]
- Hara, T.; Tanck, E.; Homminga, J.; Huiskes, R. The influence of microcomputed tomography threshold variations on the assessment of structural and mechanical trabecular bone properties. Bone 2002, 31, 107–109. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, C.-H.; Chui, C.-K.; Ong, S.-H. Fast segmentation of bone in CT images using 3D adaptive thresholding. Comput. Biol. Med. 2010, 40, 231–236. [Google Scholar] [CrossRef] [PubMed]
- Heimann, T.; Meinzer, H.-P. Statistical shape models for 3D medical image segmentation: A review. Med. Image Anal. 2009, 13, 543–563. [Google Scholar] [CrossRef] [PubMed]
- Sarkalkan, N.; Weinans, H.; Zadpoor, A.A. Statistical shape and appearance models of bones. Bone 2014, 60, 129–140. [Google Scholar] [CrossRef] [PubMed]
- Bos, E.; Scholten, T.; Song, Y.; Verlinden, J.; Wolff, J.; Forouzanfar, T.; Helder, M.; van Zuijlen, P. Developing a parametric ear model for auricular reconstruction: A new step towards patient-specific implants. J. Cranio Maxillofac. Surg. 2015, 43, 390–395. [Google Scholar] [CrossRef] [PubMed]
- Moreo, M. Parametric Design of a 3D Printable Hand Prosthesis for Children in Developing Countries. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, November 2016. [Google Scholar]
- Lee, J.H.; Singer, J.P.; Thomas, E.L. Micro-/nanostructured mechanical metamaterials. Adv. Mater. 2012, 24, 4782–4810. [Google Scholar] [CrossRef] [PubMed]
- Zadpoor, A.A. Mechanical meta-materials. Mater. Horiz. 2016, 3, 371–381. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Wegener, M. Optical metamaterials—More bulky and less lossy. Science 2010, 330, 1633–1634. [Google Scholar] [CrossRef] [PubMed]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008, 455, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Belkin, M.; Alù, A. Twisted optical metamaterials for planarized ultrathin broadband circular polarizers. Nat. Commun. 2012, 3, 870. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chan, C. Acoustic cloaking in three dimensions using acoustic metamaterials. Appl. Phys. Lett. 2007, 91, 183518. [Google Scholar] [CrossRef]
- Lu, M.-H.; Feng, L.; Chen, Y.-F. Phononic crystals and acoustic metamaterials. Mater. Today 2009, 12, 34–42. [Google Scholar] [CrossRef]
- Mei, J.; Ma, G.; Yang, M.; Yang, Z.; Wen, W.; Sheng, P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 2012, 3, 756. [Google Scholar] [CrossRef] [PubMed]
- Torrent, D.; Sánchez-Dehesa, J. Acoustic metamaterials for new two-dimensional sonic devices. New J. Phys. 2007, 9, 323. [Google Scholar] [CrossRef]
- Florijn, B.; Coulais, C.; van Hecke, M. Programmable mechanical metamaterials. Phys. Rev. Lett. 2014, 113, 175503. [Google Scholar] [CrossRef] [PubMed]
- Kadic, M.; Bückmann, T.; Stenger, N.; Thiel, M.; Wegener, M. On the practicability of pentamode mechanical metamaterials. Appl. Phys. Lett. 2012, 100, 191901. [Google Scholar] [CrossRef]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A. Ultralight, ultrastiff mechanical metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef] [PubMed]
- Amin Yavari, S.; Ahmadi, S.; Wauthle, R.; Pouran, B.; Schrooten, J.; Weinans, H.; Zadpoor, A. Relationship between unit cell type and porosity and the fatigue behavior of selective laser melted meta-biomaterials. J. Mech. Behav. Biomed. Mater. 2015, 43, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Lv, C.; Krishnaraju, D.; Konjevod, G.; Yu, H.; Jiang, H. Origami based mechanical metamaterials. Sci. Rep. 2014, 4, 5979. [Google Scholar] [CrossRef] [PubMed]
- Yasuda, H.; Yang, J. Reentrant origami-based metamaterials with negative poisson’s ratio and bistability. Phys. Rev. Lett. 2015, 114, 185502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Xu, X.; Lin, D.; Chen, W.; Xiong, G.; Yu, Y.; Fisher, T.S.; Li, H. Hyperbolically patterned 3D graphene metamaterial with negative poisson’s ratio and superelasticity. Adv Mater. 2016, 28, 2229–2237. [Google Scholar] [CrossRef] [PubMed]
- Grima, J.N.; Attard, D.; Caruana-Gauci, R.; Gatt, R. Negative linear compressibility of hexagonal honeycombs and related systems. Scr. Mater. 2011, 65, 565–568. [Google Scholar] [CrossRef]
- Grima, J.N.; Caruana-Gauci, R. Mechanical metamaterials: Materials that push back. Nat. Mater. 2012, 11, 565–566. [Google Scholar] [CrossRef] [PubMed]
- Nicolaou, Z.G.; Motter, A.E. Mechanical metamaterials with negative compressibility transitions. Nat. Mater. 2012, 11, 608–613. [Google Scholar] [CrossRef] [PubMed]
- Lavine, M.S. Folding robots and metamaterials. Science 2014, 345, 633. [Google Scholar] [CrossRef]
- Silverberg, J.L.; Evans, A.A.; McLeod, L.; Hayward, R.C.; Hull, T.; Santangelo, C.D.; Cohen, I. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 2014, 345, 647–650. [Google Scholar] [CrossRef] [PubMed]
- Walia, S.; Shah, C.M.; Gutruf, P.; Nili, H.; Chowdhury, D.R.; Withayachumnankul, W.; Bhaskaran, M.; Sriram, S. Flexible metasurfaces and metamaterials: A review of materials and fabrication processes at micro-and nano-scales. Appl. Phys. Rev. 2015, 2, 011303. [Google Scholar] [CrossRef]
- Ergin, T.; Stenger, N.; Brenner, P.; Pendry, J.B.; Wegener, M. Three-dimensional invisibility cloak at optical wavelengths. Science 2010, 328, 337–339. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Luo, Y.; Liu, X.; Barbastathis, G. Macroscopic invisibility cloak for visible light. Phys. Rev. Lett. 2011, 106, 033901. [Google Scholar] [CrossRef] [PubMed]
- Hedayati, R.; Leeflang, A.; Zadpoor, A. Additively manufactured metallic pentamode meta-materials. Appl. Phys. Lett. 2017, 110, 091905. [Google Scholar] [CrossRef]
- Joshi, M.G.; Advani, S.G.; Miller, F.; Santare, M.H. Analysis of a femoral hip prosthesis designed to reduce stress shielding. J. Biomech. 2000, 33, 1655–1662. [Google Scholar] [CrossRef]
- Nagels, J.; Stokdijk, M.; Rozing, P.M. Stress shielding and bone resorption in shoulder arthroplasty. J. Shoulder Elb. Surg. 2003, 12, 35–39. [Google Scholar] [CrossRef] [PubMed]
- Karande, T.S.; Ong, J.L.; Agrawal, C.M. Diffusion in musculoskeletal tissue engineering scaffolds: Design issues related to porosity, permeability, architecture, and nutrient mixing. Ann. Biomed. Eng. 2004, 32, 1728–1743. [Google Scholar] [CrossRef] [PubMed]
- Mitsak, A.G.; Kemppainen, J.M.; Harris, M.T.; Hollister, S.J. Effect of polycaprolactone scaffold permeability on bone regeneration in vivo. Tissue Eng. Part A 2011, 17, 1831–1839. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.; Lin, C.-Y.; Hollister, S.J. Topology optimization of three dimensional tissue engineering scaffold architectures for prescribed bulk modulus and diffusivity. Struct. Multidiscip. Optim. 2010, 42, 633–644. [Google Scholar] [CrossRef]
- Bobbert, F.; Lietaert, K.; Eftekhari, A.; Pouran, B.; Ahmadi, S.; Weinans, H.; Zadpoor, A. Additively manufactured metallic porous biomaterials based on minimal surfaces: A unique combination of topological, mechanical, and mass transport properties. Acta Biomater. 2017, 53, 572–584. [Google Scholar] [CrossRef] [PubMed]
- Amin Yavari, S.; Wauthlé, R.; Böttger, A.J.; Schrooten, J.; Weinans, H.; Zadpoor, A.A. Crystal structure and nanotopographical features on the surface of heat-treated and anodized porous titanium biomaterials produced using selective laser melting. Appl. Surf. Sci. 2014, 290, 287–294. [Google Scholar] [CrossRef]
- Amin Yavari, S.; Loozen, L.; Paganelli, F.L.; Bakhshandeh, S.; Lietaert, K.; Groot, J.A.; Fluit, A.C.; Boel, C.E.; Alblas, J.; Vogely, H.C. Antibacterial behavior of additively manufactured porous titanium with nanotubular surfaces releasing silver ions. ACS Appl. Mater. Interfaces 2016, 8, 17080–17089. [Google Scholar] [CrossRef] [PubMed]
- Zadpoor, A.A.; Hedayati, R. Analytical relationships for prediction of the mechanical properties of additively manufactured porous biomaterials. J. Biomed. Mater. Res. Part A 2016, 104, 3164–3174. [Google Scholar] [CrossRef] [PubMed]
- Kadkhodapour, J.; Montazerian, H.; Darabi, A.C.; Anaraki, A.; Ahmadi, S.; Zadpoor, A.; Schmauder, S. Failure mechanisms of additively manufactured porous biomaterials: Effects of porosity and type of unit cell. J. Mech. Behav. Biomed. Mater. 2015, 50, 180–191. [Google Scholar] [CrossRef] [PubMed]
- Babaee, S.; Shim, J.; Weaver, J.C.; Chen, E.R.; Patel, N.; Bertoldi, K. 3D soft metamaterials with negative poisson's ratio. Adv. Mater. 2013, 25, 5044–5049. [Google Scholar] [CrossRef] [PubMed]
- Overvelde, J.T.B.; Shan, S.; Bertoldi, K. Compaction through buckling in 2D periodic, soft and porous structures: Effect of pore shape. Adv. Mater. 2012, 24, 2337–2342. [Google Scholar] [CrossRef] [PubMed]
- Erdemir, A.; McLean, S.; Herzog, W.; van den Bogert, A.J. Model-based estimation of muscle forces exerted during movements. Clin. Biomech. 2007, 22, 131–154. [Google Scholar] [CrossRef] [PubMed]
- Fregly, B.J.; Besier, T.F.; Lloyd, D.G.; Delp, S.L.; Banks, S.A.; Pandy, M.G.; D’lima, D.D. Grand challenge competition to predict in vivo knee loads. J. Orthop. Res. 2012, 30, 503–513. [Google Scholar] [CrossRef] [PubMed]
- Lloyd, D.G.; Besier, T.F. An EMG-driven musculoskeletal model to estimate muscle forces and knee joint moments in vivo. J. Biomech. 2003, 36, 765–776. [Google Scholar] [CrossRef]
- Nikooyan, A.A.; Zadpoor, A.A. An improved cost function for modeling of muscle activity during running. J. Biomech. 2011, 44, 984–987. [Google Scholar] [CrossRef] [PubMed]
- Nikooyan, A.A.; Zadpoor, A.A. Effects of muscle fatigue on the ground reaction force and soft-tissue vibrations during running: A model study. IEEE Trans. Biomed. Eng. 2012, 59, 797–804. [Google Scholar] [CrossRef] [PubMed]
- Zadpoor, A.A.; Nikooyan, A.A. A mechanical model to determine the influence of masses and mass distribution on the impact force during running—A discussion. J. Biomech. 2006, 39, 388–390. [Google Scholar] [CrossRef] [PubMed]
- Campoli, G.; Borleffs, M.; Yavari, S.A.; Wauthle, R.; Weinans, H.; Zadpoor, A.A. Mechanical properties of open-cell metallic biomaterials manufactured using additive manufacturing. Mater. Des. 2013, 49, 957–965. [Google Scholar] [CrossRef]
- Zadpoor, A.A.; Sinke, J.; Benedictus, R. Experimental and numerical study of machined aluminum tailor-made blanks. J. Mater. Process. Technol. 2008, 200, 288–299. [Google Scholar] [CrossRef]
- Eyckens, P.; van Bael, A.; van Houtte, P. An extended marciniak–kuczynski model for anisotropic sheet subjected to monotonic strain paths with through-thickness shear. Int. J. Plast. 2011, 27, 1577–1597. [Google Scholar] [CrossRef]
- Marciniak, Z.; Kuczyński, K. Limit strains in the processes of stretch-forming sheet metal. Int. J. Mech. Sci. 1967, 9, 609IN1613–1612IN2620. [Google Scholar] [CrossRef]
- Zadpoor, A.A.; Sinke, J.; Benedictus, R. The mechanical behavior of adhesively bonded tailor-made blanks. Int. J. Adhes. Adhes. 2009, 29, 558–571. [Google Scholar] [CrossRef]
- Bikas, H.; Stavropoulos, P.; Chryssolouris, G. Additive manufacturing methods and modelling approaches: A critical review. Int. J. Adv. Manuf. Technol. 2016, 83, 389–405. [Google Scholar] [CrossRef]
- Turner, B.; Strong, R.; Gold, S. A review of melt extrusion additive manufacturing processes: I. Process design and modeling. Rapid Prototyp. J. 2014, 20, 192–204. [Google Scholar] [CrossRef]
- Pal, D.; Patil, N.; Zeng, K.; Stucker, B. An integrated approach to additive manufacturing simulations using physics based, coupled multiscale process modeling. J. Manuf. Sci. Eng. 2014, 136, 061022. [Google Scholar] [CrossRef]
- Bendsoe, M.P.; Sigmund, O. Topology Optimization: Theory, Methods, and Applications; Springer: Berlin, Germany, 2003. [Google Scholar]
- Langelaar, M. Topology optimization of 3D self-supporting structures for additive manufacturing. Addit. Manuf. 2016, 12, 60–70. [Google Scholar] [CrossRef]
- Qian, X. Undercut and overhang angle control in topology optimization: A density gradient based integral approach. Int. J. Numer. Methods Eng. 2017, 111, 247–272. [Google Scholar] [CrossRef]
- Jang, I.G.; Kim, I.Y. Computational study of wolff’s law with trabecular architecture in the human proximal femur using topology optimization. J. Biomech. 2008, 41, 2353–2361. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M. Structural optimization system based on trabecular bone surface adaptation. Struct. Multidiscip. Optim. 2006, 32, 241–249. [Google Scholar] [CrossRef]
- Bagge, M. A model of bone adaptation as an optimization process. J. Biomech. 2000, 33, 1349–1357. [Google Scholar] [CrossRef]
- Fernandes, P.; Rodrigues, H.; Jacobs, C. A model of bone adaptation using a global optimisation criterion based on the trajectorial theory of wolff. Comput. Methods Biomech. Biomed. Eng. 1999, 2, 125–138. [Google Scholar] [CrossRef] [PubMed]
- Wieding, J.; Wolf, A.; Bader, R. Numerical optimization of open-porous bone scaffold structures to match the elastic properties of human cortical bone. J. Mech. Behav. Biomed. Mater. 2014, 37, 56–68. [Google Scholar] [CrossRef] [PubMed]
- Zadpoor, A.A.; Campoli, G.; Weinans, H. Neural network prediction of load from the morphology of trabecular bone. Appl. Math. Model. 2013, 37, 5260–5276. [Google Scholar] [CrossRef]
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef] [PubMed]
- Barthelat, F. Designing nacre-like materials for simultaneous stiffness, strength and toughness: Optimum materials, composition, microstructure and size. J. Mech. Phys. Solids 2014, 73, 22–37. [Google Scholar] [CrossRef]
- Rossetti, L.; Kuntz, L.; Kunold, E.; Schock, J.; Müller, K.; Grabmayr, H.; Stolberg-Stolberg, J.; Pfeiffer, F.; Sieber, S.; Burgkart, R. The microstructure and micromechanics of the tendon-bone insertion. Nat. Mater. 2017, 16, 664–670. [Google Scholar] [CrossRef] [PubMed]
- Gu, G.X.; Su, I.; Sharma, S.; Voros, J.L.; Qin, Z.; Buehler, M.J. Three-dimensional-printing of bio-inspired composites. J. Biomech. Eng. 2016, 138, 021006. [Google Scholar] [CrossRef] [PubMed]
- Munch, E.; Launey, M.E.; Alsem, D.H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Tough, bio-inspired hybrid materials. Science 2008, 322, 1516–1520. [Google Scholar] [CrossRef] [PubMed]
- Wegst, U.G.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Gibson, I.; Rosen, D.; Stucker, B. Design for additive manufacturing. In Additive Manufacturing Technologies; Springer: New York, NY, USA, 2015; Volume 238, pp. 399–435. [Google Scholar]
- Vayre, B.; Vignat, F.; Villeneuve, F. Designing for additive manufacturing. Procedia CIRP 2012, 3, 632–637. [Google Scholar] [CrossRef]
- Karunakaran, K.; Suryakumar, S.; Pushpa, V.; Akula, S. Retrofitment of a CNC machine for hybrid layered manufacturing. Int. J. Adv. Manuf. Technol. 2009, 45, 690–703. [Google Scholar] [CrossRef]
- Karunakaran, K.; Suryakumar, S.; Pushpa, V.; Akula, S. Low cost integration of additive and subtractive processes for hybrid layered manufacturing. Robot. Comput. Integr. Manuf. 2010, 26, 490–499. [Google Scholar] [CrossRef]
- Houben, A.; van Hoorick, J.; van Erps, J.; Thienpont, H.; van Vlierberghe, S.; Dubruel, P. Indirect rapid prototyping: Opening up unprecedented opportunities in scaffold design and applications. Ann. Biomed. Eng. 2017, 45, 58–83. [Google Scholar] [CrossRef] [PubMed]
- Larson, D.B.; Malarik, R.J.; Hall, S.M.; Podberesky, D.J. System for verifiable CT radiation dose optimization based on image quality. Part ii. Process control system. Radiology 2013, 269, 177–185. [Google Scholar] [CrossRef] [PubMed]
- Larson, D.B.; Wang, L.L.; Podberesky, D.J.; Goske, M.J. System for verifiable CT radiation dose optimization based on image quality. Part i. Optimization model. Radiology 2013, 269, 167–176. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Smitherman, C.; Samei, E. Size-specific optimization of CT protocols based on minimum detectability. Med. Phys. 2017, 44, 1301–1311. [Google Scholar] [CrossRef] [PubMed]
- Hong, D.; Chou, D.-T.; Velikokhatnyi, O.I.; Roy, A.; Lee, B.; Swink, I.; Issaev, I.; Kuhn, H.A.; Kumta, P.N. Binder-jetting 3D printing and alloy development of new biodegradable Fe-Mn-Ca/Mg alloys. Acta Biomater. 2016, 45, 375–386. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Jiang, L.; Yang, J.; Cao, L.; Dong, J. Application of biodegradable 3D-printed cage for cervical diseases via anterior cervical discectomy and fusion (ACDF): An in vitro biomechanical study. Biotechnol. Lett. 2017. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zadpoor, A.A. Design for Additive Bio-Manufacturing: From Patient-Specific Medical Devices to Rationally Designed Meta-Biomaterials. Int. J. Mol. Sci. 2017, 18, 1607. https://doi.org/10.3390/ijms18081607
Zadpoor AA. Design for Additive Bio-Manufacturing: From Patient-Specific Medical Devices to Rationally Designed Meta-Biomaterials. International Journal of Molecular Sciences. 2017; 18(8):1607. https://doi.org/10.3390/ijms18081607
Chicago/Turabian StyleZadpoor, Amir A. 2017. "Design for Additive Bio-Manufacturing: From Patient-Specific Medical Devices to Rationally Designed Meta-Biomaterials" International Journal of Molecular Sciences 18, no. 8: 1607. https://doi.org/10.3390/ijms18081607
APA StyleZadpoor, A. A. (2017). Design for Additive Bio-Manufacturing: From Patient-Specific Medical Devices to Rationally Designed Meta-Biomaterials. International Journal of Molecular Sciences, 18(8), 1607. https://doi.org/10.3390/ijms18081607




