Developing a Novel Parameter Estimation Method for Agent-Based Model in Immune System Simulation under the Framework of History Matching: A Case Study on Influenza A Virus Infection
Abstract
1. Introduction
2. Results and Discussion
2.1. Observation Data of Influenza A Virus (IAV)
2.2. Sampling Data
2.3. Non-Implausible Space
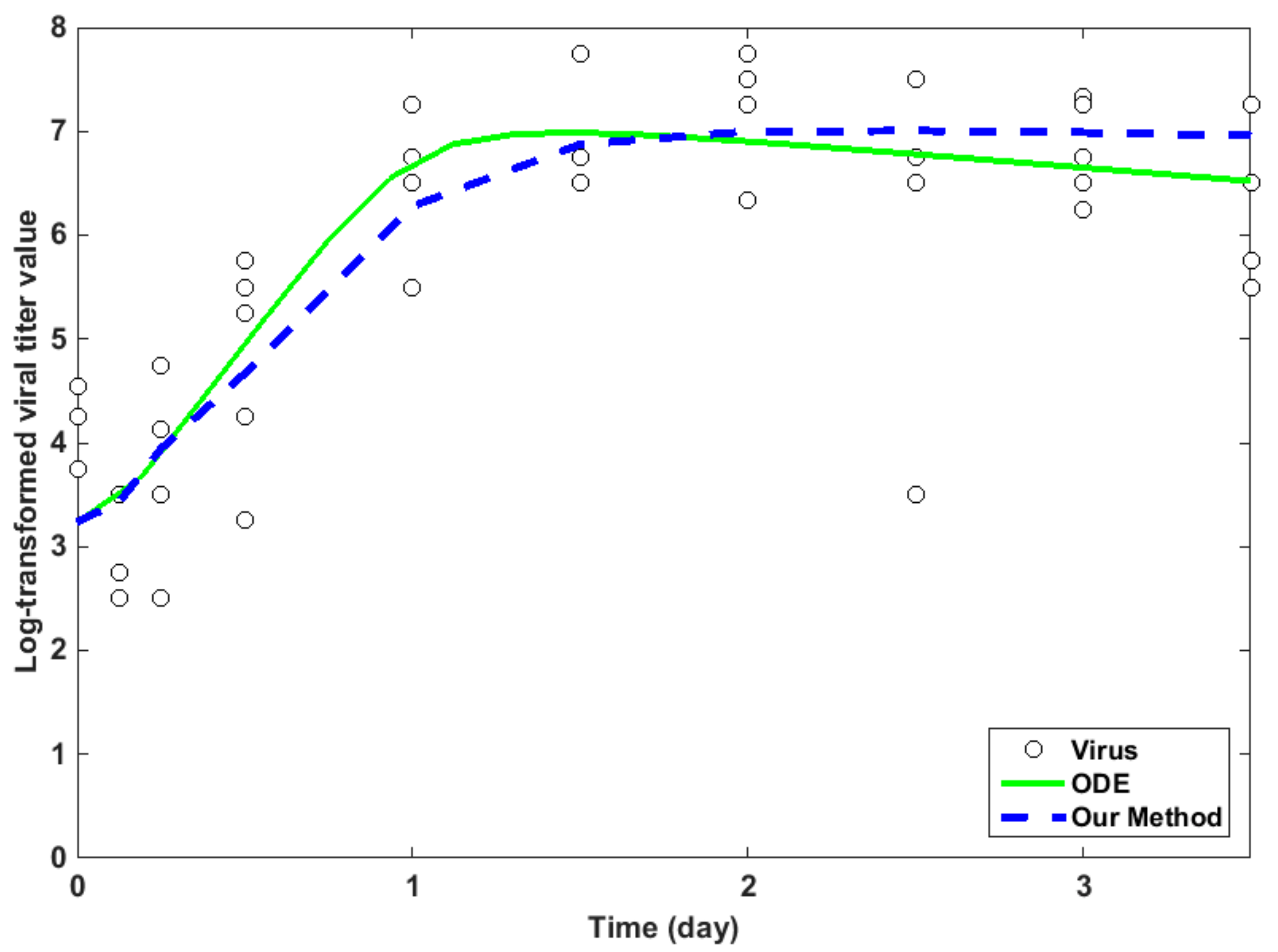
2.4. Fitting Experimental Data
2.5. Average Relative Error
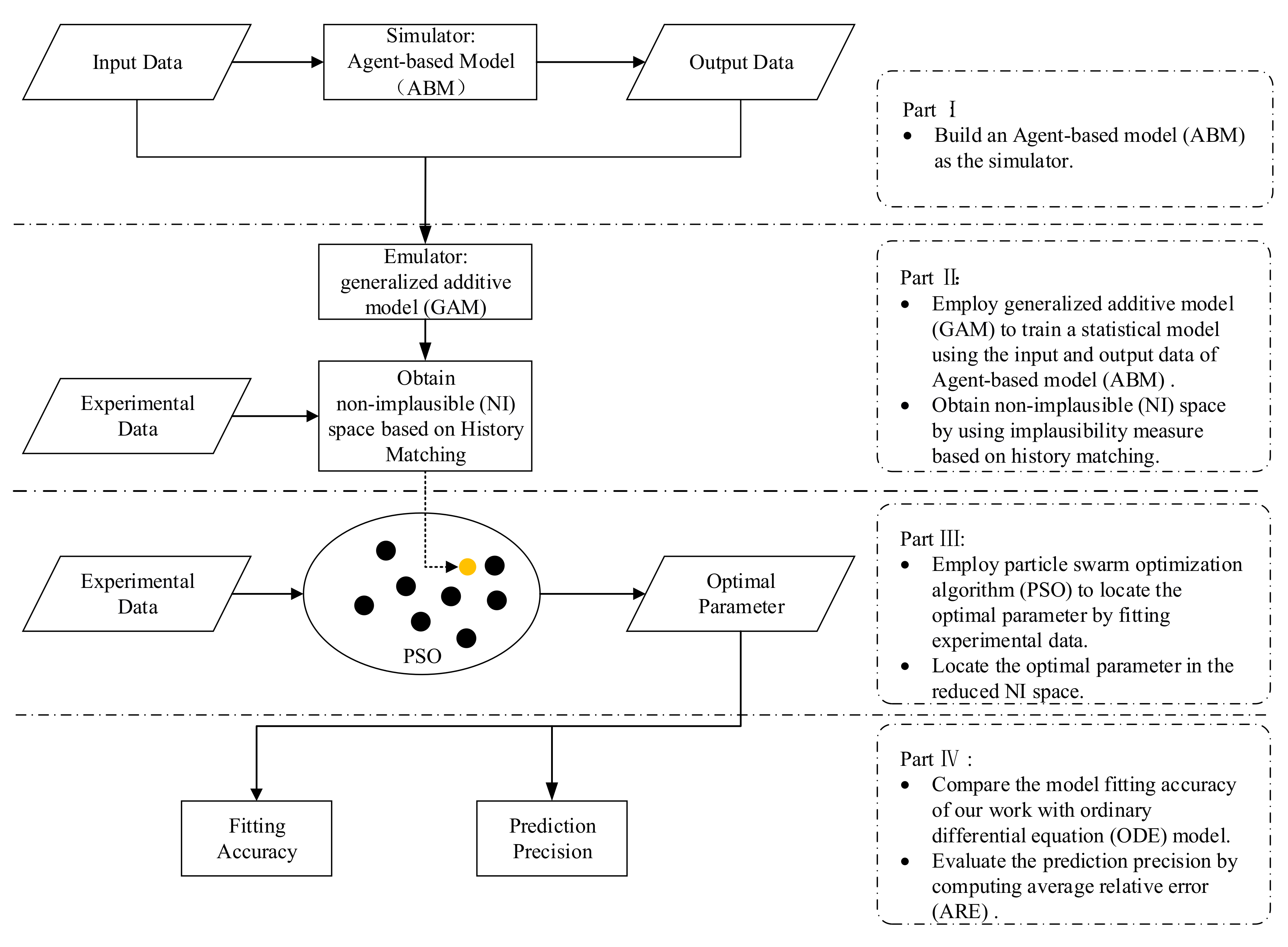
3. Methods
3.1. Simulator: Using ABM (Agent-based Model) to Simulate the Immune System
3.2. Emulator: GAM Model
3.3. Reducing the Input Space by Using Implausibility Measure
3.4. Parameter Estimation
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Miao, H.Y.; Xia, X.H.; Perelson, A.S.; Wu, H.L. On identifiability of nonlinear ode models and applications in viral dynamics. SIAM Rev. 2011, 53, 3–39. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.Y.; Hollenbaugh, J.A.; Zand, M.S.; Holden-Wiltse, J.; Mosmann, T.R.; Perelson, A.S.; Wu, H.; Topham, D.J. Quantifying the early immune response and adaptive immune response kinetics in mice infected with influenza A virus. J. Virol. 2010, 84, 6687–6698. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.Y.; Dykes, C.; Demeter, L.M.; Wu, H.L. Differential equation modeling of hiv viral fitness experiments: Model identification, model selection, and multimodel inference. Biometrics 2009, 65, 292–300. [Google Scholar] [CrossRef] [PubMed]
- Øksendal, B. Stochastic Differential Equations; Springer: Berlin, Germany, 2003. [Google Scholar]
- Jones, D.S.; Plank, M.J.; Sleeman, B.D. Differential Equations and Mathematical Biology; Food and Agriculture Organization: Rome, Italy, 2010. [Google Scholar]
- Ho, W.H.; Chan, L.F. Hybrid Taguchi-differential evolution algorithm for parameter estimation of differential equation models with application to HIV dynamics. Math. Probl. Eng. 2011, 2011, 514756. [Google Scholar] [CrossRef]
- Miao, H.; Wu, H.; Xue, H. Generalized ordinary differential equation models. J. Am. Stat. Assoc. 2014, 109, 1672. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Sullivan, A.M.; Su, C.L.; Zhao, X.P. An agent-based model for the transmission dynamics of Toxoplasma gondii. J. Theor. Biol. 2012, 293, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Folcik, V.A.; An, G.C.; Orosz, C.G. The Basic Immune Simulator: An agent-based model to study the interactions between innate and adaptive immunity. Theor. Biol. Med. Model. 2007, 4, 39. [Google Scholar] [CrossRef] [PubMed]
- Segovia-Juarez, J.L.; Ganguli, S.; Kirschner, D. Identifying control mechanisms of granuloma formation during M-tuberculosis infection using an agent-based model. J. Theor. Biol. 2004, 231, 357–376. [Google Scholar] [CrossRef] [PubMed]
- Jacob, C.; Litorco, J.; Lee, L. Immunity through swarms: Agent-based simulations of the human immune system. In Proceedings of the International Conference on Artificial Immune Systems, Sicily, Italy, 13–16 September 2014; pp. 400–412. [Google Scholar]
- Wang, Z.H.; Butner, J.D.; Kerketta, R.; Cristini, V.; Deisboeck, T.S. Simulating cancer growth with multiscale agent-based modeling. Semin. Cancer Biol. 2015, 30, 70–78. [Google Scholar] [CrossRef] [PubMed]
- Chiacchio, F.; Pennisi, M.; Russo, G.; Motta, S.; Pappalardo, F. Agent-based modeling of the immune system: Netlogo, a promising framework. BioMed Res. Int. 2014, 2014, 907171. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Jiang, B.; Wu, Y.; Strouthos, C.; Sun, P.Z.; Su, J.; Zhou, X.B. Developing a multiscale, multi-resolution agent-based brain tumor model by graphics processing units. Theor. Biol. Med. Model. 2011, 8, 46. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Qiao, M.; Gao, H.; Hu, B.; Tan, H.; Zhou, X.; Li, C.M. Investigation of mechanism of bone regeneration in a porous biodegradable calcium phosphate (CaP) scaffold by a combination of a multi-scale agent-based model and experimental optimization/validation. Nanoscale 2016, 8, 14877. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Xue, Y.; Jiang, B.N.; Strouthos, C.; Duan, Z.F.; Wu, Y.K.; Su, J.; Zhou, X.B. Multiscale agent-based modelling of ovarian cancer progression under the stimulation of the STAT 3 pathway. Int. J. Data Min. Bioinform. 2014, 9, 235–253. [Google Scholar] [CrossRef] [PubMed]
- Moedomo, R.L.; Pancoro, A.; Ibrahim, J.; Ahmad, A.S.; Mardiyanto, M.S.; Belatiff, M.B.; Tasman, H. Simulation of influenza pandemic based on genetic algorithm and agent-based modeling: A multi-objective optimization problem solving. J. Matematika Sains 2010, 15, 47–59. [Google Scholar]
- Zhang, L.; Zhang, S. Using game theory to investigate the epigenetic control mechanisms of embryo development: Comment on: “Epigenetic game theory: How to compute the epigenetic control of maternal-to-zygotic transition” by Qian Wang et al. Phys. Life Rev. 2017, 20, 140. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, Z.; Sagotsky, J.; Deisboeck, T. Multiscale agent-based cancer modeling. J. Math. Biol. 2009, 58, 545. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.M.; Chen, J.H.; Miao, H.Y.; Li, T.T.; Zhang, L. Development of an Agent-Based Model (ABM) to simulate the immune system and integration of a regression method to estimate the key abm parameters by fitting the experimental data. PLoS ONE 2015, 10, e0141295. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Honolulu, HI, USA, 12–17 May 2002; Volume 4, pp. 1942–1948. [Google Scholar]
- Kennedy, J.; Eberhart, R.C.; Shi, Y. Swarm Intelligence; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2001. [Google Scholar]
- Poli, R. An Analysis of Publications on Particle Swarm Optimization Applications; Department of Computer Science, University of Essex: Essex, UK, 2007. [Google Scholar]
- Poli, R. Analysis of the publications on the applications of particle swarm optimisation. J. Artif. Evol. Appl. 2008, 2008, 685175. [Google Scholar] [CrossRef]
- Clerc, M. Standard Particle Swarm Optimisation. 2012. Available online: https://hal.archives-ouvertes.fr/hal-00764996/ (accessed on 13 December, 2012).
- Pedersen, M.E.H.; Chipperfield, A.J. Simplifying particle swarm optimization. Appl. Soft Comput. 2010, 10, 618–628. [Google Scholar] [CrossRef]
- Fan, J.; Gijbels, R. Local Polynomial Modelling and Its Applications; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Walsh, W.A.; Kleiber, P. Generalized additive model and regression tree analyses of blue shark (Prionace glauca) catch rates by the Hawaii-based commercial longline fishery. Fish. Res. 2001, 53, 115–131. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R. Generalized Additive Models; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Trevor, H.; Tibshirani, R. Generalized additive models. Stat. Sci. 1986, 1, 297–310. [Google Scholar]
- Andrianakis, I.; Vernon, I.R.; McCreesh, N.; McKinley, T.J.; Oakley, J.E.; Nsubuga, R.N.; Goldstein, M.; White, R.G. Bayesian history matching of complex infectious disease models using emulation: A tutorial and a case study on HIV in Uganda. PLoS Comput. Biol. 2015, 11, e1003968. [Google Scholar] [CrossRef] [PubMed]
- Mckay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Pukelsheim, F. The three sigma rule. Am. Stat. 1994, 48, 88–91. [Google Scholar]
- López-Moreno, J.I.; Nogués-Bravo, D. A generalized additive model for the spatial distribution of snowpack in the Spanish Pyrenees. Hydrol. Process. 2005, 19, 3167–3176. [Google Scholar] [CrossRef]
- Ramsay, T.; Burnett, R.; Krewski, D. Exploring bias in a generalized additive model for spatial air pollution data. Environ. Health Perspect. 2003, 111, 1283–1288. [Google Scholar] [CrossRef] [PubMed]
- Murase, H.; Nagashima, H.; Yonezaki, S.; Matsukura, R.; Kitakado, T. Application of a generalized additive model (GAM) to reveal relationships between environmental factors and distributions of pelagic fish and krill: A case study in Sendai Bay, Japan. ICES J. Mar. Sci. 2009, 66, 1417–1424. [Google Scholar] [CrossRef]
- Jiang, B.N.; Struthers, A.; Sun, Z.; Feng, Z.; Zhao, X.Q.; Zhao, K.Y.; Dai, W.Z.; Zhou, X.B.; Berens, M.E.; Zhang, L. Employing graphics processing unit technology, alternating direction implicit method and domain decomposition to speed up the numerical diffusion solver for the biomedical engineering research. Int. J. Numer. Methods Biomed. Eng. 2011, 27, 1829–1849. [Google Scholar] [CrossRef]
- Jamshed, S. Graphics Processing Unit Technology; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]

| Time Points (Day−1) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Samples | 0 | 0.125 | 0.25 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 |
| 1 | 4.25 | 2.5 | 3.5 | 4.25 | 5.5 | 6.5 | 6.33 | 6.75 | 6.5 | 6.5 | 6.5 | 7 | 6.33 |
| 2 | 3.75 | 2.5 | 4.75 | 3.25 | 6.75 | 6.75 | 7.5 | 3.5 | 7.33 | 7.25 | 6.25 | 6.5 | 5.5 |
| 3 | 4.25 | 3.5 | 4.75 | 5.25 | 6.5 | 7.75 | 7.75 | 7.5 | 7.33 | 7.25 | 6.5 | 6.25 | 5.75 |
| 4 | 3.75 | 3.5 | 4.13 | 5.75 | 7.25 | NA | 7.25 | 6.5 | 6.25 | 5.5 | NA | NA | NA |
| 5 | 4.55 | 2.75 | 2.5 | 5.75 | NA | NA | NA | 7.5 | 6.75 | 6.5 | NA | NA | NA |
| 6 | 4.25 | NA | 4.75 | 5.5 | NA | NA | NA | NA | 7.25 | 5.75 | NA | NA | NA |
| Samples | ||||
|---|---|---|---|---|
| 1 | 3.466758 × 10−9 | 2.288938 × 10−7 | 2.460326 × 10−2 | 8.616152 × 10−2 |
| 2 | 8.001264 × 10−9 | 4.300130 × 10−7 | 8.741329 × 10−2 | 3.955367 × 10−1 |
| 3 | 1.081166 × 10−8 | 1.932323 × 10−7 | 1.004010 × 10−1 | 3.100995 × 10−1 |
| 4 | 1.090549 × 10−8 | 2.812863 × 10−7 | 8.654013 × 10−2 | 3.202220 × 10−1 |
| 5 | 9.102252 × 10−9 | 4.513295 × 10−7 | 4.608862 × 10−2 | 1.196989 × 10−1 |
| 6 | 3.405003 × 10−9 | 3.370440 × 10−8 | 1.130993 × 10−1 | 6.104288 × 10−1 |
| 7 | 8.092254 × 10−9 | 4.017315 × 10−8 | 2.174145 × 10−2 | 2.430601 × 10−1 |
| 8 | 2.010234 × 10−9 | 1.745676 × 10−8 | 6.418247 × 10−2 | 1.722317 × 10−1 |
| 9 | 1.691198 × 10−9 | 3.527068 × 10−7 | 1.158533 × 10−1 | 1.302177 × 10−2 |
| 10 | 2.912003 × 10−9 | 2.957414 × 10−7 | 2.715800 × 10−2 | 2.602361 × 10−1 |
| 11 | 2.554265 × 10−9 | 9.798854 × 10−8 | 1.866300 × 10−2 | 5.577698 × 10−1 |
| 12 | 6.864842 × 10−9 | 4.184238 × 10−7 | 1.079778 × 10−1 | 7.730243 × 10−1 |
| 13 | 1.121311 × 10−9 | 3.102666 × 10−7 | 2.784293 × 10−3 | 5.343298 × 10−2 |
| 14 | 9.583759 × 10−9 | 6.668325 × 10−8 | 3.832125 × 10−2 | 7.836137 × 10−1 |
| 15 | 8.762499 × 10−9 | 5.740286 × 10−8 | 6.656615 × 10−2 | 1.462840 × 10−1 |
| 16 | 1.167708 × 10−8 | 1.339571 × 10−7 | 1.286682 × 10−2 | 7.554816 × 10−1 |
| 17 | 5.319678 × 10−9 | 4.057522 × 10−7 | 7.242679 × 10−2 | 6.884958 × 10−1 |
| 18 | 7.634766 × 10−9 | 8.162650 × 10−8 | 9.417931 × 10−2 | 8.124229 × 10−1 |
| 19 | 9.973253 × 10−9 | 1.641823 × 10−7 | 5.553776 × 10−2 | 1.506380 × 10−1 |
| 20 | 6.455279 × 10−9 | 1.729994 × 10−7 | 7.591240 × 10−2 | 4.765285 × 10−1 |
| 21 | 3.989849 × 10−9 | 9.193181 × 10−8 | 9.013124 × 10−2 | 4.137486 × 10−1 |
| 22 | 1.212724 × 10−8 | 4.454997 × 10−7 | 1.593432 × 10−2 | 1.957182 × 10−1 |
| 23 | 9.163350 × 10−10 | 3.647394 × 10−7 | 7.019446 × 10−2 | 5.823037 × 10−1 |
| 24 | 4.437117 × 10−9 | 3.801312 × 10−7 | 8.076542 × 10−3 | 6.162935 × 10−1 |
| 25 | 1.186253 × 10−8 | 3.221797 × 10−7 | 6.068513 × 10−2 | 2.227833 × 10−1 |
| 26 | 5.134477 × 10−9 | 2.635175 × 10−7 | 9.752898 × 10−2 | 5.182151 × 10−1 |
| 27 | 4.222250 × 10−9 | 2.151502 × 10−7 | 1.059426 × 10−1 | 8.356908 × 10−1 |
| 28 | 1.246306 × 10−9 | 3.445810 × 10−7 | 5.116530 × 10−2 | 4.604467 × 10−1 |
| 29 | 1.134631 × 10−8 | 1.157556 × 10−7 | 3.036958 × 10−2 | 6.538406 × 10−1 |
| 30 | 2.343542 × 10−9 | 1.483302 × 10−7 | 7.804259 × 10−2 | 4.427248 × 10−1 |
| 31 | 4.911390 × 10−9 | 1.124756 × 10−8 | 1.018424 × 10−1 | 2.351053 × 10−2 |
| 32 | 1.043893 × 10−8 | 4.616473 × 10−7 | 5.736185 × 10−2 | 2.911685 × 10−1 |
| 33 | 5.792641 × 10−9 | 4.757734 × 10−7 | 1.195959 × 10−1 | 7.008772 × 10−1 |
| 34 | 7.162705 × 10−9 | 1.314465 × 10−7 | 1.195076 × 10−2 | 3.444968 × 10−1 |
| 35 | 6.743423 × 10−9 | 2.437133 × 10−7 | 5.718468 × 10−3 | 6.614001 × 10−2 |
| 36 | 8.583690 × 10−9 | 3.363820 × 10−7 | 3.510043 × 10−2 | 4.877613 × 10−1 |
| 37 | 1.832510 × 10−10 | 1.983512 × 10−7 | 4.478183 × 10−2 | 3.777456 × 10−1 |
| 38 | 5.980517 × 10−9 | 3.927292 × 10−7 | 4.956199 × 10−2 | 6.684690 × 10−1 |
| 39 | 5.754720 × 10−10 | 2.763359 × 10−7 | 4.084022 × 10−2 | 5.291611 × 10−1 |
| 40 | 9.649890 × 10−9 | 2.419316 × 10−7 | 8.210135 × 10−2 | 7.266126 × 10−1 |
| Parameters | Initial Interval | Non-Implausible Interval |
|---|---|---|
| [0, 1.240000 × 10−8] | [3.8139 × 10−14, 1.2400 × 10−8] | |
| [0, 4.840000 × 10−7] | [2.5844 × 10−14, 4.8400 × 10−7] | |
| [0, 1.196000 × 10−1] | [8.7906 × 10−7, 1.1960 × 10−1] | |
| [0, 8.460000 × 10−1] | [6.1473 × 10−6, 8.4600 × 10−1] |
| Parameters | ||||
|---|---|---|---|---|
| Model | ||||
| Initial Parameters | 6.2000 × 10−9 | 2.4200 × 10−7 | 5.9800 × 10−2 | 4.2300 × 10−1 |
| Our Estimates | 6.5656 × 10−9 | 7.2467 × 10−9 | 2.7739 × 10−2 | 1.2595 × 10−1 |
| (4.2290 × 10−9) | (6.4759 × 10−11) | (2.8178 × 10−7) | (3.1538 × 10−6) | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, T.; Cheng, Z.; Zhang, L. Developing a Novel Parameter Estimation Method for Agent-Based Model in Immune System Simulation under the Framework of History Matching: A Case Study on Influenza A Virus Infection. Int. J. Mol. Sci. 2017, 18, 2592. https://doi.org/10.3390/ijms18122592
Li T, Cheng Z, Zhang L. Developing a Novel Parameter Estimation Method for Agent-Based Model in Immune System Simulation under the Framework of History Matching: A Case Study on Influenza A Virus Infection. International Journal of Molecular Sciences. 2017; 18(12):2592. https://doi.org/10.3390/ijms18122592
Chicago/Turabian StyleLi, Tingting, Zhengguo Cheng, and Le Zhang. 2017. "Developing a Novel Parameter Estimation Method for Agent-Based Model in Immune System Simulation under the Framework of History Matching: A Case Study on Influenza A Virus Infection" International Journal of Molecular Sciences 18, no. 12: 2592. https://doi.org/10.3390/ijms18122592
APA StyleLi, T., Cheng, Z., & Zhang, L. (2017). Developing a Novel Parameter Estimation Method for Agent-Based Model in Immune System Simulation under the Framework of History Matching: A Case Study on Influenza A Virus Infection. International Journal of Molecular Sciences, 18(12), 2592. https://doi.org/10.3390/ijms18122592





