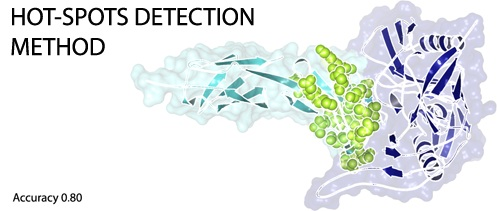
A Machine Learning Approach for Hot-Spot Detection at Protein-Protein Interfaces
Abstract
:1. Introduction
2. Results
3. Discussion
4. Material and Methods
4.1. Dataset Construction
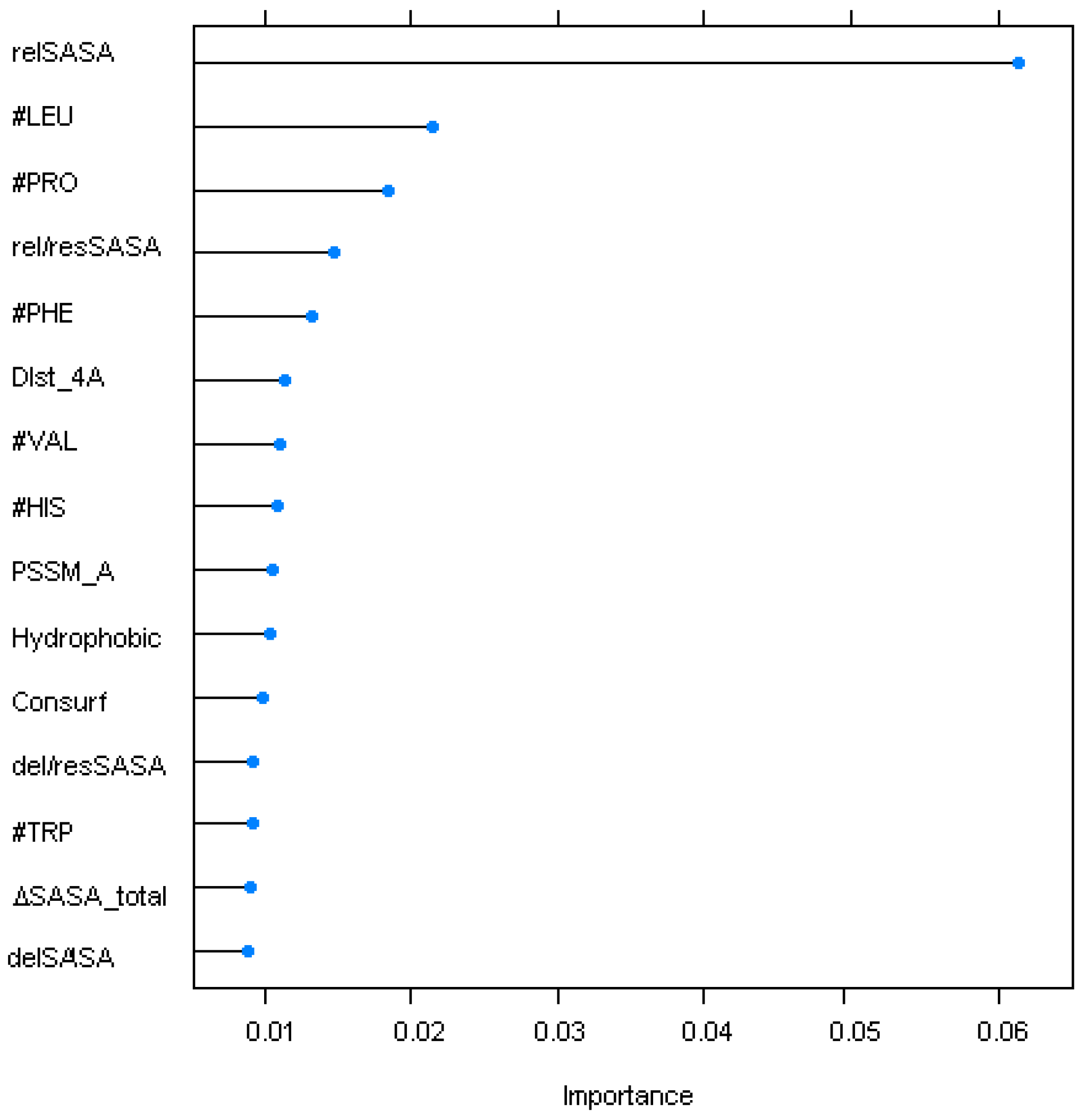
4.2. Sequence/Structural Features
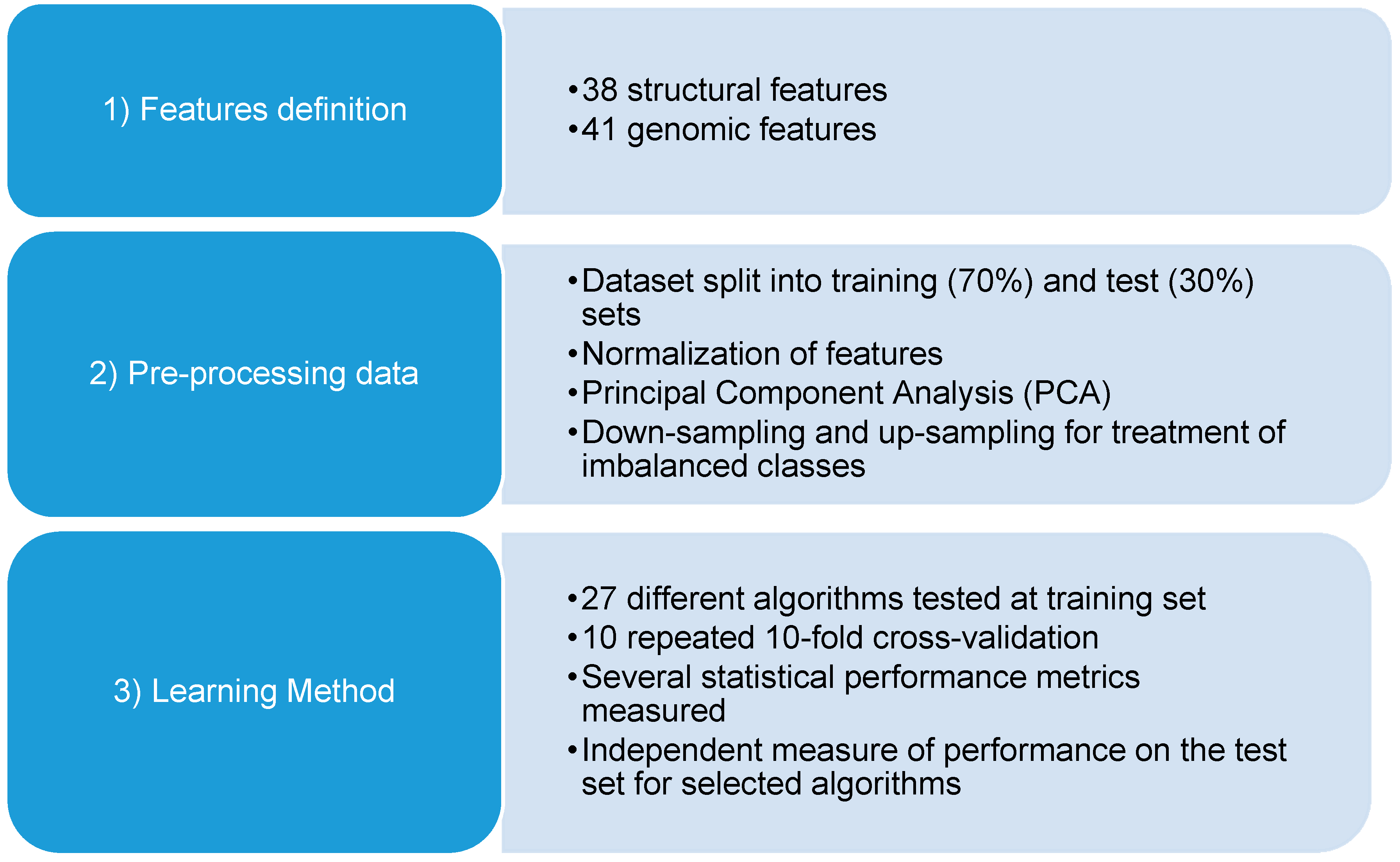
4.3. Machine Learning Techniques
4.4. Comparison with Other Software
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sudarshan, S.; Kodathala, S.B.; Mahadik, A.C.; Mehta, I.; Beck, B.W. Protein-protein interface detection using the energy centrality relationship (ECR) characteristic of proteins. PLoS ONE 2014, 9, e97115. [Google Scholar] [CrossRef] [PubMed]
- Phizicky, E.M.; Fields, S. Protein-protein interactions: Methods for detection and analysis. Microbiol. Rev. 1995, 59, 94–123. [Google Scholar] [PubMed]
- Clackson, T.; Wells, J.A. A hot spot of binding energy in a hormone-receptor interface. Science 1995, 267, 383–386. [Google Scholar] [CrossRef] [PubMed]
- Uetz, P.; Giot, L.; Cagney, G.; Mansfield, T.A.; Judson, R.S.; Knight, J.R.; Lockshon, D.; Narayan, V.; Srinivasan, M.; Pochart, P.; et al. A comprehensive analysis of protein-protein interactions in saccharomyces cerevisiae. Nature 2000, 403, 623–627. [Google Scholar] [PubMed]
- Cho, H.; Wu, M.; Bilgin, B.; Walton, S.P.; Chan, C. Latest developments in experimental and computational approaches to characterize protein–lipid interactions. Proteomics 2012, 12, 3273–3285. [Google Scholar] [CrossRef] [PubMed]
- Moreira, I.S. The role of water occulsion for the definition of a protein binding hot-spot. Curr. Top. Med. Chem. 2015, 15, 2068–2079. [Google Scholar] [CrossRef] [PubMed]
- Cunningham, B.; Wells, J. High-resolution epitope mapping of hgh-receptor interactions by alanine-scanning mutagenesis. Science 1989, 244, 1081–1085. [Google Scholar] [CrossRef] [PubMed]
- Bogan, A.A.; Thorn, K.S. Anatomy of hot spots in protein interfaces 1. J. Mol. Biol. 1998, 280, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wan, H.; Li, Y.; Fan, Y.; Meng, F.; Chen, C.; Zhou, Q. A site-directed mutagenesis method particularly useful for creating otherwise difficult-to-make mutants and alanine scanning. Anal. Biochem. 2012, 420, 163–170. [Google Scholar] [CrossRef] [PubMed]
- Massova, I.; Kollman, P.A. Computational alanine scanning to probe protein-protein interactions: A novel approach to evaluate binding free energies. J. Am. Chem. Soc. 1999, 121, 8133–8143. [Google Scholar] [CrossRef]
- Moreira, I.S.; Fernandes, P.A.; Ramos, M.J. Computational alanine scanning mutagenesis—An improved methodological approach. J. Comput. Chem. 2007, 28, 644–654. [Google Scholar] [CrossRef] [PubMed]
- Bromberg, Y.; Rost, B. Comprehensive in silico mutagenesis highlights functionally important residues in proteins. Bioinformatics 2008, 24, i207–i212. [Google Scholar] [CrossRef] [PubMed]
- Darnell, S.J.; Page, D.; Mitchell, J.C. An automated decision-tree approach to predicting protein interaction hot spots. Proteins: Struct. Funct. Bioinform. 2007, 68, 813–823. [Google Scholar] [CrossRef] [PubMed]
- Munteanu, C.R.; Pimenta, A.C.; Fernandez-Lozano, C.; Melo, A.; Cordeiro, M.N.D.S.; Moreira, I.S. Solvent accessible surface area-based hot-spot detection methods for protein–protein and protein–nucleic acid interfaces. J. Chem. Inform. Model. 2015, 55, 1077–1086. [Google Scholar] [CrossRef] [PubMed]
- Martins, J.M.; Ramos, R.M.; Pimenta, A.C.; Moreira, I.S. Solvent-accessible surface area: How well can be applied to hot-spot detection? Proteins: Struct. Funct. Bioinform. 2014, 82, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Caret: Classification and Regression Training. Available online: https://cran.r-project.org/web/packages/caret/index.html (accessed on 25 July 2016).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2010. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Kim, D.E.; Chivian, D.; Baker, D. Protein structure prediction and analysis using the robetta server. Nucleic Acids Res. 2004, 32, W526–W531. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.; Mitchell, J. KFC2: A knowledge-based hot spot prediction method based on interface solvation, atomic density and plasticity features. Proteins 2011, 79, 2671–2683. [Google Scholar] [CrossRef] [PubMed]
- De Vries, S.J.; Bonvin, A.M.J.J. Cport: A consensus interface predictor and its performance in prediction-driven docking with haddock. PLoS ONE 2011, 6, e17695. [Google Scholar] [CrossRef] [PubMed]
- Oshima, H.; Yasuda, S.; Yoshidome, T.; Ikeguchi, M.; Kinoshita, M. Crucial importance of the water-entropy effect in predicting hot spots in protein-protein complexes. Phys. Chem. Chem. Phys. 2011, 13, 16236–16246. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Hoi, S.; Kwoh, C.; Wong, L.; Li, J. Integrating water exclusion theory into betacontacts to predict binding free energy changes and binding hot spots. BMC Bioinform. 2014, 15, 57. [Google Scholar] [CrossRef] [PubMed]
- Guharoy, M.; Chakrabarti, P. Empirical estimation of the energetic contribution of individual interface residues in structures of protein–protein complexes. J. Comput. Aided Mol. Des. 2009, 23, 645–654. [Google Scholar] [CrossRef] [PubMed]
- Guharoy, M.; Pal, A.; Dasgupta, M.; Chakrabarti, P. Price (protein interface conservation and energetics): A server for the analysis of protein-protein interfaces. J. Struct. Funct. Genom. 2011, 12, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhou, H.-X. Prediction of interface residues in protein-protein complexes by a consensus neural network method: Test against NMR data. Proteins 2005, 61, 21–35. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Li, J.; Wong, L.; Kuwahara, H.; Huang, J.; Gao, X. Accurate prediction of hot spot residues through physicochemical characteristics of amino acid sequences. Proteins: Struct. Funct. Bioinform. 2013, 81, 1351–1362. [Google Scholar] [CrossRef] [PubMed]
- Darnell, S.J.; LeGault, L.; Mitchell, J.C. KFC server: Interactive forecasting of protein interaction hot spots. Nucleic Acids Res. 2008, 36, W265–W269. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Guan, J.; Wei, X.; Yi, Y.; Zhou, S. Boosting prediction performance of protein-protein interaction hot spots by using structural neighborhood properties. Res. Comput. Mol. Biol. Lecture Notes Comput. Sci. 2013, 7821, 333–344. [Google Scholar]
- Cho, K.; Kim, D.; Lee, D. A feature-based approach to modeling protein–protein interaction hot spots. Nucleic Acids Res. 2009, 37, 2672–2687. [Google Scholar] [CrossRef] [PubMed]
- Segura Mora, J.; Assi, S.A.; Fernandez-Fuentes, N. Presaging critical residues in protein interfaces: A web server to chart hot spots in protein interfaces. PLoS ONE 2010, 5, e12352. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Zhao, X.; Song, J.; Huang, D. Apis: Accurate prediction of hot spots in protein interfaces by combining protrusion index with solvent accessibility. BMC Bioinform. 2010, 11, 174. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Liu, Z.; Zhang, X.; Chen, L. Prediction of hot spots in protein interfaces using a random forest model with hybrid features. Protein Eng. Des. Sel. 2012, 25, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Wei, X.; Deng, L.; Guan, J.; Zhou, S. A semi-supervised boosting svm for predicting hot spots at protein-protein interfaces. BMC Syst. Biol. 2012, 6. [Google Scholar] [CrossRef] [PubMed]
- Ozbek, P.; Soner, S.; Haliloglu, T. Hot spots in a network of functional sites. PLoS ONE 2013, 8, e74320. [Google Scholar] [CrossRef] [PubMed]
- Strobl, C.; Malley, J.; Tutz, G. An introduction to recursive partitioning: Rationale, application and characteristics of classification and regression trees, bagging and random forests. Psychol. Methods 2009, 14, 323–348. [Google Scholar] [CrossRef] [PubMed]
- Thorn, K.S.; Bogan, A.A. ASEdb: A database of alanine mutations and their effects on the free energy of binding in protein interactions. Bioinformatics 2001, 17, 284–285. [Google Scholar] [CrossRef] [PubMed]
- Fischer, T.B.; Arunachalam, K.V.; Bailey, D.; Mangual, V.; Bakhru, S.; Russo, R.; Huang, D.; Paczkowski, M.; Lalchandani, V.; Ramachandra, C.; et al. The binding interface database (BID): A compilation of amino acid hot spots in protein interfaces. Bioinformatics 2003, 19, 1453–1454. [Google Scholar] [CrossRef] [PubMed]
- Moal, I.H.; Fernández-Recio, J. Skempi: A structural kinetic and energetic database of mutant protein interactions and its use in empirical models. Bioinformatics 2012, 28, 2600–2607. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.D.S.; Gromiha, M.M. Pint: Protein–protein interactions thermodynamic database. Nucleic Acids Res. 2006, 34, D195–D198. [Google Scholar] [CrossRef] [PubMed]
- Bernstein, F.C.; Koetzle, T.F.; Williams, G.J.; Meyer, E.F.; Brice, M.D.; Rodgers, J.R.; Kennard, O.; Shimanouchi, T.; Tasumi, M. The protein data bank. A computer-based archival file for macromolecular structures. Eur. J. Biochem. 1977, 80, 319–324. [Google Scholar] [CrossRef] [PubMed]
- Miller, S.; Janin, J.; Lesk, A.M.; Chothia, C. Interior and surface of monomeric proteins. J. Mol. Biol. 1987, 196, 641–656. [Google Scholar] [CrossRef]
- Miller, S.; Lesk, A.M.; Janin, J.; Chothia, C. The accessible surface area and stability of oligomeric proteins. Nature 1987, 328, 834–836. [Google Scholar] [CrossRef] [PubMed]
- Ashkenazy, H.; Erez, E.; Martz, E.; Pupko, T.; Ben-Tal, N. Consurf 2010: Calculating evolutionary conservation in sequence and structure of proteins and nucleic acids. Nucleic Acids Res. 2010, 38, W529–W533. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.; Gish, W.; Miller, W.; Myers, E.; Lipman, D. Basic local alignment search tool. J. Mol. Biol. 1990, 215, 403–410. [Google Scholar] [CrossRef]
- Camacho, C.; Coulouris, G.; Avagyan, V.; Ma, N.; Papadopoulos, J.; Bealer, K.; Madden, T.L. Blast+: Architecture and applications. BMC Bioinform. 2009, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Papageorgiou, A.C.; Shapiro, R.; Acharya, K.R. Molecular recognition of human angiogenin by placental ribonuclease inhibitor—An x-ray crystallographic study at 2.0 angstrom resolution. Embo J. 1997, 16, 5162–5177. [Google Scholar] [CrossRef] [PubMed]
- Huang, M.; Syed, R.; Stura, E.A.; Stone, M.J.; Stefanko, R.S.; Ruf, W.; Edgington, T.S.; Wilson, I.A. The mechanism of an inhibitory antibody on TF-initiated blood coagulation revealed by the crystal structures of human tissue factor, fab 5g9 and tf·5g9 complex1. J. Mol. Biol. 1998, 275, 873–894. [Google Scholar] [CrossRef] [PubMed]
- Buckle, A.M.; Schreiber, G.; Fersht, A.R. Protein-protein recognition: Crystal structural analysis of a barnase-barstar complex at 2.0-.Ang. Resolution. Biochemistry 1994, 33, 8878–8889. [Google Scholar] [CrossRef] [PubMed]
- Crystal structure of the E. Coli colicin E9 dnase domain with its cognate immunity protein im9. Available online: http://www.rcsb.org/pdb/explore.do?structureId=1bxi (accessed on 26 July 2016).
- Scheidig, A.J.; Hynes, T.R.; Pelletier, L.A.; Wells, J.A.; Kossiakoff, A.A. Crystal structures of bovine chymotrypsin and trypsin complexed to the inhibitor domain of alzheimer's amyloid beta-protein precursor (APPI) and basic pancreatic trypsin inhibitor (BPTI): Engineering of inhibitors with altered specificities. Protein Sci.: Publ. Protein Soc. 1997, 6, 1806–1824. [Google Scholar] [CrossRef] [PubMed]
- Banner, D.W.; D′Arcy, A.; Chène, C.; Winkler, F.K.; Guha, A.; Konigsberg, W.H.; Nemerson, Y.; Kirchhofer, D. The crystal structure of the complex of blood coagulation factor viia with soluble tissue factor. Nature 1996, 380, 41–46. [Google Scholar] [CrossRef] [PubMed]
- Braden, B.C.; Fields, B.A.; Ysern, X.; Dall'Acqua, W.; Goldbaum, F.A.; Poljak, R.J.; Mariuzza, R.A. Crystal structure of an fv–fv idiotope–anti-idiotope complex at 1.9 å resolution. J. Mol. Biol. 1996, 264, 137–151. [Google Scholar] [CrossRef] [PubMed]
- Fuentes-Prior, P.; Iwanaga, Y.; Huber, R.; Pagila, R.; Rumennik, G.; Seto, M.; Morser, J.; Light, D.R.; Bode, W. Structural basis for the anticoagulant activity of the thrombin-thrombomodulin complex. Nature 2000, 404, 518–525. [Google Scholar] [CrossRef] [PubMed]
- Kwong, P.D.; Wyatt, R.; Robinson, J.; Sweet, R.W.; Sodroski, J.; Hendrickson, W.A. Structure of an HIV gp120 envelope glycoprotein in complex with the CD4 receptor and a neutralizing human antibody. Nature 1998, 393, 648–659. [Google Scholar] [PubMed]
- Malby, R.L.; Tulip, W.R.; Harley, V.R.; McKimm-Breschkin, J.L.; Laver, W.G.; Webster, R.G.; Colman, P.M. The structure of a complex between the NC10 antibody and influenza virus neuraminidase and comparison with the overlapping binding site of the NC41 antibody. Structure 1994, 2, 733–746. [Google Scholar] [CrossRef]
- Bhat, T.N.; Bentley, G.A.; Boulot, G.; Greene, M.I.; Tello, D.; Dall'Acqua, W.; Souchon, H.; Schwarz, F.P.; Mariuzza, R.A.; Poljak, R.J. Bound water molecules and conformational stabilization help mediate an antigen-antibody association. Proc. Natl. Acad. Sci. USA 1994, 91, 1089–1093. [Google Scholar] [CrossRef] [PubMed]
- Padlan, E.A.; Silverton, E.W.; Sheriff, S.; Cohen, G.H.; Smithgill, S.J.; Davies, D.R. Structure of an antibody antigen complex: Crystal-structure of the HyHEL-10 Fab-lysozyme complex. Proc. Natl. Acad. Sci. USA 1989, 86, 5938–5942. [Google Scholar] [CrossRef] [PubMed]
- Deisenhofer, J. Crystallographic refinement and atomic models of a human Fc fragment and its complex with fragment-B of protein-A from staphylococcus-aureus at 2.9- and 2.8-ANG resolution. Biochemistry 1981, 20, 2361–2370. [Google Scholar] [CrossRef] [PubMed]
- Kobe, B.; Deisenhofer, J. A structural basis of the interactions between leucine-rich repeats and protein ligands. Nature 1995, 374, 183–186. [Google Scholar] [CrossRef] [PubMed]
- Emsley, J.; Knight, C.G.; Farndale, R.W.; Barnes, M.J.; Liddington, R.C. Structural basis of collagen recognition by integrin α2β 1. Cell 2000, 101, 47–56. [Google Scholar] [CrossRef]
- Kirsch, T.; Sebald, W.; Dreyer, M.K. Crystal structure of the BMP-2-BRIA ectodomain complex. Nat. Struct. Biol. 2000, 7, 492–496. [Google Scholar] [PubMed]
- Kvansakul, M.; Hopf, M.; Ries, A.; Timpl, R.; Hohenester, E. Structural basis for the high-affinity interaction of nidogen-1 with immunoglobulin-like domain 3 of perlecan. Embo J. 2001, 20, 5342–5346. [Google Scholar] [CrossRef] [PubMed]
- Kamada, K.; Hanaoka, F.; Burley, S.K. Crystal structure of the maze/mazf complex: Molecular bases of antidote-toxin recognition. Mol. Cell 2003, 11, 875–884. [Google Scholar] [CrossRef]
- Sauereriksson, A.E.; Kleywegt, G.J.; Uhl, M.; Jones, T.A. Crystal-structure of the C2 fragment of streptococcal protein-G in complex with the Fc domain of human-IgG. Structure 1995, 3, 265–278. [Google Scholar] [CrossRef]
- Kuszewski, J.; Gronenborn, A.M.; Clore, G.M. Improving the packing and accuracy of nmr structures with a pseudopotential for the radius of gyration. J. Am. Chem. Soc. 1999, 121, 2337–2338. [Google Scholar] [CrossRef]
- Zhang, E.; St Charles, R.; Tulinsky, A. Structure of extracellular tissue factor complexed with factor VIIa inhibited with a BPTI mutant. J. Mol. Biol. 1999, 285, 2089–2104. [Google Scholar] [CrossRef] [PubMed]
- Radisky, E.S.; Kwan, G.; Lu, C.J.K.; Koshland, D.E. Binding, proteolytic, and crystallographic analyses of mutations at the protease-inhibitor interface of the subtilisin BPN’/chymotrypsin inhibitor 2 complex. Biochemistry 2004, 43, 13648–13656. [Google Scholar] [CrossRef] [PubMed]
- Hage, T.; Sebald, W.; Reinemer, P. Crystal structure of the interleukin-4/receptor alpha chain complex reveals a mosaic binding interface. Cell 1999, 97, 271–281. [Google Scholar] [CrossRef]
- Fields, B.A.; Malchiodi, E.L.; Li, H.M.; Ysern, X.; Stauffacher, C.V.; Schlievert, P.M.; Karjalainen, K.; Mariuzza, R.A. Crystal structure of a t-cell receptor β-chain complexed with a superantigen. Nature 1996, 384, 188–192. [Google Scholar] [CrossRef] [PubMed]
- Nishida, M.; Nagata, K.; Hachimori, Y.; Horiuchi, M.; Ogura, K.; Mandiyan, V.; Schlessinger, J.; Inagaki, F. Novel recognition mode between vav and grb2 sh3 domains. Embo J. 2001, 20, 2995–3007. [Google Scholar] [CrossRef] [PubMed]
- Gamble, T.R.; Vajdos, F.F.; Yoo, S.H.; Worthylake, D.K.; Houseweart, M.; Sundquist, W.I.; Hill, C.P. Crystal structure of human cyclophilin a bound to the amino-terminal domain of HIV-1 capsid. Cell 1996, 87, 1285–1294. [Google Scholar] [CrossRef]
- Barinka, C.; Parry, G.; Callahan, J.; Shaw, D.E.; Kuo, A.; Bdeir, K.; Cines, D.B.; Mazar, A.; Lubkowski, J. Structural basis of interaction between urokinase-type plasminogen activator and its receptor. J. Mol. Biol. 2006, 363, 482–495. [Google Scholar] [CrossRef] [PubMed]
- Abergel, C.; Monchois, V.; Byrne, D.; Chenivesse, S.; Lembo, F.; Lazzaroni, J.-C.; Claverie, J.-M. Structure and evolution of the ivy protein family, unexpected lysozyme inhibitors in gram-negative bacteria. Proc. Natl. Acad. Sci. USA 2007, 104, 6394–6399. [Google Scholar] [CrossRef] [PubMed]
- Nam, T.-W.; Il Jung, H.; An, Y.J.; Park, Y.-H.; Lee, S.H.; Seok, Y.-J.; Cha, S.-S. Analyses of MLc-IIBGLc interaction and a plausible molecular mechanism of Mlc inactivation by membrane sequestration. Proc. Natl. Acad. Sci. USA 2008, 105, 3751–3756. [Google Scholar] [CrossRef] [PubMed]
- Meenan, N.A.G.; Sharma, A.; Fleishman, S.J.; MacDonald, C.J.; Morel, B.; Boetzel, R.; Moore, G.R.; Baker, D.; Kleanthous, C. The structural and energetic basis for high selectivity in a high-affinity protein-protein interaction. Proc. Natl. Acad. Sci. USA 2010, 107, 10080–10085. [Google Scholar] [CrossRef] [PubMed]
- Pelletier, H.; Kraut, J. Crystal-structure of a complex between electron-transfer partners, cytochrome-c peroxidase and cytochrome-c. Science 1992, 258, 1748–1755. [Google Scholar] [CrossRef] [PubMed]
- Prasad, L.; Waygood, E.B.; Lee, J.S.; Delbaere, L.T.J. The 2.5 angstrom resolution structure of the jei42 fab fragment hpr complex. J. Mol. Biol. 1998, 280, 829–845. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, M.; Meiss, G.; Pingoud, A.M.; London, R.E.; Pedersen, L.C. The nuclease a-inhibitor complex is characterized by a novel metal ion bridge. J. Biol. Chem. 2007, 282, 5682–5690. [Google Scholar] [CrossRef] [PubMed]
- Schutt, C.E.; Myslik, J.C.; Rozycki, M.D.; Goonesekere, N.C.W.; Lindberg, U. The structure of crystalline profilin beta-actin. Nature 1993, 365, 810–816. [Google Scholar] [CrossRef] [PubMed]
- Misaghi, S.; Galardy, P.J.; Meester, W.J.N.; Ovaa, H.; Ploegh, H.L.; Gaudet, R. Structure of the ubiquitin hydrolase uch-l3 complexed with a suicide substrate. J. Biol. Chem. 2005, 280, 1512–1520. [Google Scholar] [CrossRef] [PubMed]
- Sundquist, W.I.; Schubert, H.L.; Kelly, B.N.; Hill, G.C.; Holton, J.M.; Hill, C.P. Ubiquitin recognition by the human tsg101 protein. Mol. Cell 2004, 13, 783–789. [Google Scholar] [CrossRef]
- Huang, L.; Hofer, F.; Martin, G.S.; Kim, S.H. Structural basis for the interaction of ras with raigds. Nat. Struct. Biol. 1998, 5, 422–426. [Google Scholar] [CrossRef] [PubMed]
- Hart, P.J.; Deep, S.; Taylor, A.B.; Shu, Z.Y.; Hinck, C.S.; Hinck, A.P. Crystal structure of the human TβR2 ectodomain-TGF-β3 complex. Nat. Struct. Biol. 2002, 9, 203–208. [Google Scholar] [CrossRef] [PubMed]
- Bravo, J.; Li, Z.; Speck, N.A.; Warren, A.J. The leukemia-associated AML1 (Runx1)-CBFβ complex functions as a DNA-induced molecular clamp. Nat. Struct. Mol. Biol. 2001, 8, 371–378. [Google Scholar] [CrossRef] [PubMed]
- Gouet, P.; Chinardet, N.; Welch, M.; Guillet, V.; Cabantous, S.; Birck, C.; Mourey, L.; Samama, J.P. Further insights into the mechanism of function of the response regulator chey from crystallographic studies of the chey-chea(124–257) complex. Acta Crystallogr. Sect. D-Biol. Crystallogr. 2001, 57, 44–51. [Google Scholar] [CrossRef]
- Schneider, E.L.; Lee, M.S.; Baharuddin, A.; Goetz, D.H.; Farady, C.J.; Ward, M.; Wang, C.-I.; Craik, C.S. A reverse binding motif that contributes to specific protease inhibition by antibodies. J. Mol. Biol. 2012, 415, 699–715. [Google Scholar] [CrossRef] [PubMed]
- Hanson, W.M.; Domek, G.J.; Horvath, M.P.; Goldenberg, D.P. Rigidification of a flexible protease inhibitor variant upon binding to trypsin. J. Mol. Biol. 2007, 366, 230–243. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.J.; McCoy, J.G.; Bingman, C.A.; Phillips, G.N., Jr.; Raines, R.T. Inhibition of human pancreatic ribonuclease by the human ribonuclease inhibitor protein. J. Mol. Biol. 2007, 368, 434–449. [Google Scholar] [CrossRef] [PubMed]
- Bode, W.; Wei, A.Z.; Huber, R.; Meyer, E.; Travis, J.; Neumann, S. X-ray crystal-structure of the complex of human-leukocyte elastase (pmn elastase) and the 3rd domain of the turkey ovomucoid inhibitor. Embo J. 986, 5, 2453–2458. [Google Scholar]
- Read, R.J.; Fujinaga, M.; Sielecki, A.R.; James, M.N.G. Structure of the complex of streptomyces-griseus protease-b and the 3rd domain of the turkey ovomucoid inhibitor at 1.8-a resolution. Biochemistry 1983, 22, 4420–4433. [Google Scholar] [CrossRef] [PubMed]
- Hammel, M.; Sfyroera, G.; Ricklin, D.; Magotti, P.; Lambris, J.D.; Geisbrecht, B.V. A structural basis for complement inhibition by staphylococcus aureus. Nat. Immunol. 2007, 8, 430–437. [Google Scholar] [CrossRef] [PubMed]
- Iyer, S.; Wei, S.; Brew, K.; Acharya, K.R. Crystal structure of the catalytic domain of matrix metalloproteinase-1 in complex with the inhibitory domain of tissue inhibitor of metalloproteinase-1. J. Biol. Chem. 2007, 282, 364–371. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.-l.; Qiu, L.-y.; Kotzsch, A.; Weidauer, S.; Patterson, L.; Hammerschmidt, M.; Sebald, W.; Mueller, T.D. Crystal structure analysis reveals how the chordin family member crossveinless 2 blocks BMP-2 receptor binding. Dev. Cell 2008, 14, 739–750. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, R.; Fuentes-Prior, P.; Ong, E.; Coombs, G.; Hunter, M.; Oehler, R.; Pierson, D.; Gonzalez, R.; Huber, R.; Bode, W.; et al. Catalytic domain structures of MT-SP1/matriptase, a matrix-degrading transmembrane serine proteinase. J. Biol. Chem. 2002, 277, 2160–2168. [Google Scholar] [CrossRef] [PubMed]
- Farady, C.J.; Egea, P.F.; Schneider, E.L.; Darragh, M.R.; Craik, C.S. Structure of an Fab-protease complex reveals a highly specific non-canonical mechanism of inhibition. J. Mol. Biol. 2008, 380, 351–360. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.L.; Li, H.M.; Smith-Gill, S.J.; Mariuzza, R.A. Three-dimensional structures of the free and antigen-bound Fab from monoclonal antilysozyme antibody hyhel-63. Biochemistry 2000, 39, 6296–6309. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, K.A.; Thomson, J.M.; Corbett, K.D.; Bethel, C.R.; Berger, J.M.; Kirsch, J.F.; Bonomo, R.A.; Handel, T.M. Structural and computational characterization of the SHV-1 β-lactamase-β lactamase inhibitor protein interface. J. Biol. Chem. 2006, 281, 26745–26753. [Google Scholar] [CrossRef] [PubMed]
- Fujinaga, M.; Sielecki, A.R.; Read, R.J.; Ardelt, W.; Laskowski, M.; James, M.N.G. Crystal and molecular-structures of the complex of α-chymotrypsin with its inhibitor turkey ovomucoid 3rd domain at 1.8 a resolution. J. Mol. Biol. 1987, 195, 397–418. [Google Scholar] [CrossRef]
| Pre-Processing | Metrics | Algorithms | ||||
|---|---|---|---|---|---|---|
| Scaled | Nnet | avNNET | C5.0 Tree | C5.0 Rules | svmRadialSigma | |
| AUROC | 0.52 | 0.65 | 0.77 | 0.72 | 0.78 | |
| Accuracy | 0.92 | 0.94 | 0.96 | 0.92 | 0.91 | |
| Sensitivity | 0.92 | 0.88 | 0.88 | 0.85 | 0.80 | |
| Specificity | 0.91 | 0.98 | 1.00 | 0.96 | 0.97 | |
| PPV | 0.86 | 0.95 | 0.99 | 0.92 | 0.93 | |
| NPV | 0.95 | 0.94 | 0.94 | 0.92 | 0.89 | |
| FPR | 0.09 | 0.02 | 0.00 | 0.04 | 0.03 | |
| F1-score | 0.89 | 0.92 | 0.93 | 0.89 | 0.86 | |
| Scaled_Down | c-Forest | avNNET | C5.0Tree | C5.0Rules | GBM | |
| AUROC | 0.79 | 0.70 | 0.73 | 0.71 | 0.80 | |
| Accuracy | 0.91 | 0.95 | 0.96 | 0.90 | 1.00 | |
| Sensitivity | 0.93 | 0.96 | 0.96 | 0.89 | 0.99 | |
| Specificity | 0.90 | 0.93 | 0.95 | 0.91 | 1.00 | |
| PPV | 0.90 | 0.93 | 0.95 | 0.9 | 1.00 | |
| NPV | 0.92 | 0.96 | 0.96 | 0.89 | 0.99 | |
| FPR | 0.1 | 0.07 | 0.05 | 0.09 | 0 | |
| F1-score | 0.91 | 0.95 | 0.96 | 0.9 | 1.00 | |
| Scaled_Up | c-Forest | avNNET | C5.0Tree | C5.0Rules | GBM | |
| AUROC | 0.85 | 0.75 | 0.85 | 0.82 | 0.84 | |
| Accuracy | 0.93 | 0.94 | 0.98 | 0.95 | 0.98 | |
| Sensitivity | 0.93 | 0.96 | 0.99 | 0.96 | 0.97 | |
| Specificity | 0.93 | 0.92 | 0.97 | 0.94 | 0.99 | |
| PPV | 0.93 | 0.92 | 0.97 | 0.94 | 0.99 | |
| NPV | 0.93 | 0.96 | 0.99 | 0.95 | 0.97 | |
| FPR | 0.07 | 0.08 | 0.03 | 0.06 | 0.01 | |
| F1-score | 0.93 | 0.94 | 0.98 | 0.95 | 0.98 | |
| PCA | nnet | avNNET | C5.0Tree | C5.0Rules | svmRadialSigma | |
| AUROC | 0.69 | 0.75 | 0.61 | 0.59 | 0.76 | |
| Accuracy | 1.00 | 0.99 | 0.98 | 0.92 | 0.91 | |
| Sensitivity | 1.00 | 0.97 | 0.98 | 0.91 | 0.76 | |
| Specificity | 1.00 | 1.00 | 0.98 | 0.93 | 0.99 | |
| PPV | 1.00 | 0.99 | 0.96 | 0.89 | 0.97 | |
| NPV | 1.00 | 0.98 | 0.99 | 0.95 | 0.88 | |
| FPR | 0 | 0 | 0.02 | 0.07 | 0.01 | |
| F1-score | 1.00 | 0.98 | 0.97 | 0.90 | 0.85 | |
| PCA_Down | nnet | avNNET | C5.0Tree | C5.0Rules | svmRadialSigma | |
| AUROC | 0.70 | 0.78 | 0.67 | 0.67 | 0.75 | |
| Accuracy | 0.87 | 0.91 | 0.97 | 0.91 | 0.91 | |
| Sensitivity | 0.88 | 0.88 | 0.96 | 0.96 | 0.88 | |
| Specificity | 0.87 | 0.93 | 0.99 | 0.87 | 0.93 | |
| PPV | 0.87 | 0.92 | 0.99 | 0.88 | 0.93 | |
| NPV | 0.88 | 0.89 | 0.96 | 0.95 | 0.89 | |
| FPR | 0.13 | 0.07 | 0.01 | 0.13 | 0.07 | |
| F1-score | 0.87 | 0.90 | 0.97 | 0.92 | 0.91 | |
| PCA_Up | nnet | avNNET | C5.0Tree | C5.0Rules | svmRadialSigma | |
| AUROC | 0.75 | 0.82 | 0.80 | 0.78 | 0.80 | |
| Accuracy | 0.95 | 0.98 | 0.98 | 0.96 | 0.94 | |
| Sensitivity | 0.94 | 0.97 | 0.99 | 0.96 | 0.92 | |
| Specificity | 0.96 | 0.99 | 0.98 | 0.96 | 0.95 | |
| PPV | 0.96 | 0.99 | 0.98 | 0.96 | 0.95 | |
| NPV | 0.94 | 0.97 | 0.99 | 0.96 | 0.92 | |
| FPR | 0.04 | 0.01 | 0.02 | 0.04 | 0.05 | |
| F1-score | 0.95 | 0.98 | 0.98 | 0.96 | 0.94 | |
| Pre-Processing | Metrics | Algorithms | ||||
|---|---|---|---|---|---|---|
| Scaled | Nnet | avNNET | C5.0 Tree | C5.0 Rules | svmRadialSigma | |
| AUROC | 0.71 | 0.68 | 0.68 | 0.72 | 0.70 | |
| Accuracy | 0.74 | 0.71 | 0.71 | 0.74 | 0.73 | |
| Sensitivity | 0.57 | 0.57 | 0.5 | 0.60 | 0.55 | |
| Specificity | 0.83 | 0.79 | 0.83 | 0.82 | 0.83 | |
| PPV | 0.65 | 0.6 | 0.62 | 0.65 | 0.64 | |
| NPV | 0.78 | 0.77 | 0.75 | 0.79 | 0.77 | |
| FPR | 0.43 | 0.43 | 0.4 | 0.4 | 0.45 | |
| F1-score | 0.61 | 0.58 | 0.55 | 0.62 | 0.59 | |
| Scaled_Down | c-forest | avNNET | C5.0 Tree | C5.0 Rules | GBM | |
| AUROC | 0.75 | 0.68 | 0.63 | 0.71 | 0.73 | |
| Accuracy | 0.76 | 0.69 | 0.64 | 0.72 | 0.75 | |
| Sensitivity | 0.79 | 0.71 | 0.67 | 0.76 | 0.74 | |
| Specificity | 0.74 | 0.69 | 0.62 | 0.70 | 0.75 | |
| PPV | 0.63 | 0.55 | 0.49 | 0.59 | 0.62 | |
| NPV | 0.87 | 0.81 | 0.77 | 0.84 | 0.84 | |
| FPR | 0.21 | 0.29 | 0.33 | 0.24 | 0.26 | |
| F1-score | 0.7 | 0.62 | 0.57 | 0.66 | 0.68 | |
| Scaled_Up | c-forest | AvNNET | C5.0 Tree | C5.0 Rules | GBM | |
| AUROC | 0.78 | 0.73 | 0.65 | 0.70 | 0.80 | |
| Accuracy | 0.80 | 0.75 | 0.69 | 0.73 | 0.82 | |
| Sensitivity | 0.76 | 0.66 | 0.48 | 0.59 | 0.76 | |
| Specificity | 0.82 | 0.80 | 0.80 | 0.81 | 0.85 | |
| PPV | 0.70 | 0.64 | 0.57 | 0.63 | 0.73 | |
| NPV | 0.86 | 0.81 | 0.74 | 0.78 | 0.86 | |
| FPR | 0.24 | 0.34 | 0.52 | 0.41 | 0.24 | |
| F1-score | 0.73 | 0.65 | 0.52 | 0.61 | 0.75 | |
| PCA | Nnet | avNNET | C5.0 Tree | C5.0 Rules | svmRadialSigma | |
| AUROC | 0.65 | 0.73 | 0.68 | 0.71 | 0.71 | |
| Accuracy | 0.67 | 0.75 | 0.7 | 0.74 | 0.74 | |
| Sensitivity | 0.60 | 0.60 | 0.66 | 0.67 | 0.52 | |
| Specificity | 0.71 | 0.84 | 0.72 | 0.77 | 0.86 | |
| PPV | 0.54 | 0.67 | 0.57 | 0.62 | 0.67 | |
| NPV | 0.77 | 0.79 | 0.79 | 0.81 | 0.76 | |
| FPR | 0.4 | 0.4 | 0.34 | 0.33 | 0.48 | |
| F1-score | 0.57 | 0.64 | 0.61 | 0.64 | 0.58 | |
| PCA_Down | Nnet | avNNET | C5.0 Tree | C5.0 Rules | svmRadialSigma | |
| AUROC | 0.70 | 0.68 | 0.59 | 0.61 | 0.69 | |
| Accuracy | 0.71 | 0.69 | 0.61 | 0.63 | 0.70 | |
| Sensitivity | 0.76 | 0.71 | 0.55 | 0.60 | 0.72 | |
| Specificity | 0.68 | 0.69 | 0.64 | 0.64 | 0.69 | |
| PPV | 0.56 | 0.55 | 0.46 | 0.48 | 0.56 | |
| NPV | 0.84 | 0.81 | 0.72 | 0.74 | 0.82 | |
| FPR | 0.24 | 0.29 | 0.45 | 0.4 | 0.28 | |
| F1-score | 0.65 | 0.62 | 0.50 | 0.53 | 0.63 | |
| PCA_Up | Nnet | avNNET | C5.0 Tree | C5.0 Rules | svmRadialSigma | |
| AUROC | 0.67 | 0.75 | 0.56 | 0.61 | 0.69 | |
| Accuracy | 0.7 | 0.77 | 0.59 | 0.63 | 0.71 | |
| Sensitivity | 0.59 | 0.64 | 0.48 | 0.55 | 0.64 | |
| Specificity | 0.76 | 0.84 | 0.65 | 0.68 | 0.75 | |
| PPV | 0.58 | 0.69 | 0.43 | 0.48 | 0.59 | |
| NPV | 0.77 | 0.81 | 0.69 | 0.73 | 0.79 | |
| FPR | 0.41 | 0.36 | 0.52 | 0.45 | 0.36 | |
| F1-score | 0.58 | 0.66 | 0.46 | 0.52 | 0.61 | |
| Perfomance | Algorithms | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| c-Forest/ Up-Scaling Classes | SBHD2 | Robetta | KFC2-A | KFC2-B | CPORT | |||||||
| Training | Test | Training | Test | Training | Test | Training | Test | Training | Test | Training | Test | |
| AUROC | 0.85 | 0.78 | 0.74 | 0.69 | 0.62 | 0.62 | 0.72 | 0.66 | 0.60 | 0.67 | 0.54 | 0.54 |
| Accuracy | 0.93 | 0.80 | 0.70 | 0.71 | 0.66 | 0.66 | 0.76 | 0.71 | 0.70 | 0.73 | 0.49 | 0.49 |
| Sensitivity | 0.93 | 0.76 | 0.70 | 0.70 | 0.38 | 0.29 | 0.57 | 0.53 | 0.26 | 0.28 | 0.55 | 0.54 |
| Specificity | 0.93 | 0.82 | 0.70 | 0.71 | 0.85 | 0.88 | 0.85 | 0.81 | 0.93 | 0.96 | 0.45 | 0.47 |
| PPV | 0.93 | 0.70 | 0.55 | 0.56 | 0.61 | 0.60 | 0.67 | 0.59 | 0.65 | 0.80 | 0.34 | 0.35 |
| NPV | 0.93 | 0.86 | 0.82 | 0.82 | 0.68 | 0.67 | 0.79 | 0.77 | 0.71 | 0.72 | 0.66 | 0.66 |
| F1-score | 0.93 | 0.73 | 0.62 | 0.62 | 0.47 | 0.39 | 0.62 | 0.56 | 0.37 | 0.42 | 0.42 | 0.42 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Melo, R.; Fieldhouse, R.; Melo, A.; Correia, J.D.G.; Cordeiro, M.N.D.S.; Gümüş, Z.H.; Costa, J.; Bonvin, A.M.J.J.; Moreira, I.S. A Machine Learning Approach for Hot-Spot Detection at Protein-Protein Interfaces. Int. J. Mol. Sci. 2016, 17, 1215. https://doi.org/10.3390/ijms17081215
Melo R, Fieldhouse R, Melo A, Correia JDG, Cordeiro MNDS, Gümüş ZH, Costa J, Bonvin AMJJ, Moreira IS. A Machine Learning Approach for Hot-Spot Detection at Protein-Protein Interfaces. International Journal of Molecular Sciences. 2016; 17(8):1215. https://doi.org/10.3390/ijms17081215
Chicago/Turabian StyleMelo, Rita, Robert Fieldhouse, André Melo, João D. G. Correia, Maria Natália D. S. Cordeiro, Zeynep H. Gümüş, Joaquim Costa, Alexandre M. J. J. Bonvin, and Irina S. Moreira. 2016. "A Machine Learning Approach for Hot-Spot Detection at Protein-Protein Interfaces" International Journal of Molecular Sciences 17, no. 8: 1215. https://doi.org/10.3390/ijms17081215
APA StyleMelo, R., Fieldhouse, R., Melo, A., Correia, J. D. G., Cordeiro, M. N. D. S., Gümüş, Z. H., Costa, J., Bonvin, A. M. J. J., & Moreira, I. S. (2016). A Machine Learning Approach for Hot-Spot Detection at Protein-Protein Interfaces. International Journal of Molecular Sciences, 17(8), 1215. https://doi.org/10.3390/ijms17081215