Proteins are fundamental molecules of living organisms that participate in nearly all cell functions in an organism. Protein-protein interactions (PPIs) play an essential role in many biological processes. Thus, detection the interactions of proteins become more and more important. Knowledge of PPIs can provide insight into the molecular mechanisms of biological processes, lead to a better understanding of disease mechanisms, and suggest novel methods for practical medical applications. In recent years, a number of high-throughput technologies, such as immunoprecipitation [
1], protein chips [
2], and yeast two-hybrid screening methods [
3,
4], have been developed for detecting the large-scale PPIs. However, there are some disadvantages of these experimental approaches, such as time-intensiveness and high cost. In addition, the aforementioned methods suffer from high rates of false positives and false negatives. For these reasons, predicting unknown PPIs is considered a difficult task using only biological experimental methods. Therefore, there is a stronger motivation to exploit computational methods for PPIs.
As a result, a number of computational methods have been proposed to infer PPIs from different sources of information, including tertiary structures, phylogenetic profiles, protein domains, and secondary structures. However, these approaches cannot be employed when prior-knowledge about a protein of interest is not available. With the rapid growth of protein sequence data, the protein sequence-based method is becoming the most widely used tool for predicting PPIs. Consequently, a number of protein sequence-based methods have been developed for predicting PPIs. For example, Martin
et al. proposed the method that uses a novel descriptor called signature product to predict PPIs [
5]. The descriptor is extended to protein pairs by using signature product. The signature product is implemented within a support vector machine (SVM) classifier as a kernel function. Nanni and Lumini [
6] used the method based on an ensemble of
K-local hyperplane distance nearest neighbor (HKNN) classifiers to predict PPIs, where each classifier is trained using a different physicochemical property of the amino acids. Bock and Gough [
7] proposed a method that an SVM is used and combined with several structural and physiochemical descriptors to predict PPIs. Chou and Cai [
8] used the approach based on the gene ontology and the approach of pseudo-amino acid composition, where a predictor called “GO-PseAA” predictor was established to predict PPIs. Shen
et al. [
9] proposed a method based on a support vector machine (SVM) combined with a kernel function and a conjoint triad feature for describing amino acids to infer human PPIs. Guo
et al. [
10] proposed a sequence-based method that used a support vector machine (SVM) combined with feature representation of auto covariance (AC) descriptor to predict yeast PPIs. Chen
et al. [
11] used a domain-based random forest of decision trees to infer protein interactions. Licamele and Getoor [
12] proposed several novel relational features, where they used a Bagging algorithm to predict PPIs. Several other methods based on protein amino acid sequences have been proposed in previous works. In spite of this, there is still space to improve the accuracy and efficiency of the existing methods.
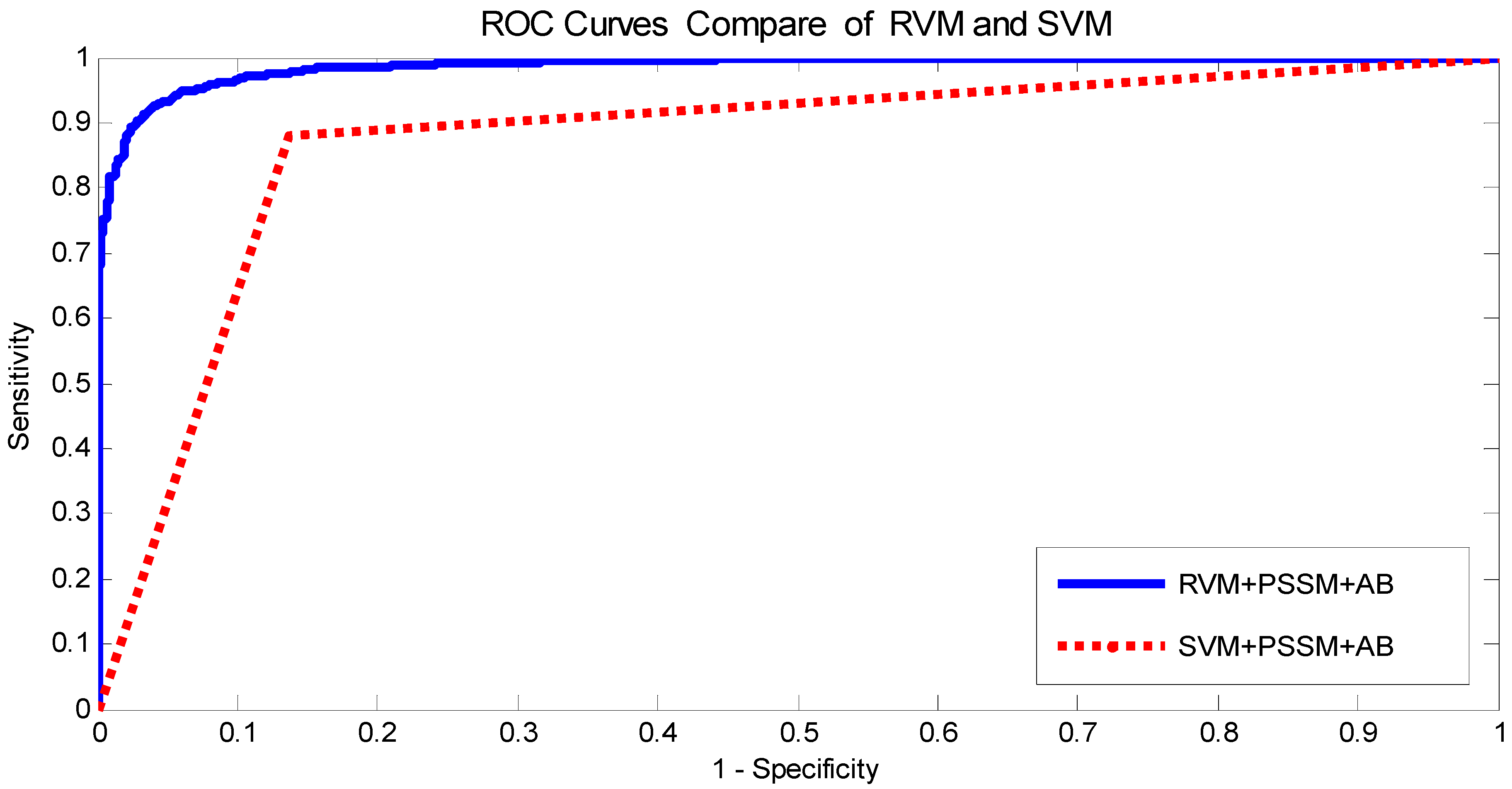
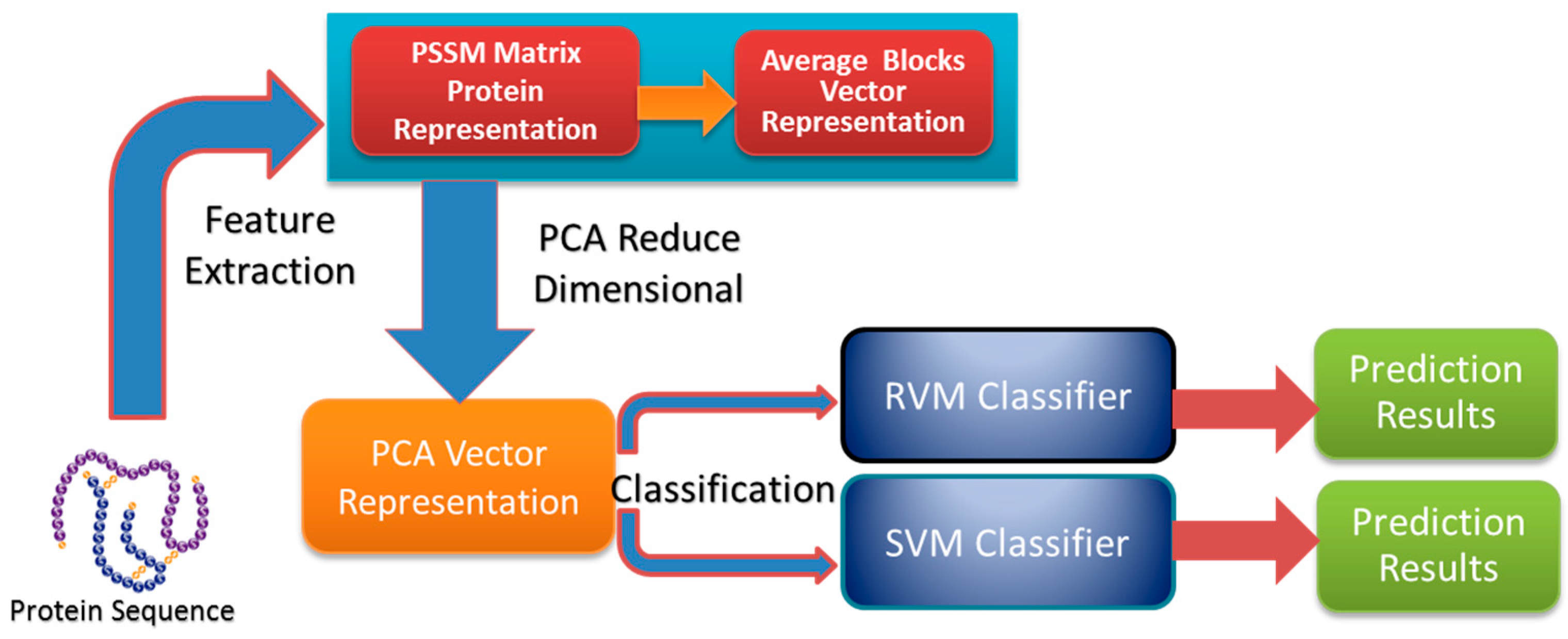
In this paper, a novel computational method was proposed, which can be used to predict PPIs using only protein sequence data. The main aim of this study is to improve the accuracy of predicting PPIs. The main improvements are the results of representing protein sequences using the Average Blocks (AB) feature representation on a Position Specific Scoring Matrix (PSSM), reducing the influence of noise by using a Principal Component Analysis (PCA), and using a Relevance Vector Machine (RVM) based classifier. More specifically, we first represent each protein using a PSSM representation. Then, an Average Blocks (AB) descriptor is employed to capture useful information from each protein PSSM and generate a 400-dimensional feature vector. Next, dimensionality reduction method PCA is used to reduce the dimensions of the AB vector and the influence of noise. Finally, the RVM model is employed as the machine learning approach to carry out classification. The proposed method was executed using two different PPIs datasets: yeast and Helicobacter pylori. The experimental results are found to be superior to SVM and other previous methods. In addition, cross-species experiments were also performed on five independent datasets C. elegans, M. musculus, H. sapiens, H. pylori, and E. coli. Thus, we also obtained good prediction accuracy in the cross-species experiments. The achieved results show that the proposed method is fit for predicting PPIs. These experimental results prove that the proposed method performs incredibly well in predicting PPIs.