Periodic CO2 Dosing Strategy for Dunaliella salina Batch Culture
Abstract
:1. Introduction
2. Results and Discussion
2.1. Model of Periodical CO2 Dosing
2.1.1. Estimation of Dosing Time
2.1.2. Estimation of Dosing Interval
2.1.3. Prediction of Final Concentration of Chlorophyll Content
2.2. Experimental Results
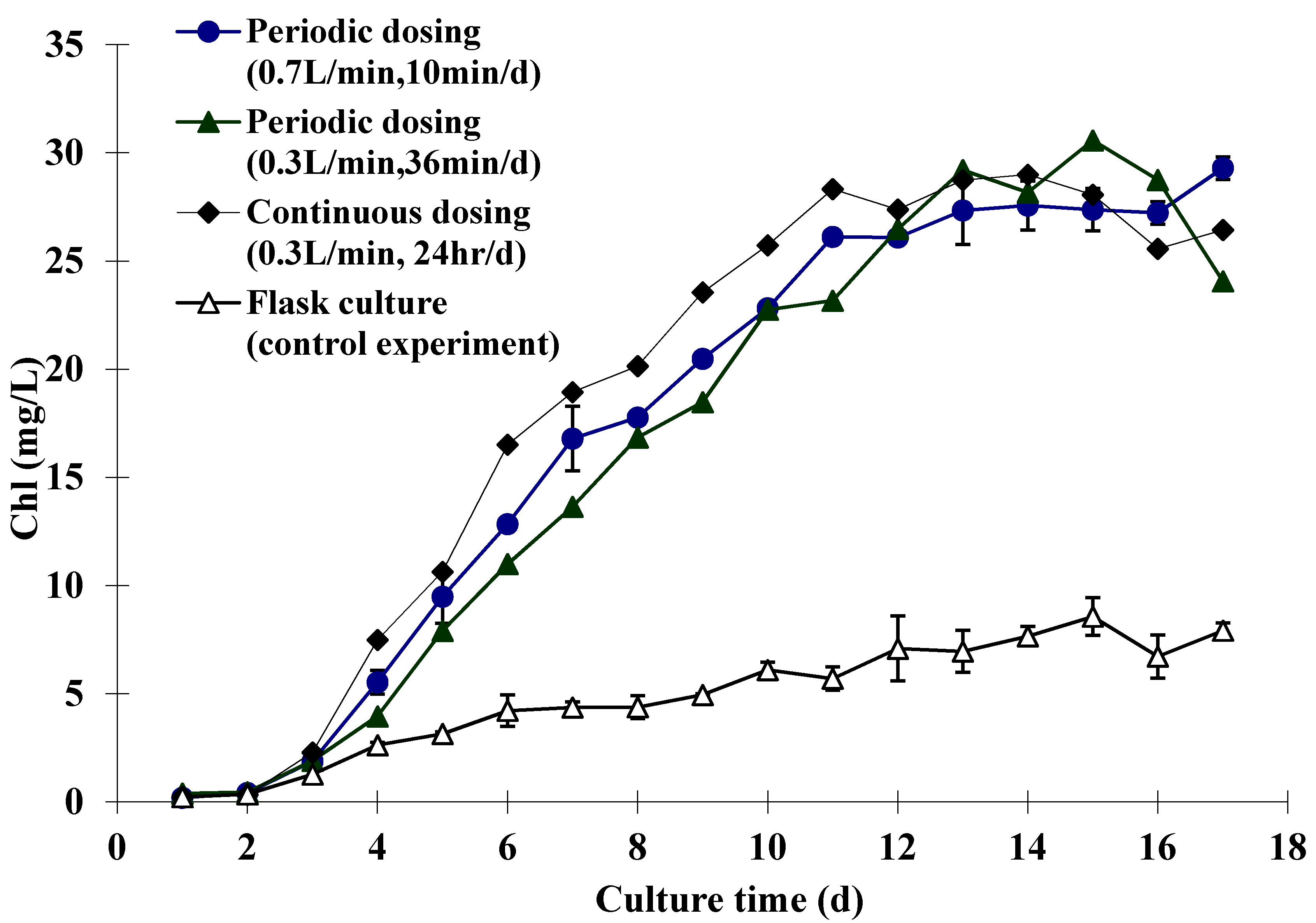
| Dosing Type (5% CO2) | Flow Rate (1 atm, 25 °C) | Dosing Time (in Total) | CO2 Total | ||
|---|---|---|---|---|---|
| Absorption | Input | η | |||
| Periodic | 0.7 L·min−1 | 10 min·d−1 × 8 d | 0.89 g | 5.03 g | 18% |
| Periodic | 0.3 L·min−1 | 36 min·d−1 × 8 d | 0.86 g | 7.75 g | 11% |
| Continuous | 0.3 L·min−1 | 24 h·d−1 × 8 d | 0.81 g | 311.1 g | 0.26% |
| Logarithmic Growth Time Period (d) | Dosing Condition | Estimated [Chl]t (mg/L) | Real [Chl]t (mg/L) | Error |
|---|---|---|---|---|
| 8 d | 0.7 L·min−1, 10 min·d−1 | 26.90 | 26.09 | 3% |
| 8 d | 0.3 L·min−1, 36 min·d−1 | 26.07 | 26.48 | 2% |
3. Experimental Section
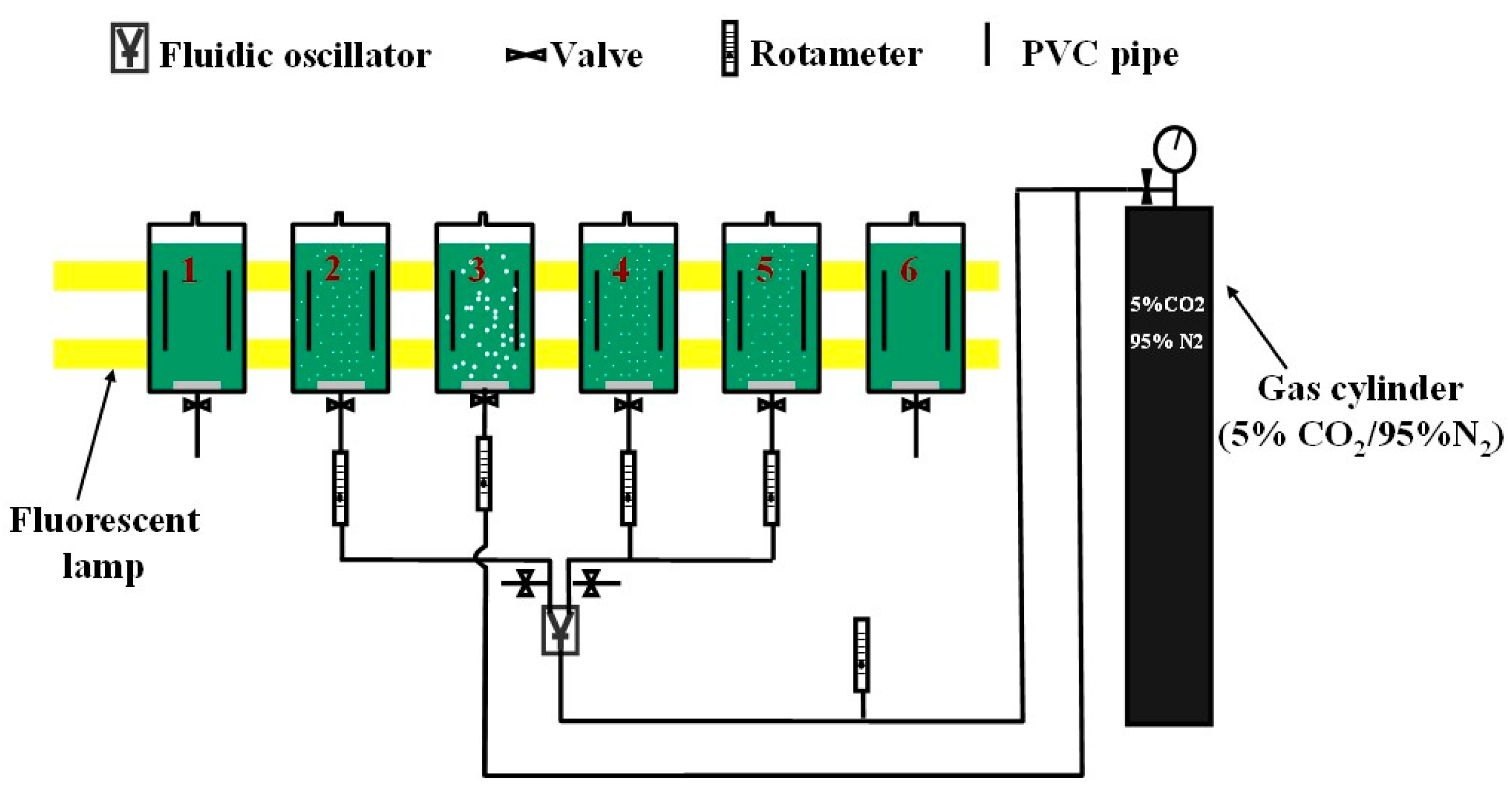
3.1. Experimental Setup
| Composition of Growth Medium Per Litre |
|---|
| 0.5 M·NaCl; 0.185 mM·H3BO3; 10 mM·KCl; 0.007 mM MnSO4; 20 mM·MgCl2; 0.8 × 10−3 mM·ZnCl2; 10 mM CaCl2; 0.2 × 10−4 mM CoCl2; 24 mM MgSO4; 0.2 × 10−6 mM·CuCl2; 5 mM NaNO3; 24 mM·Na2SO4; 0.0119 mM·NaHCO3; 0.1 mM NaH2PO4; 0.0015 mM·FeEDTA |
| Reactor | Dosing Conditions | Represent | |||
|---|---|---|---|---|---|
| Bubbles | Fluidic Oscillator | Dosing Flowrate | Dosing Time Equation (5) | ||
| No. 1 | No bubbles | Not Engaged | 0 | 0 | Flask culture |
| No. 2 | Microbubble (d32: 388 μm) | Engaged | 0.7 L·min−1 | 10 min·d−1 | Periodic dosing |
| No. 3 | Fine-bubble (d32: 719 μm) | Not Engaged | 0.3 L·min−1 | 24 h·d−1 | Continuous dosing |
| No. 4 | Microbubble (d32: 388 μm) | Engaged | 0.3 L·min−1 | 36 min·d−1 | Periodic dosing |
| No. 5 | Microbubble (d32: 388 μm) | Engaged | 0.7 L·min−1 | 10 min·d−1 | Duplication of No. 2 |
| No. 6 | No bubbles | Not Engaged | 0 | 0 | Duplication of No. 1 |
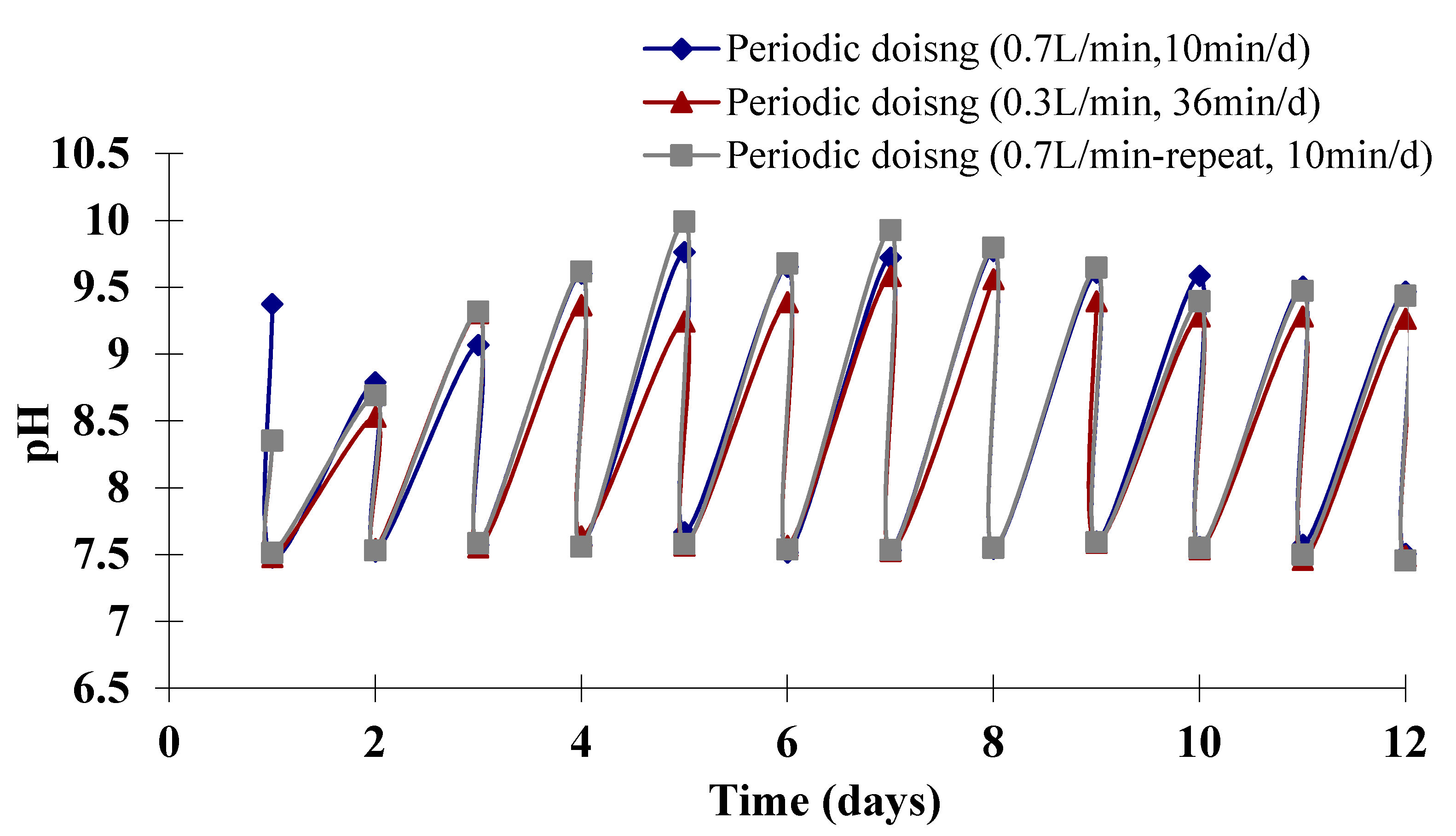
3.2. Estimation of the Dosing Time and Dosing Interval
4. Conclusions
Acknowledgments
Author Contributions
Abbreviations
| Δ[Chl] | changes in the concentration of chlorophyll content, mg·L−1 |
| Δ[CO2]dosed | the difference between the concentration of dissolved CO2 before and after dosing, mol·L−1 |
| Δ[CO2]uptake | changes in the concentration of CO2(aq) due to the CO2 consumption by algal growth, mol·L−1 |
| Δ[Na+] | the concentration of sodium ions in the liquid which comes from NaHCO3, mol·L−1 |
| CO2% | the concentration of CO2 in the gas stream, % (v/v) |
| d32 | the Sauter mean diameter of the bubbles, μm |
| η | the CO2 capture efficiency, % |
| KLa | volumetric mass transfer coefficient (min−1), where “KL” is the CO2 gas-liquid mass transfer coefficient (m·min−1); “a” means the gas-liquid interfacial area (m−1) |
| P | standard atmospheric pressure, 101.325 Kpa |
| pH | the pH value of the liquid |
| R | universal gas constant, 8.314 J·mol−1·K−1 |
| T | the temperature, K |
| tc | culture time period, d |
| td | CO2 dosing time, min |
| ti | CO2 dosing interval, min |
| ν'Chl | average productivity of chlorophyll content, mg·L−1·d−1 |
| νCO2 uptake | instantaneous algal CO2 uptake rate, mol·L−1·min−1 |
| ν'CO2 uptake | average algal CO2 uptake rate, mol·L−1·min−1 |
| Q | the gas dosing flowrate, L·min−1 |
| ν'MTR | CO2 average mass transfer rate, mol·L−1·min−1 |
| VL | the volume of the liquid, L |
| [CT] | total concentration of inorganic carbon in the liquid, mol·L−1 |
| [CT]pH=A | total concentration of inorganic carbon in the liquid at pH=A, mol·L−1 |
| [CT]pH=B | total concentration of inorganic carbon in the liquid at pH=B, mol·L−1 |
| [Chl] | concentration of chlorophyll content in the culture, mg·L−1 |
| [Chl]0 | initial concentration of chlorophyll content at the beginning of log growth phase, mg·L−1 |
| [CO2] | dissolved carbon dioxide concentration in the liquid, mol·L−1 |
| [CO2]* | dissolved carbon dioxide equilibrium concentration in the liquid, mol·L−1 |
| [CO2]0 | initial dissolved carbon dioxide concentration in the liquid, mol·L−1 |
| [CO2]pH=A | dissolved carbon dioxide concentration in the liquid at pH=A, mol·L−1 |
| [CO2]pH=B | dissolved carbon dioxide concentration in the liquid at pH=B, mol·L−1 |
| [CO32−] | the concentration of carbonate, mol·L−1 |
| [HCO3−] | the concentration of bicarbonate, mol·L−1 |
Conflicts of Interest
References
- Wang, B.; Li, Y.; Wu, N.; Lan, C.Q. CO2 bio-mitigation using microalgae. Appl. Microbiol. Biotechnol. 2008, 79, 707–718. [Google Scholar] [CrossRef] [PubMed]
- Pulz, O. Photobioreactors: Production systems for phototrophic microorganisms. Appl. Microbiol. Biotechnol. 2001, 57, 287–293. [Google Scholar] [CrossRef] [PubMed]
- Satyanarayana, K.G.; Mariano, A.B.; Vargas, J.V.C. A review on microalgae, a versatile source for sustainable energy and materials. Int. J. Energy Res. 2011, 35, 291–311. [Google Scholar] [CrossRef]
- Zimmerman, W.B.; Tesar, V.; Butler, S.; Bandulasena, H.C.H. Microbubble generation. Recent Pat. Eng. 2008, 2, 1–8. [Google Scholar] [CrossRef]
- Molina, E.; Fernandez, J.; Acien, F.G.; Chisti, Y. Tubular photobioreactor design for algal cultures. J. Biotechnol. 2001, 92, 113–131. [Google Scholar] [CrossRef] [PubMed]
- Carvalho, A.P.; Malcata, F.X. Transfer of carbon dioxide within cultures of microalgae: Plain bubbling versus hollow-fiber modules. Biotechnol. Prog. 2001, 17, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Ying, K.; Gilmour, D.J.; Shi, Y.; Zimmerman, W.B. Growth enhancement of Dunaliella salina by microbubble induced airlift loop bioreactor (ALB)—The relation between mass transfer and growth rate. J. Biomater. Nanobiotechnol. 2013, 4. [Google Scholar] [CrossRef]
- Ying, K.; Gilmour, D.J.; Zimmerman, W.B. Effects of CO2 and pH on growth of the microalga dunaliella salina. J. Microb. Biochem. Technol. 2014, 6, 167–173. [Google Scholar] [CrossRef]
- Ying, K.; Mahmood, K.H.A.; James, H.; Gilmour, D.J.; Zimmerman, W.B. Enhanced mass transfer in microbubble driven airlift bioreactor for Microalgal culture. J. Eng. 2013, 5, 735–743. [Google Scholar] [CrossRef]
- Livansky, K. Losses of CO2 in outdoor mass algal cultures: Determination of the mass transfer coefficient KL by means of measured pH course in NaHCO3 solution. Algol. Stud. 1990, 58, 87–97. [Google Scholar]
- Camacho, R.F. Prediction of dissolved oxygen and carbon dioxide concentration profiles in tubular photobioreactors for microalgal culture. Biotechnol. Bioeng. 1999, 62, 71–84. [Google Scholar] [CrossRef] [PubMed]
- Scragg, A.H. Bioreactors in Biotechnology: A Practical Approach; Ellis Horwood: London, UK, 1991; pp. 47–48. [Google Scholar]
- Stemler, A. Forms of dissolved carbon dioxide required for photosystem II activity in chloroplast membranes. Plant Physiol. 1980, 65, 1160–1165. [Google Scholar] [CrossRef] [PubMed]
- Richmond, A. Handbook of Microalgal Culture: Biotechnology and Applied Phycology; Blackwell Science: Oxford, UK, 2008. [Google Scholar]
- Borowitzka, M.A.; Borowitzka, L.J. Dunaliella. In Micro-algal Biotechnology; Borowitzka, M.A., Borowitzka, L.J., Eds.; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Zimmerman, W.B.; Zandi, M.; Bandulasena, H.C.H.; Tesar, V.; Gilmour, D.J.; Ying, K. Design of an airlift loop bioreactor and pilot scales studies with fluidic oscillator induced microbubbles for growth of a microalgae Dunaliella salina. Appl. Energy 2011, 88, 3357–3369. [Google Scholar] [CrossRef]
- Brittle, S.; Desai, P.; Ng, W.C.; Dunbar, A.; Howell, R.; Zimmerman, W.B. Optimal system desugn for minimising microbubble size through frequency control. Chem. Eng. Res. Des. submitted for publication. 2015. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ying, K.; Gilmour, D.J.; Zimmerman, W.B. Periodic CO2 Dosing Strategy for Dunaliella salina Batch Culture. Int. J. Mol. Sci. 2015, 16, 11509-11521. https://doi.org/10.3390/ijms160511509
Ying K, Gilmour DJ, Zimmerman WB. Periodic CO2 Dosing Strategy for Dunaliella salina Batch Culture. International Journal of Molecular Sciences. 2015; 16(5):11509-11521. https://doi.org/10.3390/ijms160511509
Chicago/Turabian StyleYing, Kezhen, D. James Gilmour, and William B. Zimmerman. 2015. "Periodic CO2 Dosing Strategy for Dunaliella salina Batch Culture" International Journal of Molecular Sciences 16, no. 5: 11509-11521. https://doi.org/10.3390/ijms160511509
APA StyleYing, K., Gilmour, D. J., & Zimmerman, W. B. (2015). Periodic CO2 Dosing Strategy for Dunaliella salina Batch Culture. International Journal of Molecular Sciences, 16(5), 11509-11521. https://doi.org/10.3390/ijms160511509





