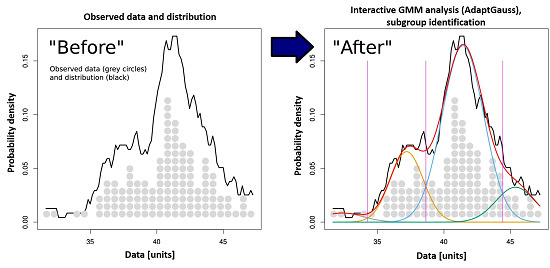
Identification of Molecular Fingerprints in Human Heat Pain Thresholds by Use of an Interactive Mixture Model R Toolbox (AdaptGauss)
Abstract
:1. Introduction
2. Results and Discussion
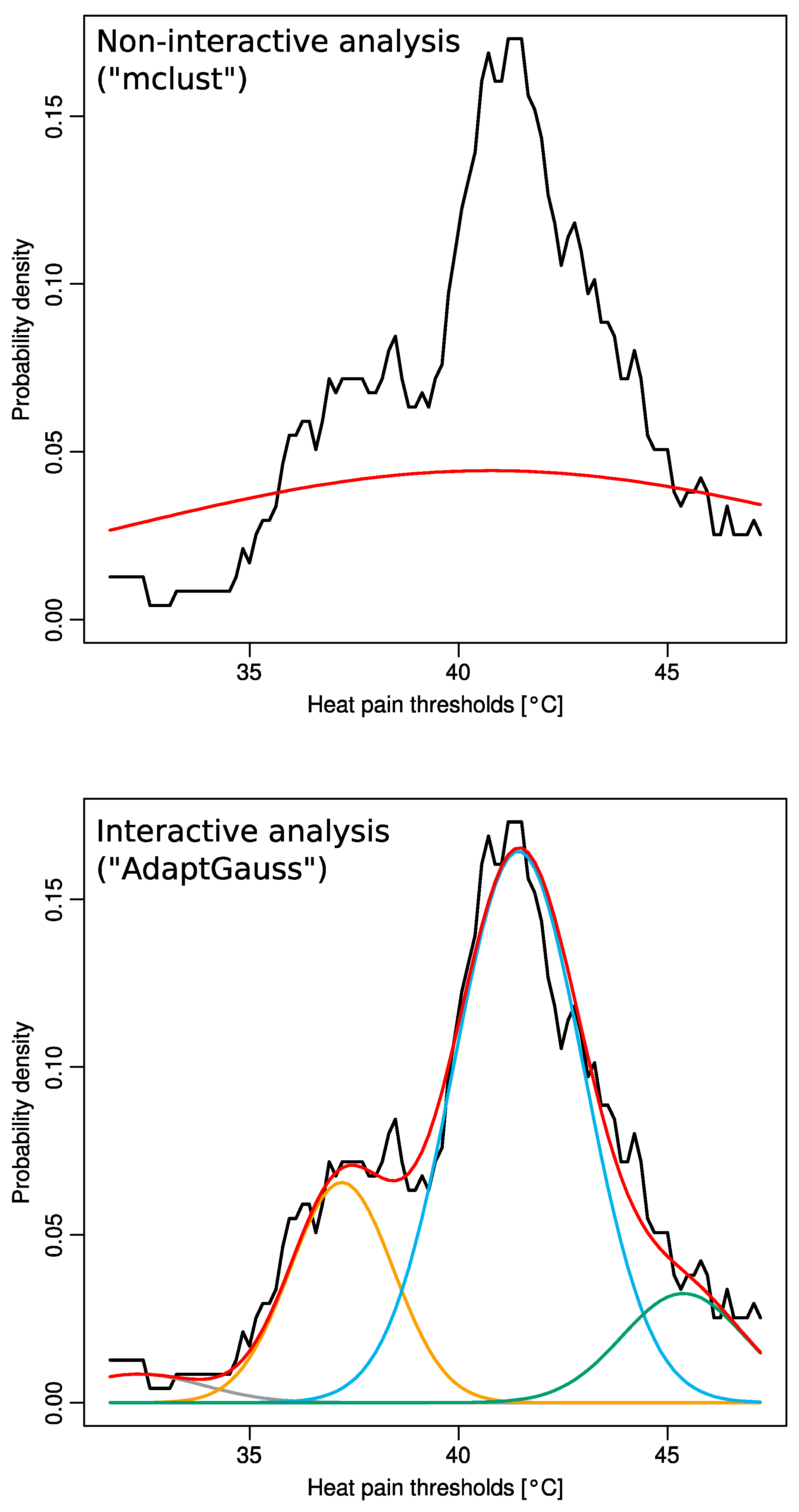
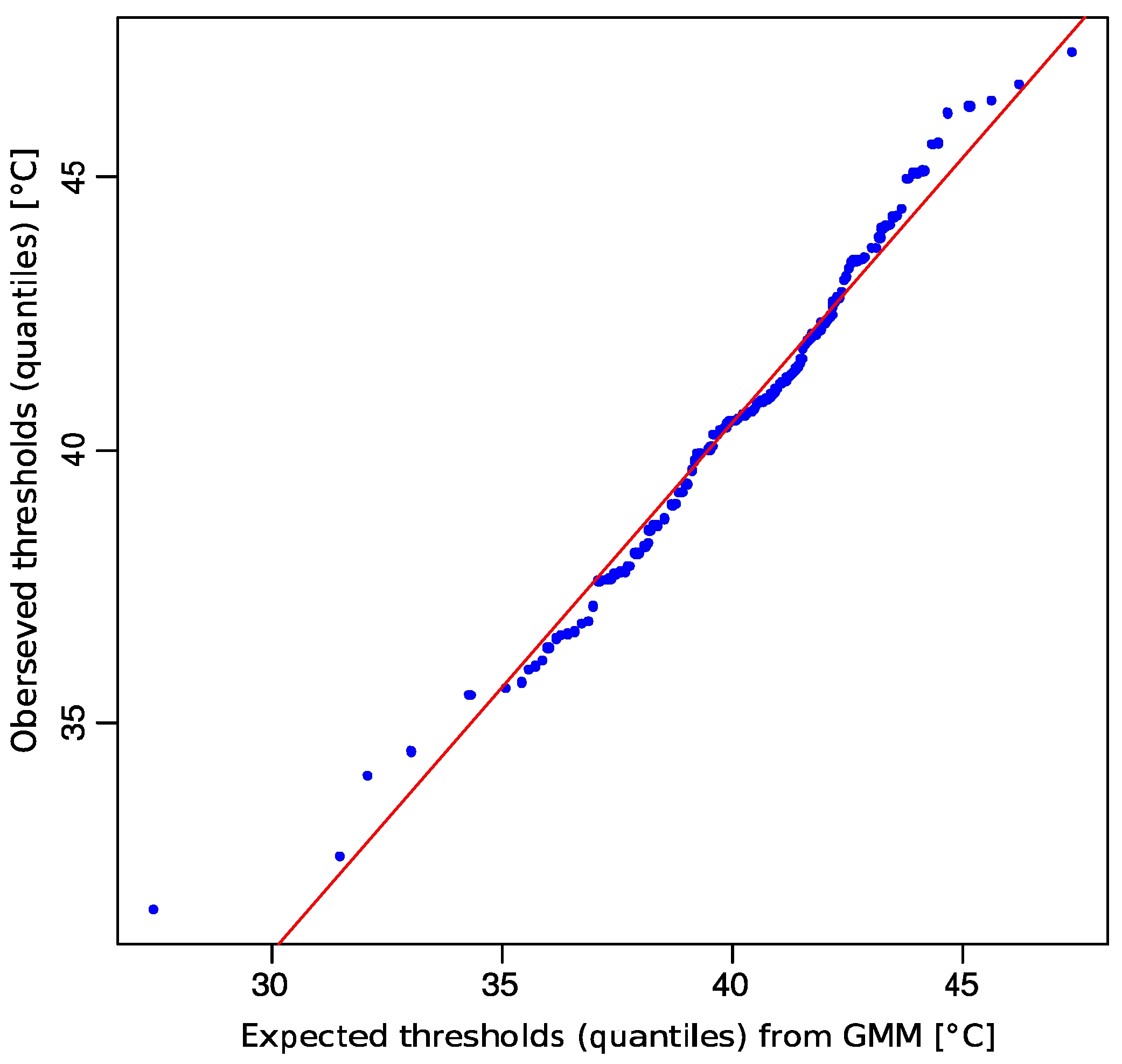
2.1. Non-Normality of Heat Pain Data

2.2. Multimodal Distribution of HPT Data
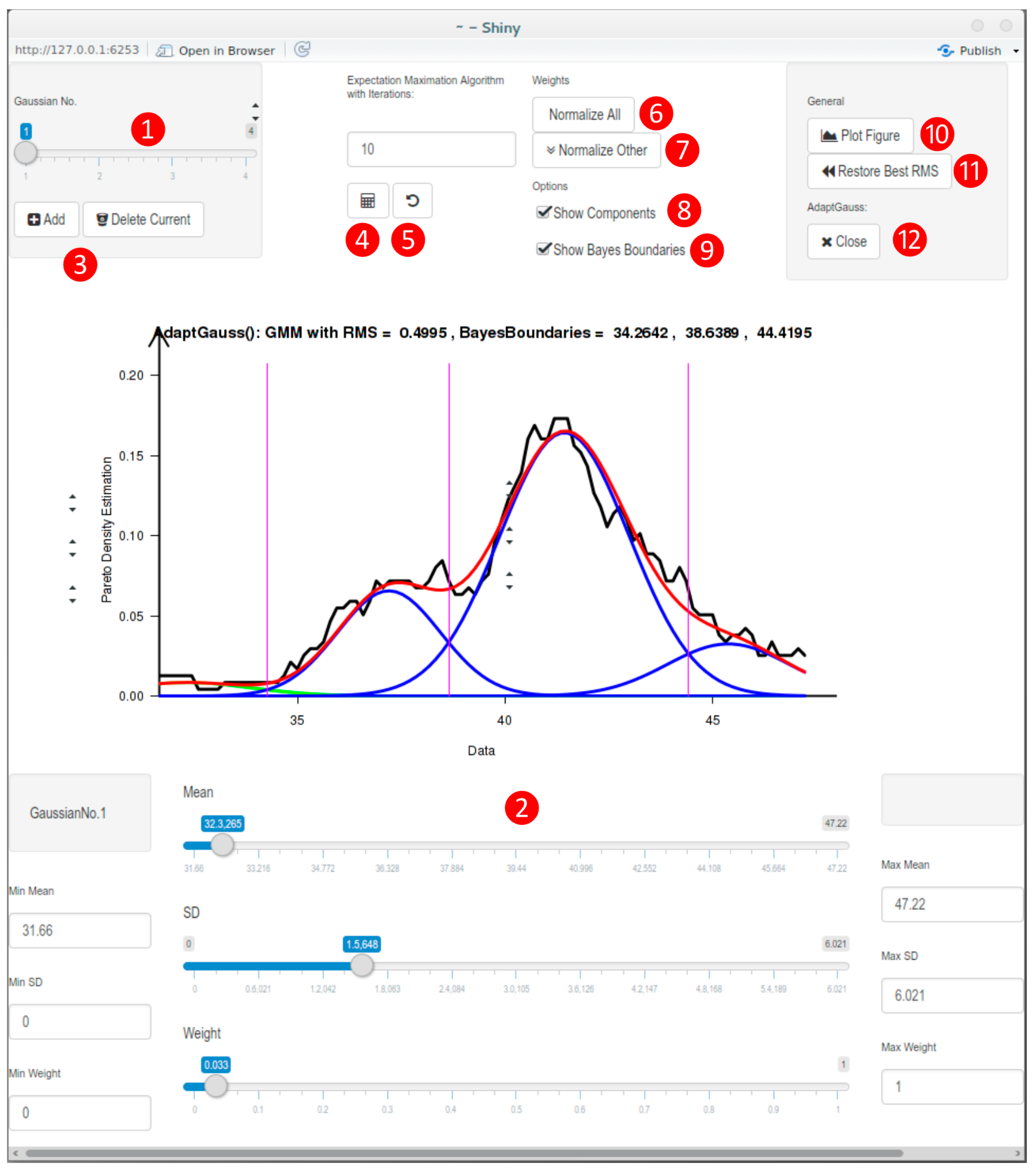
3. Methods
3.1. Heat Pain Threshold Data (HPT)
3.2. Beyond Normal Distribution: Gaussian Mixture Models
3.3. Implementation of a Visualization Guided GMM Tool: AdaptGauss
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Julius, D.; Basbaum, A.I. Molecular mechanisms of nociception. Nature 2001, 413, 203–210. [Google Scholar] [PubMed]
- Mogil, J.S. The genetic mediation of individual differences in sensitivity to pain and its inhibition. Proc. Natl. Acad. Sci. USA 1999, 96, 7744–7751. [Google Scholar] [CrossRef] [PubMed]
- Hastie, B.A.; Riley, J.L., 3rd; Robinson, M.E.; Glover, T.; Campbell, C.M.; Staud, R.; Fillingim, R.B. Cluster analysis of multiple experimental pain modalities. Pain 2005, 116, 227–237. [Google Scholar] [CrossRef] [PubMed]
- Binder, A.; May, D.; Baron, R.; Maier, C.; Tölle, T.R.; Treede, R.D.; Berthele, A.; Faltraco, F.; Flor, H.; Gierthmuhlen, J.; et al. Transient receptor potential channel polymorphisms are associated with the somatosensory function in neuropathic pain patients. PLoS ONE 2011, 6, e17387. [Google Scholar] [CrossRef] [PubMed]
- Baron, R.; Tölle, T.R.; Gockel, U.; Brosz, M.; Freynhagen, R. A cross-sectional cohort survey in 2100 patients with painful diabetic neuropathy and postherpetic neuralgia: Differences in demographic data and sensory symptoms. Pain 2009, 146, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Lötsch, J.; Dimova, V.; Lieb, I.; Zimmermann, M.; Oertel, B.G.; Ultsch, A. Multimodal distribution of human cold pain thresholds. PLoS ONE 2015, 10, e0125822. [Google Scholar] [PubMed]
- Lötsch, J.; Dimova, V.; Hermens, H.; Zimmermann, M.; Geisslinger, G.; Oertel, B.G.; Ultsch, A. Pattern of neuropathic pain induced by topical capsaicin application in healthy subjects. Pain 2015, 156, 405–414. [Google Scholar] [CrossRef] [PubMed]
- Dimova, V.; Oertel, B.G.; Kabakci, G.; Zimmermann, M.; Hermens, H.; Lautenbacher, S.; Ultsch, A.; Lötsch, J. A more pessimistic life-orientation is associated with experimental inducibility of neuropathy-like pain pattern in healthy subjects. J. Pain 2015, 16, 791–800. [Google Scholar] [CrossRef] [PubMed]
- Rolke, R.; Baron, R.; Maier, C.; Tölle, T.R.; Treede, R.D.; Beyer, A.; Binder, A.; Birbaumer, N.; Birklein, F.; Botefur, I.C.; et al. Quantitative sensory testing in the German Research Network on Neuropathic Pain (DFNS): Standardized protocol and reference values. Pain 2006, 123, 231–243. [Google Scholar] [PubMed]
- Rolke, R.; Magerl, W.; Campbell, K.A.; Schalber, C.; Caspari, S.; Birklein, F.; Treede, R.D. Quantitative sensory testing: A comprehensive protocol for clinical trials. Eur. J. Pain 2006, 10, 77–88. [Google Scholar] [CrossRef] [PubMed]
- Ultsch, A. Pareto Density Estimation: A Density Estimation for Knowledge Discovery. In Innovations in Classification, Data Science, and Information Systems, Proceedings of the 27th Annual Conference of the German Classification Society (GfKL), 12–14 March 2003; Baier, D., Werrnecke, K.D., Eds.; Springer: Berlin, Germany, 2005; pp. 91–100. [Google Scholar]
- Fraley, C.; Raftery, A.E.; Murphy, T.B.; Scrucca, L. Mclust Version 4 for R: Normal Mixture Modeling for Model-Based Clustering, Classification, and Density Estimation; Department of Statistics, University of Washington: Seattle, WA, USA, 2012. [Google Scholar]
- Smirnov, N. Table for estimating the goodness of fit of empirical distributions. Ann. Math. Stat. 1948, 19, 279–281. [Google Scholar] [CrossRef]
- Pfau, D.; Klein, T.; Blunk, J.A.; Geber, C.; Krumova, E.; Limbeck, C.; Magerl, W.; Maier, C.; Westermann, A.; Schuh-Hofer, S.; et al. QST Quantitative sensorische Testung, Handanweisung für den Untersucher, Eine standardisierte Testbatterie für die Quantitative Sensorische Testung nach den Regeln des Deutschen Forschungsverbundes Neuropathischer Schmerz (DFNS); Rolke, R., Andrews, A., Magerl, W., Treede, R.D., Eds.; Lehrstuhl für Neurophysiologie, Universitätsmedizin Mannheim: Mannheim, Germany, 2010. [Google Scholar]
- Maier, C.; Baron, R.; Tölle, T.R.; Binder, A.; Birbaumer, N.; Birklein, F.; Gierthmühlen, J.; Flor, H.; Geber, C.; Huge, V.; et al. Quantitative sensory testing in the German Research Network on Neuropathic Pain (DFNS): Somatosensory abnormalities in 1236 patients with different neuropathic pain syndromes. Pain 2010, 150, 439–450. [Google Scholar] [CrossRef] [PubMed]
- Qin, F. Time-Resolved Activation of Thermal TRP Channels by Fast Temperature Jumps. In TRP Channels; Zhu, M.X., Ed.; Llc.: Boca Raton, FL, USA, 2011. [Google Scholar]
- Melzack, R.; Rose, G.; McGinty, D. Skin sensitivity to thermal stimuli. Exp. Neurol. 1962, 6, 300–314. [Google Scholar] [CrossRef]
- Clapham, D.E. TRP channels as cellular sensors. Nature 2003, 426, 517–524. [Google Scholar] [CrossRef] [PubMed]
- Clapham, D.E.; Runnels, L.W.; Strubing, C. The TRP ion channel family. Nat. Rev. Neurosci. 2001, 2, 387–396. [Google Scholar] [CrossRef] [PubMed]
- Patapoutian, A.; Peier, A.M.; Story, G.M.; Viswanath, V. ThermoTRP channels and beyond: Mechanisms of temperature sensation. Nat. Rev. Neurosci. 2003, 4, 529–539. [Google Scholar] [CrossRef] [PubMed]
- Ferrandiz-Huertas, C.; Mathivanan, S.; Wolf, C.J.; Devesa, I.; Ferrer-Montiel, A. Trafficking of ThermoTRP Channels. Membranes 2014, 4, 525–564. [Google Scholar] [CrossRef] [PubMed]
- Reubish, D.; Emerling, D.; Defalco, J.; Steiger, D.; Victoria, C.; Vincent, F. Functional assessment of temperature-gated ion-channel activity using a real-time PCR machine. Biotechniques 2009, 47, iii–ix. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, K.; Lennerz, J.K.; Hein, A.; Link, A.S.; Kaczmarek, J.S.; Delling, M.; Uysal, S.; Pfeifer, J.D.; Riccio, A.; Clapham, D.E. Transient receptor potential cation channel, subfamily C, member 5 (TRPC5) is a cold-transducer in the peripheral nervous system. Proc. Natl. Acad. Sci. USA 2011, 108, 18114–18119. [Google Scholar] [CrossRef] [PubMed]
- Caterina, M.J.; Leffler, A.; Malmberg, A.B.; Martin, W.J.; Trafton, J.; Petersen-Zeitz, K.R.; Koltzenburg, M.; Basbaum, A.I.; Julius, D. Impaired nociception and pain sensation in mice lacking the capsaicin receptor. Science 2000, 288, 306–313. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.B.; Gray, J.; Gunthorpe, M.J.; Hatcher, J.P.; Davey, P.T.; Overend, P.; Harries, M.H.; Latcham, J.; Clapham, C.; Atkinson, K.; et al. Vanilloid receptor-1 is essential for inflammatory thermal hyperalgesia. Nature 2000, 405, 183–187. [Google Scholar] [CrossRef] [PubMed]
- Moqrich, A.; Hwang, S.W.; Earley, T.J.; Petrus, M.J.; Murray, A.N.; Spencer, K.S.R.; Andahazy, M.; Story, G.M.; Patapoutian, A. Impaired thermosensation in mice lacking TRPV3, a heat and camphor sensor in the skin. Science 2005, 307, 1468–1472. [Google Scholar] [CrossRef] [PubMed]
- McNamara, C.R.; Mandel-Brehm, J.; Bautista, D.M.; Siemens, J.; Deranian, K.L.; Zhao, M.; Hayward, N.J.; Chong, J.A.; Julius, D.; Moran, M.M.; et al. TRPA1 mediates formalin-induced pain. Proc. Natl. Acad. Sci. USA 2007, 104, 13525–13530. [Google Scholar] [CrossRef] [PubMed]
- Bautista, D.M.; Siemens, J.; Glazer, J.M.; Tsuruda, P.R.; Basbaum, A.I.; Stucky, C.L.; Jordt, S.E.; Julius, D. The menthol receptor TRPM8 is the principal detector of environmental cold. Nature 2007, 48, 204–208. [Google Scholar] [CrossRef] [PubMed]
- Colburn, R.W.; Lubin, M.L.; Stone, D.J., Jr.; Wang, Y.; Lawrence, D.; D’Andrea, M.R.; Brandt, M.R.; Liu, Y.; Flores, C.M.; Qin, N. Attenuated cold sensitivity in TRPM8 null mice. Neuron 2007, 54, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Dhaka, A.; Murray, A.N.; Mathur, J.; Earley, T.J.; Petrus, M.J.; Patapoutian, A. TRPM8 is required for cold sensation in mice. Neuron 2007, 54, 371–378. [Google Scholar] [CrossRef] [PubMed]
- Szallasi, A.; Cortright, D.N.; Blum, C.A.; Eid, S.R. The vanilloid receptor TRPV1: 10 years from channel cloning to antagonist proof-of-concept. Nat. Rev. Drug Discov. 2007, 6, 357–372. [Google Scholar] [CrossRef] [PubMed]
- Cesare, P.; McNaughton, P. A novel heat-activated current in nociceptive neurons and its sensitization by bradykinin. Proc. Natl. Acad. Sci. USA 1996, 93, 15435–15439. [Google Scholar] [CrossRef] [PubMed]
- Todaka, H.; Taniguchi, J.; Satoh, J.; Mizuno, A.; Suzuki, M. Warm temperature-sensitive transient receptor potential vanilloid 4 (TRPV4) plays an essential role in thermal hyperalgesia. J. Biol. Chem. 2004, 279, 35133–35138. [Google Scholar] [CrossRef] [PubMed]
- Grant, A.D.; Cottrell, G.S.; Amadesi, S.; Trevisani, M.; Nicoletti, P.; Materazzi, S.; Altier, C.; Cenac, N.; Zamponi, G.W.; Bautista-Cruz, F.; et al. Protease-activated receptor 2 sensitizes the transient receptor potential vanilloid 4 ion channel to cause mechanical hyperalgesia in mice. J. Physiol. 2007, 578, 715–733. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.C.; Rainville, P.; Bushnell, M.C. Noxious and innocuous cold discrimination in humans: Evidence for separate afferent channels. Pain 1996, 68, 33–43. [Google Scholar] [CrossRef]
- Peier, A.M.; Moqrich, A.; Hergarden, A.C.; Reeve, A.J.; Andersson, D.A.; Story, G.M.; Earley, T.J.; Dragoni, I.; McIntyre, P.; Bevan, S.; et al. A TRP channel that senses cold stimuli and menthol. Cell 2002, 108, 705–715. [Google Scholar] [CrossRef]
- Bandell, M.; Story, G.M.; Hwang, S.W.; Viswanath, V.; Eid, S.R.; Petrus, M.J.; Earley, T.J.; Patapoutian, A. Noxious cold ion channel TRPA1 is activated by pungent compounds and bradykinin. Neuron 2004, 41, 849–857. [Google Scholar] [CrossRef]
- Bautista, D.M.; Jordt, S.E.; Nikai, T.; Tsuruda, P.R.; Read, A.J.; Poblete, J.; Yamoah, E.N.; Basbaum, A.I.; Julius, D. TRPA1 mediates the inflammatory actions of environmental irritants and proalgesic agents. Cell 2006, 124, 1269–1282. [Google Scholar] [CrossRef] [PubMed]
- Kwan, K.Y.; Allchorne, A.J.; Vollrath, M.A.; Christensen, A.P.; Zhang, D.-S.; Woolf, C.J.; Corey, D.P. TRPA1 contributes to cold, mechanical, and chemical nociception but is not essential for hair-cell transduction. Neuron 2006, 50, 277–289. [Google Scholar] [CrossRef] [PubMed]
- Story, G.M.; Peier, A.M.; Reeve, A.J.; Eid, S.R.; Mosbacher, J.; Hricik, T.R.; Earley, T.J.; Hergarden, A.C.; Andersson, D.A.; Hwang, S.W.; et al. ANKTM1, a TRP-like channel expressed in nociceptive neurons, is activated by cold temperatures. Cell 2003, 112, 819–829. [Google Scholar] [CrossRef]
- Knothe, C.; Doehring, A.; Ultach, A.; Lötsch, J. Methadone induces hypermethylation of human DNA. Epigenomics 2015. [Google Scholar] [CrossRef] [PubMed]
- Bollati, V.; Baccarelli, A.; Hou, L.; Bonzini, M.; Fustinoni, S.; Cavallo, D.; Byun, H.M.; Jiang, J.; Marinelli, B.; Pesatori, A.C.; et al. Changes in DNA methylation patterns in subjects exposed to low-dose benzene. Cancer Res. 2007, 67, 876–880. [Google Scholar] [CrossRef] [PubMed]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics 1945, 1, 80–83. [Google Scholar] [CrossRef]
- McGlone, F.; Reilly, D. The cutaneous sensory system. Neurosci. Biobehav. Rev. 2010, 34, 148–159. [Google Scholar] [CrossRef] [PubMed]
- Meh, D.; Denislic, M. Quantitative assessment of thermal and pain sensitivity. J. Neurol. Sci. 1994, 127, 164–169. [Google Scholar] [CrossRef]
- Stevens, J.C.; Choo, K.K. Temperature sensitivity of the body surface over the life span. Somatosens. Mot. Res. 1998, 15, 13–28. [Google Scholar] [PubMed]
- Berkley, K.J. Sex differences in pain. Behav. Brain Sci. 1997, 20, 371–380. [Google Scholar] [CrossRef] [PubMed]
- Riley, J.L., 3rd; Robinson, M.E.; Wise, E.A.; Myers, C.D.; Fillingim, R.B. Sex differences in the perception of noxious experimental stimuli: A meta-analysis. Pain 1998, 74, 181–187. [Google Scholar] [CrossRef]
- Derbyshire, S.W. Gender, pain, and the brain. Pain: Clin. Updat. 2008, 16, 1–4. [Google Scholar]
- Press, W.H. Numerical Recipes 3rd Edition: The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Fraley, C.; Raftery, A.E. Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc. 2002, 97, 611–631. [Google Scholar] [CrossRef]
- Bishop, C. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Mixture model. Available online: https://en.wikipedia.org/wiki/Mixture_model (accessed on 23 October 2015).
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum Likelihood from Incomplete Data via the EM Algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- McGrayne, S.B. The Theory That Would Not Die: How Bayes’ Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy; Yale University Press: New Haven, CT, USA, 2011. [Google Scholar]
- The Comprehensive R Archive Network. Available online: http://CRAN.R-project.org/ (accessed on 23 October 2015).
- AdaptGauss: Gaussian Mixture Models (GMM). Available online: https://cran.r-project.org/web/packages/AdaptGauss/index.html (accessed on 23 October 2015).
- Duda, R.O.; Hart, P.E.; Stork, D. Pattern Classification, 2nd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2001. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ultsch, A.; Thrun, M.C.; Hansen-Goos, O.; Lötsch, J. Identification of Molecular Fingerprints in Human Heat Pain Thresholds by Use of an Interactive Mixture Model R Toolbox (AdaptGauss). Int. J. Mol. Sci. 2015, 16, 25897-25911. https://doi.org/10.3390/ijms161025897
Ultsch A, Thrun MC, Hansen-Goos O, Lötsch J. Identification of Molecular Fingerprints in Human Heat Pain Thresholds by Use of an Interactive Mixture Model R Toolbox (AdaptGauss). International Journal of Molecular Sciences. 2015; 16(10):25897-25911. https://doi.org/10.3390/ijms161025897
Chicago/Turabian StyleUltsch, Alfred, Michael C. Thrun, Onno Hansen-Goos, and Jörn Lötsch. 2015. "Identification of Molecular Fingerprints in Human Heat Pain Thresholds by Use of an Interactive Mixture Model R Toolbox (AdaptGauss)" International Journal of Molecular Sciences 16, no. 10: 25897-25911. https://doi.org/10.3390/ijms161025897
APA StyleUltsch, A., Thrun, M. C., Hansen-Goos, O., & Lötsch, J. (2015). Identification of Molecular Fingerprints in Human Heat Pain Thresholds by Use of an Interactive Mixture Model R Toolbox (AdaptGauss). International Journal of Molecular Sciences, 16(10), 25897-25911. https://doi.org/10.3390/ijms161025897