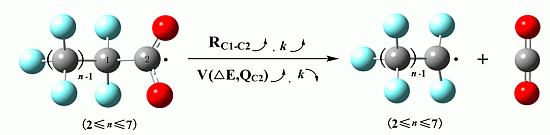Kinetics and Quantitative Structure—Activity Relationship Study on the Degradation Reaction from Perfluorooctanoic Acid to Trifluoroacetic Acid
Abstract
:1. Introduction
2. Results and Discussion
2.1. Reaction Mechanism
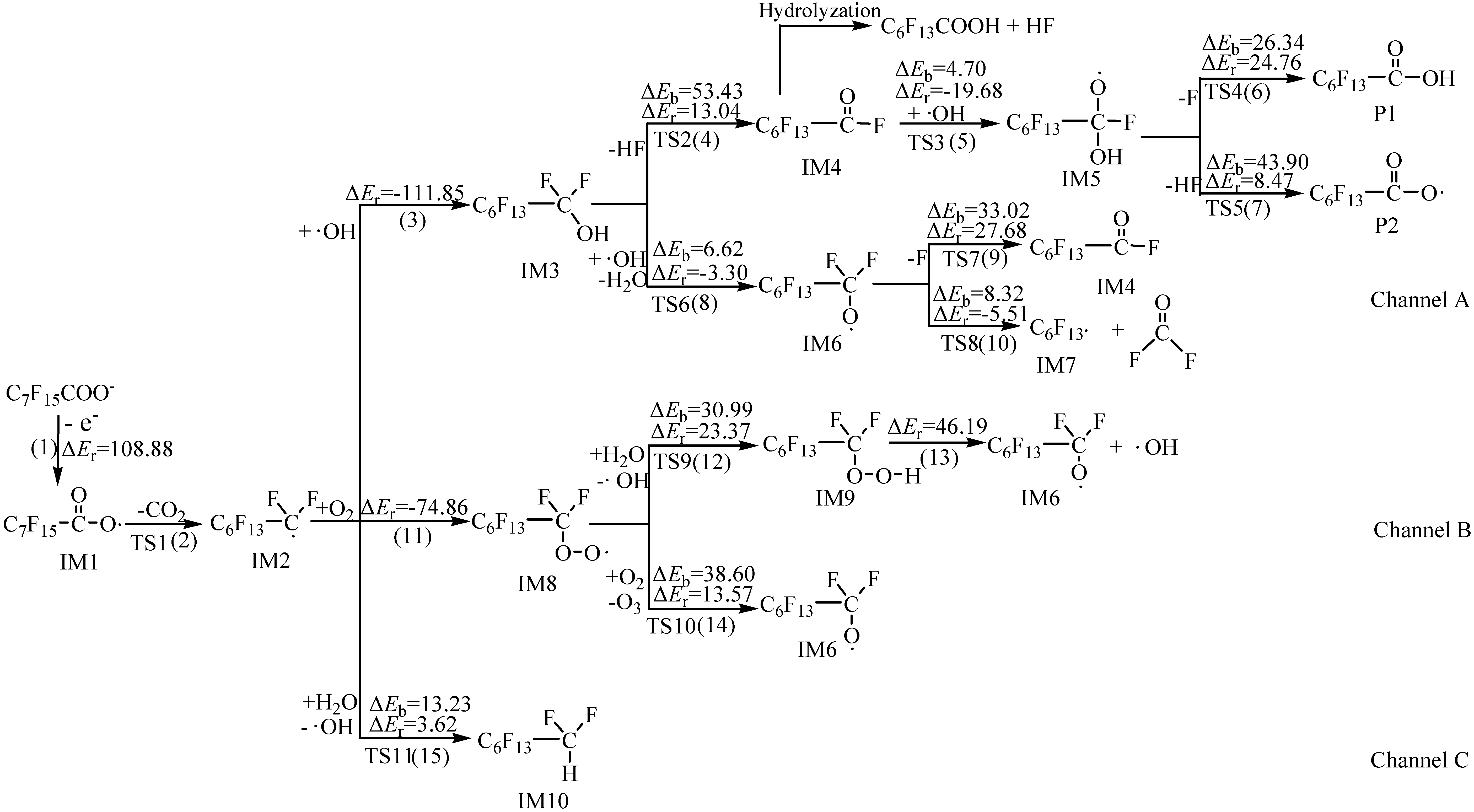
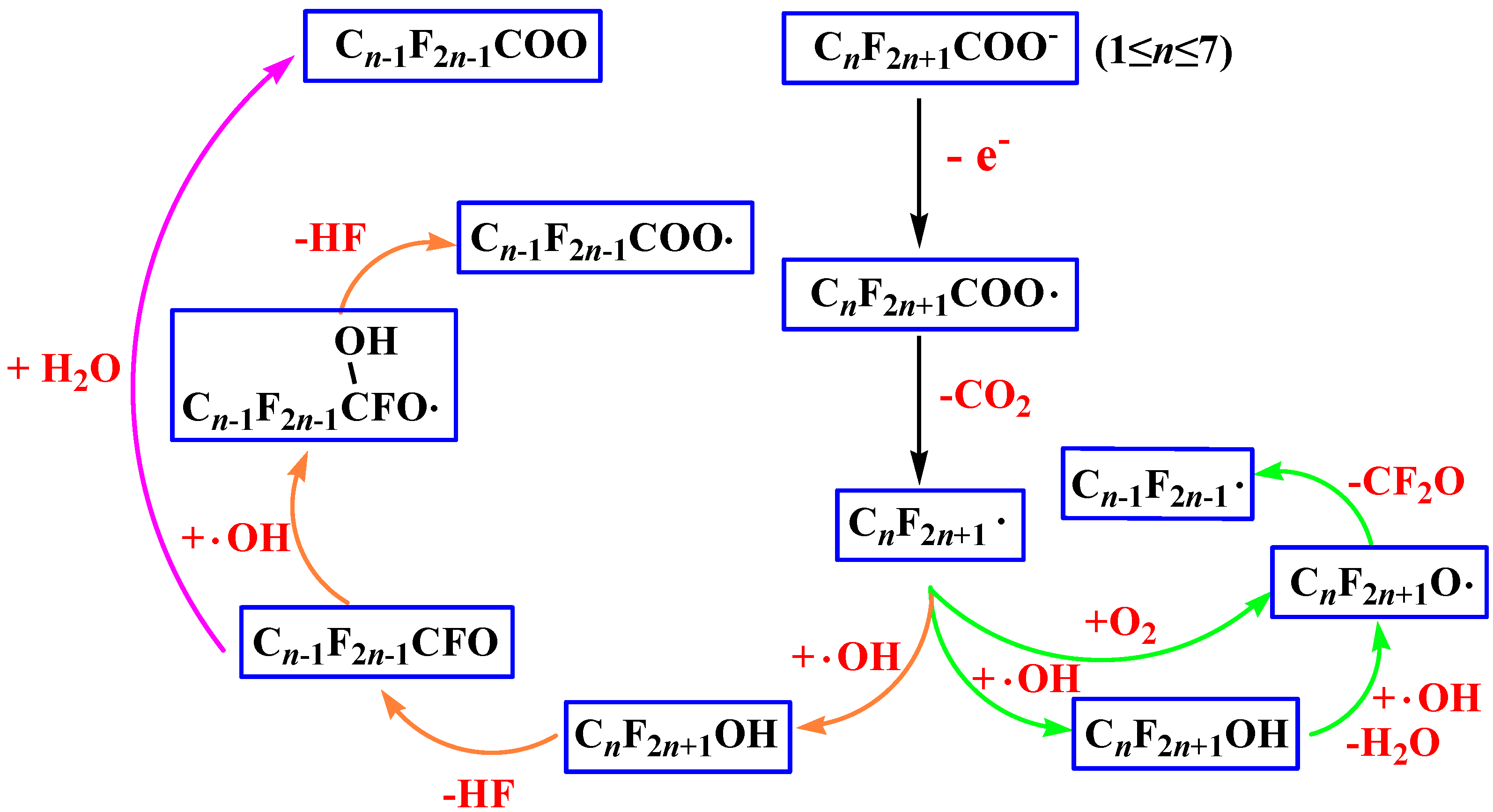
2.2. Rate Constants
| T (K) | k8C-7C a | k7C-6C a | k6C-5Ca | k5C-4Ca | k4C-3Ca | k3C-2Ca | k2C-1Ca |
|---|---|---|---|---|---|---|---|
| 200 | 1.13 × 1012 | 4.21 × 1010 | 1.34 × 1011 | 2.05 × 1011 | 3.81 × 1011 | 5.17 × 1011 | 7.62 × 1011 |
| 220 | 1.26 × 1012 | 5.01 × 1010 | 1.54 × 1011 | 2.50 × 1011 | 4.25 × 1011 | 5.22 × 1011 | 7.58 × 1011 |
| 240 | 1.39 × 1012 | 5.80 × 1010 | 1.74 × 1011 | 2.95 × 1011 | 4.67 × 1011 | 5.28 × 1011 | 7.55 × 1011 |
| 260 | 1.52 × 1012 | 6.57 × 1010 | 1.92 × 1011 | 3.40 × 1011 | 5.07 × 1011 | 5.33 × 1011 | 7.17 × 1011 |
| 280 | 1.64 × 1012 | 7.32 × 1010 | 2.10 × 1011 | 3.85 × 1011 | 5.45 × 1011 | 5.38 × 1011 | 7.19 × 1011 |
| 298.15 | 1.75 × 1012 | 7.97 × 1010 | 2.25 × 1011 | 4.25 × 1011 | 5.79 × 1011 | 5.42 × 1011 | 7.21 × 1011 |
| 320 | 1.87 × 1012 | 8.72 × 1010 | 2.43 × 1011 | 4.73 × 1011 | 6.17 × 1011 | 5.48 × 1011 | 7.25 × 1011 |
| 340 | 1.97 × 1012 | 9.38 × 1010 | 2.58 × 1011 | 5.16 × 1011 | 6.50 × 1011 | 5.52 × 1011 | 7.29 × 1011 |
| 360 | 2.08 × 1012 | 1.00 × 1011 | 2.73 × 1011 | 5.58 × 1011 | 6.82 × 1011 | 5.56 × 1011 | 7.33 × 1011 |
| 380 | 2.17 × 1012 | 1.06 × 1011 | 2.86 × 1011 | 5.98 × 1011 | 7.13 × 1011 | 5.60 × 1011 | 7.37 × 1011 |
| 400 | 2.27 × 1012 | 1.12 × 1011 | 2.99 × 1011 | 6.38 × 1011 | 7.42 × 1011 | 5.64 × 1011 | 7.41 × 1011 |
| 450 | 2.48 × 1012 | 1.25 × 1011 | 3.29 × 1011 | 7.32 × 1011 | 3.19 × 1011 | 5.73 × 1011 | 7.52 × 1011 |
| 500 | 2.68 × 1012 | 1.36 × 1011 | 3.55 × 1011 | 8.19 × 1011 | 3.38 × 1011 | 5.82 × 1011 | 7.82 × 1011 |
| T (K) | k(2) a | k(3) b | k(4) a | k(5) b | k(6) a | k(7) a | k(8) b | k(9) a | k(10) a | k(11) b | k(12) b | k(13) a | k(14) b | k(15) b |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 200 | 1.13 × 1012 | 3.21 × 10−12 | 2.80 × 10−42 | 1.06 × 10−22 | 1.64 × 10−20 | 1.54 × 10−32 | 1.15 × 10−24 | 4.21 × 10−24 | 9.70 × 106 | 9.92 × 10−18 | 1.21 × 10−58 | 4.75 × 10−21 | 2.60 × 10−70 | 3.73 × 10−38 |
| 220 | 1.26 × 1012 | 4.33 × 10−12 | 1.98 × 10−37 | 3.71 × 10−22 | 4.83 × 10−18 | 1.18 × 10−28 | 6.70 × 10−24 | 7.50 × 10−21 | 2.99 × 107 | 1.75 × 10−17 | 3.50 × 10−56 | 1.91 × 10−20 | 1.80 × 10−65 | 3.63 × 10−36 |
| 240 | 1.39 × 1012 | 5.58 × 10−12 | 2.18 × 10−33 | 1.06 × 10−21 | 1.12 × 10−15 | 2.04 × 10−25 | 2.96 × 10−23 | 3.86 × 10−18 | 7.70 × 107 | 2.82 × 10−17 | 3.85 × 10−54 | 6.17 × 10−20 | 1.98 × 10−61 | 1.67 × 10−34 |
| 260 | 1.52 × 1012 | 6.93 × 10−12 | 5.74 × 10−30 | 2.59 × 10−21 | 1.13 × 10−13 | 1.12 × 10−22 | 1.05 × 10−22 | 7.59 × 10−16 | 1.72 × 108 | 4.28 × 10−17 | 2.03 × 10−52 | 1.69 × 10−19 | 5.27 × 10−58 | 4.33 × 10−33 |
| 280 | 1.64 × 1012 | 8.35 × 10−12 | 4.90 × 10−27 | 5.62 × 10−21 | 5.89 × 10−12 | 2.49 × 10−20 | 3.14 × 10−22 | 7.02 × 10−14 | 3.46 × 108 | 6.18 × 10−17 | 6.00 × 10−51 | 4.07 × 10−19 | 4.59 × 10−55 | 7.15 × 10−32 |
| 298.15 | 1.75 × 1012 | 9.69 × 10−12 | 1.02 × 10−24 | 1.04 × 10−20 | 1.35 × 10−10 | 1.79 × 10−18 | 7.52 × 10−22 | 2.52 × 10−12 | 6.01 × 108 | 8.28 × 10−17 | 8.70 × 10−50 | 8.24 × 10−19 | 9.84 × 10−53 | 6.64 × 10−31 |
| 320 | 1.87 × 1012 | 1.13 × 10−11 | 2.84 × 10−22 | 2.01 × 10−20 | 3.63 × 10−9 | 1.62 × 10−16 | 1.91 × 10−21 | 1.09 × 10−10 | 1.08 × 109 | 1.14 × 10−16 | 1.45 × 10−48 | 1.75 × 10−18 | 2.84 × 10−50 | 7.02 × 10−30 |
| 340 | 1.97 × 1012 | 1.29 × 10−11 | 5.84 × 10−20 | 3.44 × 10−20 | 5.12 × 10−8 | 6.01 × 10−15 | 4.05 × 10−21 | 2.24 × 10−9 | 1.73 × 109 | 1.48 × 10−16 | 1.37 × 10−47 | 3.25 × 10−18 | 2.70 × 10−48 | 4.71 × 10−29 |
| 360 | 2.08 × 1012 | 1.44 × 10−11 | 3.25 × 10−18 | 5.56 × 10−20 | 5.37 × 10−7 | 1.49 × 10−13 | 7.95 × 10−21 | 3.29 × 10−8 | 2.65 × 109 | 1.87 × 10−16 | 1.01 × 10−46 | 5.66 × 10−18 | 1.56 × 10−46 | 2.58 × 10−28 |
| 380 | 2.17 × 1012 | 1.60 × 10−11 | 1.18 × 10−16 | 8.60 × 10−20 | 4.40 × 10−6 | 2.64 × 10−12 | 1.46 × 10−20 | 3.62 × 10−7 | 3.87 × 109 | 2.32 × 10−16 | 6.05 × 10−46 | 9.40 × 10−18 | 5.93 × 10−45 | 1.19 × 10−27 |
| 400 | 2.27 × 1012 | 1.75 × 10−11 | 3.01 × 10−15 | 1.06 × 10−19 | 2.93 × 10−5 | 3.50 × 10−11 | 2.55 × 10−20 | 3.14 × 10−6 | 5.45 × 109 | 2.84 × 10−16 | 3.01 × 10−45 | 1.49 × 10−17 | 1.57 × 10−43 | 4.77 × 10−27 |
| 450 | 2.48 × 1012 | 2.05 × 10−11 | 2.79 × 10−12 | 2.44 × 10−19 | 1.59 × 10−3 | 8.21 × 10−9 | 8.39 × 10−20 | 2.95 × 10−4 | 1.13 × 1010 | 4.42 × 10−16 | 8.93 × 10−44 | 4.08 × 10−17 | 1.64 × 10−40 | 9.11 × 10−26 |
| 500 | 2.68 × 1012 | 2.30 × 10−11 | 6.58 × 10−10 | 4.89 × 10−19 | 3.87 × 10−2 | 6.45 × 10−7 | 2.23 × 10−19 | 1.15 × 10−2 | 2.03 × 1010 | 6.42 × 10−16 | 1.35 × 10−42 | 9.42 × 10−17 | 4.37 × 10−38 | 1.00 × 10−24 |
| Reaction | A | Ea (kJ/mol) | Arrhenius Equation | R2 |
|---|---|---|---|---|
| (2) | 4.66 × 1012 | 2398.76 | k = 4.66 × 1012 exp(−288.52/T) | 0.997 |
| (3) | 9.13 × 10−11 | 5564.81 | k = 9.13 × 10−11 exp(−669.33/T) | 0.999 |
| (4) | 3.22 × 1012 | 207,450.90 | k = 3.22 × 1012 exp(−24,952/T) | 0.999 |
| (5) | 1.30 × 10−16 | 23,352.36 | k = 1.30 × 10−16 exp(−2808.80/T) | 0.999 |
| (6) | 8.05 × 1010 | 118,399.70 | k = 8.05 × 1010 exp(−14,241/T) | 0.999 |
| (7) | 7.89 × 1010 | 163,511.40 | k = 7.89 × 1010 exp(−19,667/T) | 0.999 |
| (8) | 6.35 × 10−16 | 33,661.72 | k = 6.35 × 10−16 exp(−4048.80/T) | 0.999 |
| (9) | 2.30 × 1012 | 136,798.60 | k = 2.30 × 1012 exp(−16,454/T) | 0.999 |
| (10) | 3.18 × 1012 | 21,194.88 | k = 3.18 × 1012 exp(−2549.30/T) | 0.999 |
| (11) | 8.98 × 10−15 | 11,478.31 | k = 8.98 × 10−15 exp(−1380.6/T) | 0.998 |
| (12) | 7.04 × 10−32 | 102,328.70 | k = 7.04 × 10−32 exp(−12,308/T) | 0.998 |
| (13) | 5.49 × 10−14 | 27,305.67 | k = 5.49 × 10−14 exp(−3284.3/T) | 0.999 |
| (14) | 1.09 × 10−16 | 205,547.02 | k = 1.09 × 10−16 exp(−24,723/T) | 0.999 |
| (15) | 7.12 × 10−16 | 85,567.69 | k = 7.12 × 10−16 exp(−10,292/T) | 0.999 |
2.3. QSAR Models
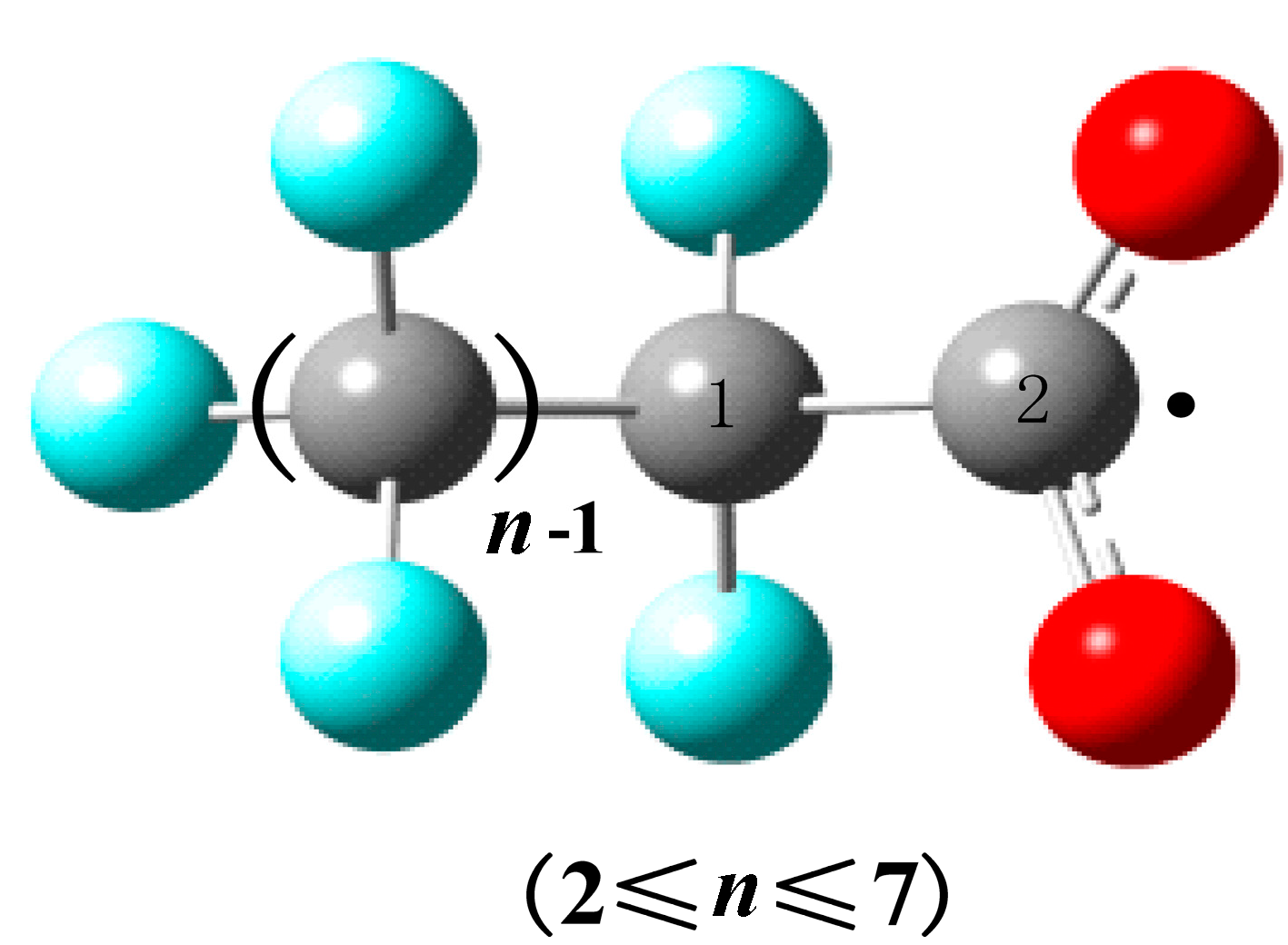
| PFCAs Radicals | RC1–C2 (Å) | M | V (cm3/mol) | ΔE (a.u.) | Dipole (Debye) | EC1–C2 (kcal/mol) | QC1 (C) | QC2 (C) |
|---|---|---|---|---|---|---|---|---|
| C7F15COO | 1.5433 | 412.9659 | 166.972 | 0.3634 | 1.1594 | 24.12 | 0.659 | 0.365 |
| C6F13COO | 1.5386 | 362.9691 | 152.634 | 0.3616 | 1.1382 | 24.22 | 0.663 | 0.367 |
| C5F11COO | 1.5388 | 312.9723 | 141.161 | 0.2728 | 1.2436 | 24.15 | 0.600 | 0.374 |
| C4F9COO | 1.5441 | 262.9755 | 118.218 | 0.2533 | 1.2094 | 24.10 | 0.455 | 0.457 |
| C3F7COO | 1.5394 | 212.9787 | 83.114 | 0.3665 | 1.2019 | 24.26 | 0.472 | 0.417 |
| C2F5COO | 1.5380 | 162.9819 | 62.998 | 0.2863 | 1.1352 | 23.03 | 0.322 | 0.418 |
| CF3COO | 1.5392 | 112.9850 | 46.759 | 0.2894 | 1.1828 | 19.69 | 0.936 | 0.419 |
| PFCAs Radicals | Lg k (Actual Values) | Lg k (Predicted Values) | Residual Values |
|---|---|---|---|
| C7F15COO | 12.2430 | 12.2439 | −8.34 × 10−4 |
| C6F13COO | 10.9015 | 10.9029 | −1.42 × 10−3 |
| C5F11COO | 11.3522 | 11.3497 | 2.43 × 10−3 |
| C4F9COO | 11.6284 | 11.6286 | −2.02 × 10−4 |
| C3F7COO | 11.7627 | 11.7603 | 2.43 × 10−3 |
| C2F5COO | 11.7340 | 11.7373 | −3.28 × 10−3 |
| CF3COO | 11.8579 | 11.8571 | 8.72 × 10−4 |
3. Experimental Section
3.1. Geometry Optimization
3.2. Kinetic Calculation
3.3. QSAR Analysis
4. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hori, H.; Hayakawa, E.; Einaga, H.; Kutsuna, S.; Koike, K.; Ibusuki, T.; Kiatagawa, H.; Arakawa, R. Decomposition of environmentally persistent perfluorooctanoic acid in water by photochemical approaches. Environ. Sci. Technol. 2004, 38, 6118–6124. [Google Scholar] [CrossRef]
- Renner, R. Growing concern over perfluorinated chemicals. Environ. Sci. Technol. 2001, 35, 154A–160A. [Google Scholar] [CrossRef]
- Giesy, J.P.; Kannan, K. Global distribution of perfluorooctane sulfonate in wildlife. Environ. Sci. Technol. 2001, 35, 1339–1342. [Google Scholar] [CrossRef]
- Schultz, M.M.; Barofsky, D.F.; Field, J.A. Fluorinated alkyl surfactants. Environ. Eng. Sci. 2003, 20, 487–501. [Google Scholar] [CrossRef]
- DeWitt, J.C.; Copeland, C.B.; Strynar, M.J.; Luebke, R.W. Perfluorooctanoic acid-induced immunomodulation in adult C57BL/6J or C57BL/6N female mice. Environ. Health Perspect. 2008, 116, 644–650. [Google Scholar] [CrossRef]
- Lin, H.; Niu, J.; Ding, S.; Zhang, L. Electrochemical degradation of perfluorooctanoic acid (PFOA) by Ti/SnO2-Sb, Ti/SnO2-Sb/PbO2 and Ti/SnO2-Sb/MnO2 anodes. Water Res. 2012, 46, 2281–2289. [Google Scholar] [CrossRef]
- Loganathan, B.G.; Sajwan, K.S.; Sinclair, E.; Senthil Kumar, K.; Kannan, K. Perfluoroalkyl sulfonates and perfluorocarboxylates in two wastewater treatment facilities in Kentucky and Georgia. Water Res. 2007, 41, 4611–4620. [Google Scholar] [CrossRef]
- Guo, R.; Sim, W.J.; Lee, E.S.; Lee, J.H.; Oh, J.E. Evaluation of the fate of perfluoroalkyl compounds in wastewater treatment plants. Water Res. 2010, 44, 3476–3486. [Google Scholar] [CrossRef]
- Loos, R.; Locoro, G.; Comero, S.; Contini, S.; Schwesig, D.; Werres, F.; Balsaa, P.; Gans, O.; Weiss, S.; Blaha, L.; et al. Pan-European survey on the occurrence of selected polar organic persistent pollutants in ground water. Water Res. 2010, 44, 4115–4126. [Google Scholar] [CrossRef]
- Falandysz, J.; Taniyasu, S.; Gulkowska, A.; Yamashita, N.; Schulte-Oehlmann, U. Is fish a major source of fluorinated surfactants and repellents in humans living on the Baltic Coast? Environ. Sci. Technol. 2006, 40, 748–751. [Google Scholar] [CrossRef]
- Keller, J.M.; Kannan, K.; Taniyasu, S.; Yamashita, N.; Day, R.D.; Arendt, M.D.; Segars, A.L.; Kucklick, J.R. Perfluorinated compounds in the plasma of loggerhead and Kemp’s ridley sea turtles from the southeastern coast of the United States. Environ. Sci. Technol. 2005, 39, 9101–9108. [Google Scholar] [CrossRef]
- Moriwaki, H.; Takagi, Y.; Tanaka, M.; Tsuruho, K.; Okitsu, K.; Maeda, Y. Sonochemical decomposition of perfluorooctane sulfonate and perfluorooctanoic acid. Environ. Sci. Technol. 2005, 39, 3388–3392. [Google Scholar] [CrossRef]
- Berthiaume, J.; Wallace, K.B. Perfluorooctanoate, perflourooctanesulfonate, and N-ethyl perfluorooctanesulfonamido ethanol; peroxisome proliferation and mitochondrial biogenesis. Toxicol. Lett. 2002, 129, 23–32. [Google Scholar] [CrossRef]
- Olsen, G.W.; Logan, P.W.; Hansen, K.J.; Simpson, C.A.; Burris, J.M.; Burlew, M.M.; Vorarath, P.P.; Venkateswarlu, P.; Schumpert, J.C.; Mandel, J.H. An occupational exposure assessment of a perfluorooctanesulfonyl fluoride production site: Biomonitoring. AIHA J. 2003, 64, 651–659. [Google Scholar] [CrossRef]
- Sanderson, H.; Boudreau, T.M.; Mabury, S.A.; Cheong, W.J.; Solomon, K.R. Ecological impact and environmental fate of perfluorooctane sulfonate on the zooplankton community in indoor microcosms. Environ. Toxicol. Chem. 2002, 21, 1490–1496. [Google Scholar] [CrossRef]
- Hines, E.P.; White, S.S.; Stanko, J.P.; Gibbs-Flournoy, E.A.; Lau, C.; Fenton, S.E. Phenotypic dichotomy following developmental exposure to perfluorooctanoic acid (PFOA) in female CD-1 mice: Low doses induce elevated serum leptin and insulin, and overweight in mid-life. Mol. Cell. Endocrinol. 2009, 304, 97–105. [Google Scholar] [CrossRef]
- Kennedy, G.L.; Butenhoff, J.L.; Olsen, G.W.; O’Connor, J.C.; Seacat, A.M.; Perkins, R.G.; Biegel, L.B.; Murphy, S.R.; Farrar, D.G. The toxicology of perfluorooctanoate. Crit. Rev. Toxicol. 2004, 34, 351–384. [Google Scholar] [CrossRef]
- Lau, C.; Anitole, K.; Hodes, C.; Lai, D.; Pfahles-Hutchens, A.; Seed, J. Perfluoroalkyl acids: A review of monitoring and toxicological findings. J. Toxicol. Sci. 2007, 99, 366–394. [Google Scholar] [CrossRef]
- US EPA. Revised Draft Hazard Assessment of Perfluorooctanoic Acid and Its Salts. Available online: http://www.fluoridealert.org/wp-content/pesticides/pfoa.epa.nov.4.2002.pdf (accessed on 4 November 2002).
- Järnberg, U.; Holmström, K.; van Bavel, B. Perfluoroalkylated Acids and Related Compounds (PFAS) in the Swedish Environment-Chemistry. Available online: http://www.diva-portal.org/smash/get/diva2:657980/FULLTEXT01.pdf (accessed on 1 May 2007).
- Hoffman, K.; Webster, T.F.; Bartell, S.M.; Weisskopf, M.G.; Fletcher, T.; Vieira, V.M. Private drinking water wells as a source of exposure to perfluorooctanoic acid (PFOA) in communities surrounding a fluoropolymer production facility. Environ. Health Perspect. 2011, 119, 92–97. [Google Scholar]
- Ochiai, T.; Moriyama, H.; Nakata, K.; Murakami, T.; Koide, Y.; Fujishima, A. Electrochemical and photocatalytic decomposition of perfluorooctanoic acid with a hybrid reactor using a boron-doped diamond electrode and TiO2 photocatalyst. Chem. Lett. 2011, 40, 682–683. [Google Scholar] [CrossRef]
- Zhuo, Q.; Deng, S.; Yang, B.; Huang, J.; Yu, G. Efficient electrochemical oxidation of perfluorooctanoate using a Ti/SnO2-Sb-Bi anode. Environ. Sci. Technol. 2011, 45, 2973–2979. [Google Scholar] [CrossRef]
- Ochiai, T.; Lizuka, Y.; Nakata, K.; Murakami, T.; Tryk, D.A.; Fujishima, A.; Koide, Y.; Morito, Y. Efficient electrochemical decomposition of perfluorocarboxylic acids by the use of a boron-doped diamond electrode. Diam. Relat. Mater. 2011, 20, 64–67. [Google Scholar] [CrossRef]
- Niu, J.; Lin, H.; Gong, C.; Sun, X. Theoretical and experimental insights into the electrochemical mineralization mechanism of perfluorooctanoic acid. Environ. Sci. Technol. 2013, 47, 14341–14349. [Google Scholar] [CrossRef]
- Niu, J.; Lin, H.; Xu, J.; Wu, H.; Li, Y. Electrochemical mineralization of perfluorocarboxylic acids (PFCAs) by Ce-doped modified porous nanocrystalline PbO2 film electrode. Environ. Sci. Technol. 2012, 46, 10191–10198. [Google Scholar]
- Zhang, Q.; Zhang, R.; Gu, Y. Kinetics and mechanism of O (3P) reaction with CH3CHF2: A theoretical study. J. Phys. Chem. A 2004, 108, 1064–1068. [Google Scholar]
- Zhang, Q.; Zhang, R.; Chan, K.; Bello, I. Ab initio and variational transition state approach to β-C3N4 formation: Kinetics for the reaction of CH3NH2 with H. J. Phys. Chem. A 2005, 109, 9112–9117. [Google Scholar]
- Sun, T.; Zhang, Q.; Qu, X.; Wang, W. Mechanism and direct dynamics studies for the reaction of monoethylsilane EtSiH3 with atomic O (3P). Chem. Phys. Lett. 2005, 407, 527–532. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Hybrid meta density functional theory methods for thermochemistry, thermochemical kinetics, and noncovalent interactions: The MPW1B95 and MPWB1K models and comparative assessments for hydrogen bonding and van der Waals interactions. J. Phys. Chem. A 2004, 108, 6908–6918. [Google Scholar]
- Hehre, W.; Ditchfield, R.; Pople, J. Theoretical investigations on the solvation process. J. Chem. Phys. 1972, 56, 2557–2562. [Google Scholar]
- Zheng, J.J.; Zhao, Y.; Truhlar, D.G. The DBH24/08 database and its use to assess electronic structure model chemistries for chemical reaction barrier heights. J. Chem. Theory Comput. 2009, 5, 808–821. [Google Scholar]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Zakrzewski, V.; Montgomery, J., Jr.; Stratmann, R.; Burant, J.; et al. Gaussian 03,Revision E.01. Available online: http://www.gaussian.com/g_misc/g03/citation_g03.htm (accessed on 11 June 2003).
- Corchado, J.C.; Chuang, Y.Y.; Fast, P.L.; Hu, W.P.; Liu, Y.P.; Lynch, G.C.; Nguyen, K.A.; Jackels, C.F.; Fernandez Ramos, A.; Ellingson, B.A.; et al. POLYRATE Version 9.7; University of Minnesota: Minneapolis, MN, USA, 2007. [Google Scholar]
- Miller, W.H. Tunneling corrections to unimolecular rate constants, with application to formaldehyde. J. Am. Chem. Soc. 1979, 101, 6810–6814. [Google Scholar] [CrossRef]
- Zhang, Q.; Yu, W.; Zhang, R.; Zhou, Q.; Gao, R.; Wang, W. Quantum chemical and kinetic study on dioxin formation from the 2, 4, 6-TCP and 2, 4-DCP precursors. Environ. Sci. Technol. 2010, 44, 3395–3403. [Google Scholar] [CrossRef]
- Qu, X.; Wang, H.; Zhang, Q.; Shi, X.; Xu, F.; Wang, W. Mechanistic and kinetic studies on the homogeneous gas-phase formation of PCDD/Fs from 2, 4, 5-trichlorophenol. Environ. Sci. Technol. 2009, 43, 4068–4075. [Google Scholar] [CrossRef]
- Gong, C.; Sun, X.; Zhang, C. The atmospheric chemical reaction of 4-tert-butylphenol initiated by OH radicals. Environ. Chem. 2013, 10, 111–119. [Google Scholar] [CrossRef]
- Hou, H.; Wang, B. Ab initio study of the reaction of propionyl (C2H5CO) radical with oxygen (O2). J. Chem. Phys. 2007, 127, 054306. [Google Scholar]
- Rogers, D.; Hopfinger, A.J. Application of genetic function approximation to quantitative structure-activity relationships and quantitative structure-property relationships. J. Chem. Inf. Comput. Sci. 1994, 34, 854–866. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gong, C.; Sun, X.; Zhang, C.; Zhang, X.; Niu, J. Kinetics and Quantitative Structure—Activity Relationship Study on the Degradation Reaction from Perfluorooctanoic Acid to Trifluoroacetic Acid. Int. J. Mol. Sci. 2014, 15, 14153-14165. https://doi.org/10.3390/ijms150814153
Gong C, Sun X, Zhang C, Zhang X, Niu J. Kinetics and Quantitative Structure—Activity Relationship Study on the Degradation Reaction from Perfluorooctanoic Acid to Trifluoroacetic Acid. International Journal of Molecular Sciences. 2014; 15(8):14153-14165. https://doi.org/10.3390/ijms150814153
Chicago/Turabian StyleGong, Chen, Xiaomin Sun, Chenxi Zhang, Xue Zhang, and Junfeng Niu. 2014. "Kinetics and Quantitative Structure—Activity Relationship Study on the Degradation Reaction from Perfluorooctanoic Acid to Trifluoroacetic Acid" International Journal of Molecular Sciences 15, no. 8: 14153-14165. https://doi.org/10.3390/ijms150814153
APA StyleGong, C., Sun, X., Zhang, C., Zhang, X., & Niu, J. (2014). Kinetics and Quantitative Structure—Activity Relationship Study on the Degradation Reaction from Perfluorooctanoic Acid to Trifluoroacetic Acid. International Journal of Molecular Sciences, 15(8), 14153-14165. https://doi.org/10.3390/ijms150814153