Excitation and Adaptation in Bacteria–a Model Signal Transduction System that Controls Taxis and Spatial Pattern Formation
Abstract
:1. Introduction

2. Signal Transduction in E. coli
2.1. Cell Movement and Taxis
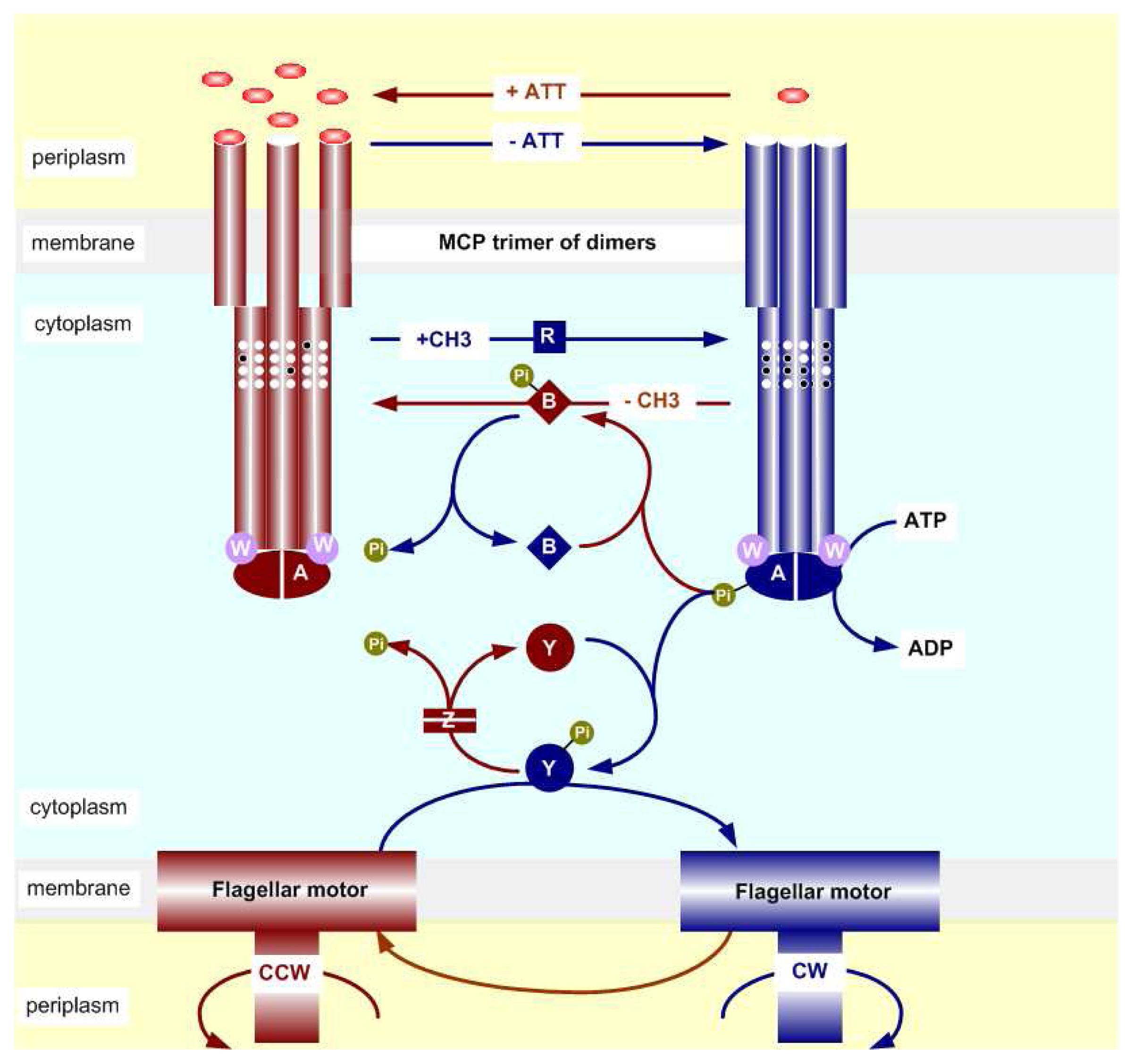
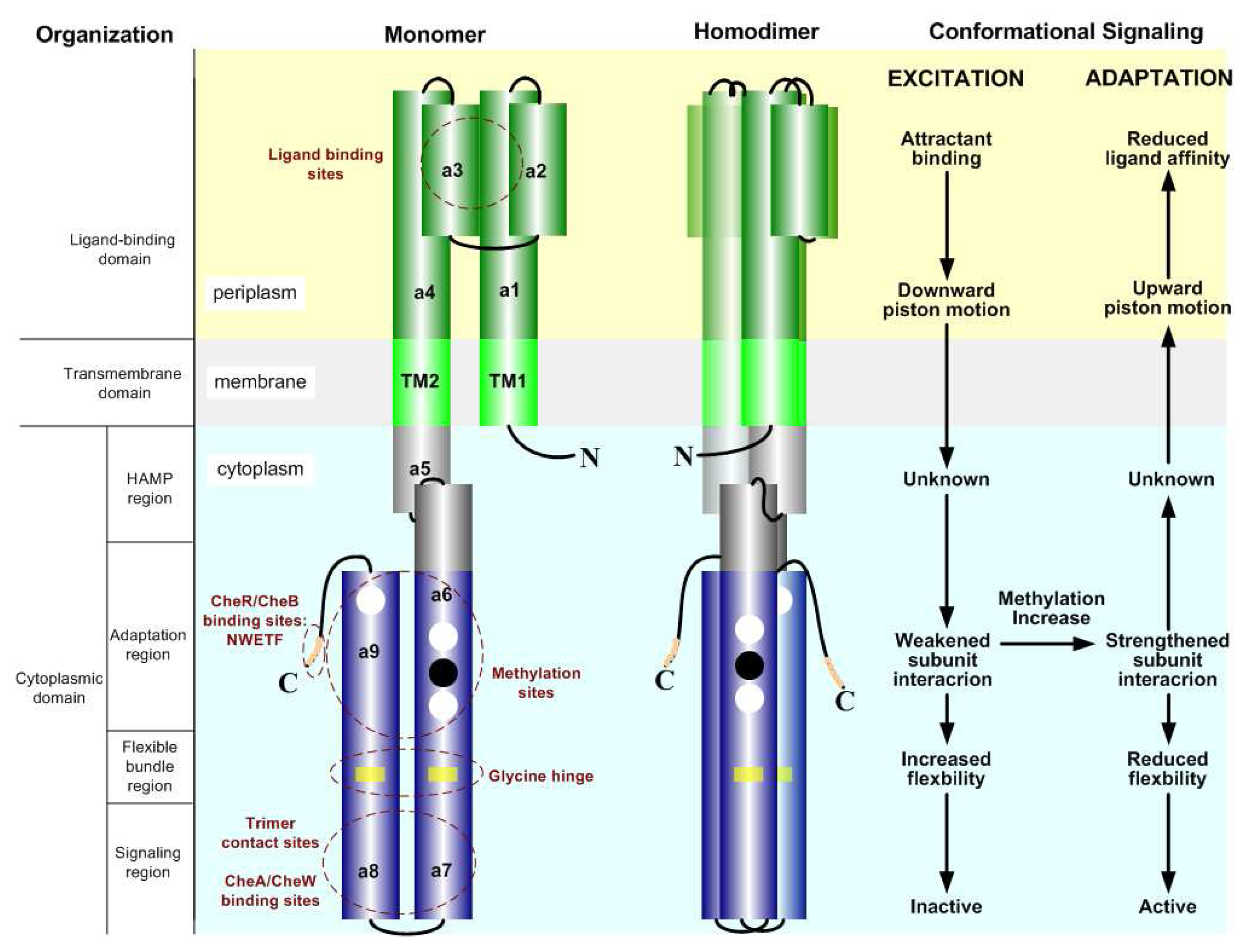
2.2. The Biochemistry of Signal Processing in E. coli
3. Models of Signal Transduction and Adaptation
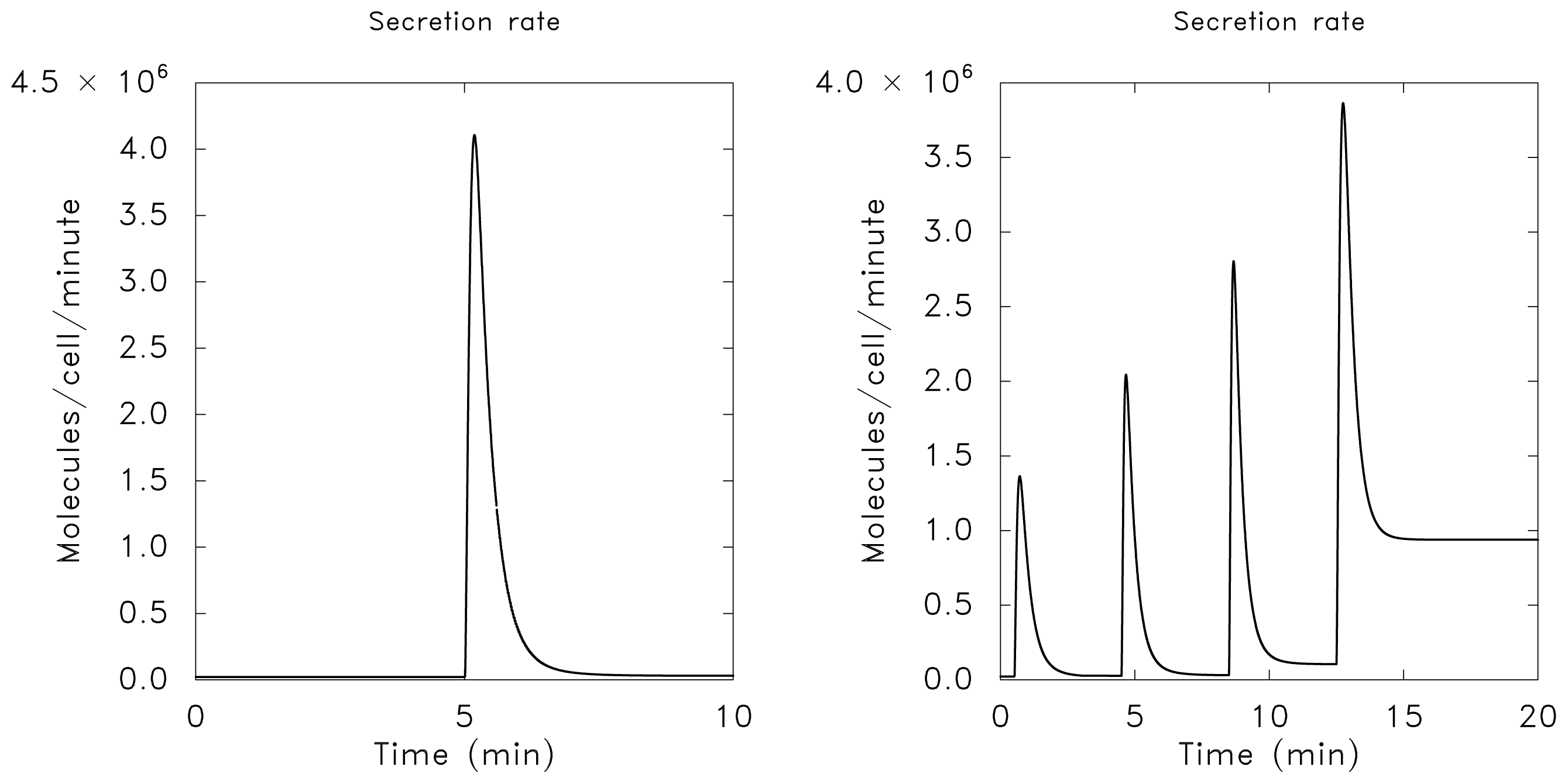
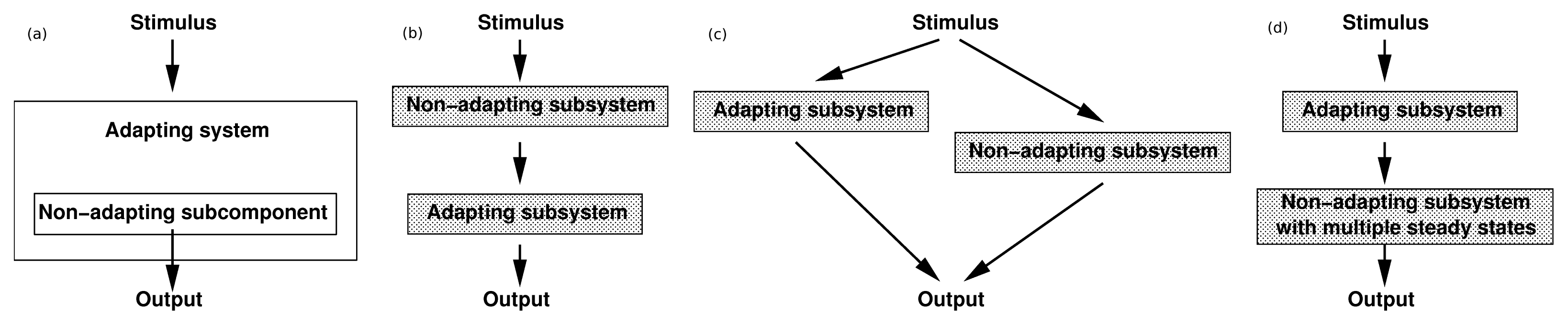
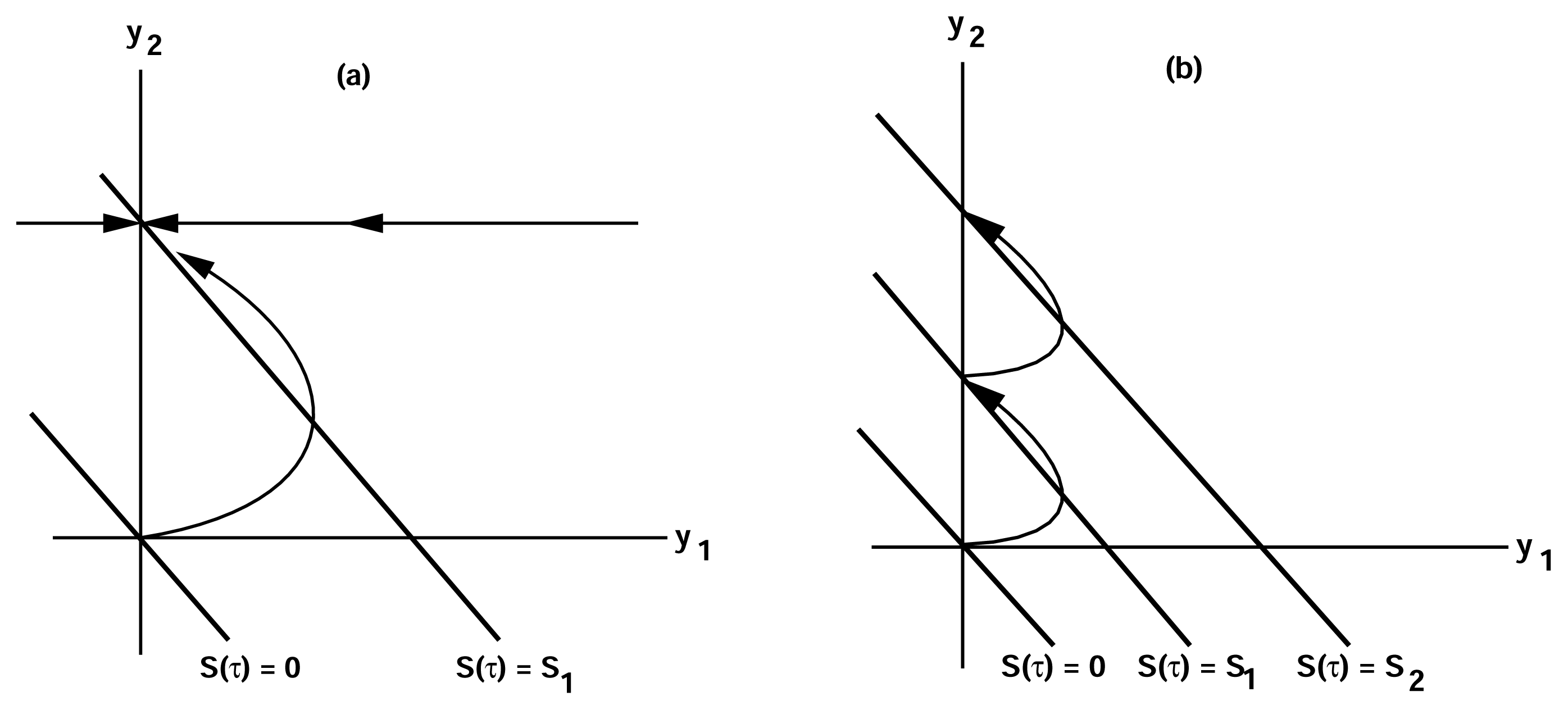
3.1. Adaptation in Model Systems
 of the state u given as follows:
of the state u given as follows: could depend on the derivatives of the state variables, their past history, or directly on the stimulus and its derivatives. If we only consider systems whose “basal dynamics” are time independent, which means that the system has an asymptotically stable steady state in the presence of any constant stimulus, we can define perfect adaptation to constant stimuli as follows.
could depend on the derivatives of the state variables, their past history, or directly on the stimulus and its derivatives. If we only consider systems whose “basal dynamics” are time independent, which means that the system has an asymptotically stable steady state in the presence of any constant stimulus, we can define perfect adaptation to constant stimuli as follows. (u(τ)) = au1(τ) where a is a constant. Then this simple scheme can be viewed as having two input pathways, an excitatory one in which the stimulus increases the production of u1 and hence increases the response, and an inhibitory one that increases the production of u2, which in turn shuts off the response.
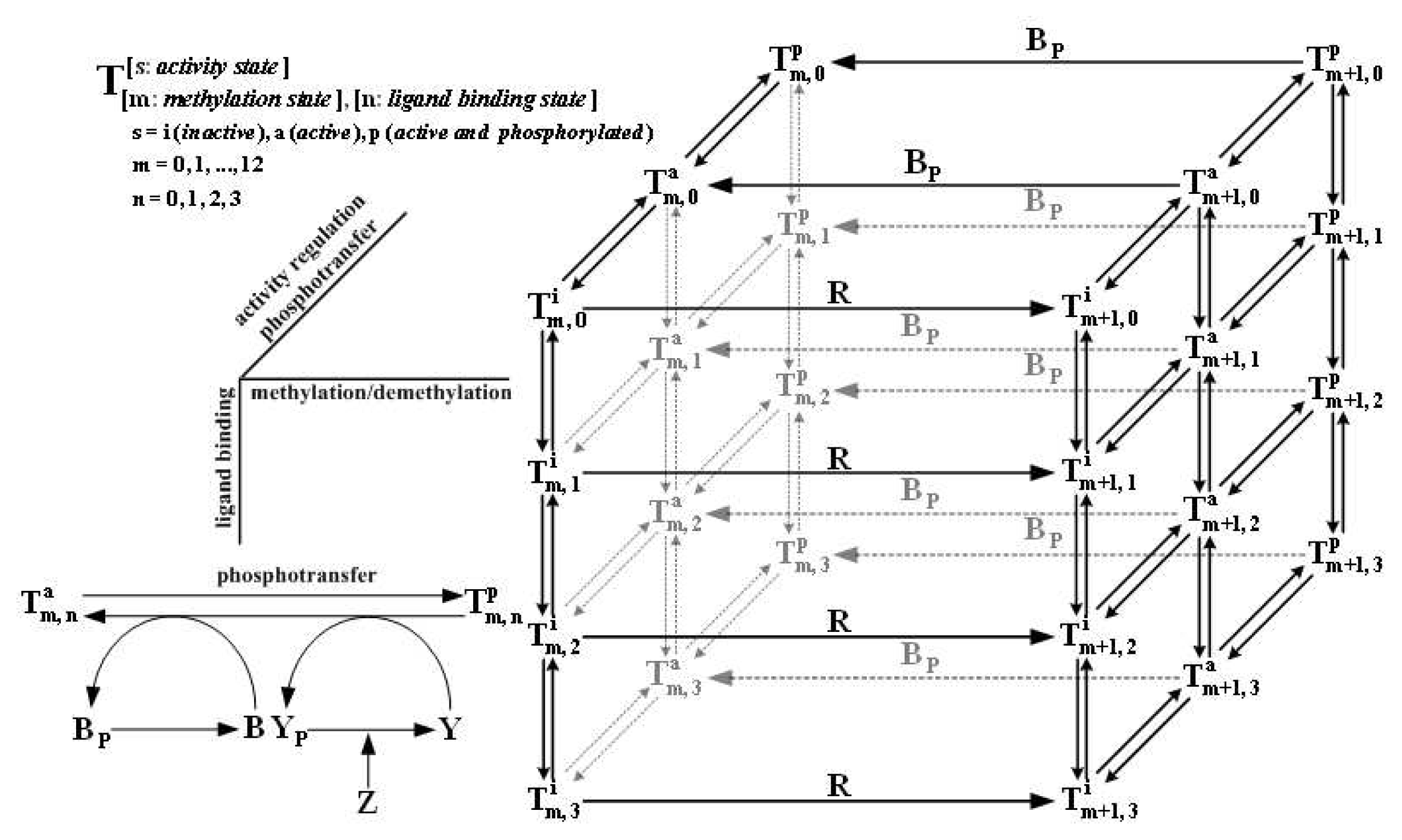
(u(τ)) = au1(τ) where a is a constant. Then this simple scheme can be viewed as having two input pathways, an excitatory one in which the stimulus increases the production of u1 and hence increases the response, and an inhibitory one that increases the production of u2, which in turn shuts off the response.4. Models of Signal Transduction in E. coli
Category I
Category II
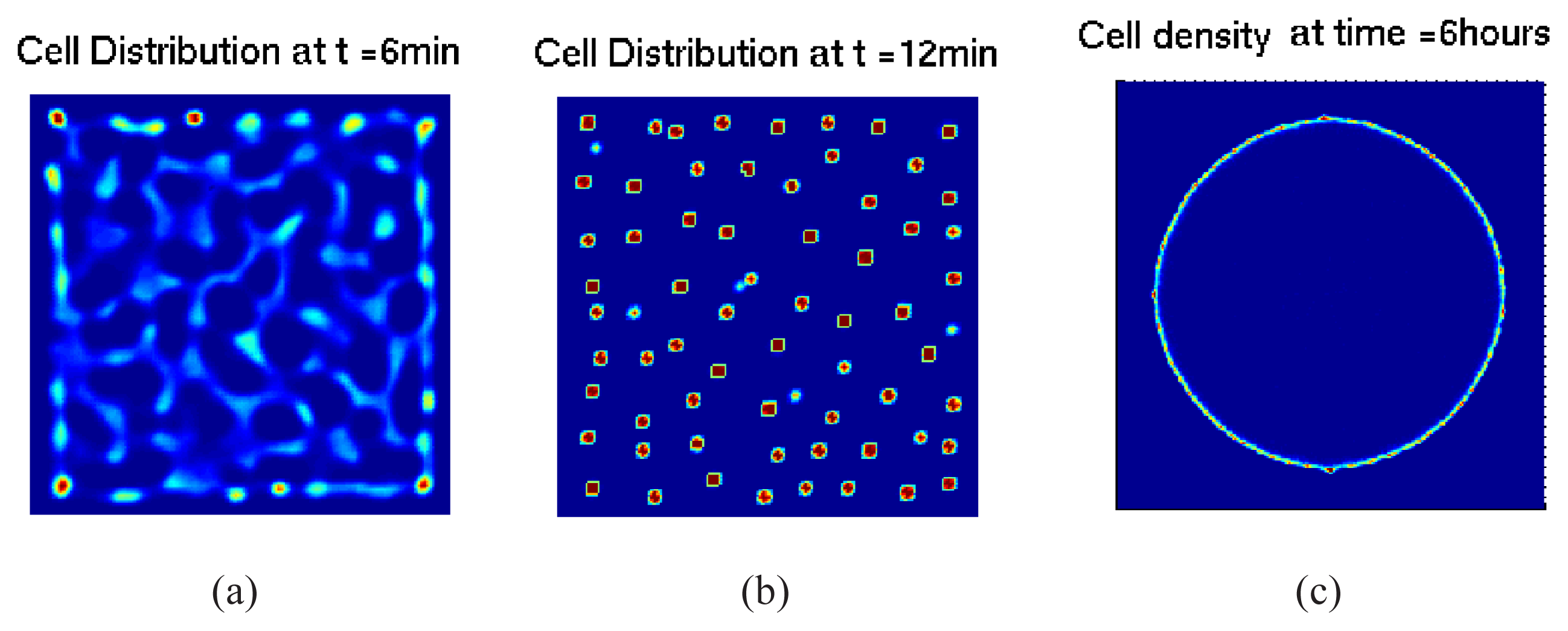
5. Spontaneous Spatial Pattern Formation in Populations
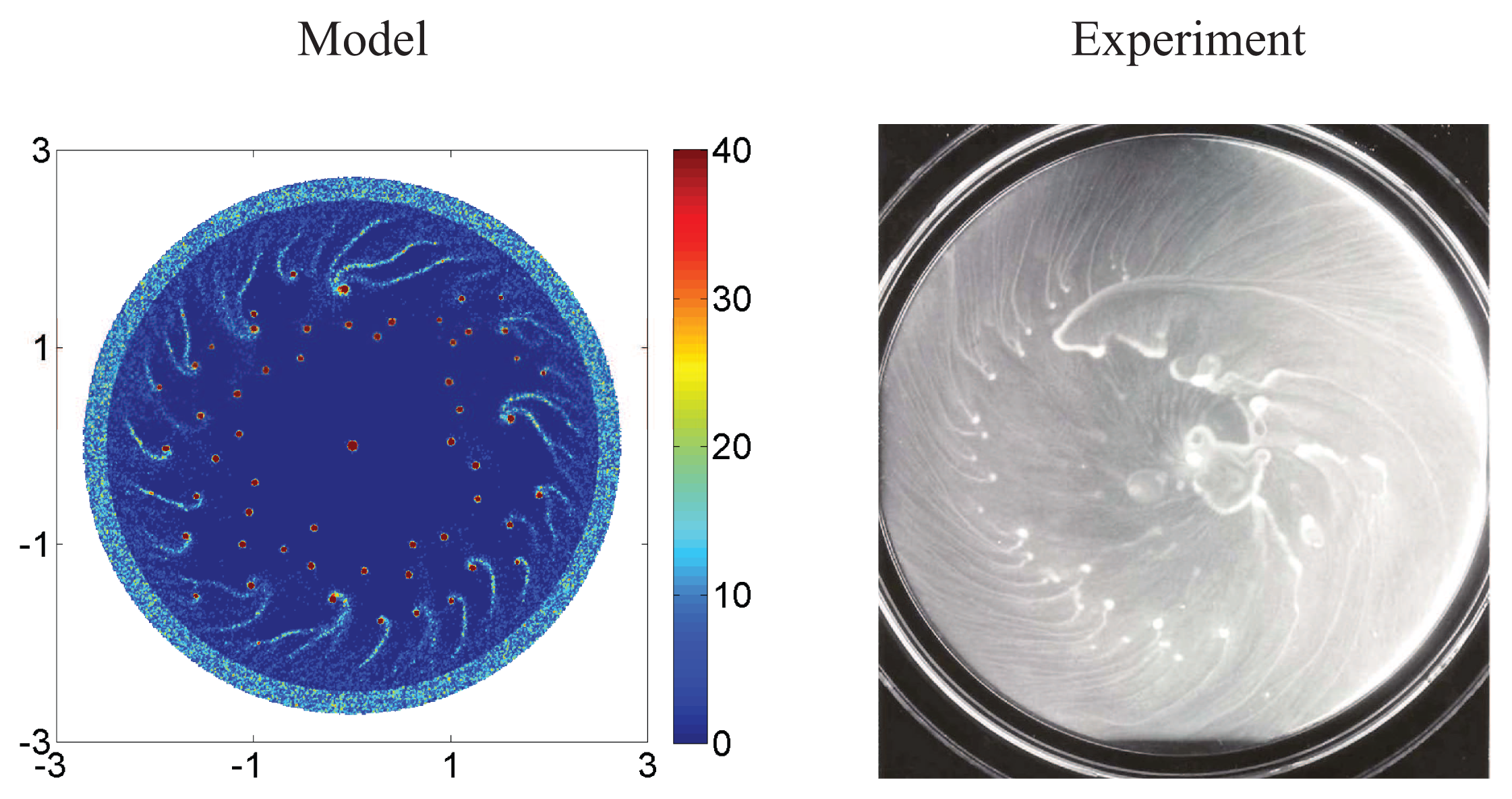
5.1. Pattern Formation in Bacterial Colonies
5.2. Mathematical Models of E. coli Pattern Formation
5.2.1. Hybrid Cell-based Models
5.2.2. From Cell-based Models to Continuum Models
6. Discussion
Acknowledgements
References
- Othmer, H.G.; Schaap, P. Oscillatory cAMP signaling in the development of Dictyostelium discoideum. Comments Theor. Biol 1998, 5, 175–282. [Google Scholar]
- Koutalos, Y.; Yau, K.Y. Regulation of sensitivity in vertebrate rod photoreceptors by calcium. Trends Neurosci 1996, 19, 73–81. [Google Scholar]
- Purcell, E.M. Life at low Reynolds number. Am. J. Phys 1977, 45, 3–11. [Google Scholar]
- Block, S.M.; Segall, J.E.; Berg, H.C. Impulse responses in bacterial chemotaxis. Cell 1982, 31, 215–226. [Google Scholar]
- Stewart, R.C.; Dahlquist, F.W. Molecular components of bacterial chemotaxis. Chem. Rev 1987, 87, 997–1025. [Google Scholar]
- Berg, H.C. Bacterial microprocessing. Cold Spring Harbor Symp. Quantit. Biol 1990, 55, 539–545. [Google Scholar]
- Berg, H.C.; Brown, D.A. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 1972, 239, 500–504. [Google Scholar]
- Berg, H.C. Random Walks in Biology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Budrene, E.O.; Berg, H.C. Complex patterns formed by motile cells of Escherichia coli. Nature 1991, 349, 630–633. [Google Scholar]
- Block, S.; Segall, J.; Berg, H. Adaptation kinetics in bacterial chemotaxis. J. Bacteriol 1983, 154, 312–323. [Google Scholar]
- Bourret, R.B.; Borkovich, K.A.; Simon, M.I. Signal transduction pathways involving protein phosphorylation in prokaryotes. Ann. Rev. Biochem 1991, 60, 401–441. [Google Scholar]
- Macnab, R.M. Motility and Chemotaxis. In Escherichia coli and Salmonella typhimurium: Cellular and Molecular Biology; American Society for Microbiology: Washington, DC, USA, 1987; pp. 732–759. [Google Scholar]
- Mesibov, R.; Adler, J. Chemotaxis toward amino acids in Escherichia coli. J. Bacteriol 1972, 112, 315–326. [Google Scholar]
- Segall, J.E.; Block, S.M.; Berg, H.C. Temporal comparisons in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 1986, 83, 8987–8991. [Google Scholar]
- Sourjik, V.; Berg, H.C. Receptor sensitivity in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 2002, 99, 123–127. [Google Scholar]
- Milburn, M.V.; Prive, G.G.; Milligan, D.L.; Scott, W.G.; Yeh, J.; Jancarik, J.; Koshland, D.E.; Kim, S.H. Three-dimensional structures of the ligand-binding domain of the bacterial aspartate receptor with and without a ligand. Science 1991, 254, 1342–1347. [Google Scholar]
- Kim, K.K.; Yokota, H.; Kim, S.H. Four-helical-bundle structure of the cytoplasmic domain of a serine chemotaxis receptor. Nature 1999, 400, 787–792. [Google Scholar]
- Moual, H.L.; Koshland, D.E., Jr. Molecular evolution of the C-terminal cytoplasmic domain of a superfamily of bacterial receptors involved in taxis. J. Mol. Biol 1996, 261, 568–585. [Google Scholar]
- Zhulin, I.B. The superfamily of chemotaxis transducers: From physiology to genomics and back. Adv. Microb. Physiol 2001, 45, 157–98. [Google Scholar]
- Hulko, M.; Berndt, F.; Gruber, M.; Linder, J.U.; Truffault, V.; Schultz, A.; Martin, J.; Schultz, J.E.; Lupas, A.N.; Coles, M. The HAMP domain structure implies helix rotation in transmembrane signaling. Cell 2006, 126, 929–940. [Google Scholar]
- Butler, S.L.; Falke, J.J. Cysteine and disulfide scanning reveals two amphiphilic helices in the linker region of the aspartate chemoreceptor. Biochemistry 1998, 37, 10746–10756. [Google Scholar]
- Surette, M.G.; Stock, J.B. Role of alpha-helical coiled-coil interactions in receptor dimerization, signaling, and adaptation during bacterial chemotaxis. J. Biol. Chem 1996, 271, 17966–17973. [Google Scholar]
- Terwilliger, T.C.; Bogonez, E.; Wang, E.A.; Koshland, D.E. Sites of methyl esterification on the aspartate receptor involved in bacterial chemotaxis. J. Biol. Chem 1983, 258, 9608–9611. [Google Scholar]
- Terwilliger, T.C.; Koshland, D.E. Sites of methyl esterification and deamination on the aspartate receptor involved in chemotaxis. J. Biol. Chem 1984, 259, 7719–7725. [Google Scholar]
- Lupas, A.; Dyke, M.V.; Stock, J. Predicting coiled coils from protein sequences. Science 1991, 252, 1162–1164. [Google Scholar]
- Alexander, R.P.; Zhulin, I.B. Evolutionary genomics reveals conserved structural determinants of signaling and adaptation in microbial chemoreceptors. Proc. Natl. Acad. Sci. USA 2007, 104, 2885–2890. [Google Scholar]
- Coleman, M.D.; Bass, R.B.; Mehan, R.S.; Falke, J.J. Conserved glycine residues in the cytoplasmic domain of the aspartate receptor play essential roles in kinase coupling and on-off switching. Biochemistry 2005, 44, 7687–7695. [Google Scholar]
- Wu, J.; Li, J.; Li, G.; David, G.; Weis, R.M. The receptor binding site for the methyltransferase of bacterial chemotaxis is distinct from the sites of methylation. Biochemistry 1996, 35, 4984–4993. [Google Scholar]
- Barnakov, A.N.; Barnakova, L.A.; Hazelbauer, G.L. Efficient adaptational demethylation of chemoreceptors requires the same enzyme-docking site as efficient methylation. Proc. Natl. Acad. Sci. USA 1999, 96, 10667–10672. [Google Scholar]
- Hazelbauer, G.L.; Falke, J.J.; Parkinson, J.S. Bacterial chemoreceptors: High-performance signaling in networked arrays. Trends Biochem. Sci 2008, 33, 9–19. [Google Scholar]
- Wang, H.; Matsumura, P. Characterization of the CheAS/CheZ complex: A specific interaction resulting in enhanced dephosphorylating activity on CheY-phosphate. Mol. Microbiol 1996, 19, 695–703. [Google Scholar]
- Falke, J.J.; Bass, R.B.; Butler, S.L.; Chervitz, S.A.; Danielson, M.A. The two-component signaling pathway of bacterial chemotaxis: A molecular view of signal transduction by receptors, kinase, and adaptation enzymes. Ann. Rev. Cell Dev. Biol 1997, 13, 457–512. [Google Scholar]
- McNamara, B.; Wolfe, A. Coexpression of the long and short forms of CheA, the chemotaxis histidine kinase, by members of the family Enterobacteriaceae. J. Bacteriol 1997, 179, 1813–1818. [Google Scholar]
- Cantwell, B.J.; Draheim, R.R.; Weart, R.B.; Nguyen, C.; Stewart, R.C.; Manson, M.D. CheZ phosphatase localizes to chemoreceptor patches via CheA-short. J. Bacteriol 2003, 185, 2354–2361. [Google Scholar]
- Shiomi, D.; Zhulin, I.B.; Homma, M.; Kawagishi, I. Dual recognition of the bacterial chemoreceptor by chemotaxis-specific domains of the CheR methyltransferase. J. Biol. Chem 2002, 277, 42325–42333. [Google Scholar]
- Li, J.; Li, G.; Weis, R.M. The serine chemoreceptor from Escherichia coli is methylated through an inter-dimer process. Biochemistry 1997, 36, 11851–11857. [Google Scholar]
- Banno, S.; Shiomi, D.; Homma, M.; Kawagishi, I. Targeting of the chemotaxis methylesterase/deamidase CheB to the polar receptor-kinase cluster in an Escherichia coli cell. Mol. Microbiol 2004, 53, 1051–1063. [Google Scholar]
- Maddock, J.R.; Shapiro, L. Polar location of the chemoreceptor complex in the Escherichia coli cell. Science 1993, 259, 1717–1723. [Google Scholar]
- Sourjik, V.; Berg, H.C. Functional interactions between receptors in bacterial chemotaxis. Nature 2004, 428, 437–441. [Google Scholar]
- Milligan, D.L.; Koshland, D.E. Site-directed crosslinking: Establishing the dimeric structure of the aspartate receptor of bacterial chemotaxis. J. Biol. Chem 1988, 263, 6268–6275. [Google Scholar]
- Pakula, A.A.; Simon, M.I. Determination of transmembrane protein structure by disulfide cross-linking: The Escherichia coli Tar receptor. Proc. Natl. Acad. Sci. USA 1992, 89, 4144–4148. [Google Scholar]
- Lee, G.F.; Burrows, G.G.; Lebert, M.R.; Dutton, D.P.; Hazelbauer, G.L. Deducing the organization of a transmembrane domain by disulfide cross-linking. The bacterial chemoreceptor Trg. J. Biol. Chem 1994, 269, 29920–29927. [Google Scholar]
- Chervitz, S.A.; Lin, C.M.; Falke, J.J. Transmembrane signaling by the aspartate receptor: Engineered disulfides reveal static regions of the subunit interface. Biochemistry 1995, 34, 9722–9733. [Google Scholar]
- Bass, R.B.; Falke, J.J. The aspartate receptor cytoplasmic domain: In situ chemical analysis of structure, mechanism and dynamics. Structure 1999, 7, 829–840. [Google Scholar]
- Ames, P.; Studdert, C.A.; Reiser, R.H.; Parkinson, J.S. Collaborative signaling by mixed chemoreceptor teams in Escherichia coli. Proc. Natl. Acad. Sci. USA 2002, 99, 7060. [Google Scholar]
- Studdert, C.A.; Parkinson, J.S. Crosslinking snapshots of bacterial chemoreceptor squads. Proc. Natl. Acad. Sci. USA 2004, 101, 2117–2122. [Google Scholar]
- Studdert, C.A.; Parkinson, J.S. Insights into the organization and dynamics of bacterial chemoreceptor clusters through in vivo crosslinking studies. Proc. Natl. Acad. Sci. USA 2005, 102, 15623–15628. [Google Scholar]
- Boldog, T.; Grimme, S.; Li, M.; Sligar, S.G.; Hazelbauer, G.L. Nanodiscs separate chemoreceptor oligomeric states and reveal their signaling properties. Proc. Natl. Acad. Sci. USA 2006, 103, 11509. [Google Scholar]
- Zhang, P.; Khursigara, C.M.; Hartnell, L.M.; Subramaniam, S. Direct visualization of Escherichia coli chemotaxis receptor arrays using cryo-electron microscopy. Proc. Natl. Acad. Sci. USA 2007, 104, 3777. [Google Scholar]
- Briegel, A.; Ding, H.J.; Li, Z.; Werner, J.; Gitai, Z.; Dias, D.P.; Jensen, R.B.; Jensen, G.J. Location and architecture of the Caulobacter crescentus chemoreceptor array. Mol. Microbiol 2008, 69, 30–41. [Google Scholar]
- Khursigara, C.M.; Wu, X.; Subramaniam, S. Chemoreceptors in Caulobacter crescentus: Trimers of receptor dimers in a partially ordered hexagonally packed array. J. Bacteriol 2008, 190, 6805–6810. [Google Scholar]
- Briegel, A.; Ortega, D.R.; Tocheva, E.I.; Wuichet, K.; Li, Z.; Chen, S.; Müller, A.; Iancu, C.V.; Murphy, G.E.; Dobro, M.J.; et al. Universal architecture of bacterial chemoreceptor arrays. Proc. Natl. Acad. Sci. USA 2009, 106, 17181–17186. [Google Scholar]
- Khursigara, C.M.; Lan, G.; Neumann, S.; Wu, X.; Ravindran, S.; Borgnia, M.J.; Sourjik, V.; Milne, J.; Tu, Y.; Subramaniam, S. Lateral density of receptor arrays in the membrane plane influences sensitivity of the E. coli chemotaxis response. EMBO J 2011, 30, 1719–1729. [Google Scholar]
- Briegel, A.; Li, X.; Bilwes, A.M.; Hughes, K.T.; Jensen, G.J.; Crane, B.R. Bacterial chemoreceptor arrays are hexagonally packed trimers of receptor dimers networked by rings of kinase and coupling proteins. Proc. Natl. Acad. Sci. USA 2012, 109, 3766–3771. [Google Scholar]
- Liu, J.; Hu, B.; Morado, D.R.; Jani, S.; Manson, M.D.; Margolin, W. Molecular architecture of chemoreceptor arrays revealed by cryoelectron tomography of Escherichia coli minicells. Proc. Natl. Acad. Sci. USA 2012, 109, E1481–E1488. [Google Scholar]
- Cardozo, M.J.; Massazza, D.A.; Parkinson, J.S.; Studdert, C.A. Disruption of chemoreceptor signalling arrays by high levels of CheW, the receptor–kinase coupling protein. Mol. Microbiol 2010, 75, 1171–1181. [Google Scholar]
- Asinas, A.E.; Weis, R.M. Competitive and cooperative interactions in receptor signaling complexes. J. Biol. Chem 2006, 281, 30512–30523. [Google Scholar]
- Levit, M.N.; Grebe, T.W.; Stock, J.B. Organization of the receptor-kinase signaling array that regulates Escherichia coli chemotaxis. J. Biol. Chem 2002, 277, 36748–36754. [Google Scholar]
- Liu, Y.; Levit, M.; Lurz, R.; Surette, M.G.; Stock, J.B. Receptor-mediated protein kinase activation and the mechanism of transmembrane signaling in bacterial chemotaxis. EMBO J 1997, 16, 7231. [Google Scholar]
- Francis, N.R.; Wolanin, P.M.; Stock, J.B.; DeRosier, D.J.; Thomas, D.R. Three-dimensional structure and organization of a receptor/signaling complex. Proc. Natl. Acad. Sci. USA 2004, 101, 17480–17485. [Google Scholar]
- Li, M.; Hazelbauer, G.L. Cellular stoichiometry of the components of the chemotaxis signaling complex. J. Bacteriol 2004, 186, 3687–3694. [Google Scholar]
- Li, M.; Hazelbauer, G.L. Core unit of chemotaxis signaling complexes. Proc. Natl. Acad. Sci. USA 2011, 108, 9390–9395. [Google Scholar]
- Thiem, S.; Kentner, D.; Sourjik, V. Positioning of chemosensory clusters in E. coli and its relation to cell division. EMBO J 2007, 26, 1615–1623. [Google Scholar]
- Lybarger, S.R.; Maddock, J.R. Clustering of the chemoreceptor complex in Escherichia coli is independent of the methyltransferase CheR and the methylesterase CheB. J. Bacteriol 1999, 181, 5527–5529. [Google Scholar]
- Lybarger, S.R.; Nair, U.; Lilly, A.A.; Hazelbauer, G.L.; Maddock, J.R. Clustering requires modified methyl-accepting sites in low-abundance but not high-abundance chemoreceptors of Escherichia coli. Mol. Microbiol 2005, 56, 1078–1086. [Google Scholar]
- Amin, D.N.; Hazelbauer, G.L. The chemoreceptor dimer is the unit of conformational coupling and transmembrane signaling. J. Bacteriol 2010, 192, 1193–1200. [Google Scholar]
- Li, G.; Weis, R.M. Covalent modification regulates ligand binding to receptor complexes in the chemosensory system of Escherichia coli. Cell 2000, 100, 357–365. [Google Scholar]
- Hall, B.A.; Armitage, J.P.; Sansom, M.S.P. Mechanism of bacterial signal transduction revealed by molecular dynamics of Tsr dimers and trimers of dimers in lipid vesicles. PLoS Comput. Biol 2012, 8, e1002685. [Google Scholar]
- Winston, S.E.; Mehan, R.; Falke, J.J. Evidence that the adaptation region of the aspartate receptor is a dynamic four-helix bundle: Cysteine and disulfide scanning studies. Biochemistry 2005, 44, 12655–12666. [Google Scholar]
- Starrett, D.J.; Falke, J.J. Adaptation mechanism of the aspartate receptor: Electrostatics of the adaptation subdomain play a key role in modulating kinase activity. Biochemistry 2005, 44, 1550. [Google Scholar]
- Bass, R.B.; Falke, J.J. Detection of a conserved α-helix in the kinase-docking region of the aspartate receptor by cysteine and disulfide scanning. J. Biol. Chem 1998, 273, 25006–25014. [Google Scholar]
- Irieda, H.; Homma, M.; Homma, M.; Kawagishi, I. Control of chemotactic signal gain via modulation of a pre-formed receptor array. J. Biol. Chem 2006, 281, 23880–23886. [Google Scholar]
- Vaknin, A.; Berg, H.C. Osmotic stress mechanically perturbs chemoreceptors in Escherichia coli. Proc. Natl. Acad. Sci. USA 2006, 103, 592–596. [Google Scholar]
- Vaknin, A.; Berg, H.C. Physical responses of bacterial chemoreceptors. J. Mol. Biol 2007, 366, 1416–1423. [Google Scholar]
- Spiro, P.A.; Parkinson, J.S.; Othmer, H.G. A model of excitation and adaptation in bacterial chemotaxis. Proc. Nat. Acad. Sci. USA 1997, 94, 7263–7268. [Google Scholar]
- Cluzel, P.; Surette, M.; Leibler, S. An ultrasensitive bacterial motor revealed by monitoring signaling proteins in single cells. Science 2000, 287, 1652–1655. [Google Scholar]
- Goldbeter, A.; Koshland, D.E., Jr. Simple molecular model for sensing and adaptation based on receptor modification with application to bacterial chemotaxis. J. Mol. Biol 1982, 161, 395–416. [Google Scholar]
- Asakura, S.; Honda, H. Two-state model for bacterial chemoreceptor proteins. J. Mol. Biol 1984, 176, 349–367. [Google Scholar]
- Othmer, H.G.; Monk, P.B.; Rapp, P.E. A model for signal relay and adaptation in Dictyostelium discoideum Part II. Analytical and numerical results. Math. Biosci 1985, 77, 77–139. [Google Scholar]
- Tang, Y.; Othmer, H.G. A G-protein-based model of adaptation in Dictyostelium discoideum. Math. Biosci 1994, 120, 25–76. [Google Scholar]
- Yi, T.M.; Huang, Y.; Simon, M.I.; Doyle, J. Robust perfect adaptation in bacterial chemotaxis through integral feedback control. Proc. Natl. Acad. Sci. USA 2000, 97, 4649–4653. [Google Scholar]
- Sontag, E.D. Adaptation and regulation with signal detection implies internal model. Syst. Control Lett 2003, 50, 119–126. [Google Scholar]
- Othmer, H.G.; Tang, Y. Oscillations and Waves in a Model of INSP3-controlled Calcium Dynamics. In Experimental and Theoretical Advances in Pattern Formation; Othmer, H.G., Maini, P.K., Murray, J.D., Eds.; Plenum Press: New York, NY, USA, 1993; pp. 277–313. [Google Scholar]
- Tang, Y.; Othmer, H.G. A model of calcium dynamics in cardiac myocytes based on the kinetics of ryanodine-sensitive calcium channels. Biophys. J 1994, 67, 2223–2235. [Google Scholar]
- Tang, Y.; Stephenson, J.L.; Othmer, H.G. Simplification and analysis of models of calcium dynamics based on IP3-sensitive calcium channel kinetics. Biophys. J 1996, 70, 246–263. [Google Scholar]
- Katz, B.; Thesleff, S. A study of the ‘desensitization’ produced by acetylcholine at the motor end-plate. J. Physiol 1957, 138, 63–80. [Google Scholar]
- Gero, A. Desensitization, two-state receptors and pharmacological parameters. J. Theor. Biol 1983, 103, 137–162. [Google Scholar]
- Segel, L. Incorporation of receptor kinetics into a model for bacterial chemotaxis. J. Theor. Biol 1976, 57, 23–42. [Google Scholar]
- Koshland, D., Jr. A response regulator model in a simple sensory system. Science 1977, 196, 1055–1063. [Google Scholar]
- Macnab, R.M.; Koshland, D.E. The Gradient-sensing mechanism in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA 1972, 69, 2509–2512. [Google Scholar]
- Goldbeter, A.; Koshland, D., Jr. Simple molecular model for sensing and adaptation based on receptor modification with application to bacterial chemotaxis. J. Mol. Biol 1982, 161, 395–416. [Google Scholar]
- Segel, L.; Goldbeter, A.; Devreotes, P.; Knox, B. A mechanism for exact sensory adaptation based on receptor modification. J. Theor. Biol 1986, 120, 151–179. [Google Scholar]
- Bray, D.; Bourret, R.B.; Simon, M.I. Computer simulation of the phosphorylation cascade controlling bacterial chemotaxis. Mol. Biol. Cell 1993, 4, 469–482. [Google Scholar]
- Bray, D.; Bourret, R.B. Computer analysis of the binding reactions leading to a transmembrane receptor-linked multiprotein complex involved in bacterial chemotaxis. Mol. Biol. Cell 1995, 6, 1367–1380. [Google Scholar]
- Morton-Firth, C.; Bray, D. Predicting temporal fluctuations in an intracellular signaling pathway. J. Theor. Biol 1998, 192, 117–128. [Google Scholar]
- Barkai, N.; Leibler, S. Robustness in simple biochemical networks. Nature 1997, 387, 913–917. [Google Scholar]
- Shi, Y.; Duke, T. Cooperative model of bacterial sensing. Phys. Rev. E 1998, 58, 6399–6406. [Google Scholar]
- Shi, Y. Adaptive Ising model and bacterial chemotactic receptor network. Europhys. Lett 2000, 50, 113–119. [Google Scholar]
- Morton-Firth, C.J.; Shimizu, T.S.; Bray, D. A free-energy-based stochastic simulation of the tar receptor complex. J. Mol. Biol 1999, 286, 1059–1074. [Google Scholar]
- Mello, B.A.; Tu, Y. Quantitative modeling of sensitivity in bacterial chemotaxis: The role of coupling among different chemoreceptor species. Proc. Natl. Acad. Sci. USA 2003, 100, 8223–8228. [Google Scholar]
- Goldman, J.; Andrews, S.; Bray, D. Size and composition of membrane protein clusters predicted by Monte Carlo analysis. Europ. Biophys. J 2004, 33, 506–512. [Google Scholar]
- Albert, R.; Chiu, Y.; Othmer, H.G. Dynamic receptor team formation can explain the high signal transduction gain in Escherichia coli. Biophys. J 2004, 86, 2650–2659. [Google Scholar]
- Liberman, L.; Berg, H.C.; Sourjik, V. Effect of chemoreceptor modification on assembly and activity of the receptor-kinase complex in Escherichia coli. J. Bacteriol 2004, 186, 6643–6646. [Google Scholar]
- Bornhorst, J.A.; Falke, J.J. Evidence that both ligand binding and covalent adaptation drive a two-state equilibrium in the aspartate receptor signaling complex. J. Gen. Physiol 2001, 118, 693–710. [Google Scholar]
- Li, M.; Hazelbauer, G.L. Adaptational assistance in clusters of bacterial chemoreceptors. Mol. Microbiol 2005, 56, 1617–1626. [Google Scholar]
- Keymer, J.E.; Endres, R.G.; Skoge, M.; Meir, Y.; Wingreen, N.S. Chemosensing in Escherichia coli: Two regimes of two-state receptors. Proc. Natl. Acad. Sci. USA 2006, 103, 1786–1791. [Google Scholar]
- Mello, B.A.; Tu, Y. An allosteric model for heterogeneous receptor complexes: Understanding bacterial chemotaxis responses to multiple stimuli. Proc. Natl. Acad. Sci. USA 2005, 102, 17354–17359. [Google Scholar]
- Shrout, A.; Montefusco, D.; Weis, R. Template-directed assembly of receptor signaling complexes. Biochemistry 2003, 42, 13379–13385. [Google Scholar]
- Lai, R.; Manson, J.; Bormans, A.; Draheim, R.; Nguyen, N.; Manson, M. Cooperative signaling among bacterial chemoreceptors. Biochemistry 2005, 44, 14298–14307. [Google Scholar]
- Endres, R.G.; Wingreen, N.S. Precise adaptation in bacterial chemotaxis through “assistance neighborhoods”. Proc. Natl. Acad. Sci. USA 2006, 103, 13040. [Google Scholar]
- Kollmann, M.; Loevdok, L.; Bartholome, K.; Timmer, J.; Sourjik, V. Design principles of a bacterial signalling network. Nature 2005, 438, 504–507. [Google Scholar]
- Tu, Y.; Shimizu, T.; Berg, H. Modeling the chemotactic response of Escherichia coli to timevarying stimuli. Proc. Natl. Acad. Sci. USA 2008, 105, 14855–14860. [Google Scholar]
- Hauri, D.C.; Ross, J. A model of excitation and adaptation in bacterial chemotaxis. Biophys. J 1995, 68, 708–722. [Google Scholar]
- Levin, M.D.; Morton-Firth, C.J.; Abouhamad, W.N.; Bourret, R.B.; Bray, D. Origins of individual swimming behavior in bacteria. Biophys. J 1998, 74, 175–181. [Google Scholar]
- Almogy, G.; Stone, L.; Ben-Tal, N. Multi-stage regulation, a key to reliable adaptive biochemical pathways. Biophysical journal 2001, 81, 3016–3028. [Google Scholar]
- Mello, B.A.; Tu, Y. Perfect and near-perfect adaptation in a model of bacterial chemotaxis. Biophys. J 2003, 84, 2943–2956. [Google Scholar]
- Arocena, M.; Acerenza, L. Necessary conditions for a minimalmodel of receptor to show adaptive response over a wide range of levels of stimulus. Jour. Theor. Biol 2004, 229, 45–57. [Google Scholar]
- Bray, D.; Levin, M.D.; Morton-Firth, C.J. Receptor clustering as a cellular mechanism to control sensitivity. Nature 1998, 393, 85–88. [Google Scholar]
- Duke, T.A.J.; Bray, D. Heightened sensitivity of a lattice of membrane receptors. Proc. Natl. Acad. Sci. USA 1999, 96, 10104–10108. [Google Scholar]
- Shi, Y. Effects of thermal fluctuation and the receptor-receptor interaction in bacterial chemotactic signaling and adaptation. Phys. Rev. E 2001, 64, 1–8. [Google Scholar]
- Shi, Y. Clustering and signalling of cell receptors. Phys. Stat. Mech. Appl 2002, 311, 199–212. [Google Scholar]
- Levin, M.; Shimizu, T.; Bray, D. Binding and diffusion of CheR molecules within a cluster of membrane receptors. Biophys. J 2002, 82, 1809–1817. [Google Scholar]
- Shimizu, T.S.; Aksenov, S.V.; Bray, D. A spatially extended stochastic model of the bacterial chemotaxis signalling pathway. J. Mol. Biol 2003, 329, 291–309. [Google Scholar]
- Mello, B.A.; Shaw, L.; Tu, Y. Effects of receptor interaction in bacterial chemotaxis. Biophys. J 2004, 87, 1578–1595. [Google Scholar]
- Monod, J.; Wyman, J.; Changeux, J.P. On the nature of allosteric transitions: A plausible model. J. Mol. Biol 1965, 12, 88–118. [Google Scholar]
- Mello, B.A.; Tu, Y. Effects of adaptation in maintaining high sensitivity over a wide range of backgrounds for Escherichia coli chemotaxis. Biophys. J 2007, 92, 2329–2337. [Google Scholar]
- Hansen, C.H.; Endres, R.G.; Wingreen, N.S.; Bourne, P.E. Chemotaxis in Escherichia coli: A molecular model for robust precise adaptation. PLoS Comput. Biol 2008, 4, e1. [Google Scholar]
- Meir, Y.; Jakovljevic, V.; Oleksiuk, O.; Sourjik, V.; Wingreen, N. Precision and kinetics of adaptation in bacterial chemotaxis. Biophys. J 2010, 99, 2766–2774. [Google Scholar]
- Skoge, M.L.; Endres, R.G.; Wingreen, N.S. Receptor-receptor coupling in bacterial chemotaxis: Evidence for strongly coupled clusters. Biophys. J 2006, 90, 4317–4326. [Google Scholar]
- Rao, C.V.; Frenklach, M.; Arkin, A.P. An allosteric model for transmembrane signaling in bacterial chemotaxis. J. Mol. Biol 2004, 343, 291–303. [Google Scholar]
- Endres, R.G.; Falke, J.J.; Wingreen, N.S. Chemotaxis receptor complexes: From signaling to assembly. PLoS Comput. Biol 2007, 3, 1385–1393. [Google Scholar]
- Park, M.J.; Dahlquist, F.W.; Doyle, F.J., III. Simultaneous high gain and wide dynamic range in a model of bacterial chemotaxis. IET Syst. Biol 2007, 1, 222–229. [Google Scholar]
- Endres, R.; Oleksiuk, O.; Hansen, C.; Meir, Y.; Sourjik, V.; Wingreen, N. Variable sizes of Escherichia coli chemoreceptor signaling teams. Mol. Syst. Biol 2008, 4, 211–219. [Google Scholar]
- Hansen, C.; Sourjik, V.; Wingreen, N. A dynamic-signaling-team model for chemotaxis receptors in Escherichia coli. Proc. Natl. Acad. Sci. USA 2010, 107, 17170–17175. [Google Scholar]
- Lipkow, K.; Andrews, S.S.; Bray, D. Simulated diffusion of phosphorylated CheY through the cytoplasm of Escherichia coli. J. Bacteriol 2005, 187, 45–53. [Google Scholar]
- Lipkow, K. Changing cellular location of CheZ predicted by molecular simulations. PLoS Comput. Biol 2006, 2, e39. [Google Scholar]
- Endres, R. Polar chemoreceptor clustering by coupled trimers of dimers. Biophys. J 2009, 96, 453–463. [Google Scholar]
- Rao, C.V.; Kirby, J.R.; Arkin, A.P. Design and diversity in bacterial chemotaxis: A comparative study in Escherichia coli and Bacillus subtilis. PLoS Biol 2004, 2, 239–252. [Google Scholar]
- Roberts, M.; August, E.; Hamadeh, A.; Maini, P.; McSharry, P.; Armitage, J.; Papachristodoulou, A. A model invalidation-based approach for elucidating biological signalling pathways, applied to the chemotaxis pathway in R. sphaeroides. BMC Syst. Biol 2009, 3, 105. [Google Scholar]
- Tindall, M.; Porter, S.; Maini, P.; Armitage, J. Modeling chemotaxis reveals the role of reversed phosphotransfer and a bi-functional kinase-phosphatase. PLoS Comput. Biol 2010, 6, e1000896. [Google Scholar]
- Hamadeh, A.; Roberts, M.; August, E.; McSharry, P.; Maini, P.; Armitage, J.; Papachristodoulou, A. Feedback control architecture and the bacterial chemotaxis network. PLoS Comput. Biol 2011, 7, e1001130. [Google Scholar]
- Clausznitzer, D.; Oleksiuk, O.; Løvdok, L.; Sourjik, V.; Endres, R. Chemotactic response and adaptation dynamics in Escherichia coli. PLoS Comput. Biol 2010, 6, e1000784. [Google Scholar]
- Xin, X.; Othmer, H. A “Trimer of Dimers”-based model for the chemotactic signal transduction network in bacterial chemotaxis. Bull. Math. Biol 2012, 74, 2339–2382. [Google Scholar]
- Tindall, M.J.; Porter, S.L.; Maini, P.K.; Gaglia, G.; Armitage, J.P. Overview of mathematical approaches used to model bacterial chemotaxis I: The single cell. Bull. Math. Biol 2008, 70, 1525–1569. [Google Scholar]
- Xin, X. Mathematical Models of Bacterial Chemotaxis. Ph.D. Dissertation, University of Minnesota, Minneapolis, MN, USA, 2010. [Google Scholar]
- Budrene, E.O.; Berg, H.C. Dynamics of formation of symmetrical patterns by chemotactic bacteria. Nature 1995, 376, 49–53. [Google Scholar]
- Woodward, D.; Tyson, R.; Myerscough, M.; Murray, J.; Budrene, E.; Berg, H. Spatio-temporal patterns generated by Salmonella typhimurium. Biophys. J 1995, 68, 2181–2189. [Google Scholar]
- Ben-Jacob, E.; Schochet, O.; Tenenbaum, A.; Cohen, I.; Czirok, A. Generic modelling of cooperative growth patterns in bacterial colonies. Nature 1994, 368, 46–49. [Google Scholar]
- Ben-Jacob, E.; Cohen, I.; Czirok, A.; Vicsek, T.; Gutnick, D.L. Chemomodulation of cellular movement, collective formation of vortices by swarming bacteria, and colonial development. Physica A 1997, 238, 181–197. [Google Scholar]
- Law, A.M.J.; Aitken, M.D. Continuous-flow capillary assay for measuring bacterial chemotaxis. Appl. Environ. Microbiol 2005, 71, 3137–3143. [Google Scholar]
- Kalinin, Y.V.; Jiang, L.; Tu, Y.; Wu, M. Logarithmic sensing in Escherichia coli bacterial chemotaxis. Biophys. J 2009, 96, 2439–2448. [Google Scholar]
- Saragosti, J.; Calvez, V.; Bournaveas, N.; Perthame, B.; Buguin, A.; Silberzan, P. Directional persistence of chemotactic bacteria in a traveling concentration wave. Proc. Nat. Acad. Sci. USA 2011, 108, 16235–16240. [Google Scholar]
- Pandey, G.; Jain, R.K. Bacterial chemotaxis toward environmental pollutants: Role in bioremediation. Appl. Environ. Microbiol 2002, 68, 5789–5795. [Google Scholar]
- Law, A.M.J.; Aitken, M.D. Bacterial chemotaxis to naphthalene desorbing from a nonaqueous liquid. Appl. Environ. Microbiol 2003, 69, 5968–5973. [Google Scholar]
- Ben-Jacob, E.; Cohen, I.; Levine, H. Cooperative self-organization of microorganisms. Adv. Phys 2000, 49, 395–554. [Google Scholar]
- Kaiser, D. Coupling cell movement to multicellular development in myxobacteria. Nat. Rev. Microbiol 2003, 1, 45–54. [Google Scholar]
- Kaiser, D. Myxococcus–from single-cell polarity to complex multicellular patterns. Ann. Rev. Genet 2008, 42, 109–130. [Google Scholar]
- Wu, Y.; Kaiser, A.D.; Jiang, Y.; Alber, M.S. Periodic reversal of direction allows Myxobacteria to swarm. Proc. Natl. Acad. Sci. USA 2009, 106, 1222–1227. [Google Scholar]
- Wu, Y.; Jiang, Y.; Kaiser, A.D.; Alber, M. Self-organization in bacterial swarming: Lessons from myxobacteria. Phys. Biol 2011, 8, 055003. [Google Scholar]
- Du, H.; Xu, Z.; Shrout, J.D.; Alber, M. Multiscale modeling of Pseudomonas aeruginosa Swarming. Math. Models Methods Appl. Sci 2011, 21, 939–954. [Google Scholar]
- Be’er, A.; Zhang, H.P.; Florin, E.L.; Payne, S.M.; Ben-Jacob, E.; Swinney, H.L. Deadly competition between sibling bacterial colonies. Proc. Natl. Acad. Sci. USA 2009, 106, 428–433. [Google Scholar]
- Be’er, A.; Ariel, G.; Kalisman, O.; Helman, Y.; Sirota-Madi, A.; Zhang, H.P.; Florin, E.L.; Payne, S.M.; Ben-Jacob, E.; Swinney, H.L. Lethal protein produced in response to competition between sibling bacterial colonies. Proc. Natl. Acad. Sci. USA 2010, 107, 6258–6263. [Google Scholar]
- Wang, Q.; Zhang, T. Review of mathematical models for biofilms. Solid State Commun 2010, 150, 1009–1022. [Google Scholar]
- Cogan, N.G.; Gunn, J.S.; Wozniak, D.J. Biofilms and infectious diseases: Biology to mathematics and back again. FEMS Microbiol. Lett 2011, 322, 1–7. [Google Scholar]
- Cogan, N.G.; Wolgemuth, C.W. Two-dimensional patterns in bacterial veils arise from self-generated, three-dimensional fluid flows. Bull. Math. Biol 2011, 73, 212–229. [Google Scholar]
- Mittal, N.; Budrene, E.O.; Brenner, M.P.; Oudenaarden, A. Motility of Escherichia coli cells in clusters formed by chemotactic aggregation. Proc. Natl. Acad. Sci. USA 2003, 100, 13259–63. [Google Scholar]
- Adler, J. Chemotaxis in bacteria. Science 1966, 153, 708–716. [Google Scholar]
- Saragosti, J.; Calvez, V.; Bournaveas, N.; Buguin, A.; Silberzan, P.; Perthame, B. Mathematical description of bacterial traveling pulses. PLoS Comput. Biol 2010, 6, e1000890. [Google Scholar]
- Saragosti, J.; Calvez, V.; Bournaveas, N.; Perthame, B.; Buguin, A.; Silberzan, P. Directional persistence of chemotactic bacteria in a traveling concentration wave. Proc. Natl. Acad. Sci. USA 2011, 108, 16235–16240. [Google Scholar]
- Xue, C.; Budrene, E.O.; Othmer, H.G. Radial and spiral stream formation in Proteus mirabilis colonies. PLoS Comput. Biol 2011, 7, e1002332. [Google Scholar]
- Frymier, P.D.; Ford, R.M.; Berg, H.C.; Cummings, P.T. Three-dimensional tracking of motile bacteria near a solid planar surface. Proc. Natl. Acad. Sci. USA 1995, 92, 6195–6199. [Google Scholar]
- DiLuzio, W.R.; Turner, L.; Mayer, M.; Garstecki, P.; Weibel, D.B.; Berg, H.C.; Whitesides, G.M. Escherichia coli swim on the right-hand side. Nature 2005, 435, 1271–1274. [Google Scholar]
- Keller, E.F.; Segel, L.A. Traveling bands of chemotactic bacteria: A theoretical analysis. J. Theor. Biol 1971, 30, 235–248. [Google Scholar]
- Lapidus, I.R.; Schiller, R. A model for traveling bands of chemotactic bacteria. Biophys J 1978, 22, 1–13. [Google Scholar]
- Lauffenburger, D.; Kennedy, C.R.; Aris, R. Traveling bands of chemotactic bacteria in the context of population growth. Bull. Math. Biol 1984, 46, 19–40. [Google Scholar]
- Ben-Jacob, E.; Cohen, I.; Shochet, O.; Aranson, I.; Levine, H. Complex bacterial patterns. Nature 1995, 373, 566–557. [Google Scholar]
- Tsimring, L.; Levine, H.; A.I.; Ben-Jacob, E.; Cohen, I.; Shochet, O.; Reynolds, W.N. Aggregation patterns in stressed bacteria. Phys. Rev. Let 1995, 75, 1859–1862. [Google Scholar]
- Tyson, R.; Lubkin, S.R.; Murray, J.D. A minimal mechanism for bacterial pattern formation. Proc. R. Soc. Lond. B 1999, 266, 299–304. [Google Scholar]
- Tyson, R.; Lubkin, S.R.; Murray, J.D. Model and analysis of chemotactic bacterial patterns in a liquid medium. J. Math. Biol 1999, 38, 359–375. [Google Scholar]
- Tyson, R.; Stern, L.G.; LeVeque, R.J. Fractional step methods applied to a chemotaxis model. J. Math. Biol 2000, 41, 455–475. [Google Scholar]
- Polezhaev, A.A.; Pashkov, R.A.; Lobanov, A.I.; Petrov, I.B. Spatial patterns formed by chemotactic bacteria Escherichia coli. Int. J. Dev. Biol 2006, 50, 311–338. [Google Scholar]
- Calvez, V.; Perthame, B. A Lyapunov function for a two-chemical species version of the chemotaxis model. BIT Numer. Math 2006, 46, 85–97. [Google Scholar]
- Hillen, T.; Painter, K.J. A user’s guide to PDE models for chemotaxis. J. Math. Biol 2009, 58, 183–217. [Google Scholar]
- Horstmann, D. From 1970 until present: The Keller-Segel model in chemotaxis and its consequences. Jahresbericht der DMV 2003, 105, 103–165. [Google Scholar]
- Brenner, M.; Levitov, L.; Budrene, E. Physical mechanisms for chemotactic pattern formation by bacteria. Biophys. J 1998, 74, 1677–1693. [Google Scholar]
- Betterton, M.D.; Brenner, M.P. Collapsing bacterial cylinders. Phys. Rev. E 2001, 64, 061904. [Google Scholar]
- Othmer, H.G.; Painter, K.J.; Umulis, D.; Xue, C. The intersection of theory and application in elucidating pattern formation in developmental biology. Math. Model. Nat. Phenom 2009, 4, 3–82. [Google Scholar]
- Franz, B.; Erban, R. Hybrid Modelling of Individual Movement and Collective Behaviour. In Dispersal, Individual Movement and Spatial Ecology: A Mathematical Perspective; 2013; to appear. [Google Scholar]
- Xue, C.; Othmer, H.G. Multiscale models of taxis-driven patterning in bacterial populations. SIAM J. Appl. Math 2009, 70, 133–167. [Google Scholar]
- Franz, B.; Xue, C.; Painter, K.J.; Erban, R. Travelling waves in hybrid chemotaxis models. submitted. 2013. [Google Scholar]
- Jiang, L.; Ouyang, Q.; Tu, Y. Quantitative modeling of Escherichia coli chemotactic motion in environments varying in space and time. PLoS Comput. Biol 2010, 6, e1000735. [Google Scholar]
- Zhu, X.; Si, G.; Deng, N.; Ouyang, Q.; Wu, T.; He, Z.; Jiang, L.; Luo, C.; Tu, Y. Frequency-dependent Escherichia coli chemotaxis behavior. Phys. Rev. Lett 2012, 108, 128101. [Google Scholar]
- Patlak, C.S. Random walk with persistence and external bias. Bull. Math. Biophys 1953, 15, 311–338. [Google Scholar]
- Alt, W. Biased random walk models for chemotaxis and related diffusion approximations. J. Math. Biol 1980, 9, 147–177. [Google Scholar]
- Othmer, H.G.; Dunbar, S.R.; Alt, W. Models of dispersal in biological systems. J. Math. Biol 1988, 26, 263–298. [Google Scholar]
- Hillen, T.; Othmer, H.G. The diffusion limit of transport equations derived from velocity-jump processes. SIAM J. Appl. Math 2000, 61, 751–775. [Google Scholar]
- Othmer, H.G.; Hillen, T. The diffusion limit of transport equations II: Chemotaxis equations. SIAM J. Appl. Math 2002, 62, 1222–1250. [Google Scholar]
- Chen, K.C.; Ford, R.M.; Cummings, P.T. Cell balance equation for chemotactic bacteria with a biphasic tumbling frequency. J. Math. Biol 2003, 47, 518–546. [Google Scholar]
- Othmer, H.G.; Stevens, A. Aggregation, blowup, and collapse: The ABC’s of taxis in reinforced random walks. SIAM J. Appl. Math 1997, 57, 1044–1081. [Google Scholar]
- Alber, M.; Chen, N.; Glimm, T.; Lushnikov, P.M. Multiscale dynamics of biological cells with chemotactic interactions: From a discrete stochastic model to a continuous description. Phys. Rev. E Stat. Nonlin. Soft Matt. Phys 2006, 73, 051901. [Google Scholar]
- Lushnikov, P.M.; Chen, N.; Alber, M. Macroscopic dynamics of biological cells interacting via chemotaxis and direct contact. Phys. Rev. E Stat. Nonlin. Soft Matt. Phys 2008, 78, 061904. [Google Scholar]
- Levy, D.; Requeijo, T. Modeling group dynamics of phototaxis: From particle systems to PDEs. Discret. Contin. Dyn. Syst. Series B 2008, 9, 103. [Google Scholar]
- Ha, S.Y.; Levy, D. Particle, kinetic and fluid models for phototaxis. Discret. Contin. Dyn. Syst. B 2009, 12, 77–108. [Google Scholar]
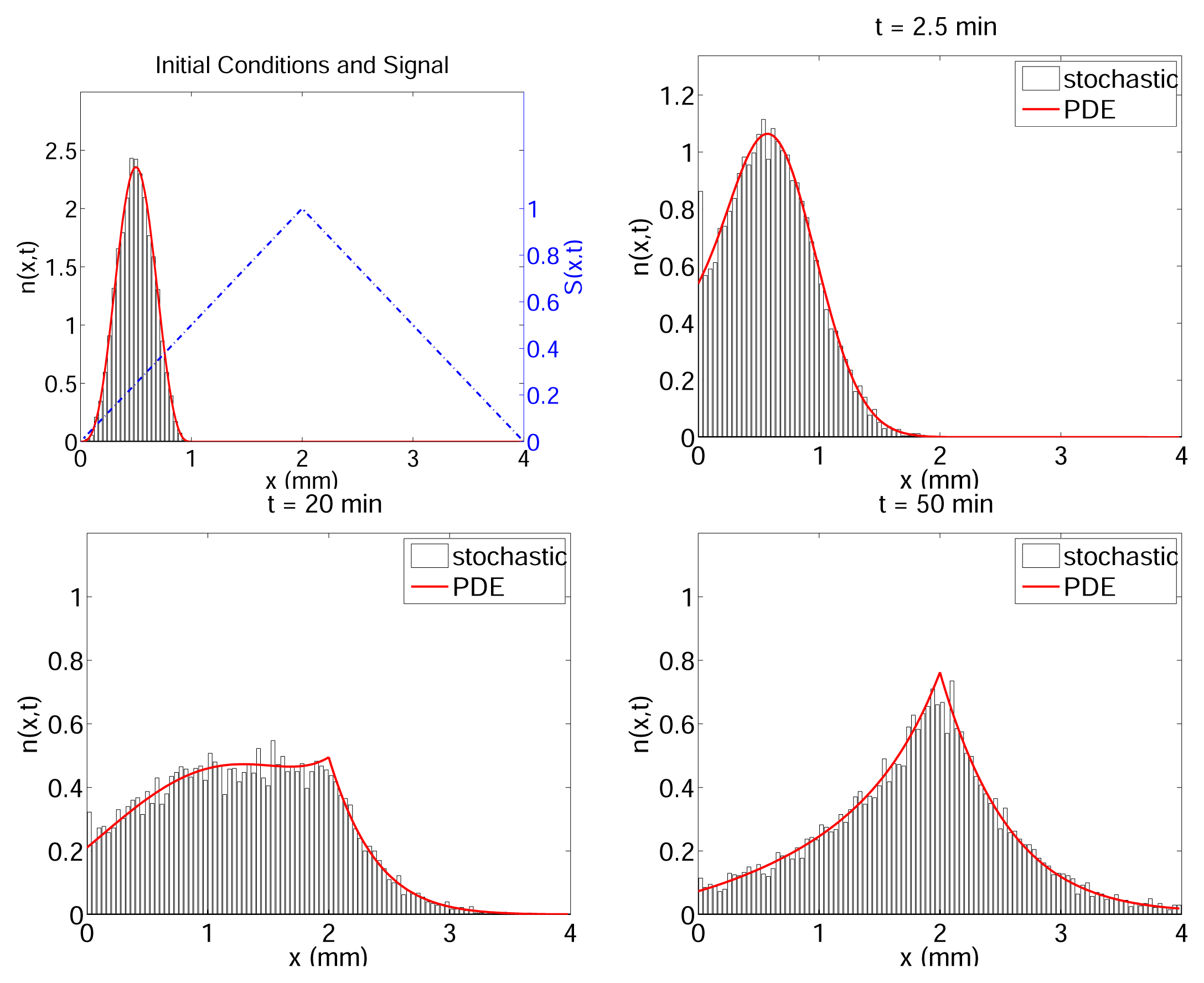
- Erban, R.; Othmer, H.G. From individual to collective behavior in bacterial chemotaxis. SIAM J. Appl. Math 2004, 65, 361–391. [Google Scholar]
- Erban, R.; Othmer, H. From signal transduction to spatial pattern formation in E. coli: A paradigm for multiscale modeling in biology. Multiscale Model. Simul 2005, 3, 362–394. [Google Scholar]
- Si, G.; Wu, T.; Ouyang, Q.; Tu, Y. Pathway-based mean-field model for Escherichia coli chemotaxis. Phys. Rev. Lett 2012, 109, 048101. [Google Scholar]
| Dimer | Trimer of dimers | Cluster of trimers | |
|---|---|---|---|
| Ligand binding | Yes minimal structural unit | Yes | Yes |
| Adaptational modification | Yes minimal structural unit | Yes | Yes |
| Transmembrane signaling | Yes minimal structural unit | Yes | Yes |
| Kinase activity control | No | Yes minimal structural unit, core functional unit (maximal kinase activation) | Yes |
| Cooperativity | Low Hill coefficient~1 | Moderate Hill coefficient~2-3; in wild-type cells and some cheR/cheB/cheRcheB mutant strains | High Hill coefficient≫3; in cheRcheB mutant strains with Tar or Tsr highly overexpressed, in receptor Tsr in vitro |
| Excitation, adaptation, and robustness | ||
|---|---|---|
| Model | Methods | Assumptions and Outcomes |
| Goldbeter and Koshland Jr [91] | ODE | Includes ligand binding and one-site methylation; Uses two-state assumption (methylated and demethylated); Demonstrates that perfect adaptation could be achieved via methylation whose reaction rates depend on receptor occupancy. |
| Block et al. [10] | ODE | Uses two-state assumption (CW and CCW); Includes adaptation; Demonstrates that transition between the run and tumble states depends on adaptation to the sensory input. |
| Asakura and Honda [78] | ODE | Includes ligand binding and multiple-site methylation; Uses two-state assumption (methylated and demethylated); Shows adaptation to attractants and repellents at both low and high background concentrations via multiple methylation. |
| Segel et al. [92] | ODE | Similar with Goldbeter and Koshland Jr [91] but allows receptor modification to occur on both ligand-free and ligand-bound receptors. |
| Bray et al. [93] | ODE | Includes ligand binding, phosphorylation cascade, and motor control; Reproduces the motor bias response to step changes in attractants and repellents ; Does not include methylation/demethylation and model for adaptation. |
| Bray and Bourret [94] | ODE | Models the ternary MCP/CheA/CheWsignaling complex formation and adds it into Bray et al. [93] to study the effect of the signaling complex formation on motor bias. |
| Hauri and Ross [113] | ODE | Models the complete signal transduction pathway and reproduces the excitation and adaptation phases of bacterial chemotaxis in the experimentally agreed timescales; Assumes that CheA autophosphorylation rate dependent on the methylation level of receptors. |
| Spiro et al. [75] | ODE | Models the complete signal transduction pathway with reduced three methylation states and reproduces excitation and adaptation in the experimentally agreed timescales. Assumes the autophosphorylation rate increases with the methylation level, the methylation rate is greater for attractant-bound than attractant-free receptors, and the demethylation rate is independent of ligand binding of receptors. |
| Barkai and Leibler [96] | ODE | Includes ligand binding and methylation/demethylation for a three-component system (MCP, CheR and CheB); Uses two-state assumption (active or inactive for receptors); Assumes that CheR works at saturation in a constant rate and CheB acts only on active receptors in a rate independent of ligand binding; Shows perfect adaptation of receptor activity and robustness of the ratio of adapted steady-state receptor activity over prestimulus activity for a wide range of parameter values. |
| Levin et al. [114] | ODE | Investigates the effect of changes in chemotactic protein expression levels on the concentration of CheYp, and compares the fine-tuned and the robust adaptation models in this aspect. |
| Morton-Firth and Bray [95] | Free-energy-based stochastic simulation | Includes phosphorylation cascade; Simulates the temporal fluctuation of CheYp. |
| Morton-Firth et al. [99] | Free-energy-based stochastic simulation | Includes phosphorylation cascade (based on [95]) and methylation/demethylation (based on [96]); Assumes that CheR only methylates inactive receptors and CheBp only demethylates active receptors; Shows excitation and adaptation; |
| Yi et al. [81] | ODE | Analyzes the Barkai and Leibler’s model and shows an integral feedback control imbedded in the system that leads to robust perfect adaptation. |
| Almogy et al. [115] | ODE | Proposes an alternative adaptation mechanism that is through dephosphorylation of CheYp by both CheZ and the CheAs–CheZ complex rather than methylation/demethylation of receptors. |
| Mello and Tu [116] | ODE | Studies the robust adaptation problem analytically and proposes six conditions for achieving perfect adaptation, confirming those key assumptions that Barkai and Leibler use [96]. |
| Arocena and Acerenza [117] | ODE | Studies the response range of bacterial chemotaxis, and shows the wider range when receptor modification is through methylation and phosphorylation than through attractant binding. |
| Kollmann et al. [111] | ODE | Uses a simplified signaling network only including a single methylation site; Shows the robustness to the intercellular variation in chemotactic protein concentrations arising from gene expression, and the variation of CheYp is much smaller than that of other proteins. |
| Tu et al. [112] | ODE, mean-field theory | Simulates chemotactic responses to time-varying exponential ramp, sine wave, and impulsive signals. |
| Receptor clustering and signaling sensitivity | ||
| Bray et al. [118] | probability analysis | Conceptual model; Shows that receptor clustering and conformational spread among neighboring receptors can explain high sensitivity. |
| Shi and Duke [97] | statistical mechanics, Ising model | Ising-type model and mean-field theory applied; Shows that receptor coupling strength affects response more than attractant binding. |
| Duke and Bray [119] | Monte Carlo methods | Monte Carlo simulation of [97]; Shows higher signaling sensitivity than the uncoupled system and ability to respond to over five order of magnitude of attractant concentrations. |
| Shi [98] | statistical mechanics, Ising model | Adaptive Ising-type model with CheR, CheBp, and their negative feedback effect on receptor activity included; More robust than [97] because of relaxation of the filed strength assumptions; Shows high sensitivity. |
| Shi [120] | Ising model | Compares simulations of the models [97,98] with experiments and shows good agreement on the ratio of attractant binding to receptor-receptor interactions, the adaptation time, as well as the ratio of pre- and post-stimulus CheA phosphorylation. |
| Shi [121] | Ising model, Monte Carlo methods | Considers the receptor movement and allows them to float; Shows strong correlation for neighboring receptors and exponential decay with increasing receptor-receptor distance. |
| Levin et al. [122] | Monte Carlo methods | Studies effect of binding and diffusion of CheR through receptor clusters with the model [99]; Shows that if binding is within the physiological limits, CheR can access and modify a large number of receptors in cluster. |
| Shimizu et al. [123] | Ising model, free-energy-based stochastic simulation | Ising model incorporated into [99]; Compares effect of receptor array size and geometry on sensitivity, gain and signal-to-noise ratio; Reproduces overshoot. |
| Mello and Tu [100] | Ising model | Deterministic version of Ising-type model; Includes receptor interactions between Tar and Tsr; Includes methylation/demethylation (same assumptions as [96,99]); Reproduces the FRET data on cheR/cheB/cheRcheB mutant and wild-type cells [15] using two different parameter sets. |
| Mello et al. [124] | Ising model, mean-field theory, Monte Carlo methods | Mean-field theory applied to and Monte Carlo simulation of [100]. |
| Goldman et al. [101] | Lattice gas model, Monte Carlo methods | Applies 2-D lattice gas model of protein association to chemoreceptor clusters. |
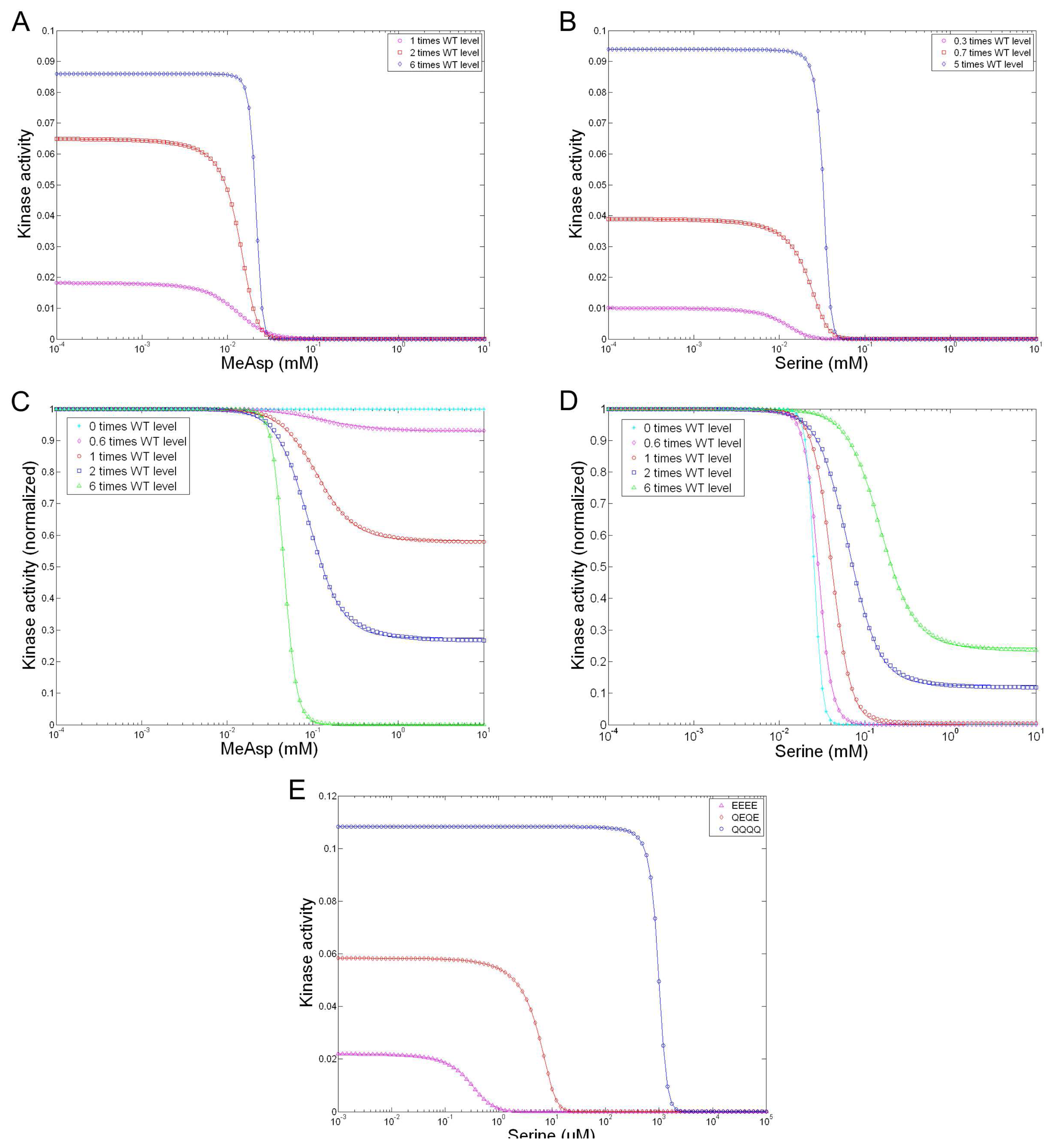
| Sourjik and Berg [39] | MWC model | Applies MWC model to explain their FERT data. |
| Albert et al. [102] | ODE | Model for dynamic formation of trimer of dimers; Assumes the time scale of association and dissociation of trimer of dimers comparable to that of ligand binding and kinase activity, which was disproved later by experiments [103]. |
| Rao et al. [130] | MWC model | Model of static trimer of dimers; Reproduces in vitro kinase activity data on Tar [104] and Tsr [67] as well as in vivo data on mutant cells [15] |
| Mello and Tu [107] | MWC model | Generalizes MWC model for allosteric interaction and multiple signal integration in heterogeneous receptor clusters; Reproduces measured responses for 14 mutant strains with varied expression levels of Tar and/or Tsr [39]. |
| Keymer et al. [106] | MWC model | Proposes two regimes for a two-state receptor: regime I is characterized by low to moderate kinase activity and a low, constant inhibition number for half-maximal activity Ki, in which coupling of receptors leads to high sensitivity (in the case of wild-type and cheR mutant cells); regime II is characterized by high kinase activity and a high Ki, increasing with the methylated level of receptors, in which coupling leads to high cooperativity (in the case of cheRcheB mutant cells); Accordingly proposes a modified MWC model; Reproduces Sourjik and Berg’s FRET data [15]. |
| Endres and Wingreen [110] | MWC model | Adaptation model based on ‘assistant-neighborhoods’ [105], using the key assumptions on CheR and CheBp as [96,99]; Incorporates the MWC model [106]; Shows sensitivity and adaptation for mixed-type receptors observed in [15]; Suggests two limits of adaptation to attractants: (1) saturation of ligand binding sites on receptors; (2) full methylation of receptors. |
| [129] | MWC model, Ising model | Compares activity response of receptor clusters generated by one-dimensional Ising-type model, two-dimensional Ising-type model, and two-regime MWC-type model; Shows that the outputs of Ising-type models are not consistent with the FRET data on activity responses to steps of attractants for wild-type and cheR mutant cells [15], which the MWC-type model can reproduce; Suggests strongly-coupled receptor clusters. |
| Mello and Tu [126] | MWC model | Studies the mechanism how the cells maintain high sensitivity over a wide range of backgrounds based on a simplified version of [107] for homogeneous receptor complexes. |
| Endres et al. [131] | statistical mechanics, MWC model | Model of static trimer of dimers; Reproduces in vitro kinase activity data on Tar [104,108,109]. |
| Park et al. [132] | sensitivity analysis | Performs sensitivity analysis for trimer of dimers and shows enhanced signaling sensitivity compared with dimers. |
| Hansen et al. [127] | MWC model | Robust adaptation model extended from [110] including binding and unbinding of CheR and CheBp; Analyzes adaptation limits from the angle of CheR and CheB kinetics. |
| Endres et al. [133] | MWC model, statistical method | Determines the sizes of signaling clusters through best fitting in vivo FRET data with the model [106] using statistical PCA method; Shows the cluster sizes increasing with methylation levels. |
| Hansen et al. [134] | statistical mechanics, MWC model | Model of dynamic signaling clusters of trimers of dimers, the boundaries of which are variable in simulation; Shows stronger coupling of active trimers of dimers than inactive. |
| Meir et al. [128] | MWC model, ODE | Analyzes the characteristics of precise adaptation and finds the asymmetries (i.e., different adaptation time) in responses to addition and removal of attractants; Proposes two possible sources of the asymmetry: (1) dynamic phosphorylation of CheB and (2) scarcity of methylation site. |
| Clausznitzer et al. [142] | MWC model, ODE | Studies the dynamics (time courses) of adaptation and evaluate the existing adaptation models. |
| Khursigara et al. [53] | MWC model | Study with experiments and simulations combined; A cutoff distance used to determine the range of interacting receptors and the size of signaling receptor clusters variable; Shows that the size of receptor arrays is relatively stable, non-correlated with the protein expression level, and the packing density is slightly varied in difficult growth media. |
| Xin and Othmer [143] | ODE | Model of trimer of dimers; Simulates dynamics for the overall pathway; Explains a line of in vitro kinase activity data on Tar and Tsr [67,104,108,109] and in vivo FRET data in mutant cells [15] with the single trimer without higher-order clusters; Shows enhanced sensitivity and robustness to protein expressions generated by trimer of dimers. |
| Other features | ||
| Rao et al. [138] | ODE | Compares signaling pathways between E. coli and Bacillus subtilis; Shows robust adaptation in both pathways but B. subtilis can perform methylation-independent chemotaxis because of existence of CheV-CheY pathway. |
| Lipkow et al. [135] | spatiotemporal stochastic simulation | 3D stochastic simulation of CheY phosphorylation, CheY/CheYp diffusion, CheYp binding to FliM and dephosphorylation; Studies effects of CheZ localization, motor position, and macromolecular crowding on spatial concentration of CheYp; Shows a constant concentration of CheYp throughout the cytoplasm when CheZ is restricted to anterior ends and an exponential gradient across the length of the cell when CheZ diffuses freely. |
| Lipkow [136] | spatiotemporal stochastic simulation | Studies the effect of CheZ localization; Suggests that clustering of CheZ–CheAs–CheYp at the cell poles, introducing a negative feedback to the CheYp level, serves a secondary adaptation mechanism and explains the overshoot of CheYp in cheRcheB mutant cells. |
| Endres [137] | statistical mechanics | Free energy-based model for formation of clusters of trimer of dimers; Studies the determining factors of the size of polar receptor clusters. |
| Roberts et al. [139] | ODE | Develops a control engineering method and applies it to elucidating the signaling pathways of Rhodobacter sphaeroides chemotaxis. |
| Tindall et al. [140] | ODE | Studies the signal integration mechanism in Rhodobacter sphaeroides chemotaxis. |
| Hamadeh et al. [141] | control theory | Studies the feedback configuration of Rhodobacter sphaeroides; Shows the role of cascade control in achieving robust functions. |
| State | Free-energy Level (unit: kBT) |
|---|---|
| On with 0 ligand bound | |
| On with 1 ligands bound | |
| On with 2 ligands bound | |
| On with 3 ligands bound | |
| Off with 0 ligand bound | Eoff |
| Off with 1 ligands bound | |
| Off with 2 ligands bound | |
| Off with 3 ligands bound | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Othmer, H.G.; Xin, X.; Xue, C. Excitation and Adaptation in Bacteria–a Model Signal Transduction System that Controls Taxis and Spatial Pattern Formation. Int. J. Mol. Sci. 2013, 14, 9205-9248. https://doi.org/10.3390/ijms14059205
Othmer HG, Xin X, Xue C. Excitation and Adaptation in Bacteria–a Model Signal Transduction System that Controls Taxis and Spatial Pattern Formation. International Journal of Molecular Sciences. 2013; 14(5):9205-9248. https://doi.org/10.3390/ijms14059205
Chicago/Turabian StyleOthmer, Hans G., Xiangrong Xin, and Chuan Xue. 2013. "Excitation and Adaptation in Bacteria–a Model Signal Transduction System that Controls Taxis and Spatial Pattern Formation" International Journal of Molecular Sciences 14, no. 5: 9205-9248. https://doi.org/10.3390/ijms14059205
APA StyleOthmer, H. G., Xin, X., & Xue, C. (2013). Excitation and Adaptation in Bacteria–a Model Signal Transduction System that Controls Taxis and Spatial Pattern Formation. International Journal of Molecular Sciences, 14(5), 9205-9248. https://doi.org/10.3390/ijms14059205




