Predicting Retention Times of Naturally Occurring Phenolic Compounds in Reversed-Phase Liquid Chromatography: A Quantitative Structure-Retention Relationship (QSRR) Approach
Abstract
:1. Introduction
2. Results and Discussion
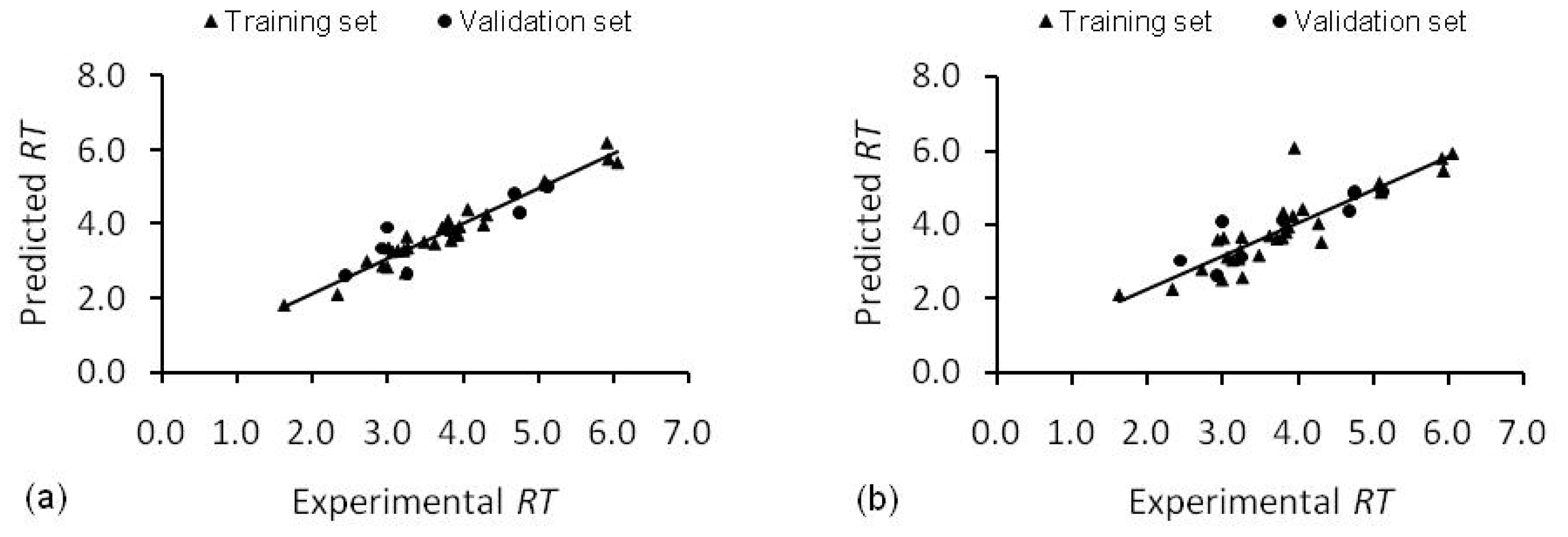
2.1. Stepwise Multiple Linear Regression Model (SMLR Model)
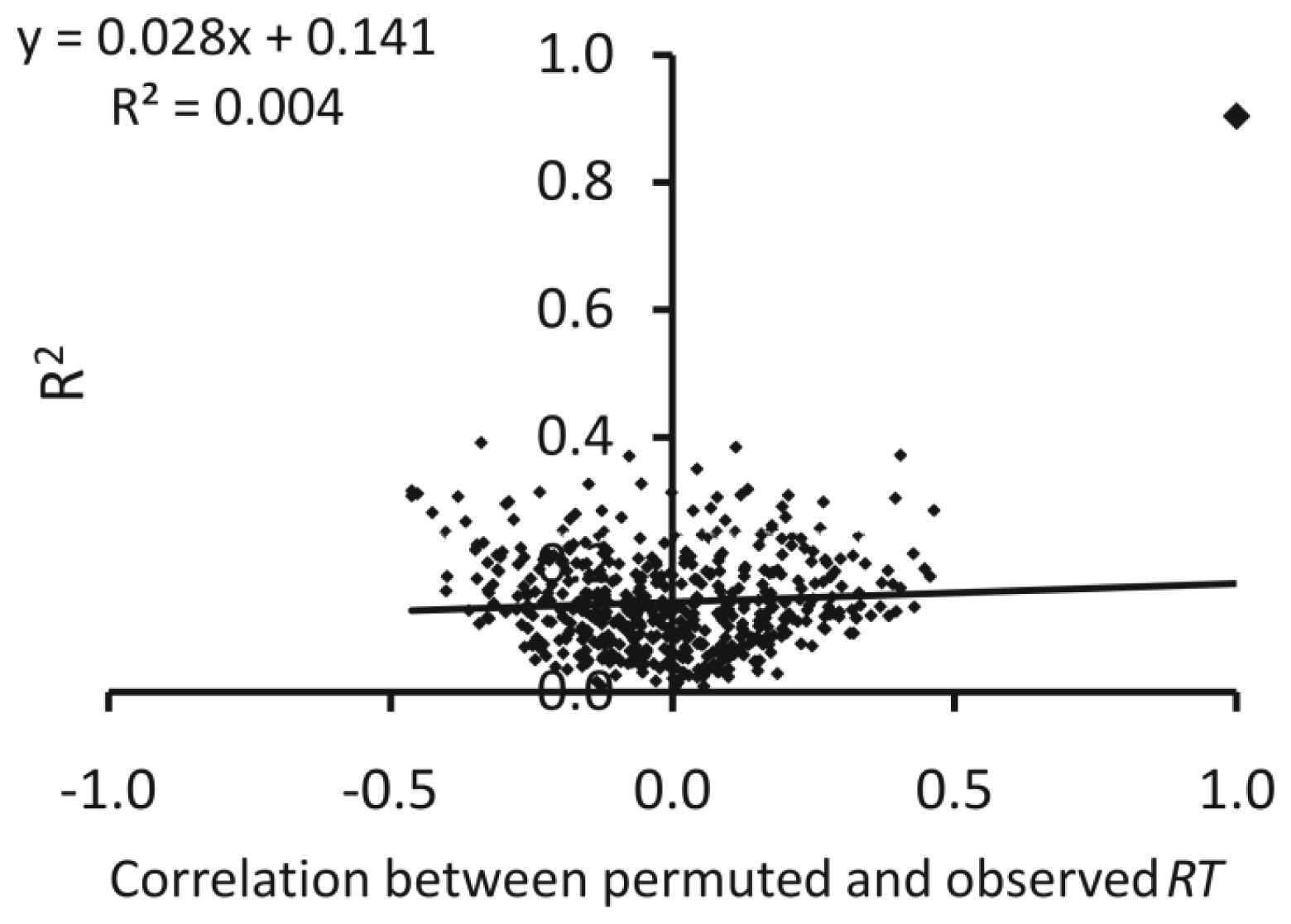
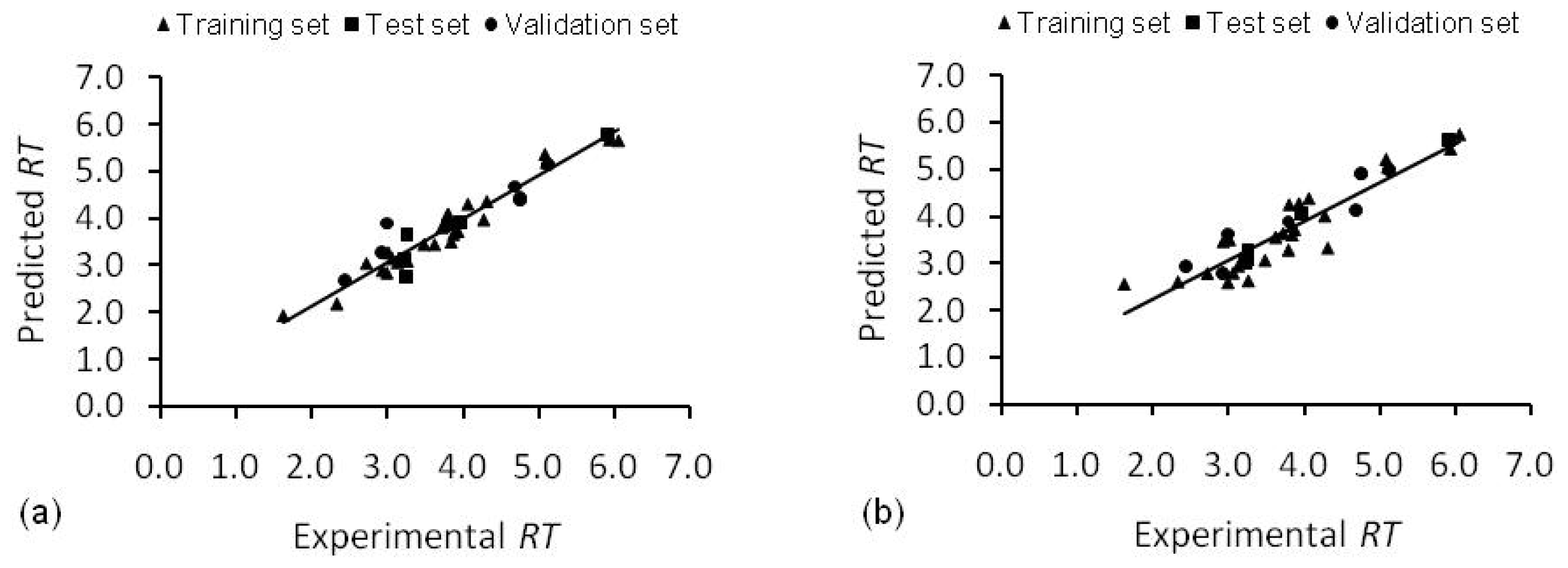
2.2. Artificial Neural Network
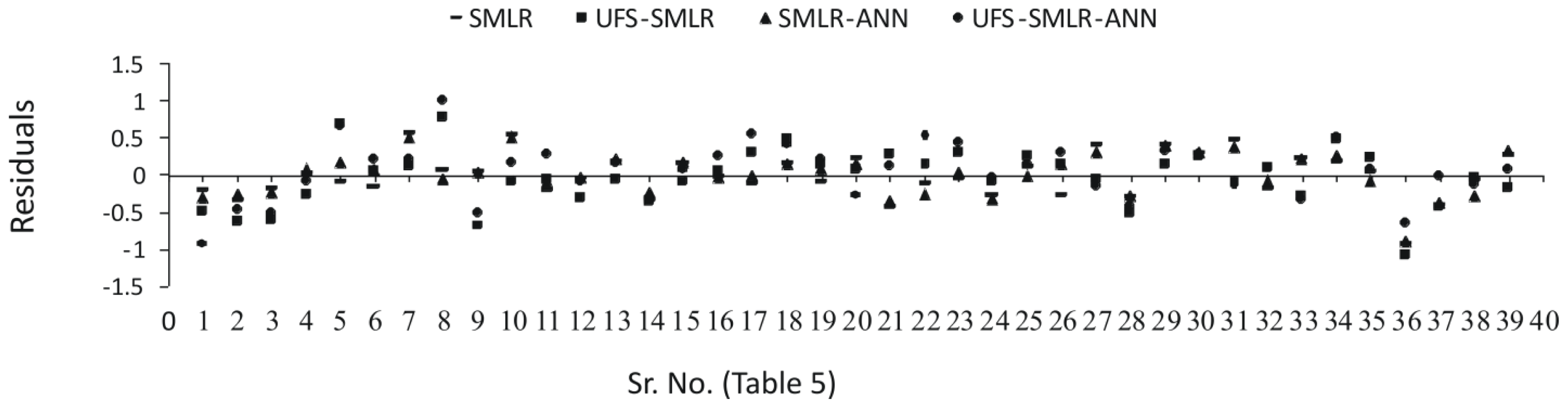
2.3. Interpretation of the Models
3. Experimental Section
3.1. Data for Retention Times of Phenolic Compounds
3.2. Descriptor Computation
3.3. Feature Selection and Model Generation
3.4. Model Validation
4. Conclusions
Supplementary Materials
ijms-13-15387-s001.pdfReferences
- Breinholt, V. Desirable versus Harmful Levels of Intake Offlavonoids and Phenolic Acids; The Royal Society of Chemistry: Cambridge, UK, 1999; pp. 93–105. [Google Scholar]
- Shahidi, F.; Naczk, M. Food Phenolics; Technomic Publishing: Lancaster, PA, USA; p. 1995.
- Naczk, M.; Shahidi, F. Phenolics in cereals, fruits and vegetables: Occurrence, extraction and analysis. J. Pharmaceut. Biomed 2006, 41, 1523–1542. [Google Scholar]
- Iqbal, S.; Younas, U.; Sirajuddin; Chan, K.W.; Sarfraz, R.A.; Uddin, M.K. Proximate composition and antioxidant potential of leaves from three varieties of Mulberry (Morus sp.): A comparative study. Int. J. Mol. Sci 2012, 13, 6651–6664. [Google Scholar]
- Herrmann, K. Ccurrence and content of hydroxycinnamic and hydroxybenzoic acid compounds in foods. Crit. Rev. Food Sci. Nutr 1989, 28, 315–347. [Google Scholar]
- Middleton, E.; Kandaswami, C. The Impact of Plant Flavonoids on Mammalian Biology: Implications for Immunity, Inflammation and Cancer; Chapman and Hall: London, UK; p. 1994.
- Hertog, M.G.L.; Hollman, P.C.H.; Venema, D.P. Optimization of a quantitative HPLC determination of potentially anticarcinogenic flavonoids in vegetables and fruits. J. Agric. Food Chem 1992, 40, 1591–1598. [Google Scholar]
- Kondratyuk, T.P.; Pezzuto, J.M. Natural product polyphenols of relevance to human health. Pharm. Biol 2004, 42, 46–63. [Google Scholar]
- Yao, L.H.; Jiang, Y.M.; Shi, J.; Tomás-Barberán, F.A.; Datta, N.; Singanusong, R.; Chen, S.S. Flavonoids in food and their health benefits. Plant Food Hum. Nutr 2004, 59, 113–122. [Google Scholar]
- Valko, M.; Leibfritz, D.; Moncola, J.; Cronin, M.T.D.; Mazura, M.; Telser, J. Free radicals and antioxidants in normal physiological functions and human disease. Int. J. Biochem. Cell Biol 2007, 39, 44–84. [Google Scholar]
- Scalbert, A.; Manach, C.; Morand, C.; Remesy, C.; Jimenez, L. Dietary polyphenols and the prevention of diseases. Crit. Rev. Food Sci. Nutr 2005, 45, 287–306. [Google Scholar]
- Bonoli, M.; Marconi, E.; Caboni, M.F. Free and bound phenolic compounds in barley (Hordeum vulgare L.) flours: Evaluation of the extraction capability of different solvent mixtures and pressurized liquid methods by micellar electrokinetic chromatography and spectrophotometry. J. Chromatogr. A 2004, 1057, 1–12. [Google Scholar]
- Zhou, Z.; Robards, K.; Helliwell, S.; Blanchard, C. The distribution of phenolic acids in rice. Food Chem 2004, 87, 401–406. [Google Scholar]
- Zadernowski, R.; Kozlowska, H. Phenolic acids in soybean and rapeseed flours. Lebensm. Wiss. Technol 1983, 16, 110–114. [Google Scholar]
- Parr, A.; Ng, A.; Waldron, K. Ester-linked phenolic components of carrot cell walls. J. Agric. Food Chem 1997, 45, 2468–2471. [Google Scholar]
- Amakura, Y.; Okada, M.; Tsuji, S.; Tonogai, Y. Determination of phenolic acids in fruit juices by isocratic column liquid chromatography. J. Chromatogr. A 2000, 891, 183–188. [Google Scholar]
- McKinney, J.D.; Richard, A.; Waller, C.; Newman, M.C.; Gerberick, F. The practice of structure activity relationships (SAR) in toxicology. Toxicol. Sci 2000, 56, 8–17. [Google Scholar]
- Amiri, A.A.; Hemmateenejad, B.; Safavi, A.; Sharghi, H.; Salimi Beni, A.R.; Shamsipur, M. Structure-retention and mobile phase-retention relationships for reversed-phase high-performance liquid chromatography of several hydroxythioxanthone derivatives in binary acetonitrile-water mixtures. Anal. Chim. Acta 2007, 605, 11–19. [Google Scholar]
- Carlucci, G.; D’Archivio, A.A.; Maggi, M.A.; Mazzeo, P.; Ruggieri, F. Investigation of retention behaviour of non-steroidal anti-inflammatory drugs in high-performance liquid chromatography by using quantitative structure-retention relationships. Anal. Chim. Acta 2007, 601, 68–76. [Google Scholar]
- Ma, W.; Luan, F.; Zhang, H.; Zhang, X.; Liua, M.; Hu, Z.; Fan, B. Quantitative structure-property relationships for pesticides in biopartitioning micellar chromatography. Quantitative retention-structure and retention-activity relationships of barbiturates by micellar liquid chromatography. J. Chromatogr. A 2006, 1113, 140–147. [Google Scholar]
- Michel, M.; Baczek, T.; Studzińska, S.; Bodzioch, K.; Jonsson, T.; Kaliszan, R.; Buszewski, B. Comparative evaluation of high-performance liquid chromatography stationary phases used for the separation of peptides in terms of quantitative structure-retention relationships. J. Chromatogr. A 2007, 1175, 49–54. [Google Scholar]
- Fatemia, M.H.; Ghorbanzad’ea, M.; Baher, E. Quantitative structure retention relationship modeling of retention time for some organic pollutants. Anal. Lett 2010, 43, 823–835. [Google Scholar]
- Garkani-Nejad, Z. Quantitative Structure-Retention Relationship Study of Some Phenol Derivatives in Gas Chromatography. J. Chormatogr. Sci 2010, 48, 317–323. [Google Scholar]
- Wei, Y.; Xi, L.; Chen, D.; Wu, X.A.; Liu, H.; Yao, X. Extraction, separation and quantitative structure-retention relationship modeling of essential oils in three herbs. J. Sep. Sci 2010, 33, 1980–1990. [Google Scholar]
- Kaliszan, R. QSRR: Quantitative Structure-(Chromatographic) Retention Relationships. Chem. Rev 2007, 107, 3212–3246. [Google Scholar]
- Kaliszan, R.; Bączek, T. QSAR in Chromatography: Quantitative Structure-Retention Relationships (QSRRs). In Recent Advances in QSAR Studies: Methods and Applications; Puzyn, T., Leszczynski, J., Cronin, M.T., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 223–259. [Google Scholar]
- Gómez-Romero, M.; Zurek, G.; Schneider, B.; Baessmann, C.; Segura-Carretero, A.; Fernández-Gutiérrez, A. Automated identification of phenolics in plant-derived foods by using library search approach. Food Chem 2011, 124, 379–386. [Google Scholar]
- Riahi, S.; Mousavi, M.F.; Shamsipur, M. Prediction of selectivity coefficients of a theophylline-selective electrode using MLR and ANN. Talanta 2006, 69, 736–740. [Google Scholar]
- Fatemi, M.H.; Ghorbannezhad, Z. Estimation of the volume of distribution of some pharmacologically important compounds from their structural descriptors. J. Serb. Chem. Soc 2011, 76, 1003–1014. [Google Scholar]
- Saquib, M.; Gupta, M.K.; Sagar, R.; Prabhakar, Y.S.; Shaw, A.K.; Kumar, R.; Maulik, P.R.; Gaikwad, A.N.; Sinha, S.; Srivastava, A.K.; et al. C-3 alkyl/arylalkyl-2,3-dideoxy hex-2-enopyranosides as antitubercular agents: Synthesis, biological evaluation, and QSAR study. J. Med. Chem 2007, 50, 2942–2950. [Google Scholar]
- Schuur, J.H.; Selzer, P.; Gasteiger, J. The Coding of the Three-Dimensional Structure of Molecules by Molecular Transforms and Its Application to Structure-Spectra Correlations and Studies of Biological Activity. J. Chem. Inf. Comput. Sci 1996, 36, 334–344. [Google Scholar]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors. In Methods and Principles in Medicinal Chemistry; Mannhold, R., Kubinyi, H., Timmerman, H., Eds.; John Wiley and Sons: Weinheim, Germany, 2000; Volume 11. [Google Scholar]
- MOPAC2009; Stewart Computational Chemistry: Colorado Springs, CO, USA, 2009.
- DRAGON Software, version 3; Talete srl: Milano, Italy, 2003.
- Whitley, D.C.; Ford, M.G.; Livingstone, D.J. Unsupervised forward selection: A method for eliminating redundant variables. J. Chem. Inf. Comput. Sci 2000, 40, 1160–1168. [Google Scholar]
- Mittermayr, S.; Olajos, M.; Chovan, T.; Bonn, G.K.; Guttman, A. Mobility modeling of peptides in capillary electrophoresis. Trends Anal. Chem 2008, 27, 407–417. [Google Scholar]
- Yan, A.X.; Hu, Z.D. Linear and non-linear modeling for the investigation of gas chromatography retention indices of alkylbenzenes on cita-4, SE-30 and Carbowax 20M. Anal. Chim. Acta 2001, 433, 145–154. [Google Scholar]
- Wold, S. Validation of QSAR’s. Quant. Struct. Act. Relat 1991, 10, 191–193. [Google Scholar]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The Importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci 2003, 22, 69–77. [Google Scholar]
- Gramatica, P. Principles of QSAR models validation: Internal and external. QSAR Comb. Sci 2007, 26, 694–701. [Google Scholar]
- Hawkins, D.M.; Basak, S.C.; Mills, D. Assessing model fit by cross-validation. J. Chem. Inf. Comput. Sci 2003, 43, 579–586. [Google Scholar]
| Method/Type | Descriptors |
|---|---|
| MOPAC2009/Quantum mechanical | Total energy, electronic energy, core-core repulsion, dielectric energy, dipole moment, ionization energy, energies of highest occupied molecular orbital (EHOMO) and lowest unoccupied molecular orbitals (ELUMO), difference of ELUMO and EHOMO, hardness, softness, molecular mass, cosmo area, cosmo volume. Logarithmic transformations of dipole moment, ionization energy, ELUMO, difference of ELUMO and EHOMO, hardness, softness, molecular mass, cosmo area and cosmo volume. |
| DRAGON/18 blocks of descriptors | Constitutional, topological, molecular walk counts, BCUT, Galvez topological charge indices, 2D autocorrelations, charge descriptors, aromaticity indices, Randic molecular profiles, geometrical, RDF, 3D-MoRSE, WHIM, GETAWAY, functional groups, atom-centered fragments, empirical and properties. |
| HNar | GATS2v | DISPe | Mor32e | Ke | |
|---|---|---|---|---|---|
| HNar | 1.0000 | ||||
| GATS2v | −0.0482 | 1.0000 | |||
| DISPe | 0.1253 | 0.1566 | 1.0000 | ||
| Mor32e | −0.4053 | −0.4069 | 0.0784 | 1.0000 | |
| Ke | 0.4727 | 0.4644 | 0.1360 | −0.3608 | 1.0000 |
| Descriptors | Name | Type |
|---|---|---|
| IDM | Mean information content on the distance magnitude | Topological |
| MATS6p | Moran autocorrelation-lag6/weighted by atomic poloarizabilities | 2D-autocorrelations |
| Mp | Mean atomic polarizability (scaled on carbon atom) | Constitutional |
| E1e | 1st component accessibility directional WHIM index/weighted by atomic Sanderson electronegativities | WHIM |
| MATS6e | Moran autocorrelation-lag6/weighted by atomic Sanderson electronegativities | 2D-autocorrelations |
| Mor30m | 3D-MoRSE-signal 30/weighted by atomic masses | 3D-MoRSE |
| AROM | Aromaticity | Aromatic indices |
| E3u | 3rd component accessibility directional WHIM index/unweighted | WHIM |
| Mor22v | 3D-MoRSE-signal 22/weighted by atomic volume | 3D-MoRSE |
| Mor28e | 3D-MoRSE-signal 28/weighted by atomic Sanderson electronegativities | 3D-MoRSE |
| Mor29m | 3D-MoRSE-signal 29/weighted by atomic masses | 3D-MoRSE |
| DISPm | d COMMA2 value/weighted by atomic masses | Geometrical |
| PJI3 | 3D petijean shape index | Geometrical |
| G3s | 3rd component accessibility directional WHIM index/weighted by atomic electrotopological states | WHIM |
| MATS5e | Moran autocorrelation-lag5/weighted by atomic Sanderson electronegativities | 2D-autocorrelations |
| PJI2 | 2D petijean shape index | Topological |
| SIC4 | Structural information content (neighbourhood symmetry of 4-order) | Topological |
| E2p | 3rd component accessibility directional WHIM index/weighted by atomic poloarizabilities | WHIM |
| Mor12e | 3D-MoRSE-signal 12/weighted by atomic Sanderson electronegativities | 3D-MoRSE |
| IVDE | Mean information content vertex degree equality | Topological |
| SPI | Superpendentic index | Topological |
| HATS7p | Leaverage-weighted autocorrelation of lag 7/weighted by atomic poloarizabilities | GETAWAY |
| SMLR-ANN | UFS-SMLR-ANN | |
|---|---|---|
| No. of neurons in the input layer | 4 | 5 |
| No. of neurons in the hidden layer | 6 | 5 |
| No. of neurons in the output layer | 1 | 1 |
| Hidden weight decay | 0.01 | 0.01 |
| Output weight decay | 0.01 | 0.01 |
| Hidden activation function | Tanh | Exponential |
| Output activation function | Tanh | Logistic |
| PRESSext | 1.4841 | 1.1021 |
| Q2ext | 0.8145 | 0.8622 |
| Training error | 0.0013 | 0.0047 |
| Test error | 0.0021 | 0.0009 |
| Validation error | 0.0042 | 0.0031 |
| Sr No. | Compound | Experimental RT (min) | Predicted RT (min) | |||
|---|---|---|---|---|---|---|
| SMLR | UFS-SMLR | SMLR-ANN | UFS-SMLR-ANN | |||
| 1 | Gallic acid | 1.63 | 1.82 | 2.12 | 1.94 | 2.54 |
| 2 | Gentisic acid | 3.02 | 3.36 | 3.65 | 3.28 | 3.49 |
| 3 | Protocatechuicacid b | 2.43 | 2.61 | 3.04 | 2.67 | 2.94 |
| 4 | Salicylic acid a | 3.96 | 3.93 | 4.23 | 3.89 | 4.04 |
| 5 | Syringic acid | 3.27 | 3.36 | 2.58 | 3.10 | 2.61 |
| 6 | Vanillic acid | 3.14 | 3.29 | 3.05 | 3.07 | 2.93 |
| 7 | 2,4-Dihydroxybenzoic acid b | 3.26 | 2.67 | 3.13 | 2.76 | 3.05 |
| 8 | 3-Methoxybenzoic acid | 4.32 | 4.25 | 3.53 | 4.37 | 3.31 |
| 9 | 4-Hydroxybenzoic acid | 2.94 | 2.88 | 3.60 | 2.90 | 3.45 |
| 10 | Caffeicacid a | 3.24 | 2.69 | 3.31 | 2.74 | 3.08 |
| 11 | Chlorogenic acid | 3.07 | 3.26 | 3.13 | 3.16 | 2.78 |
| 12 | Ferulicacid b | 3.80 | 3.84 | 4.11 | 3.84 | 3.89 |
| 13 | m-Coumaric acid | 3.88 | 3.69 | 3.94 | 3.67 | 3.71 |
| 14 | o-Coumaric acid | 4.07 | 4.39 | 4.42 | 4.31 | 4.37 |
| 15 | p-Coumaric acid | 3.63 | 3.47 | 3.70 | 3.45 | 3.54 |
| 16 | Sinapic acid | 3.85 | 3.86 | 3.80 | 3.89 | 3.59 |
| 17 | trans-Cinnamicacid b | 4.69 | 4.80 | 4.38 | 4.69 | 4.14 |
| 18 | Dihydrocaffeic acid | 3.00 | 2.84 | 2.52 | 2.85 | 2.57 |
| 19 | Homovanillicacid a | 3.22 | 3.29 | 3.08 | 3.14 | 3.00 |
| 20 | DOPAC | 2.34 | 2.11 | 2.27 | 2.19 | 2.59 |
| 21 | 4-hydroxyphenylacetic acid b | 2.92 | 3.34 | 2.64 | 3.28 | 2.79 |
| 22 | Ellagic acid | 3.80 | 3.90 | 3.65 | 4.07 | 3.27 |
| 23 | Vanillin | 3.49 | 3.52 | 3.18 | 3.45 | 3.05 |
| 24 | Tyrosol | 2.73 | 3.00 | 2.80 | 3.05 | 2.77 |
| 25 | Apigenin b | 5.14 | 5.01 | 4.88 | 5.16 | 4.99 |
| 26 | Chrysin a | 5.92 | 6.18 | 5.78 | 5.77 | 5.62 |
| 27 | Luteolin b | 4.76 | 4.33 | 4.82 | 4.45 | 4.90 |
| 28 | Luteolin-7-O-glucoside | 3.81 | 4.10 | 4.32 | 4.10 | 4.24 |
| 29 | Kaempferide | 6.06 | 5.65 | 5.91 | 5.66 | 5.74 |
| 30 | Myricetin | 4.28 | 3.98 | 4.03 | 3.98 | 4.00 |
| 31 | Quercetin b | 4.76 | 4.28 | 4.87 | 4.39 | 4.89 |
| 32 | Rutin | 3.73 | 3.91 | 3.62 | 3.82 | 3.62 |
| 33 | Hesperidin | 3.94 | 3.71 | 4.23 | 3.73 | 4.26 |
| 34 | Isosakuranetin | 5.94 | 5.74 | 5.45 | 5.68 | 5.43 |
| 35 | Naringenin | 5.11 | 5.05 | 4.87 | 5.20 | 5.04 |
| 36 | (+)-Catechin b | 2.99 | 3.91 | 4.07 | 3.89 | 3.63 |
| 37 | (−)-Epicatechin a | 3.26 | 3.66 | 3.67 | 3.63 | 3.28 |
| 38 | Genistein | 5.09 | 5.15 | 5.12 | 5.37 | 5.21 |
| 39 | (+)-Taxifolin | 3.85 | 3.57 | 4.02 | 3.51 | 3.78 |
© 2012 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Akbar, J.; Iqbal, S.; Batool, F.; Karim, A.; Chan, K.W. Predicting Retention Times of Naturally Occurring Phenolic Compounds in Reversed-Phase Liquid Chromatography: A Quantitative Structure-Retention Relationship (QSRR) Approach. Int. J. Mol. Sci. 2012, 13, 15387-15400. https://doi.org/10.3390/ijms131115387
Akbar J, Iqbal S, Batool F, Karim A, Chan KW. Predicting Retention Times of Naturally Occurring Phenolic Compounds in Reversed-Phase Liquid Chromatography: A Quantitative Structure-Retention Relationship (QSRR) Approach. International Journal of Molecular Sciences. 2012; 13(11):15387-15400. https://doi.org/10.3390/ijms131115387
Chicago/Turabian StyleAkbar, Jamshed, Shahid Iqbal, Fozia Batool, Abdul Karim, and Kim Wei Chan. 2012. "Predicting Retention Times of Naturally Occurring Phenolic Compounds in Reversed-Phase Liquid Chromatography: A Quantitative Structure-Retention Relationship (QSRR) Approach" International Journal of Molecular Sciences 13, no. 11: 15387-15400. https://doi.org/10.3390/ijms131115387
APA StyleAkbar, J., Iqbal, S., Batool, F., Karim, A., & Chan, K. W. (2012). Predicting Retention Times of Naturally Occurring Phenolic Compounds in Reversed-Phase Liquid Chromatography: A Quantitative Structure-Retention Relationship (QSRR) Approach. International Journal of Molecular Sciences, 13(11), 15387-15400. https://doi.org/10.3390/ijms131115387




