Köln-Timişoara Molecular Activity Combined Models toward Interspecies Toxicity Assessment
Abstract
:1. Introduction
2. Background Models
2.1. Köln ESIP Model for Biological Activity
- the toxicity of a compound can be subdivided into that of components (ESIP’s) in such a way that the sum of these components results in the total toxicity value;
- these components (ESIP’s) are identical in different substances;
- the ESIP’s components have a dynamical value (they depend on the determined number or are derived from newly available data) for one organism and a test-system, while varying for different test-systems. However, if a deviation between the measured M and the calculated C values is observed, there is an indication of an overlooked interaction between different parts of the molecule, or may indicate an activity of a substance specific for a certain biochemical pathway.
2.2. Timişoara Spectral-SAR Model
- ○ Any molecular structural state (dynamical, since undergoes interactions with organisms) may be represented by a | ket〉 state vector, in the abstract Hilbert space, following the 〈bra | ket〉 Dirac formalism [14]; such states are to be represented by any reliable molecular index, or, in particular in our study by hydrophobicity |LogP〉, polarizability |POL〉, and total optimized energy |Etot〉, just to be restrained only the so called Hansch parameters, usually employed for accounting the diffusion, electrostatic and steric effects for molecules acting on organisms’ cells, respectively.
- ○ The (quantum) superposition principle assuring that the various linear combinations of molecular states map onto the resulting state, here interpreted as the bio-, eco- or toxico-logical activity, e.g., |Y〉 = |Y0〉 +CLogP |LogP〉 +CPOL |POL〉 +..., with |Y0〉 meaning the free or unperturbed activity (when all other influences are absent).
- ○ The orthogonalization feature of quantum states, a crucial condition providing that the superimposed molecular states generates new molecular state (here quantified as the organism activity); analytically, the orthogonalization condition is represented by the 〈bra | ket〉 scalar product of two envisaged states (molecular indices); if it is evaluated to zero value, i.e., 〈bra | ket〉 = 0, then the convoluted states are said to be orthogonal (zero-overlapping) and the associate molecular descriptors are considered as independent, therefore suitable to be assumed as eigen-states (of a spectral decomposition) in the resulted activity state, while quantified by the degree their molecular indices enter the activity correlation. Further details on scalar product and related properties are given in Appendix A1, whereas in what follows the Spectral-based SAR correlation method (thereby called as Spectral-SAR) is resumed.
3. Spectral-SAR Results
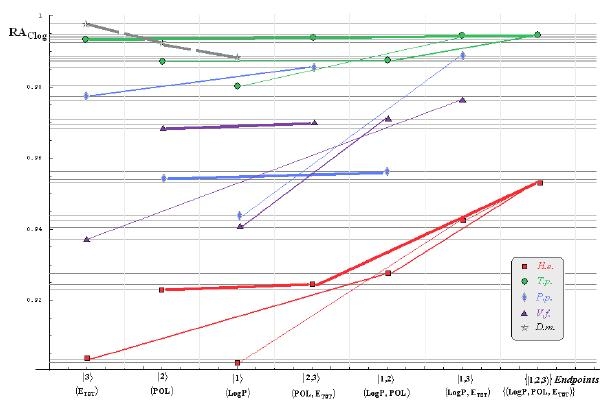
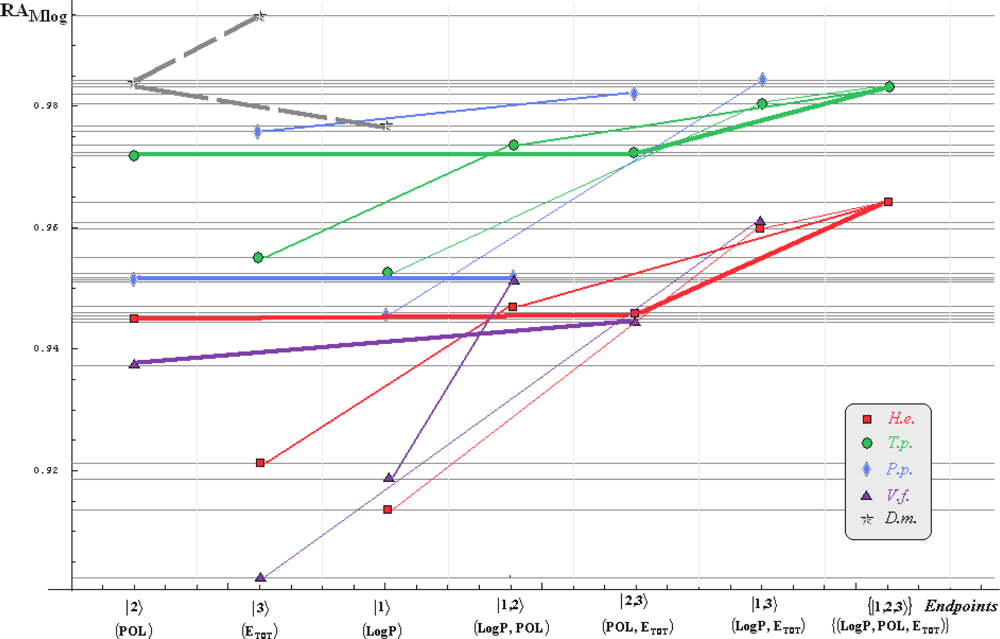
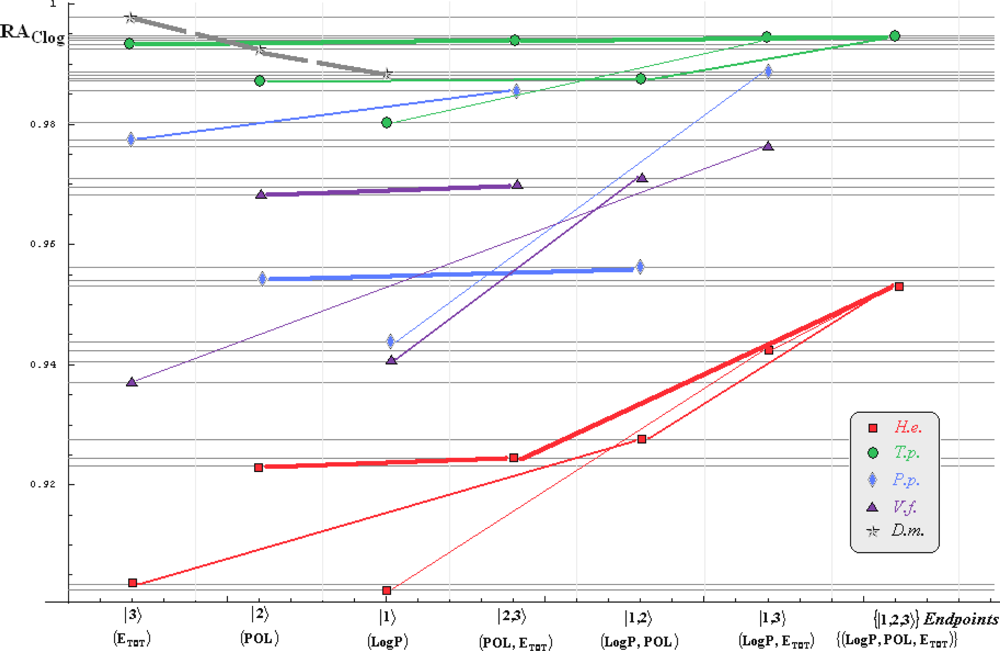
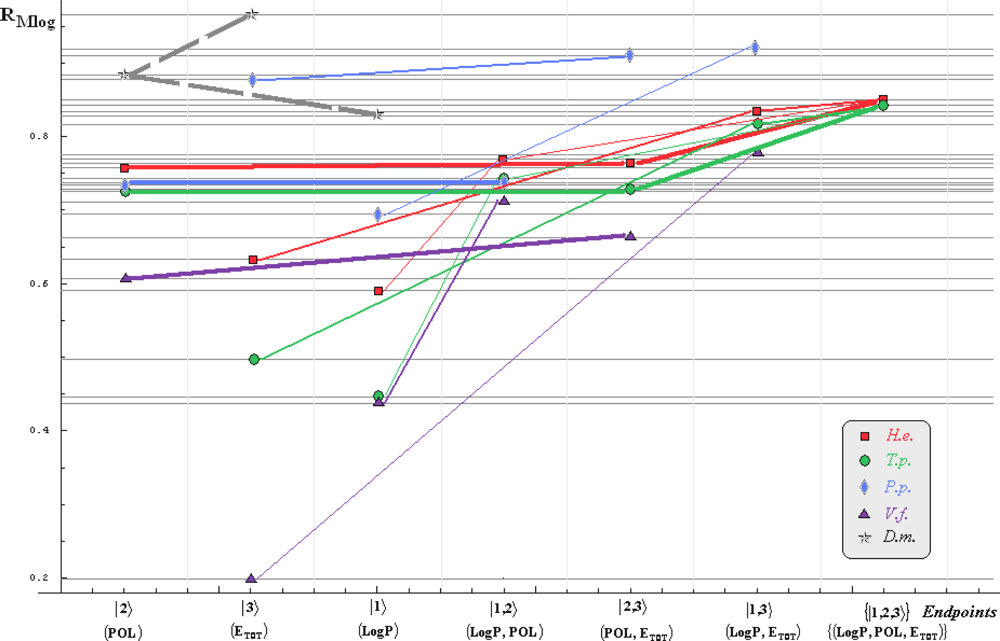
- if the overall minimum is reached by many equivalent paths (as is the case of Mlog-algebraic column for H.e. in Table 5, for instance) the minimum path will be considered that one connecting the starting endpoint with the closest endpoint in the sense of norms (as is for H.e./ Mlog the norm of |2> state the closest to the norm of |2,3> state, as compared with |1,2> and |1,3>, see Spectral-SAR norm column of Table 3, for example);
- the overall minimum path will set the dominant hierarchical path in assessing the mechanistically mode of action towards the given/measured activity; it is called as the alpha path (α);
- once the alpha path has been set the next minimum path will be looked for in such a way that the new starting endpoint is different from that one already involved in the alpha path (that is, if in the established alpha path for H.e./ Mlog the starting model correspond to the |2> state, the next path to be identified will originate either on models/states |1> or |3>);
- the remaining minimum paths are identified on the same rules as before and will be called like beta and gamma paths, β and γ, respectively;
- at the end of this procedure each mode of action is to be “touched” only one, excepting the final endpoint state {|1,2,3>} that can present degeneracy, i.e., may be found with the same influence at the end of various paths, herein called as degenerate paths (e.g., the states |1,2,3>, |2,1,3>, and |3,1,2> in the case of Hydractinia echinata and Tetrahymena pyriformis at their ending toxicity paths of Table 5); Yet, such behavior may leave with the important idea the degenerate paths, although different in the start and intermediate states, while ending with the same ordering influences, e.g., the state |2,1,3> of Table 5 (with “1” for LogP, “2” for POL, and “3” for Etot, see Tables 3 and 4), provides weaker contribution to the recorder activity since two paths have to produce the same (final) effect in order it to be activated; this is nevertheless one remarkable mechanistic consequence of the present combined (algebraic or statistical) correlations with minimization (optimization) principle applied for the spectral path lengths through Equations (6)–(10);
- the alpha, beta and gamma paths can be easily identified for algebraic and statistical treatments in Tables 5 and 6 and there are accordingly marked; the degeneracy behavior is readily verified in Table 5 where the alpha path is found as the only (non-degenerate) path out of all possible ones. Of course, the same rationalization applies also for alpha path of Table 6, however displaying the trivial situation in which the absence of any degeneracy is recorded due to the restrained structural parameters considered for activity modeling since less available data for Pimephales promelas (P.p.) and Vibrio fisheri (V.f.) species in Table 2, according with the above specified Topliss-Costello rule.
- h) models with higher correlation/probability (either within statistic or algebraic approaches) will firstly enter molecular mechanism of toxicity through their considered structural parameter, i.e., LogP, POL and Etot for the |1>, |2> and |3> end-points, respectively.
4. Discussion of ESIP
5. Conclusions and Outlook
Appendix
A1. Vectorial Scalar Product, Norms, and Cauchy-Schwarz Inequality
A2. Algebraic Correlation Factor
Acknowledgments
References
- Corvini, PFX; Vinken, R; Hommes, G; Schmidt, B; Dohmann, M. Degradation of the radioactive and non-labelled branched 4(3′,5′-dimethyl-3′-heptyl)-phenol nonylphenol isomer by SphingomonasSphingomonas TTNP3. Biodegradation 2004, 15, 9–18. [Google Scholar]
- Schwitzguebel, J-P; Aubert, S; Grosse, W; Laturnus, F. Sulphonated aromatic pollutants: Limits of microbial degradability and potential of phytoremediation. Environ. Sci. Pollut. Res 2002, 9, 62–72. [Google Scholar]
- Berking, S. Effects of the anticonvulsant drug valproic acid and related substances on developmental processes in hydroids. Toxic. in Vitro 1991, 5, 109–117. [Google Scholar]
- Chicu, SA; Berking, S. Interference with metamorphosis induction in the marine cnidaria Hydractinia echinata (hydrozoa): A structure-activity relationship analysis of lower alcohols, aliphatic and aromatic hydrocarbons, thiophenes, tributyl tin and crude oil. Chemosphere 1997, 34, 1851–1866. [Google Scholar]
- Chicu, SA; Herrmann, K; Berking, S. An approach to calculate the toxicity of simple organic molecules on the basis of QSAR analysis in Hydractinia echinata (Hydrozoa, Cnidaria). Quant. Struct.-Act. Relat 2000, 19, 227–236. [Google Scholar]
- Chicu, SA; Simu, GM. Hydractinia echinata test system. I. Toxicity determination of some benzenic, biphenilic and naphthalenic phenols. Comparative SAR-QSAR study. Rev Roum Chim 2009, 8. [Google Scholar]
- Putz, MV; Lacrămă, AM. Introducing Spectral Structure Activity Relationship (S-SAR) analysis. Application to ecotoxicology. Int. J. Mol. Sci 2007, 8, 363–391. [Google Scholar]
- Putz, MV; Lacrămă, AM; Ostafe, V. Spectral-SAR ecotoxicology of ionic liquids. The Daphnia magna Case. Res Lett Ecol 2007. [Google Scholar]
- Lacrămă, AM; Putz, MV; Ostafe, V. A Spectral-SAR Model for the anionic-cationic interaction in ionic liquids: Application to Vibrio fischeri ecotoxicity. Int. J. Mol. Sci 2007, 8, 842–863. [Google Scholar]
- Putz, MV; Putz, AM; Lazea, M; Ienciu, L; Chiriac, A. Quantum-SAR extension of the Spectral-SAR Algorithm. Application to polyphenolic anticancer bioactivity. Int. J. Mol. Sci 2009, 10, 1193–1214. [Google Scholar]
- Cronin, MTD; Netzeva, TI; Dearden, JC; Edwards, R; Worgan, ADP. Assessment and modeling of toxicity of organic chemicals to Chlorella vulgaris: Development of a novel database. Chem. Res. Toxicol 2004, 17, 545–554. [Google Scholar]
- Cronin, MTD; Dearden, J. QSAR in toxicology. 2. Prediction of acute mammalian toxicity and interspecies correlations. Quant. Struct.-Act. Relat 1995, 14, 117–120. [Google Scholar]
- Cronin, MTD; Worth, AP. (Q)SARs for predicting effects relating to reproductive toxicity. QSAR Comb. Sci 2008, 27, 91–100. [Google Scholar]
- Dirac, PAM. The Principles of Quantum Mechanics; Oxford University Press: Oxford, UK, 1944. [Google Scholar]
- Randić, M. Orthogonal molecular descriptors. New J. Chem 1991, 15, 517–525. [Google Scholar]
- Klein, DJ; Randić, M; Babić, D; Lučić, B; Nikolić, S; Trinajstić, N. Hierarchical orthogonalization of descriptors. Int. J. Quantum Chem 1997, 63, 215–222. [Google Scholar]
- Fernández, FM; Duchowicz, PR; Castro, EA. About orthogonal descriptors in QSPR/QSAR theories. MATCH Commun. Math. Comput. Chem 2004, 51, 39–57. [Google Scholar]
- Steen, LA. Highlights in the history of spectral theory. Amer. Math. Monthly 1973, 80, 359–381. [Google Scholar]
- Siegmund-Schultze, R. Der Beweis des Hilbert-Schmidt Theorem. Arch. Hist. Ex. Sc 1986, 36, 251–270. [Google Scholar]
- Chaterjee, S; Hadi, AS; Price, B. Regression Analysis by Examples, 3rd ed; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Putz, MV; Putz, AM. Timişoara Spectral – Structure Activity Relationship (Spectral-SAR) algorithm: From statistical and algebraic fundamentals to quantum consequences. In Quantum Frontiers of Atoms and Molecules; Putz, MV, Ed.; NOVA Publishers, Inc.: New York, NY, USA, 2010. [Google Scholar]
- Putz, MV; Duda-Seiman, C; Duda-Seiman, DM; Putz, A-M. Turning SPECTRAL-SAR into 3D-QSAR analysis. Application on H+K+-ATPase inhibitory activity. Int. J. Chem. Mod 2008, 1, 45–62. [Google Scholar]
- Lacrămă, A-M; Putz, MV; Ostafe, V. Designing a Spectral Structure-Activity ecotoxicologistical battery. In Advances in Quantum Chemical Bonding Structures; Putz, MV, Ed.; Transworld Research Network: Kerala, India, 2008; Chapter 16pp. 389–419. [Google Scholar]
- Putz, MV; Putz, A-M; Lazea, M; Chiriac, A. Spectral vs. statistic approach of structure-activity relationship. Application on ecotoxicity of aliphatic amines. J Theor Comput Chem 2009. [Google Scholar]
- Topliss, JG; Costello, RJ. Chance Correlation in Structure-Activity studies using multiple regression analysis. J. Med. Chem 1972, 15, 1066–1068. [Google Scholar]
- Hypercube, Inc. HyperChem 701, Program package, Semiempirical, AM1, Polak-Ribier optimization procedure, 2002.
- Hansch, C; Zhang, L. Comparative QSAR: Radical toxicity and scavenging. Two different sides of the same coin. SAR. QSAR. Environ. Res 1995, 4, 73–82. [Google Scholar]
- Baratt, MD. Prediction of toxicity from chemical structure. Cell Biol. Toxicol 2000, 16, 1–13. [Google Scholar]
- Bassan, A; Worth, AP. The integrated use of models for the properties and effects of chemicals by means of a structured workflow. QSAR Comb. Sci 2008, 27, 6–20. [Google Scholar]

| Activity | Structural predictor variables | |||||
|---|---|---|---|---|---|---|
| |YOBS (ERVED)〉 | |X0〉 | |X1〉 | … | |Xk〉 | … | |XM〉 |
| y1-OBS | 1 | x11 | … | x1k | … | x1M |
| y2-OBS | 1 | x21 | … | x2k | … | x2M |
| … | … | … | … | … | … | … |
| yN-OBS | 1 | xN1 | … | xNk | … | xNM |
| No. | Compound | Species Toxicities |Y> | Structural parameters | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hydractinia echinata | Tetrahymena pyriformis | Pimephales promelas | Vibrio fischeri | Daphnia magna | |X1> =Log P | |X2> =POL (A3) | |X3>=Etot (kcal/mol) | |||||||
| Mlog | Clog | Mlog | Clog | Mlog | Clog | Mlog | Clog | Mlog | Clog | |||||
| 1 | Water | −1.23 | −0.91 | −0.51 | 1.41 | −8038.2 | ||||||||
| 2 | Methanol | −0.22 | −0.41 | 0.33 | 0.15 | 0.04 | 0.24 | −0.27 | 3.25 | −11622.9 | ||||
| 3 | Ethanol | 0.02 | 0.09 | 0.59 | 0.60 | 0.51 | 0.74 | 0.11 | 1.11 | 0.93 | 0.25 | 0.08 | 5.08 | −15215.4 |
| 4 | 1-Butanol | 0.99 | 1.08 | 1.48 | 1.50 | 1.63 | 1.73 | 1.34 | 2.18 | 1.57 | 1.68 | 0.94 | 8.75 | −22402.8 |
| 5 | 1,2,3-Propanetriol | 0.34 | 0.37 | −1.08 | 8.19 | −33600. | ||||||||
| 6 | Triphenylmethanol | 5.69 | 5.27 | 4.87 | 32.23 | −68532.5 | ||||||||
| 7 | 1,10-Diaminodecane | 3.26 | 2.91 | 1.48 | 21.83 | −46754.2 | ||||||||
| 8 | 2-Benzylpyridine | 3.75 | 3.46 | 3.41 | 4.85 | 3.53 | 21.22 | −43675.3 | ||||||
| 9 | 4-Benzylpyridine | 4.08 | 3.46 | 3.68 | 4.85 | 3.75 | 21.22 | −43676.8 | ||||||
| 10 | 4-Phenylpyridin | 4.13 | 3.46 | 3.66 | 3.46 | 3.98 | 3.81 | 4.91 | 4.84 | 3.35 | 19.38 | −40083.1 | ||
| 11 | 4-Toluidine | 2.85 | 2.02 | 2.98 | 2.81 | 3.43 | 3.26 | 1.73 | 13.62 | −28300.3 | ||||
| 12 | 1,2-Dichlorobenzene | 3.04 | 3.45 | 4.00 | 3.66 | 4.19 | 4.17 | 3.08 | 14.29 | −36217.2 | ||||
| 13 | Phenol(3,15/2,66/2,85)* | 2.89* | 2.87 | 2.79 | 2.58 | 3.41 | 3.21 | 3.42 | 3.68 | 3.32 | 3.32 | 1.76 | 11.07 | −27003.1 |
| 14 | 2-Methylphenol(3,18/3,24)* | 3.21* | 2.82 | 2.72 | 2.58 | 3.77 | 3.21 | 3.75 | 3.68 | 3.64 | 3.32 | 2.23 | 12.91 | −30596.6 |
| 15 | 2,4,6-Trimethyphenol(3,19/4,00)* | 3.60* | 3.82 | 3.42 | 3.48 | 4.02 | 4.21 | 4.08 | 4.75 | 4.49 | 4.75 | 3.16 | 16.58 | −37783.7 |
| 16 | 1,2-Dihydroxibenzene | 5.11 | 5.11 | 3.75 | 3.47 | 4.08 | 4.08 | 3.54 | 3.54 | 4.68 | 4.24 | 1.48 | 11.71 | −34396.4 |
| 17 | 2-Methoxyphenol(2,89/2,77)* | 2.83* | 3.28 | 2.49 | 2.54 | 3.29 | 1.51 | 13.54 | −37974.4 | |||||
| 18 | 1,4-Dihydroxybenzene(6,14/6,06)* | 6.10* | 6.10 | 3.47 | 3.59 | 6.40 | 6.40 | 6.42 | 6.42 | 1.48 | 11.71 | −34395.8 | ||
| 19 | t-Butylhydroquinone(5,05/5,00)* | 5.30* | 7.60 | 4.94 | 7.78 | 8.03 | 3.11 | 19.05 | −48758.1 | |||||
| 20 | 1,2,3-Trihydroxibenzene | 5.15 | 5.15 | 3.85 | 3.65 | 1.19 | 12.35 | −41789.9 | ||||||
| 21 | 4(3',5'-dimethyl--3'-heptyl) phenol | 7.65 | 6.81 | 4.87 | 25.75 | −55742. | ||||||||
| 22 | 4-Chlorophenol | 3.25 | 3.04 | 3.55 | 3.56 | 4.18 | 3.66 | 4.19 | 3.88 | 4.13 | 3.95 | 2.28 | 13 | −35307.6 |
| 23 | 2,6-Diisopropylphenol | 3.73 | 5.31 | 4.82 | 5.21 | 6.36 | 6.90 | 4.15 | 22.08 | −48554.7 | ||||
| 24 | 2-Aminophenol | 3.15 | 3.04 | 3.94 | 2.93 | 0.98 | 12.42 | −32098.6 | ||||||
| 25 | 2,4,6-Trinitrophenol | 2.92 | 2.99 | 2.84 | 2.63 | 3.77 | −4.17 | 16.59 | −84472.1 | |||||
| 26 | Chloranil | 5.15 | − | 1.12 | 18.51 | −66928.2 | ||||||||
| 27 | Chloranilic acid | 3.40 | 2.99 | −0.48 | 15.93 | −65113.6 | ||||||||
| 28 | 4-Methoxyazobenzene | 5.20 | 3.70 | 4.10 | 24.63 | −59069.5 | ||||||||
| Mlog Model | Species | Spectral-SAR Activity Equation | Spectral-SAR Norm | RA (Algebraic) | R (Statistic) |
|---|---|---|---|---|---|
| |1> | H.e. | |YH.e|1>〉 = 2.348 + 0.595 |LogP> | 19.0572 | 0.9138 | 0.5912 |
| T.p. | |YT.p|1>〉 = 2.526+0.267 |LogP> | 12.642 | 0.9521 | 0.4446 | |
| P.p. | |YP.p|1>〉 = 1.402 +1.071 |LogP> | 12.1481 | 0.9453 | 0.6972 | |
| V.f. | |YV.f|1>〉 = 2.981 + 0.364 |LogP> | 11.1235 | 0.9189 | 0.4396 | |
| D.m. | |YD.m|1>〉 = 1.192 + 1.208 |LogP> | 9.09749 | 0.9769 | 0.8300 | |
| |2> | H.e. | |YH.e|2>〉 = 0.022 + 0.221 |POL> | 19.7048 | 0.9449 | 0.7597 |
| T.p. | |YT.p|2>〉 = 0.72 + 0.168 |POL> | 12.9074 | 0.9721 | 0.7267 | |
| P.p. | |YP.p|2>〉 = −0.109 + 0.29 |POL> | 12.2254 | 0.9513 | 0.7357 | |
| V.f. | |YV.f|2>〉 = 0.121 + 0.262 |POL> | 11.3472 | 0.9374 | 0.6092 | |
| D.m. | |YD.m|2>〉 = −0.759 + 0.355 |POL> | 9.16099 | 0.9837 | 0.8832 | |
| |3> | H.e. | |YH.e.|3>〉 = 0.433 –0.00007 |Etot > | 19.2139 | 0.9213 | 0.6355 |
| T.p. | |YT.p|3>〉 = 1.669 –3.6·10−5 |Etot > | 12.6819 | 0.9551 | 0.4969 | |
| P.p. | |YP.p.|3>〉 = –1.767 – 1.7·10−4 |Etot > | 12.5439 | 0.9761 | 0.8785 | |
| V.f. | |YV.f.|3>〉 = 2.755 – 1.89·10−5|Etot > | 10.926 | 0.9026 | 0.1982 | |
| D.m. | |YD.m|3>〉 = −1.826 –1.75·10−4 |Etot > | 9.26686 | 0.9951 | 0.9662 | |
| |1,2> | H.e. | |YH.e|1,2>〉 = 0.206 + 0.163|LogP> +0.19 |POL> | 19.7462 | 0.9468 | 0.7694 |
| T.p. | |YT.p|1,2>〉 = 0.784 +0.093|LogP> +0.152 |POL> | 12.9228 | 0.9733 | 0.7398 | |
| P.p. | |YP.p|1,2>〉 = −0.324 –0.191|LogP> + 0.337 |POL> | 12.2271 | 0.9514 | 0.7365 | |
| V.f. | |YV.f.|1,2>〉 = −0.018 + 0.307|LogP> + 0.242 |POL> | 11.5146 | 0.9512 | 0.7116 | |
| |1,3> | H.e. | |YH.e|1,3>〉 = −0.296 + 0.541|LogP> – 0.00007 |Etot > | 20.0182 | 0.9599 | 0.8307 |
| T.p. | |YT.p.|1,3>〉 = 0.433 + 0.413| LogP> – 5.27·10−5 |Etot > | 13.018 | 0.9805 | 0.8171 | |
| P.p. | |YP.p|1,3>〉 = −3.541 −1.061|LogP> −2.96·10−4 |Etot > | 12.646 | 0.9840 | 0.9203 | |
| V.f. | |YV.f.|1,3>〉 = −0.512 +0.82 |LogP> −8.1·10−5 |Etot > | 11.6329 | 0.9610 | 0.7767 | |
| |2,3> | H.e. | |YH.e.|2,3>〉 = −0.134 + 0.193|POL> – 0.00001 |Etot > | 19.7224 | 0.9457 | 0.7638 |
| T.p. | |YT.p.|2,3>〉 = 0.704 +0.163 |POL> – 2.18·10−6 |Etot > | 12.9078 | 0.9722 | 0.7270 | |
| P.p. | |YP.p.|2,3>〉 = −2.269 −0.262|POL> −2.94·10−4 |Etot > | 12.6208 | 0.9820 | 0.9101 | |
| V.f. | |YV.f.|2,3>〉 = 0.082 + 0.36 |POL> +3.35〉10−5 |Etot > | 11.4347 | 0.9446 | 0.6645 | |
| {|1,2,3>} | H.e. | |YH.e{|1,2,3>}〉 = −0.259 + 0.979|LogP> −0.214|POL> −0.00013|Etot > | 20.1085 | 0.9642 | 0.8502 |
| T.p. | |YT.p{|1,2,3>}〉 = 0.456 + 0.773 |LogP> −0.185|POL> −0.00011|Etot > | 13.0541 | 0.9832 | 0.8447 | |
| Clog Model | Species | Spectral-SAR Activity Equation | Spectral-SAR Norm | RA (Algebraic) | R (Statistic) |
|---|---|---|---|---|---|
| |1> | H.e. | |YH.e|1>〉 = 2.242 + 0.583 |LogP> | 18.1498 | 0.9027 | 0.5744 |
| T.p. | |YT.p|1>〉 = 1.248+ 0.919 |LogP> | 14.6075 | 0.9805 | 0.8572 | |
| P.p. | |YP.p|1>〉 = 1.436 + 1.107 |LogP> | 14.7182 | 0.9439 | 0.7011 | |
| V.f. | |YV.f|1>〉 = 3.598 + 0.41 |LogP> | 15.6785 | 0.9406 | 0.4605 | |
| D.m. | |YD.m|1>〉 = 0.57 + 1.483 |LogP> | 11.2079 | 0.9880 | 0.9432 | |
| |2> | H.e. | |YH.e|2>〉 = 0.242 + 0.201 |POL> | 18.5655 | 0.9234 | 0.6831 |
| T.p. | |YT.p|2>〉 = –0.118 + 0.237 |POL> | 14.7122 | 0.9875 | 0.9108 | |
| P.p. | |YP.p|2>〉 = –0.092 + 0.29 |POL> | 14.871 | 0.9537 | 0.7604 | |
| V.f. | |YV.f|2>〉 = 0.111 + 0.298 |POL> | 16.1385 | 0.9682 | 0.7565 | |
| D.m. | |YD.m|2>〉 = –1.241 + 0.379 |POL> | 11.2605 | 0.9927 | 0.9655 | |
| |3> | H.e. | |YH.e|3>〉 = 0.518 – 0.00007 |Etot > | 18.16 | 0.9033 | 0.5773 |
| T.p. | |YT.p|3>〉 = –1.176 –1.27·10−4 |Etot > | 14.8013 | 0.9935 | 0.9544 | |
| P.p. | |YP.p|3>〉 = –1.597 – 1.64·10−4 |Etot > | 15.2359 | 0.9771 | 0.8882 | |
| V.f. | |YV.f.|3>〉 = 2.546 – 4.51·10−5 |Etot > | 15.6221 | 0.9372 | 0.4106 | |
| D.m. | |YD.m|3>〉 = –2.546 –1.94·10−4 |Etot > | 11.3184 | 0.9978 | 0.9896 | |
| |1,2> | H.e. | |YH.e|1,2>〉 = 0.488 + 0.217 |LogP> + 0.16 |POL> | 18.6415 | 0.9272 | 0.7014 |
| T.p. | |YT.p|1,2>〉 = –0.208 – 0.081|LogP> + 0.255 |POL> | 14.7128 | 0.9875 | 0.9112 | |
| P.p. | |YP.p.|1,2>〉 = –1.038 – 0.931|LogP> + 0.509 |POL> | 14.908 | 0.9561 | 0.7742 | |
| V.f. | |YV.f.|1,2>〉 = 0.228 + 0.188 |LogP> + 0.268 |POL> | 16.187 | 0.9711 | 0.7816 | |
| |1,3> | H.e. | |YH.e|1,3>〉 = –0.134 + 0.522 |LogP> – 0.00006 |Etot > | 18.9449 | 0.9423 | 0.7708 |
| T.p. | |YT.p.|1,3>〉 = –0.859 + 0.219 |LogP> – 1.04·10−4 |Etot > | 14.8152 | 0.9944 | 0.9611 | |
| P.p. | |YP.p|1,3>〉 = –3.524 – 1.327|LogP>– 3.1·10−4 |Etot > | 15.4088 | 0.9882 | 0.9437 | |
| V.f. | |YV.f.|1,3>〉 = –0.12 + 0.713 |LogP> – 8.42·10−5 |Etot > | 16.2777 | 0.9766 | 0.8267 | |
| |2,3> | H.e. | |YH.e|2,3>〉 = 0.093 + 0.175 |POL> – 0.00001 |Etot > | 18.5804 | 0.9242 | 0.6868 |
| T.p. | |YT.p.|2,3>〉 = –1.045 + 0.062 |POL> – 9.77·10−5|Etot > | 14.8118 | 0.9942 | 0.9594 | |
| P.p. | |YP.p|2,3>〉 = –2.243 –0.355 |POL> –3.28·10−4 |Etot > | 15.3717 | 0.9858 | 0.9320 | |
| V.f. | |YV.f|2,3>〉 = 0.2 + 0.337 |POL> + 1.65·10−5 |Etot > | 16.1548 | 0.9692 | 0.7650 | |
| {|1,2,3>} | H.e. | |YH.e{|1,2,3>}〉 = –0.166 + 1.229|LogP> – 0.351|POL> –0.00017|Etot > | 19.1684 | 0.9534 | 0.8188 |
| T.p. | |YT.p{|1,2,3>}〉 = –0.871 + 0.199|LogP> + 0.008|POL> –0.0001|Etot > | 14.8153 | 0.9944 | 0.9611 | |
| Species Method Paths | H.e. | T.p. | ||||||
|---|---|---|---|---|---|---|---|---|
| Mlog | CLog | Mlog | Clog | |||||
| Algebraic | Statistic | Algebraic | Statistic | Algebraic | Statistic | Algebraic | Statistic | |
| |1>→|1,2>→|1,2,3> | 1.05246 | 1.08283γ | 1.01981 | 1.0476γ | 0.41325 | 0.575439γ | 0.208278 | 0.232353 |
| |1>→|1,3>→|1,3,2> | 1.05246γ | 1.08273 | 1.01981γ | 1.04754 | 0.41325γ | 0.574673 | 0.208278γ | 0.232342γ |
| |1>→|2,3>→|1,2,3> | 1.05246 | 1.08284 | 1.01981 | 1.0476 | 0.41325 | 0.575534 | 0.208278 | 0.232342 |
| |2>→|1,2>→|2,1,3> | 0.404191 | 0.413755 | 0.603637 | 0.61798 | 0.147067 | 0.188257 | 0.103313β | 0.114674β |
| |2>→|1,3>→|2,1,3> | 0.404191 | 0.413756 | 0.603637 | 0.617987 | 0.147067 | 0.188265 | 0.103313 | 0.114674 |
| |2>→|2,3>→|2,3,1> | 0.404191α | 0.413754α | 0.603637α | 0.617972α | 0.147067α | 0.188246α | 0.103313 | 0.114674 |
| |3>→|1,2>→|3,1,2> | 0.89559β | 0.920041 | 1.00961β | 1.03703 | 0.373261β | 0.510175 | 0.191347 | 0.212443 |
| |3>→|1,3>→|3,1,2> | 0.89559 | 0.919987β | 1.00961 | 1.03697β | 0.373261 | 0.509664β | 0.0140336 | 0.0155182 |
| |3>→|2,3>→|3,2,1> | 0.89559 | 0.920044 | 1.00961 | 1.03703 | 0.373261 | 0.510232 | 0.0140336α | 0.0155182α |
| Species Method Paths | P.p. | V.f. | ||||||
|---|---|---|---|---|---|---|---|---|
| Mlog | CLog | Mlog | Clog | |||||
| Algebraic | Statistic | Algebraic | Statistic | Algebraic | Statistic | Algebraic | Statistic | |
| |1>→|1,2> | 0.0792073 | 0.0881801 | 0.190201 | 0.2034 | 0.392451β | 0.476398β | 0.509418β | 0.601392β |
| |1>→|1,3> | 0.499343γ | 0.545515γ | 0.692013γ | 0.731962γ | 0.511148 | 0.61083 | 0.600329 | 0.702271 |
| |1>→|2,3> | 0.474093 | 0.518389 | 0.654817 | 0.69307 | 0.312213 | 0.383883 | 0.477152 | 0.565317 |
| |2>→|1,2> | 0.00166893α | 0.0018496α | 0.0371086α | 0.0395137α | 0.167993 | 0.196303 | 0.0485269 | 0.0545366 |
| |2>→|1,3> | 0.421805 | 0.459267 | 0.538921 | 0.568184 | 0.28669 | 0.331225 | 0.139438 | 0.155864 |
| |2>→|2,3> | 0.396554 | 0.432134 | 0.501725 | 0.529282 | 0.0877552α | 0.103489α | 0.0162612α | 0.0183134α |
| |3>→|1,2> | 0.3177 | 0.347114 | 0.328541 | 0.347126 | 0.590616 | 0.781086 | 0.565916 | 0.675813 |
| |3>→|1,3> | 0.102435 | 0.11035 | 0.173271 | 0.181596 | 0.709313γ | 0.913454γ | 0.656827γ | 0.776511γ |
| |3>→|2,3> | 0.0771849β | 0.0832042β | 0.136075β | 0.142683β | 0.510379 | 0.690032 | 0.53365 | 0.639803 |
| Computational Modes | Minimum Interspecies Paths | Ordered Endpoints | |||
|---|---|---|---|---|---|
| alpha | beta | gamma | |||
| Algebraic | Mlog | αP.p. | βP.p. | γT.p. | |
| |2>→|1,2> | |3>→|2,3> | |1>→|1,3> | |2>→|3>→|1>→|1,2>→|2,3>→|1,3>→{|1,2,3>} | ||
| Clog | αT.p. | βT.p. | γT.p. | ||
| |3>→|2,3> | |2>→|1,2> | |1>→|1,3> | |3>→|2>→|1>→|2,3>→|1,2>→|1,3>→{|1,2,3>} | ||
| Statistic | Mlog | αP.p. | βP.p. | γP.p. | |
| |2>→|1,2> | |3>→|2,3> | |1>→|1,3> | |2>→|3>→|1>→|1,2>→|2,3>→|1,3>→{|1,2,3>} | ||
| Clog | αT.p. | βT.p. | γT.p. | ||
| |3>→|2,3> | |2>→|1,2> | |1>→|1,3> | |3>→|2>→|1>→|2,3>→|1,2>→|1,3>→{|1,2,3>} | ||
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Chicu, S.A.; Putz, M.V. Köln-Timişoara Molecular Activity Combined Models toward Interspecies Toxicity Assessment. Int. J. Mol. Sci. 2009, 10, 4474-4497. https://doi.org/10.3390/ijms10104474
Chicu SA, Putz MV. Köln-Timişoara Molecular Activity Combined Models toward Interspecies Toxicity Assessment. International Journal of Molecular Sciences. 2009; 10(10):4474-4497. https://doi.org/10.3390/ijms10104474
Chicago/Turabian StyleChicu, Sergiu A., and Mihai V. Putz. 2009. "Köln-Timişoara Molecular Activity Combined Models toward Interspecies Toxicity Assessment" International Journal of Molecular Sciences 10, no. 10: 4474-4497. https://doi.org/10.3390/ijms10104474
APA StyleChicu, S. A., & Putz, M. V. (2009). Köln-Timişoara Molecular Activity Combined Models toward Interspecies Toxicity Assessment. International Journal of Molecular Sciences, 10(10), 4474-4497. https://doi.org/10.3390/ijms10104474