Intramolecular Versus Intermolecular Diels–Alder Reactions: Insights from Molecular Electron Density Theory
Abstract
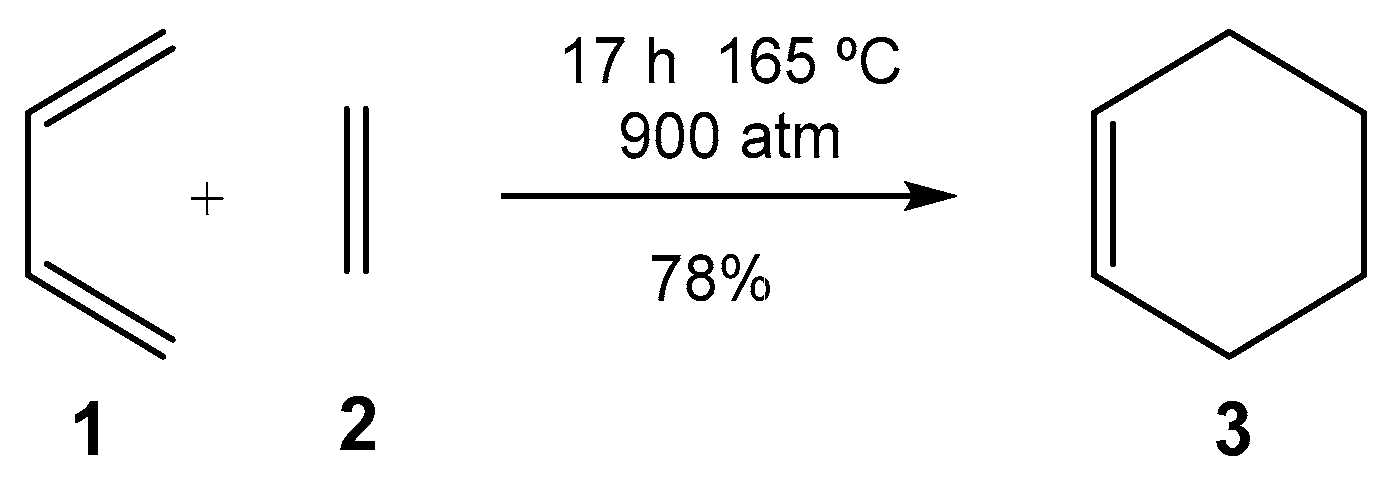
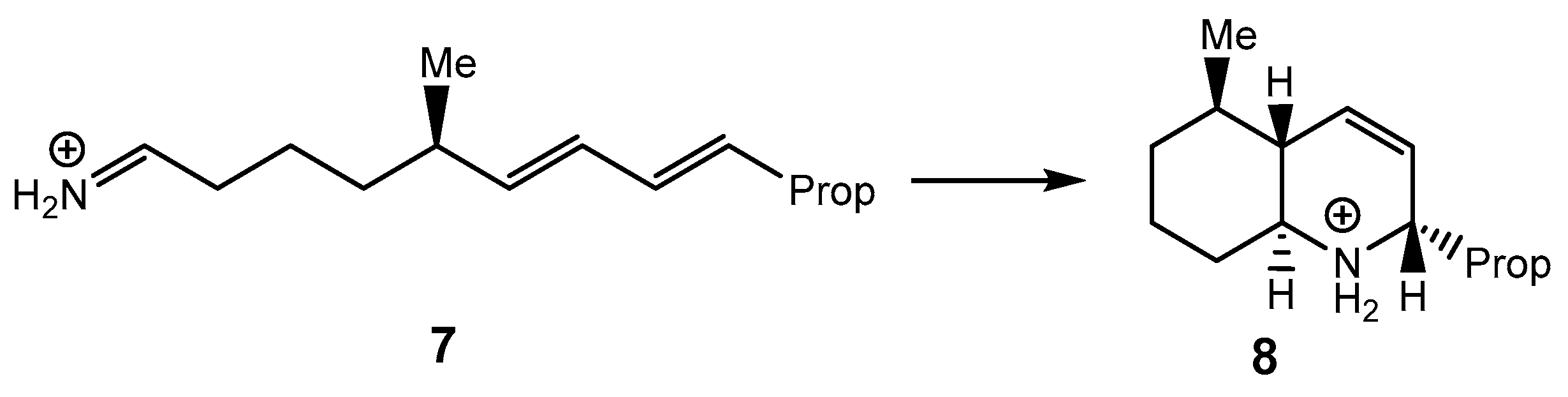
1. Introduction
2. Results and Discussion
2.1. Study of the Electronic Structure and Chemical Properties of the DTEs 5, 10, 12 and 13 and MODA 11 in the GS
2.1.1. Study of the Electronic Structure of the DTEs 5, 10, 12 and 13 and MODA 11
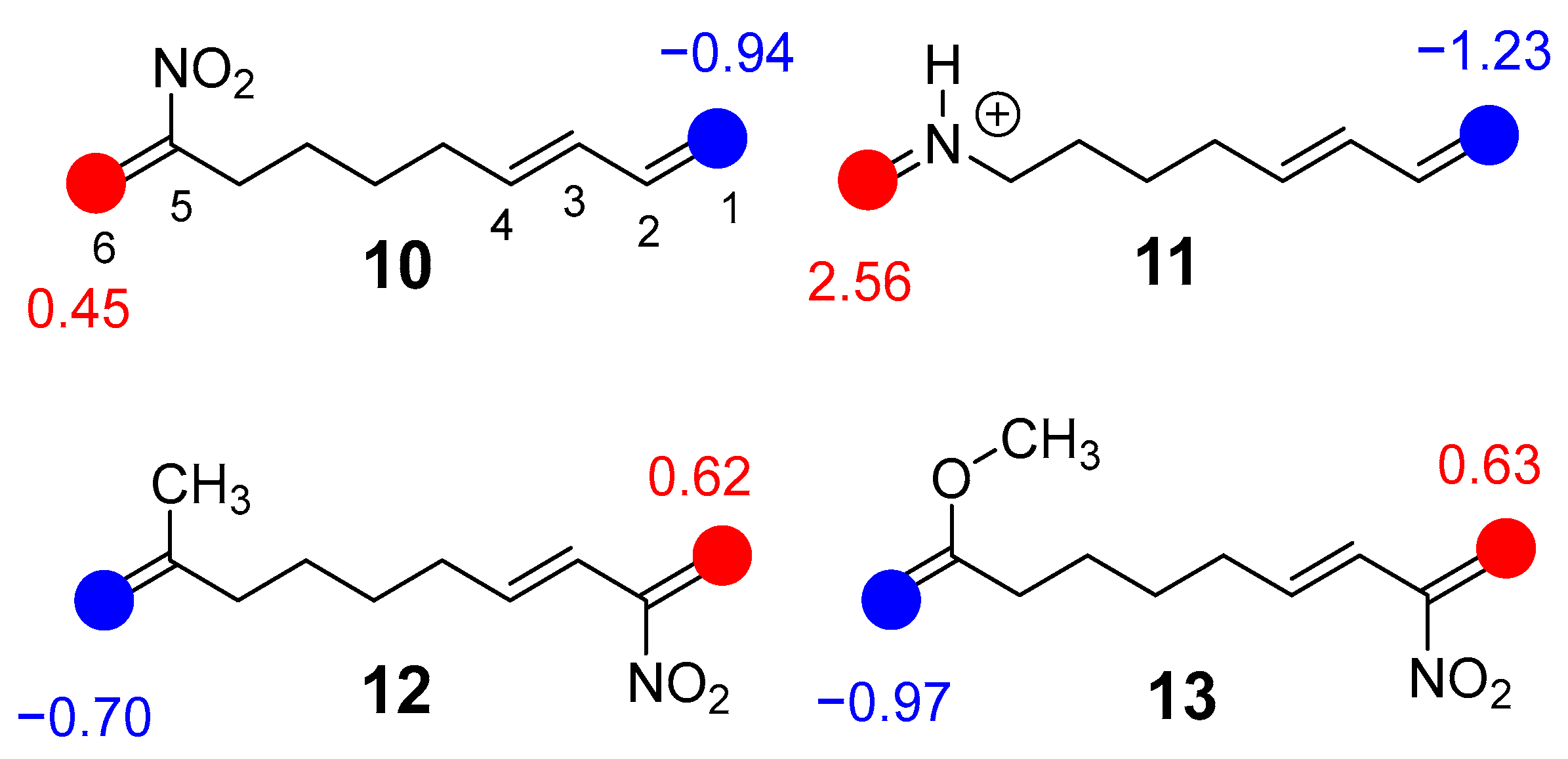
2.1.2. Analysis of the Chemical Properties of DTEs 5, 10, 12 and 13 and MODA 11
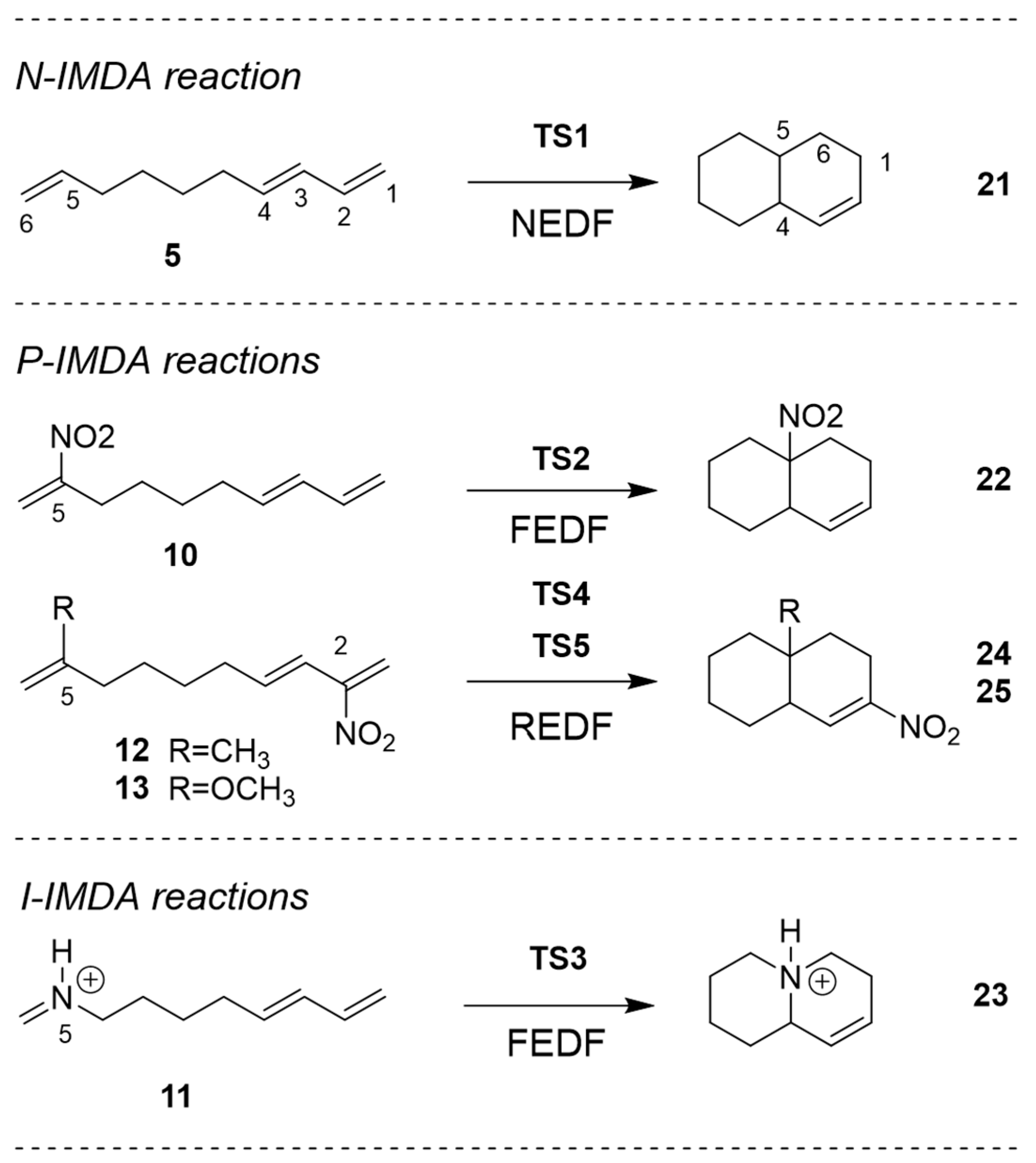
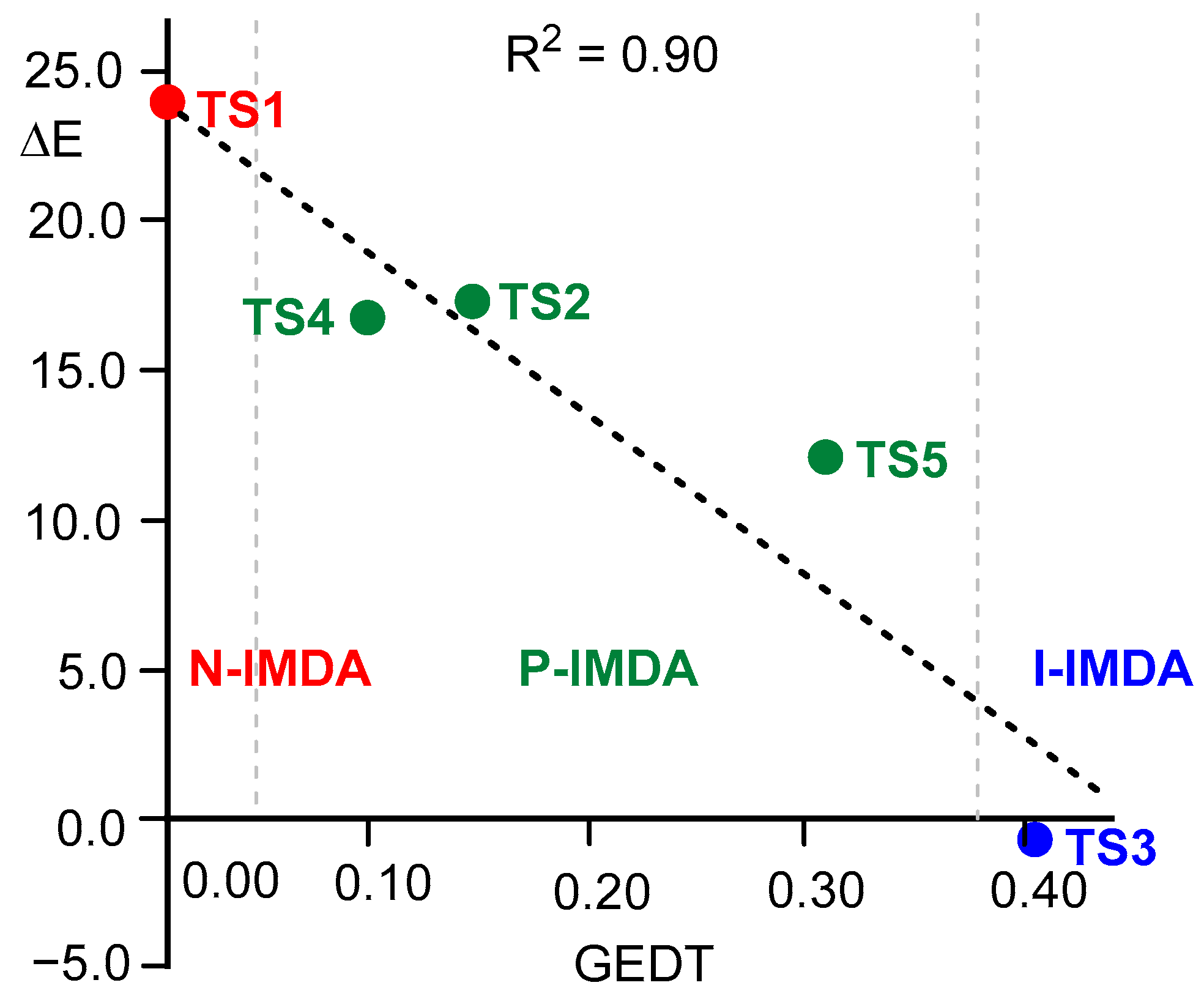
2.2. Study of the IMDA Reactions of DTEs 5, 10, 12 and 13 and MODA 11
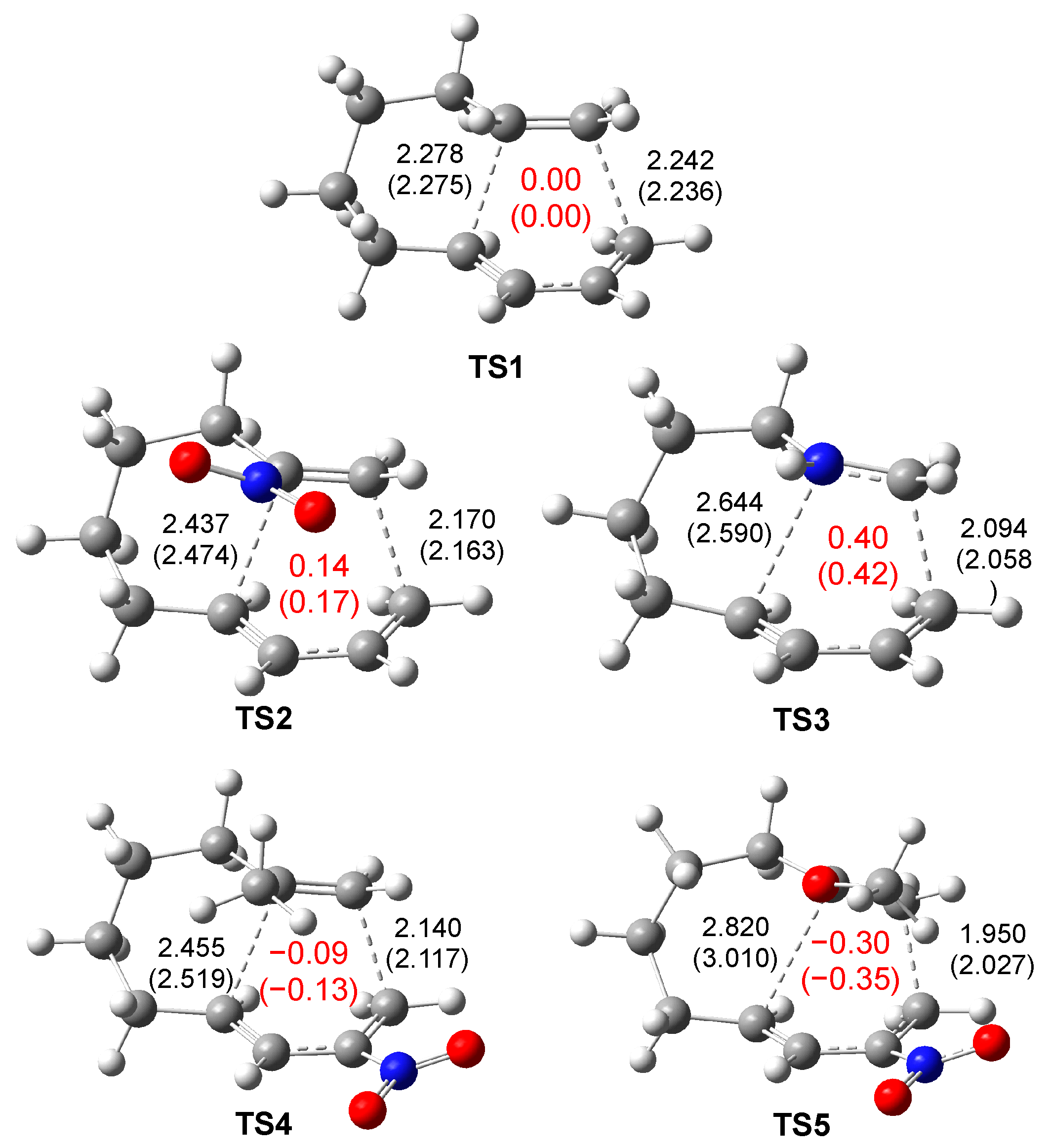
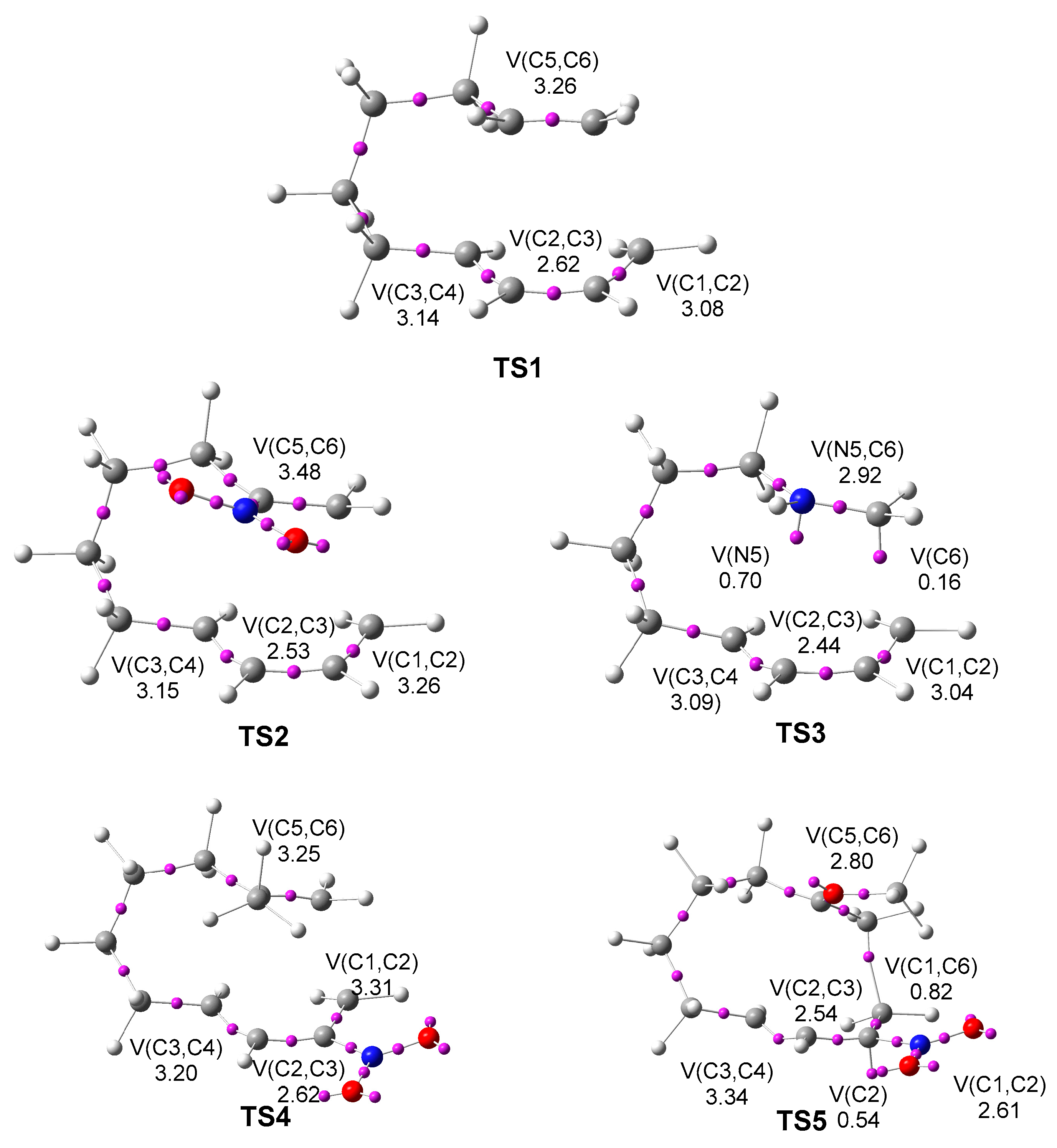
2.3. ELF Topological Analysis of the Electronic Structure of TS1–TS5
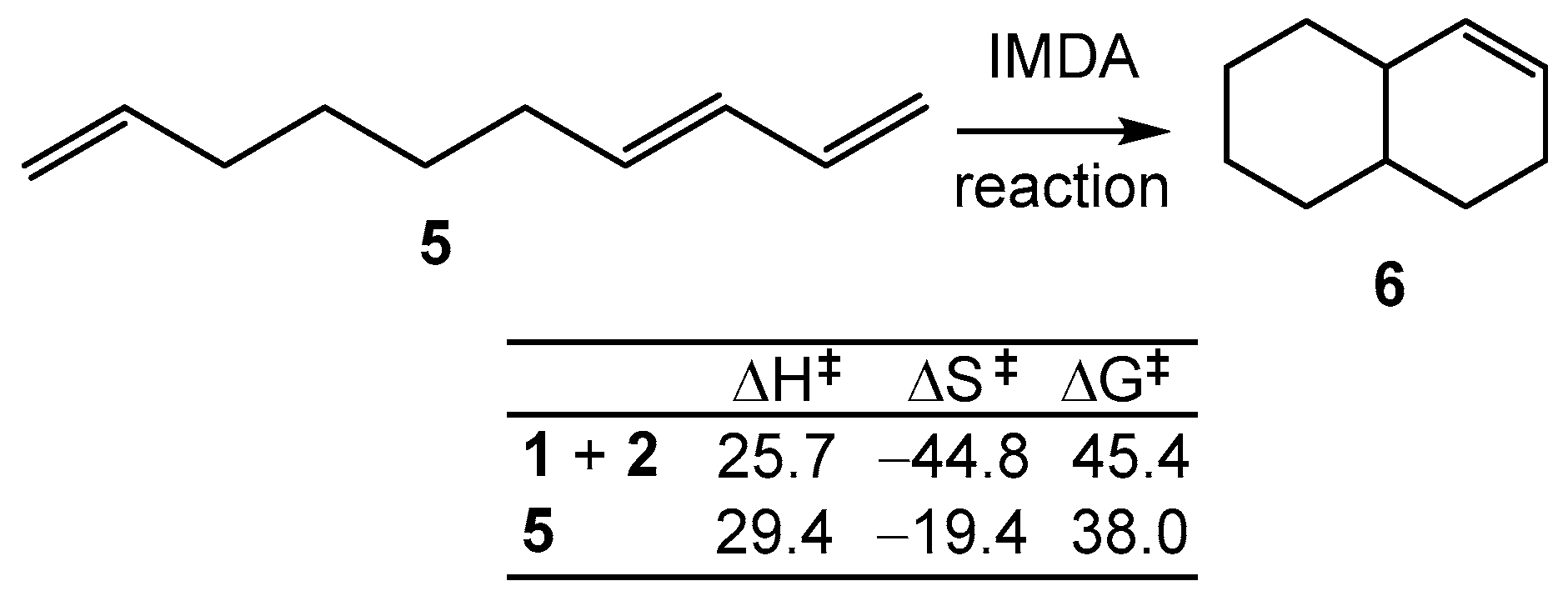
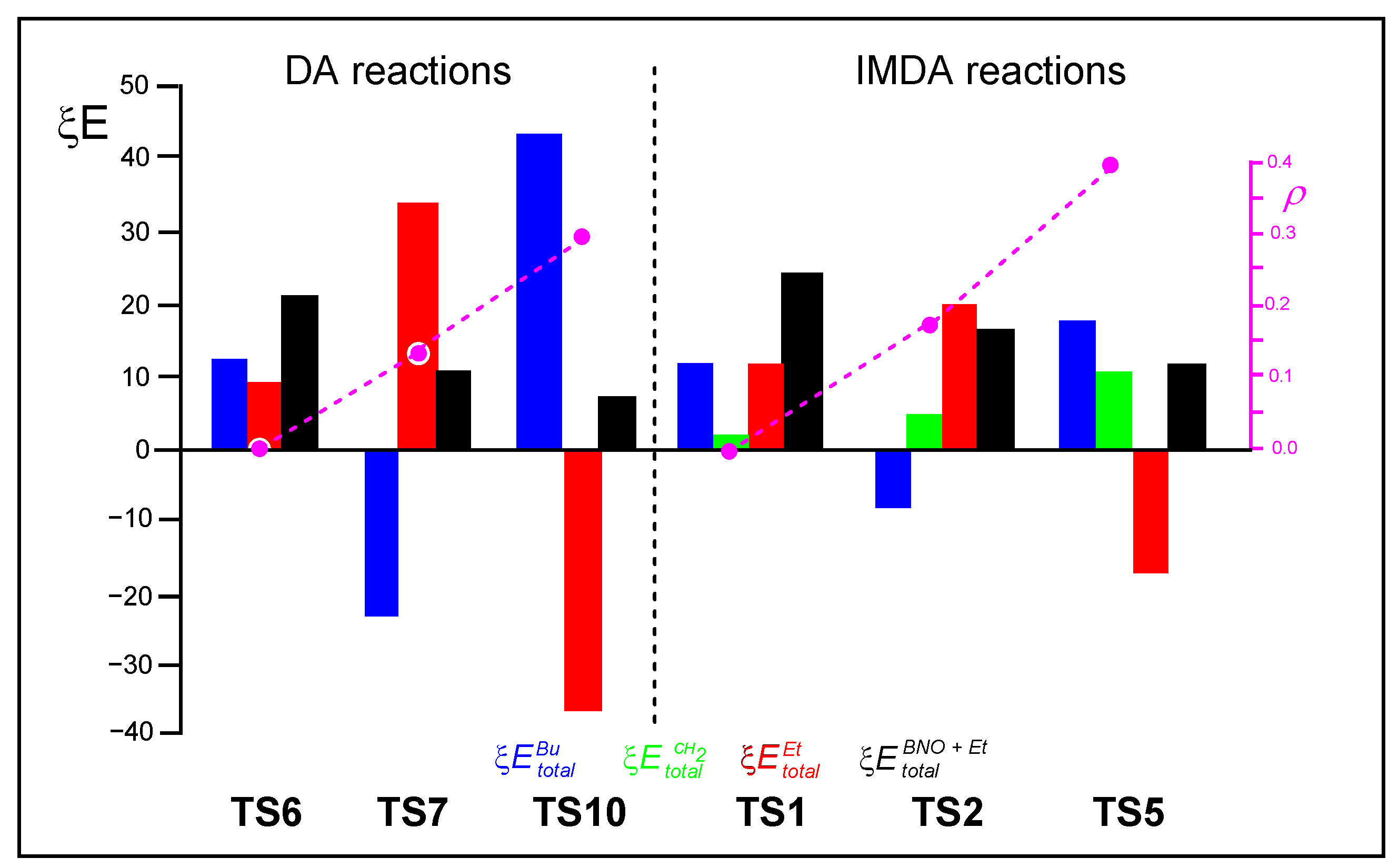
2.4. Comparative Analysis of the Kinetics of the IMDA Reactions with Respect to the Kinetics of the DA Reactions
2.5. Comparative RIAE Analysis of the DA Reactions of 14 with 16 or 17, and That of 15 with 20, and the IMDA Reactions of the DTEs 5, 10 and 13
3. Computational Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Diels, O.; Alder, K. Synthesen in der hydroaromatischen Reihe. Justus Liebigs Ann. Chem. 1928, 460, 98–122. [Google Scholar] [CrossRef]
- Carruthers, W. Some Modern Methods of Organic Synthesis, 2nd ed.; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Carruthers, W. Cycloaddition Reactions in Organic Synthesis; Pergamon: Oxford, UK, 1990. [Google Scholar]
- Woodward, R.B.; Hoffmann, R. The Conservation of Orbital Symmetry. Angew. Chem. Int. Ed. Engl. 1969, 8, 781–853. [Google Scholar] [CrossRef]
- Houk, K.N.; Gonzalez, J.; Li, Y. Pericyclic Reaction Transition States: Passions and Punctilios, 1935–1995. Acc. Chem. Res. 1995, 28, 81–90. [Google Scholar] [CrossRef]
- Rowley, D.; Steiner, H. Kinetics of diene reactions at high temperatures. Discuss. Faraday Soc. 1951, 10, 198–213. [Google Scholar] [CrossRef]
- Goldstein, E.; Beno, B.; Houk, K.N. Density Functional Theory Prediction of the Relative Energies and Isotope Effects for the Concerted and Stepwise Mechanisms of the Diels−Alder Reaction of Butadiene and Ethylene. J. Am. Chem. Soc. 1996, 118, 6036–6043. [Google Scholar] [CrossRef]
- Domingo, L.R. A new C-C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef]
- Domingo, L.R.; Sáez, J.A. Understanding the mechanism of polar Diels–Alder reactions. Org. Biomol. Chem. 2009, 7, 3576–3583. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M. Revealing the Critical Role of Global Electron Density Transfer in the Reaction Rate of Polar Organic Reactions within Molecular Electron Density Theory. Molecules 2024, 29, 1870. [Google Scholar] [CrossRef]
- Domingo, L.R. Ríos-Gutiérrez, M.; Aurell, M.J. Unveiling the Intramolecular Ionic Diels-Alder Reactions within the Molecular Electron Density Theory. Chemistry 2021, 3, 834–853. [Google Scholar] [CrossRef]
- Trost, B.M.; Fleming, I.; Winterfeldt, E. Comprehensive Organic Synthesis-Selectivity, Strategy and Efficiency in Modern Organic Chemistry; Pergamon Press: Oxford, UK, 1991. [Google Scholar]
- Pham, H.V.; Paton, R.S.; Ross, A.G.; Danishefsky, S.J.; Houk, K.N. Intramolecular Diels−Alder reactions of cycloalkenones: Stereoselectivity, Lewis acid acceleration, and halogen substituent effects. J. Am. Chem. Soc. 2014, 136, 2397–2403. [Google Scholar] [CrossRef]
- Kobuke, Y.; Sugimoto, T.; Furukawa, J. The role of attractive interactions in endo-exo stereoselectivities of Diels-Alder reactions. J. Am. Chem. Soc. 1972, 94, 3633–3635. [Google Scholar] [CrossRef]
- Takao, K.-I.; Munakata, R.; Tadano, K.-I. Recent advances in natural product synthesis by using intramolecular Diels-Alder reactions. Chem. Rev. 2005, 105, 4779–4807. [Google Scholar] [CrossRef]
- Juhl, M.; Tanner, D. Recent applications of intramolecular Diels–Alder reactions to natural product synthesis. Chem. Soc. Rev. 2009, 38, 2983–2992. [Google Scholar] [CrossRef]
- Nicolaou, K.C.; Snyder, S.A.; Montagnon, T.; Vassilikogiannakis, G. The Diels-Alder reaction in total synthesis. Angew. Chem. Int. Ed. 2002, 41, 1668–1698. [Google Scholar] [CrossRef]
- Tantillo, D.J.; Houk, K.N.; Jung, M.E. Origins of stereoselectivity in intramolecular Diels-Alder cycloadditions of dienes and dienophiles linked by ester and amide tethers. J. Org. Chem. 2001, 66, 1938–1940. [Google Scholar] [CrossRef]
- Marell, D.J.; Furan, L.R.; Woods, B.P.; Lei, X.; Bendelsmith, A.J.; Cramer, C.J.; Hoye, T.R.; Kuwata, K.T. Mechanism of the Intramolecular Hexadehydro-Diels-Alder Reaction. J. Org. Chem. 2015, 80, 11744–11754. [Google Scholar] [CrossRef]
- Rodríguez, D.; Navarro-Vázquez, A.; Castedo, L.; Domínguez, D.; Saá, C. Cyclic allene intermediates in intramolecular dehydro Diels-Alder reactions: Labeling and theoretical cycloaromatization studies. J. Org. Chem. 2003, 68, 1938–1946. [Google Scholar] [CrossRef] [PubMed]
- Cayzer, T.N.; Paddon-Row, M.N.; Moran, D.; Payne, A.D.; Sherburn, M.S.; Turner, P. Intramolecular Diels-Alder reactions of ester-linked 1,3,8-nonatrienes. J. Org. Chem. 2005, 70, 5561–5570. [Google Scholar] [CrossRef]
- Jin, S.D.; Wessig, P.; Liebscher, J. Intermolecular and intramolecular Diels-Alder cycloadditions of 3-ylidenepiperazine-2,5-diones and 5-acyloxy-2(1H)-pyrazinones. J. Org. Chem. 2001, 66, 3984–3997. [Google Scholar] [CrossRef]
- Jones, G.A.; Paddon-Row, M.N.; Sherburn, M.S.; Turner, C.I. On the Endo/Exo stereoselectivity of intramolecular Diels-Alder reactions of hexadienylacrylates: An interesting failure of density functional theory. Org. Lett. 2002, 4, 3789–3792. [Google Scholar] [CrossRef]
- Grieco, P.A.; Parker, D.T. Octahydroquinoline Synthesis via Immonium Ion Based Diels-Alder Chemistry: Synthesis of (-)-8a-Epipumiliotoxin C. J. Org. Chem. 1988, 53, 3658–3662. [Google Scholar] [CrossRef]
- Domingo, L.R. Molecular electron density theory: A modern view of reactivity in organic chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular-systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Domingo, L.R.; Ríos-Gutiérrez, M. Application of Reactivity Indices in the Study of Polar Diels–Alder Reactions. In Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory; Liu, S., Ed.; WILEY-VCH GmbH: Weinheim, Germany, 2022; Volume 2, pp. 481–502. [Google Scholar]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Electrophilicity ω and Nucleophilicity N Scales for Cationic and Anionic Species. Sci. Rad. 2025, 4, 1–17. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpaly, L.v.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study. J. Org. Chem. 2008, 73, 4615–4624. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M. A Useful Classification of Organic Reactions Bases on the Flux of the Electron Density. Sci. Rad. 2023, 2, 1–24. [Google Scholar] [CrossRef]
- Domingo, L.R.; Perez, P.; Sáez, J.A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013, 3, 1486–1494. [Google Scholar] [CrossRef]
- Chattaraj, P.K.; Duley, S.; Domingo, L.R. Understanding Local Electrophilicity/ Nucleophilicity Activation through a single Reactivity Difference Index. Org. Biomol. Chem. 2012, 10, 2855–2861. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Sáez, J.A.; Zaragoza, R.J.; Arno, M. Understanding the Participation of Quadricyclane as Nucleophile in Polar [2 sigma+2 sigma+2 pi] Cycloadditions toward Electrophilic pi Molecules. J. Org. Chem. 2008, 73, 8791–8799. [Google Scholar] [CrossRef]
- Evans, M.G.; Polanyi, M. Some applications of the transition state method to the calculation of reaction velocities, especially in solution. Trans. Faraday Soc. 1935, 31, 875–894. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Understanding the Electronic Effects of Lewis Acid Catalysts in Accelerating Polar Diels-Alder Reactions. J. Org. Chem. 2024, 89, 12349–12359. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–245. [Google Scholar]
- Hehre, M.J.; Radom, L.; Schleyer, P.V.R.; Pople, J. Ab Initio Molecular Orbital Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Schlegel, H.B. Optimization of equilibrium geometries and transition structures. J. Comput. Chem. 1982, 3, 214–218. [Google Scholar] [CrossRef]
- Schlegel, H.B. Modern Electronic Structure Theory; Yarkony, D.R., Ed.; World Scientific Publishing: Singapore, 1994. [Google Scholar]
- Fukui, K. Formulation of the reaction coordinate. J. Phys. Chem. 1970, 74, 4161–4163. [Google Scholar] [CrossRef]
- Tomasi, J.; Persico, M. Molecular interactions in solution: And overview of methods based on continuous distributions of the solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Simkin, B.Y.; Sheikhet, I.I. Quantum Chemical and Statistical Theory of Solutions–Computational Approach; Ellis Horwood: London, UK, 1995. [Google Scholar]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Cances, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M.; Tomasi, J. Geometry optimization of molecular structures in solution by the polarizable continuum model. J. Comput. Chem. 1998, 19, 404–417. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Dennington, R.; Keith, T.A.; Millam, J.M. GaussView, 6th ed.; Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
- Blanco, M.A.; Martín Pendás, A.; Francisco, E. Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [Google Scholar] [CrossRef] [PubMed]
- AIMAll (Version 19.10.12), Keith, T.A. TK Gristmill Software: Overland Park, KS, USA, 2019. Available online: https://aim.tkgristmill.com/ (accessed on 15 April 2024).

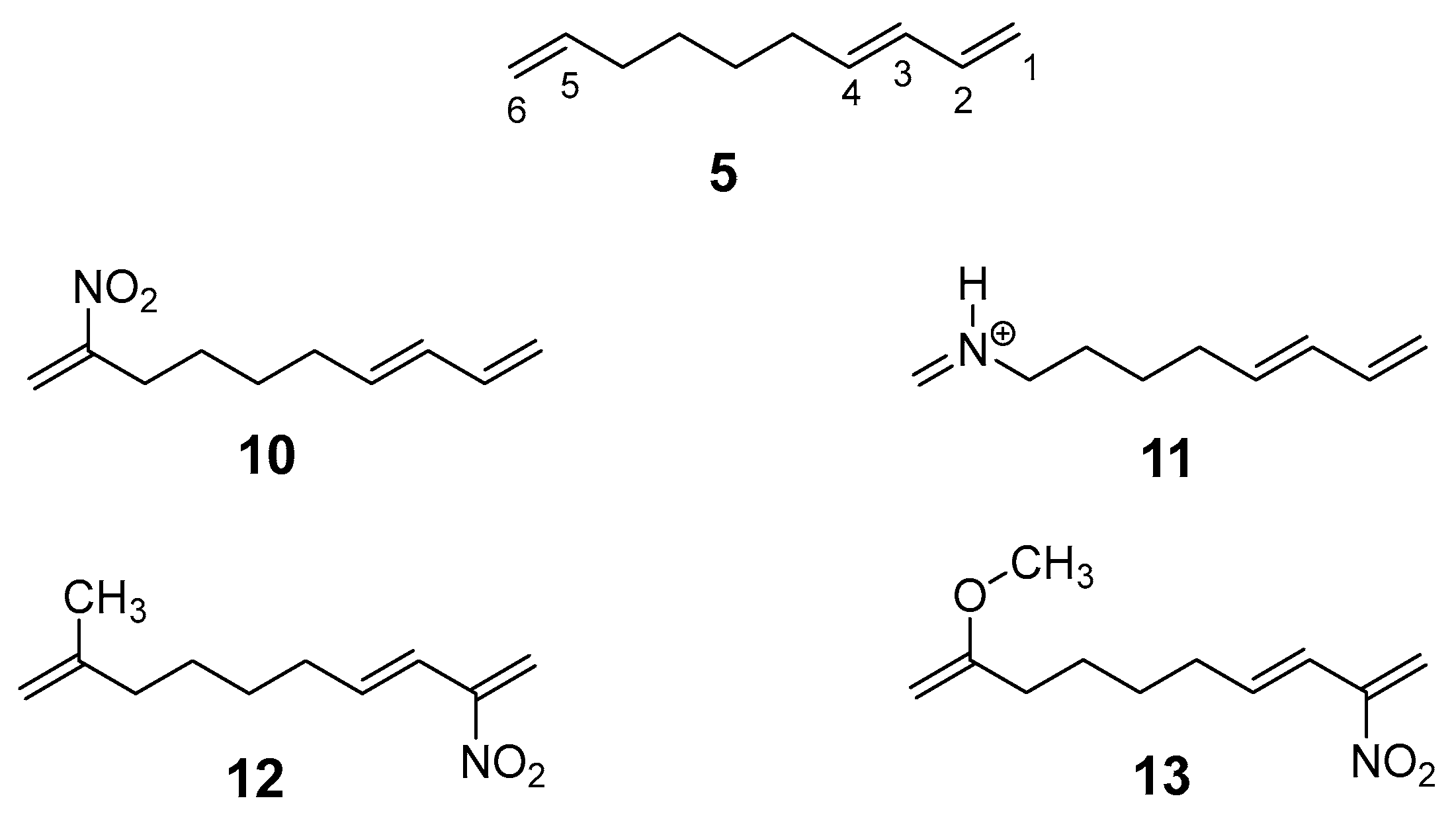
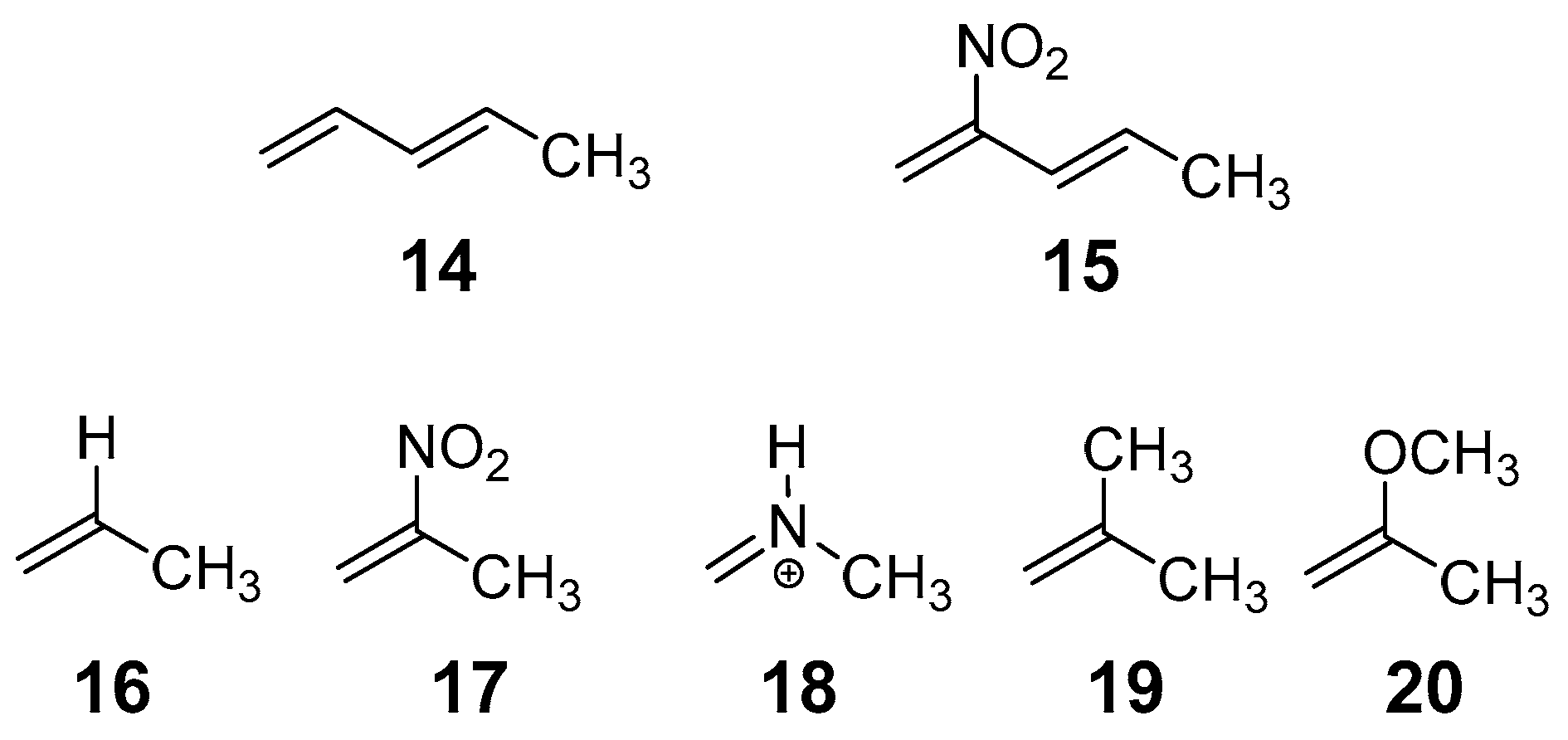

| C2 | C(N)5 | μ | η | ω | N | |
|---|---|---|---|---|---|---|
| 11 | H | H+ | −7.80 | 0.86 | 35.28 | 0.89 |
| 11 (DMSO) | −4.46 | 3.31 | 3.00 | 2.64 | ||
| 10 | H | NO2 | −4.23 | 3.60 | 2.49 | 3.09 |
| 12 | NO2 | OCH3 | −4.28 | 3.76 | 2.43 | 2.97 |
| 13 | NO2 | CH3 | −4.48 | 4.21 | 2.38 | 2.54 |
| 5 | H | H | −3.19 | 5.47 | 0.93 | 3.19 |
| Rk | Rk | |||||
|---|---|---|---|---|---|---|
| k | 10 | 11 | ||||
| 1 | 0.10 | 0.38 | −0.94 | 0.00 | 0.47 | −1.23 |
| 2 | 0.02 | 0.00 | 0.00 | 0.00 | 0.07 | −0.19 |
| 3 | 0.01 | 0.14 | −0.40 | 0.00 | 0.10 | −0.25 |
| 4 | 0.09 | 0.29 | −0.68 | 0.00 | 0.40 | −1.06 |
| 5 | −0.02 | 0.02 | −0.12 | 0.25 | 0.00 | 0.74 |
| 6 | 0.31 | 0.04 | 0.45 | 0.85 | 0.00 | 2.56 |
| k | 12 | 13 | ||||
| 1 | 0.47 | 0.20 | 0.62 | 0.46 | 0.16 | 0.63 |
| 2 | −0.02 | −0.02 | 0.00 | −0.01 | −0.01 | 0.00 |
| 3 | 0.00 | 0.14 | −0.36 | 0.00 | 0.11 | −0.33 |
| 4 | 0.08 | 0.17 | −0.24 | 0.11 | 0.14 | −0.14 |
| 5 | 0.00 | 0.12 | −0.30 | 0.00 | 0.04 | −0.11 |
| 6 | 0.00 | 0.28 | −0.70 | 0.00 | 0.33 | −0.97 |
| NEDF | FEDF | REDF | |||
|---|---|---|---|---|---|
| 5 | 0.0 | 10 | 0.0 | 12 | 0.0 |
| TS1 | 23.9 | TS2 | 17.1 | TS4 | 16.5 |
| 21 | −43.8 | 22 | −45.4 | 24 | −47.7 |
| 11 | 0.0 | 13 | 0.0 | ||
| TS3 | −0.8 | TS5 | 12.0 | ||
| 23 | −52.2 | 25 | −49.9 | ||
| ΔG‡ | ||||
|---|---|---|---|---|
| 14 + 16 | TS6 | 38.9 | 1.5 × 10−7 | |
| 14 + 17 | TS7 | 28.3 | 1.0 | |
| 14 + 18 | TS8 | 18.9 | 1.1 × 106 | |
| 15 + 19 | TS9 | 30.2 | 6.0 × 10−2 | |
| 15 + 20 | TS10 | 21.7 | 1.8 × 104 | |
| 5 | TS1 | 30.4 | 5.6 × 10−5 | 3.0 × 105 |
| 10 | TS2 | 23.8 | 1.0 | 7.9 × 102 |
| 11 | TS3 | 12.8 | 1.2 × 107 | 8.5 × 103 |
| 12 | TS4 | 21.9 | 1.7 × 101 | 2.2 × 105 |
| 13 | TS5 | 16.2 | 7.9 × 104 | 3.5 × 103 |
| TS | f(x) | ||||
|---|---|---|---|---|---|
| TS6 | Et | 36.2 | −23.8 | 12.4 | 20.9 |
| Bu | 38.3 | −29.8 | 8.5 | ||
| TS7 | Et | 31.8 | −54.9 | −23.1 | 10.9 |
| Bu | 52.8 | −18.8 | 34.0 | ||
| TS10 | Et | 95.9 | −52.4 | 43.4 | 7.1 |
| Bu | 43.5 | −79.7 | −36.3 | ||
| TS1 | Et | 29.3 | −17.6 | 11.7 | 24.5 |
| CH2 | 5.2 | −3.4 | 1.8 | ||
| Bu | 36.2 | −25.2 | 11.0 | ||
| TS2 | Et | 36.7 | −44.7 | −8.0 | 17.0 |
| CH2 | 5.8 | −1.4 | 4.4 | ||
| Bu | 41.3 | −20.6 | 20.6 | ||
| TS5 | Et | 81.1 | −63.2 | 17.8 | 11.7 |
| CH2 | 3.9 | 6.9 | 10.8 | ||
| Bu | 42.0 | −59.0 | −17.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domingo, L.R.; Pérez, P. Intramolecular Versus Intermolecular Diels–Alder Reactions: Insights from Molecular Electron Density Theory. Molecules 2025, 30, 2052. https://doi.org/10.3390/molecules30092052
Domingo LR, Pérez P. Intramolecular Versus Intermolecular Diels–Alder Reactions: Insights from Molecular Electron Density Theory. Molecules. 2025; 30(9):2052. https://doi.org/10.3390/molecules30092052
Chicago/Turabian StyleDomingo, Luis R., and Patricia Pérez. 2025. "Intramolecular Versus Intermolecular Diels–Alder Reactions: Insights from Molecular Electron Density Theory" Molecules 30, no. 9: 2052. https://doi.org/10.3390/molecules30092052
APA StyleDomingo, L. R., & Pérez, P. (2025). Intramolecular Versus Intermolecular Diels–Alder Reactions: Insights from Molecular Electron Density Theory. Molecules, 30(9), 2052. https://doi.org/10.3390/molecules30092052









