Next Article in Journal
Intramolecular Versus Intermolecular Diels–Alder Reactions: Insights from Molecular Electron Density Theory
Next Article in Special Issue
Coherent Vibrational Anti-Stokes Raman Spectroscopy Assisted by Pulse Shaping
Previous Article in Journal
Design, Synthesis, and Biological Evaluation of New Analogs of Aurein 1.2 Containing Non-Proteinogenic Amino Acids
Previous Article in Special Issue
Perfluoropropionic Acid (CF3CF2C(O)OH): Three Conformations and Dimer Formation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 30
Issue 9
10.3390/molecules30092051
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Pure Rotational Spectroscopic Study of Two Nearly-Equivalent Structures of Hexafluoroacetone Imine, (CF3)2C=NH

by
Daniel A. Obenchain
1,*,
Beppo Hartwig
1,
Daniel J. Frohman
2,
G. S. Grubbs II
3,
B. E. Long
4,
Wallace C. Pringle
2,
Stewart E. Novick
2,† and
S. A. Cooke
5,*
1
Institute of Physical Chemistry, University of Göttingen, Tammannstrasse 6, 37077 Göttingen, Germany
2
Department of Chemistry, Wesleyan University, 52 Lawn Avenue, Middletown, CT 06459, USA
3
Department of Chemistry, Missouri University of Science and Technology, 104 Schrenk Hall, 400 W. 11th St, Rolla, MO 65409, USA
4
Department of Chemistry and Biochemistry, James Madison University, Harrisonburg, VA 22807, USA
5
School of Natural and Social Sciences, Purchase College SUNY, 735 Anderson Hill Rd, Purchase, NY 10577, USA
*
Authors to whom correspondence should be addressed.
†
Deceased, October 2023.
Molecules 2025, 30(9), 2051; https://doi.org/10.3390/molecules30092051
Submission received: 31 March 2025 / Revised: 26 April 2025 / Accepted: 29 April 2025 / Published: 5 May 2025
(This article belongs to the Special Issue From Spectroscopic Insights to Structural Wonders: A Theme Issue Dedicated to Professor Jaan Laane)
Browse Figures
Versions Notes

Abstract

:
Rotational spectra for hexafluoroacetone imine, the singly substituted 13C isotopologues, and the 15N isotopologue, have been recorded using both cavity and chirped pulse Fourier transform microwave spectrometers. The spectra observed present as being doubled with separations between each pair of transitions being on the order of a few tens of kilohertz which is consistent with a large amplitude motion producing two torsional substates. The observed splitting is most likely due to the combined motions of the CF3 groups, for which the calculated barrier is small. However, no transitions between states could be observed and, similarly, no Coriolis coupling parameters were required to achieve a satisfactory fit for the transition frequencies. Hence, and somewhat curiously, the two states have been fit independently of each other such that the two states may simply be considered near-equivalent conformers. The structural properties of hexafluoroacetone imine are compared with two isoelectronic molecules hexafluoroisobutene and hexafluoroacetone. Rotational constants, quartic centrifugal distortion constants, and the 14N nuclear electric quadrupole coupling tensor have been determined and are presented together with supporting quantum chemical calculations.

1. Introduction

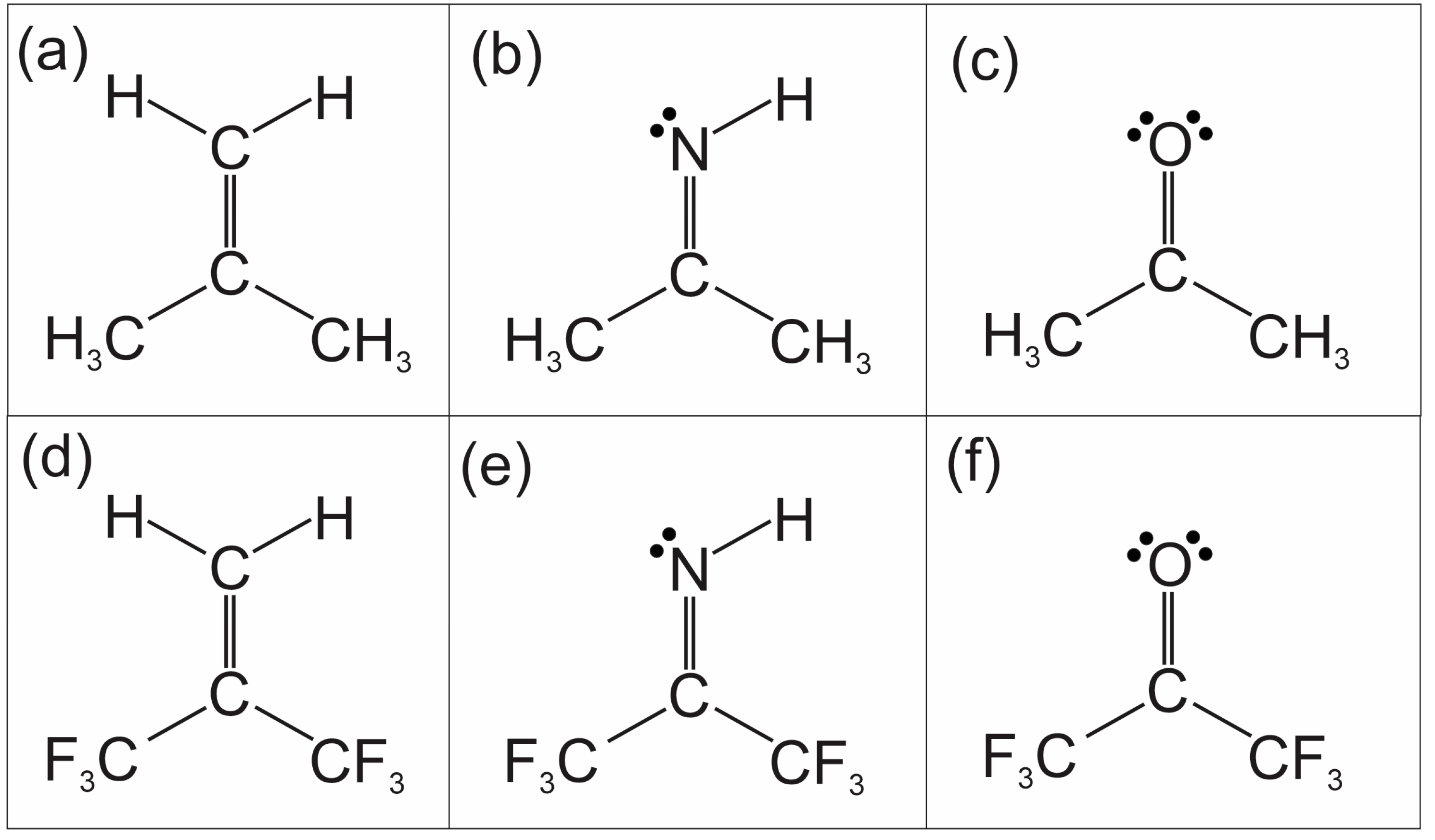
Hexafluoroacetone imine may be considered a member of a grouping of six molecules shown in Figure 1. This grouping consists of two isoelectronic series, the first being isobutene, acetone imine, and lastly acetone, and the second being the hexafluorinated analogs of the first series. Except for hexafluoroacetone imine, all these molecules have had their rotational spectra recorded at high resolution. These spectra are reported, or most recently discussed, in the following references [1,2,3,4,5]. Isobutene and acetone are well-known examples of rotational spectra in which the effects of the internal rotation of two equivalent methyl tops are manifested. At high resolution, rotational transitions from these types of molecules will appear as quartets owing to transitions occurring from within the AA, EE, AE, and EA torsional sub-levels.
These spectra have been interpreted to yield effective CH3 internal rotation tunneling barriers of 761(1) cm−1 for isobutene [1] and 251.4(26) cm−1 for acetone [3]. One would correctly assume that the tunneling barrier to CH3 internal rotation in acetone imine would be intermediate between isobutene and acetone. However, the spectra are more complex owing to the two CH3 rotors being non-equivalent. In that case, the effects of the two non-equivalent CH3 rotors result in five torsional substrates, one with A1 symmetry and four doubly degenerate states with E symmetry. Hence, rotational transitions from within these substates present to the observer as quintets. An analysis of these spectra by Zou et al. [2] has resulted in internal rotation barrier heights of 531.956(64) cm−1, attributed to the CH3 furthest from the imine hydrogen, and 465.013(26) cm−1, attributed to the CH3 nearest to the imine hydrogen. Taken as a series, then we observe that the CH3 barriers to internal rotation increase in the order of increasing hydrogenation of the apex atom, i.e., in the order O, N-H, H-C-H. From a purely classical mechanics standpoint, this is rational in the sense that the apex hydrogen(s) clearly impede the CH3 internal rotations.
We then consider the hexafluorinated analogs. The rotational spectrum of hexafuoroacetone has been recorded at high resolution with spectral line widths on the order of 7 kHz at full width, half maximum height [5]. However, none of the transitions observed for hexafluoroacetone were observed as multiplets, or broadened as they were for acetone. Now, it is generally true that, the higher the barrier heights to internal motion the closer together in energy will be the torsional substates and, hence, the rotational transitions from within those different torsional substates will appear closer together in frequency. Given that the barrier heights to CF3 internal rotation are significantly higher than those for CH3 internal rotation, together with the very small internal rotational constant for a CF3 group, F ≈ 10 GHz (compared to that for a CH3 group, F ≈ 160 GHz), then effects due to CF3 internal rotation are most often unresolvable. A helpful discussion on this topic is presented in reference [6]. Accordingly, the rotational spectrum of hexafluoroacetone presents like that of an “ordinary” semirigid rotor, with no evidence of any internal motions.
Given that isobutene has a higher barrier to CH3 internal rotation compared to that of acetone, it may be assumed that the barrier to CF3 internal rotation in hexaflouroisobutene would be higher than that in hexafluoroacetone and, therefore, would have a rotational spectrum with no observable evidence of internal motion. However, the recorded rotational spectrum of hexafluoroisobutene presented as being doubled with spacings between the rotational transitions being on the order of tens of megahertz. The spectral analyses revealed that the bis-trifluoromethyl groups of hexafluoroisobutene are staggered in the equilibrium configuration, and that a novel, out-of-phase rotation through an F-CCC-F planar configuration with a low barrier (<100 cm−1), leads to the observed doubled rotational spectra [4]. This bistrifluoromethy effect has subsequently been explored in related molecules [7,8].
In this article, we present the measurement and analyses of rotational spectra for the remaining member of the molecules in Figure 1, hexafluoroacetone imine. We ask the question of how well the spectra are present, like that of hexafluoroacetone or that of hexafluoroisobutene. And further, how do we interpret the spectra?

2. Results

2.1. Spectral Analysis

The ground-state rotational spectrum of hexafluoroacetone imine, and all of the singly substituted 13C and 15N isotopologues, exhibits both a-type and b-type transitions. The spectra consist of “doubled” transitions separated by a few tens of kilohertz, we refer to a transition as either belonging to State I or State II. An example set of transitions is shown in Figure 2.
For both State I and State II, transition quantum number assignments and measured frequencies are available in the Supplementary Data. For each state, spectroscopic constants were fitted to the observed frequencies using the SPCAT/SPFIT software [9]. The Hamiltonian used was of the simple form H = HR + HQ constructed in the coupled symmetric rotor basis set I + J = F. The Watson A reduction in the Ir representation was chosen for the semirigid rotor Hamiltonian HR [10], but only terms up to the fourth power in angular momentum were required. The second operator, HQ, represents the well-known interaction energy of the nuclear electric quadrupole moment with the electric field gradient at the nitrogen nucleus. The term HQ is not needed for the 15N isotopologue as the nuclear spin, I = 1/2, and it therefore does not possess a quadrupole moment. In all cases, the χaa and χcc were used in the fits with χbb being determined from the requirement that χaa + χbb + χcc = 0. The determined spectroscopic constants for the two states of the parent isotopologue are presented in Table 1. The spectroscopic constants of the minor isotopologues are presented in Table 2 (State I), and Table 3 (State II). Many attempts were made to (i) locate transitions that span States I and II, and (ii) to use Coriolis constants in order to link the states. However, only those constants shown in Table 1, Table 2 and Table 3 were required to fit the transition data sets.

2.2. Theoretical Calculations

The MP2/6-311G++(2d,2p) [11,12,13,14] equilibrium geometry of hexafluoroisobutene is shown in Figure 3 and this structure produces the rotational constants shown in Table 1.
Calculated centrifugal distortion constants are also shown in Table 1. It is easily seen that the agreement is very good, with only small discrepancies appearing for some of the centrifugal distortion constants. This is unsurprising given the likely internal motions.
As discussed in the introduction, curiosity surrounds the possibility of observing the hexafluoroacetone imine spectra effects due to a similar internal motion to that observed for hexafluoroisobutene. The relaxed 2D potential energy scan for hexafluoroisobutene is shown in Figure 4 (see Figure 3 for atom labeling). For reference, the staggered nature of the F-CCC-F atoms in the equilibrium structure is shown on the right-hand side of Figure 3.
The zero-degree/zero-degree center of the scan corresponds to a planar F-CCC-F configuration. A one-dimensional, diagonal slice (lower left minimum through to upper right minimum) of the potential energy scan for hexafluoroacetone imine shows a double minimum with a barrier height of approximately 116 cm−1. The barrier heights at other levels of theory are shown in Table 4, and also in the Supplementary Tables, and are generally consistent. This is, approximately, double that of the analogous barrier height in hexafluoroisobutene, and using alternative quantum mechanical methods Shahi and Arunan [8] have shown the barrier quadruples in magnitude. For reference, the Shahi and Arunan calculations have been reproduced and are shown in the Supplementary Data. The increased barrier height for this out-of-phase rotation of CF3 groups through a planar F-CCC-F local maximum is consistent with the rotational transitions within each torsional substrate being closer together in frequency than for those observed in hexafluoroisobutene.
The results of a nudged-elastic-band scan are shown in the Supplementary Data for hexafluoroacetone, hexafluoroacetone imine, and hexafluoroisobutene. The angles used here are the average of the two dihedral angles defining the rotation of the CF3 groups. The scans illustrate that both the width as well as the barrier height significantly increase in going from hexafluoroisobutene to hexafluoroacetone imine to hexafluoroacetone. From the scans, you can also see that in hexafluoroacetone and hexafluoroacetone imine the lone pair side dihedral angles are actually very similar.
For the purpose of deriving semi-experimental equilibrium structures reSE, we conducted vibrational perturbation theory of second-order calculations (VPT2) [15] to obtain vibrational corrections for the rotational constants. In particular, we used Gaussian’s generalized VPT2 (GVPT2) implementation [16,17]. Note that the VPT2 calculation was conducted separately from the geometry optimization.

2.3. Structure

From the calculations detailed above, a very accurate structure was determined that reproduced the observed rotational constants very well. The best method used was the PBE0-D3(BJ)/aug-cc-pVTZ level of the theory and key structural features are presented in Table 5. The computed rotational constants are shown in Table 6.
Attempts were made to perform r0, reSE (semi-experimental [18]) and rm(2) [19] fits using the determined experimental rotational constants and, where appropriate, with quantum mechanically calculated vibrational parameters. For a comprehensive review of these approaches, please see reference [20]. For the C=N bond, the values determined were satisfactory, but in all the attempts, the two unique C-C bonds are not in agreement with the calculated structure, having large uncertainties in the bonds, and non-converging fits. The rm2 structure converges with both ca and da, but again the bonds have non-physical values. It is most likely that these failures have to do with the effective nature of the rotational constants used together with, possibly, poorly captured large amplitude motions in the quantum mechanical calculations.
Given the availability of the rotational constants for all the singly substituted 13C- and 15N-isotopologues Kraitchman analysis [21] we can obtain the substitution principal atomic coordinates of each of the substituted atoms, with the origin of these coordinates being the center of mass of the parent isotopologue. The results are shown in Table 7. As expected, it is found that both State I and II share nearly-equivalent structures which agree well with the quantum mechanical calculations.
Regarding the structure, it is interesting to compare the second moment in the direction of the c-principal axes, Pcc = ∑ i m i c i 2 , for the three molecules: hexafluoroisobutene, hexafluoroacetone imine, and hexafluoroacetone. All these structures have two CF3- groups which are staggered with respect to each other, and so the only contributions to Pcc will be from the six out-of-plane fluorine atoms. The Pcc values may be determined from the experimental rotational constants and are found to be 89.20 amu Å2, 88.79 amu Å2, and 89.15 amu Å2, respectively. For two CF3 groups, Bohn [22] has shown that the anticipated value of Pcc should be approximately 90 amu-Å2. This is in good agreement with the present data set and is indicative of the staggered/helical tendencies of many perfluorinated molecules [23].

2.4. Nitrogen Nuclear Electric Quadrupole Coupling Tensor

The 14N-nitrogen nuclear quadrupole coupling tensor components for hexafluoroacetone imine are compared to those for CH2NH [24] and CF2NH [25,26] in Table 8. Direct comparison is difficult as each molecule has its own principal axes system. However, in all three cases, the c-principal axes are perpendicular to the C=N-H plane and therefore the χcc values are comparable. For χcc, we find that the magnitudes change in the order CH2NH > (CF3)2CNH > CF2NH. This trend may be rationalized by an appeal to the electronegativities of H, F, and CF3, and it is found that the ordering of electronegativities on the Allred-Pauling scale [27,28] is F (3.98) > CF3 (2.99) > H (2.20), the opposite trend to that observed for χcc. Nuclear quadrupole coupling tensors are often related to ionicity [29] where the quadrupole coupling tensor for an ion will be very close to zero owing to the spherical symmetry of either empty (or full) p-orbitals. So, one may rationalize that χcc will decrease in magnitude with an increase in the electronegativity of the attached groups which is consistent with experimental observations.

3. Discussion

The pure rotational spectrum of hexafluoroacetone imine presents as consisting of two nearly-equivalent conformers. However, it is undoubtedly the case that these two sets of measured rotational transitions arise from two torsional substates, State I and State II, resulting from a relatively low barrier between two equivalent F-CCC-F staggered configurations. The torsional substates most likely arise from an out-of-phase internal rotation of the two CF3 groups which is governed by an unusual potential energy function with six minima, three high barriers (V1) and three low barriers (V2) as observed in the related molecule hexafluoroisobutene [4]. The substrates arise via tunneling through the low barrier. An example of the potential energy function is given in Figure 5. For the hexafluorinated species, the global minimum corresponds to a staggered F1-CCC-F2 configuration exemplified in Figure 3.
Careful calculations by Shahi and Arunan [8] have revealed that for the isoelectronic sequence of molecules hexafluoroisobutene (HFIB), hexafluoroacetone imine (HFAI), and hexafluoacetone (HFA) the barrier height V1 varies as HFIB > HFAI > HFA, whereas the V2 barrier height varies as HFA > HFAI > HFIB. In all three cases, the V1 barrier height is too high for tunneling effects to manifest in the observed spectra consistent with the absence of groupings of rotational transitions from within four or five torsional substates. The V2 tunneling barrier height is more nuanced. With the molecule unable to tunnel through V1, we are left with a tunneling motion through a much lower barrier separating two equivalent F-CCC-F staggered configurations, more akin to a double minimum potential often observed in ring-puckering problems. The barrier V2 is lowest for hexafluoroisobutene consistent with rotational transitions from the two torsional states being separated by tens of MHz. Whereas the barrier V2 is highest for hexafluoroacetone consistent with no observed “doublets” in the rotational spectrum. Hexafluoroacetone imine is intermediate, again consistent with the observation of paired rotational transitions separated by tens of kHz.
The above trends in both V1 and V2 may be rationalized through an appeal to the molecular geometries. In regards to the trend in V1, we note that all three molecules possess a C1-C3-C2 structural component, see Figure 3. It is found that the distance C1…C2 decreases in the order HFIB > HFAI > HFA. A large value of C1…C2 means that the two CF3-groups are further away from one another, and thus easier to rotate, compared to a small value of C1…C2 which corresponds to the CF3-groups being closer together. The correspondence between V1 and C1…C2 is shown in Figure 5. In regards to V2 in which the top of the smaller barrier corresponds to a planar F1-CCC-F2 (see Figure 5), it is useful to compare the C=X distance where X = CH2, NH, and O. This C=X distance decreases in the order HFIB > HFAI > HFA. The larger C=X distance in hexafluoroisobutene corresponds to a small V2, i.e., it is easier for F-CCC-F to pass through a planar configuration, compared to the longer C=X distance in hexafluoroacetone where the planar F-CCC-F configuration is more greatly interfered with by the oxygen lone pairs. The correspondence between V2 and C=X is also shown in Figure 5.
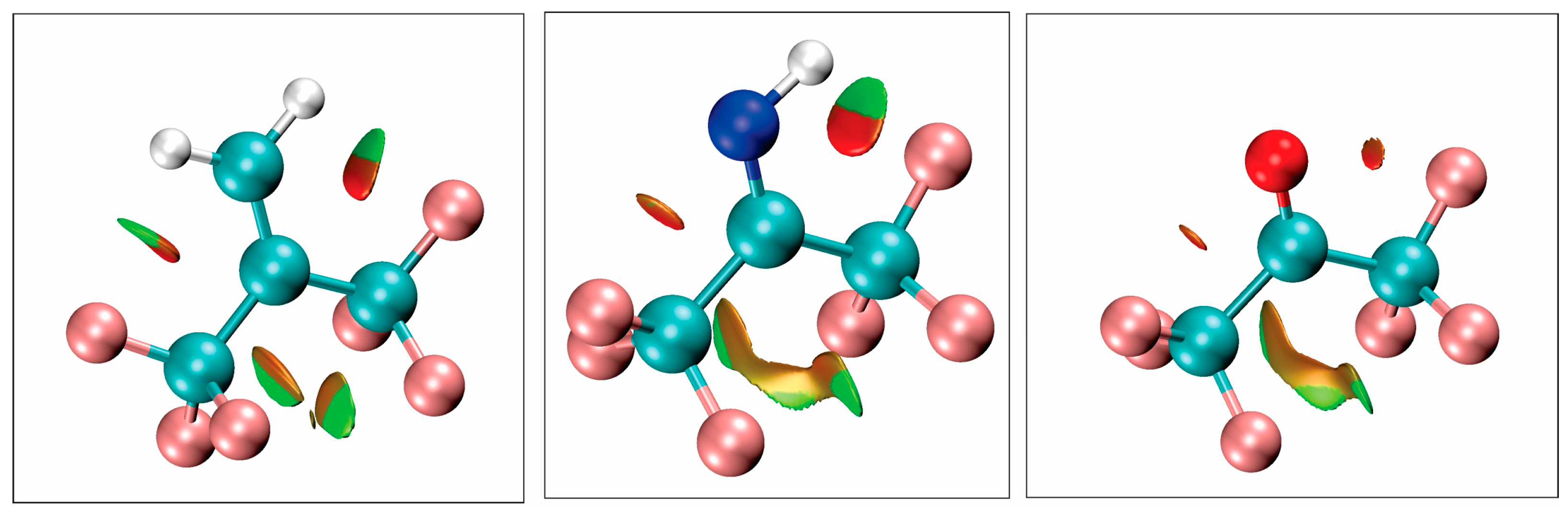
The above arguments are supported and augmented by calculations that reveal non-covalent interactions. Following the work of Johnson et al. [30] non-covalent interactions based on the electron density and its derivatives have been located for hexafluoroisobutene, hexafluoroacetone imine, and hexafluoroacetone. The results are presented in Figure 6. In this figure, green indicates weak attractive interactions whereas the orange and reddish colors indicate repulsive interactions. To obtain these plots, the electron density at the B3LYP level was analyzed using the Multiwfn [31,32] program and then visualized using VMD [33].
Within the figure, it is observed that in going from hexafluoroacetone-to-hexafluoroacetone imine to hexafluorisobutene the attractive interactions increase between the CF3 groups and O, NH and CH2, which in turn explains why the rotation of the CF3 groups becomes easier in that series. It is also observed that interactions with the lone pairs are purely repulsive whereas interactions with the NH and CH2 are partially attractive.

4. Materials and Methods

4.1. Experimental Methods

Hexafluoroacetone imine (95%, b.p. 16.5°) was purchased from Synquest Labs and used without further purification. A gas tank was pressurized to approx. 0.25 bar of hexafluoroacetone imine and then diluted with argon to a final pressure of approximately 6 bar. This solution of gases was pulsed through a solenoid valve into vacuum chambers held at approximately 10−4 bar causing a rotational cooling to approximately Trot ≈ 3 K. Rotational spectra were recorded between 5.5 GHz and 21 GHz on two types of spectrometers first a chirp-pulsed Fourier transform spectrometer, and then a Balle-Flygare cavity Fourier transform spectrometer. Both spectrometers have been explained in detail elsewhere [34,35,36,37,38]. Common to both instruments was the use of microsecond pulses of microwave radiation to bring about bulk rotational coherence of the cold target molecules. A free-induction decay, FID, was collected as a function of time as the bulk coherence is lost. FIDs are averaged to reduce random noise, and were then fast Fourier transformed to produce a frequency domain spectrum. The key difference between the spectrometers is that the chirp-pulsed spectrometer utilizes a microwave pulse of radiation containing a sweep, i.e., chirp, of frequencies from, say, 8–18 GHz. This chirp was then greatly amplified to powers of, in the present case, 5 W and then broadcast onto the molecules through a horn antenna. The FIDs collected were amplified and consisted of 800,000 points which was fast Fourier transformed on a suitably broad-banded oscilloscope. Line widths with this method were typically on the order of 80 kHz and line centers possess uncertainties of approximately 10 kHz. In the cavity experiment, monochromatic pulses of microwave radiation are amplified using a Fabry-Perot resonator which resulted in very high interrogation path lengths. FIDs were collected in the same way as above; however, the FIDs consist of approximately 1600 data points and, after mixing down, were fast Fourier transformed on a narrow band PC oscilloscope card. Line widths with this method were approximately 10 kHz and line center uncertainties were approximately 2 kHz.

4.2. Quantum Chemical Calculations

Initially, geometry optimizations and vibrational frequencies were calculated at the MP2/6-311G++(2d,2p) [11,12,13,14] level of theory using the Gaussian 16 rev. B01 software [39]. This method was relatively fast and sufficient to allow initial assignments of experimental spectroscopic transitions.
Higher-level quantum mechanical calculations were also pursued. We utilized the commonly used B3LYP [40,41,42,43], PBE0 [44,45] and CAM-B3LYP [46] hybrid density functionals as well as the B2PLYP [47,48] and DSD-PBEP86 [49,50] double-hybrid functionals. The CAM-B3LYP and DSD-PBEP86 functionals may be more accurately referred to as a range-separated hybrid functional and spin component scaled double-hybrid functional, respectively. To compensate for the inaccurate description of dispersion interactions within density functionals, Grimme’s D3 dispersion correction was used throughout in conjunction with Becke-Johnson damping (D3(BJ)) [51,52,53]. As a basis set, we utilized Dunning’s augmented triple zeta basis set aug-cc-pVTZ [54,55].
Geometry optimizations were carried out using the VeryTight optimization criterion and the very dense SuperFine integration grid. For the transition state search, the Hessian matrix was recomputed exactly at every third step. Subsequently, analytic harmonic frequency calculations were conducted to confirm the presence of a minimum of (first order) transition states. In addition, we carried out 2D relaxed surface scans with the B3LYP, PBE0 and CAM-B3LYP functionals to better understand the potential energy surface. To this end, we varied the F1C1C3N and F2C2C3N dihedral angles from 30° to −30° in steps of 2° (see Figure 3 for atom labeling). To reduce computational cost during the scan, the optimization criterion was lowered to Tight.
The zero-degree/zero-degree center of the scan corresponds to a planar F-CCC-F configuration. A one-dimensional, diagonal slice (lower left minimum through to upper right minimum) of the potential energy scan for hexafluoroacetone imine shows a double minimum.
For deriving semi-experimental equilibrium structures reSE, we conducted vibrational perturbation theory of second-order calculations (VPT2) [15] to obtain vibrational corrections for the rotational constants. In particular, we used Gaussian’s generalized VPT2 (GVPT2) implementation [16,17]. Note that the VPT2 calculation was conducted separately from the geometry optimization.
Lastly, Nudged-Elastic-Band [56] scans for the fluorinated variants using ORCA 6.0.1 [57,58] and 60 images at the B3LYP-D3(BJ)/aVTZ level were performed to further investigate the barrier heights.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/1420-3049/30/9/2051/s1, Table S1: Transition frequencies and quantum number assignments for hexafluoroacetone imine. Table S2: Overview of the electronic ( ∆ E e l ‡ ) and zero-point corrected ( ∆ E 0 ‡ ) barrier for the inversion. The singular imaginary mode ( v ~ imag) is also given associated with the transition state. Figure S1: 2-D potential energy scan for the six molecules of interest, acetone (top left), acetone imine (middle left), isobutene (bottom left), and, in each case, the hexafluorinated versions are shown to their right. Stationary points for the hexafluorinated species are shown with a white cross. See text for methods used. Figure S2: NEB scans for the fluorinated variants using ORCA 6.0.1 and 60 images and B3LYP-D3(BJ)/aVTZ (using Gaussian’s definition of B3LYP). The angle here is the average of the two dihedral angles defining the rotation of the CF3 groups.

Author Contributions

Conceptualization, S.A.C.; methodology, D.A.O., S.A.C. and B.H.; validation, D.A.O. and S.A.C.; formal analysis, D.A.O., B.H., W.C.P. and S.A.C.; investigation, D.A.O., D.J.F., G.S.G.II and B.E.L.; resources, S.E.N.; writing—original draft preparation, S.A.C.; writing—review and editing, D.A.O., B.H., D.J.F., G.S.G.II, B.E.L., W.C.P. and S.A.C.; visualization, B.H. and S.A.C.; supervision, D.A.O., S.E.N. and S.A.C.; project administration, D.A.O., S.E.N. and S.A.C.; funding acquisition, D.A.O., S.E.N. and S.A.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Science Foundation, grant number CHE-1011214. This work was also funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—389479699/GRK2455. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—OB 535/1-1.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All data presented in this study are available on request from the corresponding authors.

Acknowledgments

S. A. C. acknowledges support from the Taina Chao Fellowship.

Conflicts of Interest

The authors declare no conflicts of interest.

Correction Statement

This article has been republished with minor corrections to the title and Figure 4. This change does not affect the scientific content of the article.

References

  1. Gutowsky, H.S.; Germann, T.C. Internal Rotation and Structure of Isobutylene. J. Mol. Spectrosc. 1991, 147, 91–99. [Google Scholar] [CrossRef]
  2. Zou, L.; Guillemin, J.-C.; Belloche, A.; Jørgensen, J.K.; Margulès, L.; Motiyenko, R.A.; Groner, P. Millimeter-Wave Spectrum of 2-Propanimine. Mon. Not. R. Astron. Soc. 2023, 520, 4089–4102. [Google Scholar] [CrossRef]
  3. Groner, P. Experimental Two-Dimensional Torsional Potential Function for the Methyl Internal Rotors in Acetone. J. Mol. Struct. 2000, 550–551, 473–479. [Google Scholar] [CrossRef]
  4. Grubbs, G.S.; Novick, S.E.; Pringle, W.C.; Laane, J.; Ocola, E.J.; Cooke, S.A. Bis-Trifluoromethyl Effect: Doubled Transitions in the Rotational Spectra of Hexafluoroisobutene, (CF3)2C=CH2. J. Phys. Chem. A 2012, 116, 8169–8175. [Google Scholar] [CrossRef] [PubMed]
  5. Grabow, J.U.; Heineking, N.; Stahl, W. The Microwave Spectrum and Dipole Moment of Hexafluoropropanone. ZNA-1991-46a-0229. Z. Naturforsch 1991, 46a, 229–232. [Google Scholar] [CrossRef]
  6. Tolles, W.M.; Handelman, E.T.; Gwinn, W.D. Microwave Spectrum and Barrier to Internal Rotation in Trifluoronitromethane. J. Chem. Phys. 1965, 43, 3019–3024. [Google Scholar] [CrossRef]
  7. Cooke, S.A.; Minei, A.J. Are the CF3 Groups in 2,2-Bis(Trifluoromethyl)Oxirane Eclipsed or Staggered? Insights from Rotational Spectroscopy and Quantum Chemical Calculations. Chem. Phys. Lett. 2012, 535, 35–39. [Google Scholar] [CrossRef]
  8. Shahi, A.; Arunan, E. Microwave Spectrum of Hexafluoroisopropanol and Torsional Behavior of Molecules with a CF3–C–CF3 Group. J. Phys. Chem. A 2015, 119, 5650–5657. [Google Scholar] [CrossRef]
  9. Pickett, H.M. The Fitting and Prediction of Vibration-Rotation Spectra with Spin Interactions. J. Mol. Spectrosc. 1991, 148, 371–377. [Google Scholar] [CrossRef]
  10. Watson, J.K.G. Aspects of Quartic and Sextic Centrifugal Effects on Rotational Energy Levels. In Vibrational Spectra and Structure; Durig, J.R., Ed.; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1977; Volume 6. [Google Scholar]
  11. Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
  12. Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular-Orbital Methods. IX. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
  13. Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-Consistent Molecular Orbital Methods. XX. A Basis Set for Correlated Wave Functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
  14. Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.V.R. Efficient Diffuse Function-augmented Basis Sets for Anion Calculations. III. The 3-21+G Basis Set for First-row Elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
  15. Nielsen, H.H. The Vibration-Rotation Energies of Molecules. Rev. Mod. Phys. 1951, 23, 90–136. [Google Scholar] [CrossRef]
  16. Barone, V. Anharmonic Vibrational Properties by a Fully Automated Second-Order Perturbative Approach. J. Chem. Phys. 2005, 122, 14108. [Google Scholar] [CrossRef]
  17. Barone, V.; Bloino, J.; Guido, C.A.; Lipparini, F. A Fully Automated Implementation of VPT2 Infrared Intensities. Chem. Phys. Lett. 2010, 496, 157–161. [Google Scholar] [CrossRef]
  18. Clabo, D.A.; Allen, W.D.; Remington, R.B.; Yamaguchi, Y.; Schaefer, H.F. A Systematic Study of Molecular Vibrational Anharmonicity and Vibration—Rotation Interaction by Self-Consistent-Field Higher-Derivative Methods. Asymmetric Top Molecules. Chem. Phys. 1988, 123, 187–239. [Google Scholar] [CrossRef]
  19. Watson, J.K.G.; Roytburg, A.; Ulrich, W. Least-Squares Mass-Dependence Molecular Structures. J. Mol. Spectrosc. 1999, 196, 102–119. [Google Scholar] [CrossRef]
  20. Demaison, J. Experimental, Semi-Experimental and Ab Initio Equilibrium Structures. Mol. Phys. 2007, 105, 3109–3138. [Google Scholar] [CrossRef]
  21. Kraitchman, J. Determination of Molecular Structure from Microwave Spectroscopic Data. Am. J. Phys. 1953, 21, 17–24. [Google Scholar] [CrossRef]
  22. Bohn, R.K.; Montgomery, J.A.; Michels, H.H.; Fournier, J.A. Second Moments and Rotational Spectroscopy. J. Mol. Spectrosc. 2016, 325, 42–49. [Google Scholar] [CrossRef]
  23. Bailey, W.C.; Bohn, R.K.; Dewberry, C.T.; Grubbs, G.S., II; Cooke, S.A. The Structure and Helicity of Perfluorooctanonitrile, CF3-(CF2)6-CN. J. Mol. Spectrosc. 2011, 270, 61–65. [Google Scholar] [CrossRef]
  24. Krause, H.; Sutter, D.H. The Molecular Zeeman Effect of Imines. I. Methanimine, Its Molecular g-Tensor, Its Magnetic Susceptibility Anisotropies, Its Molecular Electric Quadrupole Moment, Its Electric Field Gradient at the Nitrogen Nucleus, and Its Nitrogen Spin-Rotation Coupling. Z. Naturforschung A 1989, 44, 1063–1078. [Google Scholar] [CrossRef]
  25. Groner, P.; Nanaie, H.; Durig, J.R.; DesMarteau, D.D. The Microwave Spectrum of Difluoromethanimine, CF2=NH. J. Chem. Phys. 1988, 89, 3983–3985. [Google Scholar] [CrossRef]
  26. Möller, K.; Winnewisser, M.; Pawelke, G.; Bürger, H. The Microwave and Millimeter Wave Spectrum of Difluoromethanimine, F2C NH: Rotational and Nuclear Hyperfine Structure Analysis. J. Mol. Struct. 1988, 190, 343–355. [Google Scholar] [CrossRef]
  27. Allred, A.L. Electronegativity Values from Thermochemical Data. J. Inorg. Nucl. Chem. 1961, 17, 215–221. [Google Scholar] [CrossRef]
  28. True, J.E.; Thomas, T.D.; Winter, R.W.; Gard, G.L. Electronegativities from Core-Ionization Energies: Electronegativities of SF5 and CF3. Inorg. Chem. 2003, 42, 4437–4441. [Google Scholar] [CrossRef]
  29. Gordy, W.; Cook, R.L. Microwave Molecular Spectra, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
  30. Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
  31. Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
  32. Lu, T. A Comprehensive Electron Wavefunction Analysis Toolbox for Chemists, Multiwfn. J. Chem. Phys. 2024, 161, 082503. [Google Scholar] [CrossRef]
  33. Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
  34. Grubbs, G.S., II; Dewberry, C.T.; Etchison, K.C.; Kerr, K.E.; Cooke, S.A. A Search Accelerated Correct Intensity Fourier Transform Microwave Spectrometer with Pulsed Laser Ablation Source. Rev. Sci. Instrum. 2007, 78, 096106. [Google Scholar] [CrossRef] [PubMed]
  35. Grubbs, G.S.; Powoski, R.A.; Jojola, D.; Cooke, S.A. Some Geometric and Electronic Structural Effects of Perfluorinating Propionyl Chloride. J. Phys. Chem. A 2010, 114, 8009–8015. [Google Scholar] [CrossRef]
  36. Balle, T.J.; Flygare, W.H. Fabry–Perot Cavity Pulsed Fourier Transform Microwave Spectrometer with a Pulsed Nozzle Particle Source. Rev. Sci. Instrum. 1981, 52, 33–45. [Google Scholar] [CrossRef]
  37. Walker, A.R.H.; Chen, W.; Novick, S.E.; Bean, B.D.; Marshall, M.D. Determination of the Structure of HBr OCS. J. Chem. Phys. 1995, 102, 7298–7305. [Google Scholar] [CrossRef]
  38. Grubbs, G.S.; Obenchain, D.A.; Pickett, H.M.; Novick, S.E. H2—AgCl: A Spectroscopic Study of a Dihydrogen Complex. J. Chem. Phys. 2014, 141, 114306. [Google Scholar] [CrossRef]
  39. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  40. Becke, A.D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
  41. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
  42. Vosko, S.H.; Wilk, L.; Nusair, M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
  43. Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
  44. Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew–Burke–Ernzerhof Exchange-Correlation Functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
  45. Adamo, C.; Barone, V. Toward Reliable Density Functional Methods without Adjustable Parameters: The PBE0 Model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  46. Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange–Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
  47. Grimme, S. Semiempirical Hybrid Density Functional with Perturbative Second-Order Correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [PubMed]
  48. Schwabe, T.; Grimme, S. Double-Hybrid Density Functionals with Long-Range Dispersion Corrections: Higher Accuracy and Extended Applicability. Phys. Chem. Chem. Phys. 2007, 9, 3397–3406. [Google Scholar] [CrossRef]
  49. Kozuch, S.; Martin, J.M.L. DSD-PBEP86: In Search of the Best Double-Hybrid DFT with Spin-Component Scaled MP2 and Dispersion Corrections. Phys. Chem. Chem. Phys. 2011, 13, 20104–20107. [Google Scholar] [CrossRef] [PubMed]
  50. Kozuch, S.; Martin, J.M.L. Spin-component-scaled Double Hybrids: An Extensive Search for the Best Fifth-rung Functionals Blending DFT and Perturbation Theory. J. Comput. Chem. 2013, 34, 2327–2344. [Google Scholar] [CrossRef]
  51. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104–154119. [Google Scholar] [CrossRef]
  52. Smith, D.G.A.; Burns, L.A.; Patkowski, K.; Sherrill, C.D. Revised Damping Parameters for the D3 Dispersion Correction to Density Functional Theory. J. Phys. Chem. Lett. 2016, 7, 2197–2203. [Google Scholar] [CrossRef]
  53. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  54. Dunning, T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
  55. Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
  56. Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef]
  57. Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
  58. Neese, F. Software Update: The ORCA Program System—Version 5.0. WIREs Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]
Molecules 30 02051 g001
Figure 1. Two series of isoelectronic molecules. (a–c) is isobutene, acetone imine, and acetone. (d–f) are the hexafluorinated analogs.
Figure 1. Two series of isoelectronic molecules. (a–c) is isobutene, acetone imine, and acetone. (d–f) are the hexafluorinated analogs.
Molecules 30 02051 g001
Molecules 30 02051 g002
Figure 2. A section of the spectra recorded for hexafluoroacetone imine using a cavity Fourier transform microwave spectrometer. The quantum number assignments given follow J′K−1K+1F ← J″K−1K+1F. The portion of spectra shown is the Fourier transform of 75 free-induction decays averaged together. Transitions appear as Doppler doublets and the average of the two Doppler components is taken as the line center. The vertical lines indicate the predicted frequencies for these transitions using the rotational constants given in Table 1.
Figure 2. A section of the spectra recorded for hexafluoroacetone imine using a cavity Fourier transform microwave spectrometer. The quantum number assignments given follow J′K−1K+1F ← J″K−1K+1F. The portion of spectra shown is the Fourier transform of 75 free-induction decays averaged together. Transitions appear as Doppler doublets and the average of the two Doppler components is taken as the line center. The vertical lines indicate the predicted frequencies for these transitions using the rotational constants given in Table 1.
Molecules 30 02051 g002
Molecules 30 02051 g003
Figure 3. Hexafluoroacetone imine calculated at the MP2/6-311G++(2d,2p) level in the ab- and bc- planes of its principal axes system.
Figure 3. Hexafluoroacetone imine calculated at the MP2/6-311G++(2d,2p) level in the ab- and bc- planes of its principal axes system.
Molecules 30 02051 g003
Molecules 30 02051 g004
Figure 4. A 2-D potential energy scan for hexafluoroacetone imine. Stationary points are shown with a white cross. Please refer to Figure 3 for the atomic number scheme, and to the text for further discussion.
Figure 4. A 2-D potential energy scan for hexafluoroacetone imine. Stationary points are shown with a white cross. Please refer to Figure 3 for the atomic number scheme, and to the text for further discussion.
Molecules 30 02051 g004
Molecules 30 02051 g005
Figure 5. Top: an example, i.e., not to any scale but just showing form, of a relevant potential energy plot with the x-axis being the F1-C1-C2-F2 dihedral angle. Middle: Bar chart showing how, for the series HFIB, HFAI, HFA the barrier V1 decreases as the distance between the C1 and C2 atoms increases. Bottom: Bar chart showing how the V2 barrier height increases as the C=X distance decreases, X=C, N, and O. HFIB is hexafluoroisobutene, HFAI is hexafluoroacetone imine, and HFA is hexafluoroacetone. See Figure 3 for the atom labeling scheme.
Figure 5. Top: an example, i.e., not to any scale but just showing form, of a relevant potential energy plot with the x-axis being the F1-C1-C2-F2 dihedral angle. Middle: Bar chart showing how, for the series HFIB, HFAI, HFA the barrier V1 decreases as the distance between the C1 and C2 atoms increases. Bottom: Bar chart showing how the V2 barrier height increases as the C=X distance decreases, X=C, N, and O. HFIB is hexafluoroisobutene, HFAI is hexafluoroacetone imine, and HFA is hexafluoroacetone. See Figure 3 for the atom labeling scheme.
Molecules 30 02051 g005
Molecules 30 02051 g006
Figure 6. From left to right regions of most attractive (green) and most repulsive (red) interactions for hexafluoroisobutene, hexafluoroacetone imine, and hexafluoroacetone. Colors between red and green indicate areas of intermediate attraction/repulsion.
Figure 6. From left to right regions of most attractive (green) and most repulsive (red) interactions for hexafluoroisobutene, hexafluoroacetone imine, and hexafluoroacetone. Colors between red and green indicate areas of intermediate attraction/repulsion.
Molecules 30 02051 g006
Table 1. Calculated and experimentally determined effective ground-state rotational constants, centrifugal distortion constants, and nitrogen nuclear electric quadrupole coupling constants for hexafluoroacetone imine.
Table 1. Calculated and experimentally determined effective ground-state rotational constants, centrifugal distortion constants, and nitrogen nuclear electric quadrupole coupling constants for hexafluoroacetone imine.
MP2/6-311G++(2d,2p)State IState II
A (MHz)2158.6102170.17085(35)2170.16744(35)
B (MHz)1045.4461043.25444(14)1043.24681(14)
C (MHz)937.933936.37030(13)936.37059(13)
ΔJ (kHz)0.0540.0576(10)0.0525(10)
ΔJK (kHz)0.150.2047(62)0.2219(62)
ΔK (kHz)−0.11−0.363(26)−0.457(26)
δJ (kHz)0.00610.00734(44)0.00471(43)
δK (kHz)−0.35−0.475(41)−0.563(41)
χaa (MHz)-−5.0732(33)
χbb (MHz)-2.9924(40)
χcc (MHz)-2.0809(40)
RMS (kHz) 1-2.7
N-176177
1 Microwave root mean square = ∑ [ o b s − c a l c 2 ] / N where N is the number of transitions.
Table 2. Experimentally determined effective ground-state rotational constants, centrifugal distortion constants, and nitrogen nuclear electric quadrupole coupling constants for the parent and isotopologues for State I of hexafluoroacetone imine.
Table 2. Experimentally determined effective ground-state rotational constants, centrifugal distortion constants, and nitrogen nuclear electric quadrupole coupling constants for the parent and isotopologues for State I of hexafluoroacetone imine.
Parent13C113C213C315N
A (MHz)2170.17085(35)2170.2055(79)2170.1985(44)2165.3028(24)2134.1858(28)
B (MHz)1043.25444(14)1039.72015(93)1039.65915(41)1043.33695(20)1043.25063(14)
C (MHz)936.37030(13)933.51356(21)933.47028(12)935.530070(95)929.59788(10)
ΔJ (kHz)0.0576(10)[0.0576][0.0576][0.0576][0.0576]
ΔJK (kHz)0.2047(62)[0.2047][0.2047][0.2047][0.2047]
ΔK (kHz)−0.363(26)[−0.363][−0.363][−0.363][−0.363]
δJ (kHz)0.00734(44)[0.00734][0.00734][0.00734][0.00734]
δK (kHz)−0.475(41)[−0.475][−0.475][−0.475][−0.475]
χaa (MHz)−5.0732(33)−5.052(31)−5.109(24)−5.070(21)-
χbb (MHz)2.9924(55)2.97(16)2.974(89)2.961(70)-
χcc (MHz)2.0809(40)2.08(16)2.135(86)2.109(67)-
RMS (kHz) 12.72.84.31.92.9
N17628392723
1 Microwave root mean square = ∑ [ o b s − c a l c 2 ] / N where N is the number of transitions.
Table 3. Experimentally determined effective ground-state rotational constants, centrifugal distortion constants, and nitrogen nuclear electric quadrupole coupling constants for the parent and isotopologues for State II of hexafluoroacetone imine.
Table 3. Experimentally determined effective ground-state rotational constants, centrifugal distortion constants, and nitrogen nuclear electric quadrupole coupling constants for the parent and isotopologues for State II of hexafluoroacetone imine.
Parent13C113C213C315N
A (MHz)2170.16744(35)2170.2155(79)2170.2607(41)2165.2925(25)2134.1836(21)
B (MHz)1043.24681(14)1039.71300(93)1039.65821(44)1043.32924(20)1043.24306(13)
C (MHz)936.37059(13)933.51364(21)933.46923(11)935.530474(96)929.59823(10)
ΔJ (kHz)0.0525(10)[0.0525][0.05764][0.05764][0.05764]
ΔJK (kHz)0.2219(62)[0.2219][0.2046][0.2046][0.2046]
ΔK (kHz)−0.457(26)[−0.457][−0.364][−0.364][−0.364]
δJ (kHz)0.00471(43)[0.00471][0.00738][0.00738][0.00738]
δK (kHz)−0.563(41)[−0.563][−0.473][−0.473][−0.473]
χaa (MHz)−5.0732(33)−5.052(31)−5.109(24)−5.070(21)-
χbb (MHz)2.9924(55)2.97(16)2.974(89)2.961(70)-
χcc (MHz)2.0809(40)2.08(16)2.135(86)2.109(67)-
RMS (kHz) 12.73.74.31.92.9
N17728392723
1 Microwave root mean square = ∑ [ o b s − c a l c 2 ] / N where N is the number of transitions.
Table 4. Overview of the electronic (ΔEel‡) and zero-point corrected (ΔE0‡) barrier for the inversion. The singular imaginary mode ( v ~ imag) is also given associated with the transition state. All methods used (i) Grimme’s dispersion correction was used throughout in conjunction with Becke-Johnson damping, D3(BJ), and (ii) the aug-cc-pVTZ basis sets were used.
Table 4. Overview of the electronic (ΔEel‡) and zero-point corrected (ΔE0‡) barrier for the inversion. The singular imaginary mode ( v ~ imag) is also given associated with the transition state. All methods used (i) Grimme’s dispersion correction was used throughout in conjunction with Becke-Johnson damping, D3(BJ), and (ii) the aug-cc-pVTZ basis sets were used.
MethodΔEel‡/cm−1ΔE0‡/cm−1 v ~ v ~ imag/i cm−1
B3LYP11811732.0
PBE011211231.3
CAM-B3LYP11211231.7
B2PLYP12712633.0
DSD-PBEP86-D313913834.2
Table 5. Key structural parameters for hexafluoroacetone imine determined from the zero-point corrected PBE0-D3(BJ)/aug-cc-pVTZ structure. See Figure 3 for the atom labeling scheme.
Table 5. Key structural parameters for hexafluoroacetone imine determined from the zero-point corrected PBE0-D3(BJ)/aug-cc-pVTZ structure. See Figure 3 for the atom labeling scheme.
ParameterValue
r (C1-C3)/Å1.534
r (C2-C3)/Å1.536
r (C3-N)/Å1.984
∠ (C1-C3-C2)/degrees116.4
D(F1-C1-C3-N)/degrees−20.5
Table 6. The PBE0-D3(BJ)/aug-cc-pVTZ equilibrium Xe, and zero-point corrected X0 rotational constants for hexafluoroacetone imine. All values are in MHz.
Table 6. The PBE0-D3(BJ)/aug-cc-pVTZ equilibrium Xe, and zero-point corrected X0 rotational constants for hexafluoroacetone imine. All values are in MHz.
AeA0BeB0CeC0
Parent2180.962168.5451045.1091038.330938.792933.093
13C=N2175.9952163.6191045.1091038.444937.871932.272
15N2145.0542132.831045.1021038.319932.072926.398
13C, N lone pair side2180.9162168.6191041.4471034.739935.829930.183
13C, NH side2180.8952168.5941041.5101034.811935.875930.243
Table 7. Kraitchman substitution coordinates, in Angstroms, for the heavy atoms in hexafluoroacetone imine. The c-coordinates are either imaginary * or are zero to two significant figures.
Table 7. Kraitchman substitution coordinates, in Angstroms, for the heavy atoms in hexafluoroacetone imine. The c-coordinates are either imaginary * or are zero to two significant figures.
State IState IIPBE0-D3(BJ)/aug-cc-pVTZ
ababab
C1−1.2867(12)0 *−1.2876(12)0 *−1.29−0.08
C21.2968(11)0 *1.2980(12)0 *1.300.07
C30 *0.7244(21)0 *0.7229(21)00.73
N0.060(25)1.9910(7)0.073(20)1.9904(7)0.061.98
* These coordinates are imaginary consistent with the atom being close, or on, a principal axis. We have taken them to indicate a coordinate of zero.
Table 8. The values of the 14N-nuclear quadrupole coupling tensor components, χ, for hexafluoroacetone imine, methanimine (CH2NH) [24] and difluomethanimine (CF2NH) [25,26].
Table 8. The values of the 14N-nuclear quadrupole coupling tensor components, χ, for hexafluoroacetone imine, methanimine (CH2NH) [24] and difluomethanimine (CF2NH) [25,26].
CH2NHCF2NH(CF3)2CNH
χaa/MHz−0.9131(16)1.029(20)−5.0732(33)
χbb/MHz−2.6688(14)−2.56(17)2.9924(40)
χcc/MHz3.5819(21)1.531(22)2.0809(40)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Obenchain, D.A.; Hartwig, B.; Frohman, D.J.; Grubbs, G.S., II; Long, B.E.; Pringle, W.C.; Novick, S.E.; Cooke, S.A. A Pure Rotational Spectroscopic Study of Two Nearly-Equivalent Structures of Hexafluoroacetone Imine, (CF3)2C=NH. Molecules 2025, 30, 2051. https://doi.org/10.3390/molecules30092051

AMA Style

Obenchain DA, Hartwig B, Frohman DJ, Grubbs GS II, Long BE, Pringle WC, Novick SE, Cooke SA. A Pure Rotational Spectroscopic Study of Two Nearly-Equivalent Structures of Hexafluoroacetone Imine, (CF3)2C=NH. Molecules. 2025; 30(9):2051. https://doi.org/10.3390/molecules30092051

Chicago/Turabian Style

Obenchain, Daniel A., Beppo Hartwig, Daniel J. Frohman, G. S. Grubbs, II, B. E. Long, Wallace C. Pringle, Stewart E. Novick, and S. A. Cooke. 2025. "A Pure Rotational Spectroscopic Study of Two Nearly-Equivalent Structures of Hexafluoroacetone Imine, (CF3)2C=NH" Molecules 30, no. 9: 2051. https://doi.org/10.3390/molecules30092051

APA Style

Obenchain, D. A., Hartwig, B., Frohman, D. J., Grubbs, G. S., II, Long, B. E., Pringle, W. C., Novick, S. E., & Cooke, S. A. (2025). A Pure Rotational Spectroscopic Study of Two Nearly-Equivalent Structures of Hexafluoroacetone Imine, (CF3)2C=NH. Molecules, 30(9), 2051. https://doi.org/10.3390/molecules30092051

Article Metrics

Back to TopTop