Chiral Pseudo-D6h Dy(III) Single-Molecule Magnet Based on a Hexaaza Macrocycle
Abstract
1. Introduction
2. Results and Discussion
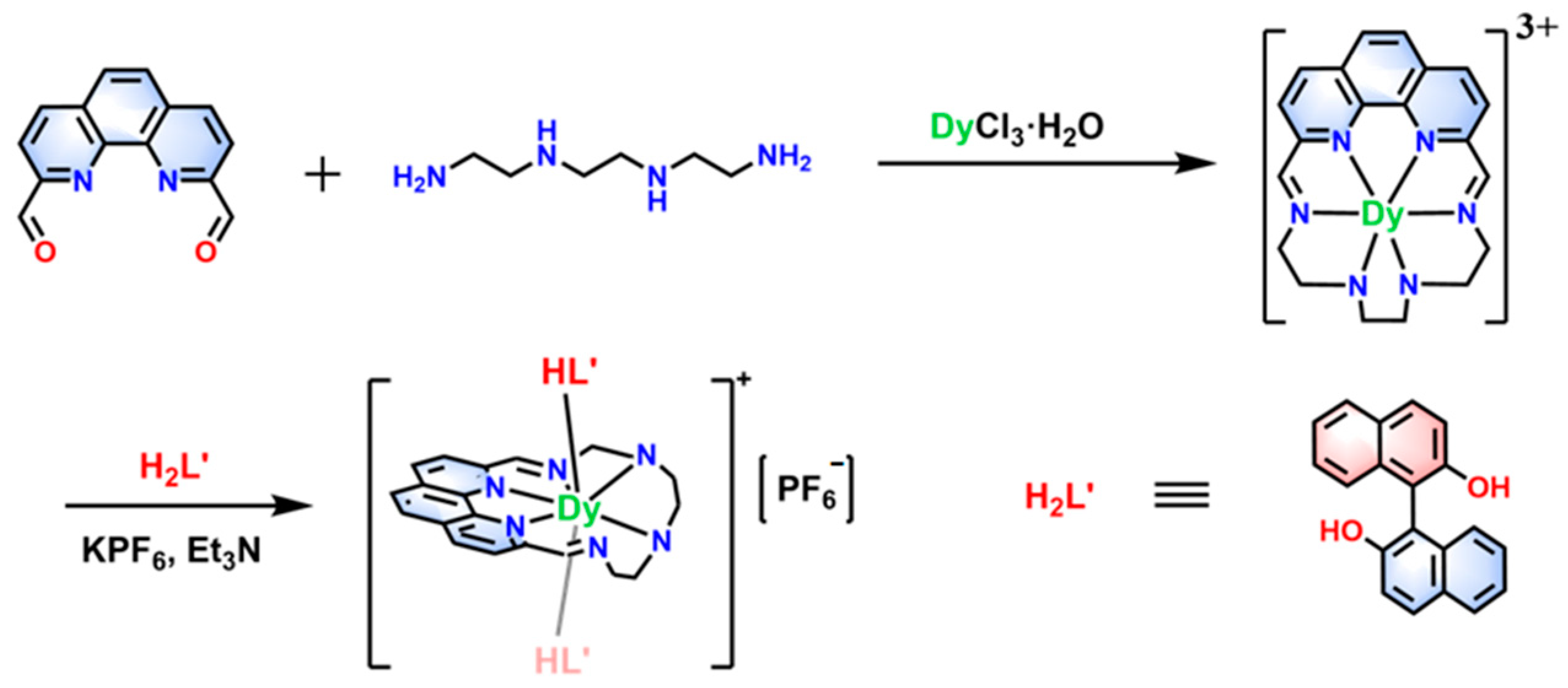
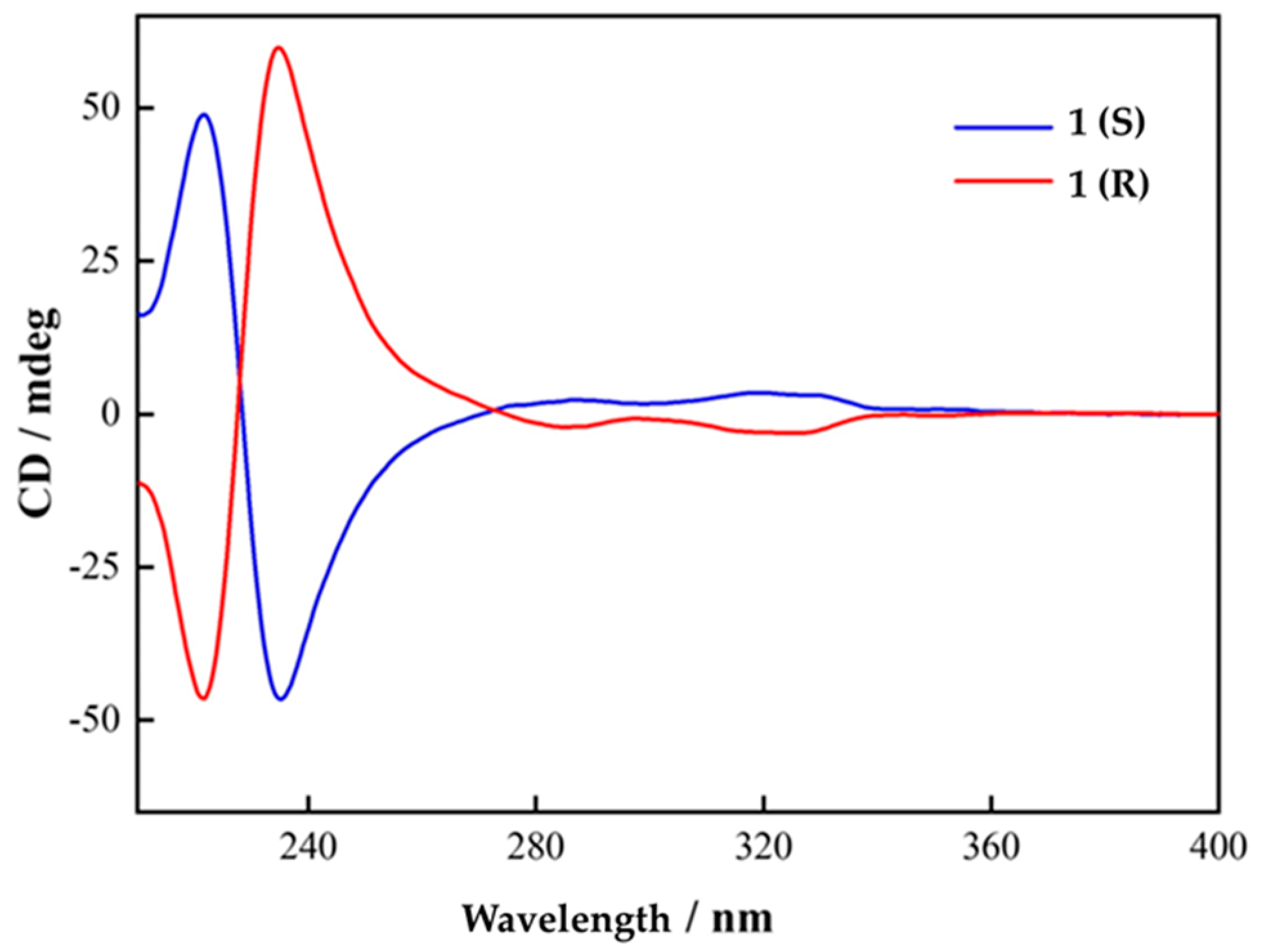
2.1. Synthesis and Circular Dichroism Spectra
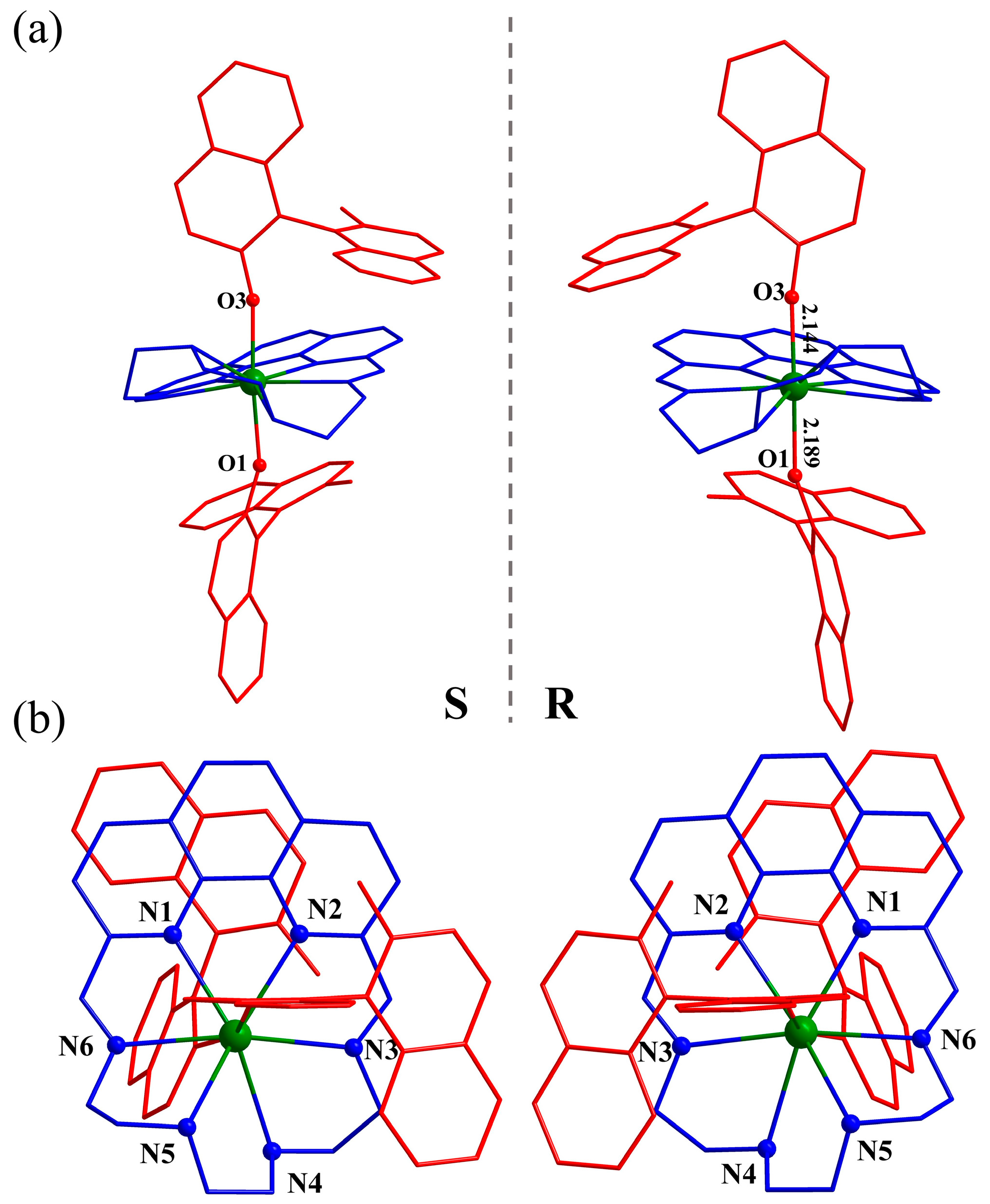
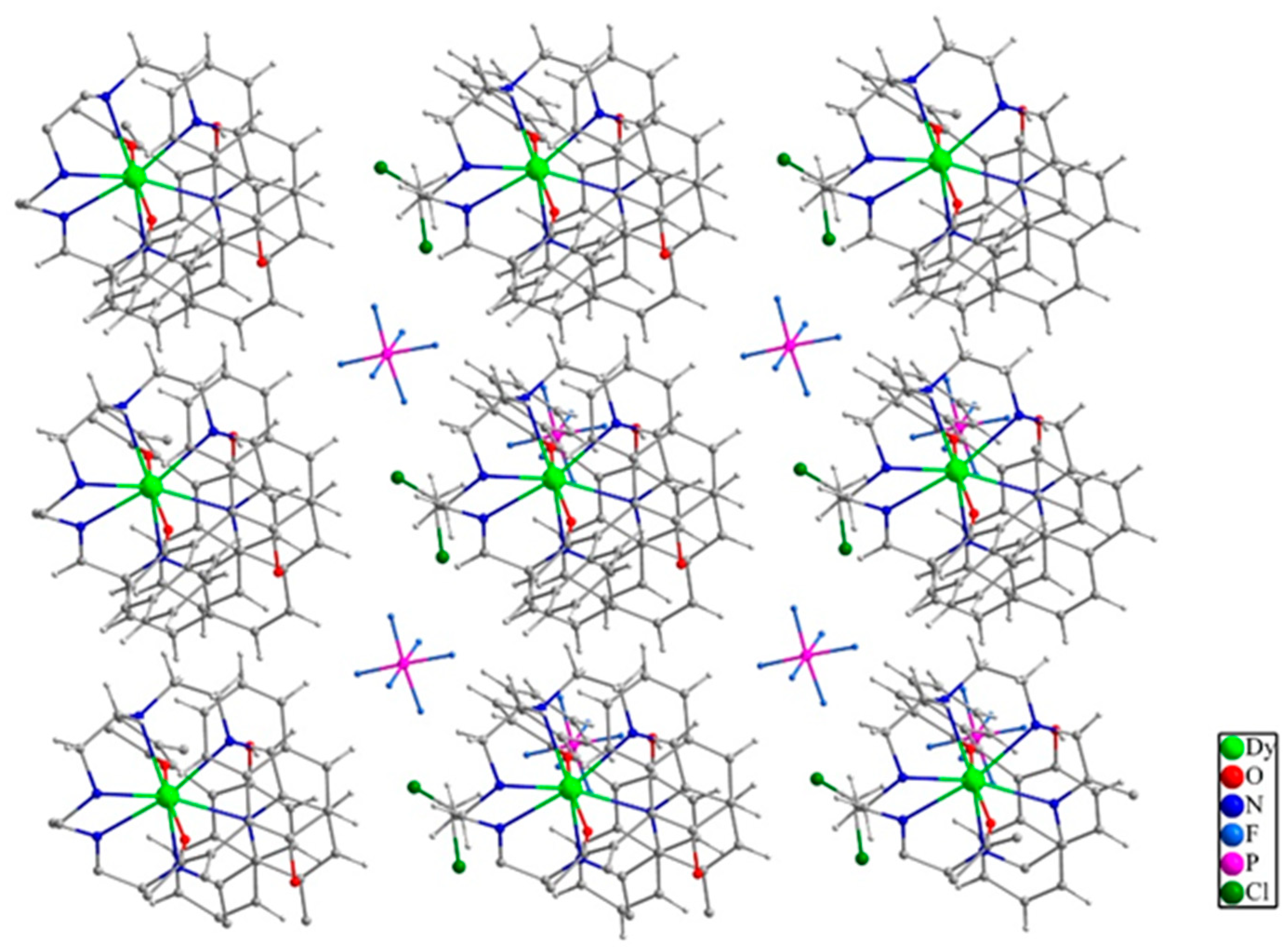
2.2. Structure
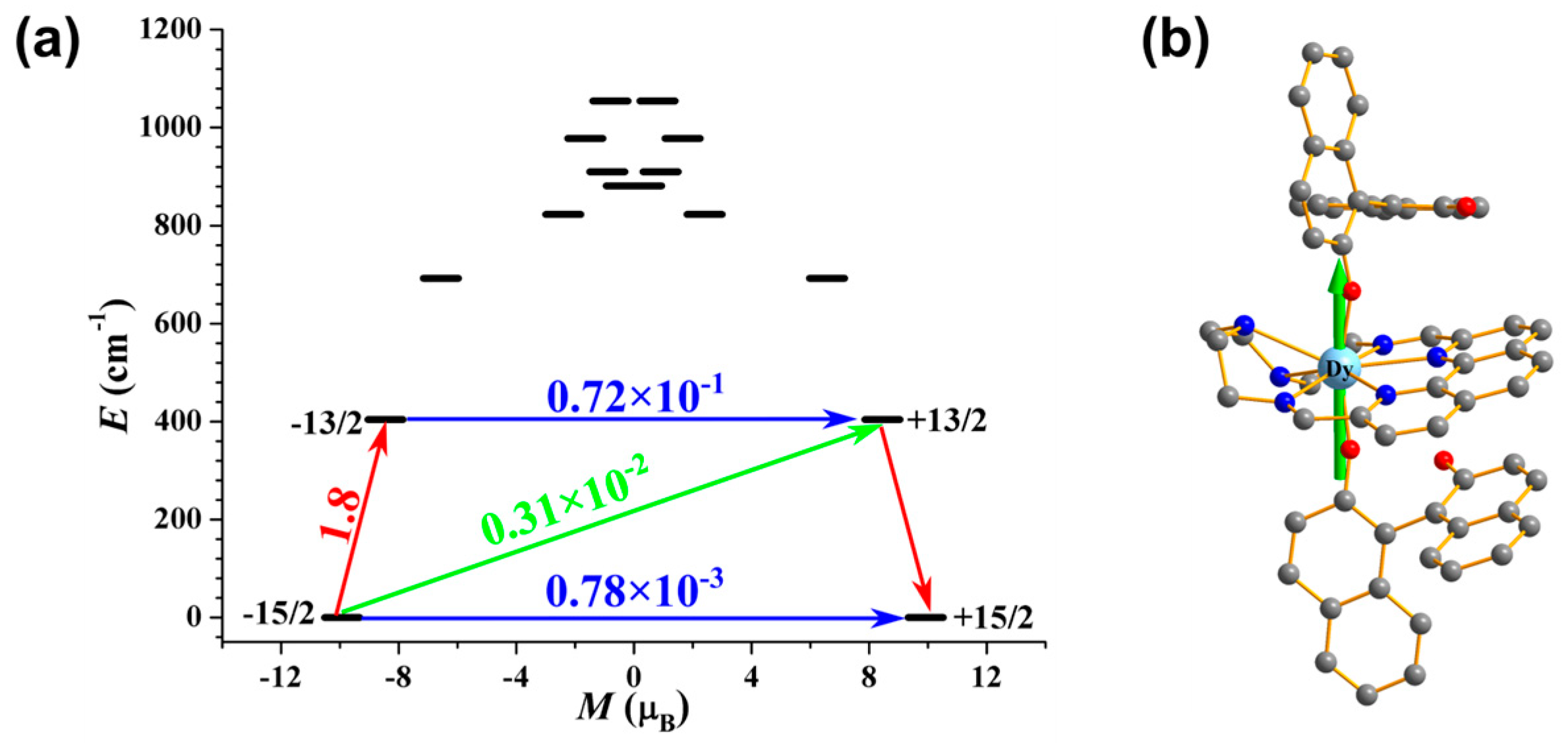
2.3. Magnetism
3. Materials and Methods
3.1. Synthesis
3.1.1. Synthesis of the Precursor phenN6-DyCl3
3.1.2. Synthesis of Complexes [Dy(phenN6)(HL′)2]PF6·CH2Cl2 (1R/1S)
3.2. Physical Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, F.-S.; Bar, A.K.; Layfield, R.A. Main Group Chemistry at the Interface with Molecular Magnetism. Chem. Rev. 2019, 119, 8479–8505. [Google Scholar] [CrossRef]
- Kragskow, J.G.C.; Mattioni, A.; Staab, J.K.; Reta, D.; Skelton, J.M.; Chilton, N.F. Spin–phonon coupling and magnetic relaxation in single-molecule magnets. Chem. Soc. Rev. 2023, 52, 4567–4585. [Google Scholar] [CrossRef] [PubMed]
- Zakrzewski, J.J.; Liberka, M.; Wang, J.; Chorazy, S.; Ohkoshi, S.-I. Optical Phenomena in Molecule-Based Magnetic Materials. Chem. Rev. 2024, 124, 5930–6050. [Google Scholar] [CrossRef] [PubMed]
- Cavallini, M.; Gomez-Segura, J.; Ruiz-Molina, D.; Massi, M.; Albonetti, C.; Rovira, C.; Veciana, J.; Biscarini, F. Magnetic Information Storage on Polymers by Using Patterned Single-Molecule Magnets. Angew. Chem. Int. Ed. 2005, 44, 888–892. [Google Scholar] [CrossRef] [PubMed]
- Damgaard-Møller, E.; Krause, L.; Tolborg, K.; Macetti, G.; Genoni, A.; Overgaard, J. Quantification of the Magnetic Anisotropy of a Single-Molecule Magnet from the Experimental Electron Density. Angew. Chem. Int. Ed. 2020, 59, 21203–21209. [Google Scholar] [CrossRef]
- Gao, C.; Genoni, A.; Gao, S.; Jiang, S.; Soncini, A.; Overgaard, J. Observation of the asphericity of 4f-electron density and its relation to the magnetic anisotropy axis in single-molecule magnets. Nat. Chem. 2020, 12, 213–219. [Google Scholar] [CrossRef]
- Raza, A.; Perfetti, M. Electronic structure and magnetic anisotropy design of functional metal complexes. Coord. Chem. Rev. 2023, 490, 215213. [Google Scholar] [CrossRef]
- Ding, Y.-S.; Chilton, N.F.; Winpenny, R.E.P.; Zheng, Y.-Z. On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet. Angew. Chem. Int. Ed. 2016, 55, 16071–16074. [Google Scholar] [CrossRef]
- Zhong, X.; Rana, R.; Luo, T.-K.; Wu, Y.-F.; Peng, Y.; Liu, S.-J.; Rajaraman, G.; Wen, H.-R. Systematically study of ligands field effect on a pseudo-D6h Dy(III) single-ion magnet with axially asymmetric ligands. J. Mol. Struct. 2025, 1338, 142270. [Google Scholar] [CrossRef]
- Deng, W.; Du, S.-N.; Ruan, Z.-Y.; Zhao, X.-J.; Chen, Y.-C.; Liu, J.-L.; Tong, M.-L. Aggregation-induced suppression of quantum tunneling by manipulating intermolecular arrangements of magnetic dipoles. Aggregate 2024, 5, e441. [Google Scholar] [CrossRef]
- Reta, D.; Kragskow, J.G.C.; Chilton, N.F. Ab Initio Prediction of High-Temperature Magnetic Relaxation Rates in Single-Molecule Magnets. J. Am. Chem. Soc. 2021, 143, 5943–5950. [Google Scholar] [CrossRef]
- Blagg, R.J.; Ungur, L.; Tuna, F.; Speak, J.; Comar, P.; Collison, D.; Wernsdorfer, W.; McInnes, E.J.L.; Chibotaru, L.F.; Winpenny, R.E.P. Magnetic relaxation pathways in lanthanide single-molecule magnets. Nat. Chem. 2013, 5, 673–678. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.-J.; Fu, Z.-Y.; Sun, R.; Yuan, J.; Liu, C.-M.; Zou, B.; Wang, B.-W.; Kou, H.-Z. Mechanochromic and Single-Molecule Magnetic Properties of a Rhodamine 6G Dy(III) Complex. ACS Appl. Electron. Mater. 2021, 3, 1368–1374. [Google Scholar] [CrossRef]
- Kong, H.; Wang, J.-Y.; Liu, J.-C.; Zhang, L.; Liao, P.-Y.; Qi, Y.-Q.; Liu, Z.; Wu, S.-G.; Tong, M.-L. Photochromic Dysprosium Single-Molecule Magnet Featuring Reversible Redox Transformation of Polyoxomolybdate Moiety. Angew. Chem. Int. Ed. 2025, 64, e202422557. [Google Scholar] [CrossRef] [PubMed]
- Osipov, N.G.; Faraonov, M.A.; Kuzmin, A.V.; Khasanov, S.S.; Dmitriev, A.A.; Gritsan, N.P.; Denisov, N.N.; Otsuka, A.; Kitagawa, H.; Konarev, D.V. Complexes (TBA+){(TMI-NPS)2·LnIIII4}− (Ln = Dy, Tb) with two axial photochromic spiropyran ligands: Photoswitching and zero-field SIM behaviour with a high magnetization blocking barrier for the Dy complex. Inorg. Chem. Front. 2025, 12, 2092–2102. [Google Scholar] [CrossRef]
- Wu, J.; Zhu, Z.; Tang, J. Recent advancements of photo-responsive lanthanide single-molecule magnets. Chin. Chem. Lett. 2025, in press. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, X.; Ying, B.; Dong, Y.; Sun, A.; Li, D.-F. Macrocyclic Hexagonal Bipyramidal Dy(III)-Based Single-Molecule Magnets with a D6h Symmetry. Cryst. Growth Des. 2023, 23, 6967–6973. [Google Scholar] [CrossRef]
- Liu, S.; Gil, Y.; Zhao, C.; Wu, J.; Zhu, Z.; Li, X.L.; Aravena, D.; Tang, J. A conjugated Schiff-base macrocycle weakens the transverse crystal field of air-stable dysprosium single-molecule magnets. Inorg. Chem. Front. 2022, 9, 4982–4989. [Google Scholar] [CrossRef]
- Wu, J.; Li, J.; Yang, Q.; Liu, D.; Tang, J.; Zhang, B. Fine-Tuning the Anisotropies of Air-Stable Single-Molecule Magnets Based on Macrocycle Ligands. Inorg. Chem. 2025, 64, 999–1006. [Google Scholar] [CrossRef]
- Cai, X.; Cheng, Z.; Wu, Y.; Jing, R.; Tian, S.-Q.; Chen, L.; Li, Z.-Y.; Zhang, Y.-Q.; Cui, H.-H.; Yuan, A. Tuning the Equatorial Negative Charge in Hexagonal Bipyramidal Dysprosium(III) Single-Ion Magnets to Improve the Magnetic Behavior. Inorg. Chem. 2022, 61, 3664–3673. [Google Scholar] [CrossRef]
- Armenis, A.S.; Mondal, A.; Giblin, S.R.; Alexandropoulos, D.I.; Tang, J.; Layfield, R.A.; Stamatatos, T.C. ‘Kick-in the head’: High-performance and air-stable mononuclear DyIII single-molecule magnets with pseudo-D6h symmetry from a [1+1] Schiff-base macrocycle approach. Inorg. Chem. Front. 2025, 12, 1214–1224. [Google Scholar] [CrossRef]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Long, J.; Tolpygin, A.O.; Mamontova, E.; Lyssenko, K.A.; Liu, D.; Albaqami, M.D.; Chibotaru, L.F.; Guari, Y.; Larionova, J.; Trifonov, A.A. An unusual mechanism of building up of a high magnetization blocking barrier in an octahedral alkoxide Dy3+-based single-molecule magnet. Inorg. Chem. Front. 2021, 8, 1166–1174. [Google Scholar] [CrossRef]
- Li, M.; Wu, H.; Xia, Z.; Ungur, L.; Liu, D.; Chibotaru, L.F.; Ke, H.; Chen, S.; Gao, S. An Inconspicuous Six-Coordinate Neutral DyIII Single-Ion Magnet with Remarkable Magnetic Anisotropy and Stability. Inorg. Chem. 2020, 59, 7158–7166. [Google Scholar] [CrossRef]
- Liu, J.-L.; Chen, Y.-C.; Tong, M.-L. Symmetry strategies for high performance lanthanide-based single-molecule magnets. Chem. Soc. Rev. 2018, 47, 2431–2453. [Google Scholar] [CrossRef]
- Wang, C.; Meng, Y.-S.; Jiang, S.-D.; Wang, B.-W.; Gao, S. Approaching the uniaxiality of magnetic anisotropy in single-molecule magnets. Sci. China Chem. 2023, 66, 683–702. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, C.; Feng, T.; Liu, X.; Ying, X.; Li, X.-L.; Zhang, Y.-Q.; Tang, J. Air-Stable Chiral Single-Molecule Magnets with Record Anisotropy Barrier Exceeding 1800 K. J. Am. Chem. Soc. 2021, 143, 10077–10082. [Google Scholar] [CrossRef]
- Zhou, Y.-Q.; Yao, C.-Y.; Ruan, Z.-Y.; Lyu, B.-H.; Du, S.-N.; Wu, S.-G.; Chen, Y.-C.; Deng, W.; Liu, J.-L.; Tong, M.-L. Proton control of Raman relaxation in bis-hydrazone single-molecule magnets. Chin. Chem. Lett. 2025, in press. [Google Scholar] [CrossRef]
- Canaj, A.B.; Dey, S.; Martí, E.R.; Wilson, C.; Rajaraman, G.; Murrie, M. Insight into D6h Symmetry: Targeting Strong Axiality in Stable Dysprosium(III) Hexagonal Bipyramidal Single-Ion Magnets. Angew. Chem. Int. Ed. 2019, 58, 14146–14151. [Google Scholar] [CrossRef]
- Li, Z.-H.; Zhai, Y.-Q.; Chen, W.-P.; Ding, Y.-S.; Zheng, Y.-Z. Air-Stable Hexagonal Bipyramidal Dysprosium(III) Single-Ion Magnets with Nearly Perfect D6h Local Symmetry. Chem. Eur. J. 2019, 25, 16219–16224. [Google Scholar] [CrossRef]
- Xu, W.-J.; Luo, Q.-C.; Li, Z.-H.; Zhai, Y.-Q.; Zheng, Y.-Z. Bis-Alkoxide Dysprosium(III) Crown Ether Complexes Exhibit Tunable Air Stability and Record Energy Barrier. Adv. Sci. 2024, 11, 2308548. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhu, Z.; Li, X.-L.; Tang, J. Air-stable chiral mono- and dinuclear dysprosium single-molecule magnets: Steric hindrance of hexaazamacrocycles. Inorg. Chem. Front. 2022, 9, 4049–4055. [Google Scholar] [CrossRef]
- Jin, Y.-S.; Liu, C.-M.; Zhang, Y.-Q.; Kou, H.-Z. Trinuclear Dy(III) Single-Molecule Magnets with Two-Step Relaxation. Chin. J. Chem. 2023, 41, 2641–2647. [Google Scholar]
- Zhu, Z.; Zhao, C.; Zhou, Q.; Liu, S.; Li, X.-L.; Mansikkamäki, A.; Tang, J. Air-Stable Dy(III)-Macrocycle Enantiomers: From Chiral to Polar Space Group. CCS Chem. 2022, 4, 3762–3771. [Google Scholar] [CrossRef]
- Li, J.; Gómez-Coca, S.; Dolinar, B.S.; Yang, L.; Yu, F.; Kong, M.; Zhang, Y.-Q.; Song, Y.; Dunbar, K.R. Hexagonal Bipyramidal Dy(III) Complexes as a Structural Archetype for Single-Molecule Magnets. Inorg. Chem. 2019, 58, 2610–2617. [Google Scholar] [CrossRef]
- Ding, Y.S.; Blackmore, W.J.A.; Zhai, Y.Q.; Giansiracusa, M.J.; Reta, D.; Vitorica-Yrezabal, I.; Winpenny, R.E.P.; Chilton, N.F.; Zheng, Y.Z. Studies of the Temperature Dependence of the Structure and Magnetism of a Hexagonal-Bipyramidal Dysprosium(III) Single Molecule Magnet. Inorg. Chem. 2022, 61, 227–235. [Google Scholar] [CrossRef]
- Deng, W.; Yao, C.-Y.; Chen, Y.-C.; Zhou, Y.-Q.; Du, S.-N.; Liu, J.-L.; Tong, M.-L. Engineering a high-barrier d-f single-molecule magnet centered with hexagonal bipyramidal Dy(III) unit. Sci. China Chem. 2024, 67, 3291–3298. [Google Scholar] [CrossRef]
- Zhong, X.; Li, D.-Y.; Cao, C.; Luo, T.-K.; Hu, Z.-B.; Peng, Y.; Liu, S.-J.; Zheng, Y.-Z.; Wen, H.-R. Effect of Substituents in Equatorial Hexaazamacrocyclic Schiff Base Ligands on the Construction and Magnetism of Pseudo D6h Single-Ion Magnets. Inorg. Chem. 2024, 63, 21909–21918. [Google Scholar] [CrossRef]
- Armenis, A.S.; Mondal, A.; Giblin, S.R.; Raptopoulou, C.P.; Psycharis, V.; Alexandropoulos, D.I.; Tang, J.; Layfield, R.A.; Stamatatos, T.C. Unveiling new [1+1] Schiff-base macrocycles towards high energy-barrier hexagonal bipyramidal Dy(III) single-molecule magnets. Chem. Commun. 2024, 60, 12730–12733. [Google Scholar] [CrossRef]
- Galván, I.F.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef]
- Chibotaru, L.F.; Ungur, L.; Soncini, A. The Origin of Nonmagnetic Kramers Doublets in the Ground State of Dysprosium Triangles: Evidence for a Toroidal Magnetic Moment. Angew. Chem. Int. Ed. 2008, 47, 4126–4129. [Google Scholar] [CrossRef] [PubMed]
- Ungur, L.; Van den Heuvel, W.; Chibotaru, L.F. Ab initio investigation of the non-collinear magnetic structure and the lowest magnetic excitations in dysprosium triangles. New J. Chem. 2009, 33, 1224–1230. [Google Scholar] [CrossRef]
- Chibotaru, L.F.; Ungur, L.; Aronica, C.; Elmoll, H.; Pilet, G.; Luneau, D. Structure, Magnetism, and Theoretical Study of a Mixed-Valence CoII3CoIII4 Heptanuclear Wheel: Lack of SMM Behavior despite Negative Magnetic Anisotropy. J. Am. Chem. Soc. 2008, 130, 12445–12455. [Google Scholar] [CrossRef] [PubMed]
- Malmqvist, P.Å.; Roos, B.O.; Schimmelpfennig, B. The restricted active space (RAS) state interaction approach with spin–orbit coupling. Chem. Phys. Lett. 2002, 357, 230–240. [Google Scholar] [CrossRef]
- Heß, B.A.; Marian, C.M.; Wahlgren, U.; Gropen, O. A mean-field spin-orbit method applicable to correlated wavefunctions. Chem. Phys. Lett. 1996, 251, 365–371. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.-H.; Jin, Y.-S.; Tang, J.; Liu, C.-M.; Zhang, Y.-Q.; Kou, H.-Z. Chiral Pseudo-D6h Dy(III) Single-Molecule Magnet Based on a Hexaaza Macrocycle. Molecules 2025, 30, 2043. https://doi.org/10.3390/molecules30092043
Liu J-H, Jin Y-S, Tang J, Liu C-M, Zhang Y-Q, Kou H-Z. Chiral Pseudo-D6h Dy(III) Single-Molecule Magnet Based on a Hexaaza Macrocycle. Molecules. 2025; 30(9):2043. https://doi.org/10.3390/molecules30092043
Chicago/Turabian StyleLiu, Jia-Hui, Yi-Shu Jin, Jinkui Tang, Cai-Ming Liu, Yi-Quan Zhang, and Hui-Zhong Kou. 2025. "Chiral Pseudo-D6h Dy(III) Single-Molecule Magnet Based on a Hexaaza Macrocycle" Molecules 30, no. 9: 2043. https://doi.org/10.3390/molecules30092043
APA StyleLiu, J.-H., Jin, Y.-S., Tang, J., Liu, C.-M., Zhang, Y.-Q., & Kou, H.-Z. (2025). Chiral Pseudo-D6h Dy(III) Single-Molecule Magnet Based on a Hexaaza Macrocycle. Molecules, 30(9), 2043. https://doi.org/10.3390/molecules30092043










